Dynamic Programming for Computing Power Indices for Weighted Voting Games with Precoalitions

Abstract

We study the efficient computation of power indices for weighted voting games with precoalitions amongst subsets of players (reflecting, e.g., ideological proximity) using the paradigm of dynamic programming. Starting from the state-of-the-art algorithms for computing the Banzhaf and Shapley–Shubik indices for weighted voting games, we present a framework for fast algorithms for the three most common power indices with precoalitions, i.e., the Owen index, the Banzhaf–Owen index and the symmetric coalitional Banzhaf index, and point out why our new algorithms are applicable for large numbers of players. We discuss implementations of our algorithms for the three power indices with precoalitions in C++ and review computing times, as well as storage requirements.

1. Introduction

Weighted voting games (also known as weighted majority games) are a common model for decision-making and voting in committees, panels or boards. There are n players and each player i is assigned a positive weight $w_i$, which, in some situations, may reflect the number of votes of a voting bloc. The decision-making body accepts a measure or motion if a certain quota q, normally more than 50 percent of the sum of all weights, is reached or exceeded, i.e., if and only if there is a winning coalition S with ${\sum }_{i\in S}{w}_i\ge q$. In cooperative game theory, weighted voting games can be regarded as a special class of simple games, i.e., games in which coalitions are either winning with value 1 or losing with value 0. Power indices are applied to simple games and provide measures for the players’ abilities to influence results in voting situations. On the basis of different bargaining models and different axiomatic assumptions, numerous power indices have been introduced; see e.g., [1] for an overview, with the two most-widely used power indices being the Banzhaf index [2,3] and the Shapley–Shubik index [4].

Weighted voting games and power indices are applicable well beyond classical voting situations in politics, described e.g., in [5,6,7,8]. For example, power indices can also be used to analyze genetic networks and rank genes that may be responsible for genetic diseases [9], to solve reliability problems in the maintenance of computer networks [10], to understand indirect control power in corporate shareholding structures [11,12,13] or to analyze social networks [14,15]. In social, economic or corporate networks, and in voting settings alike, it is common for agents to agree beforehand to form a union and act as a voting bloc.

This article deals with the special case of a partition of the player set into disjoint precoalitions (also known as a priori unions), i.e., we assume that either all or none of the members of a precoalition join a certain coalition. Precoalitions can model strict party discipline in a legislative chamber, but they can also be interpreted as a way to reduce negotiation costs, with each precoalition sending a delegate as its negotiator. The practical relevance of cooperative games with precoalitions is hard to overstate and there are practical applications abound. Vázquez-Brage et al. (1996) [16] point out that one needs to consider airlines rather than individual aircraft in order to determine aircraft landing fees; Alonso-Meijide and Bowles (2005) [17] investigate voting at the International Monetary Fund (IMF), where member states are obliged to form a limited number of groups before allowing a vote at its main decision-making committee (called the Executive Board); Alonso-Meijide et al. (2005) [18] discuss union formation in the Parliament of Catalonia during legislature from 1995 to 1999; Mayer (2018) [19] highlights the role of Luxembourg in the early days of the European Economic Community (EEC) by showing that this small country was no longer a powerless null player as soon as it formed a voting bloc together with the two other Benelux countries. 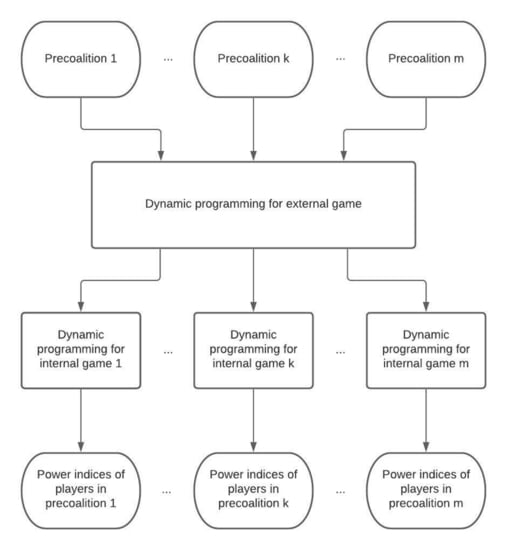As pointed out in the book by Owen [20], pp. 303, the players in such a union have agreed to keep together, but, even though they will do so in most situations, they are not forced to comply, and hence there is a need to evaluate their influence in a two-stage process. In an external stage, the power of the precoalition is evaluated, and in an internal stage, the results for the members of the precoalition are determined. Using the language of cooperative game theory, this two-stage process translates into an external game (also known as the quotient game) between the precoalitions and an internal game within each precoalition.

Owen generalized the Shapley value from the cooperative game theory to the framework with a priori unions amongst subsets of players in his seminal 1977 paper [21]. However, the internal game within each precoalition is no longer a simple game if the external game is simple. Malawski [22] pointed out how this problem can be overcome by computing more than one simple game on the internal stage. For our study, this implies that, in general, the solution of more than one weighted voting game will be necessary on the internal level. Following an article by Alonso-Meijide et al. [23], this paper studies the efficient computation of the three power indices for weighted voting games with precoalitions discussed therein: the Owen index [21] employing the Shapley–Shubik index on both the external and the internal level, the symmetric coalitional Banzhaf index [24] employing the Banzhaf index on the external level and the Shapley–Shubik index on the internal level and the Banzhaf–Owen index [25] employing the Banzhaf index on both the external and the internal level. Computing these three power indices for weighted voting games with precoalitions is challenging, as we are dealing with NP-hard problems [26], and, as the voting and network applications outlined in the first two paragraphs [5,6,7,8,9,10,11,12,13,14,15], may involve large numbers of players.

Power indices for simple games can be computed using generating functions; see, e.g., [5,27,28] and the work by Alonso-Meijide and Bowles [17] for the case of a priori unions. If the subsets of players reach only very few different weight sums, this method is favored [8] and fast-access data structures for polynomials with few coefficients in computer algebra systems, such as Mathematica [29], can be used. In this paper, we use the strongly related, though mathematically less sophisticated, paradigm of dynamic programming for power index computation [30,31,32]. The recent article [32] presents a new algorithm for the Johnston index [33], discusses algorithms for power indices based on minimal winning coalitions [34,35,36], surveys the state-of-the-art and introduces publicly available software. The work by Molinero and Blasco [37] studies algorithms for the Banzhaf–Owen and Owen indices and, to our knowledge, is the only paper on dynamic programming algorithms for weighted voting games with precoalitions. This paper presents new algorithms for the Banzhaf–Owen, Owen and symmetric coalitional Banzhaf indices with more favorable pseudopolynomial complexities. Our algorithms are based on a generalization of the concepts for computing the Banzhaf and Shapley–Shubik indices from the papers by Uno (2012) [31] and Kurz (2016) [8].

In Section 2, we introduce the basic concepts from cooperative game theory, including simple games, power indices and games with precoalitions along the lines of [23,38]. Section 3 explains how dynamic programming is used to count coalitions efficiently for weighted voting games and presents the state-of-the-art algorithms for computing the Banzhaf and Shapley–Shubik indices following the paper by Kurz [8]. Section 4 forms the heart of this paper and presents the new algorithms for the three power indices with precoalitions. We point out how our algorithms reflect both the definition of the indices as well as the internal games described by Malawski [22]. Section 5 discusses numerical experiments, reports supportive computing times and storage requirements for our methods and provides the reader with links to our C++ software and test problems. We end with some concluding remarks and an outlook to open problems in Section 6.

2. Preliminaries from Cooperative Game Theory

Cooperative game theory [39] deals with the outcomes and benefits that players can gain by forming coalitions. In the following, we briefly review some terminology for cooperative games and precoalitions along the lines of the papers by Alonso-Meijide et al. (2008) [23] and Mercik and Ramsey (2017) [38].

2.1. Cooperative Games and Simple Games

Let $N=\{1,...,n\}$ denote a finite set of n players. A group of players $S\subseteq N$ is called a coalition, whereas $2^N$ stands for the set of all subsets of N. ∅ symbolizes the empty coalition and N is called the grand coalition. By $\left|S\right|$, we express the cardinality of a coalition S, i.e., the number of its members; hence, $\left|N\right|=n$. An  n-person cooperative game can be characterized as a pair $(N,v)$, where $v:2^N\to \mathbb{R}$ is referred to as the characteristic function assigning a real value to all coalitions $S\in 2^N$, with $v\left(\mathsf{\varnothing }\right)=0$. A cooperative game is monotone if, for all coalitions $S,T\in 2^N$, the relation $S\subseteq T$ implies $v\left(S\right)\le v\left(T\right)$.

We call a cooperative game simple if it is monotone and there holds $v\left(N\right)=1$ and $v\left(S\right)=0$ or $v\left(S\right)=1$ for each coalition $S\subset N$. Coalitions for which $v\left(S\right)=1$ are classified as winning coalitions in simple games, whereas coalitions for which $v\left(S\right)=0$ are called losing coalitions. A player i is a critical player (also known as a decisive player or swing player) in a winning coalition S if $v(S\backslash \{i\left\}\right)=0$, i.e., the winning coalition S turns into a losing one if player i leaves S. We call a coalition S with at least one critical player vulnerable.

Weighted voting games (also known as weighted majority games) are possibly the most important subclass of simple games. They are useful for a large number of practical applications [5,6,7,8,9,10,11,12,13,14,15]. Weighted voting games are specified by n non-negative real weights $w_i,i=1,\dots ,n,$ and a non-negative real quota q, where normally $q>\frac{1}{2}{\sum }_{i=1}^n{w}_i$. Its characteristic function $v:2^N\to \{0,1\}$ takes the value $v\left(S\right)=1$ in case of a winning coalition S, i.e., $w\left(S\right)={\sum }_{i\in S}{w}_i\ge q$, and $v\left(S\right)=0$ otherwise, meaning that coalition S is losing.

We finally note that not every simple game allows for a representation as a weighted voting game, and refer to the article by Molinero, Riquelme and Serna (2015) [40] for an overview of different forms of representation for simple games.

2.2. Power Indices and Marginal Contributions

Let $S\subset N$ denote a coalition and $i\notin S$ a player not contained in S. We call the difference $v(S\cup \{i\left\}\right)-v\left(S\right)$ the marginal contribution of player i to coalition S. For simple games, the  marginal contribution of player i to coalition S is 1 if and only if i is a critical player in the winning coalition $S\cup \left\{i\right\}$; in any other case, the marginal contribution is 0.

A power index is a function f that obtains an n-person simple game specified by its player set N and its characteristic function v as its input, and provides a unique vector $f(N,v)=(f_1(N,v),\dots ,f_n(N,v))$ as its output. We only introduce the Banzhaf index [2,3] and the Shapley–Shubik index [4] following the notation of the paper [23]. For a deeper discussion of the subject, we refer to the overview article [1] by Bertini, Freixas, Gambarelli and Stach.

Let v be a simple n-player game. The (absolute) Banzhaf index [3] of player i and the Shapley–Shubik index [4] of player i can be written in the form

$$f_i(N,v)=\sum _{S\subseteq N\backslash \left\{i\right\}}{\alpha }_S^i·(v(S\cup \left\{i\right\})-v\left(S\right))$$

(1)

with the coefficients

$${\alpha }_S^i=\frac{1}{2^{n-1}}$$

for the Banzhaf index and

$${\alpha }_S^i=\frac{\left|S\right|!(n-|S|-1)!}{n!}$$

for the Shapley–Shubik index. We note that, for the coefficients ${\alpha }_S^i$, the cardinality of a coalition S (which is turned from a losing coalition to a winning coalition by the entrance of critical player i) plays a crucial role for the Shapley–Shubik index, whereas it can be ignored for the Banzhaf index. The coefficients ${\alpha }_S^i$ make it obvious that the Banzhaf index can seen as the probability of a player being crucial to a coalition it does not belong to, whereas the Shapley–Shubik index can be interpreted as the probability of a player being decisive over all permutations of players, i.e., assuming all sequential coalitions are equiprobable. We note that the Shapley–Shubik index is efficient, i.e., ${\sum }_{i=1}^n{f}_i(N,v)=v\left(N\right)=1$, whereas the (absolute) Banzhaf index is not.

2.3. Simple Games with Precoalitions and Coalitional Power Indices

In this subsection, we introduce simple games with precoalitions and coalitional power indices borrowing some notation from [23,38].

We are establishing an external division of our set of players $N=\{1,...,n\}$ into precoalitions (also known as a priori unions) whose members will either enter a coalition together or not at all. Let $\mathcal{P}\left(N\right)$ stand for the set of all partitions of N, a partition being a set of non-empty subsets of N satisfying the condition that N is a disjoint union of these subsets. We refer to an element $P\in \mathcal{P}\left(N\right)$ as a coalition structure (also known as a system of unions) of the set N. A simple game with a coalition structure can be identified as a triplet $(N,v,P)$. Following [23], we write our coalition structure in the form $P=\{P_1,\dots ,P_m\}$, i.e., we have m precoalitions $P_1,\dots ,P_m$ and the set $M=\{1,\dots ,m\}$ serves as the index set of the partition P. For a weighted voting game with a coalition structure P, the external game (also known as the quotient game) is defined as the weighted voting game played between the m precoalitions [22,23]. The external game is formally defined as the weighted voting game $[q;w\left(P_1\right),\dots ,w\left(P_m\right)]$, i.e., it is represented by the (unaltered) quota q and the weights $w\left(P_1\right),\dots ,w\left(P_m\right)$ of the m precoalitions, where $w\left(P_k\right)={\sum }_{i\in P_k}{w}_i$ with $k\in M$, $M=\{1,\dots ,m\}$.

A coalitional power index g is a function that obtains an n-person simple game with a coalition structure specified by its player set N, its characteristic function v and a partition P as its input, and provides a unique vector $g(N,v,P)=(g_1(N,v,P),\dots ,g_n(N,v,P))$ as its output. As in [23], we define three coalitional power indices, i.e., the Banzhaf–Owen index (hereafter BO index) [25], the symmetric coalitional Banzhaf index (SCB index) [24] and the Owen index (OW index) [21], within a unified framework.

Let $P=\{P_1,\dots ,P_m\}$ stand for a set of m precoalitions $P_1,\dots ,P_m$ and the set $M=\{1,\dots ,m\}$ serve as the index set of P. Further, let $Q_R={\cup }_{l\in R}{P}_l$ denote the subset of players belonging to any precoalition referred to by the index subset $R\subseteq M$. For any player $i\in N$ contained in precoalition k, i.e., $i\in P_k$, we write a coalitional power index as follows (cf. [38]):

$$g_i(N,v,P)=\sum _{R\subseteq M\backslash \left\{k\right\}}{\alpha }_R^k\sum _{T\subseteq P_k\backslash \left\{i\right\}}{\alpha }_T^i·(v(Q_R\cup T\cup \left\{i\right\})-v(Q_R\cup T))$$

(2)

As in [38], ${\alpha }_R^k$ is an appropriately defined weight for the external game, whereas ${\alpha }_T^i$ corresponds to internal games within a precoalition. For the BO index, we employ the weighting coefficients

$${\alpha }_R^k=\frac{1}{2^{m-1}},{\alpha }_T^i=\frac{1}{2^{|P_k|-1}},$$

For the SCB index,

$${\alpha }_R^k=\frac{1}{2^{m-1}},{\alpha }_T^i=\frac{\left|T\right|!\left(\right|P_k|-|T|-1)!}{|P_k|!},$$

and for the OW index,

$${\alpha }_R^k=\frac{\left|R\right|!(m-|R|-1)!}{m!},{\alpha }_T^i=\frac{\left|T\right|!\left(\right|P_k|-|T|-1)!}{|P_k|!}.$$

We note that the OW index is efficient, i.e., ${\sum }_{i=1}^n{g}_i(N,v,P)=v\left(N\right)=1$, whereas the BO and SCB indices are not.

Let us emphasize a crucial difference between Formulas (1) and (2). While both expressions rely on marginal contributions of player i, in  (2), we assume that precoalitions other than $P_k$ (which contains player i) have either joined with all of their members or not at all. As pointed out in [38], the power of player $i\in P_k$ comes from scenarios in which both $P_k$ is critical in the external game and i is a critical player in its precoalition in an appropriately defined internal voting game.

For illustration, we look at the coalitional game $(N,v,P)$ represented by the weighted voting game $[5;3,1,1,1,3]$ and the coalition structure $P=\left\{\right\{1\},\{2,3,4\},\{5\left\}\right\}$. We obtain

$$g^{BO}(N,v,P)=(\frac{1}{2},\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{2})$$

for the BO indices,

$$g^{SCB}(N,v,P)=(\frac{1}{2},\frac{1}{6},\frac{1}{6},\frac{1}{6},\frac{1}{2})$$

for the SCB indices and

$$g^{OW}(N,v,P)=(\frac{1}{3},\frac{1}{9},\frac{1}{9},\frac{1}{9},\frac{1}{3})$$

for the OW indices.

Looking at the extreme coalition structures $P^n=\{\left\{1\right\},\left\{2\right\},\dots ,\left\{n\right\}\}$ and $P^N=\left\{N\right\}$, we recognize that the BO index reduces to the Banzhaf index in both cases, whereas the OW index reduces to the Shapley–Shubik index in both cases. As for the SCB index, it becomes the Banzhaf index for $P^n=\{\left\{1\right\},\left\{2\right\},\dots ,\left\{n\right\}\}$ and the Shapley–Shubik index in case $P^N=\left\{N\right\}$. The BO index [25] applies the Banzhaf index in both the external game and in the internal process between unions. As pointed out by Laruelle and Valenciano [41], the BO index assesses the a priori decisiveness of every voter within their bloc in the context of the coalitional structure, i.e., assuming that all of the other precoalitions will act as voting blocs. We refer the reader to that paper [41] for a detailed discussion of the probabilistic interpretations of the BO index. The SCB index by Alonso-Meijide and Fiestras-Janeiro [24] employs the Banzhaf index for the external game and the Shapley–Shubik index for the internal processes, whereas the OW index [21] invokes the Shapley–Shubik index on both levels of a two-level decision-making process. Taking a closer look at these two-level decision-making processes will play a crucial role in Section 4, where we derive efficient dynamic programming algorithms for the BO, SCB and OW indices for weighted voting games with precoalitions.

3. Dynamic Programming for the Banzhaf and Shapley–Shubik Indices

In this section, we introduce the technique of dynamic programming for counting coalitions in weighted voting games efficiently, discuss the state-of-the-art algorithms for the Banzhaf and Shapley–Shubik indices [8,31,32] and present generalizations of existing algorithms that will prove to be useful when we deal with precoalitions and internal games within precoalitions in Section 4. In other words, we are not computing any power indices with precoalitions in this section, but lay the groundwork for doing so in Section 4.

3.1. Counting Winning and Losing Coalitions via Dynamic Programming

It is well known that every weighted voting game allows for an integer representation [8]. Hence, we assume that the weights $w_i$ of the n players in our weighted voting game, as well as the quota q, are positive integers for the rest of the article. We set $\tilde{w}=w\left(N\right)={\sum }_{i=1}^n{w}_i$ and assume $q>\frac{\tilde{w}}{2}$. Players with integer weight 0 are null players, i.e., they are never critical players, and for all power indices discussed in this paper, they can be handled in a preprocessing step and assigned the value 0 without any need to include them in any further computation.

When we want to compute the Banzhaf index of player i, we need to be able to answer one of the following two questions: How many losing coalitions are turned into winning coalitions when player i is joining? Alternatively, in how many winning coalitions is player i critical? For the Shapley–Shubik index of player i, the same two questions are relevant, but we also need to take account of cardinalities of coalitions.

Dynamic programming is an algorithmic paradigm resting on two pillars: dividing a given problem into subproblems and storing intermediate results efficiently. We will use dynamic programming to count losing and winning coalitions and present algorithms following the work by Kurz [8]. For a more general introduction to counting coalitions via dynamic programming (including examples), we refer to the recent article [32] or the textbook by Chakravarty, Mitra and Sarkar [39], chapter 12.

Algorithm 1 is a generalization of the first algorithm in the article by Kurz [8]. Equipped with the number n of players, the quota q, a vector $w=(w_1,\dots ,w_n)$ of positive integer weights and an integer vector T with $T\left(0\right)=1$ and $T\left(x\right)=0$ for $x=1,\dots ,q-1,$ as its four input arguments, it outputs a vector T, with $T\left(x\right)$ listing the number of losing coalitions attaining weight $0\le x\le q-1$. We briefly note that, in our discussion of memory space requirements, we follow the convention by Uno [31] throughout the paper and do not include the need to store the n weights itself—and, later, we also omit the memory space for the corresponding n values of the power indices—as this allows for a clearer and more concise presentation. According to this convention, Algorithm 1 needs $O\left(nq\right)$ time and $O\left(q\right)$ memory space.

Algorithm 1 Generalized counting of number of losing coalitions per weight

1: procedure LosingCoalitionsByWeight($n,q,w,T$) 2:     for i from 1 to n do 3:         if (q > w(i)) then 4:            for x from $q-1$ to $w\left(i\right)$ do 5:                if (x-w(i) == 0) then 6:                    $T\left(x\right)\leftarrow T\left(x\right)+T\left(0\right)$                                 ▹ initialize T(0)=1 for empty set 7:                else 8:                    $T\left(x\right)\leftarrow T\left(x\right)+T(x-w(i\left)\right)$ 9:                end if 10:            end for 11:         end if 12:     end for 13:     return T                                    ▹ number of losing coalitions of weight $x\in [0,q-1]$ 14: end procedure

Note that Algorithm 1 echoes a boundary condition stating that we can obtain the sum 0 in exactly one way, i.e., via the empty set, reflected in $T\left(0\right)=1$. We admit that the if-else statement in lines 5 to 8 in Algorithm 1 is superfluous, as $T(x-w(i\left)\right)=T\left(0\right)$ in case $x=w\left(i\right)$, but we wanted to highlight the role of $T\left(0\right)$. The actual recursion in line 8 in Algorithm 1 mirrors the fact that the first i weights can deliver a sum $x>0$ either with or without player i. We will find providing an initial vector T as an input useful in the following section, where we wish to incorporate results from the external game in computations of internal games.

Kurz [8] pointed out that, rather than counting losing coalitions from below, we can also count winning coalitions from above, making use of the fact that we can write the sum of all weights in exactly one way, i.e., $\tilde{w}=w\left(N\right)={\sum }_{i=1}^n{w}_i$.

Algorithm 2 is a generalization of the second algorithm in the article by Kurz [8]. Provided with the number n of players, the quota q, the sum of all weights $\tilde{w}=w\left(N\right)$, a vector $w=(w_1,\dots ,w_n)$ of positive integer weights and an integer vector T with $T\left(\tilde{w}\right)=1$ and $T\left(x\right)=0$ for $x=q,\dots ,\tilde{w}-1,$ as its five input arguments, it outputs a vector T, with $T\left(x\right)$ listing the number of winning coalitions attaining weight $q\le x\le \tilde{w}$. Algorithm 2 needs $O\left(n(\tilde{w}-q+1)\right)$ time and $O(\tilde{w}-q+1)$ space.

Algorithm 2 Generalized counting of number of winning coalitions per weight

1: procedure WinningCoalitionsByWeight($n,q,\tilde{w},w,T$) 2:     for i from 1 to n do 3:         if $(q+w\left(i\right)\le \tilde{w})$ then 4:            for x from $q+w\left(i\right)$ to $\tilde{w}$ do 5:                $T(x-w(i\left)\right)\leftarrow T\left(x\right)+T(x-w(i\left)\right)$ 6:            end for 7:         end if 8:     end for 9:     return T          ▹ number of winning coalitions of weight $x\in [q,\tilde{w}]$ 10: end procedure

Algorithms 1 and 2 can be generalized for the distribution of cardinalities of coalitions in a straightforward manner [8,32]. Given that we normally assume $q>\frac{\tilde{w}}{2}$ (and hence $\tilde{w}-q+1\le q$), we prefer to work with the winning coalitions from above. Therefore, we provide only the corresponding algorithm for winning coalitions and cardinalities from above in Algorithm 3. Provided with the number n of players, the quota q, the sum of all weights $\tilde{w}=w\left(N\right)$, a vector $w=(w_1,\dots ,w_n)$ of positive integer weights and a two-dimensional array C with $C(\tilde{w},n)=1$ and $C(x,s)=0$ for all other combinations of weights $x=q,\dots ,\tilde{w},$ and cardinalities $s=1,\dots ,n,$ as its five input arguments, it outputs a two-dimensional array C, with $C(x,s)$ listing the number of winning coalitions attaining weight $q\le x\le \tilde{w}$ and cardinalities $s=1,\dots ,n$. Algorithm 3 needs $O\left(n^2(\tilde{w}-q+1)\right)$ time and $O\left(n(\tilde{w}-q+1)\right)$ space.

Algorithm 3 Generalized counting of number of winning coalitions per weight and cardinality

1: procedure WinningCoalitionsByWeightCardinality($n,q,\tilde{w},w,C$) 2:     for i from 1 to n do 3:         if $q+w\left(i\right)\le \tilde{w}$ then 4:            for x from $q+w\left(i\right)$ to $\tilde{w}$ do 5:                for s from 2 to n do 6:                    $C(x-w(i),s-1)\leftarrow C(x,s)+C(x-w(i),s-1)$ 7:                end for 8:            end for 9:         end if 10:     end for 11:     return C    ▹ number of winning coalitions of weight $x\in [q,\tilde{w}]$ and cardinality $s\in [1,n]$ 12: end procedure

3.2. Computing the Banzhaf and Shapley–Shubik Indices

The paper by Uno (2012) [31] presented the first algorithm for computing the Banzhaf and Shapley–Shubik indices of all players in a weighted voting game in $O\left(qn\right)$ and $O\left(q{n}^2\right)$ time, respectively. By working from above, as in Algorithms 2 and 3, Kurz (2016) [8] improved this result to $O(\Delta n)$ and $O(\Delta n^2)$ with $\Delta =min(q,\tilde{w}-q+1)$ for the Banzhaf and Shapley–Shubik indices, respectively. It is worthwhile to summarize these results and their proofs, together with some new generalizations of algorithms, which we will use later in Section 4.

Theorem 1.

For an n-player weighted voting game with positive integer weights, the Banzhaf indices for all players can be computed in $O(\Delta n)$ time and $O(\Delta )$ memory space.

Proof. 

Let us focus on the case $(\tilde{w}-q+1)\le q$ and compute the Banzhaf indices from above. We obtain the vector $T\left(x\right)$ for $q\le x\le \tilde{w}$ via Algorithm 2 in $O\left((\tilde{w}-q+1)n\right)$ time and $O(\tilde{w}-q+1)$ space by calling

$$T=WinningCoalitionsByWeight(n,q,\tilde{w},w,T)$$

using an integer vector T with $T\left(\tilde{w}\right)=1$ and $T\left(x\right)=0$ for $x=q,\dots ,\tilde{w}-1,$ as our input. We set $T_{+i}\left(x\right)=T\left(x\right)$ for all $x\in \{\tilde{w}-w_i+1,\dots ,\tilde{w}\}$ and then loop for x from $\tilde{w}-w_i$ down to q in order to find

$$T_{+i}\left(x\right)=T\left(x\right)-T_{+i}(x+w_i).$$

$T_{+i}\left(x\right)$ states how frequently player i belongs to a winning coalition with weight x and

$$f_i^{BZ}(N,v)=\frac{1}{2^{n-1}}\sum _{x=q}^{q+w_i-1}{T}_{+i}\left(x\right)$$

gives us the Banzhaf index of player i.    □

Algorithm 4 is a generalization of this idea that we will use in the next section. It counts the number of coalitions containing a player with a specified weight.

Algorithm 4 Count coalitions containing a player specified by its weight

1: procedure CoalitionsWithPlayer($q,\tilde{w},weight,T$) 2:     for x from q to $\tilde{w}$ do 3:         $Tw\left(x\right)\leftarrow T\left(x\right)$ 4:     end for 5:     if $(\tilde{w}-weight\ge q)$ then 6:         for x from $\tilde{w}-weight$ to q do 7:            $Tw\left(x\right)\leftarrow T\left(x\right)-Tw(x+weight)$ 8:         end for 9:     end if 10:     return $Tw$ 11: end procedure

Theorem 1 and Algorithm 4 can be carried over to versions with cardinalities and thus to the computation of Shapley–Shubik indices.

Theorem 2.

For an n-player weighted voting game with positive integer weights, the Shapley–Shubik indices for all players can be computed in $O(\Delta n^2)$ time and $O(\Delta n)$ memory space.

Proof. 

Again, we concentrate on the case $(\tilde{w}-q+1)\le q$ and compute the Shapley–Shubik indices from above. We obtain $C(x,s)$ for $q\le x\le \tilde{w}$ and all cardinalities $1\le s\le n$ from above via Algorithm 3 in $O\left((\tilde{w}-q+1)n^2\right)$ time and $O\left((\tilde{w}-q+1)n\right)$ space by calling

$$C=WinningCoalitionsByWeightCardinality(n,q,\tilde{w},w,C)$$

using a two-dimensional array C with $C(\tilde{w},n)=1$ and $C(x,s)=0$ for all other combinations of weights $x=q,\dots ,\tilde{w},$ and cardinalities $s=1,\dots ,n,$ as our input. We set $C_{+i}(x,c)=C(x,c)$ for all weights $x\in \{\tilde{w}-w_i+1,\dots ,\tilde{w}\}$ and all cardinalities $s\in \{1,\dots ,n\}$. We loop for x from $\tilde{w}-w_i$ down to q in an outer loop and for s from 0 to $n-1$ in an inner loop in order to find

$$C_{+i}(x,s)=C(x,s)-C_{+i}(x+w_i,s+1).$$

Now, $C_{+i}(x,c)$ tells us how often player i belongs to a winning coalition with weight x and cardinality s, and via

$$f_i^{SH}(N,v)=\frac{1}{n!}\sum _{s=0}^{n-1}s!(n-s-1)!\sum _{x=q}^{q+w_i-1}{C}_{+i}(x,s+1)$$

we obtain the Shapley–Shubik index of player i.    □

Algorithm 5 is a generalization of this idea that we will need in the next section. It counts the number of coalitions and cardinalities containing a player with a specified weight.

Algorithm 5 Count coalitions and cardinalities containing a player specified by its weight

1: procedure CoalitionsCardinalityWithPlayer($n,q,\tilde{w},weight,C$) 2:     for x from q to $\tilde{w}$ do 3:         for s from 1 to n do 4:            $Cw(x,s)\leftarrow C(x,s)$ 5:         end for 6:     end for 7:     if $\tilde{w}-weight\ge q$ then 8:         for x from $\tilde{w}-weight$ to q do 9:            for s from 1 to $n-1$ do 10:                $Cw(x,s)\leftarrow C(x,s)-Cw(x+weight,s+1)$ 11:            end for 12:         end for 13:     end if 14:     return $Cw$ 15: end procedure

Finally, we wish to highlight an observation from both Theorems 1 and 2 and their proofs. In each case, the pseudopolynomial complexity estimates that computing the respective power index of only one player and computing the respective power indices of all players are identical in terms of both memory space and computing time. This is due to the fact that the setup phases in the forms of Algorithms 2 and 3, respectively, each require an additional loop over all players, whereas Algorithms 4 and 5 (which are employed to find the respective power index of an individual player) do not. Hence, in terms of the O-notation, it does not make a difference (in terms of space or speed) whether we wish to find only some or all power indices. This observation will be reflected in the results of the following section.

4. Computing Power Indices with Precoalitions via Dynamic Programming

This section forms the heart of the article. It presents new dynamic programming algorithms for the BO, SCB and OW indices. As we outlined in Section 2.3, we assume that there are m precoalitions $P_1,\dots ,P_m$. The external game (also known as the quotient game) is defined as the weighted voting game played between the precoalitions [22,23], i.e., a weighted voting game represented by the (unaltered) quota q and the m weights $w\left(P_1\right),\dots ,w\left(P_m\right)$, where $w\left(P_k\right)={\sum }_{i\in P_k}{w}_i$ with $k\in M$, $M=\{1,\dots ,m\}$. Furthermore, we define p as the maximal size of a precoalition, i.e., $p={max}_{k\in M}\left|P_k\right|$.

To our knowledge, the paper by Molinero and Blasco [37] is the only work on dynamic programming algorithms for weighted voting games with a precoalition structure. Their algorithms for the BO and OW indices combine backtracking with the algorithms from Section 5.2 of the survey paper by Matsui and Matsui (2000) [30] for power index computation. For computing the BO or OW index of a single player i with $i\in P_k$, i.e., player i contained in precoalition $P_k$, their algorithm needs $O\left(\right(n^{\prime }|P_k{\left|\right)}^{2}q)$ computing time and $O\left(n^{\prime }q\right)$ space with $n^{\prime }=m+\left|P_k\right|-2$.

In the following, we point out how the concepts and algorithms from the previous section translate into external and internal weighted voting games and algorithms for the BO, SCB and OW indices with favorable pseudopolynomial computing times and storage requirements. Each subsection will be devoted to one of the three indices, with the proof of each theorem serving as a description of an algorithm for computing the index. We follow the convention that the superscript $+k$ indicates that we count only those winning coalitions containing precoalition k on the external level, whereas the subscript $+i$ indicates that we look at only those coalitions containing player i on the level of individual players within precoalition $P_k$. Furthermore, the superscript $ext$ symbolizes the external level, i.e., the level of the precoalitions, whereas the superscript $int$ stands for the internal level, i.e., the level of individual players within a precoalition.

4.1. Efficient Computation of the Banzhaf–Owen (BO) Index

For the BO index, our idea is to reflect the external game and one internal game per precoalition via dynamic programming.

Theorem 3.

For a weighted voting game with positive integer weights and a precoalition structure $P=\{P_1,\dots ,P_m\}$, the Banzhaf–Owen (BO) indices for all players can be computed in $O(\Delta (m+p\left)\right)$ time and $O(\Delta )$ memory space, with $\Delta =min(q,\tilde{w}-q+1)$. For computing the BO index of an individual player $i\in P_k$, i.e., player i is contained in precoalition $P_k$, we need $O(\Delta (m+|P_k\left|\right))$ time and $O(\Delta )$ space.

Proof. 

Let us focus on the case $(\tilde{w}-q+1)\le q$ and compute the BO indices from above. Let $w^{ext}=(w\left(P_1\right),\dots ,w\left(P_m\right))$ be the vector of the weights of the m precoalitions. We obtain the vector $T^{ext}\left(x\right)$ for $q\le x\le \tilde{w}$ with the number of winning coalitions on the level of the precoalitions for weights $q\le x\le \tilde{w}$ via Algorithm 2 in $O\left((\tilde{w}-q+1)m\right)$ time and $O(\tilde{w}-q+1)$ space by computing

$$T^{ext}=WinningCoalitionsByWeight(m,q,\tilde{w},w^{ext},T)$$

using an integer vector T with $T\left(\tilde{w}\right)=1$ and $T\left(x\right)=0$ for $x=q,\dots ,\tilde{w}-1,$ as our input. Next, we deal with precoalition $P_k$. Algorithm 4 gives us the number of those winning coalitions containing precoalition k with weight $w_k^{ext}$ via

$$T^{ext,+k}=CoalitionsWithPlayer(q,\tilde{w},w_k^{ext},T^{ext})$$

Now, we switch to the level of precoalition $P_k$. We incorporate the individual weights $w^{int}=(w_1,\dots ,w_{|P_k|})$ of the players in precoalition $P_k$ into our vector $T^{ext,+k}$ using Algorithm 2 by computing

$$T^{int,+k}=WinningCoalitionsByWeight\left(\right|P_k|,q,\tilde{w},w^{int},T^{ext,+k})$$

The vector $T^{int,+k}\left(x\right)$ states the number of winning coalitions for weights $q\le x\le \tilde{w}$ when players from precoalition $P_k$ join on an individual level, whereas the other precoalitions join as unions. From the vector $T^{int,+k}\left(x\right)$, we can work out how frequently an individual player $i\in P_k$ with weight $w_i^{int}$ belongs to a winning coalition with weight $q\le x\le \tilde{w}$ using Algorithm 4 via

$$T_{+i}^{int,+k}=CoalitionsWithPlayer(q,\tilde{w},w_i^{int},T^{int,+k})$$

From $T_{+i}^{int,+k}$, we can assess how frequently player i is a swing player within precoalition $P_k$, i.e., assuming that all the other precoalitions are acting as unions. The expression

$$f_i^{BO}(N,v,P)=\frac{1}{2^{m-1}}\frac{1}{2^{|P_k|-1}}\sum _{x=q}^{q+w_i-1}{T}_{+i}^{int,+k}\left(x\right)$$

yields the BO index of player i. □

4.2. Efficient Computation of the Symmetric Coalitional Banzhaf (SCB) Index

As for the SCB index, our approach for the external game will be identical to the BO index. However, in the internal game of each precoalition, we will need to include cardinalities.

Theorem 4.

For a weighted voting game with positive integer weights and a precoalition structure $P=\{P_1,\dots ,P_m\}$, the symmetric coalitional Banzhaf (SCB) indices for all players can be computed in $O(\Delta m+\Delta p^2)$ time and $O(\Delta p)$ memory space with $\Delta =min(q,\tilde{w}-q+1)$. For computing the SCB index of an individual player $i\in P_k$, i.e., player i is contained in precoalition $P_k$, we need $O(\Delta m+\Delta |P_k{|}^2)$ time and $O(\Delta |P_k\left|\right)$ space.

Proof. 

Again, we discuss the case $(\tilde{w}-q+1)\le q$ and compute the SCB indices from above. On the external level, we perform the identical computations as for the BO indices. Let $w^{ext}=(w\left(P_1\right),\dots ,w\left(P_m\right))$ denote the vector of the weights of the m precoalitions. We obtain the vector $T^{ext}\left(x\right)$, with the number of winning coalitions on the level of the precoalitions for weights $q\le x\le \tilde{w}$ via Algorithm 2 by computing

$$T^{ext}=WinningCoalitionsByWeight(m,q,\tilde{w},w^{ext},T)$$

using an integer vector T with $T\left(\tilde{w}\right)=1$ and $T\left(x\right)=0$ for $x=q,\dots ,\tilde{w}-1,$ as our input. As before, Algorithm 4 gives us the number of those winning coalitions containing precoalition k with weight $w_k^{ext}$ via

$$T^{ext,+k}=CoalitionsWithPlayer(q,\tilde{w},w_k^{ext},T^{ext})$$

Now, we switch to the level of precoalition $P_k$ with the individual weights $w^{int}=(w_1,\dots ,w_{|P_k|})$. We create a two-dimensional array $C^{int,+k}$ with

$$C^{int,+k}(x,|P_k\left|\right)=T^{ext,+k}\left(x\right)$$

(3)

for all weights $q\le x\le \tilde{w}$, and $C^{int,+k}(x,s)=0$ for all other combinations of weights $x=q,\dots ,\tilde{w},$ and cardinalities $s=1,\dots ,|P_k|-1$. We note that Equation (3) states how many winning coalitions were joined by $P_k$ as a union. We incorporate the individual weights $w^{int}$ and their cardinalities using Algorithm 3 by computing

$$C^{int,+k}=WinningCoalitionsByWeightCardinality\left(\right|P_k|,q,\tilde{w},w^{int},C^{int,+k})$$

From our updated array $C^{int,+k}(x,s)$, we learn the numbers of winning coalitions with weights $x\in [q,\tilde{w}]$ with s players from $P_k$, assuming that players from precoalition $P_k$ join on an individual level whereas the other precoalitions join as unions. We can work out how frequently an individual player $i\in P_k$ with weight $w_i^{int}$ belongs to a winning coalition with s players from $P_k$ via Algorithm 5 by computing

$$C_{+i}^{int,+k}=CoalitionsCardinalityWithPlayer\left(\right|P_k|,q,\tilde{w},w_i^{int},C^{int,+k})$$

$C_{+i}^{int,+k}$ states how frequently player i is a part of a winning coalition containing s players from $P_k$, i.e., assuming that all of the other precoalitions are acting as unions. From

$$f_i^{SCB}(N,v,P)=\frac{1}{2^{m-1}}\frac{1}{|P_k|!}\sum _{s=0}^{|P_k|-1}s!\left(\right|P_k|-s-1)!\sum _{x=q}^{q+w_i-1}{C}_{+i}^{int,+k}(x,s+1)$$

we obtain the SCB index of player i. □

4.3. Efficient Computation of the Owen (OW) Index

The computation of the OW index is slightly more sophisticated. As observed by Malawski (2004) [22], more than one weighted voting game is needed on the internal level. These internal games reflect how many precoalitions have joined a vulnerable coalition for which a certain player is critical. We translate the observations from [22] into a dynamic programming algorithm.

Theorem 5.

For a weighted voting game with positive integer weights and a precoalition structure $P=\{P_1,\dots ,P_m\}$, the Owen (OW) indices for all players can be computed in $O(\Delta {\left(mp\right)}^2)$ time and $O(\Delta (m+p\left)\right)$ memory space with $\Delta =min(q,\tilde{w}-q+1)$. For computing the OW index of an individual player $i\in P_k$, i.e., player i is contained in precoalition $P_k$, we need $O(\Delta (m|P_k{\left|\right)}^2)$ time and $O(\Delta (m+|P_k\left|\right))$ space.

Proof. 

We discuss the case $(\tilde{w}-q+1)\le q$ and compute the OW indices from above. On the external level, we need to reflect cardinalities of precoalitions. As before, the vector $w^{ext}=(w\left(P_1\right),\dots ,w\left(P_m\right))$ stands for the weights of the m precoalitions. We obtain the two-dimensional array $C^{ext}(x,s)$ with the number of winning coalitions on the level of the precoalitions via Algorithm 3 for weights $x\in [q,\tilde{w}]$ and cardinalities $s=1,\dots ,m,$ in $O\left(m^2(\tilde{w}-q+1)\right)$ time and $O\left(m(\tilde{w}-q+1)\right)$ space by computing

$$C^{ext}=WinningCoalitionsByWeightCardinality(m,q,\tilde{w},w^{ext},C)$$

using a two-dimensional array C with $C(\tilde{w},m)=1$ and $C(x,s)=0$ for all other combinations of weights $x=q,\dots ,\tilde{w},$ and cardinalities $s=1,\dots ,m,$ as our input. Algorithm 5 gives us the number of those winning coalitions containing precoalition k with weight $w_k^{ext}$, together with their cardinalities, via

$$C^{ext,+k}=CoalitionsCardinalityWithPlayer(m,q,\tilde{w},w_k^{ext},C^{ext}).$$

Now, we need to loop for r from 0 to $m-1$ and work out the internal games on the level of precoalition $P_k$ with the individual weights $w^{int}=(w_1,\dots ,w_{|P_k|})$. We create a two-dimensional array $C^{int,+k}$ with

$$C^{int,r+1,+k}(x,|P_k\left|\right)=C^{ext,+k}(x,r+1)$$

(4)

for all weights $q\le x\le \tilde{w}$ and $C^{int,r+1,+k}(x,s)=0$ for all other combinations of weights $x=q,\dots ,\tilde{w},$ and cardinalities $s=1,\dots ,|P_k|-1$. We note that Equation (4) states how many winning coalitions of cardinality $r+1$ joined by $P_k$ as a union there are on the external level. We incorporate the individual weights $w^{int}$ and their cardinalities using Algorithm 3 by computing

$$C^{int,r+1,+k}=WinningCoalitionsByWeightCardinality\left(\right|P_k|,q,\tilde{w},w^{int},C^{int,r+1,+k}).$$

From our updated array $C^{int,r+1,+k}(x,s)$, we learn the numbers of winning coalitions with weights $x\in [q,\tilde{w}]$ with s players from $P_k$, assuming that players from precoalition $P_k$ join on an individual level whereas the other r precoalitions join as unions. We can work out how frequently an individual player $i\in P_k$ with weight $w_i^{int}$ belongs to a winning coalition with s players from $P_k$ via Algorithm 5 by computing

$$C_{+i}^{int,r+1,+k}=CoalitionsCardinalityWithPlayer(q,\tilde{w},w_i^{int},C^{int,r+1,+k}).$$

$C_{+i}^{int,r+1,+k}$ states how frequently player i is a part of a winning coalition containing s players from $P_k$, i.e., assuming that all of the other r precoalitions are acting as unions. From

$$f_i^{OW}(N,v,P)=\frac{1}{m!}\frac{1}{|P_k|!}\sum _{r=0}^{m-1}r!(m-r-1)!\sum _{s=0}^{|P_k|-1}s!\left(\right|P_k|-s-1)!\sum _{x=q}^{q+w_i-1}{C}_{+i}^{int,r+1,+k}(x,s+1)$$

we obtain the OW index of player i in $O(\Delta (m+|P_k{\left|\right)}^2)$ time and $O(\Delta (m+|P_k\left|\right))$ space. □

Finally, we quickly take up an observation from the final paragraph of the previous section. The proofs of Theorems 3–5 make it obvious that the pseudopolynomial complexity estimates for computing the respective power index of only one player i in a precoalition $P_k$ and for computing the respective power indices of all players in a precoalition $P_k$ are identical in terms of both computing time and memory space.

5. Numerical Results and Software

In the recent article [32], a powerful software package named EPIC (Efficient Power Index Computation) that provides efficient C++ implementations of various power indices (without precoalitions) for weighted voting games was introduced. We implemented our new algorithms for the BO, SCB and OW indices presented in the previous section in EPIC and tested our software thoroughly under MS Windows and Ubuntu Linux. Our implementations are freely available at https://github.com/jhstaudacher/EPIC/ (accessed on 25 December 2021) as parts of the software package EPIC introduced in [32].

Users can specify weighted voting games as CSV (comma separated values) files, i.e., EPIC supports a simple and widely used data format that allows for users to edit input files using notepad, MS Excel and many other text editors. An input file contains one precoalition per line, and weights of the players in the same precoalition are specified in the same line separated by commas; see https://github.com/jhstaudacher/EPIC//blob/master/readme.md (accessed on 25 December 2021) for more details.

When computing power indices for large weighted voting games, counting coalitions may force us to handle very large integers. For arbitrary-precision arithmetic, EPIC uses GMP [42], i.e., the GNU Multiple Precision Arithmetic Library. GMP [42] is a very widely used, established and well-tested C++ library for working with very large integers. We are using GMP in the same vein as described in [32].

In order to test our new algorithms, we created a number of test problems and made them available at https://github.com/jhstaudacher/EPIC/tree/master/test_cases/precoalitions (accessed on 25 December 2021).

In the following, we discuss computing times and memory requirements for three of these example problems. The numerical results in

Table 1. Computing times and memory requirements for an example with 741 players, $\tilde{w}=\mathrm{37,064}$,

40 precoalitions, a maximum coalition size of 40 and an average coalition size of 18.

	$\mathit{q}=\mathrm{18,533}$	(50% Plus 1 Vote)	$\mathit{q}=\mathrm{27,799}$	(75% of Votes)
Index	Time (s)	Memory (MB)	Time (s)	Memory (MB)
BZ	0.619	11.172	0.253	8.78
SH	594.522	2008.62	248.898	933.676
SCB	22.77	88.396	11.11	47.628
BO	0.539	10.956	0.26	8.86
OW	777.103	165.812	370.018	86.34

,

Table 2. Computing times and memory requirements for an example with 3034 players, $\tilde{w}=\mathrm{152,098}$,

60 precoalitions, a maximum coalition size of 78 and an average coalition size of 50.

	$\mathit{q}=\mathrm{76,050}$	(50% Plus 1 Vote)	$\mathit{q}=\mathrm{114,074}$	(75% of Votes)
Index	Time (s)	Memory (MB)	Time (s)	Memory (MB)
BZ	52.001	59.216	20.318	28.388
SCB	806.655	665.86	401.751	336.364
BO	9.193	23.612	4.469	15.28
OW	38,181.746	1146.04	18,638.011	574.436

and

Table 3. Computing times and memory requirements for an example with 3434 players, $\tilde{w}=\mathrm{72,068}$,

200 precoalitions, a maximum coalition size of 54 and an average coalition size of 17.

	$\mathit{q}=\mathrm{36,035}$	(50% Plus 1 Vote)	$\mathit{q}=\mathrm{54,051}$	(75% of Votes)
Index	Time (s)	Memory (MB)	Time (s)	Memory (MB)
BZ	27.694	35.768	8.959	19.324
SCB	578.455	316.324	259.954	144.224
BO	6.067	17.028	2.879	11.896
OW	86,139.148	1154.708	39,411.552	559.856

were obtained under Ubuntu 20.04 focal (64-bit) on an AMD FX(tm)-4170 Quad-Core CPU with a clock speed of 4.20 GHz and 8 GB RAM, i.e., on a standard laptop PC. In all three Table 1, Table 2 and Table 3, we report computing times and storage requirements for a quota of 50% plus 1 vote and compare them to a quota of 75% of the votes. By default, we compute power indices from above, since, normally, $q>\frac{1}{2}\tilde{w}$. As expected from our theoretical considerations, computing times and storage are approximately cut in half for the larger quota of 75%. All three Table 1, Table 2 and Table 3 investigate the BO, SCB and OW indices using the new algorithms for handling precoalition structures introduced in Section 4 and compare the Banzhaf (BZ) index (without the precoalition structure).

Table 1 is the only instance where we additionally compare the Shapley–Shubik (SH) index (without the precoalition structure). The results in Table 1 illustrate the pseudopolynomial time and space complexities reported in Theorems 2 and 5. The presence of a coalition structure makes computing the OW index slower rather than faster compared to the SH index. However, the OW index can be computed with significantly smaller storage requirements than the SH index. For the problems in Table 2 and Table 3, each containing more than 3000 players, we chose to omit the SH indices for storage reasons.

In Table 1, Table 2 and Table 3, the computations of both the BO indices and the BZ index (without a coalition structure) never need more than one minute, indicating that our algorithms could handle much larger problems. As predicted from the pseudopolynomial complexities in Theorems 1 and 3, computing times and storage needs are lower for the BO indices than for the BZ indices for large problem instances, as exemplified in the test problems in Table 2 and Table 3. In the smaller test problem in Table 1 with 741 players, this effect is not yet visible, as the implementation of the BO index is more sophisticated and more small arrays need to be allocated (in order to deal with the precoalition structure) than for the BZ index. As predicted in Section 4, the SCB indices need more storage and computing time than the BO indices due to the Shapley–Shubik computations for the internal games.

For the BZ indices (without precoalitions), we observe large time differences between Table 2 and Table 3 due to the fact that the game in Table 2 has a weight sum that is more than twice as large as the game in Table 3, even though the latter game has $13.2\%$ more players. Comparing the results from Table 2 and Table 3 for the SCB indices, we confirm the theoretical findings from Theorem 4. For computing SCB indices, it is more favorable to have more precoalitions rather than large average coalition sizes (both in terms of speed and storage). For the computation of the OW indices, no such statement can be made, as the OW index uses the Shapley–Shubik index for both the external and internal decision processes. This is reflected in the pseudopolynomial time and storage complexities from Theorem 5 and is confirmed in the numerical results in Table 2 and Table 3.

6. Outlook and Conclusions

In this paper, we present new dynamic programming algorithms for the three most common power indices with precoalitions, i.e., the Owen (OW), Banzhaf–Owen (BO) and symmetric coalitional Banzhaf (SCB) indices. Our algorithms reflect the external and internal decision processes between and within precoalitions used to specify these indices. We provide efficient C++ implementations of our new algorithms and point out that our methods can be applied for large numbers of players.

Still, there are many open questions in connection with the computation of power indices with precoalitions. Certain power indices with a priori unions, such as e.g., [43,44], do not fit the framework used in this paper, and it will be interesting to see how dynamic programming can be applied efficiently in these cases. In this context, we would like to stress that the very general framework for computing power indices via quasi-ordered binary decision diagrams [45,46,47,48], i.e., a recent approach based on relational algebra, has not yet been extended to power indices with a coalition structure. Furthermore, the mathematical relations between dynamic programming and generating functions [5,17,27,28] for power index computation justify further research, both in the cases with and without precoalitions. We expect these two paradigms to be very fruitful for each other, and such investigations have the potential to lead to even faster algorithms.

Another challenge is the parallel computation of power indices. To our knowledge, there are no publications on parallel computations of any of the power indices (without precoalitions) discussed in [32] or the dynamic programming algorithms presented therein. The new algorithms for power indices with precoalitions presented in the proofs of Theorems 3–5 appear to be particularly well suited for parallel processing, given that the internal games can be computed independently.

In terms of practical calculations for cooperative games with a coalition structure, we regret a lack of software offering more than the computation of the Owen value [21], i.e., the most widely used solution concept. In our view, even a prototypical implementation of various solution concepts for games with a partition structure, e.g., similar to the freely available R package CoopGame [49] for cooperative games, might be helpful in popularizing these ideas for analyzing real-world problems. A very concrete real-world application we wish to study using our new algorithms is the problem of indirect control in complex shareholding structures [11,12,13]. These networks are usually large and, to our knowledge, precoalitions of companies and investors within corporate networks have yet to be investigated.