3.1. Payoff Bias
In this section, we extend the model analyzed in [
18] to allow for payoff bias, where payoffs are assumed to be fitnesses. Consider a large population that lives in a environment which can exist in two states, labeled
state 1 and
state 2. Each generation, the environment switches with probability
and stays the same with probability
. This means that over the long run the environment is equally likely to be in each state. Individuals acquire one of two behaviors,
behavior 1 and
behavior 2 by either individual or social learning. Behavior 1 has fitness
when the environment is in state 1 and fitness
W when the environment is in state 2. Behavior 2 has fitness
when the environment is in state 2 and fitness
W when the environment is in state 1.
Each individual observes three cues that are predictive of the state of the environment. The adaptive problem is to determine the best way to use these cues.
Environmental cue. Individuals observe an environmental cue, y, that can take on any real value. Let and be the probability that an individual observes cue value y in environments 1 and 2 respectively. The environmental cue is a normally distributed random variable with mean and variance when the environment is in state 1 and has mean and when the environment is in state 2. This means that positive values of y indicate that it is more likely that the environment is in state 1 and negative values that it is in state 2. As the variance increases, a given cue value is a poorer predictor of environmental state.
Behavior. Each individual also observes the n models randomly sampled from the previous generation. For the jth model, social learners observe their behavior and their payoff, . Behaviors take on values 1 or 2, and payoffs are real numbers. The vector of behaviors is and the vector of payoff values is . Let p be the expected frequency of behavior 1 given that the population is experiencing environment 1. Due to the symmetry of the model, p is also the expected frequency of behavior 2 given that the population is experiencing environment 2. Then and where j is the number of individuals with the favored behavior.
Payoff. The payoff (aka fitness) of an individual with the favored behavior is a normally distributed random variable with mean and variance v and the payoff an individual with the disfavored behavior is a normally distributed variable with mean and variance v. The common mean, , is itself a normally distributed random variable with mean zero and a very large variance, V. This means that the absolute magnitudes of payoffs provide no information about the state of the environment, but that the difference between the payoffs is informative.
The information available to a given learner is the value of the non-social cue, y, and pair of vectors and . Let be the joint probability that the jth individual has the favored behavior and payoff in environment k. The probabilities of payoffs of different models conditioned on behavior and the state of the environment are independent so . The learner uses Bayesian methods to infer , the probability that the environment is in state 1 given that a learner observes an environmental cue y and models with behaviors and payoffs . Then the optimal decision rule is adopt behavior 1 if otherwise adopt behavior 2.
It is shown in
Appendix A.1 that this is equivalent to the following inequality.
where
and
If the learner knew the density of
y and frequency of the favored trait in the current environment, she could compute the values of these parameters. However, she does not know either of these things, and so cannot compute
g and
G. Instead we suppose that these are aspects of individual psychology. The value of
g gives propensity to rely on non-social cues, and
G the weight of payoff information both relative to the weight placed on the behavior of others. When
, the learner ignores payoff information and the learning rule reverts to that given in [
18]. When
, the learner is more likely to adopt the trait the exhibits the higher mean payoff among its sample of cultural models.
This rule indicates that importance of payoff differences between traits should be scaled by the term . This means that payoff bias should be more important when cultural models exhibit a mixture of behaviors than when most cultural models behave in the same way. As a result, rare beneficial innovations will be less likely to be adopted than beneficial innovations that have become established. Notice that this is not the same as the usual mass action effect which results from the probability that social learners observe an innovation. Instead, social learners are less likely to adopt even when they have observed the payoff advantage of the novel behavior. As far we know, no previous formulation of payoff bias incorporates this phenomenon.
Finally, this rule encourages a different view of payoff bias than given in other work (e.g., [
2]) where payoff bias is often conceptualized as a mechanism that determines who are the most attractive models. Here, individual payoffs are just data about the effects of alternative behaviors, and the rule simply weights the observed mean payoff of each behavior.
We assume that g and G are heritable attributes of the organism’s psychology that are shaped by natural selection. To model their evolution, we assume that the values of g and G are affected by a large number of alleles at a two haploid loci. Individuals first acquire their genotype through genetic transmission. Then, they observe members of the previous generation and an environmental cue, and determine whether they should adopt behavior 1 or behavior 2. Finally, viability selection adjusts the genotypic frequencies.
We used an agent-based simulation to investigate how natural selection shapes individual’s learning psychology, G and g, under different sets of environmental conditions. We are particularly interested in the benefits of payoff information when individual learning is hard, that is, when the environmental cues are noisy. This assumption captures the edge case that we think makes culture so adaptive: when the solution to an ecological challenge is difficult to discover through individual learning alone, but once discovered, has benefits that are easy to observe.
We also want to test the hypothesis that payoff biased transmission is helpful when the environment changes rapidly. Rapid environmental change makes social learning less adaptive because the social information acquired from previous generations become outdated. We suspect that payoff-biased transmission may help shield social learners from the deleterious impact of environmental change by providing them with another source of information that is less frequency dependent. This is important because it would mean that payoff-biased transmission can increase the range of environmental conditions under which social learning can evolve.
The agent-based simulation keeps track of the evolution of alleles that affect the values of G and g in a population of organisms. We assume haploid, asexual genetic transmission. An individual with the ith G allele and the kth g allele has a learning rule characterized by the parameters and that can take any real value. Individuals observe the behavior of the members of the previous generation, an environmental cue and a payoff cue and determine whether they should adopt behavior 1 or 2 using the optimal decision rule presented above. Then, viability selection adjusts the genotypic frequencies. Every time steps corresponds to a generation. Each generation, the following happens:
The state of the environment switches from state 1 and 2 with probability .
The individuals get a social cue, an environmental cue, and a payoff cue:
The social cue is the number j of individuals with behavior 1 among n social models drawn randomly from the previous generation. As there are two behavioral variants, the social cue is binomial with parameters p and n, where p is the frequency of behavior 1 in the population at previous generation.
The environmental cue y is drawn from a normal distribution with mean in environment 1 and in environment 2, and standard deviation .
The payoff cue, , is drawn from a normal distributed with mean d in environment 1 and in environment 2, and standard deviation .
Individuals combine those three cues using the optimal decision rule analytically derived above to chose a behavior.
Viability selection occurs. The baseline fitness is W. Individuals with the favored behavior, given the current state of the environment, get a fitness benefit d. Reproduction is based on relative fitness, which is calculated by dividing individual fitness by the maximum fitness in the population. The fitness of individuals relative to the maximum fitness in the population is used as a vector of weights in the sample function in the R language base package in order to sample the individuals that reproduce and transmit their alleles to the next generation.
Mutations in G and g alleles in the next generation occur with probability M. The values of the mutant alleles are drawn from a normal distribution with mean equal the allele of the parent and standard deviation . G and g are unlinked and mutate independently.
Several parameters of the simulation were kept constant throughout all the runs examined in this paper: number of agents = 10,000, , , , , and .
At the start of every run, the state of the environment, the behavior of each agent, as well as the values of the G and g alleles, are all set to 1. Each simulation ran for at least 5000 environmental shifts. After 5000 environmental shifts, the simulation continued until the distribution of G and g alleles became stationary. Stationary conditions were met when, for both G and g, the slope of a linear regression models fitted to the median allele value in the population, over the last 2000 generations, was smaller than 0.001.
In order to measure the fitness benefits associated with payoff information, we also ran simulations with the decision rule that includes only social and environmental cue [
18]:
The simulation results suggest that payoff bias is most adaptive when learning from the environment is hard and when the environment is unstable.
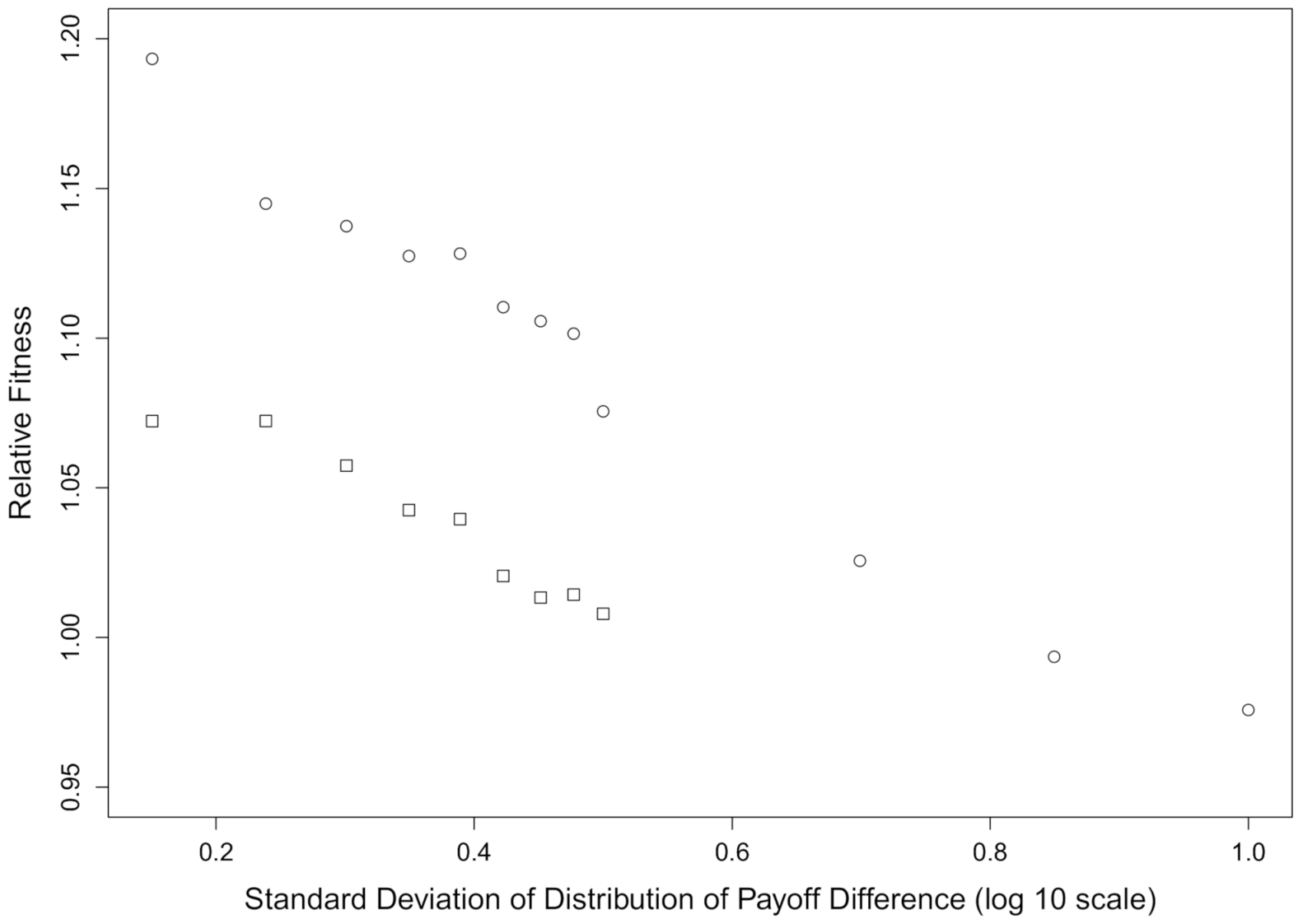
Figure 1 shows the average fitness in the population for high- and low-quality environmental information as a function of the quality of the payoff information. The fitness values plotted are relative to the average fitness in population that evolved in the same conditions but without payoff information. Thus, relative fitness greater than one mean payoff bias increases fitness, above and beyond the fitness provided by social and environmental cues alone. In the “high” regime of quality of environmental information,
(circles). In this regime, the chance of adopting the favored behavior via individual learning alone is 0.54. In the “low” regime,
(squares), i.e., the probability of adopting the favored behavior is 0.504 — a hair better than flipping a coin to make a decision.
Within each regime of environmental information quality, the relative fitness benefits of payoff biased transmission decrease with the standard deviation of the payoff cue distribution,
(
x-axis). These results plotted in
Figure 1 suggest that, unless it is very noisy, payoff information generally leads to higher fitness. More interestingly, the relative fitness benefits are highest in the low-quality of environmental information regime. As the quality of the environmental cue decreases from
to
, relative fitness increase by approximately 0.33. Notice that the evolutionary stable cultural transmission rule may reduce average fitness because selection does not maximize average fitness. Selection favors more social learning that is optimal for the population.
We also found that payoff bias leads to higher relative fitness in fast changing environments.
Figure 2 shows relative fitness in fast changing environments (
, circles) and a slow changing environments (
, squares). Given the same quality of payoff cue (x-axis), organisms in the fast changing environment condition enjoyed relative fitness benefits that were, on average, greater by 0.09 units. Payoff biases are most beneficial in rapidly changing environments because unstable environments lead to higher behavioral variation in the population. For instance, a population in a rapidly changing environment will spend more time in intermediate values of
p than a population in stable environment, in which the frequency of the favored behavior can remain high for several generations in a row. Since the value of payoffs depends in part on the variance in behavior among the social models observed, payoffs are more useful in rapidly changing environments.
Overall, our results suggests that selection will favor payoff-biased social transmission under a wide range of conditions. In particular, ecological problems that are hard to solve individually, as well as fast changing environments, will strongly favor using payoff information.
3.2. Content Bias
In both [
18] and the payoff bias model analyzed above, we assumed that the variable environment was symmetric. Each environment was equally likely, and the two behaviors had the same advantage in the environment in which they were favored. Here, we show when these assumptions are relaxed, selection favors a decision rule which is biased in favor of the behavior favored in the more common environment and the behavior which has a larger fitness advantage.
Consider a large population that lives in a environment which can exist in two states, imaginatively labeled
state 1 and
state 2. Each generation, the environment switches from state 1 to state 2 with probability
and switches from state 2 to state 1 with probability
. The means that over the long run the environment will be in state 1 with probability
Individuals acquire one of two behaviors, behavior 1 and behavior 2 by either individual or social learning. Behavior 1 has fitness in environment 1 and 1 in environment 2. Behavior 2 has fitness in environment 2 and 1 in environment 1. Each individual observes an environmental cue, x, that can takes on a range of values. Let be the probability that an individual observes cue value y in environment k. We assume that this probability is normal with mean and variance v in environment 1 and mean and variance v in environment 2. Each individual also observes n models sampled at random from the previous generation. We ignore differences in prestige, age, etc., and assume that all models are identical, so the only thing that matters is the number of models exhibits trait one or two. Let j be the number of models who exhibit the favored behavior the current environment. Let the probability of j conditioned on the environment being in state k is .
Let
be the probability that the
j individuals exhibit the favored behavior in environment
. The learner uses Bayesian methods to infer
, the probability that the environment is in state
k given that a learner observes an environmental cue
y and
j models with behavior
k. Then the optimal decision rule is adopt behavior 1 if it has higher expected fitness.
or
It is shown in the
Appendix A.2 that this is equivalent to the following inequality.
where
This is the same parameter as in the symmetric, unbiased case, except now modified to account for the asymmetric transition probabilities.
and
This learning rule indicates that nature of content bias in favor of a behavior depends on whether that behavior has relatively (1) higher fitness in environments in which it is favored, or (2) has higher frequency environments in which it is favored. In the first case, learners are more likely to adopt that behavior independent of the number of cultural models who display that behavior, while in the second case, the number of models displaying a behavior necessary to motivate the learner to adopt that behavior is reduced. To see this, set
so that the advantage of behavior 1 in environment one is the same as the advantage of behavior 2 in environment 2 and
so that both environments are equally likely. Then
, and the right-hand side of the decision rule is then same as in the unbiased case studied by [
18]. If
and
, environment 1 is more likely and behavior one has a bigger relative payoff, then both terms in the numerator are negative and
. This means that other things being equal, learners are more likely to adopt behavior 1. Similarly, if
and
, learners are more likely to adopt behavior 2. If the terms have opposite sign then the effect on the decision depends on their relative magnitude. Finally, if
, then
, and the left-hand side reduces to the same expression as in the unbiased case. Since
.
and therefore
. This means when behavior 1 is more common in environment 1 than behavior 2 is in environment 2, the rule favors behavior 1 when
. Even if fewer than half of the models exhibit behavior one, the social cue may favor the choice of behavior 1.