Abstract
In many bargaining situations, the distribution of seats or voting weights does not accurately reflect bargaining power. Maaser, Paetzel and Traub (Games and Economic Behavior, 2019) conducted an experiment to investigate the effect of such nominal power differences in the classic Baron–Ferejohn model. This paper re-analyzes the data from that experiment, looking at gender differences in bargaining behavior and in the effect of nominal weights. We find that women and men differ in particular with respect to the proposed distribution of payoffs and coalition size. By contrast, nominal weights have only minor gender-specific effects.
JEL Classification:
C78; J16; C91; C92; D7
1. Introduction
The research question of this paper is whether a non-transparent distribution of power in a bargaining situation affects individuals differently depending on their gender. This is a relevant angle in view of complex real-world negotiations. Moreover, we are, to the best of our knowledge, the first to study gender effects in the multilateral bargaining game by Baron and Ferejohn [1].
Gender differences in bargaining behavior and outcomes have, to date, almost exclusively been studied in the context of bilateral bargaining. This seems natural, as a central issue of economics, wage formation, is frequently characterized by bilateral situations, either in the form of negotiations between a labor union and an employer or as bargaining between an individual employee and his or her supervisor.
However, bargaining is also central to distributing resources in contexts where more than two agents are involved and agents have different power. For example, consider a small company with five shareholders, who have ownership shares of 26%, 23%, 20%, 17%, and 14%, and whose Articles of Association stipulate that more than 50% of the ownership interests must be behind a decision. Treating the percentage ownership shares as votes, this could be represented by the weighted voting game (51; 26,23,20,17,14), where 51 is the threshold that needs to be reached to pass a decision.
Voting weights do not always reflect individuals’ actual bargaining power in a transparent way. Due to the combinatorial nature of weighted voting, decision rules that look very different can be strategically equivalent, i.e., they result in exactly the same possibilities to form winning coalitions. In the weighted voting game presented above, the five shareholders are in fact symmetric, as any three of them can form a winning coalition. Generally, each weighted voting rule has an infinite number of representations, and we call two decision-making rules equivalent if they generate identical sets of winning and losing coalitions and thus imply the same real power. We refer to any differences between two representations that do not alter the sets of winning and losing coalitions as nominal. The voting game above is equivalent to (3; 1,1,1,1,1), which describes the distribution of power in the company in a more transparent way.
Non-transparent decision rules can have several reasons. Sometimes voting weights have been designed to conceal underlying power relations as was allegedly the case with the voting arrangements of the International Monetary Fund (see [2]). In other cases, misalignment between voting weights and actual power seems to be rather due to negligence; the Council of the European Economic Community between 1958 and 1973 is a famous example [3]. From a game-theoretic perspective, purely nominal differences in voting weights should not matter. If they are nevertheless found to influence behavior and outcomes, this indicates the presence of a “power illusion”, a possibility that has previously been studied in the context of structured multilateral bargaining [4,5,6] and in unstructured bargaining [7,8]. Guerci et al. [9] focuses on how experimental subjects learn about nominal weights, without a bargaining context.
Among the studies that considered nominal power differences in Baron–Ferejohn bargaining, evidence for power illusion is mixed. While [5] found power illusion effects to apply only to inexperienced subjects [4] (hereafter: MPT) reported that nominal differences can continue to influence agents’ behavior in spite of experience. In [6], the effect of nominal weights is a secondary aspect, as main interest is to test the effect of adding a new player to a weighted voting game. Still, their experiment included a treatment with nominal power differences, which found that nominally strong players earned more than nominally weak players, but the difference was not significant. Overall, these results suggest that transparency of voting rules is desirable in the sense that the distribution of voting weights should reflect the intended distribution of actual power as much as possible. The case for transparency becomes even stronger when it turns out that the mere appearance of a bargaining situation leads to systematic differences in outcomes between women and men.
To answer our research question, we use data from the MPT experiment. In that experiment, a group of five persons divided a budget according to the rules of the multilateral bargaining game of [1]. The decision rule in all treatments gave ex ante equal real bargaining power to all players. MPT contrasted a treatment where players’ symmetry was transparent with two ‘power illusion’ treatments that involved nominally different, non-transparent representations of the decision rule. In the present work, we first analyze whether the strategies adopted as proposer or responder differed systematically by gender in situations where influence was transparent (the Base treatment). We then compare behavior in the transparent setting to behavior in a non-transparent situation, where all group members had nominally different weights and could be subject to ‘power illusion’ (the Pit treatment). We document several behavioral differences between women and men in the absence of nominal differences. In particular, we find that women in the role of proposer claim less for themselves and also offer less to potential coalition partners than men. Women generally seek to form larger coalitions, whereas men more often form minimum winning coalitions. As a result, women earn less than men; this difference is basically unchanged by nominal weights.
Various empirical studies on wage negotiations such as, e.g., [10], show that women request and receive lower salaries compared to men. Moreover, when it is unclear whether negotiations are possible, women are less likely than men to initiate salary negotiations [11,12]. These findings largely explain the difference in negotiation outcomes [13] and point to the mechanisms behind the well-documented gender gap in wages [14]. Experimental studies have looked at the factors underlying the behavioral differences in bargaining, e.g., attitudes to norm compliance [13]. However, the existing body of experimental research has almost exclusively focused on bilateral bargaining situations, such as the ultimatum game [15,16] or two-player alternating offers bargaining [17,18].
An exception is Baranski et al. [19] who analyze how the gender composition of a committee affects the outcomes of majoritarian bargaining. In their experiment, groups of three players split a budget according to a free-form bargaining protocol with costly delay. Their evidence shows that grand coalitions—i.e., including all group members—are more often formed in predominantly female groups, whereas minimal winning coalitions are more common the larger the proportion of male group members. With respect to bargaining behavior, [19] found that men are more likely than women to make the initial offer and, when left out from a proto-coalition, men are more active in making offers to find partners (see [20]).
Our findings confirm Baranski et al.’s result that female proposers are generally more inclined than male proposers to form grand coalitions. We also agree that this inclination is probably due to women’s greater prosociality. The most important difference between the two studies is that MPT was not specifically designed to investigate gender effects, but the effect of nominal power differences. In particular, subjects in MPT did not know the gender of the other agents in the bargaining situation. Therefore, the data do not allow us to analyze group composition and gender pairing effects, which are the main focus of [19]. As a consequence, we cannot observe whether women are more likely to reject an offer if it comes from a male proposer, or whether the offers men make towards other men differ from those towards women. However, our data allow us to isolate behavioral differences between men and women when acting as proposer or responder, leaving gender pairing effects aside. Other differences between MPT and [19] concern group size and the bargaining protocol. With regard to the latter, Tremewan and Vanberg [21] have shown that the final divisions in structured and unstructured bargaining situations can be quite similar despite the different procedures.
2. Multilateral Bargaining with Nominal Power Asymmetry
2.1. Experimental Design and Treatments
The MPT experiment implemented a closed rule Baron–Ferejohn game with five players and simple majority rule. The five group members decided how to split a fixed budget of 150 Tokens according to the following rules: At first, a proposer was selected randomly with equal recognition probabilities. Next, the proposer suggested an allocation to the other players, subject to not exceeding the total budget constraint. Then players simultaneously voted yes or no, and the proposal was accepted if at least three of the five players voted in favor; in that case, the game ended and the agreed allocation was implemented. If the proposal failed, then a new proposer was selected at random with the process being repeated until an allocation was passed. In the closed rule version of the Baron–Ferejohn game, it is not possible to amend the proposal, but a new round must be started with a new proposal.
The canonical representation of the group’s voting rule is R = (3; 1,1,1,1,1), i.e., each agent has one vote, and three votes are the threshold that needs to be met or exceeded to pass a proposal. R served as a baseline in the experiment, as it reflects the real bargaining power of the players in a particularly transparent way. As an equivalent, but non-transparent representation of the same voting rule, we focused on = (18; 9,8,7,6,5), which has the smallest integer weights such that the weights of all five players differ. Using a between-subjects design, we exposed subjects to either representation R or , referred to as the Base treatment and the Pit treatment, respectively. The latter was labeled PIT2 in MPT as the original experiment also included a third treatment condition (PIT1) using representation (7; 3,3,3,2,2). In the present paper, we aim to focus on the behavior of proposers and responders by gender with and without nominal power differences. However, the PIT1 treatment potentially involves either homophily or some kind of groupiness (social identity) between members of the same weight type (weight-2 vs. weight-3). These effects could also differ by gender and would then interact with the behavioral differences we are interested in here. We therefore chose not to use that treatment in the present study.
To avoid confounding factors, MPT considered the game without discounting, i.e., the budget to be divided did not shrink from round to round. The outcome associated with the unique subgame perfect equilibrium in stationary strategies—the common benchmark prediction—then is that the proposer allocates of the budget to herself and offers the continuation value of to each of two other agents. The two remaining agents are left out of this minimal winning coalition and receive zero payoffs. The proposal is approved without delay. Clearly, these theoretical predictions apply regardless of whether voting rules R or is presented to the players.
Each session in the MPT experiment consisted of 20 bargaining periods, which were either played consecutively or with a short break of ten minutes after the first 10 periods. The relevant experimental treatments are summarized in Table 1; in total, 200 subjects participated. As can be seen from the sample breakdown in Table A1 in Appendix A, the sample was not gender-balanced, with a female share of 61%. Subjects were randomly rematched into groups between periods, but not between the rounds within a given bargaining game, and had no possibility to learn others’ gender or other characteristics. At the beginning of each period, each subject was randomly assigned her voting weight for that period (see [8] for a methodological discussion of random vs. fixed roles).

Table 1.
Treatment Conditions, Sessions and Subjects.
After learning her own voting weight as well as the voting weights of the other four group members and the quota each player was prompted to enter a proposal on how to allocate the 150 Tokens. One of the five first-round proposals was randomly chosen (with equal probabilities), displayed to all group members and then voted upon. If the proposal obtained a simple majority, the proposed distribution was agreed and the period concluded. If the proposal failed, a new round of the same game was initiated, where one player—possibly the same as before—was randomly selected (with probability ) to make a proposal. This was repeated until an allocation was agreed upon, at which point subjects were informed of their individual payoff during that period. At the end of a session, one period from the first ten periods and from the last ten periods, respectively, was randomly chosen for payment. For further details regarding the experimental procedures, we refer to MPT. The instructions are provided in Appendix B.
2.2. Results and Discussion
Comparing Base and Pit, our earlier study (MPT) demonstrated a number of power illusion effects in inexperienced players with respect to outcomes and behavior. In particular, inexperienced players’ payoffs and the proposer claims were strongly aligned with nominal weights. Similarly, the offers made to others were larger the larger the respondent’s nominal weight. Experience often but not always led to the attenuation or disappearance of these effects, making results in Pit more similar to those in Base. However, nominal weights continued to influence offering behavior for experienced players, but now larger offers were made to nominally less powerful responders. Comparing treatments with uninterrupted play over 20 bargaining situations and treatments with a break after the first 10 situations, MPT found significantly greater persistence of power illusion in the uninterrupted treatments, suggesting that the break enhanced subjects’ learning about the ‘real’ game. Overall, 63% of all coalitions were minimal; while less than predicted by theory, this share is similar to other experiments on Baron–Ferejohn bargaining. We found only very little variation across the different treatments, i.e., nominal weighting did not affect coalition size.
In our current analysis, we pool treatments with and without a short break, as also indicated in Table 1. The reason for this is that we found the effect of the break to be independent of gender. However, we include a dummy in all regressions below to control for an observation coming from a “break” or a “no-break” condition.
Another difference of our analysis here compared to MPT concerns how we define inexperienced and experienced subjects. In MPT, we referred to observations from periods 1–5 as “inexperienced” and to those from periods 16–20 as “experienced”. By contrast, in the present analysis, we take the first ten periods to be “inexperienced” and refer to the last ten periods as “experienced”. The reason is that our experimental design had each player become a proposer twice within the first or last 10 periods. Therefore, if we chose only five periods, as in MPT, it would be possible that the same person was a proposer either zero, one or two times. This would be problematic, given that women and men behave differently.
2.3. Conjectures about Gender Effects
In the present paper, we are interested in whether the introduction of nominal voting weights affects female and male players’ behavior and payoffs differently. We first draw on the previous literature on gender effects in bilateral bargaining (e.g., [15,19]) to formulate hypotheses about gender specific bargaining behavior and outcomes. Second, a growing body of literature shows that there are gender differences with respect to overconfidence (e.g., [22,23]) and motivated reasoning (e.g., [24]), finding specifically that men tend to be more overconfident and more prone to motivated reasoning about their performance. Our conjectures about gender effects of nominal weighting are based on the expectation that nominally greater power will increase individual tendencies toward overconfidence and motivated reasoning.
Hypothesis 1 (H1).
Earnings
- (a)
- Men earn more than women.
- (b)
- Nominal differences reinforce this.
The latter conjecture assumes the following behavior in the role as proposer:
Hypothesis 2 (H2).
Proposers
- (a)
- The share that a male proposer allocates to himself is greater than the share that a female proposer allocates to herself.
- (b)
- Nominal differences reinforce this.
The multilateral bargaining model suggests that players will base their decision on whether to accept or reject a proposal solely on the amount offered to them. In particular, they should accept any offer that at least corresponds to their continuation value. Alternatively, individuals’ minimal acceptable offer might be influenced by nominal weights.
Hypothesis 3 (H3).
Responders
- (a)
- Women accept lower offers than men.
- (b)
- A player’s acceptance threshold is higher the larger her or his weight.
- (c)
- Responders’ probability to accept an offer depends negatively on the share demanded by the proposer.
The literature generally finds women to be more egalitarian than men (e.g., [25,26]). In our context of multilateral bargaining, egalitarianism has two elements, first the inclusiveness of the proposed coalition and second the proposed distribution of payoffs within the coalition. We thus suggest
Hypothesis 4 (H4).
Coalitions
- (a)
- Female proposers are more inclusive than male proposers, i.e., they choose larger coalitions.
- (b)
- Female proposers propose more equal distributions among the coalition members.
3. Results
We first present our experimental results regarding players’ payoffs (Hypothesis 1) and then turn to players’ behavior following the structure of Hypotheses 2–4 above. In Section 3.5, we additionally address the question whether female proposers were motivated by risk aversion. Throughout, we focus on results from the first ten and the last ten periods, in order to distinguish clearly between inexperienced and experienced behavior.
Results in Section 3.1 (payoffs) are based on the final round of each bargaining period. Section 3.2 (proposer behavior) relies on players’ first round proposals in each bargaining period. Responder voting behavior is analyzed in Section 3.3 using “yes” and “no” votes from all rounds of a bargaining period. Coalition formation (Section 3.4) is investigated using first round proposals. Throughout the analyses, we assume that each individual first round proposal, each individual final round payoff, and each vote from all rounds of a bargaining period is an independent observation. To minimize repeated game effects, subjects were randomly rematched into groups between periods. Moreover, at the end of a session, only two periods were randomly chosen, respectively, from the first ten periods and from the last ten periods, to be paid off in private (random lottery incentive system, see [27]). Altogether, we have first round proposals and final round payoffs, respectively, per treatment. As bargaining took up to eight periods at maximum, we have (coincidentally) 2136 “yes” and “no” votes, both in Base and Pit.1
3.1. Payoffs
The upper panel of Figure 1 shows that male proposers, without and with experience, earned slightly more on average than female proposers in both treatments. Inexperienced male proposers earned 41.92 tokens in Base and 41.45 tokens in Pit, while inexperienced female proposers earned only 40.14 tokens in Base and 38.73 tokens in Pit; experienced male proposers earned 42.79 tokens in Base and 44.47 tokens in Pit, while experienced female proposers earned only 41.81 tokens in Base and 40.24 tokens in Pit (see Table A2 in Appendix A). However, the null hypothesis of equal payoffs is rejected for the Pit treatment only, using a two-tailed t-test with unequal variances. In particular, experienced male proposers earned 4.23 tokens more than experienced female proposers (). This difference amounts to 10.5% of the experienced female proposers’ average payoffs.
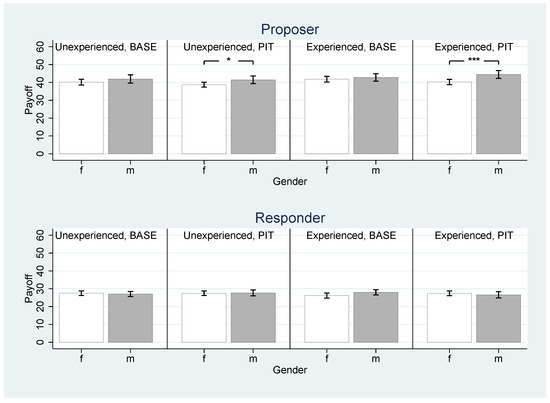
Figure 1.
Players’ Payoffs by Role, Experience, Treatment, and Gender. Average payoffs in tokens. The number of observations for each bar, means, and standard errors, as well as t-tests (Welch tests) can be taken from Table A2 in Appendix A. Significance levels: * p ≤ 0.10, ** p ≤ 0.05, and *** p ≤ 0.01. Error bars represent 90% confidence intervals.
By contrast, we find no noticeable gender effects for payoffs earned in the role of responder. As shown in the lower panels of Figure 1 and Table A2, responders earned between 26 and 28 tokens on average irrespective of gender, experience, and treatment. Inexperienced male responders in Base and experienced male responders in Pit even earned a bit less than female responders (0.46 and 0.85 tokens, respectively), but none of the payoff differences are statistically significant. There is also no difference on aggregate, i.e., when comparing the earnings of women and men in both roles (see the bottom panel in Table A2).
In Pit, players’ payoffs may additionally be influenced by their nominal voting weights and “power illusion” may reinforce payoff differences (Conjecture 1b). Figure 2 shows the marginal effect () of the voting weight on proposers’ (upper panels) and responders’ (lower panels) payoffs. The marginal effect is estimated by a random effects Tobit regression. There is 1 (of 400) left-censored (i.e., zero payoff) observations for proposers, and there are 374 (of 1600) left-censored observations for responders. Random effects panel regression with session clustered standard errors yields qualitatively identical results.
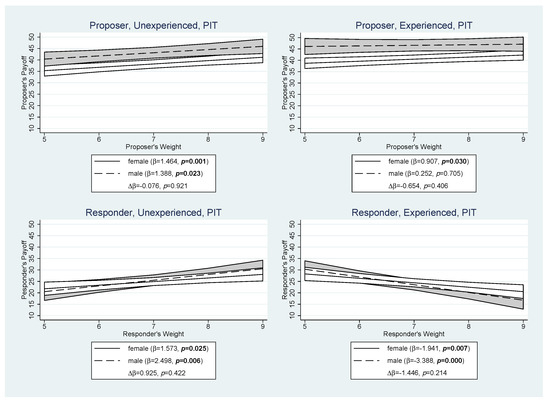
Figure 2.
Marginal Effect of Nominal Voting Weight in Pit by Role, Experience, and Gender. and are the marginal effect of the nominal voting weight and the differential slope of Gender {1 = male} estimated by a random effects Tobit regression including controls for age, siblings, lab experience, field of study, and dummies for employment and “break” (see Section 2.2). p is the significance level. Shaded areas represent 90% confidence intervals around the mean.
Figure 2 illustrates again that male proposers tend to earn more than female proposers (Conjecture 1a). For each nominal voting weight, the gender-payoff difference is statistically significant at least at the 10% level ( test at weights 5–9). The regression analysis shows that an extra nominal vote earned inexperienced female and male proposers about 1.40 tokens per nominal vote. For experienced proposers, this relationship is much weaker for both genders, and it is significant only for female proposers (0.91 tokens per extra nominal vote, ). However, with respect to Conjecture 1b, we must note that the gender difference is not significant (inexperienced, ; experienced, ), i.e., the nominal weighting does not increase the difference between female and male proposers. Figure A1 in Appendix A shows proposer payoffs by gender and weight, with women’s poorer performance in Pit attributed primarily to their low earnings in the weight-6 role.
The lower panel of Figure 2 again confirms that women and men earned the same as responders. However, it also shows an interesting pattern in which nominal vote weights had opposite effects on the payoffs of inexperienced and experienced responders. Inexperienced responders earned significantly more when they had higher nominal vote weights (women: 1.57 tokens per nominal vote; men: 2.50 tokens). In contrast, experience made higher nominal vote weights a disadvantage (female: 1.94 tokens; male: 2.54 tokens). Although this effect appears to be more pronounced for male respondents, the gender interaction with vote weight is not significant for both inexperienced and experienced respondents and therefore does not confirm Conjecture 1b. As proposers did not know the gender of the responders in our experiment, the (insignificant) gender difference must be due to responder behavior, which we will discuss in Section 3.3.
The above pattern regarding the effect of experience is explained by the fact that high-vote-weight responders’ likelihood to receive an offer decreased over time and, analogously, low-vote-weight responders became more likely to receive an offer (see Table A3 in Appendix A). The effect is especially strong in nominal-weight-9 responders, whose chance to receive an offer dropped from 85.5% to 66.7% (). Hence, significantly less experienced than inexperienced nominal-weight-9 responders voted “yes” on the final allocation (49% vs. 67.5%, ), and significantly more experienced nominal-weight-5 and nominal-weight-6 responders voted “yes” (see Table A4 in Appendix A).
Result 1:
Regarding Hypothesis 1, we conclude that
- (a)
- Male proposers on average earn more tokens than female proposers only in the Pit treatment (with nominal voting weights). Experience does not diminish the gender-payoff gap. Higher nominal voting weights have a positive impact on the payoffs of proposers of both genders, but they do not alter the gender-payoff gap.
- (b)
- Male and female responders earn equal payoffs, both in Base and in Pit. Having a higher nominal voting weight in Pit turns from an advantage to a disadvantage (in terms of tokens earned) with increasing experience. This effect seems to be stronger in male than in female responders.
3.2. Proposer Behavior
Figure 3 provides proposers’ average demand and average offer to targeted coalition members in the upper and the lower panel, respectively. In line with Conjecture 2a, we find that male proposers generally demanded significantly more for themselves than female proposers. The difference is more than 5 tokens for inexperienced proposers. In Base, the difference shrinks to 2.76 tokens when proposers become experienced, but is still significant. In Pit, the gap remains large (exactly 5 tokens).
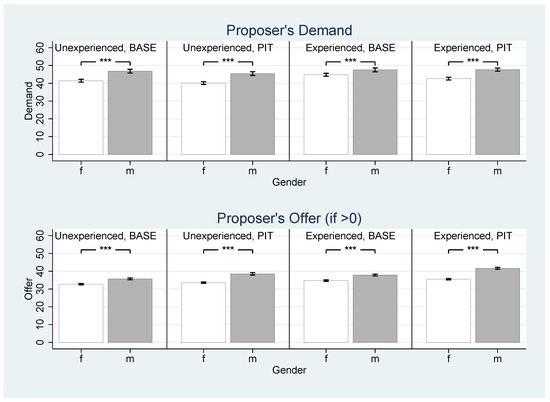
Figure 3.
Proposer Behavior by Experience, Treatment, and Gender. Upper panel: average demand in tokens; lower panel: average offer in tokens. The number of observations for each bar, means, and standard errors, as well as t-tests can be taken from Table A5 in Appendix A. Significance levels: * p ≤ 0.10, ** p ≤ 0.05, and *** p ≤ 0.01. Error bars represent 90% confidence intervals.
Additionally, the lower panel of Figure 3 shows that male proposers generally offered more than female proposers to responders when that responder was included in the proposed coalition. As the total number of tokens was fixed at 150, this implies that, on average, male proposers chose smaller coalitions than female proposers. We return to this point when we consider Conjecture 4a in Section 3.4.
Figure 4 shows how the nominal voting weight influenced proposer behavior in the Pit treatment. The upper panels show the marginal effect of the proposer’s nominal voting weight on her or his average demand in tokens. The lower panels show the marginal effect of the responder’s nominal weight on the proposer’s average offer in tokens. Both marginal effects are estimated by random effects panel regressions with session clustered standard errors (due to the exclusion of zeros, censoring is irrelevant).
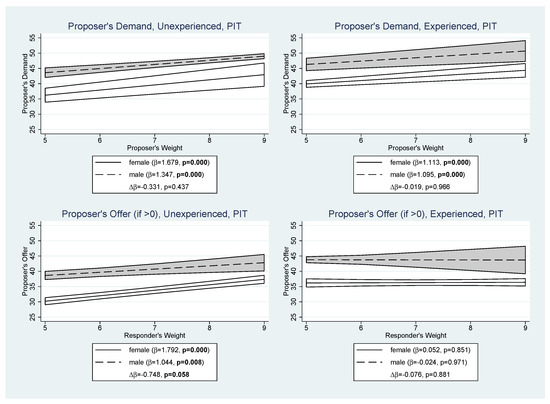
Figure 4.
Marginal Effect of Nominal Voting Weight on Proposer Behavior by Role, Experience, and Gender. Upper panel: average demand in tokens; lower panel: average offer (if < 0) in tokens. and are the marginal effect of the nominal voting weight and the differential slope of Gender {1 = male} estimated by a random effects panel regression. p is the significance level. Shaded areas represent 90% confidence intervals around the mean.
The upper panels not only confirm that male proposers allocated more to themselves than female proposers, but also show that an extra nominal vote increased the proposer’s demand by up to 1.70 tokens. The relationship between nominal voting weight and demand became less steep for experienced proposers (, ) but is still significant. There were no gender differences concerning the impact of the nominal voting weight on proposer demand (inexperienced: , ; experienced: , ). As an alternative perspective on behavior in Pit, the upper panel of Figure A2 in Appendix A shows proposer’s demand by gender and weight.
The lower panels of Figure 4 show that inexperienced proposers offer more to potential coalition members the larger their nominal voting weight (female: 1.79 tokens per vote; male 1.04 tokens per vote). The gender difference of 0.75 tokens is significant (), but disappears for experienced players. We show proposer’s offer by gender and responder’s weight in the lower panel of Figure A2 in Appendix A.
Result 2:
Regarding Hypothesis 2, we conclude that
- (a)
- Male proposers on average allocate more tokens to themselves than female proposers. Experience diminishes this gender difference only in the Base treatment. In Pit, both genders increase their demands with increasing nominal voting weights even if they are experienced.
- (b)
- Contrary to our Hypothesis 2b, nominal weighting does not affect male and female proposers differently.
3.3. Responder Voting Behavior
Responders could either vote “yes” in order to accept a proposal or “no“ in order to reject a proposal. Figure 5 shows how responders reacted to the proposer’s offer in terms of the average probability to vote “yes” on a certain offer in tokens. Note that there were almost no offers exceeding 50 tokens, which is one third of the pie. Interestingly, even offers below 30 tokens had some chance to be accepted. Offers of 50 tokens were almost always accepted.
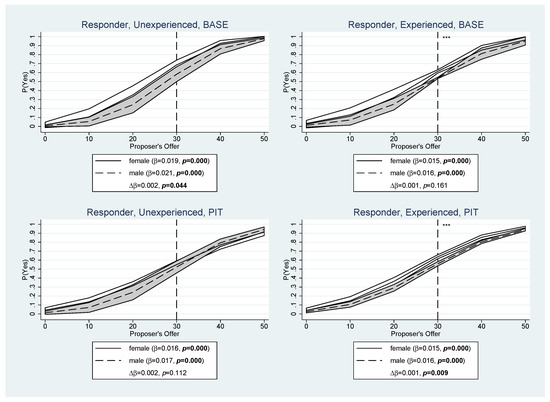
Figure 5.
Responder Voting Behavior: Proposer’s Offer. The graphs show the responder’s average probability to vote “yes” on a certain offer in tokens by experience, treatment, and gender. and are the marginal effect of the proposer’s offer and the differential slope of Gender {1 = male} estimated by a random effects probit panel regression. p is the significance level. Shaded areas represent 90% confidence intervals around the mean. Significance levels for a test on the hypothesis that female and male responders exhibit the same probability to vote “yes” on a proposal of 30 tokens are given by asterisks in the graphs: * p ≤ 0.10, ** p ≤ 0.05, *** p ≤ 0.01 (see Table A6 in Appendix A).
Although the 90% confidence intervals for female responders and male responders, in white and gray shade, respectively, largely overlap, the graphs indicate that female responders were inclined to accept lower offers than male responders. This finding supports our Conjecture 3a. In fact, the estimated coefficients show that male responders’ reaction function to the proposer’s offer was steeper than that of female responders in all four settings. For example, in inexperienced Base, the average marginal effect of one extra token on was 1.9% for female responders and 2.1% for male responders. Still, the gender difference is significant at the 10% level only in inexperienced Base and experienced Pit.
We also estimated the gender difference for at an offer of 30 tokens (see the dashed line at ). The respective means, standard errors, and tests are displayed in Table A6 in Appendix A. The graphs and the numbers reported there clearly demonstrate that experienced females were significantly more likely to vote “yes” on a 30-token proposal than experienced males (7.3% in Base, 7.8% in Pit). In light of this, we consider Conjecture 3, that women accept lower offers than men, as being confirmed by the data, at least for experienced responders.
Figure 6 additionally shows how respondents reacted to offers of at least 30 tokens (the game theoretic prediction for an acceptable offer) in Pit given their own nominal vote weight. The plots clearly show that respondents with higher nominal vote weights were less likely to accept such an offer, even if they were experienced. For example, inexperienced male respondents decreased their likelihood of voting “yes” by almost 6% per nominal vote (marginal effect). Thus, the analysis confirms Conjecture 3b. There are no significant gender differences, although the effects of nominal vote weight were somewhat weaker for female respondents.
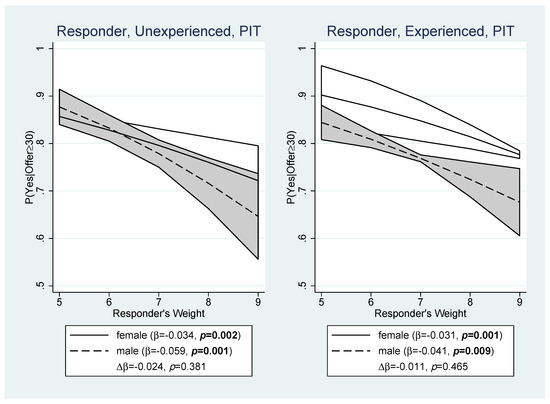
Figure 6.
Responder Voting Behavior in Pit: Proposer’s Offer ≥ 30. The graphs show the responder’s average probability to vote “yes” on an offer ≥ 30 tokens by experience, gender, and nominal weight. and are the marginal effect of the nominal voting weight and the differential slope of Gender {1 = male} estimated by a random effects panel probit regression; p is the significance level; shaded areas represent 90% confidence intervals around the mean.
Next, we examine how responders responded to the proposer’s demand (Conjecture 3c). Figure 7 focuses on responders who received an offer of at least 30 tokens, i.e., who were involved in a coalition and received an offer that should be accepted from a game theoretic perspective. The figure shows that inexperienced and experienced female responders in the Base treatment reacted negatively to the proposer’s demand. For female responders, the probability of accepting an offer shrank by about −0.5% to −0.6% per token demanded by the proposer. For the Pit treatment, the response of female responders was also negative, but much weaker and not significant. The response of male responders to the proposer’s demand was not significant in either treatment. Thus, we conclude that only female responders reacted negatively to the proposer’s demand. However, in the Pit treatment, this effect appears to have been masked by the higher complexity of the decision task with nominal vote weights. Breaking down responder behavior in Pit by responders’ nominal voting weights does not reveal additional insights and is therefore relegated to Figure A3 in Appendix A.
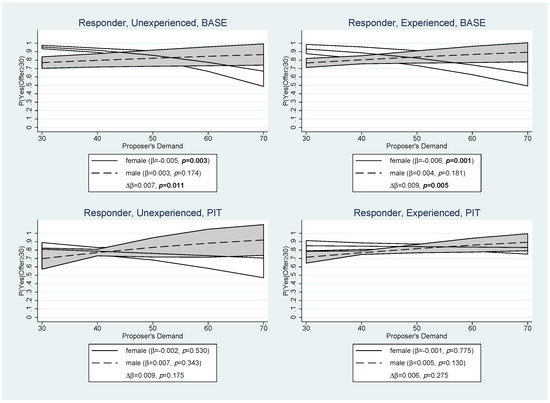
Figure 7.
Responder Voting Behavior: Proposer’s Demand. The graphs show the responder’s average probability to vote “yes” on an offer ≥ 30 tokens, given the proposer’s demand in tokens by experience, treatment, and gender. and are the marginal effect of the proposer’s demand and the differential slope of Gender {1 = male} estimated by a random effects probit panel regression. p is the significance level. Shaded areas represent 90% confidence intervals around the mean.
Result 3:
Regarding Hypothesis 3, we conclude that
- (a)
- Female responders accept lower offers than male responders.
- (b)
- Responders’ acceptance thresholds increase with their nominal voting weights.
- (c)
- In contrast to male responders, female responders, who receive an offer of at least 30 tokens, are more likely to react negatively to the proposer’s demand.
3.4. Coalition Size
Finally, we turn to the effects of gender on the proposed coalition size. Figure 8 shows the proposed coalition sizes in the top panels, the average Gini coefficient of the proposed distributions in the middle panels, and the proportion of the same distributions among coalition members in the bottom panels, by experience, treatment, and gender. Coalition size is defined as the number of players, including the proposer, who receive an offer greater than zero. The (discrete) Gini coefficient is a measure of inequality normalized to the interval , with higher values indicating greater inequality. It is calculated using the formula , where is the number of players, is the average payoff, , is the proposed payoff of player i, and the payoffs are increasingly ordered. The fraction of the proposed equal distribution refers only to the coalition members. That is, the proposal corresponds, up to permutations, to a uniform distribution in a size 3 coalition, the proposal is a uniform distribution in a size 4 coalition, and in the large coalition of all five players.
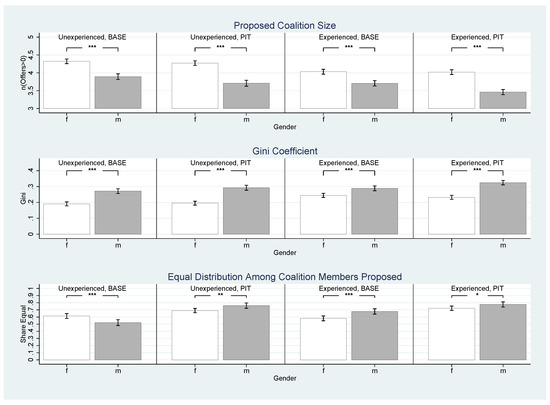
Figure 8.
Proposed Coalition Size, Gini Coefficient, and Share of Equal Distributions Proposed by Experience, Treatment, and Gender. Upper panel: average proposed coalition size (n(Offers > 0)); middle panel: Gini coefficient; lower panel: share of equal distributions among the members of the coalition proposed. The number of observations for each bar, means, and standard errors, as well as t-tests can be taken from Table A7 in Appendix A. Significance levels: * p ≤ 0.10, ** p ≤ 0.05, and *** p ≤ 0.01. Error bars represent 90% confidence intervals.
Figure 8 clearly confirms Conjecture 4a that female proposers proposed larger coalitions than male proposers. The gender difference is highly significant for both treatments and for inexperienced and experienced proposers. The middle panels of the figure show that female proposers on average proposed significantly less unequal allocations. For example, in experienced PIT, we have and , leading to a highly significant difference of (). The lower panels of the figure, however, indicate that, except for those in the inexperienced Base classification, female proposers proposed an equal distribution within the coalition significantly less often compared to male proposers. In other words, female proposers sought to build broader, more equal coalitions by offering to more respondents, but at the same time they sought to claim a relatively larger share for themselves.
Result 4:
Regarding Hypothesis 4, we conclude that
- (a)
- Female proposers form more inclusive coalitions.
- (b)
- Coalitions formed by female proposers are less unequal across all players, but more unequal within the coalition.
3.5. Discussion
One may wonder whether the female strategy—proposing more inclusive coalitions which involve more within-coalition payoff inequality—was more successful than the male strategy—proposing minimum winning coalitions with low within-coalition payoff inequality. If so, adopting this proposer behavior could be motivated by risk aversion [28]. To shed light on this, we compare the acceptance rates of minimum winning coalitions () and grand coalitions (). Together, these two types of coalitions accounted for more than 95% of all proposed coalitions. In Base with inexperienced players, we find that minimum winning coalitions were accepted at a higher rate and grand coalitions at a lower rate than would be expected under the assumption of independence (, ). The negative association between acceptance rate and size of the proposed coalition disappeared with increasing experience (, ). In Pit, however, experience tended to reinforce the relatively higher acceptance rate of minimal gain coalitions compared to large coalitions (inexperienced: , ; experienced: , ). Thus, if anything, proposing larger coalitions had a negative effect on acceptance rates.
Did proposing an equal distribution of payoffs among coalition members change the probability that the proposal was adopted? For Base, the answer is “no” (inexperienced: , ; experienced: , ). In contrast, the response in Pit is “yes” (inexperienced: , ; experienced: , ). Thus, in Pit, male proposers clearly had a greater chance of having their proposals passed because they more often proposed small coalitions with equal payoff distributions among coalition members, i.e., .
As experienced female proposers continued to propose more inclusive coalitions even though these had lower acceptance rates, exclusion aversion seems a more plausible explanation of their behavior than risk aversion (i.e., minimizing the chance that their own proposal is rejected). Note, however, that the evidence is only suggestive, as we do not know players’ beliefs regarding the probability of rejection.
Figure 9 and Table A8 in Appendix A further address this question by comparing the individual probabilities to accept a proposal between female and male responders for given coalition size n. The upper panels show the individual acceptance rates of minimum winning coalitions (). Analogously, the lower panels show graphs and numbers for the grand coalition (). With respect to minimum winning coalitions, there is almost no gender difference. If at all, male responders were a bit more inclined to accept minimum winning coalitions. In experienced Base, the difference of 8.5 percentage point is significant (). In contrast to this, female responders were, except for inexperienced Base, significantly more likely to accept grand coalitions; in experienced Pit the gender difference rises to 14.1 percentage points (). From this, we can conclude that female players showed a strong preference for including all group members in the coalition, both in their roles as proposers and responders. This suggests that women prefer less inequality in the overall group compared to men.
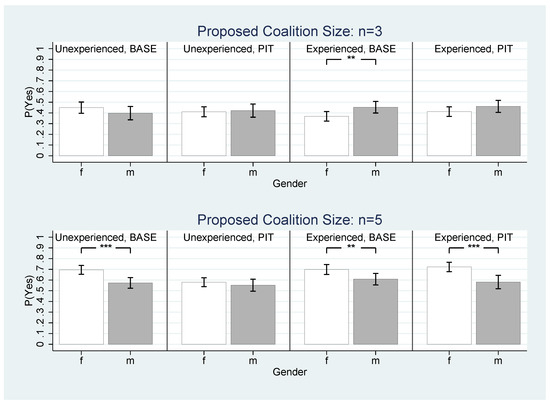
Figure 9.
Responder’s Probability to Vote “Yes” by Proposed Coalition Size, Experience, Treatment, and Gender. The number of observations for each bar, means, and standard errors, as well as t-tests can be taken from Table A8 in Appendix A. Significance levels: * p ≤ 0.10, ** p ≤ 0.05, *** p ≤ 0.01. Error bars represent 90% confidence intervals.
4. Conclusions
Using data from [4], we analyzed gender differences in bargaining situations with nominal power asymmetries. Our results show that proposer and responder behavior in Baron–Ferejohn negotiations is gendered. One of the most striking observations is the difference in the size of coalitions formed by women and men. Interestingly, although women in our experiment proposed larger coalitions, the distribution of the “pie” within the coalition was rather unequal. Male proposers, on the other hand, proposed smaller coalitions but with greater equality within the coalition. As a result, inequality, as measured by the Gini coefficients of the total group, was lower for the women’s proposals. We interpret this behavior as driven by what we tentatively call “exclusion aversion”, a reluctance to leave out any members of the group. Whether “exclusion aversion” is indeed a correct interpretation and, if so, is more general among women than among men is an interesting topic for future research. A related interesting finding is the tendency of women proposers to submit suboptimal proposals, with lower self-offers compared to male proposers and a lower chance of acceptance, which cannot, in our design, be due to gender pairing effects.
With respect to nominal differences, i.e., the framing of a voting rule, we found no strong gender-specific effects. As described in greater detail in our earlier paper, ‘power illusion’ effects are particularly evident in proposers’ claims and respondents’ probability to accept an offer. Analyzing the data separately by gender, we find that the non-transparent voting rule in Pit tended to make large claims by the proposer more acceptable among female responders. However, it is primarily the gender difference in response behavior, with men indifferent to high demand from the proposer, that warrants further investigation.
Author Contributions
Conceptualization, methodology, software, formal analysis, investigation, data curation, visualization, writing—original draft preparation, writing—review and editing, N.M., F.P. and S.T. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support for the original experiment [4] from the University of Bremen Central Research Development Fund and the German Research Foundation (Stefan Traub, reference TR 458/6-2) and a travel grant from Aarhus Universitets Forskningsfond (Nicola Maaser) are gratefully acknowledged.
Data Availability Statement
The data and STATA do files can be found here: https://www.hsu-hh.de/be/forschung (accessed on 27 December 2021).
Acknowledgments
We thank two anonymous referees and the academic editor for their constructive comments. Part of the paper was completed while Nicola Maaser was visiting the Faculty of Law, Business & Economics at the University of Bayreuth, whose hospitality is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Additional Tables and Figures

Table A1.
Breakdown of the Sample.
Table A1.
Breakdown of the Sample.
| Mean | Std. Dev. | |
|---|---|---|
| Age | 25.0 | 4.5 |
| Number of Siblings | 1.6 | 1.1 |
| Freq. | Percent | |
| Gender | ||
| Female | 121 | 61.0 |
| Male | 79 | 39.0 |
| Labexperience a | ||
| Yes | 170 | 85.0 |
| No | 30 | 15.0 |
| Works b | ||
| Yes | 131 | 65.5 |
| No | 69 | 34.5 |
| Field of Study | ||
| Economics | 66 | 33.0 |
| Other fields | 32 | 16.0 |
| Sciences | 33 | 16.5 |
| Education Sciences | 20 | 10.0 |
| Social Sciences | 19 | 9.5 |
| Humanities | 14 | 7.0 |
| Law | 11 | 5.5 |
| Philosophy | 5 | 2.5 |
Notes: a Labexperience = Yes if participation in 3 or more experiments; b Student is employed.

Table A2.
Players’ Payoffs by Role, Experience, Treatment, and Gender.
Table A2.
Players’ Payoffs by Role, Experience, Treatment, and Gender.
| Gender | Inexperienced | Experienced | |||
|---|---|---|---|---|---|
| Base | Pit | Base | Pit | ||
| Proposer | |||||
| 40.15 | 38.73 | 41.81 | 40.24 | ||
| Female | (0.99) | (0.85) | (0.96) | (0.89) | |
| 125 | 124 | 128 | 136 | ||
| 41.92 | 41.45 | 42.79 | 44.47 | ||
| Male | (1.39) | (1.27) | (1.28) | (1.32) | |
| 75 | 76 | 72 | 64 | ||
| Diff | 1.77 | 2.72 | 0.98 | 4.23 | |
| (1.71) | (1.53) | (1.60) | (1.59) | ||
| p | 0.303 | 0.078 | 0.541 | 0.009 | |
| Responder | |||||
| 27.50 | 27.49 | 26.16 | 27.43 | ||
| Female | (0.77) | (0.77) | (0.84) | (0.81) | |
| 455 | 506 | 452 | 494 | ||
| 27.03 | 27.68 | 27.99 | 26.58 | ||
| Male | (0.87) | (1.01) | (0.90) | (1.06) | |
| 345 | 294 | 348 | 306 | ||
| Diff | −0.46 | 0.19 | 1.83 | −0.85 | |
| (1.16) | (1.27) | (1.24) | (1.33) | ||
| p | 0.689 | 0.881 | 0.138 | 0.523 | |
| Aggregated | |||||
| 30.22 | 29.70 | 29.62 | 30.19 | ||
| Female | (0.67) | (0.66) | (0.74) | (0.69) | |
| 580 | 630 | 580 | 630 | ||
| 29.69 | 30.51 | 30.53 | 29.67 | ||
| Male | (0.81) | (0.98) | (0.82) | (0.97) | |
| 420 | 370 | 420 | 370 | ||
| Diff | −0.54 | 0.81 | 0.92 | −0.52 | |
| (1.05) | (1.11) | (1.10) | (1.19) | ||
| p | 0.612 | 0.468 | 0.409 | 0.661 | |
Notes: Average payoffs in tokens. First row: means, second row: standard errors in parentheses, third row: case numbers. p-value of a two-tailed t-test with unequal variances (Welch test) of the hypothesis that female and male players earned the same amount of tokens. Tests which are significant at least at the 10% level are given in boldface.

Table A3.
Responders’ Probability to Receive an Offer by Nominal Voting Weight and Experience.
Table A3.
Responders’ Probability to Receive an Offer by Nominal Voting Weight and Experience.
| Responder’s Weight | P(Offer > 0) | ||
|---|---|---|---|
| Experience | |||
| No | Yes | p-Value | |
| 5 | 76.1 | 82.1 | 0.174 |
| 6 | 73.7 | 76.9 | 0.515 |
| 7 | 79.7 | 76.7 | 0.515 |
| 8 | 77.1 | 70.6 | 0.192 |
| 9 | 85.5 | 66.7 | 0.000 |
Notes: Probability to receive an offer in percent. Data refers to groups’ last round of bargaining in a period. Note that proposers did not know the gender of responders, nor did responders know the gender of the proposer, ruling out gender pairing effects. Significance level of a χ2 independence test. Tests which are significant at least at the 10% level are given in boldface.

Table A4.
Responders’ Probability to Vote “Yes” by Gender, Nominal Voting Weight and Experience.
Table A4.
Responders’ Probability to Vote “Yes” by Gender, Nominal Voting Weight and Experience.
| Responder’s Weight | P(Vote = Yes) | ||
|---|---|---|---|
| Experience | |||
| No | Yes | p-Value | |
| All Responders | |||
| 5 | 61.3 | 73.2 | 0.021 |
| 6 | 60.3 | 69.4 | 0.090 |
| 7 | 63.9 | 66.0 | 0.693 |
| 8 | 59.9 | 54.4 | 0.323 |
| 9 | 67.5 | 49.0 | 0.001 |
| Female Responders | |||
| 5 | 62.7 | 75.5 | 0.049 |
| 6 | 60.4 | 72.4 | 0.072 |
| 7 | 69.3 | 62.2 | 0.294 |
| 8 | 60.8 | 55.9 | 0.480 |
| 9 | 69.5 | 58.5 | 0.105 |
| Male Responders | |||
| 5 | 59.0 | 69.7 | 0.209 |
| 6 | 60.0 | 64.5 | 0.615 |
| 7 | 54.4 | 72.1 | 0.045 |
| 8 | 58.3 | 51.7 | 0.471 |
| 9 | 63.9 | 33.9 | 0.001 |
Notes: Probability of voting “yes” in percent. Data refers to groups’ last round of bargaining in a period. Note that proposers did not know the gender of responders, nor did responders know the gender of the proposer, ruling out gender pairing effects. Significance level of a χ2 independence test. Tests which are significant at least at the 10% level are given in boldface.

Table A5.
Proposer Behavior by Experience, Treatment, and Gender.
Table A5.
Proposer Behavior by Experience, Treatment, and Gender.
| Gender | Inexperienced | Experienced | |||
|---|---|---|---|---|---|
| Base | Pit | Base | Pit | ||
| Demand | |||||
| 41.42 | 40.09 | 44.77 | 42.64 | ||
| Female | (0.49) | (0.46) | (0.51) | (0.48) | |
| 580 | 630 | 580 | 630 | ||
| 46.81 | 45.45 | 47.54 | 47.64 | ||
| Male | (0.64) | (0.65) | (0.65) | (0.53) | |
| 420 | 370 | 420 | 370 | ||
| Diff | 5.39 | 5.36 | 2.76 | 5.00 | |
| (0.80) | (0.80) | (0.83) | (0.72) | ||
| p | 0.000 | 0.000 | 0.001 | 0.000 | |
| Offer (if > 0) | |||||
| 32.68 | 33.53 | 34.72 | 35.54 | ||
| Female | (0.24) | (0.24) | (0.26) | (0.25) | |
| 1927 | 2065 | 1758 | 1903 | ||
| 35.67 | 38.53 | 37.85 | 41.62 | ||
| Male | (0.31) | (0.41) | (0.30) | (0.34) | |
| 1215 | 1480 | 1137 | 910 | ||
| Diff | 2.99 | 5.00 | 3.13 | 6.08 | |
| (0.39) | (0.47 | (0.40) | (0.42) | ||
| p | 0.000 | 0.000 | 0.000 | 0.000 | |
Notes: Average payoffs in tokens. First row: means, second row: standard errors in parentheses, third row: case numbers. p-value of a two-tailed t-test with unequal variances (Welch test) of the hypothesis that female and male proposers demand (upper panel) and offer (lower panel) the same amount of tokens. Offers if > 0. Tests which are significant at least at the 10% level are given in boldface.

Table A6.
Responder’s Probability to Accept an Offer of 30 Tokens.
Table A6.
Responder’s Probability to Accept an Offer of 30 Tokens.
| Gender | Inexperienced | Experienced | |||
|---|---|---|---|---|---|
| Base | Pit | Base | Pit | ||
| Female | 68.6 | 55.0 | 61.3 | 63.7 | |
| (3.2) | (2.6) | (1.1) | (1.4) | ||
| Male | 58.2 | 52.3 | 54.0 | 55.9 | |
| (5.0) | (4.0) | (4.2) | (1.4) | ||
| 2.18 | 0.40 | 26.75 | 9.33 | ||
| p | 0.140 | 0.526 | 0.000 | 0.002 | |
Notes: Responder’s probability to vote “yes” in percent when offered 30 tokens estimated by a random effects panel probit regression with session clustered standard errors (marginal effects). First row: means, second row: standard errors in parentheses. p-value of a χ2 test of the hypothesis that female and male responders exhibit the same probability to vote “yes”. Tests which are significant at least at the 10% level are given in boldface.

Table A7.
Proposed Coalition Size, Gini, and Share of Equal Distributions Proposed by Experience, Treatment, and Gender.
Table A7.
Proposed Coalition Size, Gini, and Share of Equal Distributions Proposed by Experience, Treatment, and Gender.
| Gender | Inexperienced | Experienced | |||
|---|---|---|---|---|---|
| Base | Pit | Base | Pit | ||
| Coalition Size Proposed | |||||
| 4.32 | 4.27 | 4.03 | 4.02 | ||
| Female | (0.04) | (0.04) | (0.04) | (0.04) | |
| 580 | 630 | 580 | 630 | ||
| 3.89 | 3.71 | 3.71 | 3.46 | ||
| Male | (0.05) | (0.05) | (0.05) | (0.04) | |
| 420 | 370 | 420 | 370 | ||
| Diff | −0.43 | −0.56 | −0.32 | −0.56 | |
| (0.06) | (0.06) | (0.06) | (0.06) | ||
| p | 0.000 | 0.000 | 0.000 | 0.000 | |
| Gini Coefficient | |||||
| 0.191 | 0.195 | 0.245 | 0.232 | ||
| Female | (0.008) | (0.007) | (0.008) | (0.008) | |
| 580 | 630 | 580 | 630 | ||
| 0.271 | 0.293 | 0.289 | 0.325 | ||
| Male | (0.009) | (0.009) | (0.009) | (0.009) | |
| 420 | 370 | 420 | 370 | ||
| Diff | 0.080 | 0.097 | 0.044 | 0.093 | |
| (0.012) | (0.012) | (0.012) | (0.012) | ||
| p | 0.000 | 0.000 | 0.000 | 0.000 | |
| Share of Equal Distributions | |||||
| Among Coalition Members Proposed | |||||
| 0.614 | 0.690 | 0.581 | 0.724 | ||
| Female | (0.020) | (0.080) | (0.021) | (0.018) | |
| 580 | 630 | 580 | 630 | ||
| 0.521 | 0.759 | 0.679 | 0.776 | ||
| Male | (0.024) | (0.022) | (0.023) | (0.023) | |
| 420 | 370 | 420 | 370 | ||
| Diff | 0.092 | 0.069 | 0.098 | 0.052 | |
| (0.032) | (0.029) | (0.031) | (0.028) | ||
| p | 0.004 | 0.017 | 0.002 | 0.065 | |
Notes: Average coalition size (upper panel), Gini coefficient (middle panel) and share of equal distributions among the coalition members proposed (lower panel). First row: means, second row: standard errors in parentheses, third row: case numbers. p-value of a two-tailed t-test with unequal variances (Welch test) of the hypothesis that female and male proposers propose the same coalition size (upper panel), Gini coefficient (middle panel), and equally often coalitions with an equal distribution of tokens among the coalition members (lower panel). Tests which are significant at least at the 10% level are given in boldface.

Table A8.
Responder’s Probability to Vote “Yes” by Proposed Coalition Size, Experience, Treatment, and Gender.
Table A8.
Responder’s Probability to Vote “Yes” by Proposed Coalition Size, Experience, Treatment, and Gender.
| Gender | Inexperienced | Experienced | |||
|---|---|---|---|---|---|
| Base | Pit | Base | Pit | ||
| 44.9 | 41.1 | 36.8 | 41.2 | ||
| Female | (3.2) | (2.8) | (2.7) | (2.7) | |
| 245 | 302 | 326 | 335 | ||
| 38.9 | 42.1 | 45.3 | 46.1 | ||
| Male | (3.8) | (2.8) | (3.3) | (3.4) | |
| 171 | 302 | 234 | 217 | ||
| Diff | −5.1 | 1.1 | 8.5 | 4.9 | |
| (4.9) | (4.7) | (4.2) | (4.3) | ||
| p | 0.298 | 0.818 | 0.045 | 0.260 | |
| 69.4 | 57.9 | 69.8 | 72.2 | ||
| Female | (2.5) | (2.5) | (2.8) | (2.6) | |
| 337 | 390 | 265 | 288 | ||
| 57.3 | 55.1 | 60.8 | 58.1 | ||
| Male | (3.0) | (3.4) | (3.2) | (3.8) | |
| 267 | 214 | 227 | 172 | ||
| Diff | −12.1 | −2.8 | −9.0 | −14.1 | |
| (3.9) | (4.2) | (4.3) | (4.6) | ||
| p | 0.002 | 0.507 | 0.037 | 0.002 | |
Notes: Probability to vote “Yes” in percent. First row: means, second row: standard errors in parentheses, third row: case numbers. p-value of a two-tailed t-test with unequal variances (Welch test) of the hypothesis that female and male responders exhibit the same probability to votes “Yes” on a coalition of size n. Tests which are significant at least at the 10% level are given in boldface.
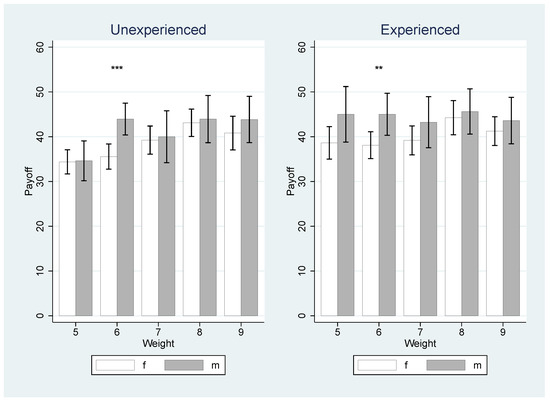
Figure A1.
Proposer’s Payoff in Pit by Experience, Weight, and Gender. Average payoffs in tokens. Significance levels: * p ≤ 0.10, ** p ≤ 0.05, *** p ≤ 0.01. Error bars represent 90% confidence intervals.
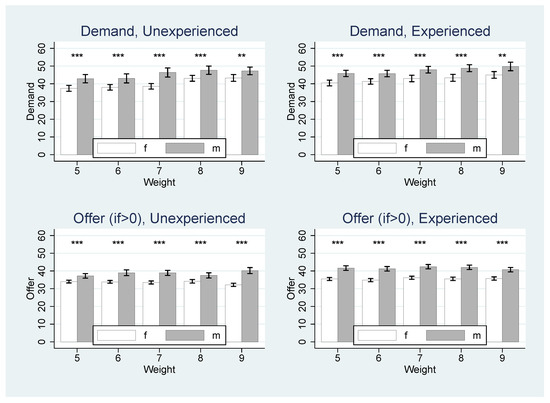
Figure A2.
Proposer’s Demand (upper panels) and Offer if > 0 (lower panels) in Pit by Nominal Voting Weight and Gender. Significance levels: * p ≤ 0.10, ** p ≤ 0.05, *** p ≤ 0.01. Error bars represent 90% confidence intervals.
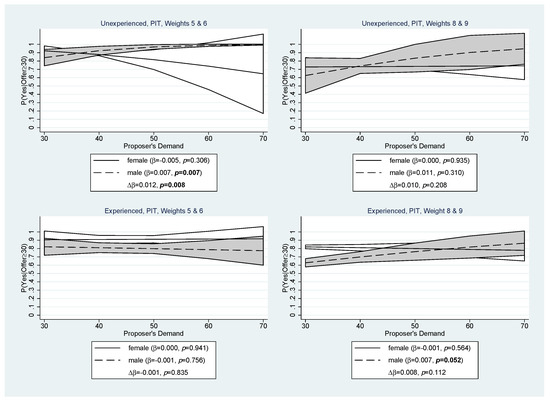
Figure A3.
Responder Voting Behavior: Proposer’s Demand in Pit by Nominal Voting Weight. The graphs show the responder’s average probability to vote “yes” on an offer ≥ 30 tokens, given the proposer’s demand in tokens by experience, nominal voting weight, and gender. and are the marginal effect of the proposer’s demand and the differential slope of Gender {1 = male} estimated by a random effects probit panel regression. p is the significance level. Shaded areas represent 90% confidence intervals around the mean.
Appendix B. Experimental Instructions
In the following we present an English translation of the German instructions. Different formulations in the various treatments are indicated in parentheses.
***
Welcome to the experiment and thank you very much for your participation!
Please read the instructions carefully. Do not talk to your neighbor during the experiment. Should you have any questions, please make sure to read the instructions again. Should you still have questions after that, please notify us. We will then come to you and answer your questions. It is of vital importance that you follow this rule. Otherwise the results of this experiment are scientifically useless to us.
Please take your time reading the explanations and making your decisions. You will not be able to influence the duration of the experiment by deciding quickly, as we will always wait for the rest of the participants to finish. The experiment is completely anonymous. You will not find out who you played with, not during the experiment or afterwards. The other participants will not find out, not during the experiment or afterwards, which role you played, what decisions you made, and how much you earned.
During the experiment, we will not talk about Euros, but about Tokens. The following exchange rate is used:
100 Tokens equal 20 Euros.
For your participation, you will receive 10 Euros as a fixed payout plus the amount of Tokens you earned during the experiment based on your and the other participant’s decisions. You will be paid in cash individually and privately after the end of the experiment. The estimated duration of the experiment is 120 min. Below you will find a detailed description of the experiment proceedings.
Instructions:
In the experiment we will ask you to decide how a specific number of Tokens will be distributed among your group of five players. This will be repeated in 20 periods. In treatments with a break: This will be repeated in 2 times 10 periods. There will be a break of 10 min after 10 periods. During the break, we serve refreshments (fruits, cookies and water). You can read in the magazines during the break. It is not allowed to talk to other participants during the break. The experiment continues after the break for the next 10 periods).
During each period, proposals are made regarding the distribution of Tokens. A distribution proposal has to distribute the available Tokens completely among the suggesting player and the other players. This proposal is presented to the other 4 players and they can either accept or reject it. A suggestion is accepted if it receives at least half of the votes. (In Pit1 and Pit2: However, the respective players each have a different number of votes. At the beginning of each period, the players are informed how many votes they have and how many votes the other players have.) (In BASE: In each Period, all players have one vote.)
Detailed Instructions:
In each bargaining period, you will form a group of five players with the other participants. You will play 20 periods. In each period, you will be placed in a group of 5 new players. Additionally, no information from previous periods will be communicated to the next period.
Each bargaining period follows the exact same procedure. First, all 5 group members anonymously and at the same time make a proposal regarding the distribution of the available Tokens. One of these five distribution proposals will be randomly selected and put to a vote.
- If this first proposal receives the majority of votes, it will be implemented. Every player receives the Tokens allocated to him during this round.
- If the proposal is rejected, one player from the group of five is randomly selected and can propose a new distribution proposal to be voted on. This can also be the player whose proposal was just rejected.
- This procedure is repeated until a distribution proposal is accepted. Once a distribution proposal is accepted, the period ends.
(In Pit1 and Pit2: At the beginning of each period, every player is allocated a number of votes. The total number of votes is constant across all bargaining periods. At the beginning of each period, the players are informed how many votes they themselves have and how many votes each other player has.) (In BASE: At the beginning of each period, every player is allocated with one vote.)
Additionally to the votes, every participant receives a symbol. The assignment of symbols is random and is independent of the assigned votes. Symbols are reassigned randomly after each period. Symbols in the experiment are +, #, O, @ and X.
A distribution proposal is accepted if at least half of the votes are cast in favor of the proposal. (In Pit1 and Pit2: During a bargaining period, each player keeps his number of votes and his symbol until an agreement is reached. However, the number of votes and the assigned symbol for each player can vary from one period to the next.) A bargaining period only ends when a distribution proposal receives the majority of the votes.
Calculation of your payout:
In each period your payout is directly determined by the distribution proposal: You will receive the number of Tokens determined by the accepted distribution. Should no Tokens have been allocated to you, you do not receive anything.
Of the 20 periods, two will be randomly selected at the end of the experiment. One of the two payoff-relevant periods is chosen from the first 10 periods and the other relevant period is chosen from the later 10 periods. Thus, each period could be relevant for the payout. The payouts for all participants are determined by these randomly selected periods.
Calculation of your final payout for participating in the experiment:
Your final payout consists of two parts:
- (i)
- Every participant receives a participation payment of 10 Euros. This is independent of your decisions or the decisions of other players.
- (ii)
- The payout for the experiment is determined by the voting behavior of all group members and by the two randomly selected periods. These periods determine the payout for all players in the experiment.
After the last period, you will receive a brief questionnaire. Following that, you will receive your payout in cash.
The experiment will start shortly. Should you have any more questions, please raise your hand and wait quietly until somebody approaches you. Please do not talk to the other participants during the whole experiment. Thank you very much for your participation.
Note
| 1 | The data and STATA do files can be found here: https://www.hsu-hh.de/be/forschung. |
References
- Baron, D.P.; Ferejohn, J.A. Bargaining in legislatures. Am. Political Sci. Rev. 1989, 83, 1181–1206. [Google Scholar] [CrossRef] [Green Version]
- Leech, D.; Leech, R. Reforming IMF and World Bank Governance: In Search of Simplicity, Transparency and Democratic Legitimacy in the Voting Rules; Warwick Economics Research Paper Series (TWERPS) No. 914; University of Warwick: Coventry, UK, 2009. [Google Scholar]
- Mayer, A. Luxembourg in the Early Days of the EEC: Null Player or Not? Games 2018, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Maaser, N.; Paetzel, F.; Traub, S. Power illusion in coalitional bargaining: An experimental analysis. Games Econ. Behav. 2019, 117, 433–450. [Google Scholar] [CrossRef] [Green Version]
- Fréchette, G.; Kagel, J.H.; Morelli, M. Nominal bargaining power, selection protocol, and discounting in legislative bargaining. J. Public Econ. 2005, 89, 1497–1517. [Google Scholar] [CrossRef]
- Drouvelis, M.; Montero, M.; Sefton, M. Gaining power through enlargement: Strategic foundations and experimental evidence. Games Econ. Behav. 2010, 69, 274–292. [Google Scholar] [CrossRef] [Green Version]
- Montero, M.; Sefton, M.; Zhang, P. Enlargement and the balance of power: An experimental study. Soc. Choice Welf. 2008, 30, 69–87. [Google Scholar] [CrossRef]
- Guerci, E.; Hanaki, N.; Watanabe, N.; Esposito, G.; Lu, X. A methodological note on a weighted voting experiment. Soc. Choice Welf. 2014, 43, 827–850. [Google Scholar] [CrossRef] [Green Version]
- Guerci, E.; Hanaki, N.; Watanabe, N. Meaningful learning in weighted voting games: An experiment. Theory Decis. 2017, 83, 131–153. [Google Scholar] [CrossRef] [Green Version]
- Säve-Söderbergh, J. Gender gaps in salary negotiations: Salary requests and starting salaries in the field. J. Econ. Behav. Organ. 2019, 161, 33–51. [Google Scholar] [CrossRef]
- Small, D.A.; Gelfand, M.; Babcock, L.; Gettman, H. Who goes to the bargaining table? The influence of gender and framing on the initiation of negotiation. J. Personal. Soc. Psychol. 2007, 93, 600–613. [Google Scholar] [CrossRef] [PubMed]
- Leibbrandt, A.; List, J.A. Do women avoid salary negotiations? Evidence from a large-scale natural field experiment. Manag. Sci. 2015, 61, 2016–2024. [Google Scholar] [CrossRef] [Green Version]
- Azmat, G.; Petrongolo, B. Gender and the labor market: What have we learned from field and lab experiments? Labour Econ. 2014, 30, 32–40. [Google Scholar] [CrossRef] [Green Version]
- Blau, F.D.; Kahn, L.M. The gender wage gap: Extent, trends, and explanations. J. Econ. Lit. 2017, 55, 789–865. [Google Scholar] [CrossRef] [Green Version]
- Eckel, C.C.; Grossman, P.J. Chivalry and solidarity in ultimatum games. Econ. Inq. 2001, 39, 171–188. [Google Scholar] [CrossRef]
- Solnick, S.J. Gender differences in the ultimatum game. Econ. Inq. 2001, 39, 189–200. [Google Scholar] [CrossRef]
- Dittrich, M.; Knabe, A.; Leipold, K. Gender differences in experimental wage negotiations. Econ. Inq. 2014, 52, 862–873. [Google Scholar] [CrossRef]
- Hernandez-Arenaz, I.; Iriberri, N. Gender Differences in Alternating-Offer Bargaining: An Experimental Study; CEPR Discussion Papers 12561; Centre for Economic Policy Research: London, UK, 2019. [Google Scholar]
- Baranski, A.; Geraldes, D.; Kovaliukaite, A.; Tremewan, J. An Experiment on Gender Representation in Majoritarian Bargaining; U.S.E. Working Paper Series No. 21-02; Utrecht University: Utrecht, The Netherlands, 2021. [Google Scholar]
- Niederle, M.; Vesterlund, L. Do women shy away from competition? Do men compete too much? Q. J. Econ. 2007, 122, 1067–1101. [Google Scholar] [CrossRef]
- Tremewan, J.; Vanberg, C. The dynamics of coalition formation—A multilateral bargaining experiment with free timing of moves. J. Econ. Behav. Organ. 2016, 130, 33–46. [Google Scholar] [CrossRef] [Green Version]
- Bengtsson, C.; Persson, M.; Willenhag, P. Gender and overconfidence. Econ. Lett. 2005, 86, 199–203. [Google Scholar] [CrossRef] [Green Version]
- Hardies, K.; Breesch, D.; Branson, J. Gender differences in overconfidence and risk taking: Do self-selection and socialization matter? Econ. Lett. 2013, 118, 442–444. [Google Scholar] [CrossRef]
- Thaler, M. Gender differences in motivated reasoning. J. Econ. Behav. Organ. 2021, 191, 501–518. [Google Scholar] [CrossRef]
- Andreoni, J.; Vesterlund, L. Which is the fair sex? Gender differences in altruism. Q. J. Econ. 2001, 116, 293–312. [Google Scholar] [CrossRef] [Green Version]
- Sharma, S. Gender and distributional preferences: Experimental evidence from India. J. Econ. Psychol. 2015, 50, 113–123. [Google Scholar] [CrossRef] [Green Version]
- Cubitt, R.P.; Starmer, C.; Sugden, R. On the Validity of the Random Lottery Incentive System. Exp. Econ. 1998, 1, 115–131. [Google Scholar] [CrossRef]
- Schubert, R.; Brown, M.; Gysler, M.; Brachinger, H.W. Financial Decision Making: Are Women Really More Risk Averse? Am. Econ. Rev. 1999, 89, 381–385. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).