Abstract
We study a model where agents face a continuum of two-player games and categorize them into a finite number of situations to make sense of their complex environment. Agents need not share the same categorization. Each agent can cooperate or defect, conditional on the perceived category. The games are fully ordered by the strength of the temptation to defect and break joint cooperation. In equilibrium agents share the same categorization, but achieve less cooperation than if they could perfectly discriminate games. All the equilibria are evolutionarily stable, but stochastic stability selects against cooperation. We model agents’ learning when they imitate successful players over similar games, but lack any information about the opponents’ categorizations. We show that imitation conditional on reaching an intermediate aspiration level leads to a shared categorization that achieves higher cooperation than under perfect discrimination.
1. Introduction
The standard approach to rational decisions presumes that the agent knows the states of the world, her available actions, and the outcomes over which he has a preference ordering. This knowledge is very difficult to attain, because an agent preliminarily needs to make sense of the environment in order to distill states, actions, and outcomes. The agent’s cognitive processes mediate between the sensory inputs and the formulation of a decision problem: according to Denzau and North ([1], p. 4), “the mental models are the internal representations that individual cognitive systems create to interpret the environment.”
The interplay between agents’ mental models and the formulation of an interactive decision problem is a quagmire, because agents’ perceptions may differ and possibly collide. Hoff and Stiglitz ([2], p. 26) argue that the “social context creates the set of mental models upon which individuals can draw, and affects the circumstances that prime alternative mental models.” This paper studies a simple model of how agents’ cognition affects their strategic interaction across games, in regard to the emergence of cooperation in social dilemmas.
There is a huge literature on this problem, especially in reference to two archetypal examples: the prisoners’ dilemma, from Hobbes [3] to Nowak and Highfield [4]; and the stag hunt game, from Rousseau [5] to Skyrms [6]. The overarching question concerns the origin of conventions that support cooperation where, as argued by Binmore ([7], p. 17), “[a] convention shared by a whole community […] is a cultural artifact that might have been different without contravening any principle of individual rationality.” We show that a cooperative convention may have a cognitive foundation.
Our approach keeps the cognition of the environment distinct from the choice of actions. The environment is a space of symmetric games that differ only over the value of a specific payoff in the interval . This space of games contains variants of the stag hunt and of the prisoners’ dilemma. In stag hunt games, both joint cooperation and joint defection are equilibria; in prisoners’ dilemmas, only joint defection is an equilibrium. The game space is fully ordered by the value of the temptation to destroy joint cooperation with a unilateral defection.
The perception of the agents is not fine enough to discriminate all the games. We assume that “[c]ategorization provides the gateway between perception and cognition” ([8], p. 520): the agent reduces the complexity of her environment to a finitenumber of categories.1 Each category defines a strategic situation: the agent is confronted with a continuum of games, but recognizes only a finite number of situations. Conditional on the perceived situation, the agent has correct expectations and maximizes her expected payoff [10]. Given his coarse perception, the agent chooses an action for each situation.
Since there are only two available actions, we restrict players to binary categorizations: each agent recognizes up to two situations. Her coarse perception directly affects the agent’s choice of an action, valid over many distinct games (perceived as one situation). For instance, if the situation perceived by an agent bundles only prisoners’ dilemmas, her only rationalizable action is defection; but, when the situation packs together stag hunts and prisoners’ dilemmas, both cooperation and defection may be rationalizable. In this latter case, an external observer may detect a behavioral spillover because the agent plays the same choice in some stag hunt games and in some prisoners’ dilemmas. The study of behavioral spillovers is outside the scope of this paper, but we remark that a failure to perceive differences across games may be a reason2 behind some spillovers reported in the literature; see Peysakhovich and Rand [12] for a related argument.
We allow agents to have different categorizations. However, because agents have no full control on their cognitive processes, we do not assume that they can choose a priori which games are bundled in the same category. This is an important assumption that differentiates our work from Heller and Winter [13], who explicitly consider the joint choice of categorizations and actions across a space of games. Mengel [14] deals with the related question of how agents learn across games when they jointly experiment over categorizations and actions, using reinforcement learning. Her work is the closest to ours in the literature, but she consider a game space that is finite and unstructured. Instead, our game space is a fully ordered continuum and we force agents’ mental models to be consistent with the ordinal structure of the underlying environment.
We inquire about three main questions. The first one concerns the mutual effects of a binary categorization and of a strategic choice between cooperation and defection. The main result is that in equilibrium agents share the same categorization and the same way to play games. In our limited setup, such common understanding—a convention—is not an assumption but a consequence of equilibration. We also find that the range of equilibrium payoffs under perfect discrimination is remarkably smaller than under binary categorizations: a coarse perception of the environment may support more cooperation.
The second question concerns which categorizations emerge when agents grope for a better understanding of their environment. Because agents lack control of their cognitive processes, we consider an evolutionary dynamics where random mutations over binary categorizations compete for success. We show that the range of evolutionarily stable strategies coincides with the range of equilibrium strategies under perfect discrimination: evolution of a coarse perception by random mutations strictly refines the set of equilibria and makes cooperation harder to attain. Moreover, a modicum of persistent mutation leads with high probability to a state where stag hunts and prisoners’ dilemmas are conflated in the same category, and agents defect most of the time. When they grope in the dark, agents are very likely to end up in distrust and play a max-min strategy of persistent defection.
The third question occupies most of the paper and concerns agents’ social learning of categories based on the imitation of successful players engaged over similar games. An agent who coarsely perceives situations cannot discriminate ex ante across games in the same category. However, after observing the play of a different pair of agents, he may compare their actions and their payoffs and reconsider how a similar game in the same category should be played. These inferences drive his search for a better categorization.
We compare three models of social imitation, where a failure to attain his aspiration level prompts an agent to initiate a search for exemplars to mimic. Our main result is that intermediate aspiration levels support the emergence of shared categorizations where agents cooperate more than in any evolutionarily stable equilibrium; see Macy and Flache [15] for a related result under reinforcement learning. Categorization conceals different games under one situation: under imitation with a reasonable aspiration level, such coarse perception is blissful.
The organization of the paper is the following. Section 2 describes the model and discusses both how the game space is categorized and which strategic choices are available to the agents. Section 3 characterizes the equilibria in pure strategies for the two cases where agents have or have not full control over their categorizations. Section 4 studies the evolutionary and stochastic stability of the equilibrium strategies, showing how these relate to the underlying categorization; in particular, we prove that stochastic stability selects against cooperation. Section 5 provides a computational model of social imitation, where agents play randomly chosen games and update their categorizations by imitating successful behavior from other players over similar games. An agent initiates an attempt to imitate when his payoff falls below some aspiration level: we consider three rules that set this level differently. Our main result is that for intermediate aspiration levels cooperation extends to a sizable subset of prisoners’ dilemmas. Section 6 analyzes the dynamics and explains how social imitation may escape the straitjacket of defection in prisoners’ dilemmas. Section 7 tests the resilience of the imitation dynamics and shows that this is largely amenable to its ability to blend the incumbent and the entrant categorizations. Section 8 concludes.
2. The Model
2.1. The Game Space
We consider a class of symmetric games that encompasses both the prisoners’ dilemma and the stag hunt. The strategic form for each game has two players (named 1 and 2), who choose between C (for cooperation) and D (for defection). If cooperates, he bears a cost and the other player receives a benefit . Defection incurs no cost but, when it is unilateral, the benefit b received by the defector is reduced by a factor x in : this downsizing may be attributed to multiple sources, such as punishment, guilt feeling, etc. The resulting bimatrix is the following.
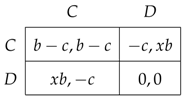
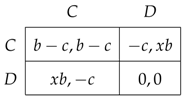
Given , the value of x decides the nature of the game: when , we have a stag hunt game; if , we have a prisoners’ dilemma. Increasing x makes defection more attractive and shifts the strategic tension from coordination to cooperation. Our class of games focuses on the dimension x, yielding a simple and compact representation. In particular, we conveniently set and in the bimatrix (1) and let x vary in . See Rankin et al. [16] for another one-dimensional parameterization, limited to stag hunt games.
A typical element in the space of games is shown below. The action D is always risk-dominant and the profile is always a strict Nash equilibrium.
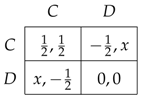

The payoff x received by a unilateral defector is called the temptation. This temptation payoff x parameterizes the games in : as it increases from 0 to 1, playing C becomes a less attractive reply than D to the opponent’s choice of C. If , the temptation is high: a player is lured away from C by the strictly dominant strategy D and we have a prisoners’ dilemma. If , the temptation is low and the profile is payoff-dominant: we have a stag hunt with the two strict Nash equilibria and .
Because the games in differ only in the value of the temptation x, we identify each game in with the point x in . Hence, the game space is completely ordered: if , then the game has a higher temptation than the game . We assume that the temptation x is a random variable X with uniform distribution on .
2.2. Discriminating Games
We are interested in how the ability of players to perceive and discriminate games affects their choices. In general, let K be a partition of and let k denote a cell (or situation) of K. Our model identifies with and we consider partitions over the interval . Each cell is a similarity class: two games in the same cell are not perceived as distinct before being played [17]. We say that an agent perceives the same situation when he is facing two games from the same cell.
Given a partition K, a (pure) strategy is a mapping from the situations of K to the set of actions . The payoffs attributed to a cell k match expected values across all games in k; that is, conditional on his ability to discriminate, an agent has correct expectations. Agents choose strategies that maximize expected utility. After a game is played, the agents receive their actual payoffs. In short, ex ante the games are perceived and categorized as situations; ex post, the payoffs from the actual game played are realized and received.
Under perfect discrimination, a player perceives each game in as distinct. If , he perceives a prisoners’ dilemma where D is the dominant strategy. Otherwise, he perceives a stag hunt because C is payoff-dominant and D is both the risk-dominant and the max-min strategy.3 Thus, his best reply is to play D if and C or D otherwise. If both players perfectly discriminate, the equilibria in pure strategies are for and one of the two profiles or for . The expected equilibrium payoffs range from 0 (if they defect for any x) to (if they defect only for ).
Under no discrimination, a player cannot distinguish two games in : all games are perceived as the same situation. Because the expected value for X is , the payoff matrix perceived by the agent for this situation is
The strategy D weakly dominates C. Under no discrimination, playing is the only equilibrium in weakly dominant strategies, with an expected payoff of 0.
| C | D | |
| C | ||
| D |
This paper studies a population of agents that simultaneously learn to partially discriminate games and to play equilibrium strategies adapted to their discriminating ability. The key cognitive process is categorization: an agent partitions the space in a finite number of cells. The agent perceives different situations, but cannot discriminate games within a situation. Because the game space is completely ordered (by the temptation value x), the cells of a partition are intervals and we can associate any (finite) partition with a set of thresholds that define contiguous cells.4
In particular, any threshold t in defines a binary (interval) partition with two situations named ℓ (low) and h (high). When , the agent perceives a situation with low temptation that we denote ℓ; similarly, if , he perceives a situation with high temptation denoted h. (What happens at the null event is immaterial.) Given his threshold t, the agent has correct expectations: he has an expected value for X that is when the temptation is low and when it is high. Depending on t and whether he perceives a situation with low or high temptation, the agent faces one of the two payoff matrices in Table 1.

Table 1.
The two situations under a binary categorization with threshold t.
2.3. Strategies and Binary Categorizations
We focus on learning across games when agents use binary (interval) categorizations. Any binary categorization over is identified by a single threshold t in . We allow for the special case of no discrimination by adding the convention that all the games are bundled in the same category when , and in the same category when , respectively. Therefore, we assume that the threshold t is in .
Given the binary categorization defined by a threshold t in , a player perceives two situations (ℓ and h) and has two possible actions (C and D). Hence, she has only four possible strategies: (always play C); (always play D); (play C when ℓ and D when h); (play D when ℓ and C when h). If or , the player cannot discriminate at all and plays always the same action: we associate the strategy with and with . We emphasize that the agent cannot perceive x and does not consciously use the threshold t to discriminate between situations with a low or a high temptation. The threshold is only a modeling device to compactly describe the categories used by an agent. We write to denote the case where the threshold is t and the agent plays action A when and action B when . For instance, the strategy cooperates when and defects when .
Table 1 shows that, for any t in , a situation ℓ is perceived as a stag hunt game and a situation h as a prisoners’ dilemma. Clearly, any agent with a binary categorization prefers to plays D whenever she perceives the situation h. The strategic uncertainty concerns how she should play in situation ℓ. Thus, given any t in , the only two rationalizable strategies are or . In the special cases when or and the agent cannot discriminate situations, our convention has for “always D” and for “always C”. Both “always D” and “always C” are rationalizable strategies; however, because “always D” weakly dominates “always C”, this latter is not evolutionary stable. Without loss of generality, we restrict the search for optimal strategies to the class for some t in .
The rest of the paper focuses on the dynamics by which agents evolve or learn their understanding of situations (and hence their strategies). Given the mapping between binary categorizations and thresholds, this can be done by studying the evolution of agents’ thresholds in the set .
3. Equilibria over Thresholds
In our model, the viable strategies are written as for some t in . Heller and Winter [13] suppose that an agent can choose how he partitions the space of games, and thus has full control on his own threshold t. In their setup, our first result is that all the equilibria in pure strategies require that agents share the same categorization for some threshold t in . Intuitively, if agents start off with different categorizations, there are games where they miscoordinate and play , making one of them a “sucker” who scores and regrets how his categorization led him to play.
Proposition 1.
Assume binary categorizations with t in . If agents have full control on their thresholds, the only equilibria in pure strategies are symmetric: they share a common threshold t in and play .
Proof.
Suppose . If 1 plays and 2 plays , then the pair plays with probability , plays with probability and plays with probability . The expected utility is for Player 1 and for Player 2. In particular, if , each player scores . The payoff submatrix of Player 1 for two arbitrary strategies is
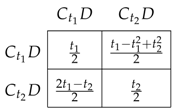 Clearly, if 2 is using , then playing gives 1 a strictly lower expected payoff than ; hence, it is never optimal for an agent to have a strictly higher threshold than his opponent. On the other hand, suppose that 2 uses : if , then 1 maximizes his expected payoff when ; if , then 1 maximizes his expected payoff at . Combining these two conditions yields the result. □
Clearly, if 2 is using , then playing gives 1 a strictly lower expected payoff than ; hence, it is never optimal for an agent to have a strictly higher threshold than his opponent. On the other hand, suppose that 2 uses : if , then 1 maximizes his expected payoff when ; if , then 1 maximizes his expected payoff at . Combining these two conditions yields the result. □

Proposition 1 implies that the range of equilibrium payoffs is when agents have full control on their categorizations, as in Heller and Winter [13]. Our model, instead, insists that agents lack full control and this expands the set of equilibria. If two agents share the same threshold t in , then their strategies are perfectly coordinated: they play when and when . Because they never miscoordinate (except perhaps at the null event ), they are at an equilibrium for any t in . In particular, for , each agent receives an expected payoff but the “non-equilibrium” threshold t is not upset because agents are unaware that they could profitably deviate to another categorization with a lower threshold.
When agents have no full control on their thresholds, any shared categorization t in may survive and the range of equilibrium payoffs expands to . When agents happen to share a threshold , they achieve a higher payoff: here, ignorance is bliss. However, if agents start with different thresholds, it is not clear how they come to have a shared categorization and which ones might emerge. The rest of this paper explores the social dynamics of agents who have no full control on their perception, but use concurrent play from other players to draw inferences and revise their categorizations.
4. Evolutionary and Stochastic Stability
Even if agents have no full control on their categorizations, they may grope for a better understanding of their environment. We model an agent who changes his binary categorization to have a smaller (resp., greater) cell ℓ by a shift to a lower (higher) threshold. If t decreases, the agent is more likely to perceive a prisoners’ dilemma situation, and thus plays D more often; otherwise, if t increases, he is more likely to perceive a stag hunt situation where C is also rationalizable. Therefore, agents who increase their thresholds may learn to cooperate more often. In particular, when , some prisoners’ dilemma games () are bundled under a stag hunt situation and cooperation may spill over to them.
This section draws an analogy between the biological evolution of genes and the cognitive evolution of categorizations; see Gracia-Lázaro et al. [18] for a related approach to cognitive hierarchies. We imagine that, occasionally, an agent experiments with a different categorization and becomes a “mutant”. If her new threshold is sufficiently successful in the current environment, it replicates and possibly displaces the predominant threshold. These random mutations model a search process over categorizations by trial and error, because agents cannot pursue purposeful selections on how they perceive the environment.
The natural first step is to consider the evolutionary stability of agents’ threshold-based strategies. Abusing notation, we refer to a strategy by the value t in of the threshold. Please note that in our model the interaction among agents may be viewed both as a two-player symmetric game and as a population game.
A strategy t is evolutionarily stable (ES) if, for every strategy , there is such that
for any . This definition tests the evolutionary stability of the strategy against one mutant at a time; in particular, need not be uniform across all . The first result of this section is that all the Nash equilibria in Proposition 1 are evolutionarily stable.
Proposition 2.
Assume binary categorizations with t in . The only evolutionarily stable strategies are with t in .
Proof.
Consider any strategy in and a mutant . The payoff matrix over and is the same as in (3). Then is a strict Nash equilibrium and thus it is evolutionary stable against any mutation to a higher threshold. Similarly, consider a strategy in and a mutant . Using again the payoff matrix in (3), we see that is a strict Nash equilibrium and thus it is evolutionary stable against any mutation to a lower threshold. However, if , then this strategy is no longer a best reply against a mutant . Combining all the conditions above yields the result. □
Our model is based on a unidimensional continuous strategy space, because of the mapping from to t in . This allows for stronger notions of stability that control for success over a neighborhood of mutants; see f.i. Cressman and Apaloo [19]. However, none of the standard notions of stability selects a unique strategy: once we include deviations to other strategies in the interval between t and , the fine details of the process may help or hinder the evolutionary success of a mutant . Nonetheless, we appeal to long-run stochastic stability (SS) and argue that with is very likely to prevail most of the time among all ES strategies.
Suppose that agents undergo a process of stochastic strategy revision over a set S of strategies (or just t for simplicity), based on a Darwinian selection dynamics and independent random mutations [20]. We assume that S has a finite nonempty intersection with the set of ES strategies and denote by the minimum threshold associated with a strategy in S. Our main result is that the strategy is the only long run stochastically stable strategy in S. In particular, if , defection everywhere will be persistently and recurrently played as the rate of mutation approaches zero.
Proposition 3.
Assume binary categorizations with t in . If is the minimum threshold in S, then the only stochastically stable strategy is .
Proof.
Consider the game where two players can choose any strategy t in S. Its strategic form associates with any two strategies the payoffs given in the submatrix (3). For any ES strategy , the strategic profile is a symmetric equilibrium with payoff . We say that the symmetric equilibrium is -dominant if is a strict best reply against any mixed strategy placing at least probability on [21]. Then the proof follows from Corollary 1 in Ellison ([22], p. 27), provided we show that is -dominant. In fact, for any t in S,
or, equivalently, if . This holds if and only if , establishing the claim. □
5. Social Learning for Categorizers
Section 4 shows that the random mutations underlying evolutionary stability yield low levels of cooperation. A strategy is evolutionary stable only if . In any finite set that includes at least one ES strategy, the only stochastically stable strategy is at the lowest threshold : cooperation is minimal. If is available and the search for a shared categorization is driven by random mutations over a finite support, after a sufficiently long wait agents would be led to always defect, effectively unlearning to discriminate stag hunt situations from prisoners’ dilemmas.
We argue that the dynamic process underlying evolutionary stability or its variants may not be a realistic model of the search for useful categorizations. Roughly speaking, the evolutionary dynamics tests whether random mutants perform better than the current population and, if so, favor their reproduction. This is plausible when the agents of change do not know which mutations are more promising and thus their search is undirected.
On the other hand, even if an agent has no full control on his cognitive processes, he is aware that his own categories affect his choice and hence his performance. Because it takes considerable effort to change how one perceives the world, an agent is unlikely to experiment (and “mutate”) randomly. We posit that the agent tries to amass sufficient cause for attempting a change, and that these changes tend to occur in a direction that he hopes to be favorable. In short, we expect that changes are not purposeless, and abide by some form of bounded rationality.
We use two well-known mechanisms to model such bounded rationality. First, an agent initiates an attempt to change his categorization only if his performance in a situation is sufficiently low. Second, an agent tries to imitate successful categorizations. These two mechanisms are usually known as aspiration levels and learning by imitation. When dealing with categorizations, their application requires a modicum of care.
Consider the aspiration level. An agent compares her payoff in (say) situation ℓ with others’ payoffs in situation ℓ. Because an agent perceives different games as the same situation, she is actually comparing her payoff in a game in ℓ against others’ payoffs in different games in ℓ. Moreover, if two agents have different categorizations, then and they make their comparisons based on different sets of games.
Concerning imitation, agents do not know others’ categorization thresholds and hence cannot imitate how others categorize the world. However, they can use observed play to make inferences about how others view the world and approach what appears to be a more successful viewpoint. Recall our assumption that each agent plays a strategy for some t in . Consider an agent with threshold who faces a game with , categorizes it as ℓ and plays C. Unbeknown to him, his opponent has a threshold and plays D. The first player receives a payoff while the second player scores ; see the payoff matrix in (2). After observing payoffs and actions, the first player learns that . He can infer that the second player has a smaller category ℓ than his () but does not know what is and cannot imitate it; however, because he observes x and , he may review his own categories so as to shift x from ℓ to h (and play D in the future). That is, he can “imitate” the second player by updating his t towards x.
In the following, we present a few variants for a model of social learning where agents use aspiration levels to initiate change and learn by imitation. We show that, even under the limitations imposed by their categorical perceptions, agents learn to cooperate much more than a mere argument of evolutionary stability suggests. Within our modest scope, this is consistent with the general argument that cultural evolution may achieve different outcomes than biological evolution; see f.i. Boyd and Richerson [23].
At a high level, the main features of our model for learning categorizations by imitation are the following. Agents play only strategies for some threshold t in . This is just a modeling device: an agent may not be consciously using a threshold t to classify games – it suffices that he perceives the two (interval) categories ℓ and h and that he plays C when ℓ and D when h. Agents do not know and cannot observe others’ thresholds. Also, we speak for simplicity of agents who learn their threshold value t instead of agents who learn binary categorizations.
There is a population of n agents, who are randomly matched in each period. Each pair may play a different game . Any agent categorizes the game according to his threshold and plays accordingly. Agents do not review their categorization after each interaction. Once in a while, an agent who realizes a performance below his aspiration level attempts to review his categorization. He compares his performance against the performance of others who played games that he ascribes to the same situation. Drawing on his observations, he infers the direction in which he should move his threshold and adjust it accordingly.
5.1. Learning by Imitation
This section describes the model and some variants in detail, using a pseudo-code notation. We use two classes ( for agents and for games) as well as a few functions. We eschew a formal definition for the simple functions random_pairs, random_member and random_number because their meaning is obvious.5
There is a finite population of n agents. The state of an agent a in is described by four features:
- a.threshold: the current threshold that separates a’s categories (ℓ and h);
- a.action: the last action (C or D) played by a;
- a.xValue: the value x for the last game played by a;
- a.payoff: the last payoff received by a after playing .
An agent gathers information about other agents by observing their actions and their payoffs. When a player considers an agent a who has played a game , she observes what a chose (a.action), what game a played (a.xValue), and which payoff a received (a.payoff). The player ignores the threshold value of agent a (a.threshold), because a’s mental model cannot be observed. In short, a player can use three of the four features that describe the state of an agent in order to imitate the fourth one.
Figure 1 provides the pseudo-code describing the structure of the Threshold Imitation (TI) algorithm that implements the simulation model. The input parameters are in lines 1–4, the initialization is in line 5, the agents’ interaction is in lines 7–18, and the learning is in lines 19–22.

Figure 1.
The TI algorithm (Threshold Imitation).
The input parameters are self-explanatory: we provide more details in the next subsection. Each agent is initialized with her own threshold (line 5). Agents are matched and play games at each simulation round, until a break condition B is reached (line 6). At each round of interaction, agents’ features are updated (lines 7–18) as follows:
- line 7: the agents in are randomly matched in pairs;
- lines 8–10: each pair of agents plays a game from where x is an independent uniform draw from ;
- lines 13–16: for each agent a,
- the agent’s game a.xValue is set equal to x (line 12);
- the agent’s played action action is set by the strategy to be C if xValuethreshold and D otherwise (lines 13–16);
- lines 17–18: the two paired agents play their chosen action in the game and the payoff a.payoff is computed for each of them.
No agent updates her threshold value during these rounds. Learning by imitation takes place separately, at the end of a round of interaction (lines 19–22). The learning part works as follows. The choice rule selects an agent, labeled as the imitator agent, who attempts to change his categorization (line 19). The choice rule captures how bounded rationality affects the willingness of an agent to undertake this laborious effort. We tested a few different choice rules that are presented in the next section.
The imitator considers only successful agents: f.i., someone who scored better in the same situation as is. The agent who is targeted for imitation is labeled as the exemplar agent (line 20). An imitator applies three criteria to select his exemplar: (1) she must have scored better than ; (2) she must have played a different action from ; (3) she must have played in a game that categorizes as the same situation that himself played. These three criteria are implemented respectively by the function random_member_with_higher_payoff described in Appendix A.1, by the test action≠.action, and by the function is_in_same_situation given in Appendix A.2.
For instance, if a target agent a plays the same action as in the same situation (according to ) but gets a higher payoff, then screens him out of consideration because he (correctly) attributes a’s higher payoff to noise: she must have either faced a different opponent’s action or another game (categorized by under the same situation).
The three criteria require only information about that is ex post observable by , namely payoff, xValue and action. When all three criteria are met, the imitator concludes that the higher payoff received by the exemplar is due to playing a different action than when facing the same situation. This prompts to initiate an effort to imitate .
The imitator , however, cannot imitate ’s categorization, because .threshold is not observable. He must be subtler and use the available information to move his categorization closer to ’s. This is possible because the game space is fully ordered. There are two cases:
- suppose faced situation ℓ and thus played C. Because played the different action D, he knows that must have played a game that perceives as situation h. Thus infers .xValue.threshold. On the other hand, because played a game that perceives as situation ℓ, knows that .xValue.threshold. Combining the two inequalities gives .threshold.xValue.threshold. Therefore, knows that decreasing her threshold from .threshold to .xValue moves her categorization closer to ’s.
- conversely, suppose faced situation h and played D. Because played C, he knows that faced a game that perceives as situation ℓ. Then infers .xValue.threshold. In addition, because played a game that perceives as situation h, knows that .xValue.threshold. This yields .threshold.xValue.threshold. Hence, knows that increasing her threshold to .xValue makes her categorization closer to ’s.
In either case, moves her threshold closer to ’s by shifting the boundary between her two new categories at the observed game .xValue (line 22). Pivoting on the observed game acknowledges the recognition problem: the agent needs to experience a game before using it to categorize other games [24].
This imitation dynamics also implies that the imitator may only decrease his threshold after playing in situation ℓ, or increase it after playing in situation h. This property plays an important role in the analysis of the dynamics given in Section 6. Next, we present the output for some variants of the TI algorithm.
5.2. Simulations
The first three of the four input parameters for the TI algorithm are set as follows. (1) The size of the population of agents is . Testing higher values for n produced no notable impact on the results of the simulation. (2) The threshold initialization rule follows an equidspaced allocation, where agent i’s threshold value is set to , for . Using a random allocation, where each agent is initialized with a random threshold value, yields similar results. We adopt the first rule to avoid injecting additional noise in the simulations. (3) The break condition B terminates a simulation when the distance between the maximum and the minimum value for the current agents’ thresholds drops strictly below . All our experiments eventually reached this condition, so the population came to share (approximately) the same threshold.
The fourth and last input parameter is the choice rule for the imitator , stating under what conditions an agent attempts a revision of his categorization. Our experiments show that the choice rule has a clear impact on the threshold value that the population eventually learns to use. Therefore, we present three different lines of experiments that differ solely in the choice rule . We performed 100 simulation runs in each experiment and all of them reached the break condition B: agents always learned to (approximately) share the same categorization, as discussed in Section 3.
5.2.1. Experiment I: Only Suckers Imitate
A “sucker” is an agent who plays C against an opponent who plays D: the “sucker” receives a payoff of , which is by far the worst possible outcome. The first line of experiments assumes that only “suckers” attempt to update their thresholds. Equivalently, one may assume that players initiate change only if they receive a strictly negative payoff. (Except for the sucker’s payoff, all the games in have positive payoffs.)
Accordingly, the choice rule (called “suckers imitate”) is
- , where .payoff
In each run, the population of agents always approximates and thus learns to defect over the whole game space . This dismal outcome matches the stochastically stable strategy discussed in Section 4.
5.2.2. Experiment II: All Imitate
The second line of experiments lets everyone attempt to update his threshold. The choice rule (called “ALL imitate”) is
We recorded the value for the (approximate) shared threshold learned by the population. The datapoints for from 100 simulations are reported using the boxplot labeled [II (ALL)] in Figure 2. (See keys on the right.)
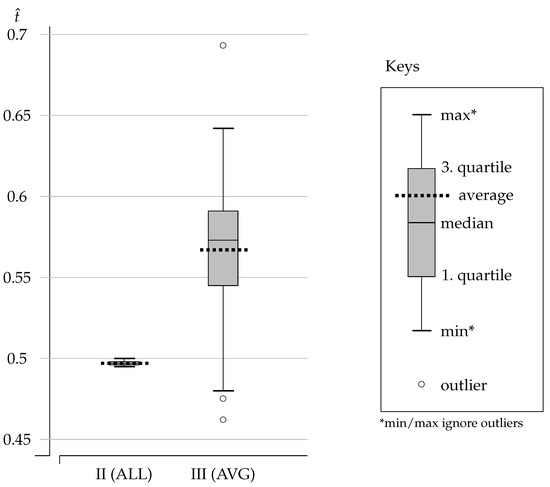
Figure 2.
Boxplots for the shared threshold from Experiments II and III.
The results of Experiment II show that the population of agents converges to an average threshold value of . Half of the datapoints are between (first quartile) and (third quartile), with a median at . The dispersion is minute and we conclude that agents come to a shared categorization where the common threshold is very close to the payoff-best ES value (). Agents categorize games so as to play C over almost all stag hunts ( with ) and to play D over all prisoners’ dilemmas ( with ). There is no cooperation spillover from the stag hunts to the prisoners’ dilemmas.
5.2.3. Experiment III: Agents Imitate When below Average
“Suckers imitate” restrict imitation to a very specific case. “ALL imitate” opens it to everybody. The third line of experiments postulates an intermediate choice rule. We assume that an agent considers imitation only if he has scored below the average payoff achieved by players who (from the agent’s viewpoint) faced the same situation as he did. Accordingly, the choice function (called “AVG imitate”) is
- , where
The function below_average_same_situation is described in Appendix A.3.
We recorded the value for the (approximate) shared threshold learned by the population. The datapoints for from 100 simulations are reported using the boxplot labeled [III (AVG)] in Figure 2.
The results of Experiment III show that the population of agents converges to an average threshold value of . Half of the datapoints are between (first quartile) and (third quartile), with a median at . The dispersion is much higher than in Experiment II, but the average threshold achieved by the population is clearly above the payoff-best ES value (). In fact, more than of the simulation runs produced a value above . Experiment III exhibits frequent cooperation spillovers from the stag hunts to the prisoners’ dilemmas.
A visual summary of the main results for the three experiments is in Figure 3.
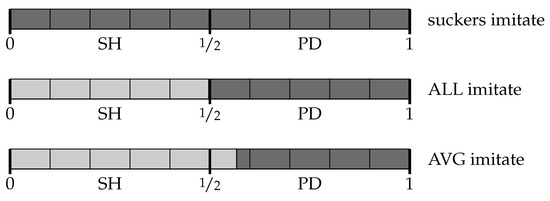
Figure 3.
Categorization thresholds that determine where to cooperate (light gray) and defect (dark gray) over a space of stag hunt games (SH, ) and prisoners’ dilemmas (PD, ).
Under “suckers imitate”, agents learn the threshold : they defect over the whole space and achieve the lowest equilibrium payoff of 0. Under “ALL imitate”, agents learn a threshold very close to : approximately, they cooperate over the stag hunts and defect over the prisoners’ dilemma, achieving close to the highest equilibrium payoff of . Finally, under “AVG imitate” agents usually learn a threshold higher than : on average, they cooperate over the stag hunts as well as over about 13% of the prisoners’ dilemmas, achieving a payoff of about . The third (intermediate) imitation dynamics achieves an outcome that is socially superior to either of the other two extreme cases. This outcome is supported by a strategy that is not evolutionarily stable: the random emergence of those mutants that could displace it is kept under control by the purposefulness of the rules that initiate imitation. The following section explains this mechanism in detail.
6. Analysis of the Results
The choice rule used to select imitators is a reduced form for the aspiration level that prompts agents to reconsider their categorization. Under “suckers imitate”, only suckers attempt to review their mental model. Under “ALL imitate”, everybody tries. Under “AVG imitate”, only a subset of lower-performing agents initiate imitation. Clearly, the choice rule remarkably affects the shared categorization learned by the population. This section takes a closer look and explains how the choice rule impacts on the dynamics of the process.
After playing a game, an agent obtains one of four possible outcomes. Depending on the outcome realized, we label him as follows:
- sucker (S-agent): unilateral cooperation—agent played C, the opponent chose D;
- rewarded (R-agent): mutual cooperation—both played C;
- punished (P-agent): mutual defection—both played D;
- tempted (T-agent): unilateral defection—agent played D, the opponent chose C.
Consider separately what happens when only one of these four types may attempt imitation and change his threshold. Recall that simulations are initialized assuming equispaced thresholds to reduce exogenous noise.
- Experiment I concerns the case where only S-agents (suckers) may imitate: the entire population learns to share the threshold . This follows from two simple reasons. First, an S-agent played C when facing situation ℓ and, as discussed in Section 5.1, imitation may only decrease the threshold. Second, an S-agent received the lowest possible payoffs so any agent who is not a sucker is a potential exemplar. In sum, under “suckers imitate”, a player who experience the pain of being a sucker expands her category h, increasing the chance to defect later and to make other (more cooperative) agents turn out as suckers themselves.
- Suppose that only R-agents may imitate. Then imitation stops once all agents’ thresholds lie below . The reason is again twofold. First, an R-agent played C when facing situation ℓ: then imitation can only decrease his threshold. Moreover, the realized game must have a temptation value smaller than the imitator’s threshold , so . Second, because an R-agents received the payoff , his only viable exemplars have a payoff above . Any of these exemplars must be a T-agent who scored against an S-agent with a threshold . Once all agents’ thresholds are below , no R-agent finds viable exemplars to imitate and learning stops.
- Assume that only P-agents imitate. Then the population learns to share the highest threshold in the initial population. First, a P-agent played D when facing situation h: then imitation can only increase her threshold. Second, a P-agents received the payoff 0, so R-agents (who score ) are viable exemplars. As threshold values increase, cooperation becomes more likely and thus there are more and more R-agents that P-agents try to imitate.
- Finally, suppose that only T-agents imitate. Then imitation stops once all agents’ thresholds are above . First, a T-agent played D when facing situation h: imitation can only increase his threshold. Second, because a T-agent received a payoff above 0, his only viable exemplars are R-agents who score . (A T-agent never imitates another T-agent because both of them have played the same action.) Once all agents’ thresholds are above , a T-agent defects only when facing a game with and receives a payoff , which is higher than what any R-agent receives. Therefore, a T-agents finds no agents to imitate and learning stops.
Figure 4 summarizes this analysis, showing both the direction in which thresholds are updated and their basins of attraction for the four single-type choice rules.
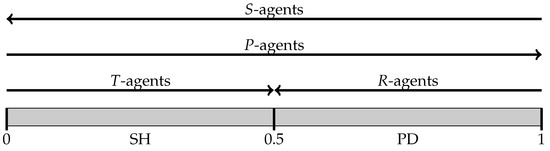
Figure 4.
Updating thresholds by imitation for the four single-type choice rules.
We are ready to consider the dynamics for the two choice rules “ALL imitate” and “AVG imitate”. Figure 5 (left) shows the cumulated number of threshold updates made by each of the four types of agents (R-, S-, T-, P-) for the first 500 update steps of one simulation run for “ALL imitate”. Initially, updates are roughly equidistributed across the four types. Over time, agents’ thresholds get closer and thus they choose similar actions over more games. This makes both joint cooperation () and joint defection ( more frequent and thus R- or P-agents more likely. Updating from the R-agents drives thresholds down towards , whereas updating from the P-agents pushes them up; see Figure 4. These two countervailing forces strike a balance at a threshold around .

Figure 5.
Percentages of the cumulated number of updates steps from R-, S-, T-, and P-agents for “ALL imitate” (left) and “AVG imitate” (right).
Figure 5 (right) provides the analogous plot for “AVG imitate”. The R-agents never imitate because they score and the average payoff of agents in their same situation cannot be higher than . On the other hand, S-agents and P-agents, who score respectively and 0, are very likely to attempt imitation. Simultaneously, as thresholds get closer, P-agents become more frequent than S-agents. The prevalence of P-agents eventually drives updating and pushes thresholds up, often way above .
7. The Stability of Learning by Imitation
7.1. Long-Term Behavior
Proposition 3 shows that low thresholds are the most likely long-run outcome under an evolutionary dynamics with a small rate of mutation. This section tests how “ALL imitate” and “AVG imitate” fare under a persistent and sizable flow of random mutants.
We initialize the TI algorithm with randomly chosen thresholds and let it run until the population settles around a threshold . (We use the break condition B to adjudicate convergence.) Once a shared categorization is found, we replace a portion of the population with an equally sized group of invaders, who are given a random threshold. The rate of replacement is randomly and independently chosen between and . We run the algorithm with the new population until they find another shared threshold ; then we iterate the above and let a new invasion occur.
After 1000 iterations, we record the values of the shared thresholds and count how frequently they fall in one of the ten equispaced intervals , for . The output of these experiments is presented in Figure 6 for both “ALL imitate” (on the left) and “AVG imitate” (on the right).

Figure 6.
Distribution of shared thresholds under persistent invasions for “ALL imitate” (left) and “AVG imitate” (right).
The frequency histogram for “ALL imitate” shows that the population converges to a shared threshold in the interval for about of the cases, and otherwise to a value in . Threshold values slightly short of not only are most likely to emerge, but they recur under random invasions of mutants. This stability is due to the counterbalancing effects from T-agents and R-agents around , adjusted for the stronger impact of R-agents in the final steps as described in the previous section.
The frequency histogram for “AVG imitate” shows that the population converges to a shared threshold that has a roughly bell-shaped distribution around , with of the datapoints above . The long-term behavior under persistent and constant invasion sustains a substantial rate of cooperation: when the shared threshold is , agents cooperate in about of all prisoners’ dilemmas. Experiment III found shared thresholds mostly between and . This discrepancy follows because R-agents never imitate: the predominant imitators are P-agents, who tend to push the threshold towards 1. However, as thresholds increase, defection becomes less likely and P-agents rarer, making room for the imitation by S-agents or T-agents that decreases thresholds.
7.2. Resilience after Invasions
Under “AVG imitate”, the population learns to share a categorization associated with a strategy that is not evolutionarily stable. This section explains what prevents random mutations from taking over and destroying the cooperation achieved under “AVG imitate”.
Generally speaking, most evolutionary dynamics share three features: (1) a population playing an ES strategy repels any invasion by a sufficiently small group of mutants; (2) if both the current and the invading strategy are ES, the latter has to overcome an invasion barrier to displace the current strategy; (3) if the population plays a strategy that is not ES, this is eventually displaced by some ES strategy. Importantly, the thresholds t for the incumbent and for the mutant strategy never change: either t or will prevail, because invasion is an all-or-nothing contest between these two strategies.
On the other hand, imitation makes agents change their thresholds. An incumbent strategy t responds to an invasion from another strategy by adjusting the value of t, and so does . Intuitively, evolutionary stability adjudicates between two fixed strategies while imitation lets t and influence each other. Instead of two strategies fighting for the survival of the fittest, imitation helps two categorizations blend into each other.
Under “AVG imitate”, two strategies t and affect each other more when their initial distance is greater. Moreover, t is more responsive to than to . Finally, the group with an initial larger size tends to exercise more pull on the competing group. Figure 7 illustrates these features. As usual, we identify the strategy with its threshold t: we color the values for t in light gray if the strategy is ES, and in dark gray otherwise. Thick arrows represent the displacement of a population’s strategy with threshold t. Shifts in the invading strategy are shown as thin arrows for small invasions and as regular arrows for large invasions.
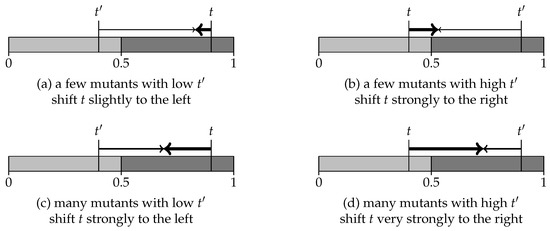
Figure 7.
Dynamics under “AVG imitate”.
The dynamics under “AVG imitate” leads almost always to shared categorizations with a threshold above ; see Figure 6 (on the right). This induces cooperation over some prisoners’ dilemmas. Nonetheless, the associated strategies are not ES: let us review what prevents them from being displaced by some ES strategy. Note first that, once the population achieves a shared categorization, all agents play similarly. This implies that there may be only mutual cooperation or mutual defection: hence, we have only R-agents and P-agents.
Suppose : the shared categorization is not ES and this population is more likely to see R-agents than P-agents. Consider an invasion from a small group of mutants who play an ES strategy with . The interaction of mutants with incumbents over a game with generates T-agents. Mutants with a low , who imitate R-agents, increase their threshold. Incumbent agents decrease their threshold when they turn out as S-agents or R-agents. However, R-agents are more frequent, because incumbents are more likely to interact within their group than across. Moreover, R-agents never imitate; see Figure 5 (right). Because T-agents imitate R-agents (but not vice versa), the incumbent population with resists invasion from mutants with at the cost of a small change in their new shared threshold.
8. Conclusions
This paper studies the emergence of a cooperative convention across a space of games that are variants of the archetypes known as prisoners’ dilemma and stag hunt. Our work speaks to a strand of literature that deals with laboratory experiments about cohorts of subject facing similar (but not identical) strategic situations. Rankin et al. [16] present evidence that players engaged over similar stag hunt games may establish a convention of payoff dominance: they attribute its emergence to cutoff strategies that implicitly define a binary categorization. van Huyck and Stahl [8] follow up on this study and show that increasing the diversity of the game space fosters the emergence of a cooperative convention. They argue for the importance of categories in helping players organize their beliefs and their strategies. Another larger strand deals with spillover effects across games, but eschews explicit consideration of the cognitive issues. In particular, Rusch and Luetge [25] provide evidence of coordination in stag hunt games spilling over to cooperation in prisoners’ dilemmas. Knez and Camerer [26] offer a related approach in the context of repeated games, enriched by an insightful distinction between descriptive and payoff similarity.
Our contribution is a step in the study of the cognitive foundations for some cooperative conventions.6 Bednar and Page ([28], p. 89) note that “[n]orms that are cognitively costly for some societies may be less so for others. Agents can evolve encodings or representations of the world that are coarse partitionings of the ‘real’ world.” We posit that agents use categories to distill their complex environment into a simpler set of situations. We consider a space of stag hunt games and prisoners’ dilemmas. We prove that in equilibrium agents must share the same categorization: this implies that they end up playing similar but different games in the same way, establishing a convention. Consistent with Binmore (2008)’s dictum that conventions are cultural artifacts, Section 3 shows that many different conventions are possible in equilibrium.
Next, we examine which conventions may emerge. Binmore ([7], p. 25) summarizes Hume [29] by claiming that “most conventions arise gradually and acquire force by a slow progression , they are the product of a largely unconscious process of cultural evolution.” We prove that the dynamics underlying evolutionary stability moves away from cooperation; in particular, stochastic stability selects as much defection as possible. We attribute this dismal outcome to the purposeless nature of evolutionary search and argue that the difficulty of changing categorizations prompt agents to act only if they fail to achieve some appropriate aspiration level.
We model how agents can use observable actions and payoff to imitate successful behavior from other players over similar (but not identical) games, although individual categorizations cannot be observed. Because cognitive adjustments are laborious, we postulate that agents initiate them only when failing to meet their aspiration level. When this level is not extreme, we show that the imitation process leads to cooperative conventions that spill over a sizable portion of the prisoners’ dilemmas. An advantage of our approach is that incumbent and entrant categorizations blend with each other, consistent with the intuition that a better understanding of the world comes not from a tug-of-war between two fixed views but from their proper amalgamation.
Author Contributions
conceptualization, M.L. and R.M.; software, R.M.; validation, M.L. and R.M.; formal analysis, M.L. and R.M.; writing-original draft preparation, M.L. and R.M.; writing-review and editing, M.L. and R.M.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation 604 programme under grant agreement no. 732942.
Acknowledgments
We acknowledge the anonymous reviewers for their valuable comments, that improved the clarity and quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ES | evolutionarily stable |
| SS | stochastically stable |
| TI | threshold imitation |
| ALL | all agents |
| AVG | agents that scored below the average score of all agents in the same situation |
| S-agent | sucker agent |
| R-agent | rewarded agent |
| P-agent | punished agent |
| T-agent | tempted agent |
Appendix A. Implemented Functions
Appendix A.1. random_member_with_higher_payoff
| 1 | Input: | set of n agents , | |||
| 2 | imitator agent | ||||
| 3 | : | ||||
| 4 | for: | ||||
| 5 | if.payoff.payoff: | ||||
| 6 | |||||
| 7 | returnrandom_member(O) | ||||
Appendix A.2. is_in_same_situation
| 1 | Input: | imitator agent , | |||
| 2 | example agent | ||||
| 3 | false | ||||
| 4 | if.xValue.thresholdand.xValue.threshold: | ||||
| 5 | true | ||||
| 6 | if.xValue.thresholdand.xValue.threshold: | ||||
| 7 | true | ||||
| 8 | returnc | ||||
Appendix A.3. below_average_same_situation
| 1 | Input: | set of n agents , | |||
| 2 | : | ||||
| 3 | for: | ||||
| 4 | accumulated_payoff | ||||
| 5 | num_opponents | ||||
| 6 | for: | ||||
| 7 | ifis_in_same_situation(a, ): | ||||
| 8 | accumulated_payoff = accumulated_payoff + .payoff | ||||
| 9 | num_opponents = num_opponents | ||||
| 10 | avg_payoff = accumulated_payoff/num_opponents | ||||
| 11 | ifa.payoff < avg_payoff: | ||||
| 12 | |||||
| 13 | returnM | ||||
References
- Denzau, A.; North, D. Shared mental models: Ideologies and institutions. Kyklos 1994, 47, 3–31. [Google Scholar] [CrossRef]
- Hoff, K.; Stiglitz, J.E. Striving for balance in economics: Towards a theory of the social determination of behavior. J. Econ. Behav. Organ. 2016, 126, 25–57. [Google Scholar] [CrossRef]
- Hobbes, T. Leviathan; Shapiro, I., Ed.; Yale University Press: New Haven, CT, USA, 2010. [Google Scholar]
- Nowak, M.; Highfield, R. Supercooperators: Altruism, Evolution, and Why We Need Each Other to Succeed; Free Press: New York, NY, USA, 2011. [Google Scholar]
- Rousseau, J.J. Discours sur l’origine et les fondements de l’inégalité parmi les hommes; Bedford/St. Martins: New York, NY, USA, 2011. [Google Scholar]
- Skyrms, B. The Stag Hunt and the Evolution of Social Structure; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Binmore, K. Do conventions need to be common knowledge? Topoi 2008, 27, 17–27. [Google Scholar] [CrossRef]
- Van Huyck, J.; Stahl, D. Conditional behavior and learning in similar stag hunt games. Exp. Econ. 2018, 21, 513–526. [Google Scholar] [CrossRef]
- Cohen, H.; Lefebvre, C. Handbook of Categorization in Cognitive Science; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Gibbons, R.; LiCalzi, M.; Warglien, M. What Situation Is This? Coarse Cognition and Behavior over a Space of Games; Working Paper 9/2017; Department of Management, Università Ca’ Foscari Venezia: Venice, Italy, 2017. [Google Scholar]
- Steiner, J.; Stewart, C. Contagion through learning. Theor. Econ. 2008, 3, 431–458. [Google Scholar]
- Peysakhovich, A.; Rand, D.G. Habits of virtue: Creating norms of cooperation and defection in the laboratory. Manag. Sci. 2016, 62, 631–647. [Google Scholar] [CrossRef]
- Heller, Y.; Winter, E. Rule rationality. Int. Econ. Rev. 2016, 57, 997–1026. [Google Scholar] [CrossRef]
- Mengel, F. Learning across games. Games Econ. Behav. 2012, 74, 601–619. [Google Scholar] [CrossRef]
- Macy, M.W.; Flache, A. Learning dynamics in social dilemmas. Proc. Natl. Acad. Sci. USA 2002, 99, 7229–7236. [Google Scholar] [CrossRef] [PubMed]
- Rankin, F.W.; van Huyck, J.B.; Battalio, R.C. Strategic similarity and emergent conventions: Evidence from similar stag hunt games. Games Econ. Behav. 2000, 32, 315–337. [Google Scholar] [CrossRef]
- LiCalzi, M. Fictitious play by cases. Games Econ. Behav. 1995, 11, 64–89. [Google Scholar] [CrossRef]
- Gracia-Lázaro, C.; Floría, L.M.; Moreno, Y. Cognitive hierarchy theory and two-person games. Games 2017, 8, 1. [Google Scholar] [CrossRef]
- Cressman, R.; Apaloo, J. Evolutionary game theory. In Handbook on Dynamic Game Theory; Başar, T., Zaccour, G., Eds.; Springer: Cham, Switzerland, 2018; pp. 461–510. [Google Scholar]
- Kandori, M.; Mailath, G.; Rob, R. Learning, mutation and long run equilibrium in games. Econometrica 1993, 61, 29–56. [Google Scholar] [CrossRef]
- Morris, S.; Rob, R.; Shin, H. p-dominance and belief potential. Econometrica 1995, 63, 145–157. [Google Scholar] [CrossRef]
- Ellison, G. Basins of attraction, long-run stochastic stability, and the speed of step- by-step evolution. Econometrica 2000, 67, 17–45. [Google Scholar] [CrossRef]
- Boyd, R.; Richerson, P.J. Culture and the evolution of human cooperation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2009, 364, 3281–3288. [Google Scholar] [CrossRef] [PubMed]
- Ellison, G.; Holden, R. A theory of rule development. J. Law Econ. Organ. 2014, 30, 649–682. [Google Scholar] [CrossRef]
- Rusch, H.; Luetge, C. Spillovers from coordination to cooperation: Evidence for the interdependence hypothesis? Evolut. Behav. Sci. 2016, 10, 284–296. [Google Scholar] [CrossRef]
- Knez, M.; Camerer, C. Increasing cooperation in prisoner’s dilemmas by establishing a precedent of efficiency in coordination games. Organ. Behav. Hum. Decis. Process. 2000, 82, 194–216. [Google Scholar] [CrossRef] [PubMed]
- Bacharach, M. Beyond Individual Choice: Teams and Frames in Game Theory; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Bednar, J.; Page, S. Can game(s) theory explain culture? Rational. Soc. 2007, 19, 65–97. [Google Scholar] [CrossRef]
- Hume, D. A Treatise of Human Nature; Selby-Bigge, L.A., Nidditch, P., Eds.; Oxford University Press: Oxford, UK, 1978. [Google Scholar]
| 1. | See Cohen and Lefebvre [9] for extensive surveys on the cognitive primacy of categorization processes. |
| 2. | See Steiner and Stewart [11] for a formal model of spillovers due to learning across games. |
| 3. | This remains true at the null event , when Player 1 gets the same payoff under and . |
| 4. | Technically, thresholds define partitions up to zero-measure sets because cells overlap at the boundary. |
| 5. | An implementation of the model (using python) is available at the GitHub repository: https://github.com/muehlenbernd/temptation_threshold_imitation. |
| 6. | See Bacharach [27] for a different approach. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).