On Adaptive Heuristics that Converge to Correlated Equilibrium

Abstract

I study the path properties of adaptive heuristics that mimic the natural dynamics of play in a game and converge to the set of correlated equilibria. Despite their apparent differences, I show that these heuristics have an abstract representation as a sequence of probability distributions that satisfy a number of common properties. These properties arise due to the topological structure of the set of correlated equilibria. The characterizations that I obtain have useful applications in the study of the convergence of the heuristics.

1. Introduction

Given the large fraction of economic interactions intermediated by algorithms today, it is becoming increasingly important for economists to understand the collective play properties of algorithmic procedures. Important work by several researchers (see the books by Fudenberg and Levine [1], Hart and Mas-Colell [2], and Shoham and Leyton-Brown [3]) has uncovered a number of algorithmic procedures that converge to an assortment of economic equilibria. In particular, a variety of algorithmic procedures has been discovered that mimic aspects of the natural dynamics of play in a game and converge to the set of correlated equilibria (see, for example, Foster and Vohra [4], Hart and Mas-Colell [5], Hart and Mas-Colell [6], and Blum and Mansour [7]). The typical setup involves repeated play of a game, with player responses improving over time according to some defined rule. The rules used seem natural, in the sense that they respect general principles by which players learn and compute, and the dynamics of play arise from the repeated local decisions made at the level of the players. In an influential paper, Hart [8] introduced the term adaptive heuristics to define such algorithmic play in games.

In this paper, I explore a number of general characterizations for such heuristics. These characterizations provide a complementary way to think about adaptive heuristics: instead of emphasizing the distinct behavioral or decision rules in each heuristic, as is common practice in the literature, they highlight the shared properties that underlie the entire class of procedures that converge to particular equilibria. Thus, this paper goes some way in answering Hart’s important question about general links between heuristics and equilibrium behavior (refer to Section 9 in Hart [8]).

Hart [8] documented the convergence of empirical play of most of the well-known adaptive heuristics to the set of correlated equilibria.1 This is the starting point of my analysis. The set of correlated equilibria is compact and convex. Thus, in a certain sense, all these heuristics generate paths that converge to a common compact and convex set. In the case of sequences on the real line that converge to a limit point, we have alternative characterizations of convergence in terms of the path; for instance, the Cauchy convergence criterion. Here, I examine whether comparable path characterizations are feasible for adaptive heuristics. Such characterizations, when available, are useful to understand the links between the dynamics of play and equilibrium, as emphasized in Hart [8]. The task, however, is tricky for a number of reasons. First, it is not clear how one may consistently extract a single sequence from heuristic procedures to check for convergence to equilibrium. An obvious candidate is the sequence of empirical distributions generated from the play of a heuristic procedure, but this sequence is unhelpful because the same heuristic may generate different sequences if it involves randomization.2 To overcome this problem, I define the notion of an explicit scheme.

Explicit schemes are abstract representations of heuristics where all randomization is centralized, and they provide a simple way to generate a single sequence from any heuristic procedure. The mapping from a heuristic to its explicit scheme, in certain ways, echoes the mapping from an ordinary mechanism to a direct mechanism in mechanism design theory. At various points in the paper, I allude to this similarity and also point out the differences. The sequence generated in an explicit scheme is a succession of probability distributions, so the original task is now reduced to the problem of characterization of such sequences. The problem is still non-trivial because the probability distributions may inhabit a high dimensional space, and more importantly, the convergence is to a limit set, not a point. For this reason, I need to establish a definition of convergence in terms of set containment relations, and this eventually provides the characterization of adaptive heuristics in terms of their paths. A useful result from this exercise is the insight that the outlines of a compact, convex set can be discerned from the path, as a sequence progresses, if a heuristic ultimately converges to the set of correlated equilibria. This idea can have interesting applications, some of which I outline in the last part of the paper.

The paper is organized as follows. I start by introducing the notation and basic definitions in Section 2. Section 3 discusses the properties of explicit schemes, defines the notion of convergence, and then provides the main characterization results. Section 4 discusses some applications and potential extensions of the current work. The proof of Proposition 2 is in the Appendix A.

2. Preliminaries

Let $\mathsf{\Gamma }=\left(N,{\left(S^i\right)}_{i\in N},{\left(u^i\right)}_{i\in N}\right)$ be a finite N-person strategic-form game, where N is the set of players, $S^i$ is the set of pure strategies of player i, and $u^i:{✕}_{i\in N}{S}^i\to \mathbb{R}$ is player i’s payoff function. $S={✕}_{i\in N}{S}^i$ denotes the set of pure strategy vectors with generic element $s={\left(s^i\right)}_{i\in N}$, and $S^{-i}$ denotes the set of pure strategy vectors with i’s strategy set excluded, i.e., $S^{-i}={✕}_{j\ne i,j\in N}{S}^j$. $s^{-i}$ denotes a generic element of the set $S^{-i}$, i.e., $s^{-i}={\left(s^{i^{\prime }}\right)}_{i^{\prime }\ne i}$. All sets N and $S_i$ are assumed finite.

For any finite set A, denote by $\Delta \left(A\right)$ the set of probability distributions over A. In other words, $\Delta \left(A\right)=\{\delta :A\to [0,1]:{\sum }_{a\in A}\delta \left(a\right)=1\}$. A mixed strategy of player i, denoted by ${\rho }_i$, is a probability distribution over the player’s set of pure strategies. Thus, $\Delta \left(S^i\right)$ represents the set of mixed strategies of player i, and ${\rho }^i\in \Delta \left(S^i\right)$.

I use the standard definition for correlated equilibrium (Aumann [10]).

Definition 1

(Correlated equilibrium). A probability distribution p on S is a correlated equilibrium for the game Γ if for every player $i\in N$,

$$\sum _{s^{-i}\in S^{-i}}p\left(s^i,s^{-i}\right)u^i\left(s^i,s^{-i}\right)\ge \sum _{s^{-i}\in S^{-i}}p\left(s^i,s^{-i}\right)u^i\left({\widehat{s}}^i,s^{-i}\right),\hspace{1em}\forall s^i,{\widehat{s}}^i\in S^i.$$

(1)

The set of probability distributions satisfying Condition (1) is called the set of correlated equilibria of the game. This set has a number of well-known topological and algebraic properties: particularly useful for the analysis in this paper will be the fact that this set is compact and convex (Aumann [11]).

Let $\tau =\left\{1,2,\dots \right\}$ denote a countable index set with generic element t, and let the tuple ${\mathcal{G}}_{\mathsf{\Gamma }}=\left({\mathsf{\Gamma }}_1,{\mathsf{\Gamma }}_2,\dots \right)$ represent repeated play of the game $\mathsf{\Gamma }$ over the index set. The index set is interpreted as a count of the number of repetitions, and ${\mathsf{\Gamma }}_t$ denotes the play in the $t\mathrm{th}$ repetition of $\mathsf{\Gamma }$. The basic structure of the game remains the same in all the repetitions. In other words, ${\mathsf{\Gamma }}_t=\mathsf{\Gamma }=\left(N,{\left(S^i\right)}_{i\in N},{\left(u^i\right)}_{i\in N}\right)$ $\forall t$. When the subscript t is affixed to a mixed strategy, it represents a mixed strategy in ${\mathsf{\Gamma }}_t$. That is to say, ${\rho }_t^i\in \Delta \left(S^i\right)$ represents a mixed strategy of player i in the $t\mathrm{th}$ repetition of the game.

In this paper, the focus is on heuristics that arise in repeated play. A heuristic for a player i is a sequence of mixed strategies chosen by i as the game gets repeated. A heuristic scheme for a game is simply the collection of heuristics adopted by the players.

Definition 2

(Heuristic scheme). A heuristic for a player $i\in N$ is a sequence of mixed strategies:

$${\mathcal{H}}_i=\left({\rho }_1^i,{\rho }_2^i,\dots \right),$$

(2)

where the cardinality of ${\mathcal{H}}_i$ is the same as τ, and ${\rho }_t^i\in \Delta \left(S^i\right)$ $\forall t\in \tau$.

A heuristic scheme $\mathcal{H}$ for ${\mathcal{G}}_{\mathsf{\Gamma }}$ is the tuple of player heuristic schemes:

$$\mathcal{H}=\left({\left({\mathcal{H}}_i\right)}_{i\in N}\right).$$

(3)

Heuristic schemes are outcomes of decision rules adopted by players, and they can guide the play of a game to an equilibrium. Thus, there are two complementary ways to describe particular classes of heuristic schemes: in terms of player decision rules, or equivalently, in terms of the equilibrium attained. In this paper, I follow the second description. Hart [8] termed a decision rule adaptive if it improved the long-run utility of players as the game progressed and showed that such decision rules guide play to correlated equilibrium. Therefore, in this paper, I analyze the set of heuristic schemes that guide play to correlated equilibrium. Focusing on this set—instead of examining specific decision rules—allows me to draw inferences that apply to all adaptive heuristics (refer to Hart and Mas-Colell [2] for details of the decision rules-based approach).

Note that the concept of the heuristic scheme is completely general, in the sense that a heuristic scheme by itself is not tied to any decision rule or equilibrium notion. On the other hand, interesting features of player behavior in games, like the adaptiveness described above, are captured only in particular decision rules or equilibrium outcomes. Thus, for fruitful analysis, one links a heuristic scheme to a particular decision rule or equilibrium notion and then studies the characteristics of the schemes that are pinned down. This is the broad strategy adopted in this paper.

3. Main Results

Even with the restriction that they converge to the set of correlated equilibria, there are myriads of approaches to generate heuristic schemes. Such schemes may differ in any number of ways: in terms of the information set accessible to players at each round, or the rationality required of the players, or the autonomy granted to each player, and so on. While heuristic schemes are abstractions themselves, we thus need a further layer of abstraction to generate a single sequence for analyzing convergence. This abstraction, which I call the explicit scheme, has a physically-meaningful interpretation. A very rough metaphor to get a high-level overview of the mapping could be to think of heuristic schemes as similar to mechanisms and explicit schemes as similar to direct mechanisms. Just as direct mechanisms circumscribe the huge space of mechanisms potentially possible, explicit schemes restrict the variety of heuristic schemes and facilitate useful analysis. The characterizations developed later in this section are for probability distribution sequences generated from explicit schemes.

3.1. Explicit Scheme

Consider the following procedure: for every round of the game $\mathsf{\Gamma }$ over the index set $\tau =\left\{1,2,\dots \right\}$, a scheme operator uses a probability distribution $p_t$ over the set of strategy vectors $S={✕}_{i\in N}{S}^i$ to generate a realization and then recommends to each player i a pure strategy from the set $S^i$. This provides an interpretation for the definition of an explicit scheme.

Definition 3

(Explicit scheme). An explicit scheme $\mathcal{E}$ is a single sequence of probability distributions,

$$\mathcal{E}=\left(p_1,p_2,\dots \right)$$

over the set of strategy vectors $S={✕}_{i\in N}{S}^i$, where the cardinality of $\mathcal{E}$ is the same as τ, and $p_t\in \Delta \left(S\right)$ $\forall t\in \tau$.

The content of the definition can be elucidated through an example.

Example 1.

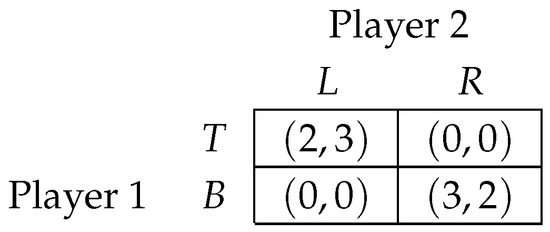
Consider the normal form game in Figure 1:

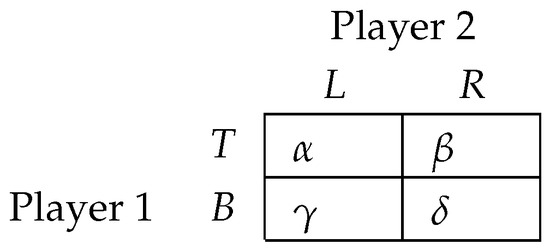
An explicit scheme would be a sequence of probability distributions over the set $\left\{TL,TR,BL,BR\right\}$. The probability distribution $p_t$ used by the scheme operator in round t may be represented graphically by Figure 2, with $\alpha +\beta +\gamma +\delta =1$ and $\alpha ,\beta ,\gamma ,\delta \ge 0$.

If the realization from $p_t$ is, say, the element $TL$, the scheme operator recommends pure strategy T to Player 1 and pure strategy L to Player 2 in round t.

A few remarks about explicit schemes are in order at this point:

Remark 1.

Explicit schemes, like heuristic schemes, are not tied to any equilibrium concept.

In fact, there is no particular requirement for play from an explicit scheme to even converge to an equilibrium. There are also no rationality restrictions on player actions. Delinking explicit schemes from the notion of equilibrium and rationality allows us to focus on just the sequence of probability distributions.

Remark 2.

A scheme operator’s function in an explicit scheme is similar in spirit to an outside observer’s role in a correlated equilibrium.

The difference in the roles arises because there is no rationality requirement imposed on players in the explicit scheme. Further, a scheme operator has to generate a sequence of probability distributions while the outside observer generates a probability distribution just once in a correlated equilibrium.

Explicit schemes are useful because they provide a common substratum for heuristic schemes: any heuristic scheme can be converted to an explicit scheme. Instead of the players randomizing locally—as happens in heuristic schemes—randomization is centralized for explicit schemes.

Proposition 1.

For every heuristic scheme, there exists a corresponding explicit scheme.

Proof. 

The proof is by construction. Recall that a heuristic scheme is a collection of sequences of mixed strategies, one for each player. One may rewrite Condition (3) as $\mathcal{H}=\left({\left({\rho }_1^i,{\rho }_2^i,\dots \right)}_{i\in N}\right)$, where the ${\rho }_t^i$ are probability distributions over player strategy sets $S^i$. An explicit scheme, on the other hand, is a single sequence of probability distributions over the set of strategy vectors. Define the probability distribution $p_t={✕}_{i\in N}{\rho }_t^i$. Since the product ${✕}_{i\in N}{\rho }_t^i$ is a probability distribution over $S={✕}_{i\in N}{S}^i$, we get an explicit scheme $\mathcal{E}=\left({✕}_{i\in N}{\rho }_1^i,{✕}_{i\in N}{\rho }_2^i,\dots \right)$.

Since this construction can be undertaken for any heuristic scheme, the proof is complete.  □

Example 2.

(Continued) In round t of a heuristic scheme, suppose Player 1 uses the probability distribution ${\rho }_t^1=\left\{0.5,0.5\right\}$ over $\left\{T,B\right\}$, and Player 2 uses the probability distribution ${\rho }_t^2=\left\{0.25,0.75\right\}$ over $\left\{L,R\right\}$. Then, the explicit scheme corresponding to the heuristic scheme would use $p_t=\left\{0.125,0.125,0.375,0.375\right\}$ over $\left\{TL,BL,TR,BR\right\}$ to generate realizations.

One possible interpretation of Proposition 1 could be that in every round, a scheme operator asks each player to reveal the probability distribution that the player would use. The scheme operator then consolidates the player distributions in the manner described above, obtains a realization, and recommends strategies to the players. In this sense, Proposition 1 has a flavor of the revelation principle in mechanism design theory. However, since heuristic schemes are free from notions of equilibrium or rationality, we do not need extra constraints like incentive compatibility or individual rationality. The conversion, as such, is purely mechanical. However, converting a heuristic scheme to its corresponding explicit scheme is very useful because it allows us to extract a single sequence of probability distributions. This allows us to take a fresh look at convergence to equilibrium for heuristics.

3.2. Convergence

To study the convergence properties of heuristic schemes, one way could be to examine the asymptotic behavior of empirical distributions generated from the scheme. The empirical distribution, after t rounds of play, is simply the relative frequency that each N tuple $s\in S$ has been played in the first t rounds $\left\{1,\dots ,t\right\}.$ In other words, if the relative frequency of s is denoted by $z_t\left(s\right):=\frac{1}{t}\left|\left\{n\le t:s_n=s\right\}\right|$, then $z_t\in \Delta \left(S\right)$ is the empirical distribution after t rounds.3

Definition 4.

(Hart and Mas-Colell [5]) A heuristic scheme converges to the set of correlated equilibria if for any $ϵ>0$, there exists an element T in the index set τ such that for all $t>T$, one can find a correlated equilibrium distribution at a distance less than ϵ from the empirical distribution.

In Definition 4, convergence to the set of correlated equilibria is asymptotic; therefore, one might switch to the theoretical distribution generating the empirical distribution.

Proposition 2.

The empirical distribution converges to the set of correlated equilibria in the space of probability distributions over a finite set if the theoretical distributions from which the empirical distributions are generated have converged to the same set.

Note the minor subtlety in the statement of the proposition; for us to assert that the empirical distributions will converge, we must know that the theoretical distributions have already converged. The proof of the proposition is in the Appendix A and follows from the strong law of large numbers for set valued probability measures.

Explicit schemes provide a convenient route to make the switch from empirical to theoretical distributions. Any heuristic scheme can be converted to a corresponding explicit scheme. Therefore, if one wants to characterize all heuristic schemes that converge to the set of correlated equilibria, one may focus attention on just explicit schemes, without loss of generality. Proposition 2 assures us that if the explicit scheme distributions have converged to the correlated equilibria set, so will the empirical distribution. Consequently, our task is to investigate the properties of the probability distribution sequences generated from explicit schemes that converge to the set of correlated equilibria.

Let C denote the set of correlated equilibria of game $\mathsf{\Gamma }$ and $ConvHull\left(p_k,\dots ,p_n\right)$ the convex hull of the sequence $\left(p_k,\dots ,p_n\right)$. Then, the discussion above means that one can re-cast the definition of convergence in the following manner.

Definition 5

(Convergence). An explicit scheme $\mathcal{E}=\left(p_1,p_2,\dots \right)$ converges to the set of correlated equilibria C if for any $C^{\prime }\supseteq C$, there exists a $T\in \tau$ such that:

$$p_t,p_{t+1},\dots \in C^{\prime }\hspace{1em}\forall t\ge T.$$

(4)

Definition 5 resembles the familiar definition for sequences converging to a limit, the only difference being that the limit is a set instead of a point. Since the set of correlated equilibria is convex, we can rewrite Condition (4) in the definition as:

$$ConvHull\left(p_t,\dots \right)\subseteq C^{\prime }\hspace{1em}\forall t\ge T.$$

(5)

Just as convergence of a sequence to a point implies that for any ball centered around the point, one can find a cutoff beyond which all members of the sequence lie in the ball, the definition of convergence to a set implies that for any superset of the given set, one can find a cutoff beyond which the sequence lies completely within the superset. Definition 5 is useful in highlighting important properties of converging heuristic schemes, the focus of the next section.

3.3. Characterizing Heuristic Schemes

Whether a heuristic is adaptive or not is essentially a question about set convergence. However, we have very few tools to probe questions about convergence in sets. On the other hand, there is an abundance of techniques to investigate the properties of sequences that converge to points. The theorems in this section provide the analytical machinery to make the switch from set convergence to point convergence in the case of heuristics. This is one of the important contributions of the paper.

The algebraic and topological concepts used in this section are standard, and the reader is referred to standard texts in analysis (Rudin [12]) or point-set topology (Steen and Seebach [13]) for detailed descriptions. For completeness, let me provide brief definitions of a few terms that come up repeatedly. A set U is called compact if every collection of open sets that covers U also has a finite subcollection that covers U. A neighborhood of a point x is any open set containing x. A point y is called an accumulation point of a sequence if every neighborhood of y contains infinitely many points from the sequence. A set U is called convex if for any two points $x,y\in U$, all points $\lambda x+(1-\lambda )y$, $0<\lambda <1$, are also in U. As noted earlier, the set of correlated equilibria is compact and convex.4

Recall that an explicit scheme generates an infinite sequence of probability distributions over S from a heuristic scheme, and if the heuristic scheme converges to the set of correlated equilibria, this sequence is eventually confined to a compact, convex set. Now, any infinite sequence in a compact set has to accumulate eventually about points in that space. For example, if our set were the first 100 positive integers $\{1,2,\dots ,100\}$, an infinite sequence that takes all its values from this set would eventually accumulate at one or more of these integers. This is the content of Theorem 1 below.

Theorem 1.

If an explicit scheme $\mathcal{E}$ converges to the set of correlated equilibria, it has an accumulation point that satisfies the correlated equilibrium Condition (1).

Proof. 

The proof is by contraposition. Denote the set of correlated equilibria by C. Since the explicit scheme $\mathcal{E}=\left(p_1,p_2,\dots \right)$ converges to this set, from Definition 5, there exists a T such that all points $p_t,p_{t+1},\dots$ for $t\ge T$ lie in C. If $\mathcal{E}$ had no accumulation point in C, then each $c\in C$ would have a neighborhood $V_c$, which would contain at most a finite number of terms of $\mathcal{E}$. Now, consider the set of such neighborhoods $\left\{V_c\right\}$, $c\in C$. This collection of sets covers C. However, no finite subcollection of $\left\{V_c\right\}$, $c\in C$, could cover the sequence $\left(p_t,p_{t+1},\dots \right)$, because the product of finites is finite. This in turn implies that no finite subcollection of $\left\{V_c\right\}$, $c\in C$, could cover C. However, this contradicts the compactness property of the set of correlated equilibria; thus the result.  □

Theorem 1 is a partial step in converting the complicated problem—of convergence to correlated equilibria sets—to a relatively simple question of checking a condition for a point. The condition to be checked is the correlated equilibrium condition in (1), and the point for which the condition is checked is an accumulation point of the explicit scheme corresponding to the heuristic. Theorem 1 is only a necessary condition, however. Thus, Theorem 1 does not immediately guarantee that finding such a point implies a heuristic scheme converges. For this, we require the next theorem.

Theorem 2.

An explicit scheme $\mathcal{E}$ converges to the set of correlated equilibria if and only if all its accumulation points satisfy the correlated equilibrium Condition (1).

Proof. 

Denote the set of correlated equilibria by C.

(Only if) The proof is by contraposition. Suppose $\mathcal{E}$ had an accumulation point that did not satisfy the correlated equilibrium condition. In other words, it was not in C. Call this point m. Then, m would have a neighborhood $V_m$ with infinitely many points from $\mathcal{E}$, and these points would not lie in C. Any infinite subsequence of $\mathcal{E}$ would now need to have points in $V_m$. In particular, for any T, and $t\ge T$, a non-empty subset of points in $\{p_t,p_{t+1},\dots \}$ would not lie in C. Thus, $\mathcal{E}$ would not have converged to C.

(If) Denote the set of accumulation points of $\mathcal{E}$ by $\left\{l\right\}$. Let $V_{\left\{l\right\}}={\bigcup }_{l\in \left\{l\right\}}{V}_l$ denote a union of neighborhoods of the accumulation points with the property $V_{\left\{l\right\}}\subseteq C$. Since $V_{\left\{l\right\}}$ contains all the accumulation points of $\mathcal{E}$, one can always find a T such that points $p_t,p_{t+1},\dots$ lie in $V_{\left\{l\right\}}\subseteq C$ for $t\ge T$; thus the result.  □

Theorem 2 provides a condition that is both necessary and sufficient for convergence. Taken together, Theorems 1 and 2 say that the explicit scheme corresponding to any heuristic scheme that converges has one or more accumulation points, and all the accumulation points satisfy Condition (1). Thus, to check for convergence to the set of correlated equilibria, it is enough to just examine a heuristic scheme’s accumulation points.

These theorems represent a significant simplification of the original problem and lead to other interesting characterizations. Recall that the Cauchy criterion on the real line asserts that for convergent sequences, elements of the sequence become arbitrarily close to each other as the sequence progresses. Something broadly similar can be established even for heuristic schemes. Since all the accumulation points of a converging explicit scheme lie in the set of correlated equilibria, the outlines of a compact, convex set may be discerned from the path of such sequences.

Theorem 3.

Let $\mathcal{E}=\left(p_1,p_2,\dots \right)$ denote an explicit scheme that converges to the set of correlated equilibria. Then, for any $p_k$ in $\mathcal{E}$, there exists a $p_m$ in $\mathcal{E}$, $m\ge k$, satisfying the correlated equilibrium Condition (1), such that:

$$ConvHull\left(p_k,\dots ,p_m\right)\supseteq ConvHull\left(p_k,\dots \right).$$

(6)

Proof. 

Denote the set of correlated equilibria by C and the set of accumulation points of $\mathcal{E}$ by A. From Theorem 1, set A is non-empty. Further, from Theorem 2, $A\subseteq C$. Represent a generic accumulation point in A by a. For any given n, denote by $V_a\left(p_n\right)$ the smallest neighborhood of a that contains the sequence $\left(p_{n+1},p_{n+2},\dots \right)$.

Now, given the point $p_k$ in the statement of the theorem, choose a point $p_x$, $x\ge k$, such that $p_x,p_{x+1},\dots \in C$. Since $A\subseteq C$, such an x always exists. Next, for each accumulation point $a\in A$, choose a point $p_b$, $b\ge x$, that satisfies two conditions: (i) $V_a\left(p_b\right)\in ConvHull\left(p_x,\dots ,p_b\right)$; (ii) for any $p_{b^{\prime }}$ such that $V_a(p_{b^{\prime }})\in ConvHull\left(p_x,\dots ,p_{b^{\prime }}\right)$, $b\le b^{\prime }$. That is, b is the smallest index for which Condition (i) is satisfied. Since a is an accumulation point, such a point $p_b$ always exists.

Finally, choose $\beta =max\left\{b\right\}$. Then, by construction, $ConvHull\left(p_k,\dots ,p_{\beta }\right)\supseteq ConvHull\left(p_k,\dots \right)$, and $p_{\beta }\in C$; thus the result.  □

In fact, there is a very simple algorithm to obtain a $p_m$ in Theorem 3 for any given point $p_k$: Construct $ConvHull\left(p_k,\dots ,p_{m^{\prime }}\right)$ for an arbitrary $m^{\prime }\ge k$, $p_{m^{\prime }}\in C$. Then, move further along the sequence, and for any $m^{″}>m^{\prime }$, if $p_{m^{″}}\notin ConvHull\left(p_k,\dots ,p_{m^{\prime }}\right)$, replace the original convex set by $ConvHull\left(p_k,\dots ,p_{m^{″}}\right)$. Since the sequence converges to the set of correlated equilibria, repeating this process eventually gives us our $p_m$. Note, however, that m in the above theorem is countable, not necessarily finite.5 Thus, such an exhaustive search algorithm may not be efficient.

The formulation in Theorem 3 is useful because it can give an idea of the pattern into which a heuristic scheme finally settles. Further, in many cases, the more the number of points one has to traverse along the sequence to find a $p_m$ for a given point, the more the distance of the point from the ultimate convergence set. This is helpful in gauging the distance of the current state of play from the ultimate equilibrium when using a heuristic. These notions are examined in more detail in the next section.

4. Discussion

This section discusses some applications of the characterizations described in the previous sections and potential extensions of the current work.

The first application concerns the rates of convergence of theoretical distributions generated from explicit schemes. Proposition 3 below shows that one may obtain heuristics with extremely fast rates of convergence. This is because one may, in principle, repeatedly jump arbitrary number of steps in any heuristic scheme, speeding up its convergence. A note of caution though: the convergence of empirically-measured distributions to the theoretical distribution (from which the empirical distributions are generated) happens only asymptotically through an appropriate law of large numbers.6 Thus, theoretical distributions converging faster to the destination set does not automatically guarantee that the empirically-measured distributions would converge faster, as well.

Proposition 3.

For any game, there exist explicit schemes whose sequence of probability distributions converges at arbitrarily fast rates to the set of correlated equilibria of the game.

Proof. 

Take any established heuristic scheme converging to the set of correlated equilibria7, and convert it to its corresponding explicit scheme. Denote this explicit scheme by ${\mathcal{E}}_1=\left(p_1,p_2,\dots \right)$. Next, define the explicit schemes ${\mathcal{E}}_2=\left(p_2,p_4,\dots \right)$, ${\mathcal{E}}_3=\left(p_3,p_6,\dots \right)$, and so on, i.e., more generally, ${\mathcal{E}}_n=\left(p_n,p_{2n},\dots \right)$. If the starting points are not already in the set of correlated equilibria, the sequence ${\mathcal{E}}_2$ converges to the destination set faster than ${\mathcal{E}}_1$; ${\mathcal{E}}_3$ converges faster than ${\mathcal{E}}_2$; and so on. Since n can be arbitrarily large, the result follows.  □

While Proposition 3 is useful, the limitation of working with explicit schemes is that the analysis does not provide a clear recipe for implementation in terms of heuristic procedures. This highlights another parallel between heuristics and mechanisms. Direct mechanisms make the analysis of arbitrary mechanisms much simpler, but come at a similar cost: it is not always clear whether an optimal mechanism in the space of direct mechanisms has an implementation in ordinary mechanisms. An interesting avenue for future work would be to investigate further the connection between explicit schemes and heuristic schemes. The mapping from explicit scheme to heuristic schemes is one-to-many, but not all explicit schemes have a simple or natural implementation like, say, calibrated forecast (Foster and Vohra [4]) or regret matching (Hart and Mas-Colell [5]). It would be interesting to understand the restrictions needed on explicit schemes so that they can yield simple, implementable heuristic schemes.

Theorem 3 can also provide useful tools to study the convergence of explicit schemes. Recall that for any converging explicit scheme $\mathcal{E}$, the theorem guarantees that for any index k, there exists an $m\ge k$ such that $ConvHull\left(p_k,\dots ,p_m\right)\supseteq ConvHull\left(p_k,\dots \right)$, with $p_m$ in the correlated equilibria set. Now, let $m_k$ denote the smallest m for which this condition holds. In other words, let $m_k$ denote the smallest index such that $p_{m_k}$ lies in the set of correlated equilibria and:

$$ConvHull\left(p_k,\dots ,p_{m_k}\right)\supseteq ConvHull\left(p_k,\dots \right).$$

(7)

Denote ${\mu }_k=\left(m_k-k\right)$ and call this the mu measure of point k. In other words, ${\mu }_k$ measures the minimum number of steps one needs to move forward, starting k, to form a convex set that contains the rest of the sequence. In the same vein,

$${\mu }_{\infty }=\underset{t\to \infty }{lim}\left({\mu }_t-t\right).$$

The limit ${\mu }_{\infty }$, when it exists, gives an idea of the pattern into which the explicit scheme ultimately settles. For instance, ${\mu }_{\infty }=0$ implies that the scheme converges to a point equilibrium. The mu measure also helps in gauging the distance of the scheme from the subset of correlated equilibria to which the scheme ultimately converges. For instance, if ${\mu }_k\approx {\mu }_{\infty }$ or if ${\mu }_k$ repeats a pattern over successive k, then it is likely that the scheme is close to the equilibrium set to which it ultimately converges. Similarly, if two explicit schemes start at the same point and the mu measure of the point under the first scheme is lower than the second, it is likely that the first scheme converges faster. Such rules of thumb can lead to analytical measures for examining convergence rates of heuristic schemes from path properties and would be another interesting direction for future work.