Evolution of Groupwise Cooperation: Generosity, Paradoxical Behavior, and Non-Linear Payoff Functions
Abstract
1. Introduction
2. Model
2.1. The -Player Repeated Prisoner’s Dilemma
2.2. Evolutionary Dynamics
3. Results
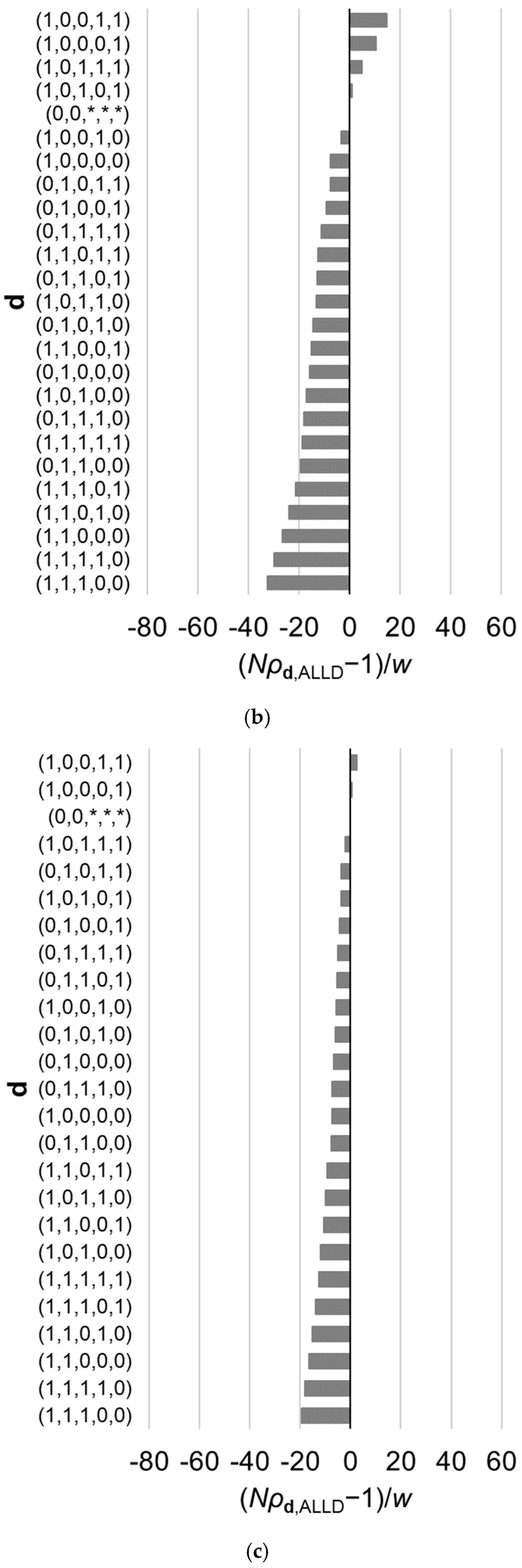
3.1. General Case
3.2. Linear Payoff
3.3. Non-Linear Payoff
3.3.1. Evolution of Generosity with Non-Linear Payoff
Constant Cost with Non-Linear Benefit
Variable Cost with Non-Decelerating Benefit
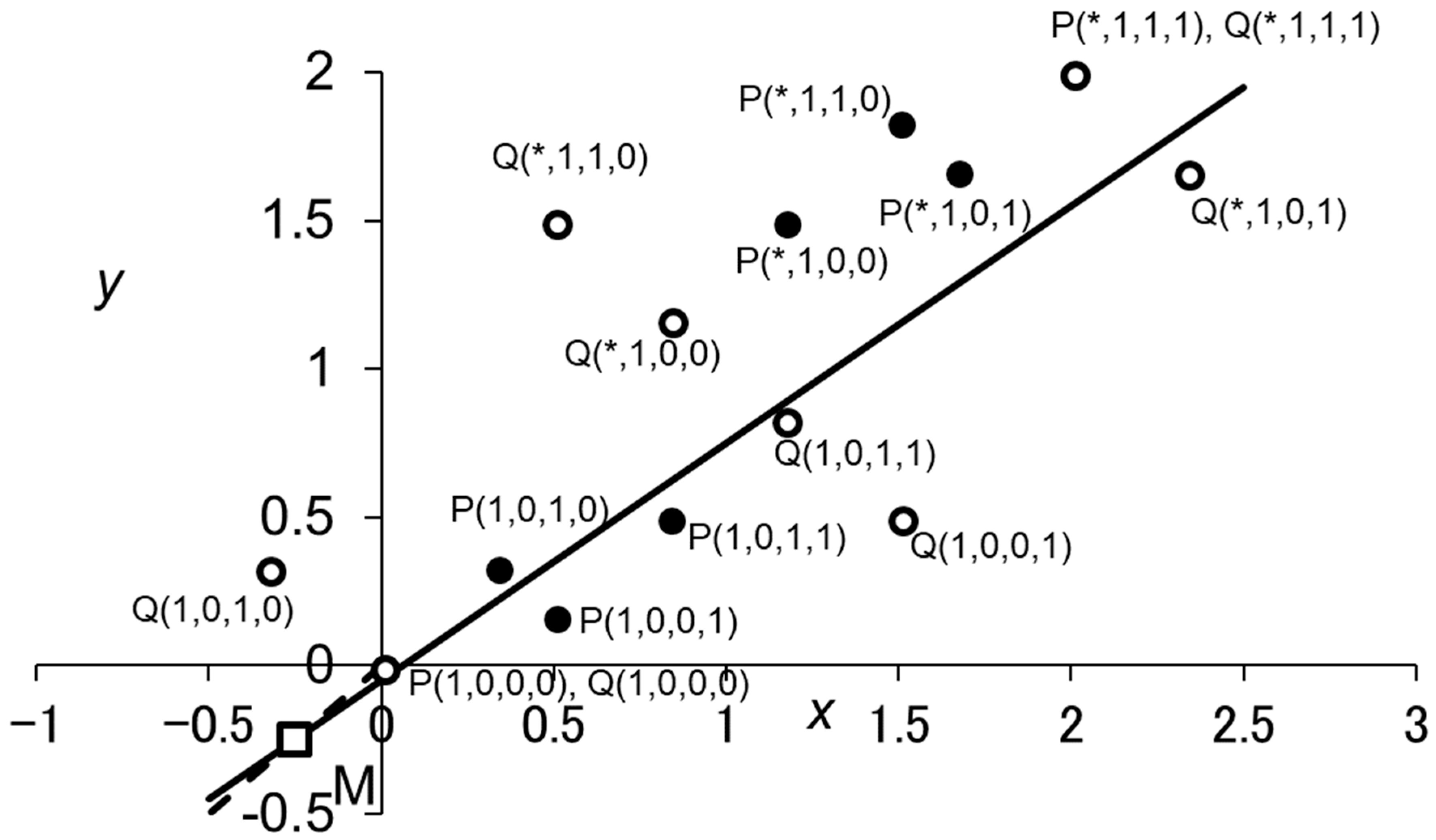
A Numerical Example
3.3.2. Evolution of Paradoxical Behavior with Non-Linear Payoff
Non-Increasing Cost and Non-Linear Benefit
A Numerical Example
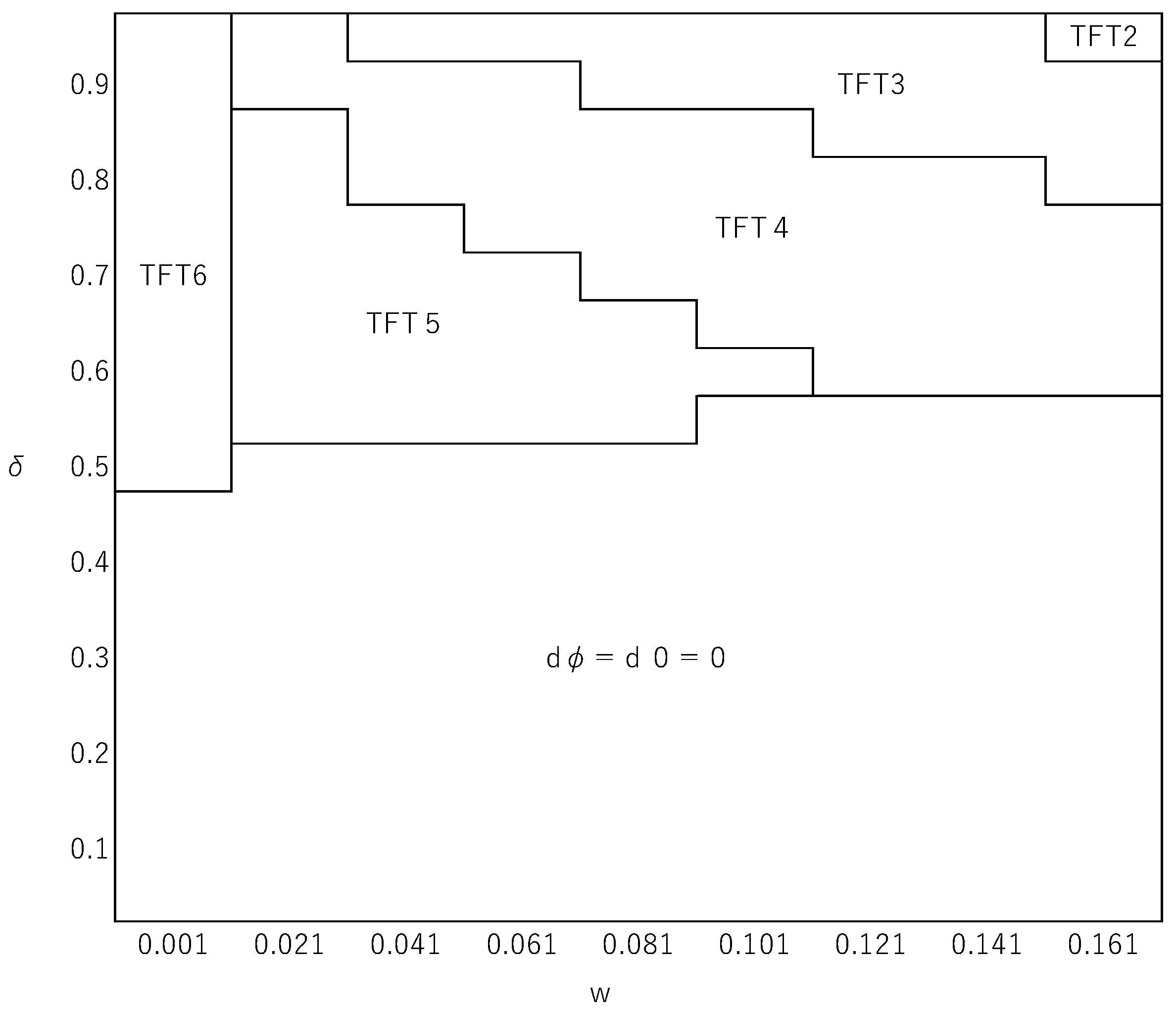
3.4. The Best Reactive Strategy under Moderate Selection Intensity
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
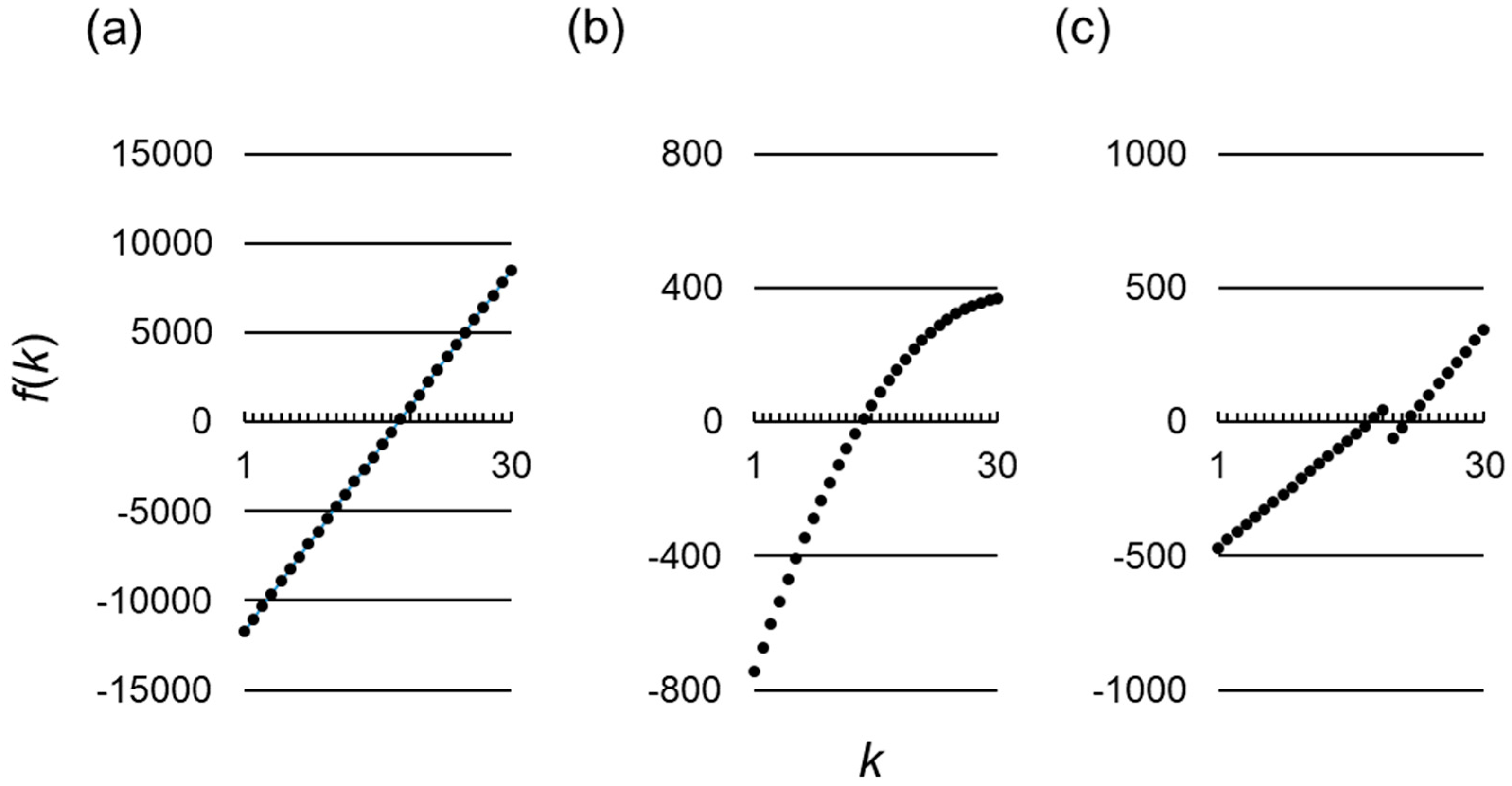
Solving (15)
Appendix B
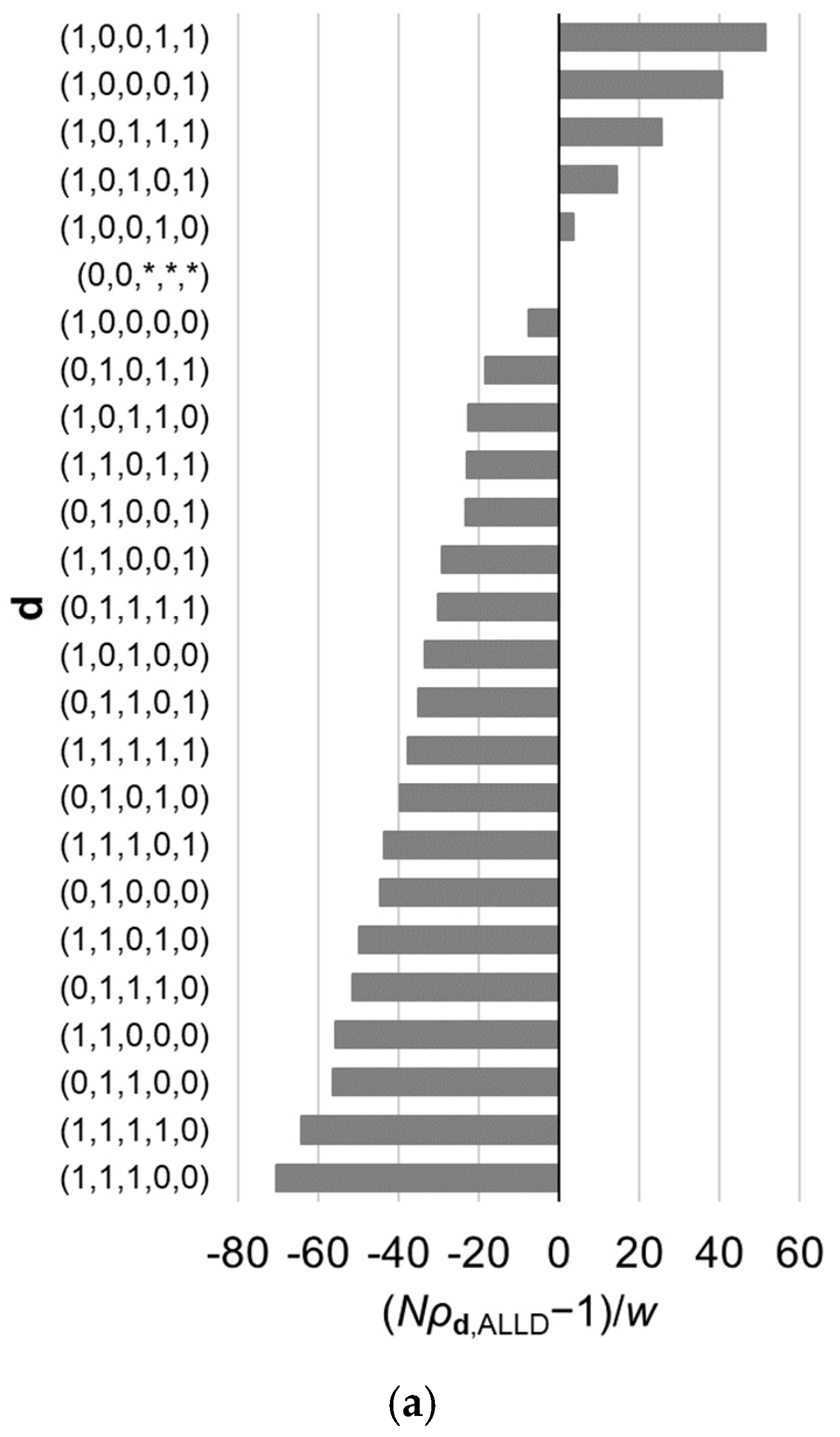
The Fixation Probability of ALLD as a Single Mutant in a Population of d
Appendix C
The Ratio of the Fixation Probabilities
Appendix D
The Conditions for Reactive Strategies to Be Selectively Favored over ALLD
References
- Trivers, R. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef]
- Joshi, N.V. Evolution of cooperation by reciprocation within structured demes. J. Genet. 1987, 6, 69–84. [Google Scholar] [CrossRef]
- Boyd, R.; Richerson, P.J. The evolution of reciprocity in sizable groups. J. Theor. Biol. 1988, 132, 337–356. [Google Scholar] [CrossRef]
- Nowak, M.A. Stochastic strategies in the prisoner’s dilemma. Theor. Popul. Biol. 1990, 38, 93–112. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. The evolution of stochastic strategies in the prisoner’s dilemma. Acta Appl. Math. 1990, 20, 247–265. [Google Scholar] [CrossRef]
- Press, W.H.; Dyson, F.J. Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl. Acad. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef]
- Stewart, A.J.; Plotkin, J.B. Extortion and cooperation in the prisoner’s dilemma. Proc. Natl. Acad. Sci. USA 2012, 109, 10134–10135. [Google Scholar] [CrossRef]
- Stewart, A.J.; Plotkin, J.B. From extortion to generosity, evolution in the iterated prisoner’s dilemma. Proc. Natl. Acad. Sci. USA 2013, 110, 15348–15353. [Google Scholar] [CrossRef]
- Stewart, A.J.; Plotkin, J.B. Collapse of cooperation in evolving games. Proc. Natl. Acad. Sci. USA 2014, 111, 17558–17563. [Google Scholar] [CrossRef]
- Hilbe, C.; Traulsen, A.; Sigmund, K. Partners or rivals? strategies for the iterated prisoner’s dilemma. Games Econ. Behav. 2015, 92, 41–52. [Google Scholar] [CrossRef] [PubMed]
- Hilbe, C.; Chatterjee, K.; Nowak, M.A. Partners and rivals in direct reciprocity. Nature Hum. Behaviour. 2018, 2, 469–477. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. Evolutionary games and spatial chaos. Nature 1992, 359, 826–829. [Google Scholar] [CrossRef]
- Killingback, T.; Doebeli, M. Self-organized criticality in spatial evolutionary game theory. J. Theor. Biol. 1998, 191, 335–340. [Google Scholar] [CrossRef] [PubMed]
- Fudenberg, D.; Harris, C. Evolutionary dynamics with aggregate shocks. J. Econ. Theory 1992, 57, 420–441. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar] [CrossRef]
- Kurokawa, S.; Ihara, Y. Emergence of cooperation in public goods games. Proc. R. Soc. Lond. B Biol. Sci. 2009, 276, 1379–1384. [Google Scholar] [CrossRef]
- Kurokawa, S.; Wakano, J.Y.; Ihara, Y. Generous cooperators can outperform non-generous cooperators when replacing a population of defectors. Theor. Popul. Biol. 2010, 77, 257–262. [Google Scholar] [CrossRef]
- Kollock, P. Social dilemmas: The anatomy of cooperation. Annu. Rev. Sociol 1998, 24, 183–214. [Google Scholar] [CrossRef]
- Milinski, M.; Semmann, D.; Krambeck, H.J.; Marotzke, J. Stabilizing the Earth’s climate is not a losing game: Supporting evidence from public goods experiments. Proc. Natl. Acad. Sci. USA 2006, 103, 3994–3998. [Google Scholar] [CrossRef] [PubMed]
- Hauert, C.; Schuster, H.G. Effects of increasing the number of players and memory size in the iterated Prisoner’s Dilemma: A numerical approach. Proc. R. Soc. Lond. B Biol. Sci. 1997, 264, 513–519. [Google Scholar] [CrossRef]
- Taylor, M. Anarchy and Cooperation; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Boyd, R.; Lorberbaum, J.P. No pure strategy is evolutionarily stable in the repeated prisoner’s dilemma game. Nature 1987, 327, 58–59. [Google Scholar] [CrossRef]
- Boyd, R. Mistakes allow evolutionary stability in the repeated prisoner’s dilemma game. J. Theor. Biol. 1989, 136, 47–56. [Google Scholar] [CrossRef]
- van Veelen, M. Robustness against indirect invasions. Games Econ. Behav. 2012, 74, 382–393. [Google Scholar] [CrossRef]
- van Veelen, M.; García, J.; Rand, D.G.; Nowak, M.A. Direct reciprocity in structured populations. Proc. Natl. Acad. Sci. USA 2012, 109, 9929–9934. [Google Scholar] [CrossRef]
- García, J.; van Veelen, M. In and out of equilibrium I: Evolution of strategies in repeated games with discounting. J. Econ. Theor. 2016, 161, 161–189. [Google Scholar] [CrossRef]
- Bonner, J.T. The Social Amoeba; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Yip, E.C.; Powers, K.S.; Aviles, L. Cooperative capture of large prey solves scaling challenge faced by spider societies. Proc. Natl. Acad. Sci. USA 2008, 105, 11818–11822. [Google Scholar] [CrossRef]
- Packer, C.; Scheel, D.; Pusey, A.E. Why lions form groups: Food is not enough. Am. Nat. 1990, 136, 1–19. [Google Scholar] [CrossRef]
- Creel, S. Cooperative hunting and group size: Assumptions and currencies. Anim. Behav. 1997, 54, 1319–1324. [Google Scholar] [CrossRef]
- Stander, P.E. Foraging dynamics of lions in semi-arid environment. Can. J. Zool. 1991, 70, 8–21. [Google Scholar] [CrossRef]
- Bednarz, J.C. Cooperative hunting Harris’ hawks Parabuteo unicinctus. Science 1988, 239, 1525–1527. [Google Scholar] [CrossRef]
- Rabenold, K.N. Cooperative enhancement of reproductive success in tropical wren societies. Ecology 1984, 65, 871–885. [Google Scholar] [CrossRef]
- Pacheco, J.M.; Santos, F.C.; Souza, M.O.; Skyrms, B. Evolutionary dynamics of collective action in N-person stag hunt dilemmas. Proc. R. Soc. Lond. B Biol. Sci. 2009, 276, 315–321. [Google Scholar] [CrossRef]
- Bach, L.A.; Helvik, T.; Christiansen, F.B. The evolution of n-player cooperation—Threshold games and ESS bifurcations. J. Theor. Biol. 2006, 238, 426–434. [Google Scholar] [CrossRef] [PubMed]
- Souza, M.O.; Pacheco, J.M.; Santos, F.C. Evolution of cooperation under n-person snowdrift games. J. Theor. Biol. 2009, 260, 581–588. [Google Scholar] [CrossRef] [PubMed]
- De Jaegher, K. Harsh environments and the evolution of multi-player cooperation. Theor. Popul. Biol. 2017, 113, 1–12. [Google Scholar] [CrossRef]
- Taylor, C.; Nowak, M.A. Transforming the dilemma. Evolution 2007, 61, 2281–2292. [Google Scholar] [CrossRef]
- Nowak, M.A.; Tarnita, C.E.; Wilson, E.O. The evolution of eusociality. Nature 2010, 466, 1057–1062. [Google Scholar] [CrossRef]
- Allen, B.; Nowak, M.A.; Wilson, E.O. Limitations of inclusive fitness. Proc. Natl. Acad. Sci. USA 2013, 110, 20135–20139. [Google Scholar] [CrossRef]
- Allen, B.; Nowak, M.A. Games among relatives revisited. J. Theor. Biol. 2015, 378, 103–116. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, S. Payoff non-linearity sways the effect of mistakes on the evolution of reciprocity. Math. Biosci. 2016, 279, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, S. Imperfect information facilitates the evolution of reciprocity. Math. Biosci. 2016, 276, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Peña, J.; Lehmann, L.; Nöldeke, G. Gains from switching and evolutionary stability in multi-player matrix games. J. Theor. Biol. 2014, 346, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M.; Scheuring, I. Review: Game theory of public goods in one-shot social dilemmas without assortment. J. Theor. Biol. 2012, 299, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Bomze, I.; Pawlowitsch, C. One-third rules with equality: Second-order evolutionary stability conditions in finite populations. J. Theor. Biol. 2008, 254, 616–620. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; García, J.; Hauert, C.; Traulsen, A. Extrapolating weak selection in evolutionary games. Plos. Comput. Biol. 2013, 9, e1003381. [Google Scholar] [CrossRef] [PubMed]
- Slade, P.F. On risk-dominance and the ‘1/3—Rule’ in 2X2 evolutionary games. IJPAM 2017, 113, 649–664. [Google Scholar] [CrossRef]
- Moran, P.A.P. Random processes in genetics. Math. Proc. Camb. 1958, 54, 60–71. [Google Scholar] [CrossRef]
- Deng, K.; Li, Z.; Kurokawa, S.; Chu, T. Rare but severe concerted punishment that favors cooperation. Theor. Popul. Biol. 2012, 81, 284–291. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Z. The public goods game with a new form of shared reward. J. Stat. Mech. Theor. Exp. 2016, 10, 103201. [Google Scholar] [CrossRef]
- Kurokawa, S.; Ihara, Y. Evolution of social behavior in finite populations: A payoff transformation in general n-player games and its implications. Theor. Popul. Biol. 2013, 84, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, C.S.; Traulsen, A. Evolutionary games in the multiverse. Proc. Natl. Acad. Sci. USA 2010, 107, 5500–5504. [Google Scholar] [CrossRef] [PubMed]
- Hirshleifer, J. From weakest-link to best-shot: The voluntary provision of public goods. Public Choice 1983, 41, 371–386. [Google Scholar] [CrossRef]
- Diekmann, A. Volunteer’s dilemma. J. Confl. Resolut. 1985, 29, 605–610. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gachter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef]
- Kocher, M.G.; Cherry, T.; Kroll, S.; Netzer, R.J.; Sutter, M. Conditional cooperation on three continents. Econ. Lett. 2008, 101, 175–178. [Google Scholar] [CrossRef]
- Herrmann, B.; Thöni, C. Measuring conditional cooperation: A replication study in Russia. Exp. Econ. 2009, 12, 87–92. [Google Scholar] [CrossRef]
- Martinsson, P.; Pham-Khanh, N.; Villegas-Palacio, C. Conditional cooperation and disclosure in developing countries. J. Econ. Psychol. 2013, 34, 148–155. [Google Scholar] [CrossRef]
- Takezawa, M.; Price, M.E. Revisiting “the evolution of reciprocity in sizable groups”: Continuous reciprocity in the repeated n-person prisoner’s dilemma. J. Theor. Biol. 2010, 264, 188–196. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the prisoner’s dilemma game. Nature 1993, 364, 56–58. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, S. Persistence extends reciprocity. Math. Biosci. 2017, 286, 94–103. [Google Scholar] [CrossRef] [PubMed]
- Hayden, B.Y.; Platt, M.L. Gambling for gatorade: Risk-sensitive decision making for fluid rewards in humans. Anim. Cogn. 2009, 12, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Scheibehenne, B.; Wilke, A.; Todd, P.M. Expectations of clumpy resources influence predictions of sequential events. Evol. Hum. Behav. 2011, 32, 326–333. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, B.; Zhou, H.-J. Social cycling and conditional responses in the rock-paper-scissors game. Sci. Rep. 2014, 4, 5830. [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Masuda, N. Win-stay lose-shift strategy in formation changes in football. EPJ 257 Data Sci. 2015, 4, 9. [Google Scholar] [CrossRef]
- Kurokawa, S. Evolution of cooperation: The analysis of the case wherein a different player has a different benefit and a different cost. Lett. Evol. Behav. Sci. 2016, 7, 5–8. [Google Scholar] [CrossRef]
- Bowles, S.; Gintis, H. A Cooperative Secies: Human Reciprocity and its Evolution; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Kurokawa, S. Does imperfect information always disturb the evolution of reciprocity? Lett. Evol. Behav. Sci. 2016, 7, 14–16. [Google Scholar] [CrossRef]
- Kurokawa, S. Evolutionary stagnation of reciprocators. Anim. Behav. 2016, 122, 217–225. [Google Scholar] [CrossRef]
- Kurokawa, S. Unified and simple understanding for the evolution of conditional cooperators. Math. Biosci. 2016, 282, 16–20. [Google Scholar] [CrossRef]
- Kurokawa, S. The extended reciprocity: Strong belief outperforms persistence. J. Theor. Biol. 2017, 421, 16–27. [Google Scholar] [CrossRef] [PubMed]
- Kurokawa, S.; Ihara, Y. Evolution of group-wise cooperation: Is direct reciprocity insufficient? J. Theor. Biol. 2017, 415, 20–31. [Google Scholar] [CrossRef] [PubMed]
| Strategy of the focal individual | ||||||
| A | ||||||
| B | ||||||
| Ranking | ||
|---|---|---|
| 1 | (1,0,0,0,0,0,0,1,1,1,1) | 40.39 |
| 2 | (1,0,0,0,0,0,1,1,1,1,1) | 38.14 |
| 3 | (1,0,0,0,0,0,0,0,1,1,1) | 36.35 |
| 4 | (1,0,0,0,0,0,1,0,1,1,1) | 34.1 |
| 5 | (1,0,0,0,0,1,0,1,1,1,1) | 31.85 |
| 6 | (1,0,0,0,0,0,0,1,0,1,1) | 30.06 |
| 7 | (1,0,0,0,0,1,1,1,1,1,1) | 29.59 |
| 8 | (1,0,0,0,0,1,0,0,1,1,1) | 27.81 |
| 8 | (1,0,0,0,0,0,1,1,0,1,1) | 27.81 |
| 10 | (1,0,0,0,0,0,0,0,0,1,1) | 26.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurokawa, S.; Wakano, J.Y.; Ihara, Y. Evolution of Groupwise Cooperation: Generosity, Paradoxical Behavior, and Non-Linear Payoff Functions. Games 2018, 9, 100. https://doi.org/10.3390/g9040100
Kurokawa S, Wakano JY, Ihara Y. Evolution of Groupwise Cooperation: Generosity, Paradoxical Behavior, and Non-Linear Payoff Functions. Games. 2018; 9(4):100. https://doi.org/10.3390/g9040100
Chicago/Turabian StyleKurokawa, Shun, Joe Yuichiro Wakano, and Yasuo Ihara. 2018. "Evolution of Groupwise Cooperation: Generosity, Paradoxical Behavior, and Non-Linear Payoff Functions" Games 9, no. 4: 100. https://doi.org/10.3390/g9040100
APA StyleKurokawa, S., Wakano, J. Y., & Ihara, Y. (2018). Evolution of Groupwise Cooperation: Generosity, Paradoxical Behavior, and Non-Linear Payoff Functions. Games, 9(4), 100. https://doi.org/10.3390/g9040100




