An Approach to Chance Constrained Problems Based on Huge Data Sets Using Weighted Stratified Sampling and Adaptive Differential Evolution †
Abstract
1. Introduction
2. Problem Formulation
- A vector of decision variables
- A vector of random variables
- A huge number of data, or a full data set
- Measurable function for constraints ,
- Objective function to be minimized
- Sufficiency level given by a probability .
2.1. Chance Constrained Problem (CCP)
2.2. Equivalence Problem of CCP
3. Data Reduction Methods
3.1. Simple Random Sampling (SRS)
3.1.1. Procedure of SRS
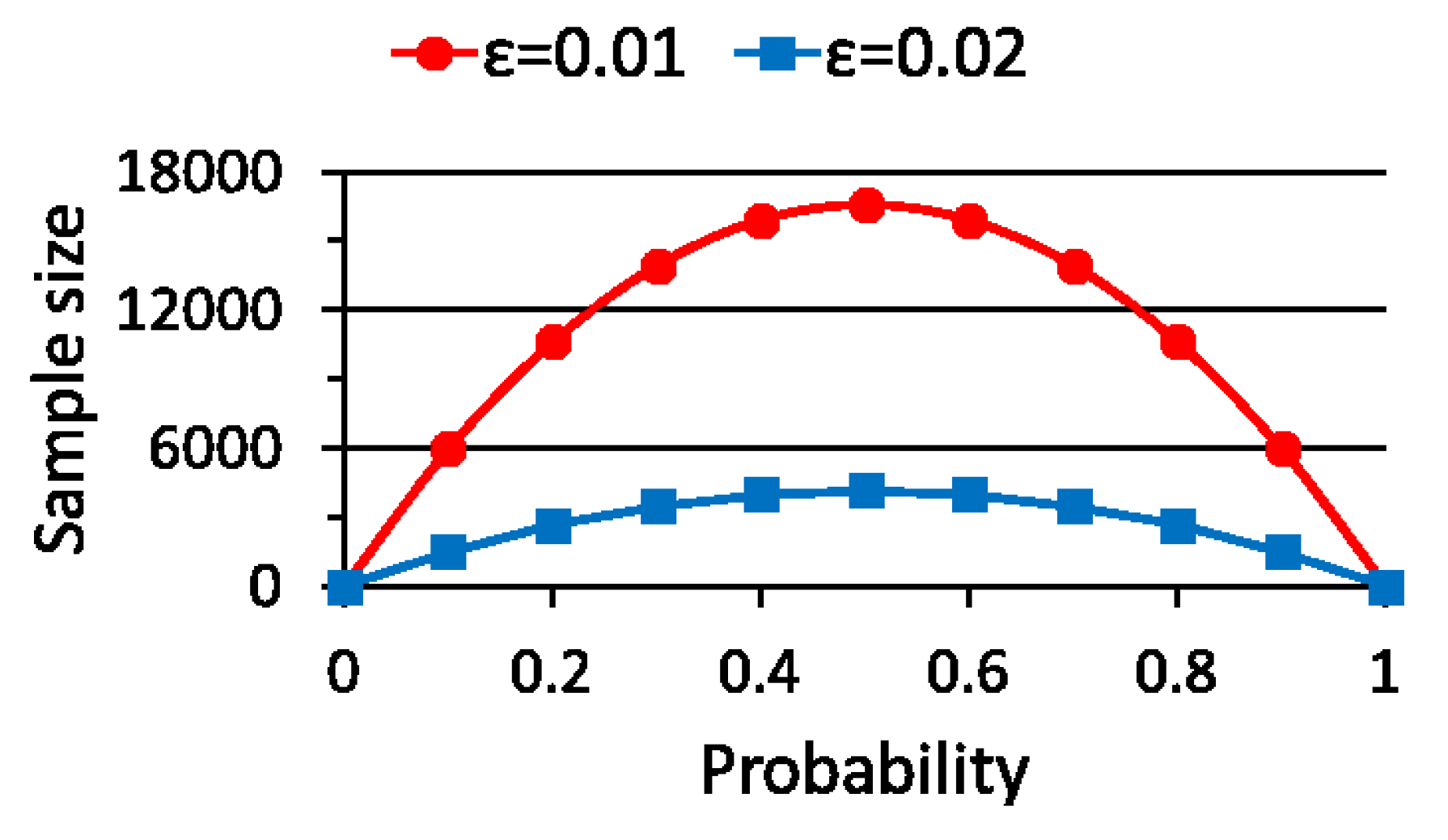
3.1.2. Theoretical Sample Size
3.2. Weighted Stratified Sampling (WSS)
3.2.1. Procedure of WSS
- Step 1:
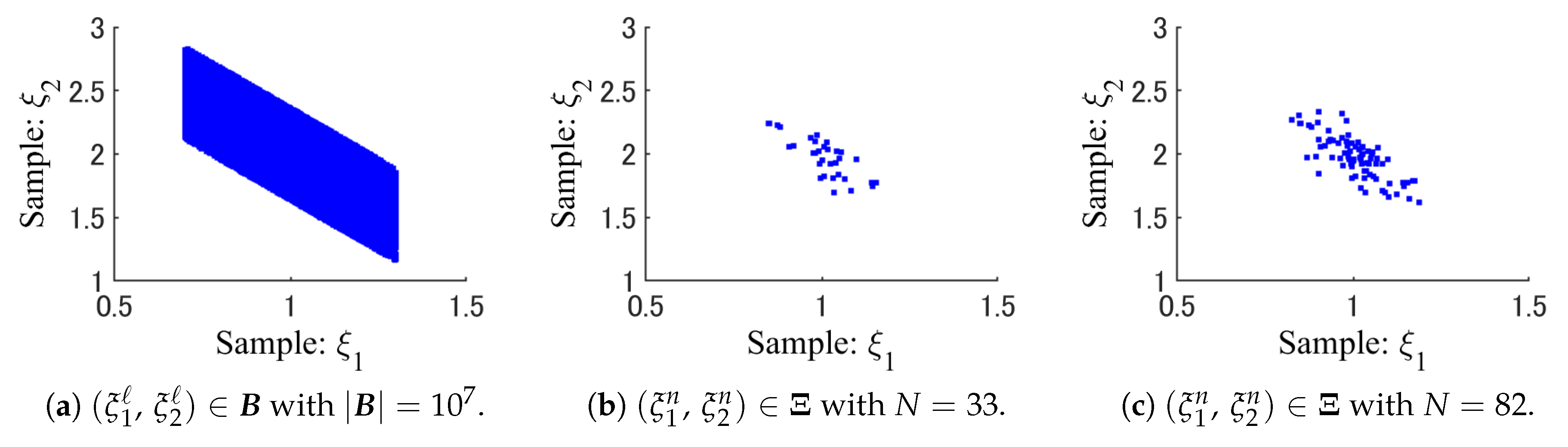
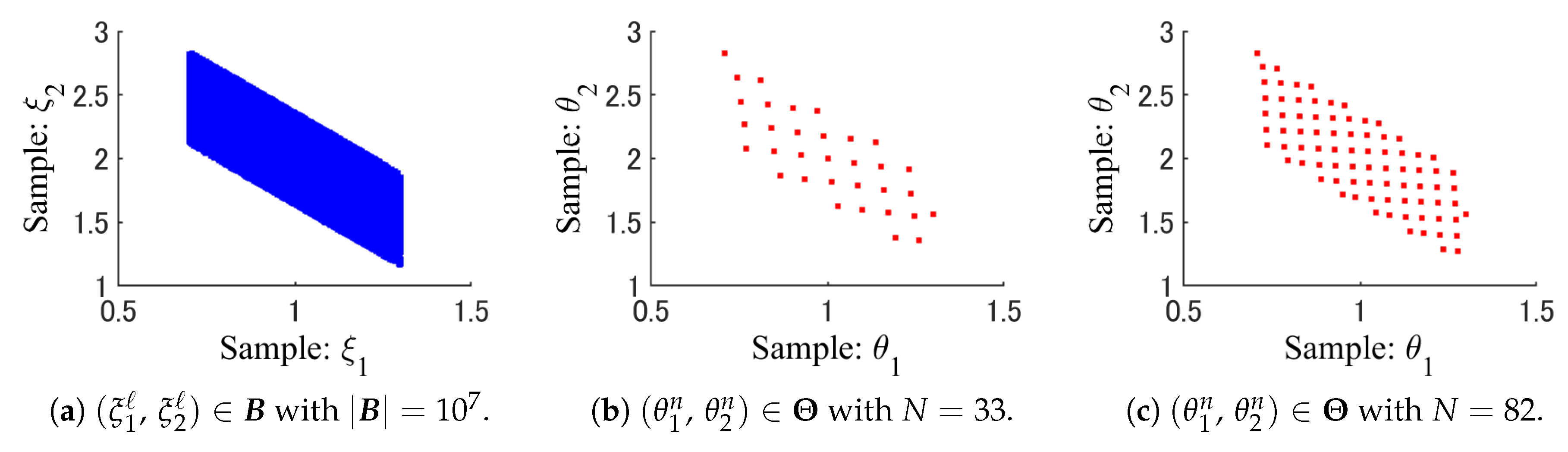
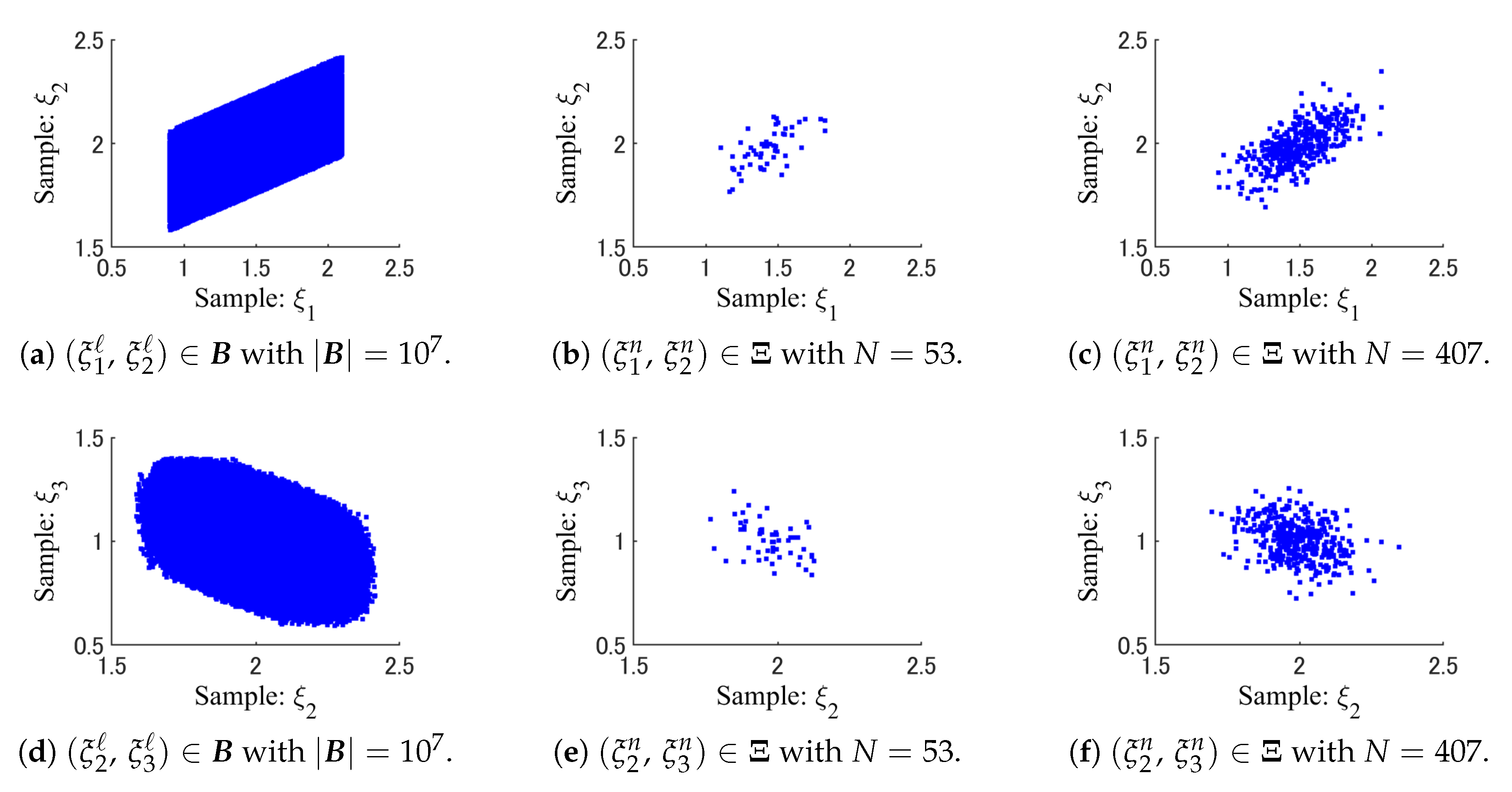
- By using a K-dimensional histogram, the full data set is divided exclusively into some strata , aswhere and , .Specifically, the K-dimensional histogram is a K-dimensional hypercube that contains the full data set . On each side of the K-dimensional hypercube, the entire range of data is divided into a series of intervals. In this paper, the number of intervals is the same on all sides. Moreover, all intervals on each side have equal widths. Therefore, the K-dimensional histogram is an equi-width histogram [26]. Each bin of the K-dimensional histogram is also a K-dimensional hypercube. Then, nonempty bins are used to define strata , .
- Step 2:
- A new sample point is generated for each stratum , . Then, the sample set is defined as .
- Step 3:
- The weight of each sample is given by the size of as .
3.2.2. Sample Generation by WSS
3.3. Relaxation Problems of CCP
4. Adaptive Differential Evolution with Pruning Technique
4.1. Strategy of DE
4.2. Adaptive Control of Parameters
4.3. Constraint Handling and Pruning Technique in Selection
4.4. Proposed Algorithm of ADEP
- Step 1:
- Randomly generate the initial population , . .
- Step 2:
- For to , evaluate and for each vector .
- Step 3:
- If holds, output the best solution and terminate ADEP.
- Step 4:
- For to , generate the trial vector from the target vector .
- Step 5:
- For to , evaluate for the trial vector .
- Step 6:
- For to , evaluate for only if the condition in (24) is not satisfied.
- Step 7:
- For to , select either or for . .
- Step 8:
- Go back to Step 3.
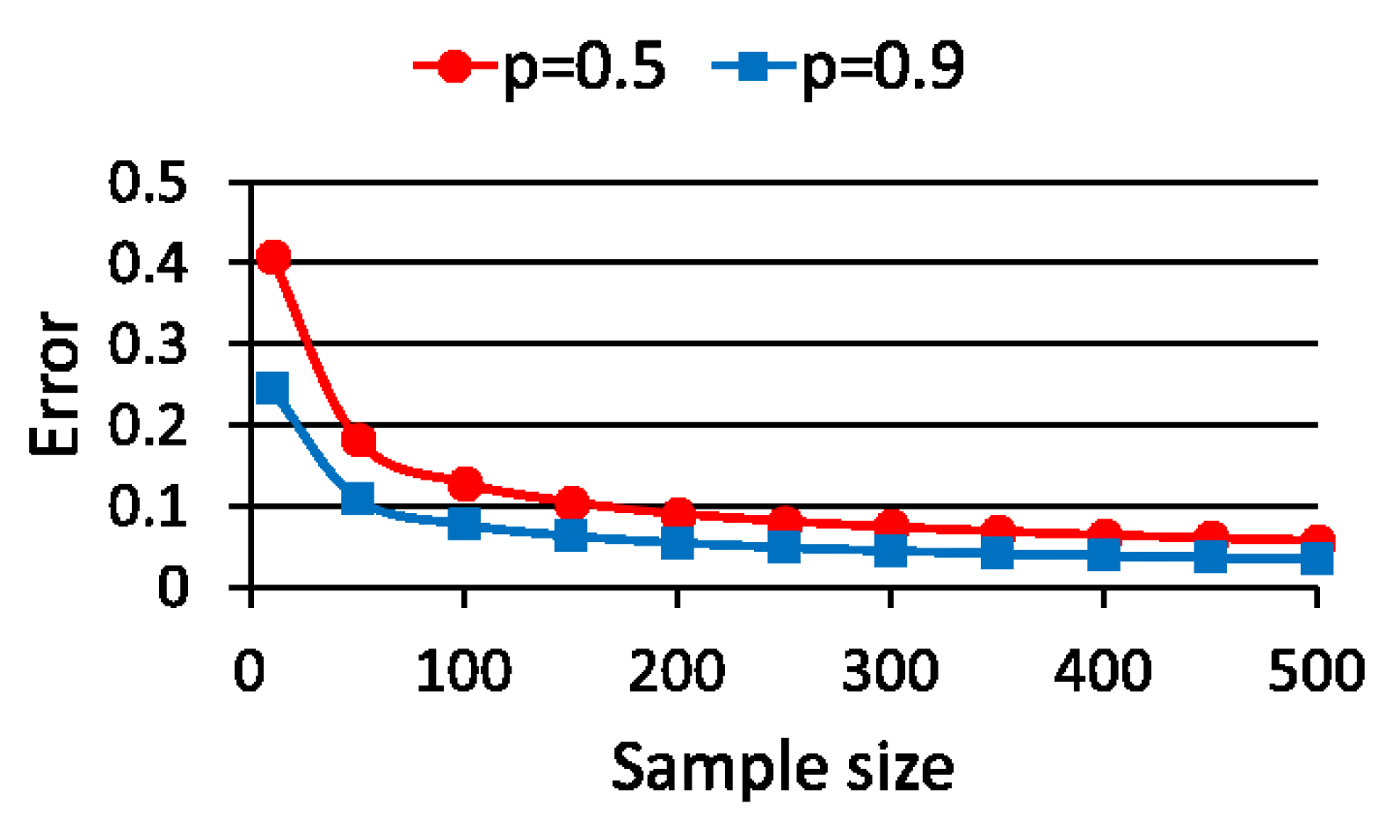
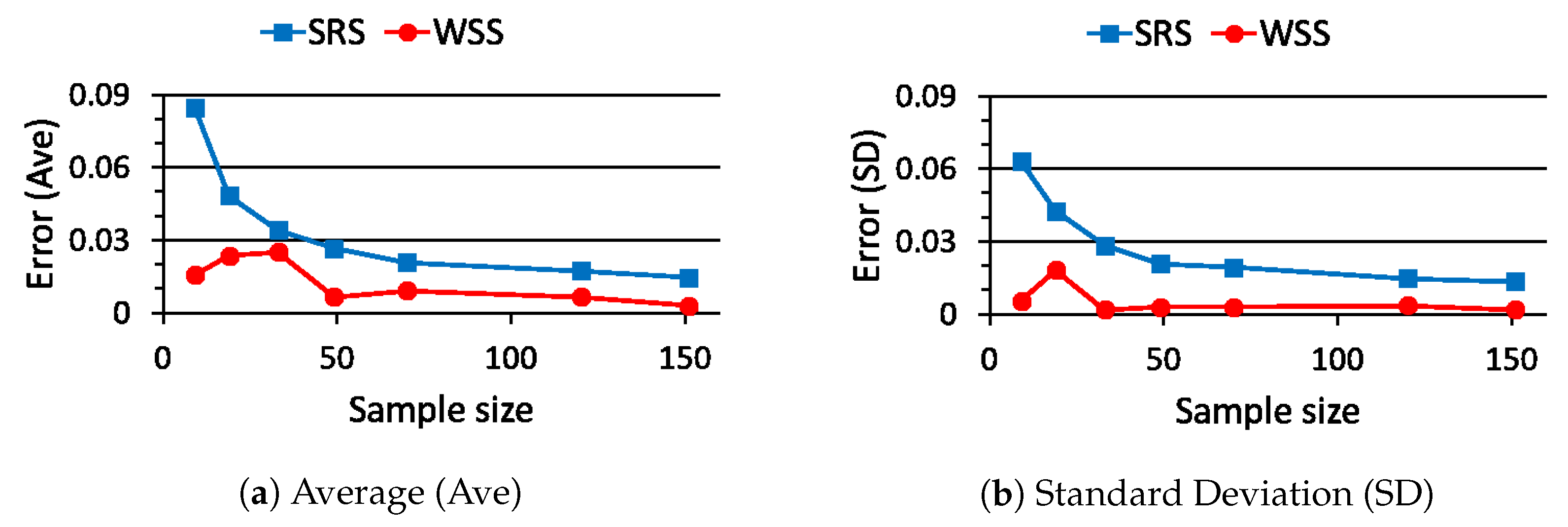
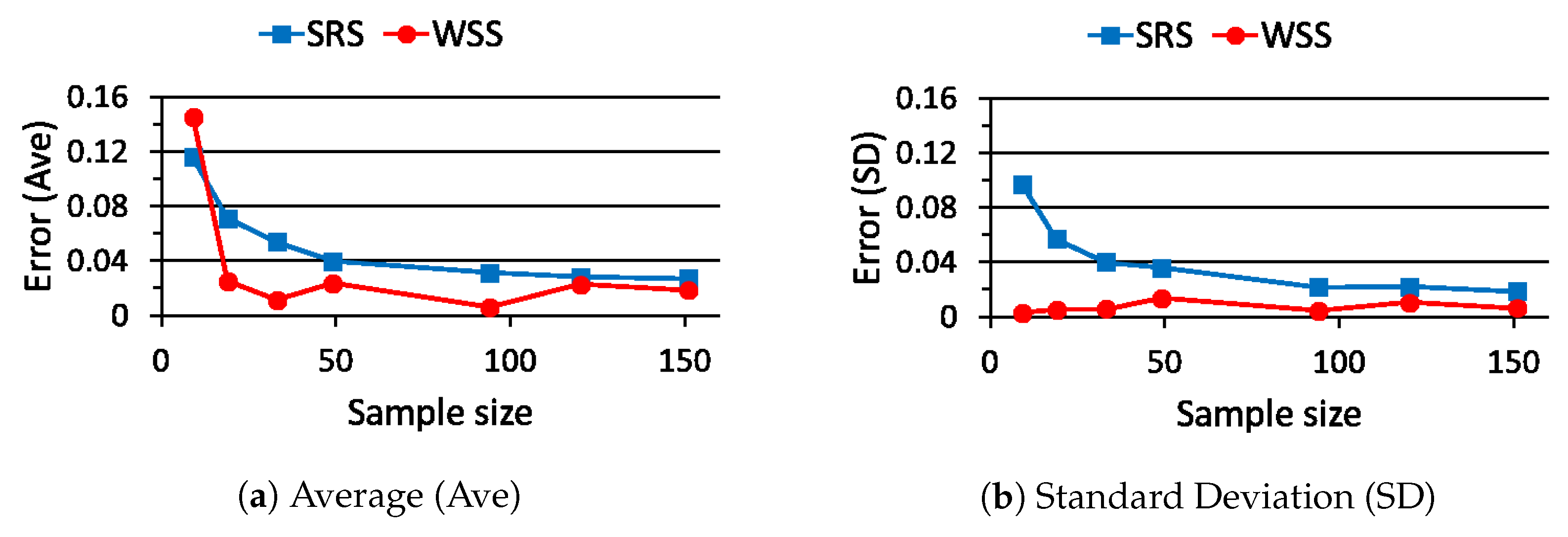
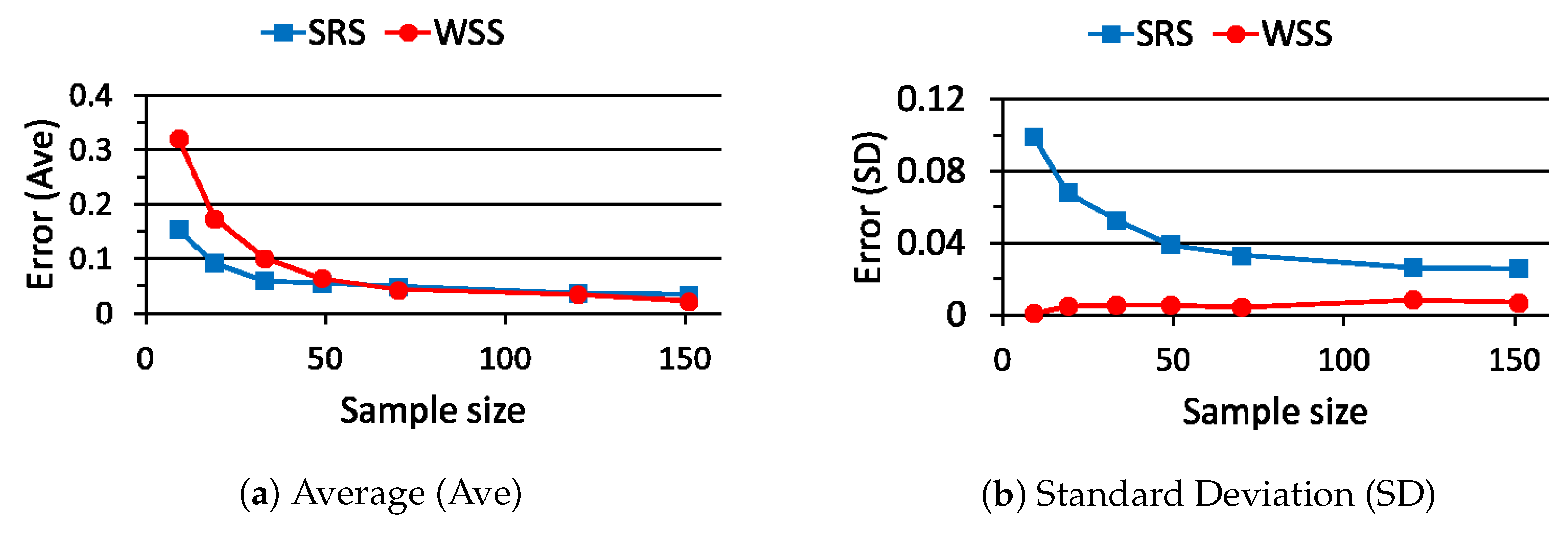
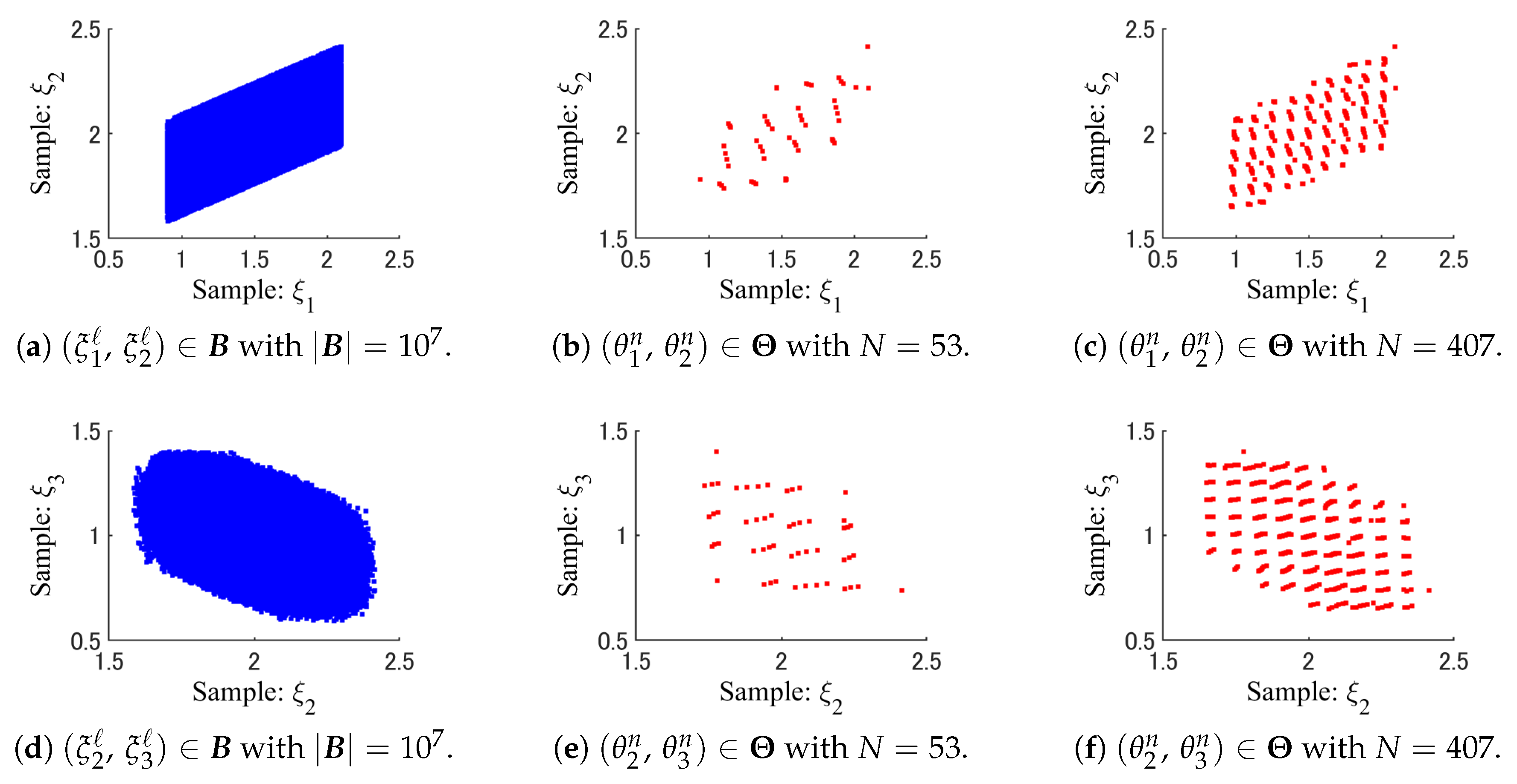
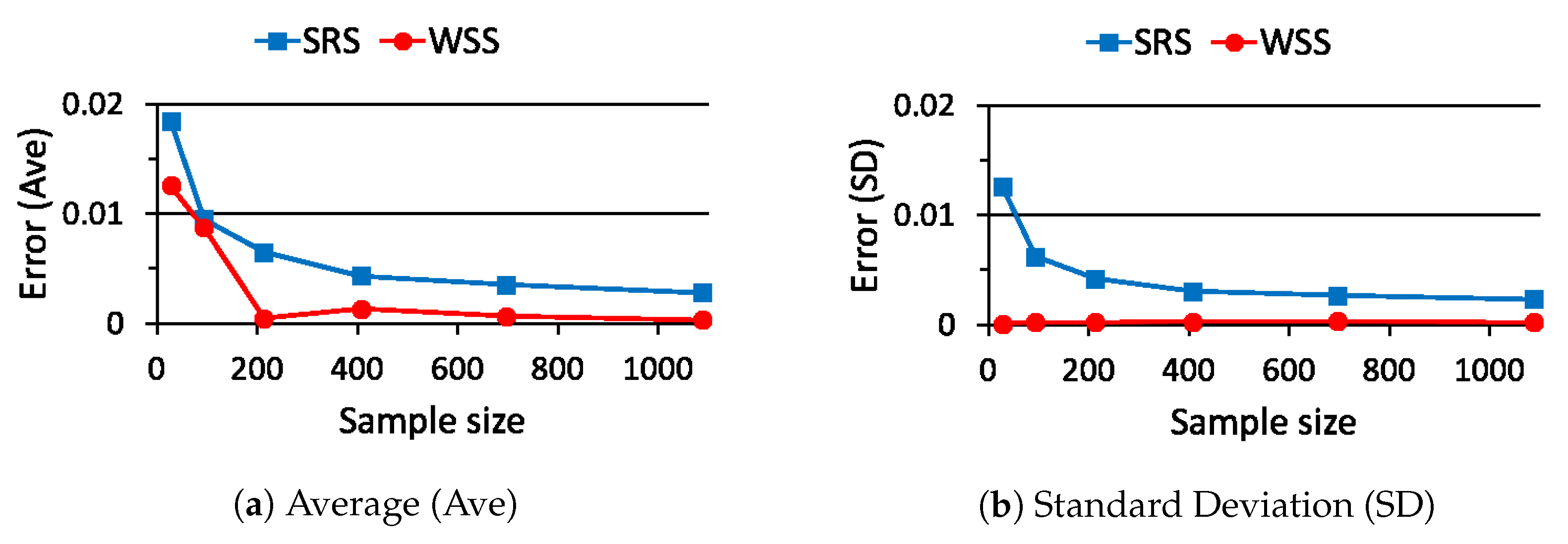
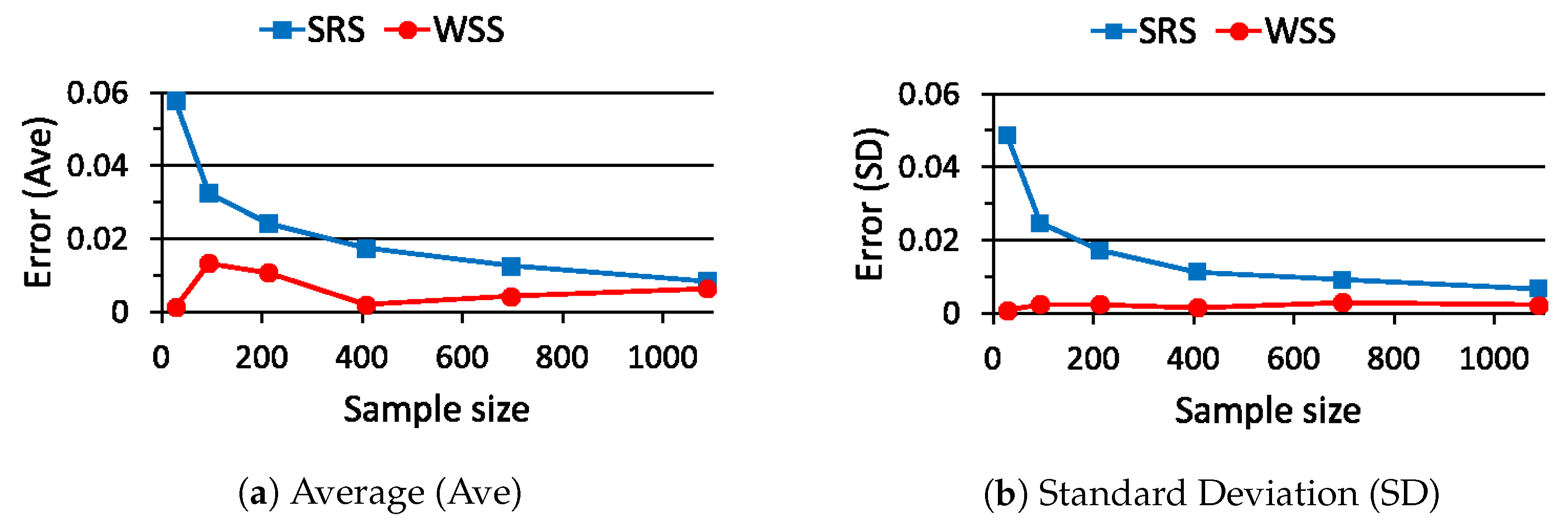
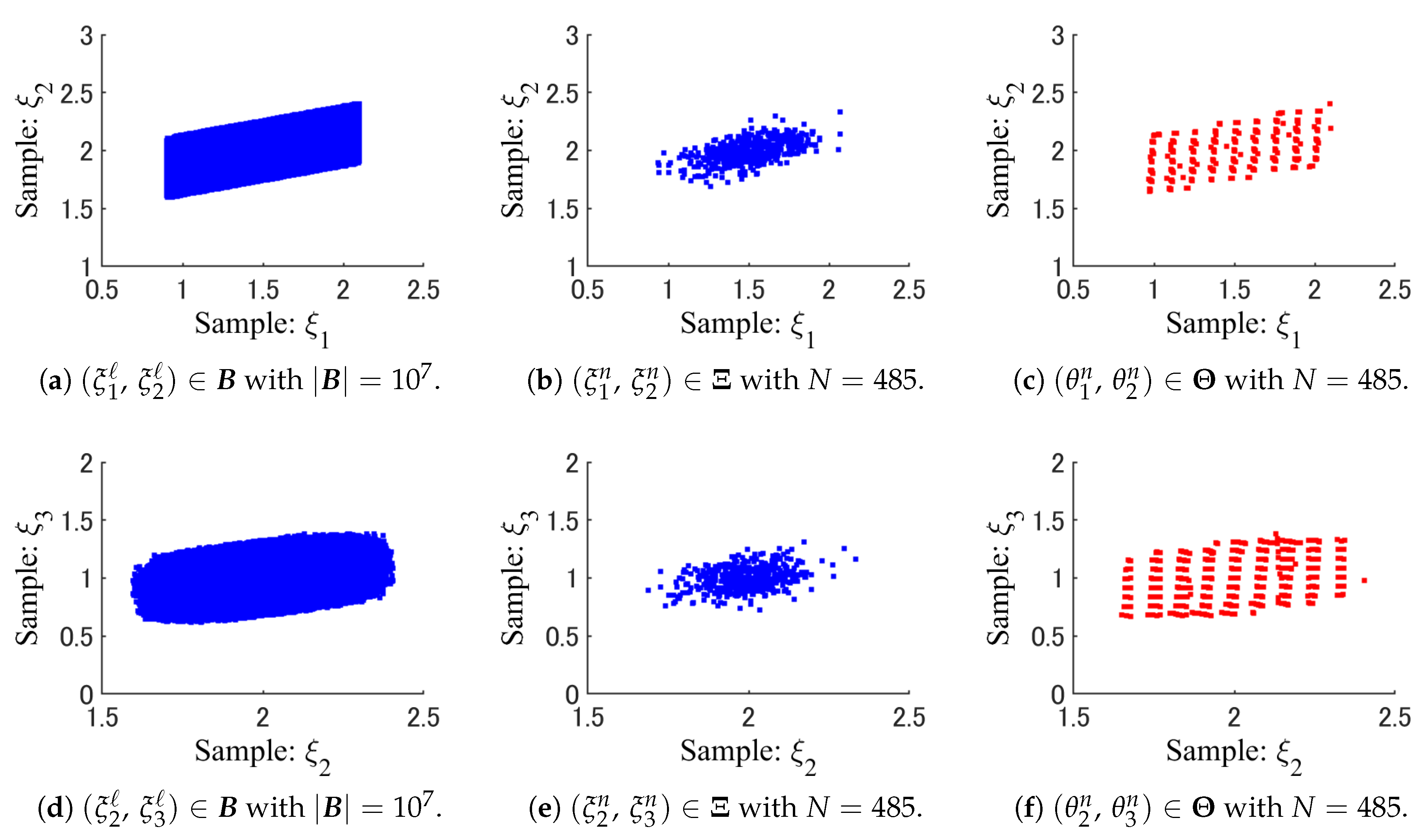
5. Performance Evaluation of WSS
5.1. Case Study 1
5.2. Case Study 2
5.3. Case Study 3
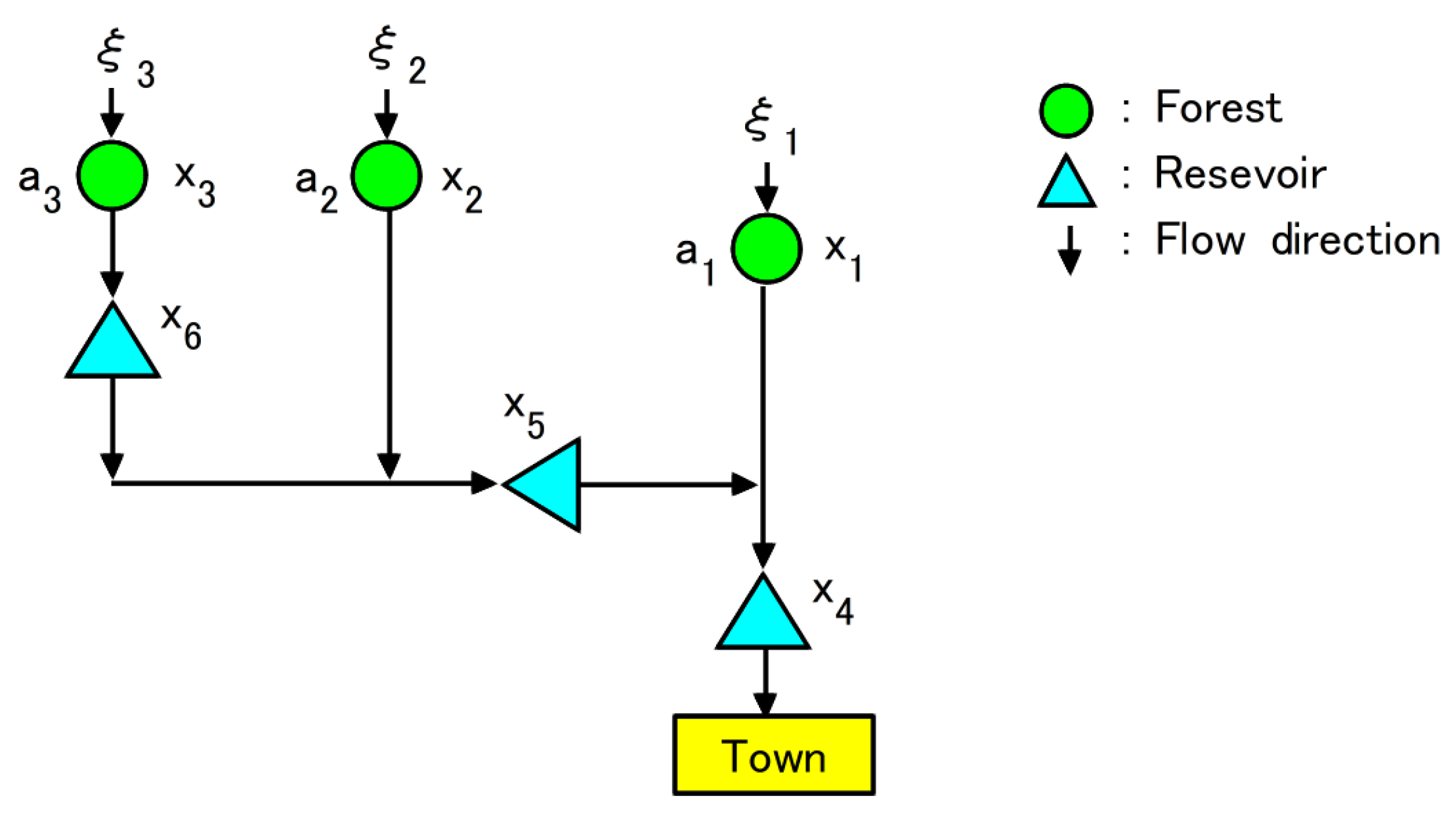
6. Flood Control Planning
6.1. Formulation of CCP
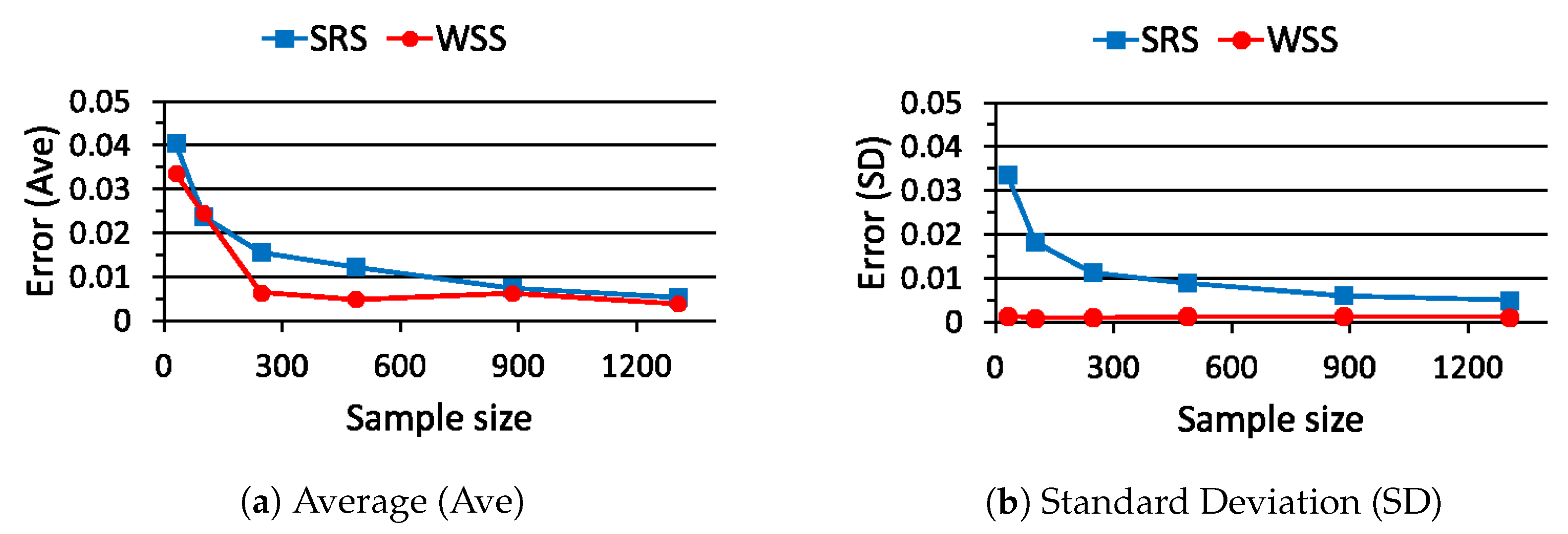
6.2. Comparison of SRS and WSS
6.3. Solution of CCP
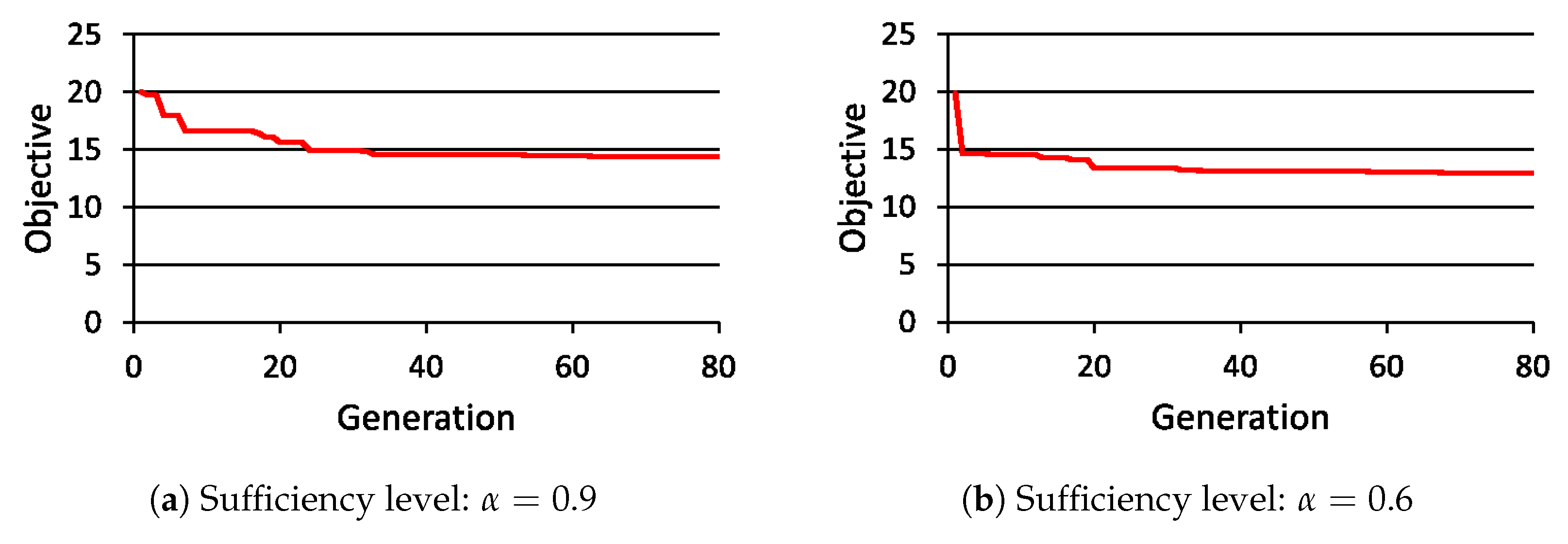
7. Performance Evaluation of ADEP
8. Conclusions
- How to properly make the strata from a full data set for WSS: The performance of WSS depends on the stratification method such as the number of strata and the shape of each stratum. By improving the stratification method, the optimal sample size of WSS will also be found.
- How to feedback the values of functions to generate samples : If we can use the function values effectively, we must be able to make the strata for WSS adaptively.
- How to cope with high-dimensional data sets: Since the similarity of data which are assigned in the same stratum is reduced in proportion to the dimensionality of the full data set, it may be hard to represent all data only by one sample .
Funding
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| ADE | Adaptive Differential Evolution |
| ADEP | Adaptive Differential Evolution with Pruning technique |
| CCP | Chance Constrained Problem |
| CHT | Constraint Handling Technique |
| DE | Differential Evolution |
| EA | Evolutionary Algorithm |
| SRS | Simple Random Sampling |
| WSS | Weighted Stratified Sampling |
References
- Ben-Tal, A.; Ghaoui, L.E.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Prékopa, A. Stochastic Programming; Kluwer Academic Publishers: Berlin, Germany, 1995. [Google Scholar]
- Uryasev, S.P. Probabilistic Constrained Optimization: Methodology and Applications; Kluwer Academic Publishers: Berlin, Germany, 2001. [Google Scholar]
- Lubin, M.; Dvorkin, Y.; Backhaus, S. A robust approach to chance constrained optimal power flow with renewable generation. IEEE Trans. Power Syst. 2016, 31, 3840–3849. [Google Scholar] [CrossRef]
- Tagawa, K.; Miyanaga, S. An approach to chance constrained problems using weighted empirical distribution and differential evolution with application to flood control planning. Electron. Commun. Jpn. 2019, 102, 45–55. [Google Scholar] [CrossRef]
- Bazaraa, M.S.; Sherali, H.D.; Shetty, C.M. Nonlinear Programming: Theory and Algorithm; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Poojari, C.A.; Varghese, B. Genetic algorithm based technique for solving chance constrained problems. Eur. J. Oper. Res. 2008, 185, 1128–1154. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, Q.; Fernández, F.V.; Gielen, G.G.E. An efficient evolutionary algorithm for chance-constrained bi-objective stochastic optimization. IEEE Trans. Evol. Comput. 2013, 17, 786–796. [Google Scholar] [CrossRef]
- Tagawa, K.; Miyanaga, S. Weighted empirical distribution based approach to chance constrained optimization problems using differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC2017), San Sebastian, Spain, 5–8 June 2017; pp. 97–104. [Google Scholar]
- Kroese, D.P.; Taimre, T.; Botev, Z.I. Handbook of Monte Carlo Methods; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tagawa, K. Group-based adaptive differential evolution for chance constrained portfolio optimization using bank deposit and bank loan. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC2019), Wellington, New Zealand, 10–13 June 2019; pp. 1556–1563. [Google Scholar]
- Xu, L.D.; He, W.; Li, S. Internet of things in industries: A survey. IEEE Trans. Ind. Inform. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Rossi, E.; Rubattion, C.; Viscusi, G. Big data use and challenges: Insights from two internet-mediated surveys. Computers 2019, 8, 73. [Google Scholar] [CrossRef]
- Kile, H.; Uhlen, K. Data reduction via clustering and averaging for contingency and reliability analysis. Electr. Power Energy Syst. 2012, 43, 1435–1442. [Google Scholar] [CrossRef]
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A. A survey of clustering algorithms for big data: Taxonomy and empirical analysis. IEEE Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- Jayaram, N.; Baker, J.W. Efficient sampling and data reduction techniques for probabilistic seismic lifeline risk assessment. Earthq. Eng. Struct. Dyn. 2010, 39, 1109–1131. [Google Scholar] [CrossRef]
- Tagawa, K. Data reduction via stratified sampling for chance constrained optimization with application to flood control planning. In Proceedings of the ICIST 2019, CCIS 1078, Vilnius, Lithuania, 10–12 October 2019; Springer: Cham, Switzerland, 2019; pp. 485–497. [Google Scholar]
- Price, K.; Storn, R.M.; Lampinen, J.A. Differential Evolution: A Practical Approach to Global Optimization; Springer: Cham, Switzerland, 2005. [Google Scholar]
- Brest, J.; Greiner, S.; Boskovic, B.; Merink, M.; Zumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Yazdi, J.; Neyshabouri, S.A.A.S. Optimal design of flood-control multi-reservoir system on a watershed scale. Nat. Hazards 2012, 63, 629–646. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, P.; Chen, X.; Wang, L.; Ai, X.; Feng, M.; Liu, D.; Liu, Y. Optimal operation of multi-reservoir systems considering time-lags of flood routing. Water Resour. Manag. 2016, 30, 523–540. [Google Scholar] [CrossRef]
- Zhou, C.; Sun, N.; Chen, L.; Ding, Y.; Zhou, J.; Zha, G.; Luo, G.; Dai, L.; Yang, X. Optimal operation of cascade reservoirs for flood control of multiple areas downstream: A case study in the upper Yangtze river basin. Water 2018, 10, 1250. [Google Scholar] [CrossRef]
- Ash, R.B. Basic Probability Theory; Dover: Downers Grove, IL, USA, 2008. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining—Concepts and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2012. [Google Scholar]
- Tempo, R.; Calafiore, G.; Dabbene, F. Randomized Algorithms for Analysis and Control of Uncertain Systems: With Applications; Springer: Cham, Switzerland, 2012. [Google Scholar]
- Poosala, V.; Ioannidis, Y.E.; Haas, P.J.; Shekita, E.J. Improved histograms for selectivity estimation of range predicates. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Montreal, QC, Canada, 4–6 June 1996; pp. 294–305. [Google Scholar]
- Cormode, G.; Garofalakis, M. Histograms and wavelets on probabilistic data. IEEE Trans. Knowl. Data Eng. 2010, 22, 1142–1157. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Eltaeib, T.; Mahmood, A. Differential evolution: A survey and analysis. Appl. Sci. 2018, 8, 1945. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Reviewing and benchmarking parameter control methods in differential evolution. IEEE Trans. Evol. Comput. 2020, 50, 1170–1184. [Google Scholar] [CrossRef]
- Montes, E.E.; Coello, C.A.C. Constraint-handling in nature inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Prékopa, A.; Szántai, T. Flood control reservoir system design using stochastic programming. Math. Progr. Study 1978, 9, 138–151. [Google Scholar]
- Maita, E.; Suzuki, M. Quantitative analysis of direct runoff in a forested mountainous, small watershed. J. Jpn. Soc. Hydrol. Water Resour. 2009, 22, 342–355. [Google Scholar] [CrossRef][Green Version]
- Martinez, A.R.; Martinez, W.L. Computational Statistics Handbook with MATLAB ®, 2nd ed.; Chapman & Hall/CRC: London, UK, 2008. [Google Scholar]
- Monrat, A.A.; Islam, R.U.; Hossain, M.S.; Andersson, K. Challenges and opportunities of using big data for assessing flood risks. In Applications of Big Data Analytics; Alani, M.M., Tawfik, H., Saeed, M., Anya, O., Eds.; Springer: Cham, Switzerland, 2018; Chapter 2; pp. 31–42. [Google Scholar]
- Reddy, P.C.; Babu, A.S. Survey on weather prediction using big data analytics. In Proceedings of the IEEE 2nd International Conference on Electrical, Computer and Communication Technologies, Coimbatore, India, 22–24 February 2017; pp. 1–6. [Google Scholar]
- Brociek, R.; Słota, D. Application of real ant colony optimization algorithm to solve space and time fractional heat conduction inverse problem. In Proceedings of the 22nd International Conference on Information and Software Technologies, ICIST2016, Communications in Computer and Information Science, Druskininkai, Lithuania, 13–15 October 2016; Springer: Cham, Switzerland, 2016; Volume 639, pp. 369–379. [Google Scholar]
| Generation: | Population Size: | Sample Size: N | Correction Level: |
|---|---|---|---|
| 80 | 30 | 482 |
| ADE | ADEP | ||||||
|---|---|---|---|---|---|---|---|
| Time [s] | Time [s] | Rate | |||||
| () | () | () | () | () | () | () | |
| () | () | () | () | () | () | () | |
| () | () | () | () | () | () | () | |
| () | () | () | () | () | () | () | |
| ADE | ADEP | ||||||
|---|---|---|---|---|---|---|---|
| Time [s] | Time [s] | Rate | |||||
| () | () | () | () | () | () | () | |
| () | () | () | () | () | () | () | |
| () | () | () | () | () | () | () | |
| () | () | () | () | () | () | () | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tagawa, K. An Approach to Chance Constrained Problems Based on Huge Data Sets Using Weighted Stratified Sampling and Adaptive Differential Evolution. Computers 2020, 9, 32. https://doi.org/10.3390/computers9020032
Tagawa K. An Approach to Chance Constrained Problems Based on Huge Data Sets Using Weighted Stratified Sampling and Adaptive Differential Evolution. Computers. 2020; 9(2):32. https://doi.org/10.3390/computers9020032
Chicago/Turabian StyleTagawa, Kiyoharu. 2020. "An Approach to Chance Constrained Problems Based on Huge Data Sets Using Weighted Stratified Sampling and Adaptive Differential Evolution" Computers 9, no. 2: 32. https://doi.org/10.3390/computers9020032
APA StyleTagawa, K. (2020). An Approach to Chance Constrained Problems Based on Huge Data Sets Using Weighted Stratified Sampling and Adaptive Differential Evolution. Computers, 9(2), 32. https://doi.org/10.3390/computers9020032





