Abstract
Wearable sensors play a significant role for monitoring the functional ability of the elderly and in general, promoting active ageing. One of the relevant variables to be tracked is the number of stair steps (single stair steps) performed daily, which is more challenging than counting flight of stairs and detecting stair climbing. In this study, we proposed a minimal complexity algorithm composed of a hierarchical classifier and a linear model to estimate the number of stair steps performed during everyday activities. The algorithm was calibrated on accelerometer and barometer recordings measured using a sensor platform worn at the wrist from 20 healthy subjects. It was then tested on 10 older people, specifically enrolled for the study. The algorithm was then compared with other three state-of-the-art methods, which used the accelerometer, the barometer or both. The experiments showed the good performance of our algorithm (stair step counting error: 13.8%), comparable with the best state-of-the-art (p > 0.05), but using a lower computational load and model complexity. Finally, the algorithm was successfully implemented in a low-power smartwatch prototype with a memory footprint of about 4 kB.
1. Introduction
Ageing is a physiological process characterised by many factors including a progressive loss of muscular strength, reduction of contraction speed and lower power production. These impairments might affect many aspects of functional abilities of older people that are essential to independent mobility [1]. In this regard, there is great interest in identifying clinical physical performance measures able to characterise the functional impairment of older adults, particularly for balance, gait, and stair climbing. Regarding the latter, the Stair Climb Power Test, 1-minute Stair Climb Test, 4-Step Stair Climb Power Test and 12-Step Stair Test have been developed for clinical evaluation [2,3,4]. Indeed, since climbing stairs involves a full control of balance and gait, as well as a sufficient muscular strength, assessing functional parameters while climbing stairs is clinically important for an overall description of how healthy the ageing process is. Despite the wide use of such clinical tests, their evaluation is limited within the clinical environment, typically when loss of functional ability has already occurred. On the contrary, frequent assessments would enable early detection of functional decline and initiate preventive measures [5].
Among the relevant functional parameters, it is well known that the number of steps performed daily is an indicator of healthy ageing. It therefore might be further relevant to investigate sensing modalities and algorithms capable of estimating the number of stair steps climbed on a daily basis, outside the clinical environment, as important clinical information about the ageing process and for the early detection of functional decline.
Human Activity Recognition (HAR) using wearable sensors is a branch of Computer Science that finds applications in a wide range of scenarios, such as fitness and sports [6], the entertainment industry [7], health monitoring and rehabilitation [8]. A comprehensive review on HAR can be found in [9]. HAR for active ageing using wearable sensors became an important ally to promote an active life style and to reduce age-related issues, such as movement, mental and cognitive disorders. In addition, along with the diffusion of inertial measurement units (IMUs), that are small in size and cheap, plenty of initiatives currently aim to promote active ageing, by quantifying the amount of physical activity performed by older people and their functional ability, [10,11].
In the context of HAR for detection of stair climbing, approaches mainly differ for the sensing modality, position of the sensor/s, features, algorithms used for classification, and target users. Sensors comprise IMUs [5,12,13,14,15] and their combined use with barometers [16,17,18,19,20,21]. Positions include wrist [16,17], chest [16,18,20], waist [5,12,17,19], calf and foot [13,14,15,16,21]. Common features are averages, ranges, Fourier Transform and Wavelet coefficients, statistical moments of sensor data, whereas classifiers are Support Vector Machine (SVM) [5,12,16,17,19], K-Nearest Neighbour (KNN) [5,16,17], Decision Tree and Random Forest [5,13,17,19], Artificial Neural Network (ANN) [22], and also convolutional NN [15]. Users span from healthy young people up to elderly patients with severe conditions such as Parkinson’s disease or stroke [5,16,20].
The main outcomes shared by all these relevant works are the following: (i) the use of the barometer highly improves classification accuracy for stair climbing detection; (ii) the only use of the accelerometer results in limited performance; (iii) sensor fusion of nine-axial sensors (accelerometer, gyroscope and magnetometer) achieves high performance but at the cost of complexity; (iv) the type of classifier plays a small role in the performance; and (v) position matters, with the trunk is the most reliable one [16] and the wrist is likely the most comfortable for the user, but with the highest amount of noise.
In this work, despite the current trend in Machine and Deep Learning where complex models are used for HAR, we investigated the design of a low-complexity algorithm to be deployed on a wearable device worn at the wrist to determine the number of stair steps (specifically: single stair steps) climbed by a population of older people. In fact, the application of interest is long-term monitoring that requires minimal battery consumption (and the avoidance of too frequent charges to improve usage by older people) which is easier to obtain by means of constraint hardware infrastructures and low-complexity algorithms. There are several innovations in the current work. First, we determined the actual number of stair steps climbed while the reported works only detect the phase of climbing stairs. Second, to achieve the final counting, we only used three simple features, despite the dozens of features normally computed for HAR. Thirdly, threshold-based classifiers were employed to further reduce the model complexity and battery expenditure. Fourthly, we considered only a limited set of sensors to perform the task, i.e., one triaxial accelerometer and one barometer. In fact, previous evidence questioned the advantage of a gyroscope for stair climbing detection [23], unless it is mounted on the foot [13]. Moreover, a gyroscope has typically a large energy requirement with respect to accelerometers [24]. Moreover, sensor fusion was excluded to further reduce complexity and energy consumption.
The algorithm was then tested and compared with two state-of-the-art methods in experiments performed outside the clinical environment, achieving good performance in terms of stair step counting. It was also successfully implemented in a wrist-worn prototype device. The work proved that in the case of a highly constraint hardware infrastructure and for the very specific task of counting the number of stair steps, a simple algorithm might be a sufficient trade-off between performance and model complexity.
2. Materials and Methods
2.1. Study Population and Data Acquisition
Data were collected by means of two different acquisition campaigns.
The first one comprised 56 acquisition sessions (total duration: 103.79 min) performed by 20 healthy volunteers (6 females and 14 males; age: years, range: 16–61 years). Data were recorded while performing common everyday activities such as walking, running, staying still, taking the elevator and climbing or running on the stairs. These recordings were carried out varying, for example, the speed of some actions or choosing environments with different slopes to have a wide range of situations. The first dataset was used as the training set.
Triaxial accelerometer data and pressure readings of the training set were collected through a Wearable Medical Platform (WMP) device (Flex Design srl, Milan, Italy). The device was not employed in its standard modality (medical patch), but it was adapted to be worn at the wrist to emulate the usage of a smartwatch. The sampling rates of the accelerometer and barometer sensors were set to 50 Hz and 25 Hz, respectively, whereas their resolutions were g and millibar.
The second dataset comprised 10 recordings (total duration: 28.73 min) performed by ten older people living independently that were informed about the aim of the research and accepted to participate to the study (3 females and 7 males; age: years, range: 63–77 years). To simulate a real everyday scenario, participants were invited in a public space where they were asked to perform a common experimental protocol. Each subject freely walked about 10 meters in a hallway at the ground floor of the selected building, including walking uphill and downhill on a ramp. Then, they climbed stairs up to the second floor and returned to the initial position at the ground floor. Finally, subjects went up and down to the second floor by the elevator. In two situations, the protocol was slightly modified to accommodate participant’s requirements (i.e., one asked to avoid the elevator due to claustrophobia; a second did not stop and climbed an extra flight of stairs). These changes did not jeopardize the objectives of the experiments and thus, the recordings were anyhow included. This second dataset was our test set.
Accelerometer and barometer data of the test set were collected using an ad-hoc device, developed and described in Section 4. Briefly, the sampling rates and resolutions of the two sensors were identical to those in the WMP, with the exception of the accelerometer whose resolution was g.
During the experiments, each activity was labeled to describe the content of the action and then used as gold standard. Given the objectives of the study, we categorized the activities into three groups: (i) going upstairs; (ii) going downstairs; and (iii) any other activity (to identify and measure the number of false positives detected while not climbing stairs). It is worth noting that walking uphill and downhill were included in the third group (making the distinction with climbing more challenging). We manually tracked the starting and ending times of each action by means of a commercial stopwatch. Afterwards, the accelerometer and barometric signals were manually segmented to separate the various activities and split into 5 s segments (each segment containing only one type of activity). Segments shorter than 5 s were discarded during the training phase.
2.2. Algorithm for Stair-Step Counting
In this section, we proposed a pipeline comprising of a hierarchical classifier and a linear regression model to count the number of stair steps climbed. Hereafter, we named our algorithm .
The algorithm is composed of three main blocks. In the first one, we used the barometric data to detect the time intervals in which the sensor likely changed its altitude. The block also discarded intervals in which the altitude changed too quickly with respect to human movement capabilities. The outcome of the first block was then further processed by the second block, meant to detect periodic movements in the range of physiological step frequency. Finally, in the third block, the time intervals during which the periodic movement was detected were then used to estimate the number of stair steps through a linear regression model. Figure 1 shows the diagram of the entire pipeline developed.
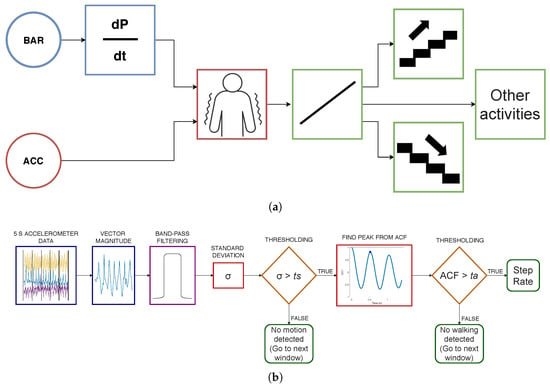
Figure 1.
Diagram of the three blocks composing the proposed pipeline (a). Colors indicate different blocks. In the first one, the time derivative of pressure data in a 5 s window is computed and then two thresholds ( and ) are used to detect whether the derivative resembles that of the range of human movement while climbing stairs. Once a change in altitude is detected, the second block (depicted in details in (b)) identifies movements, quantified by thresholding the accelerometer signal using the standard deviation (). Then, if the peak of the autocorrelation function of the accelerometer signal in the range 1 step/s to 2.5 step/s is above a threshold (), the periodicity of the movements is associated to the activity of climbing steps. Finally, the number of stair steps is computed using the step frequency associated to the peak of the autocorrelation function.
Signal processing algorithms and classifiers were built using the “Signal Processing Toolbox” and “Statistics and Machine Learning Toolbox” of Matlab (Matlab 2019a, The MathWorks, Inc., Natick, Massachusetts, United States), whereas the analyses were ad-hoc implemented using the same software.
2.2.1. First Block
In order to detect changes in altitude, we computed the time derivative of the barometric signal by means of a linear fitting on consecutive windows of 5 s. This approach was already found to be effective in [17].
Considering going upstairs, the time derivative of the signal was compared with two thresholds (, ) to determine the time intervals in which the altitude of the sensor changed, likely due to human movements. In particular, the threshold set a lower boundary to discard low slopes, while the upper threshold rejected quick changes due to, for example, elevators (or light slopes performed very fast). In case of going downstairs, the sign of the thresholds was inverted. In this way, each window was categorized into three possible states: going upstairs, going downstairs, no change in altitude (see Section 2.3 for the selection of the thresholds).
2.2.2. Second Block
For each window identified by the first block as either going upstairs or downstairs, we detected whether a periodic change resembling the human step frequency was present within the triaxial accelerometer signals. To do so, we divided this second block into three parts. First, the vector magnitude (VM) was determined as the square root of the squared sum of the three accelerometer components, and then, VM was filtered in a frequency range such to mainly include frequency components of the human movements (3rd-order, zero-phase, Butterworth filter from 0.25 to 5 Hz) [25,26]. Second, we computed the standard deviation of the filtered vector magnitude and compared it with the threshold to identify the presence of a movement (see Section 2.3 for the selection of the threshold). Third, we computed the normalized autocorrelation function (ACF) of the filtered VM signal, and the main peak in the range from 1 to 2.5 step/s was identified [27]. Examples of normalized ACF during two different activities are reported in Figure 2. When the amplitude of the peak was above the threshold , the window was marked as “climbling stairs” (see Section 2.3 for the selection of the threshold). The step frequency associated with the identified peak above threshold was then used as input for the third block.
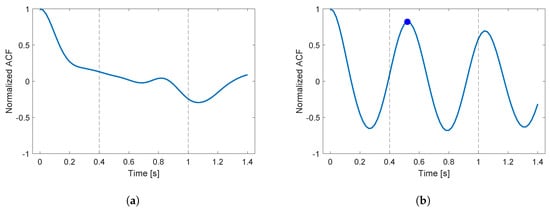
Figure 2.
Examples of normalized ACF obtained from a portion of data (a) while using the elevator (no peak above threshold is found), and (b) during climbing stairs, where a peak associated with a step frequency of 1.92 step/s was located. Black dashed lines mark the interval of the step rates considered (1 to 2.5 step/s).
2.2.3. Third Block
In the third block, we estimated the number of stair steps by using a linear regression model of the form , where s was the step frequency obtained from the second block and n was the number of stair steps to be estimated. We set these values to and s, so that the latter corresponded to the duration of the time window in the other blocks. While these values could be further calibrated through a fitting procedure, we excluded it to avoid overfitting.
2.3. Identification of the Thresholds for the Classifier
Three different analyses were performed on the training set. In the first one, we determined the lower and upper thresholds for the time derivative of the pressure signal . The upper threshold was set as the maximum derivative value within all the time intervals labelled as climbing stairs, i.e., millibar/s. The lower threshold was estimated using a ROC analysis meant to distinguish climbing stairs from all other activities using the absolute value of the time derivative as input. In particular, we chose the threshold that balanced the true recognition rates of the two classes. The value obtained for the lower threshold was millibar/s. The simple threshold-based classifier achieved an AUC of on the training set. The thresholds were then used symmetrically to detect both ascending and descending stairs. In summary, the classification scheme was as follows:
- “going downstairs”: if and ;
- “going upstairs”: if and ;
- “no change in altitude”: otherwise.
Figure 3 reports the probability density function (PDF) of the time derivative for each of the three activities considered and the ROC curve used for the selection of the lower threshold .
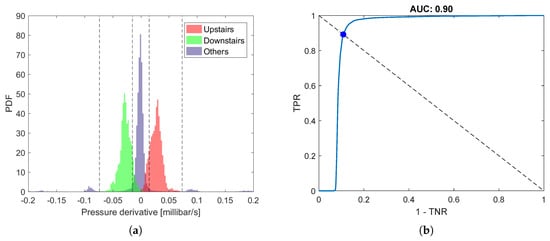
Figure 3.
(a) Distribution of the time derivative of barometric data in the training set, for each of the three activities to be classified by the first block of our algorithm. Black dashed lines represented the thresholds and . (b) ROC curve for the absolute value of the derivative to differentiate climbing stairs and others. TPR and TNR stand for true positive rate and true negative rate, respectively.
In the second analysis, we estimated the threshold of the standard deviation carrying out several measurements during activities with no significant movements like standing, taking the elevator or staying still. The threshold identified for our sensor was g. When the time derivative is above this value, an acceleration window is marked as containing a movement.
Finally, we estimated the threshold on the amplitude of the peak of the normalized autocorrelation function of the filtered VM signal (meant to determine whether the movement performed during a specific activity was periodic). Even in this case, a ROC analysis was carried out comparing the data in the training set related to periodic activities (i.e., walking, running, climbing stairs) and all the others. The optimal identified threshold was , with a corresponding recall for periodic activities of 0.98. To summarize, if the amplitude of the autocorrelation peak associated with the step frequency was greater than , then a periodic movement was recognized, and its correspondent step frequency considered further.
2.3.1. Comparison with an Accelerometer-Based Classifier
We compared the performance of our algorithm with that of a state-of-the-art accelerometer-based classification scheme for stair detection proposed by Ravi et al. [12]. Hereafter, we named this algorithm as . The algorithm required several time- and frequency-domain features to be extracted from the raw accelerometer data on windows of 5 s. For each of the three axes, the sample mean, standard deviation and power in the step frequency range 1 to 2.5 step/s (i.e., area under the power spectral density) were estimated. Also, the cross-correlation between all pairs of accelerometer axes was computed since, as stated by the authors, it can help differentiating among walking and climbing stairs. In total, the algorithm required the computation of twelve features.
In the original manuscript [12], the authors tested the performance of several classifiers, including a linear SVM. To be in line with their tests, we then selected the same classifier. However, we adapted the classification pipeline by training a hierarchical classifier composed by two SVMs. The first one was trained to classify all types of activities vs climbing stairs, whereas the second one to distinguish between going upstairs and downstairs.
In order to allow a comparison with , since the algorithm did not estimate the number of stair steps (single stair steps climbed) but only the stair climbing phase (i.e., the initial and ending time instants of stair climbing), we used its output to determine the number of stair steps climbed by first estimating the step frequency from the autocorrelation function of the VM signal, as in our second block (but without the use of our thresholds and ), and then multiplying it with the duration of the window.
The training of the classifiers was performed on the training set after downsampling to balance the classes.
2.3.2. Comparison with a Barometer-Based Classifier
We compared the performance of our algorithm with a simplified version that did not include the second and third block, i.e., no accelerometer data were used. Hereafter, we named this algorithm as . After the classification carried out by the first block using the pressure readings, we computed the number of stair steps by multiplying the duration of the time window identified with an average measure of step frequency for older people, i.e., 1.5 steps/s, according to previous works [26,28,29]. The comparison with such method provided evidence about the possible improvement achievable by the combined use of the accelerometer in terms of stair step counting, in particular for estimating the number of stair steps detected while not climbing stairs (false positives during other activities).
2.3.3. Comparison with an Accelerometer and Barometer-Based Classifier
We further compared the performance of our algorithm with that of a recent state-of-the-art methodology based on both accelerometer and barometric data for climbing stair detection proposed by Leuenberger et al. [16]. Hereafter, we named this algorithm as . Briefly, it made use of two different blocks, the first one used to classify whether the person was walking and the second one to determine the climbing stair phase using pressure readings. The first block made use of a SVM while the second one utilized a KNN. The whole method required a total number of fifteen features. Features included signal energy, range, variance, 10th and 90th percentiles, derivative of sensor data, and skewness, kurtosis, maximum value and scale from the Continuous Wavelet Transform of accelerometer data. Features were extracted from time windows lasting 7.5 s. For a better description of the features, please refer to the original manuscript [16]. The training of the classifiers was performed on the training set after downsampling to balance the classes. In addition, features were normalized and outliers removed, as performed in [16].
As for the algorithm, did not estimate the number of stair steps. To overcome the issue, we used the same strategy reported in Section 2.3.1.
Given the fact that a longer duration of the time window might negatively affect the performance of the classifier, as suggested in [17], especially around 8 s, we repeated the comparison by retraining the classifier using windows of 5 s. We named this second version of as .
2.3.4. Performance Evaluation
Performances were estimated by dividing the test set into two subsets, according to the labels available. The first one contained all the phases with climbing stair activities and, the second one, all other activities together. Confusion matrices and recalls for each activity and method were then computed on the test set.
Afterwards, we computed the absolute stair step counting error for climbing stair activities and the number of stair steps detected during other activities (false positives while not climbing stairs).
The expected number of stair steps used as a gold standard did not include those steps performed on the stair landings.
The stair step counting error, produced by each method, was reported using the median and interquartile range (median [IQR]) across the entire test set, while the Wilcoxon sign rank test and test were used for testing statistical hypotheses. Tests were considered statistically significant for .
3. Results
The total duration of stair climbing phase on the training set was min, with min and min for going upstairs and downstairs, respectively. The total duration of all other activities together was min. The duration of the stair climbing phases were s (mean ± standard deviation), with s and s for going upstairs and downstairs, respectively. Regarding the test set, we had min of going upstairs ( s), min for going downstairs ( s) and min for the other activities.
Table 1 shows the confusion matrices for , , , and on the whole test set, for stair climbing detection. In terms of classification performance, the only use of accelerometer data proved limited performance as shown by the recalls achieved by the algorithm (<0.5 for stair climbing and 0.79 for “others”), obtaining statistically significant differences between recalls when compared with all the other methodologies ( test; ).

Table 1.
Confusion matrices, along with the three recalls, for the different methods, as computed on the test set. “U”, “D” and “O” refer to going upstairs, downstairs and all other activities, respectively. Please notice that for the duration of the time window is 7.5 s. For this reason, the overall number of events (the sum along each column) is different from the other methods. is the proposed algorithm. refers to the algorithm in [12], and to the one in [16] (the latter with time windows of 5 s), is our algorithm when only barometer data were used.
When combining the accelerometer and barometer data, and obtained similar recalls (in the range 0.79–0.91), although slightly in favor for (0.84–0.91). However, the difference in terms of recalls between vs were not statistically significant ( test; ). Moreover, it was possible to achieve very high recalls for the activities labeled as “other” (≈0.90 for , and ). However, the only use of barometer in did not protect against false positives while not climbing stairs (recall of 0.65 for ). Recalls of , , vs. were statistically significantly different ( test; ). The duration of the time window did not show any improvements in the recalls ( vs. and vs. ; test; ). Figure 4 reports an example of classification performed by , and .
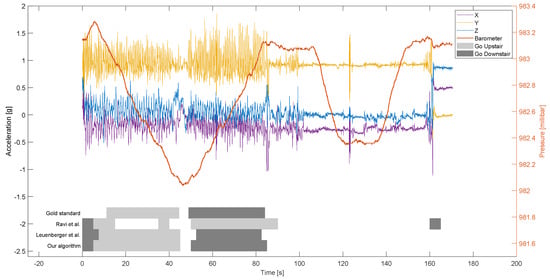
Figure 4.
Example of triaxial accelerometer and barometer data, along with the values of the gold standard and the classifications performed by , and our algorithm . The sequence of activities recorded in these signals (gold standard) was: (i) walking downhill and uphill (approximately the first ten seconds); (ii) walking upstairs and downstairs; (iii) short pause for approximately 30 s; and (iv) taking the elevator (ascending and descending).
Table 2 shows the results of the stair step counting for each algorithm and acquisition in the test set. The total number of stair steps climbed in the whole test set was 795, while the number of stair steps estimated while climbing stairs were 905, 345, 890, 914 and 881 for , , , and , respectively, achieving an overall error of , , , and . When considering going upstairs, no difference in terms of stair step counting error was found between vs ( vs steps; ), vs (; ) and vs (; ). Similar results were obtained for going downstairs where the errors were for , for , for and for (all comparisons were not statistically significant; ). obtained instead errors of and steps for going upstairs and downstairs, respectively. Both errors were statistically significantly different from those of the other four methodologies ().

Table 2.
Number of expected (“Exp.”) and estimated number of stair steps during climbing stair phases, for each method and subject (“Subj.”) of the test set. “U” and “D” refer to going upstairs and downstairs, respectively. “” indicates the number of stair steps detected while not climbing stairs but doing other activities (false positives during other activities). is the proposed algorithm. refers to the algorithm in [12], and to the one in [16] (the latter with time windows of 5 s), is our algorithm when only barometer data were used.
In case of false positives during other activities in the test set, , and did not show any difference between the wrongly detected stairs (error of , , ; ). On the contrary, and resulted in a higher number of false positives ( and , respectively; ), that are stair steps detected while not climbing stairs. Results are reported in the column of Table 2.
4. Discussion
In this work, we proposed an algorithm to estimate the number of stair steps climbed during everyday life, for the aim of long term monitoring of this functional parameter in a population of older people. The computational load and model complexity was kept as minimal as possible to reduce power consumption and hardware requirements of the wearable device where it might be implemented.
The first block of our algorithm was characterized by the use of two thresholds and on the derivative of the pressure readings. Such simple approach was able to achieve high performance in detecting the climbing of stairs within the set of activities considered. In particular, the upper threshold, estimated using the maximum derivative of the barometric pressure in our training set, made the classifier robust to quick changes in altitude, like those due to elevators. Indeed, for the data collected while using an elevator, the maximum derivative was 0.2 millibar/s, that was three times higher than the maximum derivative obtained during running on the stairs. The high performance achieved in detecting stairs corroborated the validity of previous studies involving barometer data [17,19]. In addition, as shown in Figure 5, the time derivative of the barometric pressure varies very slowly across different altitudes (it is substantially constant in the range 0 to 3000 m and in particular around 0.028 millibar/s, which is the average variation in the training set), thus it is not necessary to re-calibrate the values of and , when employing the algorithm at altitudes relevant for older people. Finally, atmospheric pressure variations due to weather phenomena will generally not affect the values of the thresholds. In fact, very rapid changes of the order of 6 millibars/3 h (or 0.00056 millibar/s) [30] are, on average, far smaller than and .
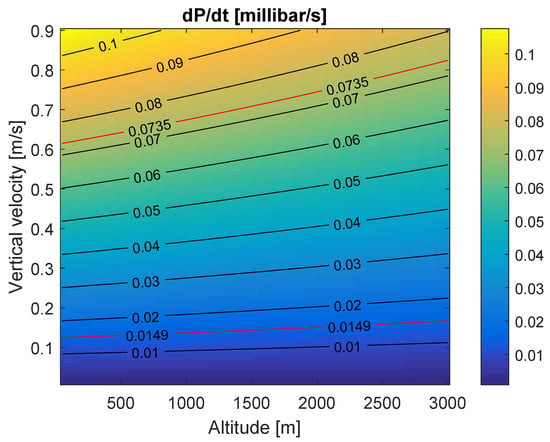
Figure 5.
Barometric pressure derivative values (absolute value) as a function of vertical velocity and altitude in the International Standard Atmosphere (ISA) model (ISO 2533:1975). The two red lines correspond to the thresholds millibar/s and millibar/s.
The stair step counting block achieved an overall error of about while considering only those phases when the subject was actually climbing stairs. This error is in line with the best of the other methods considered, while obtained with a lower computational load and model complexity. Stairs climbed in less than 5 s (very small number of steps) were completely undetected due to the size of the time window selected. However, shortening the time window would have compromised a reliable estimate of the step frequency through the accelerometer data, leading to a larger counting error. In addition, considering that the target users of our study were older people, only stair flights longer than just a few steps (hence, likely longer than 5 s) may be a relevant effort for improving active ageing. A second source of error was the noise in the barometric sensor contained in the prototype, which was further enhanced by the derivative operator in the first block (although limited by a low pass filter). The impact of noise might decrease in future with technological improvements leading to better signal-to-noise ratio.
When was compared with other algorithms, it was clear that the use of the barometer played an important role and made the proposed pipeline reliable for stair climbing detection with acceptable stair step counting error ( vs. ). On the contrary, the only use of the barometer data resulted in a high recall for stair climbing detection but with high error for stair step counting ( vs. ). The main reason was that reported a high number of false positives while not climbing stairs ( column in Table 2) with 499 steps estimated whereas our methodology estimated 129 steps, obtaining about 4 times less in terms of stair step counting error. We believe that for were underestimated with respect a real life scenario. For example, common activities such as escalators and car driving will likely trigger a stair climbing detection, and thus counting stair steps when they are not supposed to exist.
As expected, and reported similar results, slightly in favor for the latter in terms of classification performance, but with non significant differences in terms of stair step counting error. Despite such similar performance, a few differences are worth to be discussed. First, the number of features used in our algorithm was lower than the ones required by (three vs fifteen), reducing then the computational cost needed. In addition, required the computation of both time- and frequency-domain features, while only time domain. The calculation of time-domain features is recommended over frequency domain ones as their computation consumes less energy [31,32]. Second, made use of a KNN classifier, that would require the entire training set to be stored locally on the device. Third, the order of the blocks presented in (opposite than ) was not energy efficient. Indeed, since climbing stairs is supposed to happen a fewer amount of times during a day with respect to walking, detecting the change in altitude in the first place (as in our case) would reduce the time windows in which the features required by the walking classifier would be needed to be computed. It is though necessary to mention that was supposed to be utilized during ambulatory visits, therefore the power consumption and model complexity were minor issues for Leuenberger et al. [16].
Regarding the duration of the time window, we found no difference between the original version of and with windows of 5 s. This result might be explained by the fact that most of the recordings of the test set during stair climbing lasted at least 15 s. Consequently, it was not possible to determine whether our algorithm would perform better on shorter stairs.
Another important point regarding the number of sensors and their positions has to be discussed. Despite the fact that the use of sensors placed in different parts of the body is known to improve the performance [33], in the context of active ageing, it is mandatory to reduce the intrusiveness of the wearable devices for an effective and prolonged monitoring. Therefore, a wearable sensor resembling a watch would likely require the least effort for its use. However, the wide spectrum of movements performed by the upper limbs would likely produce false detection of stairs climbing only using acceleration data, further favoring the insertion of a barometric sensor.
Finally, it is worth noting that the accelerometer resolution was 16 times lower in the test set with respect to the training set, given the fact that different devices were employed for data collection. To assess the possible effect this might have on the results described in the paper, we artificially decreased the resolution of the training set and evaluated accuracy before and after. The change in resolution did not have any relevant effect (the difference in accuracy on the training set was 0.0014%), suggesting that the method is robust in the range of the resolutions considered, despite different hardware characteristics.
The present work contains several limitations, particularly regarding the definition of the gold standard. In particular, we considered walking uphill and downhill as separate from climbing stairs, even though older people would benefit from this activity [34,35] and thus it is worth to be proper monitored. However, given the limited amount of data acquired during walking uphill and downhill, we preferred to focus our effort only on climbing stairs, a more common scenario for in-home monitoring during ageing.
Another problem regarded the presence of short stair landings in which we observed that two or three steps were performed by the subjects but not counted as stairs in the gold standard. Although the performances reported might suffer for this bias across all algorithms (and thus not a relevant problem here), to the best of our knowledge, there is little discussion in the scientific community with respect to the impact of the length of the stair landings on the fatigue of climbing stairs (longer stair landings favor recovery). We leave the issue open to future discussions.
Finally, although the main target user for our smartwatch implementation were healthy young-old people where preventive measures are most effective for active ageing, we believe that old-old and very-old people, as well as sarcopenic or disease population, may also benefit from a proper monitoring of this functional parameter. However, the oldest subject in our test set was 77 years old, and thus, it was impossible to assess the performance for a higher range of ages. In this regard, a further test of the algorithm on data collected from very-old people is therefore necessary.
Online Implementation
Among the numerous initiatives aimed to promote active ageing, the H2020 NESTORE project (see the Acknowledgement section for details) objective is to support healthy older people’s wellbeing and capacity to live independently. In the context of the project, an ad-hoc wristband form-factor device was designed and built to monitor physical and social status of older people during both daily living and physical activities. The device was based on a low-power wireless dual core microcontroller targeting Bluetooth 4.2 and Bluetooth 5 Low Energy (BLE) applications (first core: 32 bit ARM-Cortex M3 @48 MHz, RAM: 28 kB, flash memory: 128 kB; second core: ARM-Cortex M0, completely dedicated to manage BLE stack). It interacted with the user using a TFT color display and a motor vibrator, while exchanging data with a smartphone and other nearby devices through BLE connectivity. The architecture was specifically meant to limit the overall battery energy expenditure of the system. The device collected data from: (i) an heart rate optical sensor; (ii) a triaxial accelerometer; and (iii) a barometer. Raw data obtained by these sensors were used for the computation of elaborated measures like number of steps, number of stair steps, travelled distance, elevation gain, activity intensity, burned calories, and social interaction through proximity to beacon devices.
The algorithm described in this paper was effectively implemented in firmware for the computation of the number of stair steps climbed. Given the high number of tasks that the RTOS (Real-Time Operating System) preemptive architecture had to run concurrently, along with the overall RAM limitation (only 28 kB), constrained the stair step counting algorithm to fit into a RAM memory footprint of about 4 kB (and a time slice of 40 ms @48 MHz). A part from being used in practice for the collection of our test set (see Section 2.1), the device will soon be tested for the long term monitoring of older people living independently in a community house.
5. Conclusions
In this study, we proposed an algorithm meant to estimate the stair steps climbed by older people in everyday life, based on accelerometer and barometer data collected by a wearable sensor worn on the wrist. The algorithm was composed of a hierarchical classifier and a linear regression model.
In addition, to classify the climbing stair phases, the work described an algorithm able to count the number of stair steps, achieving satisfactory performance with only three simple features and threshold-based classifiers. In this regard, the computational cost for climbing stair detection was lower with respect to other state-of-the-art algorithms, while achieving similar stair step counting errors. Therefore, the entire pipeline is suitable for online computation on a wearable device dedicated to the described purpose.
Author Contributions
Conceptualization: D.C., M.W.R., R.S.; Data curation: A.M., D.C., G.R., S.P.; Investigation: D.C., M.W.R., R.S.; Methodology: D.C., M.W.R., R.S.; Software: D.C., E.D., M.L.M., M.T.L.C., M.W.R.; Validation: A.M., E.D., G.R., M.L.M., M.T.L.C., S.P.; Writing—Original draft preparation: all authors. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partly funded by the Horizon 2020 project “NESTORE—Novel Empowering Solutions and Technologies for Older people to Retain Everyday life activities”, http://nestore-coach.eu (grant agreement No 769643).
Acknowledgments
The authors are grateful to the volunteers who participated in data acquisition. Each volunteer was informed about the objective of this study, following the principles outlined in the Helsinki Declaration. They gave their full informed consent to use data for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elsawy, B.; Higgins, K.E. The Geriatric Assessment. Am. Fam. Physician 2011, 83, 48–56. [Google Scholar] [PubMed]
- Bean, J.F.; Kiely, D.K.; LaRose, S.; Alian, J.; Frontera, W.R. Is Stair Climb Power a Clinically Relevant Measure of Leg Power Impairments in At-Risk Older Adults? Arch. Phys. Med. Rehabil. 2007, 88, 604–609. [Google Scholar] [CrossRef] [PubMed]
- Zech, A.; Steib, S.; Sportwiss, D.; Freiberger, E.; Pfeifer, K. Functional Muscle Power Testing in Young, Middle-Aged, and Community-Dwelling Nonfrail and Prefrail Older Adults. Arch. Phys. Med. Rehabil. 2011, 92, 967–971. [Google Scholar] [CrossRef] [PubMed]
- Ni, M.; Brown, L.G.; Lawler, D.; Bean, J.F. Reliability, Validity, and Minimal Detectable Change of Four-Step Stair Climb Power Test in Community-Dwelling Older Adults. Phys. Ther. 2017, 97, 767–773. [Google Scholar] [CrossRef]
- Hellmers, S.; Kromke, T.; Dasenbrock, L.; Heinks, A.; Bauer, J.M.; Hein, A.; Fudickar, S. Stair Climb Power Measurements via Inertial Measurement Units—Towards an Unsupervised Assessment of Strength in Domestic Environments. In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies, Funchal, Madeira, Portugal, 19–21 January 2018; pp. 39–47. [Google Scholar] [CrossRef]
- Li, R.T.; Kling, S.R.; Salata, M.J.; Cupp, S.A.; Sheehan, J.; Voos, J.E. Wearable Performance Devices in Sports Medicine. Sport. Health 2016, 8, 74–78. [Google Scholar] [CrossRef] [PubMed]
- Ayata, D.; Yaslan, Y.; Kamasak, M.E. Emotion Based Music Recommendation System Using Wearable Physiological Sensors. IEEE Trans. Consum. Electron. 2018, 64, 196–203. [Google Scholar] [CrossRef]
- Patel, S.; Park, H.; Bonato, P.; Chan, L.; Rodgers, M. A review of wearable sensors and systems with application in rehabilitation. J. Neuroeng. Rehabil. 2012, 9, 21. [Google Scholar] [CrossRef]
- Lara, O.D.; Labrador, M.A. A Survey on Human Activity Recognition using Wearable Sensors. IEEE Commun. Surv. Tut. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- McPhee, J.S.; French, D.P.; Jackson, D.; Nazroo, J.; Pendleton, N.; Degens, H. Physical activity in older age: Perspectives for healthy ageing and frailty. Biogerontology 2016, 17, 567–580. [Google Scholar] [CrossRef]
- Pigini, L.; Bovi, G.; Panzarino, C.; Gower, V.; Ferratini, M.; Andreoni, G.; Sassi, R.; Rivolta, M.W.; Ferrarin, M. Pilot test of a new personal health system integrating environmental and wearable sensors for telemonitoring and care of elderly people at home (SMARTA project). Gerontology 2017, 63, 281–286. [Google Scholar] [CrossRef]
- Ravi, N.; Dandekar, N.; Mysore, P.; Littman, M.L. Activity recognition from accelerometer data. In Proceedings of the IAAI’05 17th Conference on Innovative Applications of Artificial Intelligence, Barcelona, Spain, 8–10 June; AAAI Press/The MIT Press: Menlo Park, CA, USA, 2005; Volume 3, pp. 1541–1546. [Google Scholar]
- McCarthy, M.; James, D.; Lee, J.; Rowlands, D. Decision-tree-based human activity classification algorithm using single-channel foot-mounted gyroscope. Electron. Lett. 2015, 51, 675–676. [Google Scholar] [CrossRef]
- Liang, J.; Duan, H.; Li, J.; Sun, H.; Sha, X.; Zhao, Y.; Liu, L. Accurate Estimation of Gait Altitude Using One Wearable IMU Sensor. In Proceedings of the IEEE 1st International Conference on Micro/Nano Sensors for AI, Healthcare, and Robotics (NSENS), Shenzhen, China, 5–7 December 2018; pp. 64–67. [Google Scholar] [CrossRef]
- Chen, W.H.; Lee, Y.S.; Yang, C.J.; Chang, S.Y.; Shih, Y.; Sui, J.D.; Chang, T.S.; Shiang, T.Y. Determining motions with an IMU during level walking and slope and stair walking. J. Sport Sci. 2020, 38, 62–69. [Google Scholar] [CrossRef] [PubMed]
- Leuenberger, K.; Gonzenbach, R.; Wiedmer, E.; Luft, A.; Gassert, R. Classification of Stair Ascent and Descent in Stroke Patients. In Proceedings of the 11th International Conference on Wearable and Implantable Body Sensor Networks Workshops, Zurich, Switzerland, 16–19 June 2014; pp. 11–16. [Google Scholar] [CrossRef]
- Gu, F.; Kealy, A.; Khoshelham, K.; Shang, J. User-Independent Motion State Recognition Using Smartphone Sensors. Sensors 2015, 15, 30636–30652. [Google Scholar] [CrossRef]
- Brodie, M.A.; Wang, K.; Delbaere, K.; Persiani, M.; Lovell, N.H.; Redmond, S.J.; Del Rosario, M.B.; Lord, S.R. New Methods to Monitor Stair Ascents Using a Wearable Pendant Device Reveal How Behavior, Fear, and Frailty Influence Falls in Octogenarians. IEEE Trans. Biomed. Eng. 2015, 62, 2595–2601. [Google Scholar] [CrossRef] [PubMed]
- Xie, L.; Tian, J.; Ding, G.; Zhao, Q. Human activity recognition method based on inertial sensor and barometer. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Moltrasio, Italy, 26–29 March 2018; IEEE Press: Piscataway, NJ, USA, 2018; p. 4. [Google Scholar] [CrossRef]
- Carpinella, I.; Gervasoni, E.; Anastasi, D.; Lencioni, T.; Cattaneo, D.; Ferrarin, M. Instrumental Assessment of Stair Ascent in People With Multiple Sclerosis, Stroke, and Parkinson’s Disease: A Wearable-Sensor-Based Approach. IEEE Trans. Neural. Syst. Rehabil. Eng. 2018, 26, 2324–2332. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liang, J.; Sha, X.; Yu, J.; Duan, H.; Shi, G.; Li, W.J. Estimation of Pedestrian Altitude Inside a Multi-Story Building Using an Integrated Micro-IMU and Barometer Device. IEEE Access 2019, 7, 84680–84689. [Google Scholar] [CrossRef]
- Kwapisz, J.R.; Weiss, G.M.; Moore, S.A. Activity Recognition Using Cell Phone Accelerometers. SIGKDD Explor. Newsl. 2011, 12, 74–82. [Google Scholar] [CrossRef]
- Moncada-Torres, A.; Leuenberger, K.; Gonzenbach, R.; Luft, A.; Gassert, R. Activity classification based on inertial and barometric pressure sensors at different anatomical locations. Phys. Meas. 2014, 35, 1245–1263. [Google Scholar] [CrossRef]
- Fortune, E.; Lugade, V.; Morrow, M.; Kaufman, K. Validity of Using Tri-Axial Accelerometers to Measure Human Movement—Part II: Step Counts at a Wide Range of Gait Velocities. Med. Eng. Phys. 2014, 36, 659–669. [Google Scholar] [CrossRef]
- Weiss, A.; Herman, T.; Plotnik, M.; Brozgol, M.; Giladi, N.; Hausdorff, J.M. An instrumented timed up and go: The added value of an accelerometer for identifying fall risk in idiopathic fallers. Physiol. Meas. 2011, 32, 2003–2018. [Google Scholar] [CrossRef]
- Oh-Park, M.; Wang, C.; Verghese, J. Stair Negotiation Time in Community Dwelling Older Adults: Normative Values and Association with Functional Decline. Arch. Phys. Med. Rehabil. 2011, 92, 2006–2011. [Google Scholar] [CrossRef] [PubMed]
- Pachi, A.; Ji, T. Frequency and velocity of people walking. Inst. Struct. Eng. 2005, 83, 36–40. [Google Scholar]
- Hinman, M.R.; O’Connell, J.K.; Dorr, M.; Hardin, R.; Tumlinson, A.B.; Varner, B. Functional Predictors of Stair-Climbing Speed in Older Adults. J. Geriatr. Phys. Ther. 2014, 37, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Tiedemann, A.C.; Sherrington, C.; Lord, S.R. Physical and psychological factors associated with stair negotiation performance in older people. J. Gerontol. A Biol. Sci. Med. Sci. 2007, 62, 1259–1265. [Google Scholar] [CrossRef]
- Watts, A. The Weather Handbook, 2nd ed.; Sheridan House: Dobbs Ferry, NY, USA, 1999. [Google Scholar]
- Del Rosario, M.B.; Redmond, S.J.; Lovell, N.H. Tracking the Evolution of Smartphone Sensing for Monitoring Human Movement. Sensors 2015, 15, 18901–18933. [Google Scholar] [CrossRef]
- Ben Abdesslem, F.; Phillips, A.; Henderson, T. Less is more: Energy-efficient mobile sensing with senseless. In Proceedings of the 1st ACM Workshop on Networking, Systems, and Applications for Mobile Handhelds—MobiHeld ’09, Barcelona, Spain, 16–21 August 2009; ACM Press: Barcelona, Spain, 2009; p. 61. [Google Scholar] [CrossRef]
- Gao, L.; Bourke, A.K.; Nelson, J. Evaluation of accelerometer based multi-sensor versus single-sensor activity recognition systems. Med. Eng. Phys. 2014, 36, 779–785. [Google Scholar] [CrossRef]
- Figueiredo, S.; Finch, L.; Mai, J.; Ahmed, S.; Huang, A.; Mayo, N.E. Nordic walking for geriatric rehabilitation: A randomized pilot trial. Disabil. Rehabil. 2013, 35, 968–975. [Google Scholar] [CrossRef]
- Brach, J.S.; Van Swearingen, J.M. Interventions to Improve Walking in Older Adults. Curr. Transl. Geriatr. Exp. Gerontol. Rep. 2013, 2, 1–13. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).