Chance-Constrained Optimization Formulation for Ship Conceptual Design: A Comparison of Metaheuristic Algorithms
Abstract
1. Introduction
2. Chance-Constrained Optimization
3. Bulk Carrier Conceptual Design
4. Selected Methods and Experimental Setup
4.1. Brief Description of Selected Methods
4.2. Experimental Setup
5. Results and Discussion
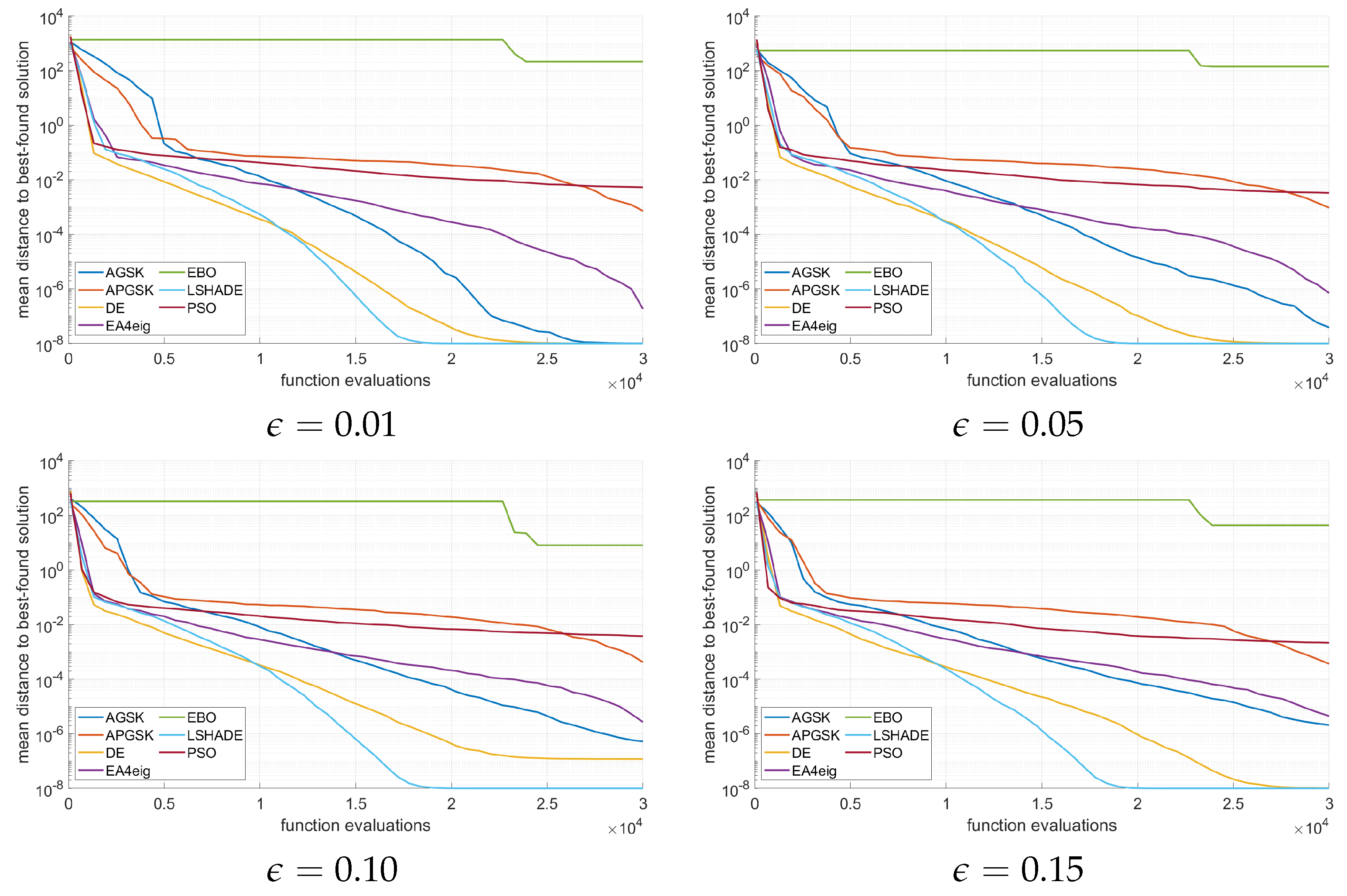
5.1. Performance Comparison of the Selected Methods
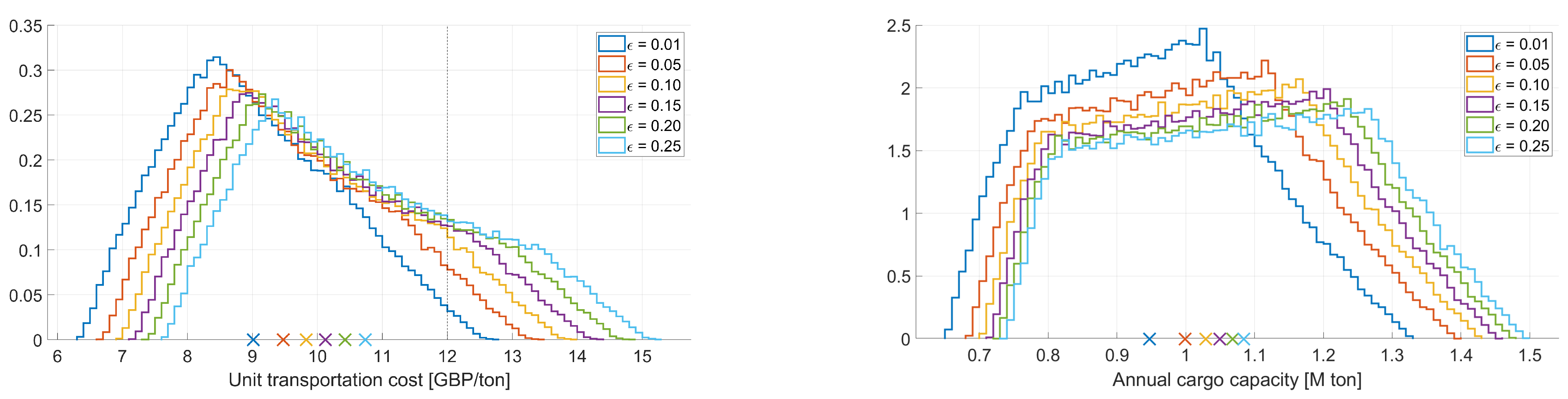
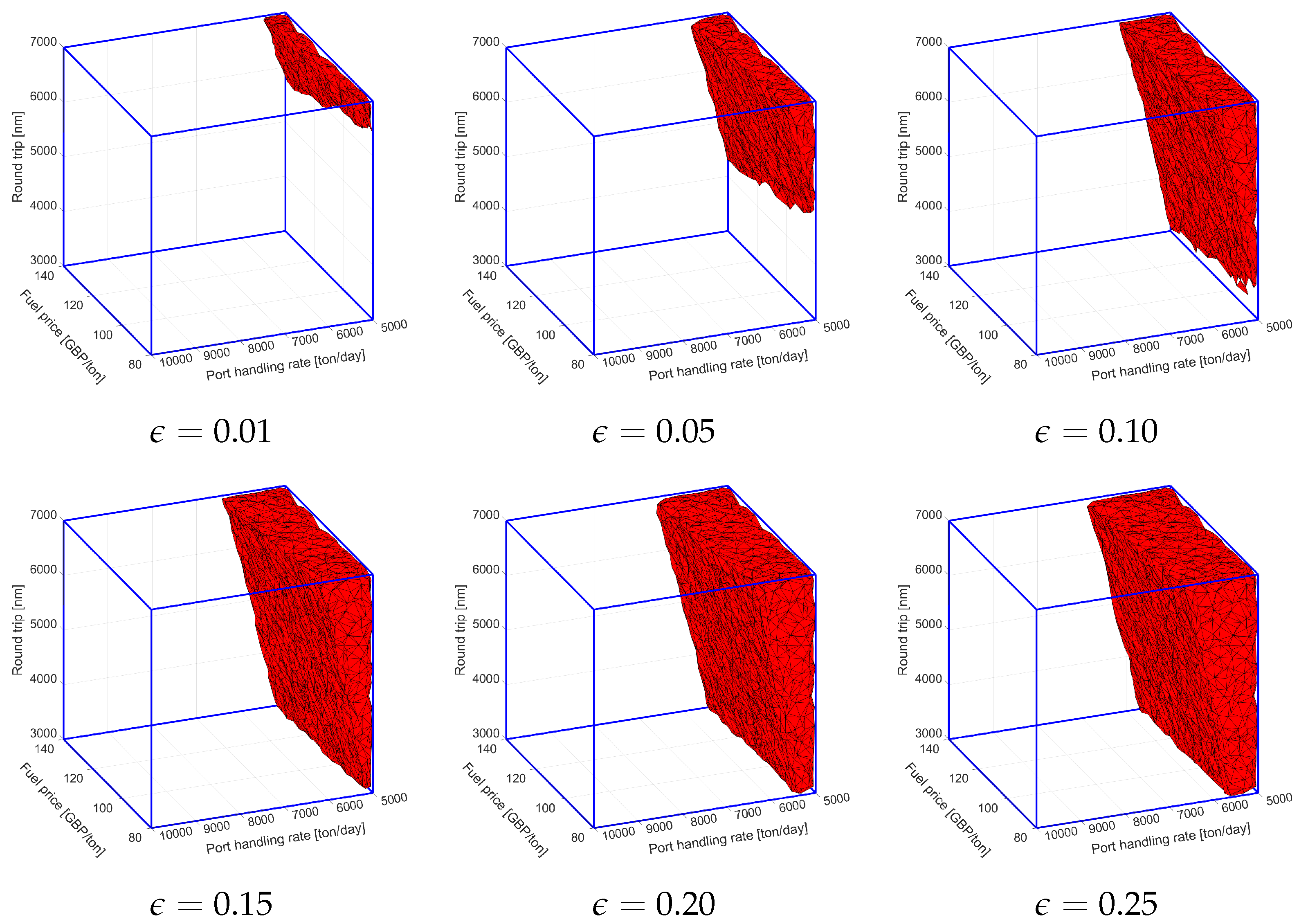
5.2. Evaluation of the Best-Found Solutions
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AGSK | adaptive gaining-sharing knowledge |
| annual cargo capacity | |
| annual cost | |
| B | beam |
| block coefficient | |
| capital costs | |
| cargo deadweight | |
| CEC | Congress on Evolutionary Computation |
| CMA-ES | covariance matrix adaptation evolutionary strategy |
| cruise speed | |
| daily consumption | |
| deadweight | |
| D | depth |
| DE | differential evolution |
| displacement | |
| DIRECT | dividing rectangles |
| T | draft |
| EBO | effective butterfly optimizer |
| EA | evolutionary algorithms |
| ES | evolutionary strategy |
| Froude number | |
| fuel carried | |
| fuel cost | |
| fuel price | |
| GA | genetic algorithm |
| CCO | chance-constrained optimization |
| L | length |
| light shipweight | |
| LPSR | linear population size reduction |
| machinery weight | |
| metacentric radius | |
| miscellaneous deadweight | |
| outfit weight | |
| PSO | particle swarm optimization |
| port cost | |
| port days | |
| port handling rate | |
| P | power |
| round trip miles | |
| round trips per year | |
| running costs | |
| sea days | |
| ship cost | |
| steel weight | |
| SHBA | success history based adaption |
| LSHADE | success-history based adaptive DE with LPSR |
| threshold (for probability) | |
| unit transportation cost | |
| vertical center of buoyancy | |
| vertical center of gravity | |
| voyage costs |
References
- Diez, M.; Peri, D. Robust optimization for ship conceptual design. Ocean. Eng. 2010, 37, 966–977. [Google Scholar] [CrossRef]
- Kochenderfer, M.J.; Wheeler, T.A. Algorithms for Optimization; Mit Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Ben-Tal, A.; El Ghaoui, L.; Nemirovski, A. Robust Optimization; Princeton University Press: Princeton, NJ, USA, 2009; Volume 28. [Google Scholar]
- Prékopa, A. Stochastic Programming; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 324. [Google Scholar]
- Shafer, G. Dempster-shafer theory. Encycl. Artif. Intell. 1992, 1, 330–331. [Google Scholar]
- Zimmermann, H.J. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility theory and its applications: Where do we stand? In Springer Handbook of Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015; pp. 31–60. [Google Scholar]
- Ben-Haim, Y. Info-Gap Decision Theory: Decisions under Severe Uncertainty; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kudela, J. A critical problem in benchmarking and analysis of evolutionary computation methods. Nat. Mach. Intell. 2022, 4, 1238–1245. [Google Scholar] [CrossRef]
- Tzanetos, A.; Blondin, M. A qualitative systematic review of metaheuristics applied to tension/compression spring design problem: Current situation, recommendations, and research direction. Eng. Appl. Artif. Intell. 2023, 118, 105521. [Google Scholar] [CrossRef]
- Žufan, P.; Bidlo, M. Advances in evolutionary optimization of quantum operators. Mendel 2021, 27, 12–22. [Google Scholar] [CrossRef]
- Abu Khurma, R.; Aljarah, I.; Sharieh, A.; Abd Elaziz, M.; Damaševičius, R.; Krilavičius, T. A review of the modification strategies of the nature inspired algorithms for feature selection problem. Mathematics 2022, 10, 464. [Google Scholar] [CrossRef]
- Akinola, O.O.; Ezugwu, A.E.; Agushaka, J.O.; Zitar, R.A.; Abualigah, L. Multiclass feature selection with metaheuristic optimization algorithms: A review. Neural Comput. Appl. 2022, 34, 19751–19790. [Google Scholar] [CrossRef]
- Ma, J.; Xia, D.; Wang, Y.; Niu, X.; Jiang, S.; Liu, Z.; Guo, H. A comprehensive comparison among metaheuristics (MHs) for geohazard modeling using machine learning: Insights from a case study of landslide displacement prediction. Eng. Appl. Artif. Intell. 2022, 114, 105150. [Google Scholar] [CrossRef]
- Muller, J. Improving initial aerofoil geometry using aerofoil particle swarm optimisation. Mendel 2022, 28, 63–67. [Google Scholar] [CrossRef]
- Febrianti, W.; Sidarto, K.A.; Sumarti, N. Approximate Solution for Barrier Option Pricing Using Adaptive Differential Evolution With Learning Parameter. Mendel 2022, 28, 76–82. [Google Scholar] [CrossRef]
- Jones, D.R.; Martins, J.R. The DIRECT algorithm: 25 years Later. J. Glob. Optim. 2021, 79, 521–566. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. Recent advances and applications of surrogate models for finite element method computations: A review. Soft Comput. 2022, 26, 13709–13733. [Google Scholar] [CrossRef]
- Greiner, H. Robust optical coating design with evolutionary strategies. Appl. Opt. 1996, 35, 5477–5483. [Google Scholar] [CrossRef] [PubMed]
- Wiesmann, D.; Hammel, U.; Back, T. Robust design of multilayer optical coatings by means of evolutionary algorithms. IEEE Trans. Evol. Comput. 1998, 2, 162–167. [Google Scholar] [CrossRef]
- Branke, J. Creating robust solutions by means of evolutionary algorithms. In Proceedings of the Parallel Problem Solving from Nature—PPSN V: 5th International Conference, Amsterdam, The Netherlands, 27–30 September 1998; Proceedings 5; Springer: Berlin/Heidelberg, Germany, 1998; pp. 119–128. [Google Scholar]
- Tsutsui, S.; Ghosh, A. Genetic algorithms with a robust solution searching scheme. IEEE Trans. Evol. Comput. 1997, 1, 201–208. [Google Scholar] [CrossRef]
- Forouraghi, B. A genetic algorithm for multiobjective robust design. Appl. Intell. 2000, 12, 151–161. [Google Scholar] [CrossRef]
- Loughlin, D.H.; Ranjithan, S.R. Chance-constrained optimization using genetic algorithms: An application in air quality management. In Proceedings of the Bridging the Gap: Meeting the World’s Water and Environmental Resources Challenges, Orlando, FL, USA, 20–24 May 2001; pp. 1–9. [Google Scholar]
- Asafuddoula, M.; Singh, H.K.; Ray, T. Six-sigma robust design optimization using a many-objective decomposition-based evolutionary algorithm. IEEE Trans. Evol. Comput. 2014, 19, 490–507. [Google Scholar] [CrossRef]
- Paenke, I.; Branke, J.; Jin, Y. Efficient search for robust solutions by means of evolutionary algorithms and fitness approximation. IEEE Trans. Evol. Comput. 2006, 10, 405–420. [Google Scholar] [CrossRef]
- Kim, C.; Choi, K.K. Reliability-based design optimization using response surface method with prediction interval estimation. ASME J. Mech. Des. 2008, 130, 121401. [Google Scholar] [CrossRef]
- Ma, W.; Ma, D.; Ma, Y.; Zhang, J.; Wang, D. Green maritime: A routing and speed multi-objective optimization strategy. J. Clean. Prod. 2021, 305, 127179. [Google Scholar] [CrossRef]
- Fagerholt, K.; Gausel, N.T.; Rakke, J.G.; Psaraftis, H.N. Maritime routing and speed optimization with emission control areas. Transp. Res. Part C Emerg. Technol. 2015, 52, 57–73. [Google Scholar] [CrossRef]
- Andersson, H.; Fagerholt, K.; Hobbesland, K. Integrated maritime fleet deployment and speed optimization: Case study from RoRo shipping. Comput. Oper. Res. 2015, 55, 233–240. [Google Scholar] [CrossRef]
- Cheaitou, A.; Cariou, P. Greening of maritime transportation: A multi-objective optimization approach. Ann. Oper. Res. 2019, 273, 501–525. [Google Scholar] [CrossRef]
- Zhou, C.; Ma, N.; Cao, X.; Lee, L.H.; Chew, E.P. Classification and literature review on the integration of simulation and optimization in maritime logistics studies. IISE Trans. 2021, 53, 1157–1176. [Google Scholar] [CrossRef]
- Jin, X.; Duan, Z.; Song, W.; Li, Q. Container stacking optimization based on Deep Reinforcement Learning. Eng. Appl. Artif. Intell. 2023, 123, 106508. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, J.B.; Ding, C.; Zhang, H.; Lin, M.; Cheng, J. Joint optimization of trajectory and communication resource allocation for unmanned surface vehicle enabled maritime wireless networks. IEEE Trans. Commun. 2021, 69, 8100–8115. [Google Scholar] [CrossRef]
- Sen, P.; Yang, J.B. Multiple Criteria Decision Support in Engineering Design; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Parsons, M.G.; Scott, R.L. Formulation of multicriterion design optimization problems for solution with scalar numerical optimization methods. J. Ship Res. 2004, 48, 61–76. [Google Scholar] [CrossRef]
- Hart, C.G.; Vlahopoulos, N. An integrated multidisciplinary particle swarm optimization approach to conceptual ship design. Struct. Multidiscip. Optim. 2010, 41, 481–494. [Google Scholar] [CrossRef]
- Serani, A.; Leotardi, C.; Iemma, U.; Campana, E.F.; Fasano, G.; Diez, M. Parameter selection in synchronous and asynchronous deterministic particle swarm optimization for ship hydrodynamics problems. Appl. Soft Comput. 2016, 49, 313–334. [Google Scholar] [CrossRef]
- Chen, X.; Diez, M.; Kandasamy, M.; Zhang, Z.; Campana, E.F.; Stern, F. High-fidelity global optimization of shape design by dimensionality reduction, metamodels and deterministic particle swarm. Eng. Optim. 2015, 47, 473–494. [Google Scholar] [CrossRef]
- Serani, A.; Fasano, G.; Liuzzi, G.; Lucidi, S.; Iemma, U.; Campana, E.F.; Stern, F.; Diez, M. Ship hydrodynamic optimization by local hybridization of deterministic derivative-free global algorithms. Appl. Ocean. Res. 2016, 59, 115–128. [Google Scholar] [CrossRef]
- Campana, E.F.; Diez, M.; Liuzzi, G.; Lucidi, S.; Pellegrini, R.; Piccialli, V.; Rinaldi, F.; Serani, A. A multi-objective DIRECT algorithm for ship hull optimization. Comput. Optim. Appl. 2018, 71, 53–72. [Google Scholar] [CrossRef]
- Diez, M.; Campana, E.F.; Stern, F. Stochastic optimization methods for ship resistance and operational efficiency via CFD. Struct. Multidiscip. Optim. 2018, 57, 735–758. [Google Scholar] [CrossRef]
- Serani, A.; Stern, F.; Campana, E.F.; Diez, M. Hull-form stochastic optimization via computational-cost reduction methods. Eng. Comput. 2022, 38, 2245–2269. [Google Scholar] [CrossRef]
- Calafiore, G.; Campi, M.C. Uncertain convex programs: Randomized solutions and confidence levels. Math. Program. 2005, 102, 25–46. [Google Scholar] [CrossRef]
- Kudela, J. Zenodo Repository: Chance-Constrained Optimization Formulation for Conceptual Ship Design: A Comparison of Metaheuristic Algorithms. 2023. Available online: https://zenodo.org/records/8178768 (accessed on 9 October 2023).
- Rockafellar, R.T.; Uryasev, S. Optimization of conditional value-at-risk. J. Risk 2000, 2, 21–42. [Google Scholar] [CrossRef]
- Rockafellar, R.T.; Royset, J.O. On buffered failure probability in design and optimization of structures. Reliab. Eng. Syst. Saf. 2010, 95, 499–510. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Symonds, G.H. Cost horizons and certainty equivalents: An approach to stochastic programming of heating oil. Manag. Sci. 1958, 4, 235–263. [Google Scholar] [CrossRef]
- Nemirovski, A. On safe tractable approximations of chance constraints. Eur. J. Oper. Res. 2012, 219, 707–718. [Google Scholar] [CrossRef]
- Kudela, J.; Popela, P. Pool & discard algorithm for chance constrained optimization problems. IEEE Access 2020, 8, 79397–79407. [Google Scholar]
- Neumann, A.; Neumann, F. Optimising monotone chance-constrained submodular functions using evolutionary multi-objective algorithms. In Proceedings of the International Conference on Parallel Problem Solving from Nature; Springer: Berlin/Heidelberg, Germany, 2020; pp. 404–417. [Google Scholar]
- Doerr, B.; Doerr, C.; Neumann, A.; Neumann, F.; Sutton, A. Optimization of chance-constrained submodular functions. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 1460–1467. [Google Scholar]
- Xie, Y.; Neumann, A.; Neumann, F. Specific single-and multi-objective evolutionary algorithms for the chance-constrained knapsack problem. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancun, Mexico, 8–12 July 2020; pp. 271–279. [Google Scholar]
- Campi, M.C.; Garatti, S. The exact feasibility of randomized solutions of uncertain convex programs. SIAM J. Optim. 2008, 19, 1211–1230. [Google Scholar] [CrossRef]
- Camacho-Villalón, C.L.; Dorigo, M.; Stützle, T. The intelligent water drops algorithm: Why it cannot be considered a novel algorithm. Swarm Intell. 2019, 13, 173–192. [Google Scholar] [CrossRef]
- Camacho Villalón, C.L.; Stützle, T.; Dorigo, M. Grey wolf, firefly and bat algorithms: Three widespread algorithms that do not contain any novelty. In Proceedings of the International Conference on Swarm Intelligence; Springer: Berlin/Heidelberg, Germany, 2020; pp. 121–133. [Google Scholar]
- Weyland, D. A rigorous analysis of the harmony search algorithm: How the research community can be misled by a “novel” methodology. Int. J. Appl. Metaheuristic Comput. (IJAMC) 2010, 1, 50–60. [Google Scholar] [CrossRef]
- Aranha, C.; Camacho Villalón, C.L.; Campelo, F.; Dorigo, M.; Ruiz, R.; Sevaux, M.; Sörensen, K.; Stützle, T. Metaphor-based metaheuristics, a call for action: The elephant in the room. Swarm Intell. 2022, 16, 1–6. [Google Scholar] [CrossRef]
- Kudela, J. Commentary on:“STOA: A bio-inspired based optimization algorithm for industrial engineering problems”[EAAI, 82 (2019), 148–174] and “Tunicate Swarm Algorithm: A new bio-inspired based metaheuristic paradigm for global optimization”[EAAI, 90 (2020), no. 103541]. Eng. Appl. Artif. Intell. 2022, 113, 104930. [Google Scholar]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Del Ser, J.; Herrera, F. A prescription of methodological guidelines for comparing bio-inspired optimization algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K. Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm. Int. J. Mach. Learn. Cybern. 2020, 11, 1501–1529. [Google Scholar] [CrossRef]
- Mohamed, A.W.; Hadi, A.A.; Mohamed, A.K.; Awad, N.H. Evaluating the performance of adaptive gaining-sharing knowledge based algorithm on CEC 2020 benchmark problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Kůdela, J.; Juříček, M.; Parák, R. A Collection of Robotics Problems for Benchmarking Evolutionary Computation Methods. In Proceedings of the International Conference on the Applications of Evolutionary Computation (Part of EvoStar); Springer: Berlin/Heidelberg, Germany, 2023; pp. 364–379. [Google Scholar]
- Sallam, K.M.; Elsayed, S.M.; Chakrabortty, R.K.; Ryan, M.J. Improved multi-operator differential evolution algorithm for solving unconstrained problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential Evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Bujok, P.; Lacko, M.; Kolenovský, P. Differential Evolution and Engineering Problems. Mendel 2023, 29, 45–54. [Google Scholar] [CrossRef]
- Kůdela, J.; Matoušek, R. Combining Lipschitz and RBF surrogate models for high-dimensional computationally expensive problems. Inf. Sci. 2023, 619, 457–477. [Google Scholar] [CrossRef]
- Hansen, N.; Müller, S.D.; Koumoutsakos, P. Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 2003, 11, 1–18. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A.S. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–1 July 2014; pp. 1658–1665. [Google Scholar]
- Piotrowski, A.P.; Napiorkowski, J.J. Step-by-step improvement of JADE and SHADE-based algorithms: Success or failure? Swarm Evol. Comput. 2018, 43, 88–108. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 December–1 November 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Particle swarm optimization or differential evolution—A comparison. Eng. Appl. Artif. Intell. 2023, 121, 106008. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. Population size in particle swarm optimization. Swarm Evol. Comput. 2020, 58, 100718. [Google Scholar] [CrossRef]
- Kazikova, A.; Pluhacek, M.; Senkerik, R. Why tuning the control parameters of metaheuristic algorithms is so important for fair comparison? Mendel 2020, 26, 9–16. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 65–70. [Google Scholar]
- Aickin, M.; Gensler, H. Adjusting for multiple testing when reporting research results: The Bonferroni vs Holm methods. Am. J. Public Health 1996, 86, 726–728. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, M.J.; Napiorkowski, J.J.; Rowinski, P.M. Swarm intelligence and evolutionary algorithms: Performance versus speed. Inf. Sci. 2017, 384, 34–85. [Google Scholar] [CrossRef]
- García-Martínez, C.; Gutiérrez, P.D.; Molina, D.; Lozano, M.; Herrera, F. Since CEC 2005 competition on real-parameter optimisation: A decade of research, progress and comparative analysis’s weakness. Soft Comput. 2017, 21, 5573–5583. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J.; Piotrowska, A.E. How Much Do Swarm Intelligence and Evolutionary Algorithms Improve Over a Classical Heuristic From 1960? IEEE Access 2023, 11, 19775–19793. [Google Scholar] [CrossRef]
- Bujok, P.; Tvrdík, J.; Poláková, R. Comparison of nature-inspired population-based algorithms on continuous optimisation problems. Swarm Evol. Comput. 2019, 50, 100490. [Google Scholar] [CrossRef]
- Kudela, J.; Zalesak, M.; Charvat, P.; Klimes, L.; Mauder, T. Assessment of the performance of metaheuristic methods used for the inverse identification of effective heat capacity of phase change materials. Expert Syst. Appl. 2023, 122373. [Google Scholar] [CrossRef]
- Kudela, J.; Matousek, R. New benchmark functions for single-objective optimization based on a zigzag pattern. IEEE Access 2022, 10, 8262–8278. [Google Scholar] [CrossRef]
- Bäck, T.H.; Kononova, A.V.; van Stein, B.; Wang, H.; Antonov, K.A.; Kalkreuth, R.T.; de Nobel, J.; Vermetten, D.; de Winter, R.; Ye, F. Evolutionary Algorithms for Parameter Optimization—Thirty Years Later. Evol. Comput. 2023, 31, 81–122. [Google Scholar] [CrossRef]
- Auger, A.; Teytaud, O. Continuous lunches are free plus the design of optimal optimization algorithms. Algorithmica 2010, 57, 121–146. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]

| Uncertain Parameter | Symbol | Unit | Distribution Type | Lower Bound | Upper Bound |
|---|---|---|---|---|---|
| Port handling rate | ton/day | uniform | 5000 | 10,000 | |
| Round trip miles | nm | uniform | 3000 | 7000 | |
| Fuel price | GBP/ton | uniform | 80 | 140 |
| Variable | Symbol | Unit | Lower Bound | Upper Bound |
|---|---|---|---|---|
| Length | L | m | 100 | 600 |
| Beam | B | m | 10 | 100 |
| Depth | D | m | 5 | 30 |
| Draft | T | m | 5 | 30 |
| Block coefficient | - | 0.63 | 0.75 | |
| Cruise speed | knots | 14 | 18 |
| AGSK | APGSKI | DE | EA4eig | EBO | LSHADE | PSO | |
|---|---|---|---|---|---|---|---|
| min | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2546087 |
| mean | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2513056 |
| max | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593538 | −1.2593536 | −1.2593538 | −1.2485806 |
| std | 0.000 | 0.000 | 0.000 | 0.000 | 4.472 × 10 | 0.000 | 1.594 × 10 |
| AGSK | APGSKI | DE | EA4eig | EBO | LSHADE | PSO | ||
|---|---|---|---|---|---|---|---|---|
| 0.01 | min | −0.9473943 | −0.9473939 | −0.9473943 | −0.9473943 | −0.8491422 | −0.9473943 | −0.9446069 |
| mean | −0.9473943 | −0.9466775 | −0.9473943 | −0.9473941 | 212.9033097 | −0.9473943 | −0.9420872 | |
| max | −0.9473943 | −0.9403836 | −0.9473943 | −0.9473932 | 1043.7700147 | −0.9473943 | −0.9367206 | |
| std | 0.000 | 1.548 × 10 | 0.000 | 3.278 × 10 | 3.248 × 10 | 0.000 | 2.166 × 10 | |
| 0.05 | min | −0.9991552 | −0.9991529 | −0.9991552 | −0.9991552 | −0.9691110 | −0.9991552 | −0.9982688 |
| mean | −0.9991552 | −0.9982114 | −0.9991552 | −0.9991545 | 139.6795100 | −0.9991552 | −0.9958583 | |
| max | −0.9991550 | −0.9962695 | −0.9991552 | −0.9991514 | 607.0723893 | −0.9991552 | −0.9910965 | |
| std | 6.156 × 10 | 8.508 × 10 | 0.000 | 1.106 × 10 | 2.198 × 10 | 0.000 | 1.668 × 10 | |
| 0.10 | min | −1.0291039 | −1.0290552 | −1.0291039 | −1.0291039 | −0.9795876 | −1.0291039 | −1.0279124 |
| mean | −1.0291034 | −1.0286804 | −1.0291038 | −1.0291013 | 7.1408294 | −1.0291039 | −1.0252982 | |
| max | −1.0291014 | −1.0276915 | −1.0291017 | −1.0290916 | 159.0656498 | −1.0291039 | −1.0194222 | |
| std | 9.305 × 10 | 3.949 × 10 | 4.919 × 10 | 3.574 × 10 | 35.76 | 0.000 | 2.111 × 10 | |
| 0.15 | min | −1.0496266 | −1.0496254 | −1.0496266 | −1.0496266 | −1.0363353 | −1.0496266 | −1.0492396 |
| mean | −1.0496245 | −1.0492608 | −1.0496266 | −1.0496221 | 42.7607508 | −1.0496266 | −1.0474384 | |
| max | −1.0496125 | −1.0479015 | −1.0496266 | −1.0496049 | 871.4141031 | −1.0496266 | −1.0431568 | |
| std | 3.512 × 10 | 4.669 × 10 | 0.000 | 6.710 × 10 | 1.950 × 10 | 0.000 | 1.631 × 10 | |
| 0.20 | min | −1.0679705 | −1.0679607 | −1.0679705 | −1.0679705 | −1.0284986 | −1.0679705 | −1.0675095 |
| mean | −1.0679691 | −1.0673805 | −1.0679705 | −1.0679699 | −0.8312606 | −1.0679705 | −1.0657167 | |
| max | −1.0679652 | −1.0660410 | −1.0679705 | −1.0679684 | 1.5861289 | −1.0679705 | −1.0628487 | |
| std | 1.900 × 10 | 6.352 × 10 | 0.000 | 7.343 × 10 | 5.802 × 10 | 0.000 | 1.160 × 10 | |
| 0.25 | min | −1.0843175 | −1.0843083 | −1.0843175 | −1.0843175 | −1.0461846 | −1.0843175 | −1.0833582 |
| mean | −1.0843142 | −1.0837891 | −1.0843175 | −1.0843170 | −1.0317051 | −1.0843175 | −1.0809449 | |
| max | −1.0843052 | −1.0817133 | −1.0843175 | −1.0843145 | −0.9836282 | −1.0843175 | −1.0772805 | |
| std | 4.584 × 10 | 6.152 × 10 | 0.000 | 7.545 × 10 | 1.475 × 10 | 0.000 | 1.761 × 10 |
| p | p | p | |||||
| LSHADE vs other methods | DE | 1.00 | 1.00 ✗ | 1.00 | 1.00 ✗ | 1.00 | 1.00 ✗ |
| AGSK | 1.00 | 1.00 ✗ | 5.00 × 10 | 1.00 ✗ | 3.91 × 10 | 7.81 × 10 | |
| EA4eig | 3.13 × 10 | 9.38 × 10 ✗ | 9.77 × 10 | 2.93 × 10 | 1.22 × 10 | 3.66 × 10 | |
| APGSKI | 8.86 × 10 | 5.31 × 10 | 8.86 × 10 | 5.31 × 10 | 8.86 × 10 | 5.31 × 10 | |
| PSO | 8.86 × 10 | 5.31 × 10 | 8.86 × 10 | 5.31 × 10 | 8.86 × 10 | 5.31 × 10 | |
| EBO | 8.86 × 10 | 4.43 × 10 | 8.86 × 10 | 4.43 × 10 | 8.86 × 10 | 4.43 × 10 | |
| p | p | p | |||||
| LSHADE vs other methods | DE | 1.00 | 1.00 ✗ | 1.00 | 1.00 ✗ | 1.00 | 1.00 ✗ |
| AGSK | 6.10 × 10 | 3.66 × 10 | 1.22 × 10 | 3.66 × 10 | 1.24 × 10 | 3.73 × 10 | |
| EA4eig | 2.90 × 10 | 5.80 × 10 | 2.44 × 10 | 4.88 × 10 | 1.68 × 10 | 3.73 × 10 | |
| APGSKI | 8.86 × 10 | 4.43 × 10 | 8.86 × 10 | 5.31 × 10 | 8.86 × 10 | 5.31 × 10 | |
| PSO | 8.86 × 10 | 4.43 × 10 | 8.86 × 10 | 5.31 × 10 | 8.86 × 10 | 5.31 × 10 | |
| EBO | 8.86 × 10 | 3.54 × 10 | 8.86 × 10 | 4.43 × 10 | 8.86 × 10 | 4.43 × 10 | |
| Variable | Symbol | 0.01 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | Deterministic |
| Length | L | 275.5554 | 295.3920 | 308.5694 | 318.4319 | 327.2925 | 334.3526 | 412.3332 |
| Beam | B | 45.9271 | 49.2330 | 51.4290 | 53.0728 | 54.5495 | 55.7262 | 68.7358 |
| Depth | D | 24.9640 | 26.6760 | 27.8068 | 28.6498 | 29.4037 | 30.0000 | 30.0000 |
| Draft | T | 18.1749 | 19.3732 | 20.1648 | 20.7549 | 21.2826 | 21.7000 | 21.7010 |
| Block coefficient | 0.7500 | 0.7500 | 0.7500 | 0.7500 | 0.7500 | 0.7500 | 0.7500 | |
| Cruise speed | 14.0000 | 14.0000 | 14.0051 | 14.0236 | 14.1336 | 14.4225 | 18.0000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudela, J. Chance-Constrained Optimization Formulation for Ship Conceptual Design: A Comparison of Metaheuristic Algorithms. Computers 2023, 12, 225. https://doi.org/10.3390/computers12110225
Kudela J. Chance-Constrained Optimization Formulation for Ship Conceptual Design: A Comparison of Metaheuristic Algorithms. Computers. 2023; 12(11):225. https://doi.org/10.3390/computers12110225
Chicago/Turabian StyleKudela, Jakub. 2023. "Chance-Constrained Optimization Formulation for Ship Conceptual Design: A Comparison of Metaheuristic Algorithms" Computers 12, no. 11: 225. https://doi.org/10.3390/computers12110225
APA StyleKudela, J. (2023). Chance-Constrained Optimization Formulation for Ship Conceptual Design: A Comparison of Metaheuristic Algorithms. Computers, 12(11), 225. https://doi.org/10.3390/computers12110225






