Abstract
Artificial neural networks are widely established models of computational intelligence that have been tested for their effectiveness in a variety of real-world applications. These models require a set of parameters to be fitted through the use of an optimization technique. However, an issue that researchers often face is finding an efficient range of values for the parameters of the artificial neural network. This paper proposes an innovative technique for generating a promising range of values for the parameters of the artificial neural network. Finding the value field is conducted by a series of rules for partitioning the original set of values or expanding it, the rules of which are generated using grammatical evolution. After finding a promising interval of values, any optimization technique such as a genetic algorithm can be used to train the artificial neural network on that interval of values. The new technique was tested on a wide range of problems from the relevant literature and the results were extremely promising.
1. Introduction
Artificial neural networks (ANNs) are widespread machine learning models, which base their dynamics on a series of parameters that are also called computational units or weights in the relevant literature [1,2]. Neural networks are widely used in a variety of scientific applications, such as problems from physics [3,4,5], solutions of differential equations [6,7], agriculture problems [8,9], chemistry problems [10,11,12], problems that appear in the area of economic sciences [13,14,15], problems related to medicine [16,17], etc. Commonly, the neural networks are expressed as a function , with the assumption that the vector stands for the input vector to the neural network and the vector is the parameter vector that should be estimated. The first vector is called pattern in the bibliography and the second one weight vector. Techniques that adjust the parameter vector minimize the so-called training error, defined as:
In Equation (1), the set is denoted as the training set of the neural network. The are considered the target outputs for the points. As proposed in [18], neural networks can be expressed as the following summation:
The number of processing units is denoted by H and the value d stands for the dimension of input vector . The function denotes the well-known sigmoid function expressed as:
From the above equations one can calculate the total number of parameters in the neural network as:
The training of neural networks has been performed by a variety of numerical methods in the recent literature, such as: the Back Propagation method [19], the RPROP method [20], the Adam optimizer [21], etc. Furthermore, more advanced optimization methods have been incorporated to optimize the parameter vector of neural networks by minimizing Equation (1) such as quasi-Newton methods [22], the Tabu search method [23], Simulated Annealing [24], genetic algorithms [25], particle swarm optimization (PSO) [26], Differential Evolution [27], Ant Colony Optimization [28], etc.
Moreover, recently, a series of hybrid optimization methods were proposed to tackle the minimization of the training error, such as a method that combines PSO and genetic algorithms [29,30], the incorporation of a particle swarm optimization algorithm and gravitational search algorithm [31], a combination of a genetic algorithm and controlled gradient method [32], etc.
In addition, an important topic for artificial neural networks such as parameter initialization has been studied by several researchers in recent years. In this area appeared papers such as initialization with decision trees [33], incorporation of the Cauchy’s inequality [34], discriminant learning [35], etc. Another interesting topic in the area of neural networks is weight decaying, where some regularization is applied to the parameters of the neural network to avoid the overfitting problem. For this topic, several research papers have been suggested, such as a method that incorporates positive correlation [36], the SarProp algorithm [37], usage of pruning techniques [38], etc.
This paper proposes a two-stage method for efficient training of the parameters of artificial neural networks. In the first stage, a value interval is constructed for the parameters of the neural network through grammatical evolution [39]. In the first stage of this work, after an initial estimate of the interval for the parameters of the neural network is made, a series of rules for partitioning and expanding the initial value interval are applied with the usage of grammatical evolution, until a promising value interval is found. In the second stage of the method, a genetic algorithm is applied to train the parameters of the artificial neural network. Training is performed within the optimal interval of values found in the first stage of the method. The proposed method utilizes a genetic algorithm in the second stage to train the neural network, but any other optimization method can be used instead of genetic algorithms. However, genetic algorithms are used because they are easily adaptable to many optimization problems as they are fault tolerant, and because they can be easily parallelized using modern computing techniques.
The proposed method seeks in its first stage to find, using an evolutionary rule technique, a range of values for the parameters of the artificial neural networks. This interval should on the one hand be small enough to speed up the method of the second stage that will be used to train the model, and on the other hand, the artificial neural network should have satisfactory generalization abilities within the interval of values of the first stage.
2. Method Description
In this section a detailed description of the grammatical evolution technique is provided, accompanied by the proposed language that creates intervals for the parameters of the neural networks. Subsequently, the first phase of the proposed technique is described, and finally, the second phase, with the application of a genetic algorithm to the outcome of the first phase, is thoroughly analyzed.
2.1. Grammatical Evolution
Grammatical evolution is an evolutionary process, where the chromosomes represent production rules of some provided BNF (Backus–Naur form) grammar [40], and this evolutionary process can evolve programs in the underlying language. Grammatical evolution has been used successfully in many real-world problems, such as function approximation [41,42], the solution of trigonometric equations [43], automatic music composition [44], neural network construction [45,46], creating numeric constraints [47], video games [48,49], estimation of energy demand [50], combinatorial optimization [51], cryptography [52], the evolution of decision trees [53], the automatic design of analog electronic circuits [54], etc. Any BNF grammar can be described as the set where
- N is the set of the non-terminal symbols. Every symbol in N has a series of production rules, used to produce terminal symbols.
- T is the set of terminal symbols.
- S denotes the start symbol of the grammar, with .
- P is the set of production rules, to create terminal symbols non-terminal symbols. These rules are in the form or .
The algorithm initiates from the symbol S and iteratively produces terminal symbols by replacing non-terminal symbols with the right hand of the selected production rule. Every production rule is selected using the following steps:
- Obtain the next element V from the current chromosome.
- Select the next production rule according to: Rule = V mod , where is the total number of production rules for the current non-terminal symbol.
The grammar used in the current work is shown in Figure 1.

Figure 1.
BNF grammar used in the current work. The value n stands for the number of total parameters in the neural network.
The symbols in <> represent the non-terminal symbols of the grammar. The numbers in parentheses in the right part of each rule indicate production rule sequence numbers. In the proposed language described by the grammar of the scheme, three distinct operations can be applied to parameters of the artificial neural network either on the left end of the parameter’s value range (described by <lcommand>) or on the right end of the value range (described by the <rcommand> symbol). These commands are
- 1.
- NOTHING. This command means that no action takes place.
- 2.
- EXPAND. With this command, the corresponding end of the value field is extended by 50% of the width of the field.
- 3.
- DIVIDE. With this command, the corresponding end of the value field is shrunk by 50% of the width of the field.
As a complete example, consider a neural network with hidden nodes and the dimension of the objective problem is set to . Hence, the total number of parameters in the neural network is . In addition, for reasons of simplicity, we consider that the initial range of values for all parameters of the artificial neural network is the interval [−2, 2] and is denoted as the set of intervals
and also consider the chromosome
The steps to produce the final program
are shown in Table 1.

Table 1.
Steps to produce a valid expression from the BNF grammar.
After the application of the program to the original interval of Equation (5), the new set has as follows:
2.2. The First Phase of the Proposed Method
Before starting the process of creating partitioning rules and expanding the value interval of the neural network weights, an initial estimate of this interval should be made. In the present work, only a few steps of a genetic algorithm are applied to make an initial estimate of the value interval. At the end of the genetic algorithm, the chromosome with the best value is
This, the initial interval set for the parameters of the neural network is calculated as
The first phase of the proposed technique will accept the set as input and seek to compute a new set by reducing the training error of the artificial neural network. The first step is mainly a genetic algorithm and the corresponding steps are as follows:
- 1.
- Set as the number of chromosomes for the grammatical evolution.
- 2.
- Set H as the number of weights for the neural network.
- 3.
- Set as the maximum number of allowed generations.
- 4.
- Set as the selection rate, with .
- 5.
- Set as the mutation rate, with .
- 6.
- Set as the number of randomly created neural networks, which will be used in the fitness calculation.
- 7.
- Initialize randomly the chromosomes. Every chromosome is a set of integer numbers used to produce valid programs through grammatical evolution and the associated grammar of Figure 1.
- 8.
- Set , the best discovered fitness. For this algorithm, we consider the fitness function of any given chromosome g as an interval
- 9.
- Set iter=0.
- 10.
- For do
- (a)
- Create for the chromosome the corresponding program using the grammar of Figure 1.
- (b)
- Apply the program to in order to produce the bounds .
- (c)
- Set
- (d)
- For do
- i.
- Create randomly as a set for the parameters of neural network.
- ii.
- Calculate the associated training error
- iii.
- If then
- iv.
- If then
- (e)
- EndFor
- (f)
- Set as the fitness value for the chromosome .
- 11.
- EndFor
- 12.
- Apply the selection procedure. Firstly, the chromosomes are sorted with correspondence to their fitness values. Since fitness is considered an interval, a fitness comparison function is required. For this reason, the operator is used to compare two fitness values and as follows:In practice this means that the fitness value is considered smaller than if . The first chromosomes with the lowest fitness values are copied to the next generation. The remaining chromosomes are substituted by chromosomes produced by the crossover procedure. During the selection process, for every new offspring, two chromosomes are selected as parents from the population using the well-known procedure of tournament selection.
- 13.
- Apply the crossover procedure. For each pair of parents, two new chromosomes and are created using the one-point crossover, graphically shown in Figure 2.
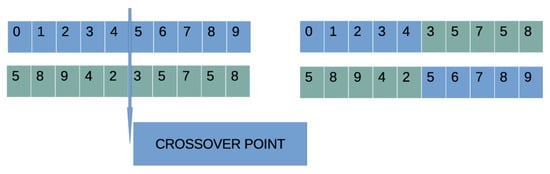 Figure 2. The one-point crossover, used in the grammatical evolution. The numbers in figure denote sequential number of production rules used in the Grammatical Evolution procedure.
Figure 2. The one-point crossover, used in the grammatical evolution. The numbers in figure denote sequential number of production rules used in the Grammatical Evolution procedure. - 14.
- Apply the mutation procedure. For each element of every chromosome alter the corresponding element with probability .
- 15.
- Set iter=iter+1
- 16.
- If goto step 10.
2.3. The Second Phase of the Proposed Method
The result of the first phase of the proposed method is an interval of values for the parameters of the artificial neural network. This interval of values can be used to minimize the error function of the network with the parameters taking values exclusively in the above interval of values. Any optimization method can be used for this purpose, but in this work, a genetic algorithm was chosen, the steps of which are given below.
- 1.
- Initialization Step
- (a)
- Set as the number of chromosomes that participate in the genetic algorithm.
- (b)
- Set as the maximum number of allowed iterations.
- (c)
- Set H as the number of weights for the neural network.
- (d)
- Obtain the best interval S from the previous step of Section 2.2.
- (e)
- Initialize using uniform distribution the chromosomes in S.
- (f)
- Set as the selection rate, with .
- (g)
- Set as the mutation rate, with .
- (h)
- Set iter=0.
- 2.
- Fitness calculation Step
- (a)
- For do
- i.
- Calculate the fitness of chromosome as
- (b)
- EndFor
- 3.
- Genetic operations step
- (a)
- Selection procedure: Initially, the chromosomes are sorted according to their fitness values. The first chromosomes with the lowest fitness values are copied to the next generation. The remaining chromosomes are substituted by chromosomes produced by the crossover procedure. During the selection process, for every new offspring, two chromosomes are selected as parents from the population using the well-known procedure of tournament selection.
- (b)
- Crossover procedure: For each pair of selected parents, two chromosomes and are constructed using the following equations:where is a random number with the property [55].
- (c)
- Mutation procedure: For each element of every chromosome, alter the corresponding element with probability .
- 4.
- Termination Check Step
- (a)
- Set
- (b)
- If go to step 2, otherwise apply a local search procedure to the best chromosome of the population. In the current work, the BFGS variant of Powell [56] was used.
3. Experiments
The effectiveness of the proposed method was evaluated on a series of classification and regression datasets, used in the relevant literature. These datasets can be downloaded from the following online databases:
- 1.
- UCI dataset repository, https://archive.ics.uci.edu/ml/index.php [57] (accessed on 4 November 2023).
- 2.
- Keel repository, https://sci2s.ugr.es/keel/datasets.php [58] (accessed on 4 November 2023).
- 3.
- The Statlib URL ftp://lib.stat.cmu.edu/datasets/index.html (accessed on 4 November 2023).
3.1. Experimental Datasets
The classification datasets used in this paper are the following:
- 1.
- Appendicitis dataset, a medical purpose dataset, suggested in [59].
- 2.
- Australian dataset [60], a dataset related to credit card transactions.
- 3.
- Balance dataset [61], related to psychological states.
- 4.
- Cleveland dataset, which is a medical dataset [62,63].
- 5.
- Dermatology dataset [64], a medical dataset related to erythemato-squamous diseases.
- 6.
- Heart dataset [65], a medical dataset related to heart diseases.
- 7.
- Hayes roth dataset [66].
- 8.
- HouseVotes dataset [67], related to votes in the U.S. House of Representatives Congressmen.
- 9.
- Ionosphere dataset, used for classification of radar returns from the ionosphere [68,69].
- 10.
- Liverdisorder dataset [70], a medical dataset related to liver disorders.
- 11.
- Mammographic dataset [71], used to identify breast tumors.
- 12.
- Parkinsons dataset, a medical dataset related to Parkinson’s disease (PD) [72].
- 13.
- Pima dataset [73], used to detect the presence of diabetes.
- 14.
- Popfailures dataset [74], a dataset related to climate measurements.
- 15.
- Regions2 dataset, medical dataset related to hepatitis C [75].
- 16.
- Saheart dataset [76], a medical dataset related to heart diseases.
- 17.
- Segment dataset [77], an image processing dataset.
- 18.
- Wdbc dataset [78], a medical dataset related to breast tumors.
- 19.
- Wine dataset, used to detect the origin of wines [79,80].
- 20.
- Eeg datasets, a medical dataset related to EEG measurements [81]. There are three different cases from this dataset used here denoted as Z_F_S, ZO_NF_S, ZONF_S.
- 21.
- Zoo dataset [82], used to classify animals.
The descriptions of the used regression datasets are as follows:
- 1.
- Abalone dataset [83], used to to predict the age of abalone from physical measurements.
- 2.
- Airfoil dataset, derived from NASA [84].
- 3.
- Baseball dataset, used to estimate the salary of baseball players.
- 4.
- BK dataset [85], used to predict the points scored in a basketball game.
- 5.
- BL dataset, an electrical engineering dataset.
- 6.
- Concrete dataset [86].
- 7.
- Dee dataset, used to predict the price of electricity.
- 8.
- Diabetes dataset, a medical dataset.
- 9.
- Housing dataset, provided in [87].
- 10.
- FA dataset, used to predict the fit body fat.
- 11.
- MB dataset, available from from Smoothing Methods in Statistics [85].
- 12.
- MORTGAGE dataset, related to economic data from the USA.
- 13.
- PY dataset, (Pyrimidines problem) [88].
- 14.
- Quake dataset, used to predict the strength of earthquakes.
- 15.
- Treasure dataset, related to economic data from the USA.
- 16.
- Wankara dataset, a dataset related to weather.
3.2. Experimental Results
The proposed method was coded in ANSI C++, and the optimization methods were obtained from the freely available OPTIMUS computing environment, downloaded from https://github.com/itsoulos/OPTIMUS/ (accessed on 9 September 2023). The results were validated using the 10-fold validation technique in all datasets. The experiments were executed 30 times for each dataset using a different seed for the random generator each time. The average classification error is reported for the case of classification datasets and the average mean test error for the regression datasets. The machine used in the experiments was an AMD Ryzen 5950X with 128GB of RAM, running the Debian Linux operating system. The experimental settings are listed in Table 2. The experimental results for the classification datasets are shown in Table 3, while for the regression datasets, the results are shown in Table 4. The following apply to the results tables:

Table 2.
Experimental parameters.

Table 3.
Experimental results for classification datasets. The values in cells indicate average classification error as measured on test set. The numbers in parentheses denote the standard deviation.

Table 4.
Experimental results for regression datasets. The values indicate average regression error as measured on test set. The numbers in parentheses denote the standard deviation.
- 1.
- A genetic algorithm where the parameters have the values of Table 2 used to train a neural network with H hidden nodes. The results in the experimental tables are denoted by the label GENETIC.
- 2.
- The Adam optimization method is used to train a neural network with H hidden nodes. The column ADAM denotes the results for this method.
- 3.
- The RPROP method is used to train a neural network with H hidden nodes. The corresponding results are denoted by RPROP in the relevant tables.
- 4.
- The NEAT method (NeuroEvolution of Augmenting Topologies) [89], where the maximum number of allowed generations is the same as in the case of the genetic algorithm.
- 5.
- The proposed method (denoted as PROPOSED) was used with the experimental settings and are shown in Table 2.
- 6.
- An extra line was also added to the experimental tables under the title AVERAGE. This line represents the average classification or regression error for all datasets.
In general, the proposed technique outperforms the rest of the techniques in the experiments. In fact, in many cases, the test error is reduced by more than 70%. Additionally, more experiments were conducted using the number of processing nodes (H) as well as the number of generations (), to determine the stability of the proposed technique. The average classification error for the classification datasets using different values for the H parameter is shown graphically in Figure 3. Furthermore, the average classification error of the proposed method for different numbers of maximum generations is shown graphically in Figure 4. The proposed technique does not show significant changes in its behavior as the critical parameters change, and therefore, its stability to changes is evident. Moreover, the average execution time for different values of the parameter is outlined in Figure 5. Judging from the above experiments, it can be said that the choice of values for the critical parameters H and is a compromise between performance and speed for the proposed technique.
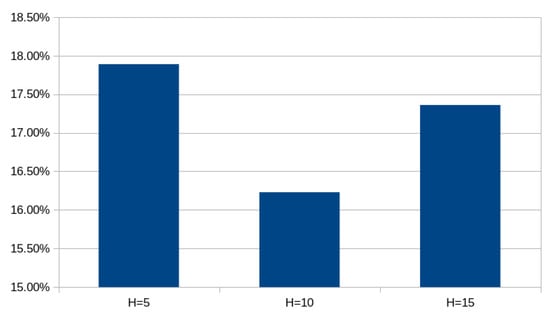
Figure 3.
Average classification error using the proposed method and different values for the number of hidden nodes H.
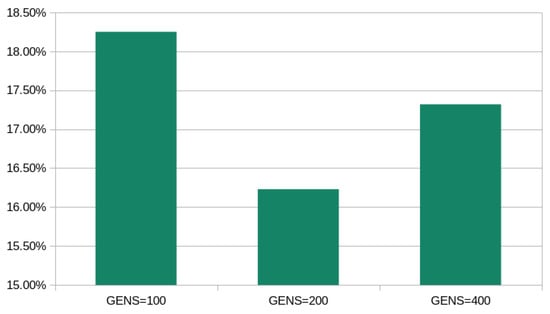
Figure 4.
Average classification error of the proposed method using different values for the maximum number of allowed generations .
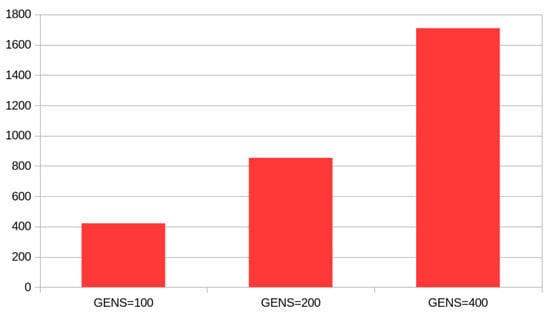
Figure 5.
Average execution time of the proposed method, using different values of the parameter.
The numerical superiority of the proposed technique over the others in the performed experiments is presented graphically in Figure 6 and Figure 7, where Wilcoxon signed-rank tests were performed on the executed experiments. However, since the proposed technique consists exclusively of a series of genetic algorithms, it can be significantly accelerated by the use of parallel computing techniques, since one of the main characteristics of genetic algorithms is their ease of parallelization [90,91]. Programming techniques that can be used to parallelize the method could be the MPI programming interface [92] or the OpenMP programming library [93].
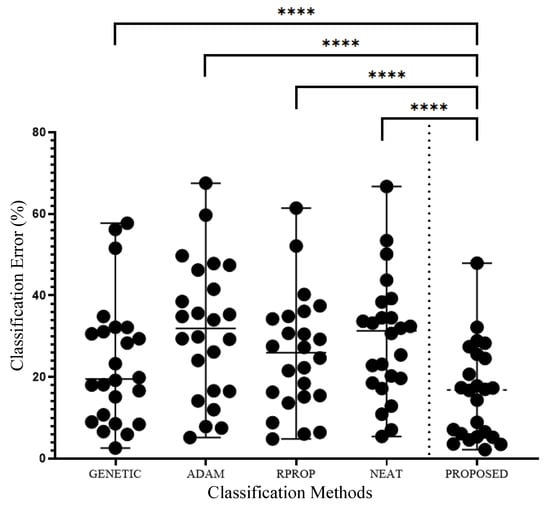
Figure 6.
Scatter plot representation and the two-sample paired (Wilcoxon) signed-rank test results of the comparison for each of the four (4) classification methods (GENETIC, ADAM, RPROP, and NEAT) with the PROPOSED method regarding the classification error in twenty-four (24) different public available classification datasets. The stars only intend to flag significance levels for the two most used groups. A p-value of less than 0.0001 is flagged with four stars (****).
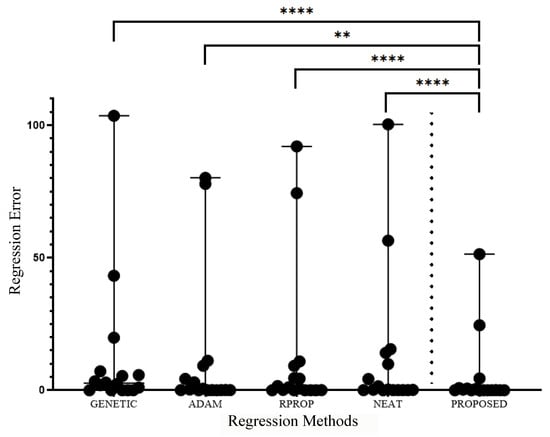
Figure 7.
Scatter plot representation and the Wilcoxon signed-rank test results of the comparison for each of the four (4) regression methods (GENETIC, ADAM, RPROP, and NEAT) with the PROPOSED method regarding the regression error in sixteen (16) different publicly available regression datasets. Star links join significantly different values: two stars (**) stands for p < 0.001, and four stars (****) stand for p < 0.0001.
4. Conclusions
This paper proposed a two-step technique to efficiently find a reliable interval of values for the parameters of artificial neural networks. In the first stage with partitioning techniques and using grammatical evolution, a range of parameter values was searched, and in the second stage, a genetic algorithm trained the artificial neural network within the optimal range of values of the first stage. The proposed technique is highly general and was successfully applied to both data fitting and classification problems. In both cases, the experimental results demonstrate its superiority over other techniques appearing in the relevant literature on the training of artificial neural networks. In fact, in many cases in the performed experiments, the proposed method outperforms others that were tested in percentages that exceed 70%. In the future, a series of actions can be carried out to improve the results and speed up the proposed method, such as:
- 1.
- There is a need for more efficient techniques for initializing the value space for artificial neural network parameters. In the present work, the optimal result from the execution of a limited number of steps by a genetic algorithm was used as an initial estimate of the value interval.
- 2.
- In the present work, the same techniques as in any whole-chromosome genetic algorithm were used to perform the crossover and mutation operations. Research could be conducted at this point to find more focused crossover and mutation techniques for this particular problem.
- 3.
- The present technique consists of two phases, in each of which a problem-adapted genetic algorithm is executed. This means that significant computational time is required to complete the algorithm. However, since genetic algorithms are inherently parallelizable, modern parallel programming techniques could be used here.
Author Contributions
I.G.T., A.T. and E.K. conceived the idea and methodology and supervised the technical part regarding the software. I.G.T. conducted the experiments, employing several datasets, and provided the comparative experiments. A.T. performed the statistical analysis. E.K. and all other authors prepared the manuscript. E.K. and I.G.T. organized the research team and A.T. supervised the project. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This research was financed by the European Union: Next Generation EU through the Program Greece 2.0 National Recovery and Resilience Plan, under the call RESEARCH—CREATE—INNOVATE, project name “iCREW: Intelligent small craft simulator for advanced crew training using Virtual Reality techniques” (project code: TAEDK-06195).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Baldi, P.; Cranmer, K.; Faucett, T.; Sadowski, P.; Whiteson, D. Parameterized neural networks for high-energy physics. Eur. Phys. J. C 2016, 76, 235. [Google Scholar] [CrossRef]
- Valdas, J.J.; Bonham-Carter, G. Time dependent neural network models for detecting changes of state in complex processes: Applications in earth sciences and astronomy. Neural Netw. 2006, 19, 196–207. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef]
- Shirvany, Y.; Hayati, M.; Moradian, R. Multilayer perceptron neural networks with novel unsupervised training method for numerical solution of the partial differential equations. Appl. Soft Comput. 2009, 9, 20–29. [Google Scholar] [CrossRef]
- Malek, A.; Beidokhti, R.S. Numerical solution for high order differential equations using a hybrid neural network—Optimization method. Appl. Math. Comput. 2006, 183, 260–271. [Google Scholar] [CrossRef]
- Topuz, A. Predicting moisture content of agricultural products using artificial neural networks. Adv. Eng. Softw. 2010, 41, 464–470. [Google Scholar] [CrossRef]
- Escamilla-García, A.; Soto-Zarazúa, G.M.; Toledano-Ayala, M.; Rivas-Araiza, E.; Gastélum-Barrios, A. Applications of Artificial Neural Networks in Greenhouse Technology and Overview for Smart Agriculture Development. Appl. Sci. 2020, 10, 3835. [Google Scholar] [CrossRef]
- Shen, L.; Wu, J.; Yang, W. Multiscale Quantum Mechanics/Molecular Mechanics Simulations with Neural Networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [Google Scholar] [CrossRef]
- Manzhos, S.; Dawes, R.; Carrington, T. Neural network-based approaches for building high dimensional and quantum dynamics-friendly potential energy surfaces. Int. J. Quantum Chem. 2015, 115, 1012–1020. [Google Scholar] [CrossRef]
- Wei, J.N.; Duvenaud, D.; Aspuru-Guzik, A. Neural Networks for the Prediction of Organic Chemistry Reactions. ACS Cent. Sci. 2016, 2, 725–732. [Google Scholar] [CrossRef] [PubMed]
- Falat, L.; Pancikova, L. Quantitative Modelling in Economics with Advanced Artificial Neural Networks. Proc. Econ. Financ. 2015, 34, 194–201. [Google Scholar] [CrossRef]
- Namazi, M.; Shokrolahi, A.; Sadeghzadeh Maharluie, M. Detecting and ranking cash flow risk factors via artificial neural networks technique. J. Bus. Res. 2016, 69, 1801–1806. [Google Scholar] [CrossRef]
- Tkacz, G. Neural network forecasting of Canadian GDP growth. Int. J. Forecast. 2001, 17, 57–69. [Google Scholar] [CrossRef]
- Baskin, I.I.; Winkler, D.; Tetko, I.V. A renaissance of neural networks in drug discovery. Expert Opin. Drug Discov. 2016, 11, 785–795. [Google Scholar] [CrossRef]
- Bartzatt, R. Prediction of Novel Anti-Ebola Virus Compounds Utilizing Artificial Neural Network (ANN). World J. Pharm. Res. 2018, 2018 7, 16. [Google Scholar]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Neural network construction and training using grammatical evolution. Neurocomputing 2008, 72, 269–277. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Kingma, D.P.; Ba, J.L. ADAM: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Robitaille, B.; Payre, B.M. Modified quasi-Newton methods for training neural networks. Comput. Chem. Eng. 1996, 20, 1133–1140. [Google Scholar] [CrossRef]
- Sexton, R.S.; Alidaee, B.; Dorsey, R.E.; Johnson, J.D. Global optimization for artificial neural networks: A tabu search application. Eur. J. Oper. Res. 1998, 106, 570–584. [Google Scholar] [CrossRef]
- Yamazaki, A.; de Souto, M.C.P.; Ludermir, T.B. Optimization of neural network weights and architectures for odor recognition using simulated annealing. In Proceedings of the 2002 International Joint Conference on Neural Networks. IJCNN’02, Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 547–552. [Google Scholar]
- Leung, F.H.F.; Lam, H.K.; Ling, S.H.; Tam, P.K. Tuning of the structure and parameters of a neural network using an improved genetic algorithm. IEEE Trans. Neural Netw. 2003, 14, 79–88. [Google Scholar] [CrossRef]
- Zhang, C.; Shao, H.; Li, Y. Particle swarm optimisation for evolving artificial neural network. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Nashville, TN, USA, 8–11 October 2000; IEEE: Toulouse, France, 2000; pp. 2487–2490. [Google Scholar]
- Lonen, J.; Kamarainen, J.K.; Lampinen, J. Differential Evolution Training Algorithm for Feed-Forward Neural Networks. Neural Process. Lett. 2003, 17, 93–105. [Google Scholar]
- Salama, K.M.; Abdelbar, A.M. Learning neural network structures with ant colony algorithms. Swarm Intell. 2015, 9, 229–265. [Google Scholar] [CrossRef]
- Zhang, J.R.; Zhang, J.; Lok, T.M.; Lyu, M.R. A hybrid particle swarm optimization—Back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 2007, 185, 1026–1037. [Google Scholar] [CrossRef]
- Mishra, S.; Patra, S.K. Short Term Load Forecasting Using Neural Network Trained with Genetic Algorithm & Particle Swarm Optimization. In Proceedings of the 2008 First International Conference on Emerging Trends in Engineering and Technology, Nagpur, India; 2008; pp. 606–611. [Google Scholar] [CrossRef]
- Mirjalili, S.; Hashim, S.Z.M.; Sardroudi, H.M. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput. 2012, 218, 11125–11137. [Google Scholar] [CrossRef]
- Kobrunov, A.; Priezzhev, I. Hybrid combination genetic algorithm and controlled gradient method to train a neural network. Geophysics 2016, 81, 35–43. [Google Scholar] [CrossRef]
- Ivanova, I.; Kubat, M. Initialization of neural networks by means of decision trees. Knowl.-Based Syst. 1995, 8, 333–344. [Google Scholar] [CrossRef]
- Yam, J.Y.F.; Chow, T.W.S. A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Chumachenko, K.; Iosifidis, A.; Gabbouj, M. Feedforward neural networks initialization based on discriminant learning. Neural Netw. 2022, 146, 220–229. [Google Scholar] [CrossRef] [PubMed]
- Shahjahan, M.D.; Kazuyuki, M. Neural network training algorithm with possitive correlation. IEEE Trans. Inf. Syst. 2005, 88, 2399–2409. [Google Scholar] [CrossRef]
- Treadgold, N.K.; Gedeon, T.D. Simulated annealing and weight decay in adaptive learning: The SARPROP algorithm. IEEE Trans. Neural Netw. 1998, 9, 662–668. [Google Scholar] [CrossRef]
- Leung, C.S.; Wong, K.W.; Sum, P.F.; Chan, L.W. A pruning method for the recursive least squared algorithm. Neural Netw. 2001, 14, 147–174. [Google Scholar] [CrossRef]
- O’Neill, M.; Ryan, C. Grammatical evolution. IEEE Trans. Evol. Comput. 2001, 5, 349–358. [Google Scholar] [CrossRef]
- Backus, J.W. The Syntax and Semantics of the Proposed International Algebraic Language of the Zurich ACM-GAMM Conference. In Proceedings of the International Conference on Information Processing, UNESCO, Paris, France, 15–20 June 1959; pp. 125–132. [Google Scholar]
- Ryan, C.; Collins, J.; O’Neill, M. Grammatical evolution: Evolving programs for an arbitrary language. In Genetic Programming. EuroGP 1998; Lecture Notes in Computer Science; Banzhaf, W., Poli, R., Schoenauer, M., Fogarty, T.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1391. [Google Scholar]
- O’Neill, M.; Ryan, M.C. Evolving Multi-line Compilable C Programs. In Genetic Programming. EuroGP 1999; Lecture Notes in Computer Science; Poli, R., Nordin, P., Langdon, W.B., Fogarty, T.C., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; Volume 1598. [Google Scholar]
- Ryan, C.; O’Neill, M.; Collins, J.J. Grammatical Evolution: Solving Trigonometric Identities. In Proceedings of the Mendel ’98: 4th International Conference on Genetic Algorithms, Optimization Problems, Fuzzy Logic, Neural Networks and Rough Sets, Anchorage, AK, USA, 4–9 May 1998; Volume 98. [Google Scholar]
- Puente, A.O.; Alfonso, R.S.; Moreno, M.A. Automatic composition of music by means of grammatical evolution. In Proceedings of the APL ’02: 2002 Conference on APL: Array Processing Languages: Lore, Problems, and Applications, Madrid, Spain, 22–25 July 2002; pp. 148–155. [Google Scholar]
- Campo, L.M.L.; Oliveira, R.C.L.; Roisenberg, M. Optimization of neural networks through grammatical evolution and a genetic algorithm. Expert Syst. Appl. 2016, 56, 368–384. [Google Scholar] [CrossRef]
- Soltanian, K.; Ebnenasir, A.; Afsharchi, M. Modular Grammatical Evolution for the Generation of Artificial Neural Networks. Evol. Comput. 2022, 30, 291–327. [Google Scholar] [CrossRef]
- Dempsey, I.; Neill, M.O.; Brabazon, A. Constant creation in grammatical evolution. Int. J. Innov. Appl. 2007, 1, 23–38. [Google Scholar] [CrossRef]
- Galván-López, E.; Swafford, J.M.; O’Neill, M.; Brabazon, A. Evolving a Ms. PacMan Controller Using Grammatical Evolution. In Applications of Evolutionary Computation. EvoApplications 2010; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6024. [Google Scholar]
- Shaker, N.; Nicolau, M.; Yannakakis, G.N.; Togelius, J.; O’Neill, M. Evolving levels for Super Mario Bros using grammatical evolution. In Proceedings of the 2012 IEEE Conference on Computational Intelligence and Games (CIG), Granada, Spain, 11–14 September 2012; pp. 304–311. [Google Scholar]
- Martínez-Rodríguez, D.; Colmenar, J.M.; Hidalgo, J.I.; Micó, R.J.V.; Salcedo-Sanz, S. Particle swarm grammatical evolution for energy demand estimation. Energy Sci. Eng. 2020, 8, 1068–1079. [Google Scholar] [CrossRef]
- Sabar, N.R.; Ayob, M.; Kendall, G.; Qu, R. Grammatical Evolution Hyper-Heuristic for Combinatorial Optimization Problems. IEEE Trans. Evol. Comput. 2013, 17, 840–861. [Google Scholar] [CrossRef]
- Ryan, C.; Kshirsagar, M.; Vaidya, G.; Cunningham, A.; Sivaraman, R. Design of a cryptographically secure pseudo random number generator with grammatical evolution. Sci. Rep. 2022, 12, 8602. [Google Scholar] [CrossRef] [PubMed]
- Pereira, P.J.; Cortez, P.; Mendes, R. Multi-objective Grammatical Evolution of Decision Trees for Mobile Marketing user conversion prediction. Expert Syst. Appl. 2021, 168, 114287. [Google Scholar] [CrossRef]
- Castejón, F.; Carmona, E.J. Automatic design of analog electronic circuits using grammatical evolution. Appl. Soft Comput. 2018, 62, 1003–1018. [Google Scholar] [CrossRef]
- Kaelo, P.; Ali, M.M. Integrated crossover rules in real coded genetic algorithms. Eur. J. Oper. Res. 2007, 176, 60–76. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Kelly, M.; Longjohn, R.; Nottingham, K. The UCI Machine Learning Repository. 2023. Available online: https://archive.ics.uci.edu (accessed on 20 September 2023).
- Alcalá-Fdez, J.; Fernandez, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. -Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1991. [Google Scholar]
- Quinlan, J.R. Simplifying Decision Trees. Int. Man-Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Hayes-Roth, B.; Hayes-Roth, B.F. Concept learning and the recognition and classification of exemplars. J. Verbal Learn. Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef]
- Dy, J.G.; Brodley, C.E. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Input Feature Extraction for Multilayered Perceptrons Using Supervised Principal Component Analysis. Neural Process. Lett. 1999, 10, 243–252. [Google Scholar] [CrossRef]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Spielman, J.; Ramig, L.O. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Symposium on Computer Applications and Medical Care; IEEE Computer Society Press: Piscataway, NJ, USA; American Medical Informatics Association: Bethesda, MD, USA, 1988; pp. 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; IEEE: Toulouse, France, 2015. November 2015; art. no. 7319047. pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression. JRSS-C (Appl. Stat.) 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Wolberg, W.H.; Mangasarian, O.L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 1990, 87, 9193–9196. [Google Scholar] [CrossRef] [PubMed]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. Publ. IEEE Syst. Cybern. Soc. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061967. [Google Scholar] [CrossRef] [PubMed]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]
- Nash, W.J.; Sellers, T.L.; Talbot, S.R.; Cawthor, A.J.; Ford, W.B. The Population Biology of Abalone (_Haliotis_ species). In Tasmania. I. Blacklip Abalone (_H. rubra_) from the North Coast and Islands of Bass Strait, Sea Fisheries Division; In Blacklip Abalone (H. rubra) from the North Coast and Islands of Bass Strait; Tasmania, I., Ed.; Technical Report; Sea Fisheries Division: Tasmania, Australia, 1994. [Google Scholar]
- Brooks, T.F.; Pope, D.S.; Marcolini, A.M. Airfoil Self-Noise and Prediction; Technical Report, NASA RP-1218; NASA: Washington, DC, USA, 1989.
- Simonoff, J.S. Smooting Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Yeh, I.C. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic prices and the demand for clean ai. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- King, R.D.; Muggleton, S.; Lewis, R.; Sternberg, M.J.E. Drug design by machine learning: The use of inductive logic programming to model the structure-activity relationships of trimethoprim analogues binding to dihydrofolate reductase. Proc. Nat. Acad. Sci. USA 1992, 89, 11322–11326. [Google Scholar] [CrossRef] [PubMed]
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks through Augmenting Topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef]
- Cantu-Paz, E.; Goldberg, D.E. Efficient parallel genetic algorithms: Theory and practice. Comput. Methods Appl. Mech. Eng. 2000, 186, 221–238. [Google Scholar] [CrossRef]
- Harada, T.; Alba, E. Parallel genetic algorithms: A useful survey. ACM Comput. Surv. (CSUR) 2022, 53, 1–39. [Google Scholar] [CrossRef]
- Gropp, W.; Lusk, E.; Doss, N.; Skjellum, A. A high-performance, portable implementation of the MPI message passing interface standard. Parallel Comput. 1996, 22, 789–828. [Google Scholar] [CrossRef]
- Chandra, R.; Dagum, L.; Kohr, D.; Maydan, D.; Menon, J.M.R. Parallel Programming in OpenMP; Morgan Kaufmann Publishers Inc.: San Diego, CA, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).