Mind Your Outcomes: The ΔQSD Paradigm for Quality-Centric Systems Development and Its Application to a Blockchain Case Study ^†

1. Introduction

In order to avoid expensive design and implementation failures, it is critical to establish sufficiently early in the design cycle that software systems will meet both their functional requirements and their non-functional requirements. This paper describes $\Delta \mathrm{Q}$SD, a novel metrics-based and quality-centric paradigm that uses formalised outcome diagrams to explore the performance consequences of design decisions, and so to determine system viability ahead of expensive implementation work. The paradigm has been successfully used in a number of commercial settings, including telecommunications, avionics, and space and defence. The paper introduces the concepts underlying $\Delta \mathrm{Q}$SD, formalises these, and shows the use of $\Delta \mathrm{Q}$SD in the context of a real-world commercial case study: globally distributed and time-limited block diffusion in the Cardano blockchain.

1.1. Motivation

The modern world depends on large-scale software systems to run its critical infrastructure: telecommunications, energy, finance, transport, government, the military, and major multi-national companies all rely on correct and reliable software to carry out their day-to-day operations. Individuals in many countries increasingly rely on online systems for many aspects of their daily lives. Such systems are complex and expensive to construct and maintain. However, all too often, they fail to deliver the intended performance or sometimes even to meet the most basic requirements of reliability and usability. One example of the economic impact of failing to adequately manage performance is OnLive. OnLive was a cloud gaming platform that attempted to deliver high-quality video and real-time interactivity but failed to provide an acceptable experience [1]. As a consequence, the company folded, wiping out a $1.8B valuation and costing investors several hundred million US dollars [2,3].

Such results are, fundamentally, a failure both of design and of management. This has a major social and economic cost: fixing a problem in development typically costs 10 times as much as fixing it in design, and fixing a problem in a released product typically costs 100 times as much as fixing it in development [4]. Overall, the cost of failed software projects in the US in 2020 was approximately $260B (up from $177.5B in 2018) [5].

One core cause of such problems is that modern software development practices successfully emphasise rapid and flexible software construction but fail to adequately consider essential quality requirements or even to consider properly whether a system can actually meet its intended outcomes, particularly when deployed at scale. In complex system development, there is a tendency for cost/performance hazards to appear late in the System Development Life Cycle (SDLC). Unfortunately, such issues can invalidate design choices, requiring major redesign or implementation changes. This can lead to time and cost overruns and sometimes project cancellation. Thus, there is an urgent need for the verification and validation of resource cost and system performance (as opposed to simply functional correctness) and for this to be part of an ongoing design process rather than applied late in the development [6]. This process must be applicable to distributed and complex hierarchical systems, and it must support both initial and incremental development. This methodology becomes increasingly important as such systems are used for cyber-physical, mission-critical, or even safety-of-life applications. Several factors make this task more difficult:

• System requirements are often vague and/or contradictory, and they can change both during and after development;
• Complexity forces hierarchical decomposition of the problem, creating boundaries, including commercial boundaries with third-party suppliers, that may hinder optimal development and hide risks;
• Time pressure forces parallel development that may be at odds with that hierarchical decomposition, and it encourages leaving ‘tricky’ issues for later, when they tend to cause re-work and overruns and leave tail-risks;
• Cost and resource constraints force resources to be shared both within the system and with other systems (e.g., when network infrastructure or computing resources are shared); they may also require re-use of existing assets (own or third-party), introducing a degree of variability in the delivered performance;
• The performance of particular components or subsystems may be incompletely quantified;
• System performance and resource consumption may not scale linearly (which may not become apparent until moving from a lab/pilot phase to a wider deployment);
• At scale, exceptional events (transient communications and/or hardware issues) can no longer be treated as negligibly rare, and their effects and mitigation need to be considered along with the associated performance impacts.

Thus, what is needed is (1) a way of capturing performance and resource requirements that accommodate all the various sources of uncertainty; and (2) a process for decomposing a top-level requirement into subsystem requirements that provides confidence that satisfying all the lower-level requirements will also satisfy the top-level one. For functional aspects of system behaviour, there are various ways of dealing with this [7]. However, while established software engineering approaches do exist for dealing with performance [8], these all have significant limitations.

1.2. The $\Delta \mathrm{Q}$SD Systems Development Paradigm

This paper directly addresses those issues by defining the $\Delta \mathrm{Q}$SD systems development paradigm and providing a high-level formalism that can be used throughout the system development process. $\Delta \mathrm{Q}$SD is a quality-centric paradigm, focusing on meeting timeliness constraints and an acceptable failure rate of the top-level outcomes with acceptable resource consumption. The paradigm has been used successfully by a small team in Predictable Network Solutions in a variety of large industrial projects, collectively saving billions of dollars and person-centuries of development effort. It informs high-level management and system design decisions by showing where conflicts exist (or may exist) between system designs and required outcomes. It is able to compute the predicted performance at any stage of the design process, where performance is seen broadly as comprising timeliness, behaviour under load, resource consumption, and other key system metrics.

Central to $\Delta \mathrm{Q}$SD is the concept of an outcome, which is defined as a specific system behaviour with specified start and end points, localised in space and time. In $\Delta \mathrm{Q}$SD, the system engineer models the system as an outcome diagram, which is a graph that captures the causal relationships between system outcomes. $\Delta \mathrm{Q}$SD defines a system design as a sequence of outcome diagrams that capture the essential observational properties of the system, independent of the details of system structure and behaviour. This sequence starts with a fully unspecified system and ends with either (i) a fully specified (or a convincingly specified-enough) system (deemed as constructible), or (ii) the conclusion that the system goals are infeasible.

The formalism allows exploration of the design space by assessing the consequences of the decisions that are taken (and possibly retracted) at each refinement step, giving rise to threaded decision trees. For each partially specified system, we compute the predicted timeliness and behaviour and resource consumption of the system under load, obtaining one of three possible conclusions: (1) infeasibility—hence, ceasing further development and revising former design decisions; (2) slack—hence, ceasing further optimisation because the system is good enough; or (3) indecisiveness—hence, requiring additional scrutiny until one of the alternative conclusions can be drawn. The paper gives one large example, blockchain diffusion, that illustrates how $\Delta \mathrm{Q}$SD can be used in practice, explaining how the formalism can be used to drive the design process and associated decision making. This example is a real-world application that is in continuous use as a core part of the Cardano blockchain technology (https://cardano.org/ (accessed on 14 December 2021)).

Most performance analysis approaches require the system to be fully specified, or even implemented, which is a serious disadvantage, since it does not allow the properties of subsystems to be encapsulated and hierarchically (de)composed. By contrast, $\Delta \mathrm{Q}$SD satisfies compositionality, the principle that the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules that are used to combine them. For compositional properties, what is “true” about subsystems (e.g., their timeliness, their resource consumption) is also “true” about their (appropriate) combination: there exists an invariant (e.g., timeliness, aspects of functional correctness) that must hold over the reified components of the system. This is key to managing complexity within the systems’ development life-cycle.

In the broader software development space, functional programming techniques are improving the compositionality of functional aspects of software systems, and they can deliver high assurance of functional correctness when combined with appropriate formal methods [9]. The $\Delta \mathrm{Q}$SD paradigm represents a similar step change in handling the “non-functional” aspects of performance and resource consumption. By treating delay and failure as a single object, called ‘quality attenuation’, our paradigm can be thought of as a combination of passage time analysis and failure mode effects analysis (FMEA).

1.3. Main Contributions of this Paper

The main contributions of this paper are as follows:

• Introduce $\Delta \mathrm{Q}$SD, a formalism (Section 5) that focuses on rapidly exploring the performance consequences of design and implementation choices, where:

  (a)

  Performance is a first-class citizen, ensuring that we can focus on details relevant to performance behaviour;

  (b)

  The whole software development process is supported, from checking the feasibility of initial requirements to making decisions about subtle implementation choices and potential optimisations;

  (c)

  We can measure our choices against desired outcomes for individual users (customer experience);

  (d)

  Analysis of saturated systems is supported (where a “saturated system” is one with resources that have reached their limits, e.g., systems with high load or high congestion);

  (e)

  Analysis of failure is supported.

  We use term-rewriting for formalising refinements (Definition 3 in Section 5) and denotational semantics for formalising timeliness analysis (Section 5.3) as well as load analysis (Section 5.4).
• Describe key decisions made in the development process of a real system—i.e., the Cardano blockchain, which is presented as a running example—and show how $\Delta \mathrm{Q}$SD is able to quickly rule out infeasible decisions, predict behaviour, and indicate design headroom (slack) to decision makers, architects, and developers (Section 4).

While the $\Delta \mathrm{Q}$ concept has been described in earlier papers [10,11] and used to inform a number of large-scale system designs, these previous contributions have only used it in an informal manner. By providing a formal definition of $\Delta \mathrm{Q}$SD, and showing how it can be used in practice, we are taking an important step towards a general evidence-based engineering methodology for developing real-time distributed systems.

1.4. Structure of the Paper

This paper has the following structure:

• Section 2 introduces the running example that we will use throughout the paper: block diffusion in the Cardano blockchain.
• Section 3 defines the basic concepts that underlie the $\Delta \mathrm{Q}$SD formalism: outcomes, outcome diagrams, and quality attenuation ($\Delta \mathrm{Q}$). We also compare outcome diagrams with more traditional diagrams such as block diagrams.
• Section 4 gives a realistic example of the $\Delta \mathrm{Q}$SD paradigm, showing a step-by-step design of block diffusion (introduced in Section 2) based on quality analysis. This example introduces the basic operations of $\Delta \mathrm{Q}$SD in a tutorial fashion. The example uses realistic system parameters that allow us to compute predicted system behaviour.
• Section 5 gives the formal mathematical definition of $\Delta \mathrm{Q}$SD and its main properties. With this formal definition, it is possible to validate the computations that are used by $\Delta \mathrm{Q}$SD as well as to build tools based on $\Delta \mathrm{Q}$SD.
• Section 6 gives a comprehensive discussion about related work from three different viewpoints: theoretical approaches for performance analysis (Section 6.1), performance design practices in distributed systems (Section 6.3), and programming languages and software engineering (Section 6.4).
• Section 7 summarises our conclusions, discusses some limitations of the paradigm, and describes our plans to further validate $\Delta \mathrm{Q}$SD and to build a dedicated toolset for real-time distributed systems design that builds on the $\Delta \mathrm{Q}$SD paradigm.

2. Running Example: Block Diffusion in the Cardano Blockchain

A blockchain is a form of distributed ledger. It comprises a number of blocks of data, each of which provides a cryptographic witness to the correctness of the preceding blocks, back to some original ‘genesis’ block (a ‘chain’ of blocks, hence ‘blockchain’) [12]. Nodes in the system use some specified protocol to arrive at a distributed consensus as to the correct sequence of blocks, even in the presence of one or more ‘adversaries’ that aim to convince other nodes that a different sequence is correct. One such consensus protocol is Ouroboros Praos [13], which underpins Cardano (https://www.cardano.org (accessed on 14 December 2021)), one of the world’s leading cryptocurrencies. Ouroboros Praos uses the distribution of ‘stake’ in the system (i.e., the value of the cryptocurrency tokens that are controlled by each node) to randomly determine which node (if any) is authorised to produce a new block in the chain during a specific time interval (a ‘slot’); the more stake a node controls, the more likely it is to be authorised to produce a block. For this to be effective, it is important that the block-producing node has a copy of the most recently produced block, so that the new block can correctly extend the existing chain. Since the block producer is selected at random, this means that the previous block needs to have been copied to all block-producing nodes; we call this process ‘block diffusion’. Since blocks are produced on a predetermined schedule and each block depends on its predecessor, block diffusion is a real-time problem; each block must be diffused before the next block can be produced. In order to be robust, the consensus algorithm is designed to withstand some imperfections in block diffusion; hence, the effective requirement is that blocks should be well-diffused “sufficiently often”. Put another way, the probability that a block fails to arrive in time for the production of the next block must be suitably bounded. The engineering challenge is to quantify this probability as a function of the design and of the parameter choices of the implementation.

The scale of the challenge is illustrated by Cardano. Cardano is a global-scale distributed system that eschews centralised management. At the time of writing, 2948 globally-distributed nodes cooperate to produce and distribute blocks for $45.77B of cryptocurrency that is associated with 956,092 distinct user addresses. The stake distribution at the time of writing is shown in Figure 1.

In Cardano, slots are one second long and blocks are produced every 20 s on average. An initial implementation of Cardano (code-named ‘Byron’) was functionally correct but proved incapable of effective block diffusion without rigid control of the nodes and their topology; a re-implementation (called ‘Jormungandr’) targeted higher performance by using a different programming language (Rust instead of Haskell), but this also missed the block diffusion target by a wide margin. A further, and ultimately successful, re-implementation (called ‘Shelley’ [14]) used Haskell to retain strong correctness assurances but applied the principles that are discussed in this paper to also ensure adequate performance in a fully decentralised deployment.

2.1. Key Design Decisions

In the design of Shelley, a number of inter-related decisions had to be made. These included the following:

• How frequently should blocks be produced? Proof-of-Work systems are limited in their throughput by the time taken to ‘crack’ the cryptographic puzzle; proof-of-stake systems do not have this limitation and so have the potential for much higher performance both in terms of the volume of transactions embedded into blocks and the time take for a transaction to be fully incorporated in the immutable part of the chain. Thus, the interval between blocks is a key parameter.
• How are nodes connected? It might seem that connecting every node to every other would minimise block diffusion time; however, the lack of any control over the number and capabilities of nodes makes this infeasible. Nodes can only be connected to a limited number of peer nodes; then, the number of connected peers and how they are chosen become important.
• How much data should be in a block? Increasing the amount of data in a block improves the overall throughput of the system but makes block diffusion slower.
• How should blocks be forwarded? Simply forwarding a new block to all connected nodes would seem to minimise delay, but this wastes resources, since a node may receive the same block from multiple peers. In the extreme case, this represents a potential denial-of-service attack. Splitting a block into a small header portion (sufficient for a node to decide whether it is new) and a larger body that a node can choose to download if it wishes mitigates this problem but adds an additional step into the forwarding process.
• How much time can be spent processing a block? Validating the contents of a block before forwarding it mitigates adversarial behaviour but can be computationally intensive, since the contents may be programs that need to be executed (called ‘smart contracts’); allowing more time for such processing permits more, and more complex, programs but makes block diffusion slower.

The remainder of this paper shows how such design decisions can be quantified using the $\Delta \mathrm{Q}$SD paradigm.

2.2. Formulating the Problem

We assume that a collection of blockchain nodes is assembled into a random graph (randomness is important in a blockchain setting for mitigating certain adversarial behaviours). In each time slot, a randomly chosen node may generate a block, and we are interested in the probability that the next randomly chosen node has received that block before it generates the next block.

Since the graph is random with some limited node degree N, there is a strong chance that A is not directly connected to Z, and so, the block will have to pass through a sequence of intermediate nodes B, C, …The length of this sequence is a function of the size and node degree of the graph [15]. The (distribution of) time to forward a block directly from one node to another is known (e.g., by measurement).

3. Foundations

In the remainder of this paper, we will take the system of discourse to be fixed for the design engineer. We assume that this system has a number of tasks that must be performed. In order to perform a task that is not considered to be atomic by the design engineer, the system might need to perform several other subtasks. The process of clarifying the details of the system by breaking higher-level tasks into such subtasks is what we call refinement (Definition 3 in Section 5). By refining a system, one goes from a coarser granularity of the design to a finer one (see Section 4.1, Section 4.2 and Section 4.3 for examples). Sometimes, the design engineer will return to a coarser grained design, as discussed in Section 7.1.2, in order to take a different direction of refinement (see Section 4.4, Section 4.5, Section 4.6 and Section 4.7 for examples). Reasons why they might want to do so include: to investigate other aspects of their system; to compare two alternative design choices; or because a refinement fails to meet the necessary performance or other requirements. Thus, $\Delta \mathrm{Q}$SD is design exploration in the world of refinements.

This section sets the stage for presenting design exploration in action (Section 4) by introducing the fundamental concepts: outcomes (Section 3.1), outcome diagrams (Section 3.2), and quality attenuation (Section 3.3). Then, it gives a simple example of how to approach problems à la $\Delta \mathrm{Q}$SD (Section 3.4). This section ends in a discussion on why $\Delta \mathrm{Q}$SD advises a new diagram in the presence of all the existing ones in Software Engineering (Section 3.5).

3.1. Outcomes

An outcome is what the system obtains by performing one of its tasks. Each task has precisely one corresponding outcome, and each outcome has precisely one corresponding task. We say that an outcome is ‘performed’ to mean that the corresponding task of an outcome is performed. Likewise, we might use task adjectives for outcomes too, even though outcomes and tasks are inherently different. For example, by an atomic outcome, we mean an outcome whose corresponding task is itself atomic.

We take an event-based perspective, in which each outcome has two distinct sets of events: the starting set of events (any one of which must happen before the task can commence) and the terminating set of events (at least one of which must happen before the task can be considered complete). Each of those sets consists of events that are of particular interest (as opposed to just any event). We call such events of interest the observables. For example, an observable in the starting set, $S_o$, of an outcome o is of interest because it signifies the point in time and 3D location at which o begins. Likewise, an observable from the terminating set, $T_o$ of o is an event that contains information regarding the location where o finishes. While it may seem unusual to refer explicitly to location in a computer science context, when considering distributed systems, the outcomes of interest are precisely those that begin at one location and finish at another. Of course, once an observable from $S_o$ occurs, there is no guarantee that one from $T_o$ will occur within o’s duration limit, $d\left(o\right)$ (i.e., the relative time by which o is required to complete). However, when an observable $T_o$ does occur within the duration limit after one from $S_o$, o is said to be done.

Diagrammatically, we show an outcome using an orange circle. As shown in Figure 2, we depict the starting set and the terminating set of an outcome using small boxes to the left and right of the outcome’s circle, respectively. The starting set is connected to the outcome from the left, and the terminating set is connected to the outcome from the right. When they are unimportant for an outcome, we do not include the starting set and the terminating set of that particular outcome in the diagram.

We consider one special kind of outcome. Consider the situation where a design engineer is aware that an outcome is not atomic. They will eventually need to further break the outcome into its suboutcomes. Nevertheless, the current level of granularity is sufficient to carry out a particular analysis (see Section 5.3 and Section 5.4 for two example analyses). In $\Delta \mathrm{Q}$SD, a black box can be used for that particular outcome. Black boxes are those outcomes that achieve one of the following:

• Can be easily quantified without even a need for them to be named;
• Are beyond the design engineer’s control (and so may need to be quantified by external specification or measurement); or,
• Are ones for which the design engineer has intentionally left the details for later.

Outcome variables are the variables that we use to refer to a given outcome.

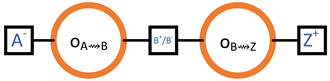
3.2. Outcome Diagrams and Outcome Expressions

The description of a system in terms of its outcomes requires the causal relationships between the outcomes to be captured. In $\Delta \mathrm{Q}$SD, these relationships are captured in outcome diagrams. In addition to its graphical presentation, each outcome diagram can be presented algebraically, using its corresponding outcome expression. As shown in Figure 3, outcome diagrams offer four different ways to describe the relationships between outcomes.

We now explain Figure 3 from left to right.

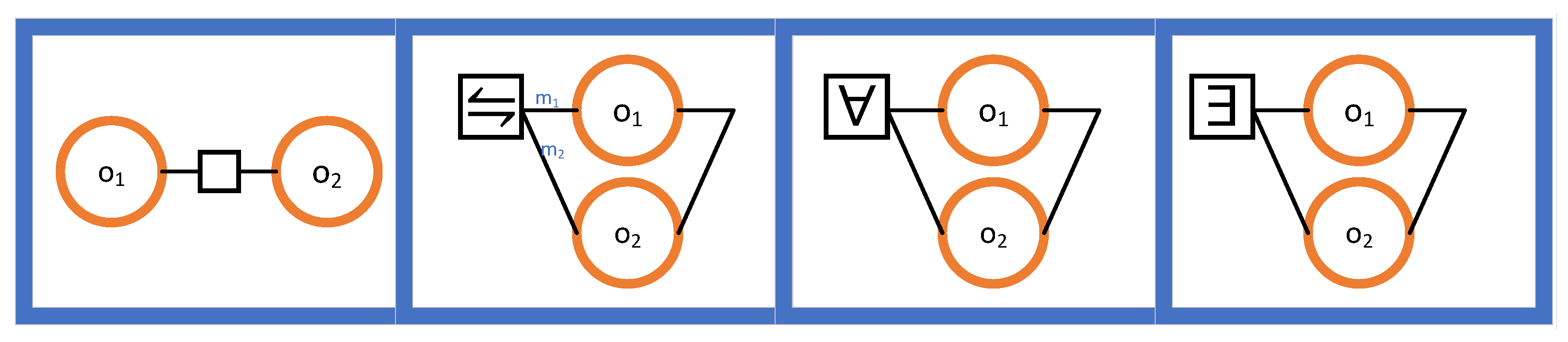
• In the first case, the outcomes $o_1$ and $o_2$ are said to be sequentially composed. Therefore, $o_2$ causally depends on $o_1$. We maintain a directional convention to avoid showing directions explicitly: when an edge connects two outcomes, the right one causally depends on the left one. The corresponding outcome expression is “$o_1•\to -•o_2$”.
• In the second case, a probabilistic choice is made between $o_1$ and $o_2$. Notice the weights $m_1$ and $m_2$. The outcome of the choice is the same as $o_1$ with probability $\frac{m_1}{m_1+m_2}$ and the same as $o_2$ with probability $\frac{m_2}{m_1+m_2}$. The corresponding outcome expression is “$o_1\begin{array}{c}{m}_1\\ {\displaystyle \leftrightharpoons }\\ m_2\end{array}{o}_2$”.
• In the third case, an all-to-finish (i.e., last-to-finish) combination is produced from $o_1$ and $o_2$. For two outcomes $o_1$ and $o_2$ that are started at the same time and that are run in parallel, the outcome is done when both $o_1$ and $o_2$ are done. The corresponding outcome expression is “$\forall (o_1\Vert o_2)$”.
• In the final case, a first-to-finish combination is produced from $o_1$ and $o_2$. For two outcomes $o_1$ and $o_2$ that are started at the same time and that are run in parallel, the outcome is done when either $o_1$ or $o_2$ is done. The corresponding outcome expression is “$\exists (o_1\Vert o_2)$”.

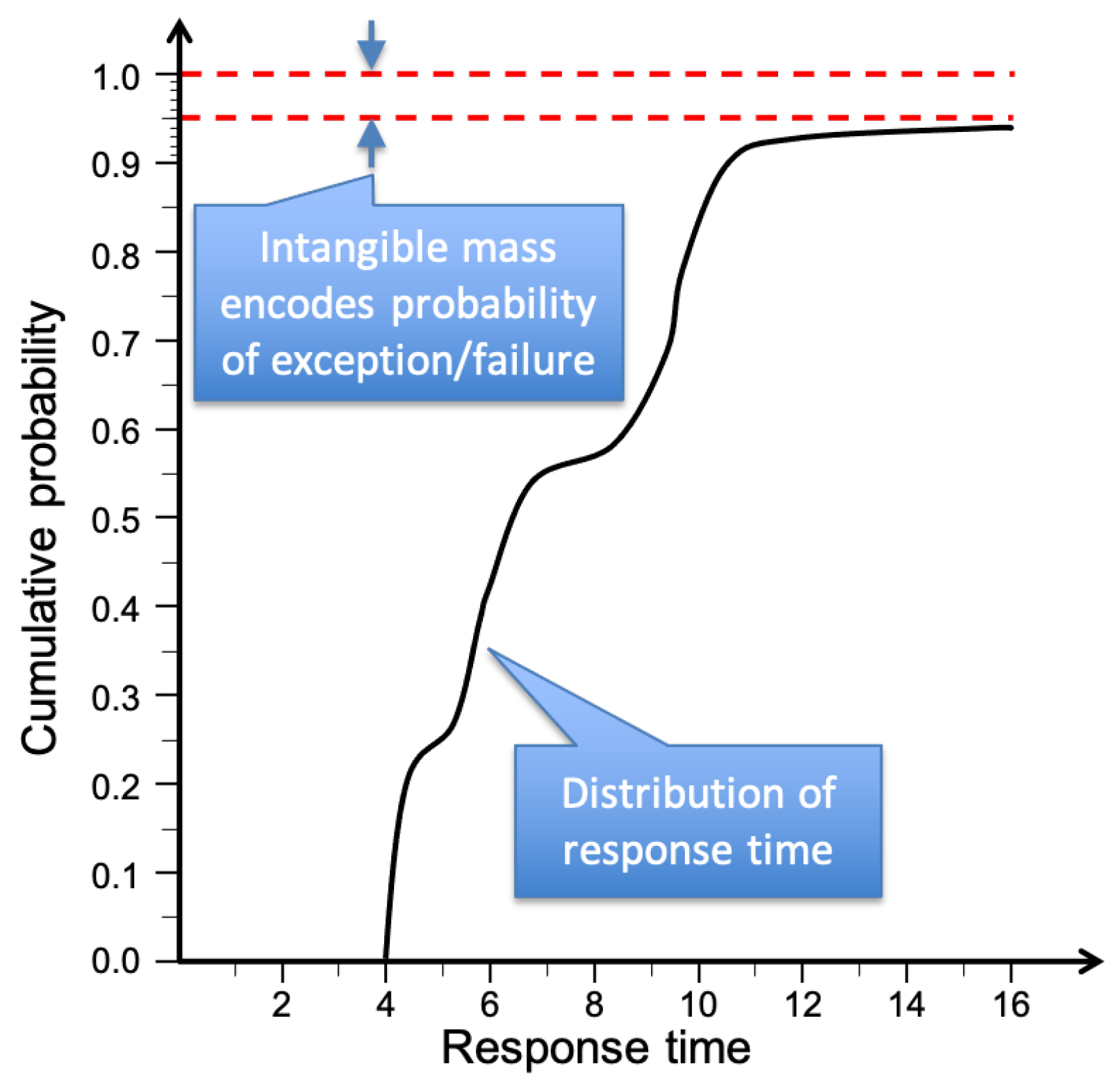
3.3. Quality Attenuation ($\Delta \mathrm{Q}$)

From the perspective of a user, a perfect system would deliver the desired outcome without error, failure, or delay, whereas real systems always fall short of this; we can say that the quality of their response is attenuated relative to the ideal. We denote this ‘quality attenuation’ by the symbol $\Delta \mathrm{Q}$ and reformulate the problem of managing performance as one of maintaining suitable bounds on $\Delta \mathrm{Q}$ [16]. This is an important conceptual shift because ‘performance’ may appear to be something that can be increased arbitrarily, whereas $\Delta \mathrm{Q}$ (similar to noise) is something that may be minimised but that can never be completely eliminated. Indeed, some aspects of $\Delta \mathrm{Q}$, such as the time for signals to propagate between components of a distributed system, cannot be reduced below a certain point.

Since the response of the system in any particular instance can depend on a wide range of factors, including the availability of shared resources, we model $\Delta \mathrm{Q}$ as a random variable. This allows various sources of uncertainty to be captured and modelled, ranging from as-yet-undecided aspects of the design, to resource use by other processes, to behavioural dependence on data values.

In capturing the deviation from ideal behaviour, $\Delta \mathrm{Q}$ incorporates both delay (a continuous random variable) and exceptions/failures (discrete variables). This can be modelled mathematically using Improper Random Variables (IRVs), whose total probability is less than one [17]. If we write $\Delta \mathrm{Q}$(x) for the probability that an outcome occurs in a time $t\le x$, then we can define the ‘intangible mass’ of such an IRV as $1-{lim}_{x\to \infty }\Delta \mathrm{Q}\left(x\right)$. In $\Delta \mathrm{Q}$, this encodes the probability of exception or failure. This is illustrated in Figure 4, which shows the cumulative distribution function (CDF) of an IRV (with arbitrary time units).

We can define a partial order on such variables, in which the ‘smaller’ attenuation is the one that delivers a higher probability of completing the outcome in any given time:

$$({\forall }_x\Delta {\mathrm{Q}}_1\left(x\right)\ge \Delta {\mathrm{Q}}_2\left(x\right))\equiv \Delta {\mathrm{Q}}_1\le \Delta {\mathrm{Q}}_2$$

(1)

This partial order has a ‘top’ element, which is simply perfect performance: $\top \equiv ({\forall }_x\Delta \mathrm{Q}\left(x\right)$$=1)$, and a ‘bottom’ element, which is total failure (an outcome that never occurs): $\perp \equiv ({\forall }_x\Delta \mathrm{Q}\left(x\right)=0)$. We can write specifications for system performance using this partial order by requiring the overall $\Delta \mathrm{Q}$ to be less than or equal to a predefined bounding case. Where the $\Delta \mathrm{Q}$ is strictly less than the requirement, we say there is performance slack; when it is strictly greater than the requirement, we say there is a performance hazard (cf. Definitions 5 and 8).

Assessments might also find the current level of information about a system to be indecisive—neither slack nor hazard. The simplest reason for indecisiveness is the partiality of ≤ in Equation (1). Another reason for indecisiveness might be conflict between different analyses. For example, timeliness analysis (Section 5.3) might show slack whilst load analysis (Section 5.4) shows hazard. A third reason might be that even though the formulations end up indicating slack or hazard, the system is still detailed so little that the result of the analysis should not be counted on.

The relationships between outcomes that are shown in Figure 3 then induce corresponding relationships between the $\Delta \mathrm{Q}$s of those outcomes, as explained in Section 5.3. The key to the compositionality of the paradigm is that the partial order is preserved by the operations that combine $\Delta \mathrm{Q}$s. Thus, for example, considering the sequential composition of either of two alternative outcomes with a third,

$$\Delta \mathrm{Q}{}_1\le \Delta \mathrm{Q}{}_2\Rightarrow \Delta \mathrm{Q}{}_1\ast \Delta \mathrm{Q}{}_3\le \Delta \mathrm{Q}{}_2\ast \Delta \mathrm{Q}{}_3$$

This enables an overall timeliness requirement to be broken into ‘budgets’ for sub-outcomes. More details of this approach are given in [11].

3.4. Simple Example

Consider the simple distributed system of a web browser interacting with a set of servers that collectively provide a web page. The outcome that is of interest to the user starts with the event of clicking on a URL, and it ends with the event of the page being fully rendered. This corresponds to the first row of Figure 5. The second row shows the distinction between the user and the browser, and the third row exposes the back-end servers. A typical web page will contain a variety of elements that are served by servers from different host domains. So, for each element, the browser (and its supporting O/S) must first resolve the corresponding domain name, then establish a connection to the given server, and finally download and then render the provided content. Thus, for each element that needs to be displayed, the $\Delta \mathrm{Q}$ is the sequential composition of the $\Delta \mathrm{Q}$s of the component steps described above; and the $\Delta \mathrm{Q}$ of rendering the whole page is an all-to-finish combination of the $\Delta \mathrm{Q}$s of all the elements. Note that this formulation automatically deals with the possibility that any of the steps may fail, and it provides the resultant failure probability for the whole process in addition to the distribution of expected completion times.

This simple model can be further refined as needed to meet real-world requirements. For example, DNS resolution might provide alternative server addresses for load-balancing purposes, and each of these servers might have different $\Delta \mathrm{Q}$s when providing the same content to the user (perhaps because they are located in different geographical locations or are provisioned using systems with different CPU or storage capabilities). We can represent this as a probabilistic choice between these outcomes, which is weighted by the probability that a specific server is used. This weights the corresponding $\Delta \mathrm{Q}$. In addition, we might also consider the effect of load and contention for shared resources, for example network interface bandwidth or rendering capacity, or the impact of different DNS caching architectures on performance. These aspects of system performance design are formalised in Section 5.

3.5. Alternatives to Outcome Diagrams—Why a New Diagram?

The $\Delta \mathrm{Q}$SD paradigm introduces the concept of outcome diagrams. It is perfectly reasonable to ask at this point: “Why another diagram? What is it that outcome diagrams capture that UML diagrams, for example, cannot?’’ Let us answer these questions by comparing outcome diagrams with UML. We first recall the two main properties of outcome diagrams in the $\Delta \mathrm{Q}$SD paradigm:

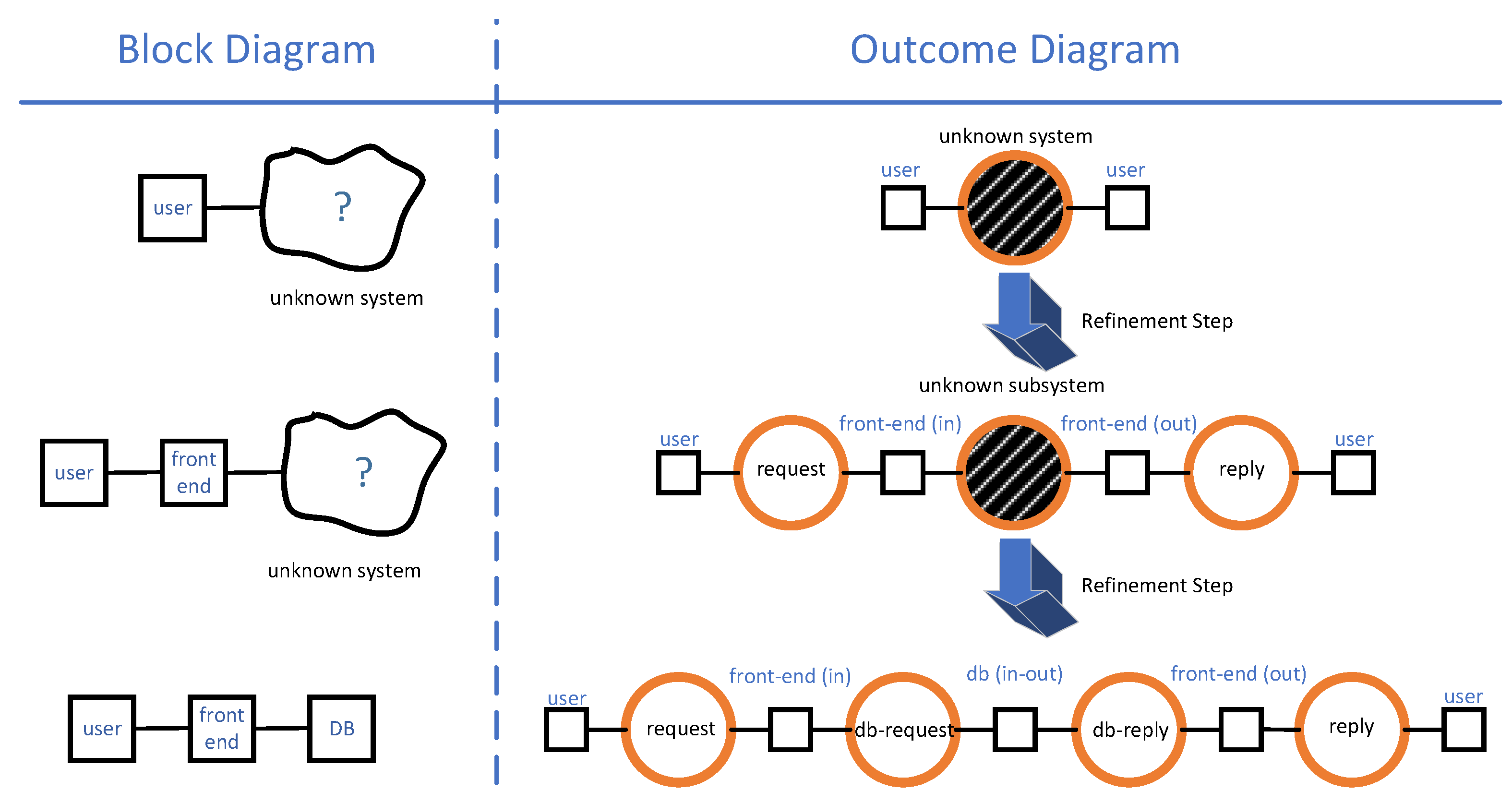
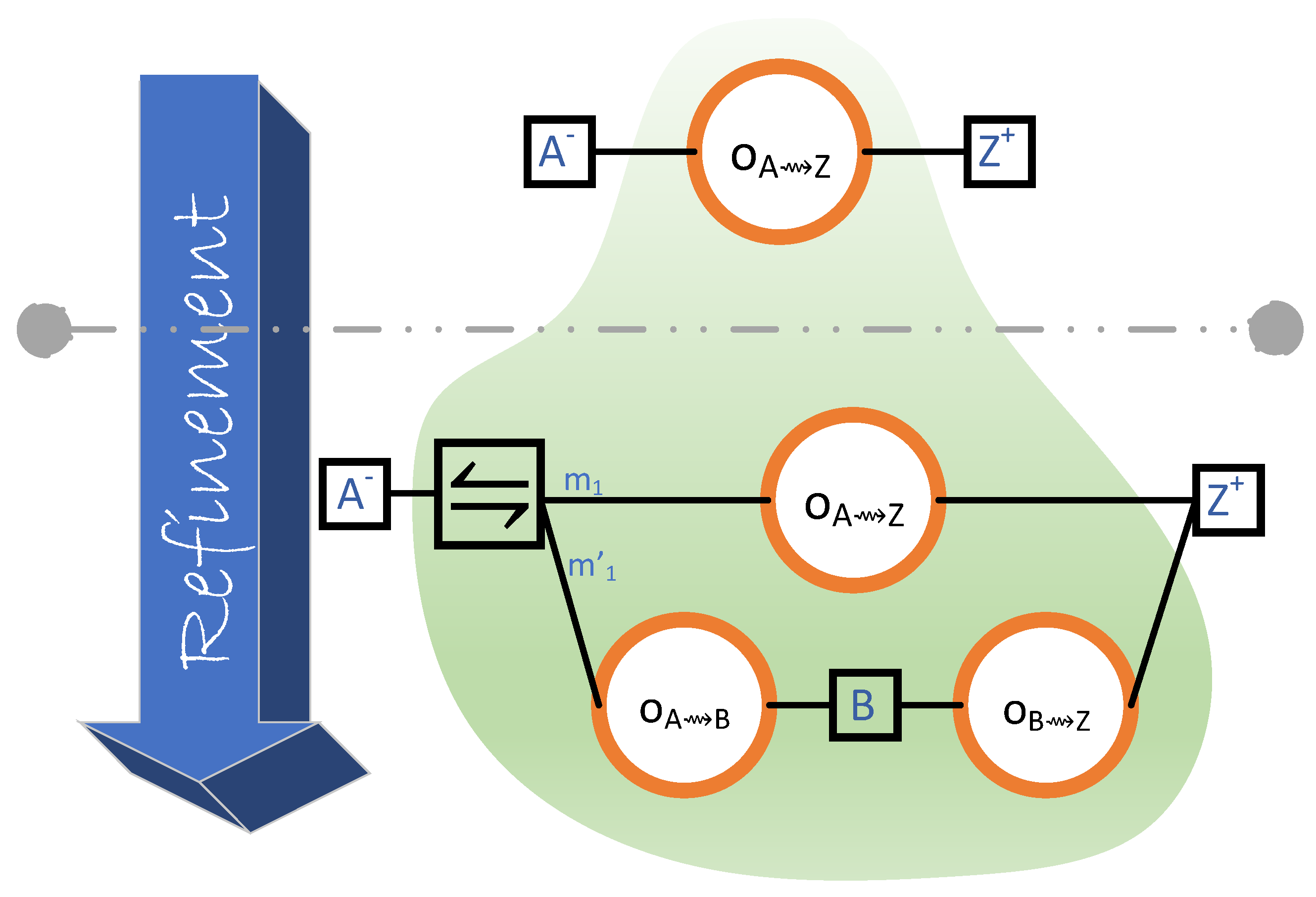
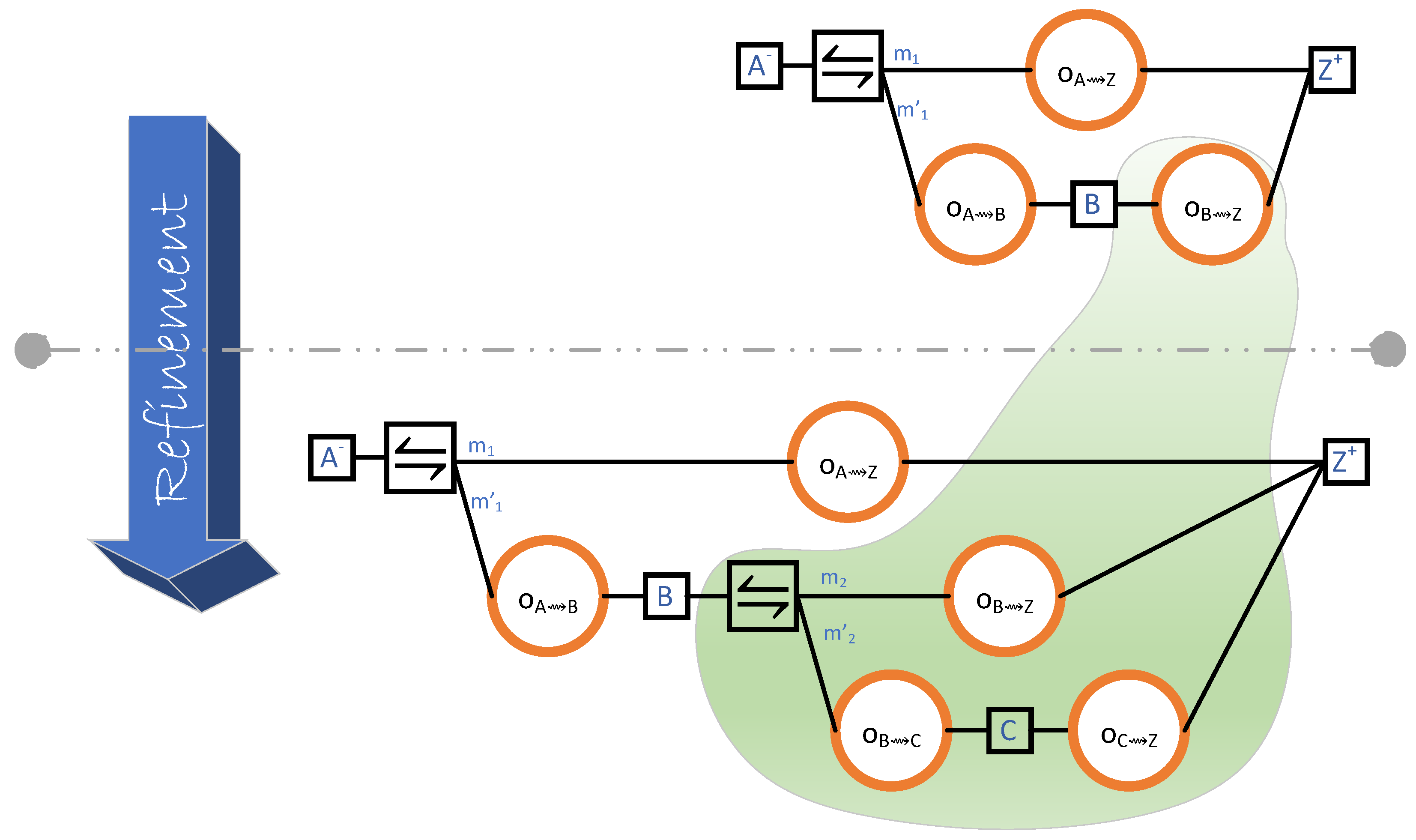
• An outcome diagram specifies the causal relations between outcomes. An outcome is a specific system behaviour defined by its possible starting events and its possible terminating events. For example, sending a message to a server is an outcome defined by the beginning of the send operation and the end of the send operation. The action of sending a message and receiving a reply is observed as an outcome, which is defined by the beginning of the send operation and the end of the receive operation. Outcomes can be decomposed into smaller outcomes, and outcomes can be causally related. For example, the send–receive outcome can be seen as a causal sequence of a send outcome and a receive outcome.
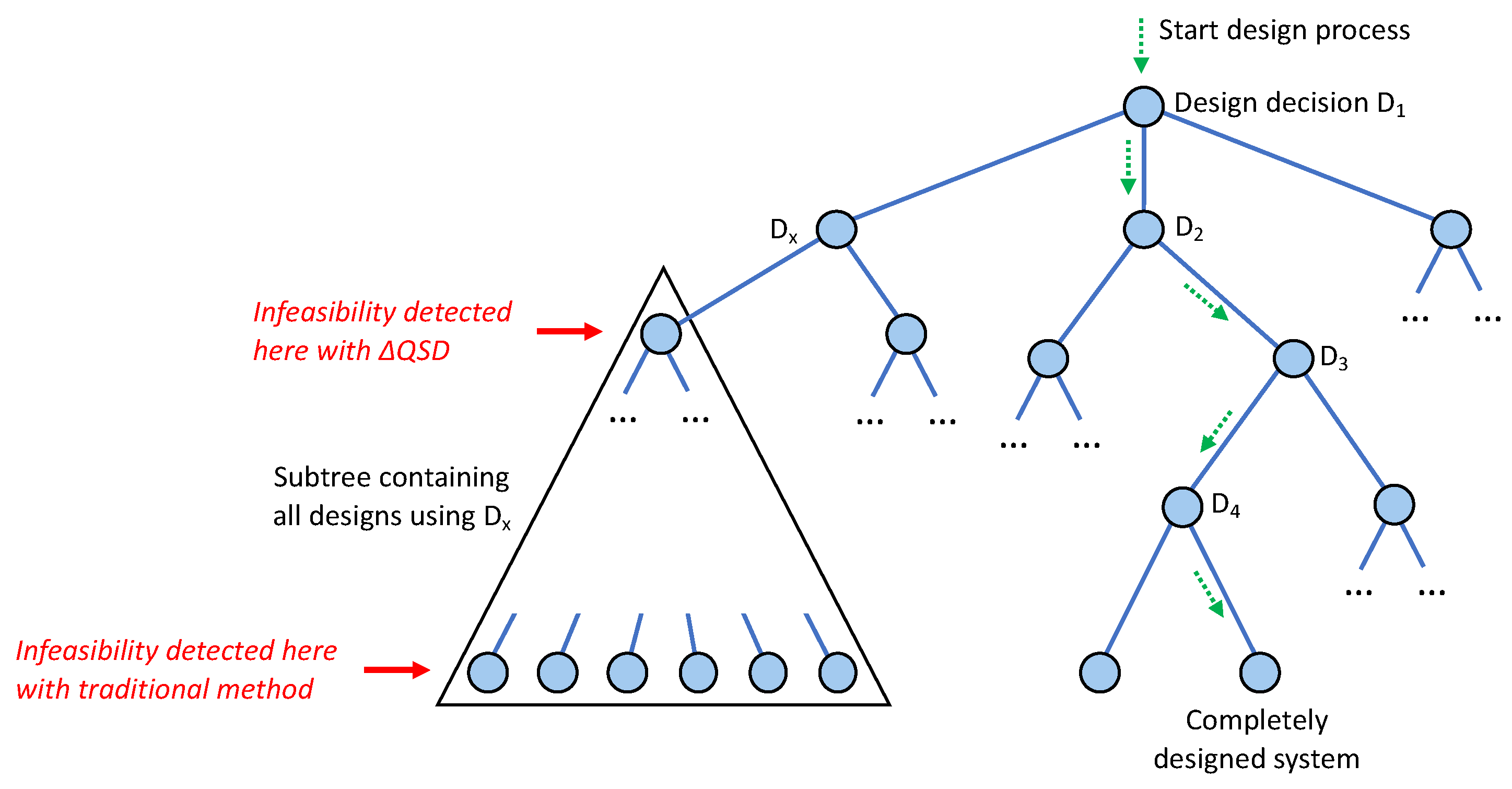
• An outcome diagram can be defined for a partially specified system. Such an outcome diagram can contain undefined outcomes, which are called black boxes. A black box does not correspond to any defined part of the system, but it still has timeliness and resource constraints. Refining an outcome diagram can consist in replacing one of its black boxes with a subgraph of outcomes.

A crucial property of an outcome diagram is that it is an observational concept. That is, it says something about what can be observed of a system from the outside, but it does not say anything about how the system is constructed internally.

3.5.1. UML Diagrams

UML is a rich language defined to model many different aspects of software, including its structure, behaviour, and the processes it is part of. The UML 2 standard defines 14 kinds of diagrams, which are classified into structural diagrams and behavioural diagrams. We first note two general properties of outcome diagrams that UML diagrams do not share:

• Observational property: All UML diagrams, structural and behavioural, define what happens inside the system being modelled, whereas outcome diagrams define observations from outside the system. The outcome diagram makes no assumptions about the system’s components or internal states.
• Wide coverage property: It is possible for both UML diagrams and outcome diagrams to give partial information about a system, so that they correspond to many possible systems. As long as the systems are consistent with the information in the diagram, they will have the same diagram. However, an outcome diagram corresponds to a much larger set of possible systems than a UML diagram. For an outcome diagram, a system corresponds if it has the same outcomes, independent of its internal structure or behaviour. For a UML diagram, a system corresponds if its internal structure or behaviour is consistent with the information in the diagram. This means that a UML diagram is already making decisions w.r.t. the possible system structures quite early in the design process. The outcome diagram does not make such decisions.

In the rest of this section, we compare outcome diagrams to two UML diagrams, namely the state machine diagram and the component diagram.

3.5.2. State Machine Diagram

A state machine diagram is a finite state automaton. It defines the internal states of a system and the transitions between them. The state diagram captures the causality between the actions taken when the system changes states, but this does not map directly to the outcomes observed by an external user. However, there is a relationship between a state diagram and an outcome diagram. An outcome can map to a sequence of state transitions, whereas, by examining the actions of a state diagram, it is possible to deduce the outcomes to expect from taking those actions.

3.5.3. Block Diagram

A block diagram specifies a system as a set of elements with their interconnections. We illustrate the difference between block diagrams and outcome diagrams using a simple example system: a user querying a front end that is connected to a database (Figure 5). The figure shows the refinement process: a system with an initially unknown structure is refined stepwise into a system that has a completely known structure. For the outcome diagram, the system performance can be obtained directly by composing the $\Delta \mathrm{Q}$s of the outcomes, using the rules described in Section 5. For the block diagram, it is harder to obtain system performance. This is because the block diagram does not define the expected outcomes of a system or their causality. The block diagram by itself does not have sufficient information to allow system performance to be calculated: we also need to know the expected outcome and the sequence of messages sent between blocks needed to achieve that outcome. As a final remark, the block diagram constrains the system structure to always have a front end and a database, whereas the outcome diagram is consistent with many alternative system structures.

4. Design Exploration Using Outcome Diagrams

This section simulates how a design engineer could explore the blockchain diffusion example that was described in Section 2, using outcome diagrams. Figure 6 depicts that design exploration in the form of a threaded decision tree in the search space. Each node in the tree is an outcome diagram. Every node is labelled with a description plus the section in this paper where it is discussed. There are two types of edges: solid edges represent refinement steps (Definition 7), whilst dashed edges represent backtracks to take alternative directions of refinement. The formalism used in this section is presented in Section 5.

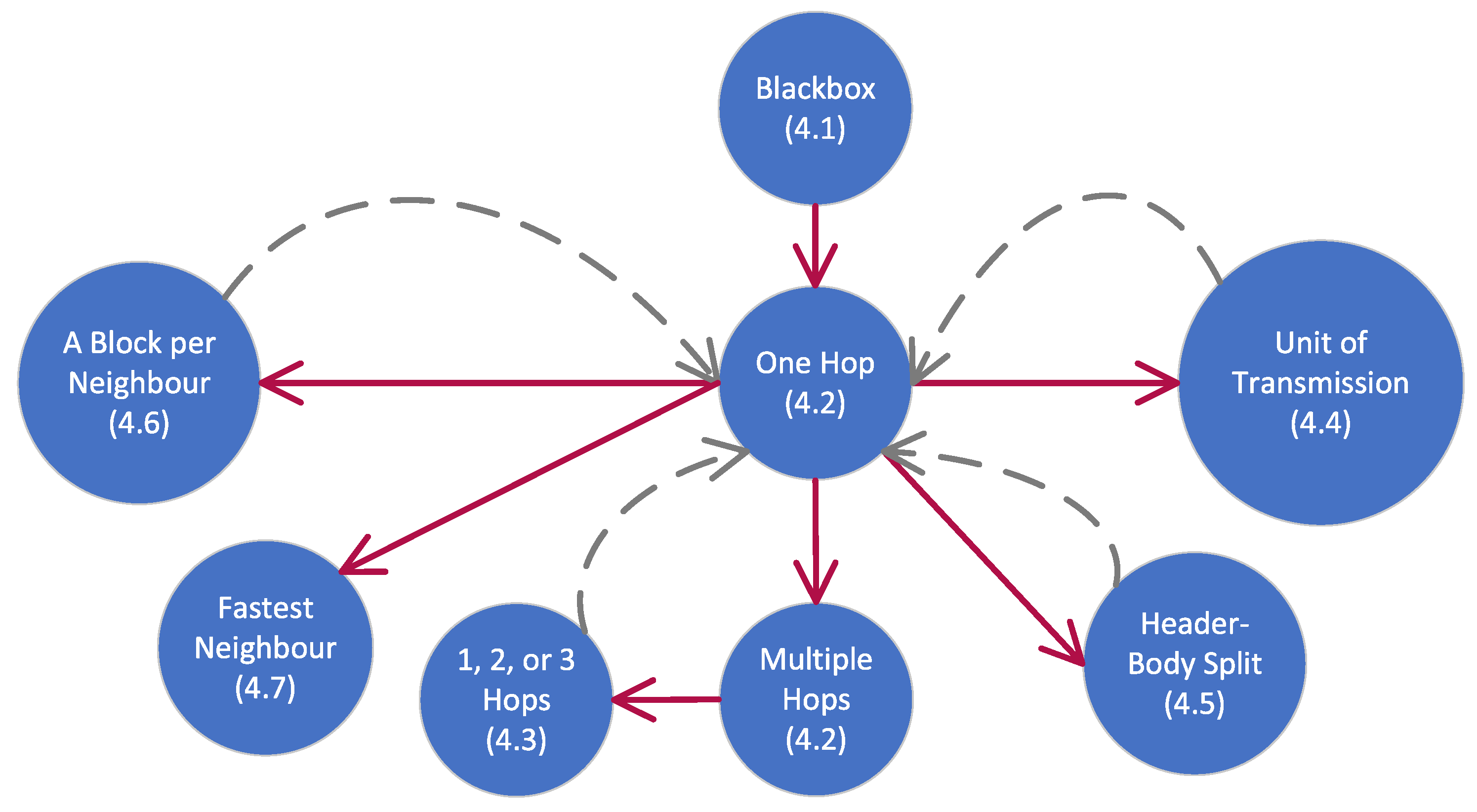
4.1. Starting Off

Initially, the design engineer knows almost nothing about the system. Perhaps, all they know is that there will be the following two observation locations:

• $A^{-}$: Block is ready to be transmitted by A.
• $Z^{+}$: Block is received and verified by Z.

The corresponding outcome diagram is

in which the only outcome is a black box. As will be detailed in Section 5, the outcome expression to describe that outcome diagram is a ♭ (♭ for black boxes).

4.2. Early Analysis

Given that the design engineer is not content with the current level of granularity, they wish to further detail the diagram by giving the black box a name, such as $o_{A⇝Z}$. In $\Delta \mathrm{Q}$SD, we call adding that further detail a refinement. That refinement step is depicted below.

Here, the outcome diagram that is above the dashed line is refined into the one below the dashed line. As will be discussed in Section 5, the (rewrite) rule that authorises this refinement is

$$\mathcal{C}[♭]\to \mathcal{C}\left[o\right].$$

We call this rule (Unbx) for unboxing (a black box). The rule states that in a context $\mathcal{C}$, a black box can be rewritten to any other outcome expression (but not to a black box). In this case, we choose the black box to be rewritten to an outcome variable called $o_{A⇝Z}$. This indicates the outcome of hopping directly from A to Z.

Before producing more of our block diffusion algorithm’s outcome diagram, we would like to take the time to apply some analysis. Refinements aside, suppose for a moment that there are two hops to make from A to Z: first from A to an intermediate node B, and, then, from B to Z. The corresponding outcome diagram for the two-hop journey from A to Z would then be:

Here, $o_{A⇝B}$ and $o_{B⇝Z}$ are the outcomes of hopping from A to B and from B to Z, respectively. Note also that the observation location between the above two outcomes is labelled $B^{+}/B^{-}$. That is because the observation $B^{+}$ and $B^{-}$ take place at the same location. For that reason, we will simply write B to refer to that observation location. The same convention is used for similar intermediate locations. Then, it is easy to obtain the outcome diagram for three hops:

While outcome diagrams are visually more attractive, outcome expressions are algebraically more attractive. For example, the corresponding expression for two hops is $o_{A⇝B}•\to -•o_{B⇝Z}$, where “$•\to -•$” is the symbol we use for sequential composition: The sequential composition of $o_{A⇝B}$ and $o_{B⇝Z}$ is needed because the latter causally depends on the former. Likewise, the outcome expression for three hops is $o_{A⇝B}•\to -•o_{B⇝C}•\to -•o_{C⇝Z}$. Then, generalising that to n hops is easy: $o_{A⇝B_1}•\to -•o_{B_1⇝B_2}•\to -•\dots •\to -•o_{B_n⇝Z}$, which we abbreviate as $o_{A⇝B_1}•\to -•\left({\begin{array}{c}•\to -•\\ •\to -•\end{array}}_1^{n-1}{o}_{B_i⇝B_{i+1}}\right)•\to -•o_{B_n⇝Z}$. Parameterisation by n hops is useful because it helps the design engineer determine the right n for their blockchain. For example, a relevant question is: What is the optimal n for block diffusion to be timely and for its load to be bearable? The formalisation in Section 5 instructs the design engineer as to how to achieve that and other goals. Before detailing the how, we take our moment to analyse a smaller example. Consider the two-hop scenario. Provided that the design engineer has $\Delta \mathrm{Q}$s for both $o_{A⇝B}$ and $o_{B⇝Z}$, they can use Definition 4 to work out the $\Delta \mathrm{Q}$ of $o_{A⇝B}•\to -•o_{B⇝Z}$, which is the convolution of the two constituent $\Delta \mathrm{Q}$s:

$$\Delta \mathrm{Q}\left(o_{A⇝B}•\to -•o_{B⇝Z}\right)=\Delta \mathrm{Q}\left(o_{A⇝B}\right)\ast \Delta \mathrm{Q}\left(o_{B⇝Z}\right).$$

In a similar vein, the design engineer can work out the n-hop scenario’s $\Delta \mathrm{Q}$ for $n>1$.

$$\begin{array}{c}\Delta \mathrm{Q}\left(o_{A⇝B_1}•\to -•\left(\begin{array}{c}•\to -•n-1\\ •\to -•i=1\end{array}{o}_{B_i⇝B_{i+1}}\right)•\to -•o_{B_n⇝Z}\right)=\hfill \\ \Delta \mathrm{Q}\left(o_{A⇝B_1}\right)\ast {\ast }_{n=1}^{n-1}\Delta \mathrm{Q}\left(o_{B_i⇝B_{i+1}}\right)\ast \Delta \mathrm{Q}\left(o_{B_n⇝Z}\right)\hfill \end{array}.$$

(2)

Then, using the formulation given in Definition 5, the design engineer can determine the constraints on n that are needed in order for block diffusion to meet the overall timeliness requirements.

In practice, the time that is needed to transfer a block of data one hop depends on four main factors:

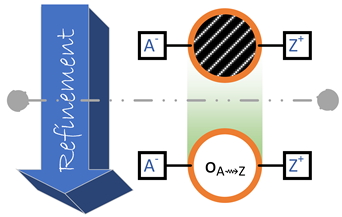
• The size of the block;
• The speed of the network interface;
• The geographical distance of the hop (as measured by the time to deliver a single packet);
• Congestion along the network path.

When we consider blockchain nodes that are located in data centres (which most block producers tend to be), the interface speed will typically be 1 Gb/s or more. This is not a significant limiting factor for the systems of interest (see Section 5.4 for an analysis that explains this). In the setting that we are considering, congestion is generally minimal, and so this can also be ignored in the first instance. This leaves (i) block size, which we will take as a design parameter to be investigated later; and (ii) distance, which we will consider now. For simplicity, we will consider three cases of geographical distance:

• Short: The two nodes are located in the same data centre;
• Medium: The two nodes are located in the same continent;
• Long: The two nodes are located in different continents.

For pragmatic reasons, Cardano relies on the standard TCP protocol for data transfers. TCP transforms loss into additional delay, so the residual loss is negligible. At this point, we could descend into a detailed refinement of the TCP protocol, but equally we could simply take measurements; the compositionality of $\Delta \mathrm{Q}$SD means that it makes no difference where the underlying values come from.

Table 1. Representative times in seconds and round-trip times (RTTs) for one-way TCP transmission of varying block sizes for short, medium, and long distances between blockchain nodes.

		64 kB		256 kB		512 kB		1024 kB		2048 kB
Distance	Time (s)	Time (s)	RTTs	Time (s)	RTTs	Time (s)	RTTs	Time (s)	RTTs	Time (s)	RTTs
Short	0.012	0.024	1.95	0.047	3.81	0.066	5.41	0.078	6.36	0.085	6.98
Medium	0.069	0.143	2.07	0.271	3.94	0.332	4.82	0.404	5.87	0.469	6.81
Long	0.268	0.531	1.98	1.067	3.98	1.598	5.96	1.598	5.96	1.867	6.96

shows measurements of the transit time of packets and the corresponding transfer time of blocks of various sizes, using hosts running on AWS data centre servers in Oregon, Virginia, London, Ireland, and Sydney. Since we know that congestion is minimal in this setting, the spread of values will be negligible, and so in this case, the CDFs for the $\Delta \mathrm{Q}$s will be step functions. The transfer time for each block size is given both in seconds and in multiples of the basic round-trip time (RTT) between the hosts in question. Since the TCP protocol relies on the arrival of acknowledgements to permit the transmission of more data, it is unsurprising to see a broadly linear relationship, which could be confirmed by a more detailed refinement of the details of the protocol.

Given the randomness in the network structure and the selection of block-producing nodes, there remains some uncertainty on the length of an individual hop. At this point, we will assume that short, medium, and long hops are equally likely, which we can think of as an equally-weighted probabilistic choice. In numerical terms, this becomes a weighted sum of the corresponding $\Delta \mathrm{Q}$s, as given in Table 1. This gives the distribution of transfer times per block size shown in Figure 7.

4.3. Refinement and Probabilistic Choice

Recall that A and Z are names for randomly chosen nodes, so the number of hops between A and Z is unkown. $\Delta \mathrm{Q}$SD tackles that uncertainty by offering an outcome diagram that involves probabilistic choice between the different number of hops that might be needed. Strictly speaking, a probabilistic choice is a binary operation. Hence, when there are more than two choices, the outcome diagram will cascade probabilistic choices. In the general formulation, there are at most n hops. In order to produce that, the design engineer exercises a step-by-step refinement of the single-hop outcome diagram. The first refinement introduces the choice between one or two or more hops, as shown in Figure 8.

There are two outcome diagrams in Figure 8: the one above the dashed line and the one below. The underlying green area is not a part of the two outcome diagrams itself, but it is there to indicate which part of the diagram above the dashed line is being refined into which part of the diagram below. In the absence of the left-side arrow, the direction of refinement can also be determined using the colour of the underlying green area. The pale side of an underlying green area is for what is being refined, whereas the dark side is for the result of the refinement.

The equivalent outcome expression of the lower diagram in Figure 8 is $o_{A⇝Z}\begin{array}{c}{m}_1\\ {\displaystyle \leftrightharpoons }\\ m_1^{\prime }\end{array}\left(o_{A⇝B}•\to -•o_{B⇝Z}\right)$, which is a probabilistic choice between one or two hops with respective weights $m_1$ and $m_1^{\prime }$. The corresponding (rewrite) rule of the figure is:

$$\mathcal{C}\left[o\right]\to \mathcal{C}\left[o^{\prime }\begin{array}{c}{m}^{\prime }\\ {\displaystyle \leftrightharpoons }\\ m^{″}\end{array}{o}^{″}\right]$$

which we call (Prob) (for probabilistic choice). Here is how we applied (Prob) to arrive from the single hop to the probabilistic choice between one hop and two hops:

$$o_{A⇝Z}\to o_{A⇝Z}\begin{array}{c}{m}_1\\ {\displaystyle \leftrightharpoons }\\ m_1^{\prime }\end{array}\left(o_{A⇝B}•\to -•o_{B⇝Z}\right)$$

That is, $\mathcal{C}$ in the above refinement is an empty context.

Next, the design engineer further refines the two+-hop part to the probabilistic choice between two or three hops, as shown in Figure 9. Again, in that figure, the underlying green area is not a part of either diagram. It only serves as a visual indicator, showing which part of the upper diagram is being refined into which part of the lower one.

For the equivalent term rewriting of Figure 9, we use (Prob) again. However, instead of an empty context, here, the context is $o_{A⇝Z}\begin{array}{c}{m}_1\\ {\displaystyle \leftrightharpoons }\\ m_1^{\prime }\end{array}\left(o_{A⇝B}•\to -•[.]\right)$:

$$o_{A⇝Z}\begin{array}{c}{m}_1\\ {\displaystyle \leftrightharpoons }\\ m_1^{\prime }\end{array}\left(o_{A⇝B}•\to -•o_{B⇝Z}\right)\to o_{A⇝Z}\begin{array}{c}{m}_1\\ {\displaystyle \leftrightharpoons }\\ m_1^{\prime }\end{array}\left(o_{A⇝B}•\to -•(o_{B⇝Z}\begin{array}{c}{m}_2\\ {\displaystyle \leftrightharpoons }\\ m_2^{\prime }\end{array}\left(o_{B⇝C}•\to -•o_{C⇝Z}\right)\right).$$

The design engineer can continue refinement until a predetermined number of hops is reached. Alternatively, they can keep the number of hops as a parameter and analyse the corresponding parameterised outcome expression for timeliness, behaviour under load, etc.

Figure 10 shows the result of applying Equation (2) to the sequence of outcome expressions corresponding to one, two, …five sequential hops using the transfer delay distribution shown in Figure 7, for a 64 kB block size. It can be seen that there is a $95\%$ probability of the block arriving within 2 s. In contrast, Figure 11 shows the corresponding sequence of delay distributions for a 1024 kB block size, where the 95th percentile of transfer time is more than 5 s.

If we know the distribution of expected path lengths, we can combine the $\Delta \mathrm{Q}$s for different hop counts using (Prob).

Table 2. Percentage of paths having a given length in a random graph of 2500 nodes of varying degree.

Length	Node Degree
	5	10	15	20
1	0.20	0.40	0.60	0.80
2	1.00	3.91	8.58	14.72
3	4.83	31.06	65.86	80.08
4	20.18	61.85	24.95	4.40
5	47.14	2.78	0.00
6	24.77	0.00
7	1.83
8	0.05

shows the distribution of paths lengths in simulated random graphs having 2500 nodes and a variety of node degrees [18]. Using the path length distribution for nodes of degree 10, for example, then gives the transfers delay distribution shown in Figure 12.

Alternative Refinements

Suppose that instead of investigating the number of hops, the design engineer is now interested in studying the steps within a single hop. There are various ways to do this. In Section 4.4, Section 4.5, Section 4.6 and Section 4.7, we will consider four different ways that can be used when A and Z are neighbours, each of which refines $o_{A⇝Z}$. These refinements are all instances of the (Elab) (rewrite) rule (for elaboration):

$$\mathcal{C}\left[o_v\right]\to \mathcal{C}\left[o\right].$$

The following sections are also important for another reason. So far, we have traversed the threaded tree of refinement in a depth-first way; the upcoming subsections traverse that tree in a breadth-first way. $\Delta \mathrm{Q}$SD allows the design engineer to choose between depth-first and breadth-first refinement at any point in their design exploration.

4.4. Breaking Down Transmissions into Smaller Units

Network transmissions are typically broken down into the transmission of smaller units. Depending on the layering of the network protocols, that might, for example mean dividing a high-level message into several smaller packets. In a similar vein, the design engineer might decide to study block diffusion in terms of smaller units of transmission. For example, they might want to study the division of $o_{A⇝Z}$ into n smaller unit operations $o_{A⇝Z}^{u_1},\cdots ,o_{A⇝Z}^{u_n}$. The resulting outcome diagram is shown in Figure 13. Then, the corresponding outcome expression would be $o_{A⇝Z}\to o_{A⇝Z}^{u_1}•\to -•\dots •\to -•o_{A⇝Z}^{u_n}$, which we abbreviate as $o_{A⇝Z}\to {\begin{array}{c}•\to -•\\ •\to -•\end{array}}_1^n{o}_{A⇝Z}^{u_i}$. This refinement can happen at different levels of granularity and is fairly repetitive. However, this is the level at which details of the transmission protocol such as TCP could be introduced if required.

4.5. Header–Body Split

In Cardano Shelley, an individual block transmission involves a dialogue between a sender node, A, and a recipient node, Z. We represent the overall transmission as $o_{A⇝Z}$. This can be refined into the following sequence:

• Permission for Header Transmission ($o_{Z⇝A}^{\mathit{ph}}$): Node Z grants the permission to node A to send it a header.
• Transmission of the Header ($o_{A⇝Z}^{\mathit{th}}$): Node A sends a header to node Z.
• Permission to for Body Transmission ($o_{Z⇝A}^{\mathit{pb}}$): Node Z analyses the header that was previously sent to it by A. Once the suitability of the block is determined via the header, node Z grants permission to A to send it the respective body of the previously sent header.
• Transmission of the Body ($o_{A⇝Z}^{\mathit{tb}}$): Finally, A sends the block body to Z.

The motivation for the header/body split and the consequential dialogue is optimisation of transmission costs. Headers are designed to be affordably cheap to transmit. In addition, they carry enough information about the body to enable the recipient to verify its suitability. The body is only sent once the recipient has done this. This prevents the unnecessary transmission of block bodies when they are not required. Since bodies are typically several orders of magnitude larger than headers, considerable network bandwidth can be saved in this way. Moreover, the upstream node is not permitted to send another header until given permission to do so by the downstream node in order to prevent a denial-of-service attack in which a node is bombarded with fake headers, so this approach also reduces latency when bodies are rejected. In practice, the first permission is sent when the connection between peers is established and the permission renewed immediately after the header is received, so that the upstream peer does not have to wait unnecessarily. Therefore, the design engineer can refine $o_{A⇝Z}$ into the finer-grained outcomes shown in Figure 14. The corresponding outcome expression is $o_{Z⇝A}^{\mathit{ph}}•\to -•o_{A⇝Z}^{\mathit{th}}•\to -•o_{Z⇝A}^{\mathit{pb}}•\to -•o_{A⇝Z}^{\mathit{tb}}$.

Note that the protocol described here is between directly connected neighbours—these requests are not forwarded to other nodes. Thus, this is a refinement of the one-hop block transfer process. The significance of this refinement is that it shows that an individual outcome that, at a given level of granularity, is unidirectional (i.e., only from one entity in the system to another) might, at a lower level of granularity, very well be a multi-directional conversation.

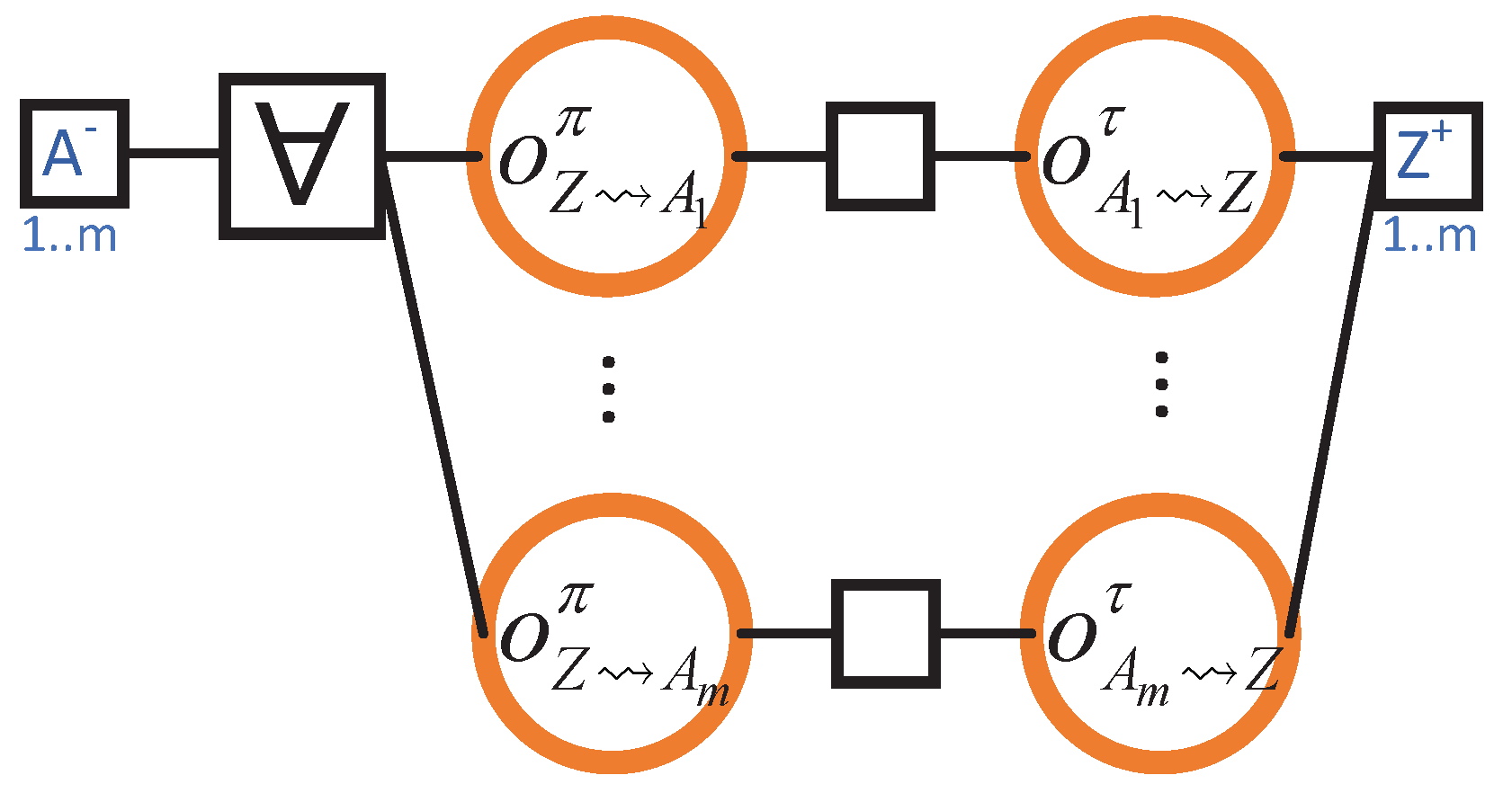
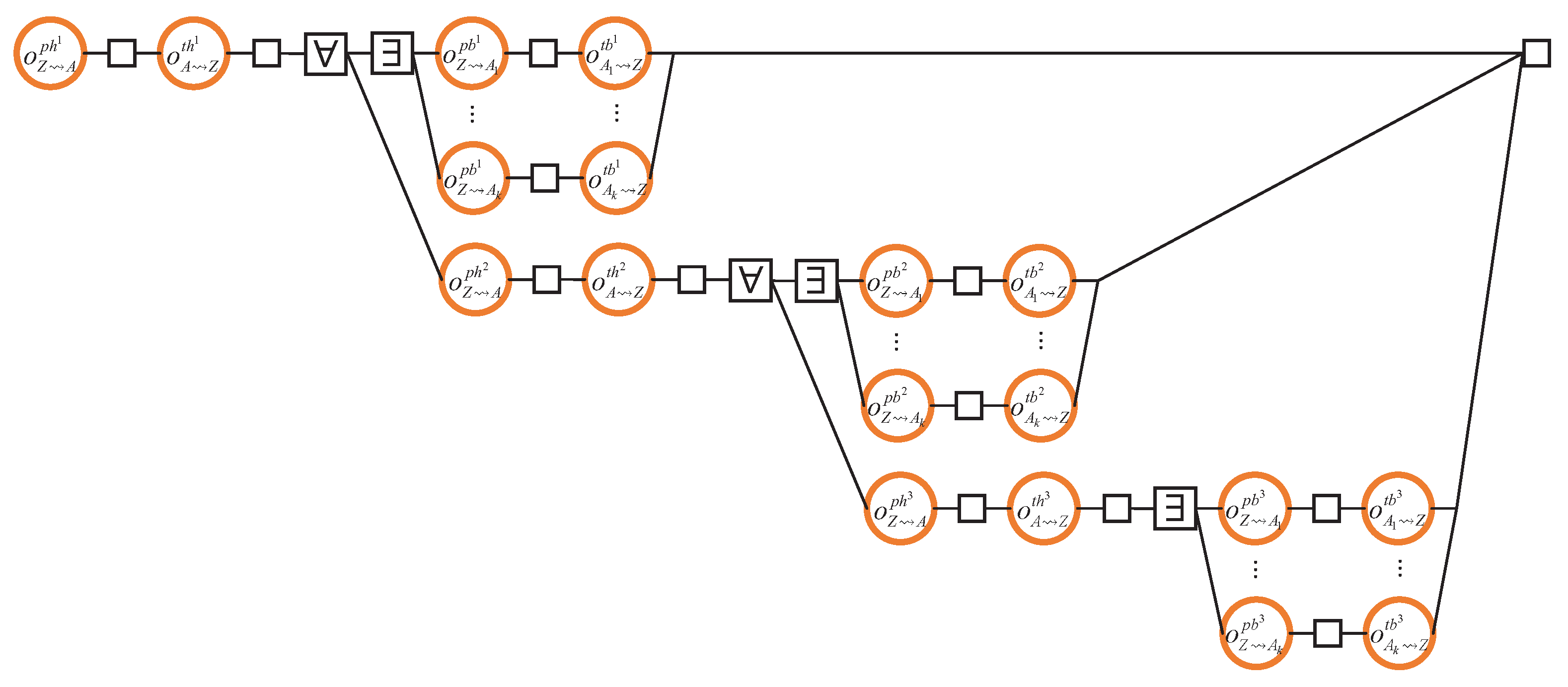
4.6. Obtaining One Block from each Neighbour when Rejoining the Blockchain

Consider the situation where a node Z rejoins the blockchain after being disconnected for some period of time. Z will be out-of-date w.r.t. the recently generated blocks and will need to update itself. Let us consider the lucky situation where Z can acquire all the blocks that it is missing from its neighbours; that is, it can acquire the blocks with only one hop but from different neighbours. For demonstration purposes, we now make a number of simplifying assumptions:

• Upon its return to the blockchain, Z is m blocks behind, where m is less than or equal to the number of Z’s neighbours.
• Each neighbour $A_i$ of Z transmits precisely one block to Z.
• The header–body split refinement of Section 4.5 is not considered. Therefore, there are only two steps (instead of the actual four):
  • $o_{Z⇝A_i}^{\pi }$ for when Z grants permission to $A_i$. And,
  • $o_{Z⇝A_i}^{\tau }$ for when $A_i$transmits the (entire) block to Z.

With those simplifications in place, the outcome diagram will be as shown in Figure 15. This shows that Z will be up-to-date when all its m (selected) neighbours are granted permission and have finished sending their blocks to Z. Note that the outcome diagram has, in fact, m starting observation locations and m terminating observation locations. This is the reason for the $1\dots m$ notation immediately below each of those observation locations. The corresponding outcome expression is

$$\forall (\left(o_{Z⇝A_1}^{\pi }•\to -•o_{A_1⇝Z}^{\tau }\right)\Vert \cdots \Vert \left(o_{Z⇝A_m}^{\pi }•\to -•o_{A_m⇝Z}^{\tau }\right))$$

which we abbreviate as ${\Vert }^{\forall }{\left(o_{Z⇝A_i}^{\pi }•\to -•o_{A_i⇝Z}^{\tau }\right)}_1^m$.

Load Analysis

One reason why this refinement is particularly interesting is that it allows an easy demonstration of our load analysis from Section 5.4. Fix a resource $\rho$ such as network capacity. Pick a time t between the first observation made at an $A_i^{-}$ and the last observation made at a $Z_i^{+}$. According to Definition 10, the static amount of work S at time t that is required for performing ${\Vert }^{\forall }{\left(o_{Z⇝A_i}^{\pi }•\to -•o_{A_i⇝Z}^{\tau }\right)}_1^m$ is the sum of the static amounts of work S that is required at t for performing each $o_{Z⇝A_i}^{\pi }•\to -•o_{A_i⇝Z}^{\tau }$ (where $1\le i\le m$):

$$S⟦{\Vert }^{\forall }{\left(o_{Z⇝A_i}^{\pi }•\to -•o_{A_i⇝Z}^{\tau }\right)}_{i=1}^m⟧\left(t\right)=\sum _{i=1}^{m}S⟦o_{Z⇝A_i}^{\pi }•\to -•o_{A_i⇝Z}^{\tau }⟧\left(t\right).$$

(3)

Equation (3) describes an approach to aggregating offered load on a resource. Considering an ephemeral resource—such as a communications network interface—a design interest might be to understand the intensity of use of this interface. We say a resource is ephemeral if it is lost if unused. For example, for a design requirement to be (at this level of detail) feasible, the average use of the interface has to be less than its capacity. This is the basic precondition for the demand on the resource to possess a feasible schedule. The RHS of Equation (3) captures this process as a piece-wise summation of the load intensities. Building on the time to transfer blocks (Table 1), and noting (from Section 2.1) that the body of a block is forwarded in response to a request (which takes one round-trip time), the total block volume is delivered in the total time minus the round trip time. For the ‘Near’ peers shipping a $64kB$ block, this means an intensity of 42.7 Mb/s (8 $\times 64,000/(0.024-0.012)$) before incorporating any other network-related overheads (such as layered headers).

Table 3. Average load intensities (in Mbit/s) implied by time to load from Table 1.

Distance	Block Size (kB)
	64	256	512	1024	2048
Short	42.7	58.5	75.9	151.7	224.4
Medium	6.9	10.1	15.6	31.1	41.0
Long	1.9	2.6	3.1	6.2	10.2

captures that load intensity approximation.

This provides an insight into the likely capacity constraints for differing degrees of connectivity and, by inference, an insight into the system-level design trades. From Table 1 and Table 3, it can be seen that smaller geographic distribution can lead to lower forwarding times assuming that (for a fixed communications capacity) the number of associating peers is suitably reduced. Assessments such as this give a measure of the likely “slack” in the design; those portions of the design that have less “slack” represent design elements that might need more detailed refinement and/or other strategies to ensure their feasibility. Note that a dedicated support tool for $\Delta \mathrm{Q}$SD would easily be able to manipulate these complex outcome diagrams, giving a formally correct analysis, with very little mental burden for the design engineer.

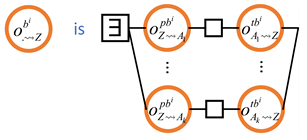
4.7. Obtaining a Block from the Fastest Neighbour

Section 4.5 discussed splitting the header and body for optimisation reasons. One assumption in that design is that the header and the body will be taken from the same neighbour. It turns out that this assumption will not necessarily lead to the fastest solution. In fact, when Z determines that it is interested in a block that it has received the header of, it may obtain it from any of its neighbours that have signalled that they have it. In particular, Cardano nodes keep a record of the $\Delta \mathrm{Q}$s of their neighbours’ block delivery. This allows them to obtain bodies from their fastest neighbour(s). In other words, once a node determines the desirability of a block (via its header), it is free to choose to take the body from any of its neighbours that have provided the corresponding header. As long as only timeliness is a concern—and not when resource consumption is also of interest—a race can occur between all neighbours, with the fastest neighbour winning the race. The diagrams in this section assume such a race.

Now, as in Section 4.6, consider the situation where Z reconnects to the blockchain after being disconnected for some time. Our design in Section 4.6 assumes that there is no causality between the m blocks that Z needs to obtain. In reality, that is not correct: there is a causal order between those blocks, and that order can be rather tricky to define; it might take a couple of reads before the matter is fully digested. There are two separate total orders between blocks:

CO1. 

For each block, the header must be transmitted before the body (so that the recipient node can determine the suitability of the block before the body transmission);

CO2. 

Headers of the older blocks need to be transmitted before those of the younger blocks (note, however, that there is no causal relationship between the body transmissions).

This section considers the situation when the design engineer investigates the above race as well as CO1 and CO2. Suppose that once Z reconnects to the blockchain, it is exactly $m=3$ blocks behind the current block. Suppose also that Z has k neighbours. The corresponding outcome diagram is shown in Figure 16. The fork that is causally dependent on $o_{A⇝Z}^{{\mathit{th}}^3}$ is done when any of its prongs is done, that is, as soon as any neighbour of Z has finished transmitting the third block to Z. The other “∃” forks are similar.

The corresponding outcome expression is:

$$\begin{array}{c}{o}_{Z⇝A}^{{\mathit{ph}}^1}•\to -•o_{A⇝Z}^{{\mathit{th}}^1}•\to -•\forall (\exists [\left(o_{Z⇝A_1}^{{\mathit{pb}}^1}•\to -•o_{A_1⇝Z}^{{\mathit{tb}}^1}\right)\Vert \cdots \Vert \left(o_{Z⇝A_k}^{{\mathit{pb}}^1}•\to -•o_{A_k⇝Z}^{{\mathit{tb}}^1}\right)]\Vert \\ (o_{Z⇝A}^{{\mathit{ph}}^2}•\to -•o_{A⇝Z}^{{\mathit{th}}^2}•\to -•\forall (\exists [\left(o_{Z⇝A_1}^{{\mathit{pb}}^2}•\to -•o_{A_1⇝Z}^{{\mathit{tb}}^2}\right)\Vert \cdots \Vert \left(o_{Z⇝A_k}^{{\mathit{pb}}^2}•\to -•o_{A_k⇝Z}^{{\mathit{tb}}^2}\right)]\Vert \\ (o_{Z⇝A}^{{\mathit{ph}}^3}•\to -•o_{A⇝Z}^{{\mathit{th}}^3}•\to -•\exists [\left(o_{Z⇝A_1}^{{\mathit{pb}}^3}•\to -•o_{A_1⇝Z}^{{\mathit{tb}}^3}\right)\Vert \cdots \Vert \left(o_{Z⇝A_k}^{{\mathit{pb}}^3}•\to -•o_{A_k⇝Z}^{{\mathit{tb}}^3}\right)\left]\right)\left)\right)).\end{array}$$

We would like to invite the reader to take their time to pair the above diagram with our explanations above. We understand that the diagram and to a greater degree the expression can look impenetrable. The compositionality of our formalism (inherited from that of $\Delta \mathrm{Q}$SD) comes to the rescue! Indeed, we can observe that the race pattern is rather repetitive. Thus, we can wrap the entire race into three new outcomes $o_{.⇝Z}^{b^1}$, $o_{.⇝Z}^{b^2}$, and $o_{.⇝Z}^{b^3}$. The intention is for $o_{.⇝Z}^{b^1}$, for example, to be the outcome of obtaining the first body transmitted to Z by any one of its k neighbours (that is, we are using “.” in the subscript of $o_{.⇝Z}^{b^1}$ as a wildcard). This makes the outcome diagram considerably simpler:

where

These new diagrams make it easy to spot the lack of causal relationship between the $o_{.⇝Z}^{b^i}$s. Hence, there is no causal order between the body transmission despite the existence of CO1 and CO2. The corresponding outcome expression also becomes considerably simpler:

$$\begin{array}{c}{o}_{Z⇝A}^{{\mathit{ph}}^1}•\to -•o_{A⇝Z}^{{\mathit{th}}^1}•\to -•\forall (o_{.⇝Z}^{b^1}\Vert (o_{Z⇝A}^{{\mathit{ph}}^2}•\to -•o_{A⇝Z}^{{\mathit{th}}^2}•\to -•\forall (o_{.⇝Z}^{b^2}\Vert \left(o_{Z⇝A}^{{\mathit{ph}}^3}•\to -•o_{A⇝Z}^{{\mathit{th}}^3}•\to -•o_{.⇝Z}^{b^3}\right))))\end{array}$$

where

$$o_{.⇝Z}^{b^i}=\exists [\left(o_{Z⇝A_1}^{{\mathit{pb}}^i}•\to -•o_{A_1⇝Z}^{{\mathit{tb}}^i}\right)\Vert \cdots \Vert \left(o_{Z⇝A_k}^{{\mathit{pb}}^i}•\to -•o_{A_k⇝Z}^{{\mathit{tb}}^i}\right)]$$

which we abbreviate as

$${\Vert }^{\exists }{\left(o_{Z⇝A_j}^{{\mathit{pb}}^i}•\to -•o_{A_j⇝Z}^{{\mathit{tb}}^i}\right)}_{j=1}^m.$$

The latter outcome diagrams and outcome expressions are now relatively easy to follow.

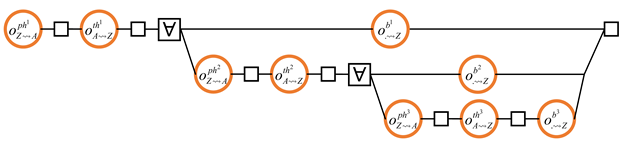
4.8. Summary

The refinements and analysis that are described in this section capture an important part of the design journey for the Shelley implementation of Cardano. In Section 4.1, we defined a ‘top level’ outcome of interest: that of diffusing a block from an arbitrary source node to an arbitrary destination in a bounded time and with bounded resource consumption. In Section 4.2, we refined this to examine the implications of forwarding the block through a sequence of intermediate nodes, and in Section 4.3, we factored in the expected distribution of path lengths. This allows an exploration of the trade-offs between graph size, node degree, block size, and diffusion time. In Section 4.4, we showed how $\Delta \mathrm{Q}$SD can be used to explore orthogonal aspects of the design, in this case how blocks of data are in fact transmitted as a sequence of packets. This could be extended into a full analysis of some transmission protocol such as TCP or QUIC. In Section 4.5, we analysed the effects of splitting blocks into a header and a body in order to reduce resource consumption, and in Section 4.6, we analysed the potential for speeding up block downloading by using multiple peers in parallel. This analysis informed critical design decisions in the Cardano Shelley implementation, in particular the block header/body split, which was shown to significantly improve the resource consumption while increasing the diffusion time only slightly. An analysis of the network resource consumption in this case gave a flavour of how the $\Delta \mathrm{Q}$SD paradigm encompasses resource as well as timeliness constraints. Finally, in Section 4.7, we discussed how $\Delta \mathrm{Q}$ is used in the Shelley implementation of Cardano in operation as well as in design, to optimise the choice of peer from which to obtain a block.

All of this, together with further optimisations such as controlling the formation of the node graph to achieve a balance between fast block diffusion and resilience to partitioning, has produced an industry-leading blockchain implementation that reliably and consistently delivers blocks of up to 72 kB every 20 s on average across a globally distributed network of collaborating block producing nodes. Figure 17 gives a snapshot of the 95th percentile of block diffusion times over a period of nearly 48 h. This clearly shows highly consistent timing behaviour regardless of block size, with the vast majority of blocks diffused across the global network within 1–2 s. Such measurements, based on the $\Delta \mathrm{Q}$SD paradigm, are used on an ongoing basis to avoid performance regressions as new features such as smart contracts are added to the Cardano blockchain.

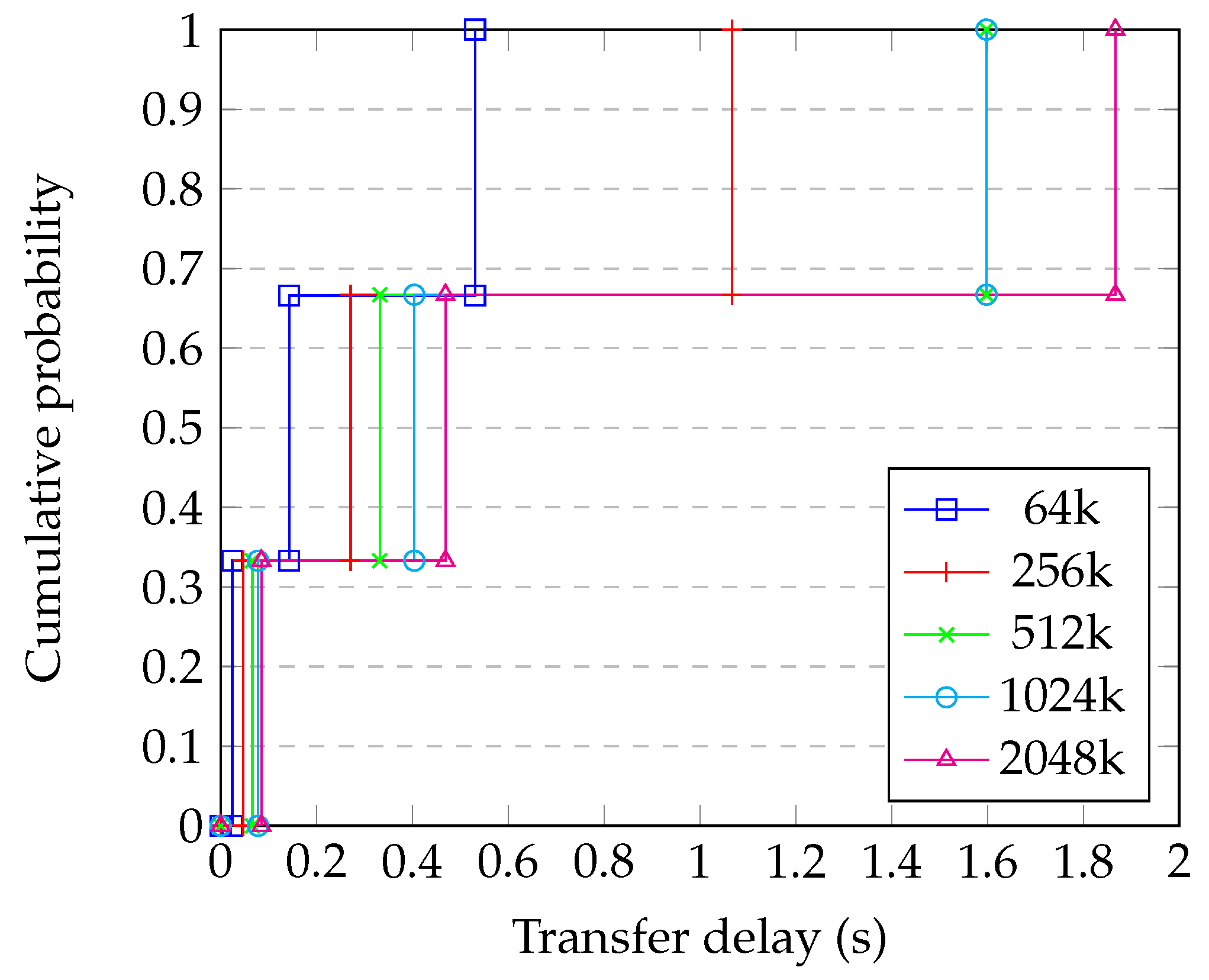
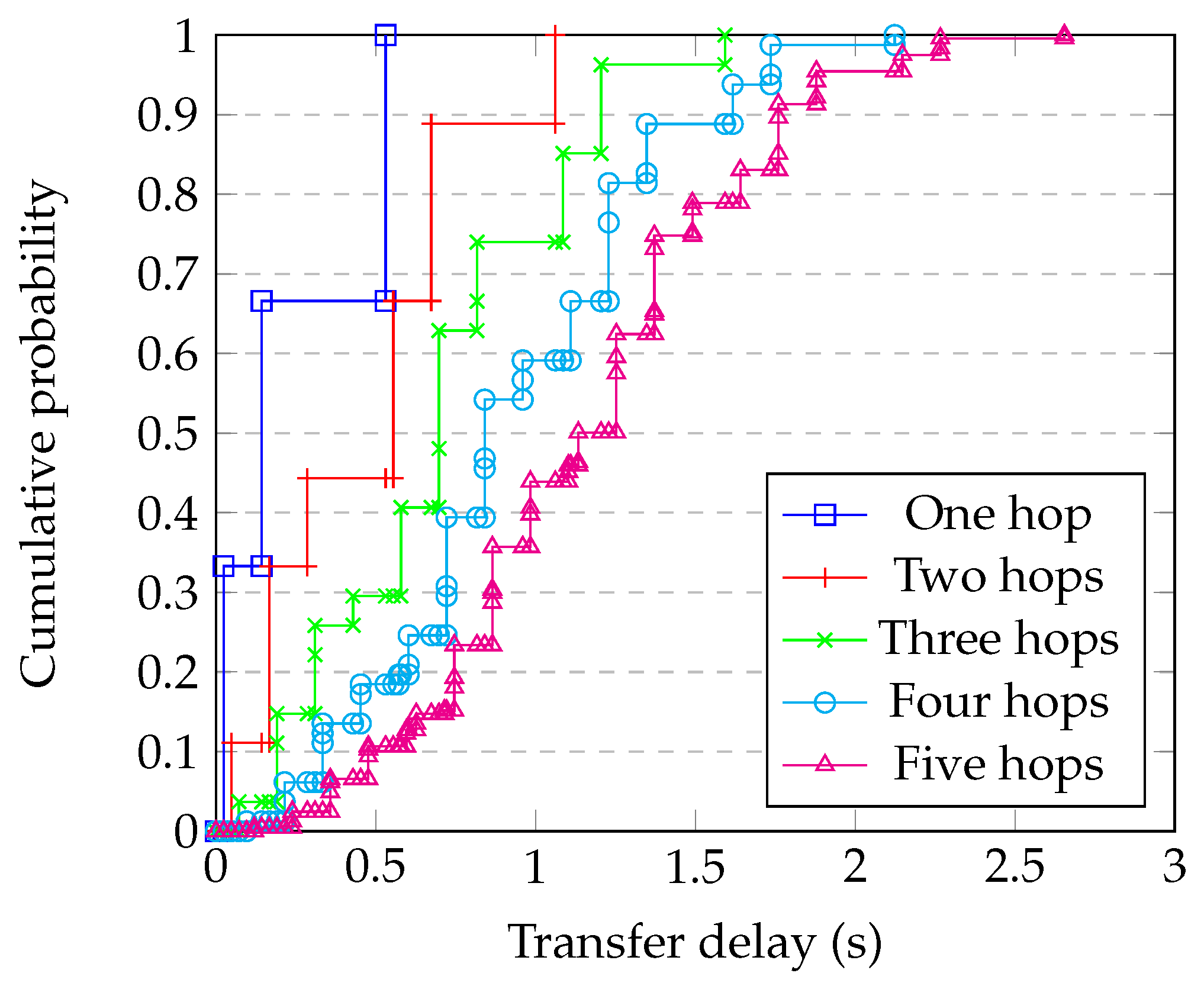
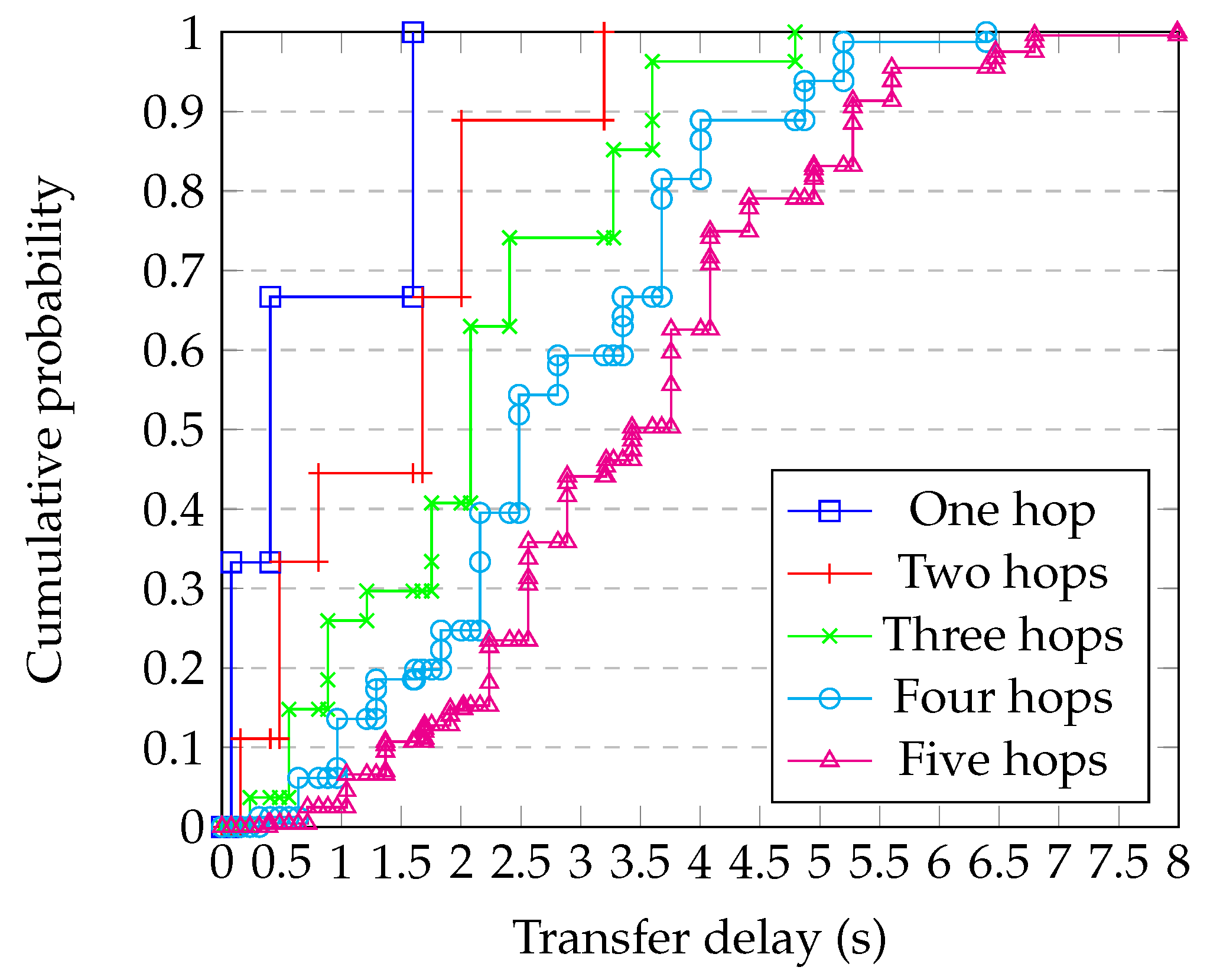
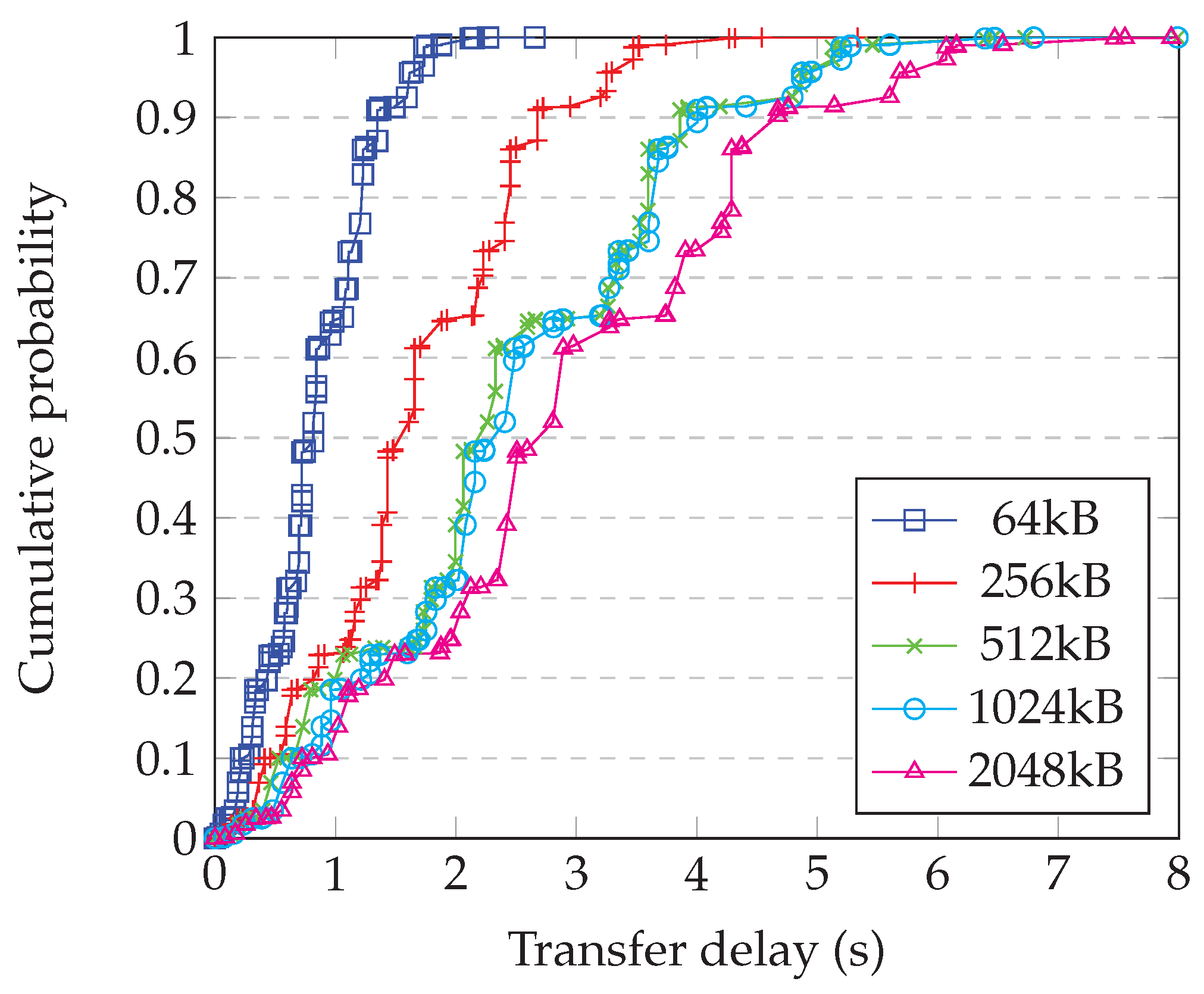
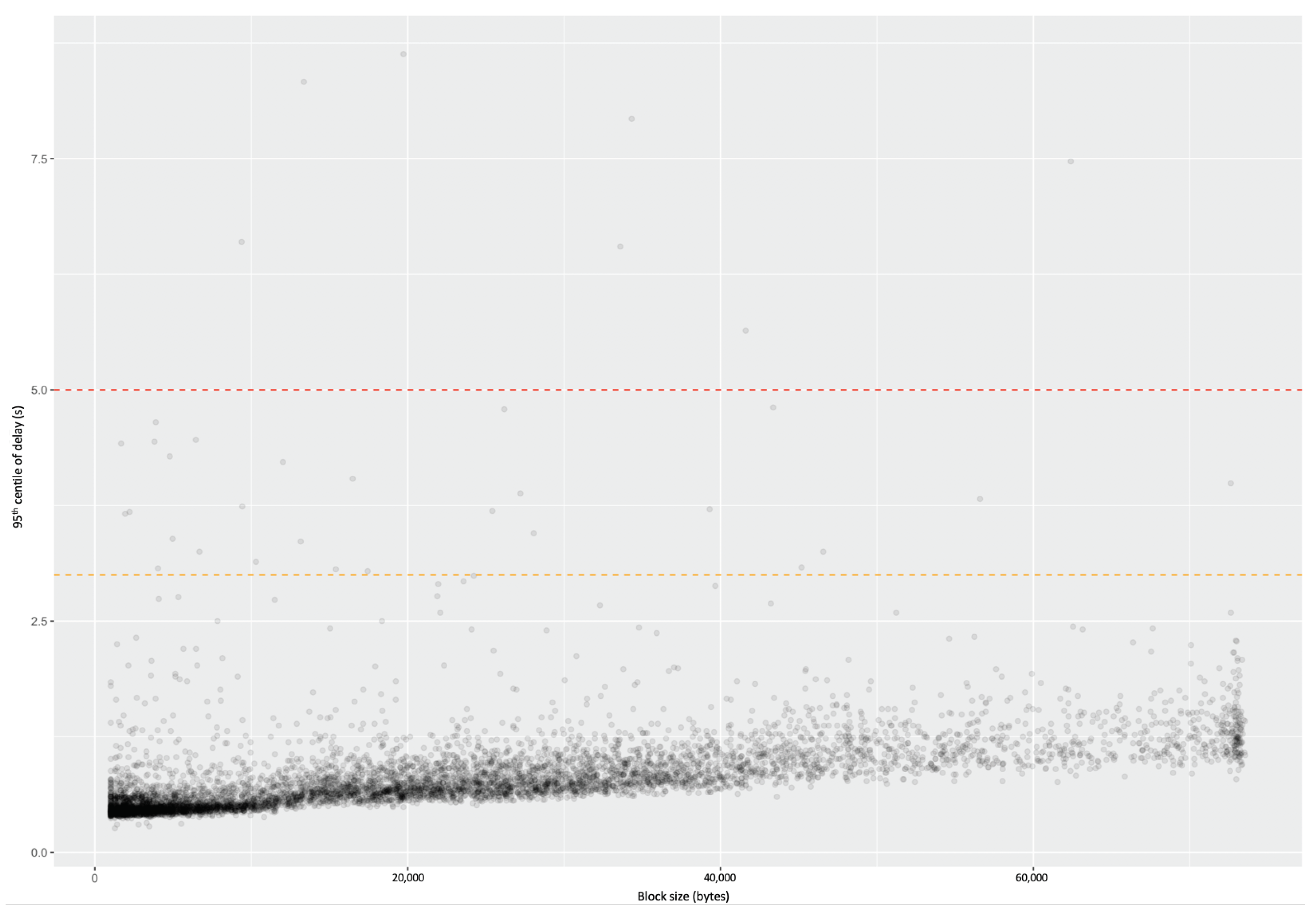
4.9. Comparison with Simulation

It is informative to consider how the insights delivered by using $\Delta \mathrm{Q}$SD could have been obtained otherwise, using, e.g., discrete-event simulations. This would require implementing the design to a sufficient level of detail for the timing to be considered accurate and then running many instances of the simulation to explore the variability of the context. For instance, obtaining the results of Figure 12 would require the following:

• Generating a random graph with 2500 nodes having degree 10;
• Randomly choosing whether each link is ‘short’, ‘medium’, or ‘long’, and applying the corresponding delay from Table 1;
• Running the simulation of the whole system for enough steps to obtain statistical confidence;
• Repeating for each block size;
• Repeating this for enough different graphs to have confidence in the results.

Let us estimate how many simulation runs might be required. As a rule of thumb, we could consider that having any confidence in a 99th percentile result requires at least 1000 samples, so we would need to measure the diffusion time of at least 1000 blocks of the selected size; following Table 2, this would typically require each block to traverse four hops, hence needing 4000 simulation steps.

So far, this seems quite tractable. However, let us consider how many graphs would need to be considered to have confidence in the results. According to McKay [19], if $k\le 2n/9$ and $nk$ is even, then the number of labelled k-regular graphs (i.e., having degree k) on n vertices is given by:

$$M(n,k)=\frac{\left(nk\right)!}{(nk/2)!{(k!)}^n}{e}^{(1-k^2)/4+O(k^3/n)}$$

Taking logarithms and using Stirling’s approximation for factorials $ln(n!)\sim n\left(ln\right(n)-1)$, we can rewrite this as:

$$\begin{array}{cc}\hfill ln\left(M\right(n,k\left)\right)& =ln(\left(nk\right)!)-ln((nk/2)!)-nln(k!)-(k^2-1)/4+O(k^3/n)\hfill \\ \hfill & \sim \left(nk\right)ln\left(nk\right)-nk-(nk/2)ln(nk/2)+nk/2-\left(nk\right)ln\left(k\right)+nk-(k^2-1)/4\hfill \\ \hfill & =\frac{nk}{2}(ln\left(n\right)-ln\left(k\right)+ln\left(2\right)+1)-\frac{k^2-1}{4}\hfill \end{array}$$

If we substitute $k=10$ and $n=2500$, we get $ln\left(M\right(n,k\left)\right))\sim 12,500\times 7.21-99/4\simeq 90,158$ which means $M(n,k)\sim {10}^{39,155}$. So, obtaining a reasonable coverage of the set of possible random graphs with 2500 nodes of degree 10 is clearly infeasible. Using $\Delta \mathrm{Q}$SD, we only process enough information to establish the performance hazard instead of constructing a lot of detail that is then discarded; combining probability distributions is a highly computationally efficient way to derive the distribution of interest (all the figures in this paper were produced on an ordinary laptop in a matter of seconds). This is not to say that $\Delta \mathrm{Q}$SD replaces simulation, far from it: simulations can produce precise results whereas $\Delta \mathrm{Q}$SD delivers probabilistic estimates. The limitation of $\Delta \mathrm{Q}$SD are discussed further in Section 7.2.

5. A Formalisation of $\Delta \mathrm{Q}$SD

The examples that were presented in Section 4 all build on the formalisms that we will present in this section. We start by describing the notational conventions that we will use here (Section 5.1). Then, we provide the syntax (Definition 1) for outcome expressions and formalise the rewrite rules that define the valid transitions between possible outcomes (Definition 3). In Section 5.3 and Section 5.4, we provide corresponding denotational semantics for both timeliness and load. These provide the bases for constructing formal timeliness and load analyses that can be used as part of $\Delta \mathrm{Q}$SD. The analyses have so far been deployed manually to inform design decisions for a number of complex real-world systems. Our longer-term intention is that they should be implemented as part of a design exploration toolset that will support $\Delta \mathrm{Q}$SD. Additional semantics and analyses are also possible, of course, and could be used to support alternative design explorations or to provide further details about timeliness, load, etc.

5.1. Notational Conventions

Let $\mathbb{A}$, $\mathbb{B}$, $\mathbb{C}$, … range over sets of values, and let lower-case letters, a, b, c, … range over elements of those sets. Subscripts and priming do not change the syntactic category of a symbol. For example, for a set A, we write $A\ni a$ to indicate that $a,a^{\prime },a^{″},\dots ,a_1,a_2,\dots$ all range over A. For predicates, we write $\mathsf{pred}\left(x\right)$.

5.2. Syntax

Let $\mathbb{B}\ni ♭$ and ${\mathbb{O}}_v\ni o_v$. We refer to black boxes and outcome variables together as base variables: $\overline{\mathbb{B}}={\mathbb{O}}_v\cup \mathbb{B}$, where $\overline{\mathbb{B}}\ni \beta$.

Definition 1.

The abstract syntax of outcome expressions is:

$$\begin{array}{cccc}\hfill o& ::=& ♭|o_v\hfill & \\ & |& o•\to -•o^{\prime }\hfill & \mathit{sequential}\mathit{composition}\hfill \\ & |& o\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m^{\prime }\end{array}{o}^{\prime }\hfill & \mathit{probabilistic}\mathit{choice}\hfill \\ & |& \forall (o\Vert o^{\prime })\hfill & \mathit{all}\text{-}\mathit{to}\text{-}\mathit{finish}(a.k.a.\mathit{last}\text{-}\mathit{to}\text{-}\mathit{finish})\hfill \\ & |& \exists (o\Vert o^{\prime })\hfill & \mathit{first}\text{-}\mathit{to}\text{-}\mathit{finish}\hfill \end{array}$$

We take $o\Vert o^{\prime }$ to be commutative.

In Section 4, we used these syntax elements as follows:

• ♭ in Section 4.1.
• $o_v$ and $o•\to -•o^{\prime }$ throughout Section 4.
• $o\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m^{\prime }\end{array}{o}^{\prime }$ in Section 4.3.
• $\forall (o\Vert o^{\prime })$ in Section 4.6 and Section 4.7.
• $\exists (o\Vert o^{\prime })$ in Section 4.7.

Definition 2.

The evaluation contexts $\mathcal{C}$ of an outcome are defined as follows:

$$\mathcal{C}::=[ ]|\mathcal{C}•\to -•o|o•\to -•\mathcal{C}|\mathcal{C}\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m^{\prime }\end{array}o|o\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m^{\prime }\end{array}\mathcal{C}|\forall (\mathcal{C}\Vert o)|\exists (\mathcal{C}\Vert o).$$

where “$[ ]$” is the empty context.

Evaluation contexts are useful in the definition of outcome transitions, which we define next.

Definition 3.

Outcome transitions ${\tau }_o:o\to o^{\prime }$ are defined by the following rewrite rules:

$$\begin{array}{ccc}\mathcal{C}[♭]\to \mathcal{C}\left[o\right]\hfill & o\notin \mathbb{B}\hfill & \left(\mathrm{U}\mathrm{NBX}\right)\hfill \\ \mathcal{C}\left[o_v\right]\to \mathcal{C}\left[o\right]\hfill & o\notin \overline{\mathbb{B}}\hfill & \left(\mathrm{E}\mathrm{LAB}\right)\hfill \\ \mathcal{C}\left[o\right]\to \mathcal{C}\left[o^{\prime }\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m^{\prime }\end{array}{o}^{″}\right]\hfill & \mathit{for}\mathit{some}m,m^{\prime }\in {\mathbb{R}}^{+},o^{\prime },o^{″}\in \mathbb{O}\hfill & \left(\mathrm{P}\mathrm{ROB}\right)\hfill \\ \mathcal{C}\left[o\right]\to \mathcal{C}[\forall (o^{\prime }\Vert o^{″})]\hfill & \mathit{for}\mathit{some}{o}^{\prime },o^{″}\in \mathbb{O}\hfill & \left(\mathrm{A}2\mathrm{F}\right)\hfill \\ \mathcal{C}\left[o\right]\to \mathcal{C}[\exists (o^{\prime }\Vert o^{″})]\hfill & \mathit{for}\mathit{some}{o}^{\prime },o^{″}\in \mathbb{O}\hfill & \left(\mathrm{F}2\mathrm{F}\right).\hfill \end{array}$$

Formally speaking, a refinement step is an instance of an outcome transition. The formal description of the system is refined when one or more refinement steps are taken.

The restriction on (Unbx) is because it makes no sense to replace a black box with another black box. (See the trailing discussion of Section 3.1 on the intention behind black boxes.) The restriction on (Elab) is because it makes no sense for an outcome variable to be replaced by another outcome variable or a black box.

Considering Definition 3 to be part of the syntax is unusual. After all, evaluation contexts are a formalism for the semantics of programming languages. However, for $\Delta \mathrm{Q}$SD, it turns out that the rewrites only cause syntactic changes to the outcome expressions (and the corresponding diagrams). Note that a refinement is not a system evolution, but rather, an update in the system description. It is only at analysis time that one tries to understand the meaning of an outcome diagram/expression.

5.3. Timeliness Analysis

We are now ready to describe the process of $\Delta \mathrm{Q}$ analysis. The idea is that the design engineer provides the basic $\Delta \mathrm{Q}$ analysis to the formulation in Definition 4. Then, our formulation enables them to determine the $\Delta \mathrm{Q}$ analysis of the larger parts of their system or even all of it. This formulation is both compositional and simple. We call the $\Delta \mathrm{Q}$ analysis that is provided by the design engineer the basic ($\Delta \mathrm{Q}$) assignment (Definition 4). In the basic assignment, the design engineer only maps $\overline{\mathbb{B}}$ expressions. They map those expressions to either CDFs or $\Delta \mathrm{Q}$ variables. In return, they receive more complex $\Delta \mathrm{Q}$ expressions. This is shown in Figure 18. The process is similar for load analysis except that there, the values exchanged between the design engineer and the respective formulation refer instead to static amounts of work.

The reason for including the CDFs in the input type of basic assignments is rather obvious. The choice to allow $\Delta \mathrm{Q}$ variables here might be less so. The assignment of those $\overline{\mathbb{B}}$ expressions that are mapped to $\Delta \mathrm{Q}$ variables are considered to be left by the design engineer for later. As such, the formulation in Definition 4 takes the $\Delta \mathrm{Q}$ value of those expressions to be ⊤, which lets the design engineer investigate feasibility even when those particular expressions are disregarded for the moment.

Fix a set $\Gamma \ni \gamma$ of all CDFs. Fix also a countable set of $\Delta \mathrm{Q}$ variables ${\Delta }_v\ni {\delta }_v$. Let $\Delta ={\Delta }_v\cup \Gamma$, where $\Delta \ni \delta$.

Definition 4.

Given a basic assignment ${\Delta }_{\circ }⟦.⟧:\overline{\mathbb{B}}\to \Delta$, define $\Delta \mathrm{Q}{[.]}_{{\Delta }_{\circ }}:\mathbb{O}\to \Gamma$ such that

$$\begin{array}{cc}\Delta \mathrm{Q}{⟦\beta ⟧}_{{\Delta }_{\circ }}\hfill & =\left\{\begin{array}{cc}\top \hfill & \mathit{when}{\Delta }_{\circ }⟦\beta ⟧\notin \Gamma \hfill \\ {\Delta }_{\circ }⟦\beta ⟧\hfill & \mathit{otherwise}\hfill \end{array}\right.\hfill \\ \Delta \mathrm{Q}{⟦o•\to -•o^{\prime }⟧}_{{\Delta }_{\circ }}\hfill & =\Delta \mathrm{Q}{⟦o⟧}_{{\Delta }_{\circ }}\ast \Delta \mathrm{Q}{⟦o^{\prime }⟧}_{{\Delta }_{\circ }}\hfill \\ \Delta \mathrm{Q}{⟦o\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m\end{array}{o}^{\prime }⟧}_{{\Delta }_{\circ }}\hfill & =\frac{m}{m+m^{\prime }}\Delta \mathrm{Q}{⟦o⟧}_{{\Delta }_{\circ }}+\frac{m^{\prime }}{m+m^{\prime }}\Delta \mathrm{Q}{⟦o^{\prime }⟧}_{{\Delta }_{\circ }}\hfill \\ {\Delta \mathrm{Q}⟦\forall (o\Vert o^{\prime })⟧}_{{\Delta }_{\mathrm{o}}}\hfill & {=\Delta \mathrm{Q}⟦o⟧}_{{\Delta }_{\circ }}{\times \Delta \mathrm{Q}⟦o^{\prime }⟧}_{{\Delta }_{\circ }}\hfill \\ {\Delta \mathrm{Q}⟦\exists (o\Vert o^{\prime })⟧}_{{\Delta }_{\circ }}\hfill & {=\Delta \mathrm{Q}⟦o⟧}_{{\Delta }_{\circ }}{+\Delta \mathrm{Q}⟦o^{\prime }⟧}_{{\Delta }_{\circ }}{-\Delta \mathrm{Q}⟦o⟧}_{{\Delta }_{\circ }}\times {\Delta \mathrm{Q}⟦o^{\prime }⟧}_{{\Delta }_{\circ }}\hfill \end{array}$$

where ∗ denotes the convolution of two $\Delta \mathrm{Q}s$. We denote the set of all basic assignments by {${\Delta }_{\circ }⟦.⟧$}.

We demonstrated the use of this definition in Section 4.2. In programming language theory, Definition 4 is said to give a denotational semantics for $\mathbb{O}$. This is because the formulation works by compositionally denoting the $\mathbb{O}$ syntax into a familiar domain, which is deemed to be simpler (in our case, it is Γ). Definition 4 gives the design engineer the possibility of determining the $\Delta \mathrm{Q}$ behaviour of a snapshot of their system. Armed with that information, the design engineer needs to figure out whether such $\Delta \mathrm{Q}$ behaviour is affordable. In other words, they need to make sure the actual $\Delta \mathrm{Q}$ is within the acceptable bounds. In order to do that, we assume that the design engineer’s customer will provide them with a demand CDF: one that defines the acceptable bounds. Definition 5 below is a recipe for comparing the actual behaviour against a demand CDF.

Definition 5.

Given a demand CDF γ and a partial order < on $\Gamma$, say that a basic assignment ${\Delta }_{\circ }$ is a witness that an outcome o is a hazard w.r.t. γ

$${\Delta }_{\circ }{\vDash }_{<}{\mathsf{hazard}}_{\gamma }\left(o\right)$$

when

$$\Delta \mathrm{Q}{⟦o⟧}_{{\Delta }_{\circ }}\nless \gamma .$$

Likewise, say ${\Delta }_{\circ }$ is a witness that an outcome o has slack once compared with γ

$${\Delta }_{\circ }{\vDash }_{<}{\mathsf{slack}}_{\gamma }\left(o\right)$$

when

$$\Delta \mathrm{Q}{⟦o⟧}_{{\Delta }_{\circ }}<\gamma .$$

The formulation of Definition 5 enables the design engineer to perform the $\Delta \mathrm{Q}$ analysis of a single snapshot of their system. In some cases, that is enough because it can, for example, reveal the absolute infeasibility of a design. However, for the majority of cases, it is not enough. After all, a snapshot $\Delta \mathrm{Q}$ analysis might not be conclusive for a variety of reasons. For example, one might not see any indication of a hazard by employing just Definition 5 because more detail is required. That takes us to Definition 8. When a design engineer works out the $\Delta \mathrm{Q}$ analysis of a snapshot, the results might be favourable at the given level of refinement but still inaccurate. In such a case, a design engineer may wish to refine the system and perform the snapshot $\Delta \mathrm{Q}$ again to check whether the refinement confirms the initial $\Delta \mathrm{Q}$ analysis. Definition 8 examines that overall confirmation. Definitions 6 and 7 set the stage.

Definition 6.

Let ${\Delta }_{\circ }$ be a basic assignment. Write

$$D_{\Gamma }\left({\Delta }_{\circ }\right)=\{\beta \in \overline{\mathbb{B}}|{\Delta }_{\circ }\left(\beta \right)\in \Gamma \}$$

for those $\overline{\mathbb{B}}$ outcomes in the domain of ${\Delta }_{\circ }$ that ${\Delta }_{\circ }$ maps to CDFs.

Definition 7.

Say ${\Delta }_{\circ }^{\prime }$ refines ${\Delta }_{\circ }$ (write ${\Delta }_{\circ }{\to }_{\Delta }{\Delta }_{\circ }^{\prime }$) when

• $D_{\Gamma }\left({\Delta }_{\circ }\right)\subseteq D_{\Gamma }\left({\Delta }_{\circ }^{\prime }\right)$;
• $\forall \beta \in D_{\Gamma }\left({\Delta }_{\circ }\right).{\Delta }_{\circ }\left(\beta \right)={\Delta }_{\circ }^{\prime }\left(\beta \right)$.

In such a case, call ${\Delta }_{\circ }{\to }_{\Delta }{\Delta }_{\circ }^{\prime }$ a $\Delta \mathrm{Q}$ refinement. When clear, we will replace ${\to }_{\Delta }$ by →.

In other words, a basic assignment refines another one when it keeps all the CDFs in place and possibly adds more. We are now ready for Definition 8.

Definition 8.

Fix an outcome transition $o\to o^{\prime }$ and a $\Delta \mathrm{Q}$ refinement ${\Delta }_{\circ }\to {\Delta }_{\circ }^{\prime }$. Given a partial order < on $\Gamma$, we say that ${\Delta }_{\circ }\to {\Delta }_{\circ }^{\prime }$ witnesses that $o\to o^{\prime }$ arms a hazard

$${\Delta }_{\circ }\to {\Delta }_{\circ }^{\prime }{\vDash }_{<}{\mathsf{hazard}}_{}(o\to o^{\prime })$$

when $\Delta \mathrm{Q}{⟦o⟧}_{{\Delta }_{\circ }}\nless \Delta \mathrm{Q}{⟦o^{\prime }⟧}_{{\Delta }_{\circ }^{\prime }}$. Likewise, say ${\Delta }_{\circ }\to {\Delta }_{\circ }^{\prime }$ witnesses that $o\to o^{\prime }$ leaves the system slack

$${\Delta }_{\circ }\to {\Delta }_{\circ }^{\prime }{\vDash }_{<}{\mathsf{slack}}_{}(o\to o^{\prime })$$

when $\Delta \mathrm{Q}{⟦o⟧}_{{\Delta }_{\circ }}<\Delta \mathrm{Q}{⟦o^{\prime }⟧}_{{\Delta }_{\circ }^{\prime }}$.

As can be seen from Definitions 5 and 8, all the decisions for the timeliness analysis are made by scrutinising the CDFs (which represent $\Delta \mathrm{Q}$ values). This is a consequence of the simple denotational semantics of Definition 4. The fact that the latter formalism is denotational implies that comparisons can be made in the domain of CDFs. Moreover, these comparisons are affordable because the denotational semantics is simple (as well as being effective).

5.4. Load Analysis

This section describes how the same approach can be used to analyse the load on given resources. Resources can be of different types; in particular, we distinguish ephemeral resources that are available at a certain rate and fixed resources that are available in a fixed number or amount. Examples of ephemeral resources are CPU cycles, network interface capacity, and disk IO operations. Fixed resources include CPU cores, memory capacity, and disk capacity. In this paper, we consider only ephemeral resources. The analysis that we want is an answer to the following question: will the resource manage the amount of work assigned to it in the available time frame?

We first need to set up some terminology for specifying the available time frame as well as the amount of work that is assigned to a given resource. Write $t^{\circ }\left(o\right)$ for the time an observable from the starting set of an outcome o occurs. Let $t^{\infty }\left(o\right)=t^{\circ }\left(o\right)+d\left(o\right)$, where $d\left(o\right)$ denotes the duration limit of o. Fix a set of resources $\mathbb{H}\ni \rho$. Note that the amount of work that is assigned to a resource ρ is not scalar. Of course, it is necessary to provide the unit of measurement. For example, when ρ represents CPU resources, a sensible unit of measurement is the number of CPU cycles. When ρ represents network resources, a sensible unit of measurement is the message size. However, at the current level of formalisation, we wish to set ourselves free from thinking about units of measurement. Therefore, given a resource ρ, we write $W_{\rho }$ for the set of values of the right unit of measurement for an amount of work that has been assigned to ρ.

The design engineer utilises our load analysis in the same way that they utilise our $\Delta \mathrm{Q}$ analysis. That is, they must provide some basic load analysis (Definition 9). Then, exactly as shown in Figure 18, they use the formulation in Definition 10 to determine the load analysis for larger parts of their system or possibly all of it. We now formalise what we mean by a basic load analysis.

Definition 9.

For a given ρ, a basic “static (amount of) work assignment for ρ” is a function:

$$\rho \Vert \stackrel{W}{—}{S}_{\circ }⟦.⟧:\overline{\mathbb{B}}\to W_{\rho }.$$

Definition 10.

Given a basic static work assignment $S_{\circ }$ for ρ, the static work assignment (i.e., the amount of work to perform a single outcome per unit of size)

$$\rho \Vert \stackrel{W}{—}⟦.⟧S_{\circ }(.):\mathbb{O}\to T\to W_{\rho }$$

(where T stands for time) is defined as

$$\begin{array}{cc}\rho \Vert \stackrel{W}{—}S{⟦\beta ⟧}_{S_{\circ }}\left(t\right)=\rho \Vert \stackrel{W}{—}{S}_{\circ }⟦\beta ⟧\hfill & \hfill t\in [t^{\circ }\left(o\right),t^{\infty }\left(o\right)]\\ \rho \Vert \stackrel{W}{—}S{⟦o•\to -•o^{\prime }⟧}_{S_{\circ }}\left(t\right)=\left\{\begin{array}{c}\rho \Vert \stackrel{W}{—}S{⟦o⟧}_{S_{\circ }}\left(t\right)\hfill \\ \rho \Vert \stackrel{W}{—}S{⟦o^{\prime }⟧}_{S_{\circ }}\left(t\right)\hfill \end{array}\right.\hfill & \hfill \begin{array}{c}\hfill t\in [t^{\circ }\left(o\right),t^{\infty }\left(o\right))\\ \hfill t\in [t^{\circ }\left(o^{\prime }\right),t^{\infty }\left(o^{\prime }\right)]\end{array}\\ \rho \Vert \stackrel{W}{—}S{⟦o\begin{array}{c}m\\ {\displaystyle \leftrightharpoons }\\ m^{\prime }\end{array}{o}^{\prime }⟧}_{S_{\circ }}\left(t\right)=\frac{m}{m+m^{\prime }}\times \rho \Vert \stackrel{W}{—}S{⟦o⟧}_{S_{\circ }}\left(t\right)+\frac{m^{\prime }}{m+m^{\prime }}\times \rho \Vert \stackrel{W}{—}S{⟦o^{\prime }⟧}_{S_{\circ }}\left(t\right)\hfill & \\ \multicolumn{2}{c}{t\in [min(t^{\circ }\left(o\right),t^{\circ }\left(o^{\prime }\right)),max(t^{\circ }\left(o\right),t^{\circ }\left(o^{\prime }\right))]}\\ \rho \Vert \stackrel{W}{—}S{⟦\forall (o\Vert o^{\prime })⟧}_{S_{\circ }}\left(t\right)=\hfill & \\ \rho \Vert \stackrel{W}{—}S{⟦\exists (o\Vert o^{\prime })⟧}_{S_{\circ }}\left(t\right)=\rho \Vert \stackrel{W}{—}S{⟦o⟧}_{S_{\circ }}\left(t\right)+\rho \Vert \stackrel{W}{—}S{⟦o^{\prime }⟧}_{S_{\circ }}\left(t\right)\hfill \\ \multicolumn{2}{c}{t\in [min(t^{\circ }\left(o\right),t^{\circ }\left(o^{\prime }\right)),max(t^{\circ }\left(o\right),t^{\circ }\left(o^{\prime }\right))].}\end{array}$$

Whether or not a given resource ρ is overloaded when performing an outcome o is determined by whether ρ can bear the offered load in the required duration, $d\left(o\right)$. The smaller that $d\left(o\right)$ is, the faster (i.e., the more intensely) o must be performed. However, that can only be done up to a certain threshold that is determined by the system’s configuration. In other words, whether the intensity brought to ρ passes a given threshold is what determines whether ρ is overloaded. As with $W_{\rho }$, at our current level of abstraction, we wish to disregard the units of measurement for intensity. That is, we write $I_{\rho }$ for the set of values of the right unit of measurement for the intensity of the load that is imposed on ρ. We single out ${\theta }_I\left(\rho \right)\in I_{\rho }$ for the threshold of intensity ρ can bear. When it is clear, we write ${\theta }_I$ for ${\theta }_I\left(\rho \right)$.

Definition 11.

For a fixed ρ, given a threshold of intensity ${\theta }_I\left(\rho \right)$ and a basic static work assignment $S_{\circ }$ for ρ, the static slack of an outcome in ρ-consumption:

$$S_{\circ }{\vDash }_{\rho }{\mathsf{slack}}_{{\theta }_I}(.):\mathbb{O}\to T\to I_{\rho }$$

is defined as

$$S_{\circ }{\vDash }_{\rho }{\mathsf{slack}}_{{\theta }_I}\left(o\right)={\theta }_I-\frac{\rho WS{⟦o⟧}_{S_{\circ }}}{d\left(o\right)}.$$

Define the static hazard of an outcome in ρ-consumption:

$$S_{\circ }{\vDash }_{\rho }{\mathsf{hazard}}_{{\theta }_I}\left(o\right)=-S_{\circ }{\vDash }_{\rho }{\mathsf{slack}}_{{\theta }_I}\left(o\right).$$

Our emphasis on considering the analyses of Definitions 9–11 “static” is intentional. Firstly, they all assume that a base outcome’s work is spread uniformly over its duration limit. That is obviously not always correct. The work assignment typically varies over the duration limit. However, if to every base outcome β, the design engineer chooses to assign the highest amount of work that β needs to do during its duration limit, the analyses given in Definition 11 would lead to a safe upper bound, which is useful as a first estimate. Secondly, Definitions 9–11 assume that an outcome’s amount of work is always the same throughout its execution. Again, that is not realistic. Various reasons might cause the amount of work assigned to a base outcome to change over time. Examples are congestion, nonlinear correlations between outcomes, and cascading effects. This suggests more advanced load analyses that are “dynamic” rather than the “static” ones we have described here. We leave the development of such analyses to future work.

6. Related Work

Several theoretical or practical approaches have previously been proposed that address parts of the problem that has been identified above, but none of these addresses the whole problem in a comprehensive way.

6.1. Alternative Theoretical Approaches

6.1.1. Queuing Theory

Steady-state performance has been widely studied as an aid to analysis, for example in queuing theory. Such approaches tend to take a resource-centric view of the system components, focusing on their individual utilisation/idleness. Where job/customer performance is considered, such as in mean-value analysis [20] or Jackson/BCMP networks [21], it is also in the context of steady-state averages. However, these traditional approaches cannot deliver metrics such as the time distribution of the system’s response to an individual stimulus or even the probability that such a response will occur within a given time bound. These metrics are key for any time-critical and/or customer-experience-centric service.

6.1.2. Extending Existing Modelling Approaches

With the exception of hard real-time systems, it is rare to see performance treated as a “first-class citizen” in a system design process. At best, performance is considered as a property that will emerge during the system development life-cycle and thus something that can only be retrospectively validated. Thus, in contrast with $\Delta \mathrm{Q}$SD, performance is unverifiable when using such an approach.

A common approach has been to extend existing approaches to modelling distributed systems such as Petri nets or process calculi with the goal of integrating performance modelling. Examples include stochastic Petri nets [22], timed and probabilistic process calculi [23,24], and performance evaluation process algebra (PEPA) [25]. These systems consider passage-time [26], which is the time taken for the system to follow a particular path to a state, that path being characteristic of an outcome of interest [27,28,29,30]. As mentioned above, these are all retrospective validation tools, requiring fully specified systems, that will give probabilistic measures of outcomes under steady-state assumptions. These systems are susceptible to state space explosion as a model grows in complexity, and therefore, this limits their usage to less complex systems. Furthermore, as with queuing models, they do not model failure nor do they model typical real-world responses to failure such as timeouts and retries.

6.1.3. Real-Time Systems and Worst-Case Execution Time

In real-time systems, actions must be completed by strict deadlines. Missed deadlines can be catastrophic (hard real-time systems) or lead to significant delay and loss caused by roll-backs or recovery (soft real-time systems). Performance analysis has focused on giving guarantees that deadlines can be met by studying worst-case execution time [31]. These approaches generally aim to analyse the behaviour of specific implementations, providing information about specific interactions. Thus, this approach is complementary to design-time approaches such as $\Delta \mathrm{Q}$SD.

6.2. Block Propagation

Bitcoin’s block propagation has been measured by Decker and Wattenhofer [32] and later by Croman et al. [33], who proposed guidelines on block size and interval to ensure adequate throughput for 90% of nodes. Shahsavari et al. [34] propose a random graph model for modelling the performance of block propagation. The recent survey article of Dotan et al. [35] covers block propagation (Section 3) and the mapping of blockchain networks.

6.3. Distributed System Design

Designing large distributed systems is costly and error-prone. This might seem paradoxical given the proliferation of modern Internet-based companies whose core business is based on large distributed systems, such as Google, Facebook, Amazon, Twitter, Netflix, and many others. Given the existence of these successful companies, it might seem that building large distributed systems is a solved problem. It is not: successful companies have built their systems over many years, using vast amounts of effort and ingenuity to find usable solutions to difficult problems. Unsuccessful companies are forgotten.

6.3.1. Iterative Design

There does not exist a standard approach for designing large distributed systems that allows prediction of high-load performance early on during the design process. We explain the problem by giving an overview of the current design approach for distributed systems. The approach is iterative. It starts with a specification of the system’s desired performance and scale. Then, the system architecture is designed by determining the system components according to the system’s scale and estimating the performance they must have to give the required overall performance. The next step is performance validation to verify that the design satisfies the performance requirements.

Performance validation is performed either as part of unit, subsystem, and/or system testing or via discrete-event simulation. Testing the performance of a component or subsystem is inconclusive without a reliable means to relate it to the resulting system performance, and testing of the whole system only reveals issues very late in the system development life-cycle. It is good practice to perform integration testing at this late stage. However, this is a poor and expensive substitute for performance analysis throughout the development process. Simulation can be performed earlier in the development process, and it may be less costly than testing, but it is limited in its ability to expose rare cases and hence cannot test tight bounds on the performance.

In the final analysis, obtaining reliable performance numbers at high load requires actually building a large part of the final system and subjecting it to a realistic load. If the system does not satisfy the requirements, then it is back to the drawing board. The system architecture is redesigned to remove observed and predicted bottlenecks and rebuilt.

Several iterations of the design may be necessary until the system behaves satisfactorily. It often happens that the system only behaves satisfactorily at a fraction of the required load, but because of market constraints, this is considered acceptable, and the system is deployed. In parallel to the deployment, the design engineers continue to work on a system that will accept the larger load under the assumption that the deployment will be successful so that the load will increase.

This methodology is workable, but it is highly risky due to its high cost and development time. To have a good chance of success, it requires experienced developers. The development budget may be exhausted before achieving a satisfactory system; it may even be determined that the requirements are impossible to satisfy (infeasibility). If this is discovered early on, then the company may be able to retarget itself to become viable. Otherwise, the company simply folds.

6.3.2. Role of the $\Delta \mathrm{Q}$SD Paradigm in Distributed System Design

The $\Delta \mathrm{Q}$SD paradigm is designed specifically to reduce cost and development time. The system is designed as a sequence of increasingly refined outcome diagrams. At each stage, performance is computed using the $\Delta \mathrm{Q}$ parameters. If the system is infeasible, this is detected early on, and it is immediately possible to change the design. If the design has sufficient slack, then the design process continues. The $\Delta \mathrm{Q}$SD paradigm is effective insofar as the $\Delta \mathrm{Q}$ computations provide realistic results. This depends on (i) having correct $\Delta \mathrm{Q}$ distributions for the basic components and (ii) correctly specifying causality and resource constraints. Experience with $\Delta \mathrm{Q}$SD in past industrial designs gives us confidence in the validity of the results. The additional rigour that is provided by the $\Delta \mathrm{Q}$SD formalism that has been introduced in this paper gives us confidence that the paradigm is being applied correctly and allows the paradigm to be integrated into new design tools.

6.4. Programming Languages and Software Engineering

6.4.1. Programming Paradigms

Programming paradigms each focus on their particular discipline for bringing more opportunities for code reuse. The most familiar examples are perhaps Object-Oriented Programming, Functional Programming, and Genericity by Type, which promote code-reuse between a base class and derived ones by refactoring into functions and type parameterisation. Gibbons [36] has an excellent survey on different flavours of Generic Programming with the different opportunities for code reuse that each provides. Some programming paradigms have widely accepted formalisms, and some do not. Regardless of the underlying programming paradigm, $\Delta \mathrm{Q}$SD is a paradigm for systems development rather than simply for programming, and it comes with its own formalism.

6.4.2. Software Development Paradigms

Three paradigms focus on the process of software development and hence are closer to $\Delta \mathrm{Q}$SD:

• Design-by-Contract. [37] Similarly to $\Delta \mathrm{Q}$SD, in this paradigm, the programmer begins by coding by describing the pre-conditions and the post-condition. Over the years, the concept of refining initial designs from specification to code has gained increasing weight [38]. However, unlike $\Delta \mathrm{Q}$SD, the focus is on functional correctness rather than performance.
• Software Product Lines. [39] This paradigm targets families of software systems that are closely related and that clearly share a standalone base. The aim is to reuse the development effort of and the code for the base across all the different variations in the family. The similarity with $\Delta \mathrm{Q}$SD is that this approach also allows variation in the implementation so long as the required quality constraints are met. In other words, variations can share a given expected outcome and its quality bounds.
• Component-Based Software Engineering. [40] Components, in this paradigm, are identified by their so-called ‘requires’ and ‘provides’ interfaces. That is, so long as two components have the same ‘requires’ and ‘provides’ interfaces, they are deemed equivalent in this paradigm, and they can be used interchangeably. In $\Delta \mathrm{Q}$SD, subsystems can also have quality contracts that involve quantitative ‘demand’ and ‘supply’ specifications. Such contracts impose quality restrictions (say, timeliness or pattern of consumption) on the respective outcomes of those subsystems. However, we have not shown examples of quality contracts in this paper, because their formalisation is not yet complete.

6.4.3. Algebraic Specification and Refinement

Algebraic specification languages such as CLEAR [41], Extended ML [42], Institutions [43], and CASL [44] work on the basis of specifying requirements using algebraic signatures and equations that are then refined progressively until one makes it to the level of actual code. Refinement in such languages is managed using various media, for example by module systems with rigorously defined formal semantics. Whilst the focus of such languages is almost exclusively on functional correctness, studying possibilities for enhancing algebraic specifications so that they also accommodate the quality of outcomes would be an interesting avenue for future work.

6.4.4. Amortised Analysis

Amortised resource analysis is an approach for promoting resource analysis as a first-class citizen of programming languages specification. Various operational semantics, type systems, and category theoretical approaches have been employed. See [45,46,47], for example, where memory consumption for functional languages such as HASKELL and ML are automatically calculated for programs written in those languages. $\Delta \mathrm{Q}$SD advises on specification at the much higher level of outcomes and outcome diagrams, leaving the actual implementation and its host language completely unconstrained. As a result, $\Delta \mathrm{Q}$SD is much more flexible and permits rapid performance estimation throughout the system development life-cycle.

7. Conclusions

This paper has presented the $\Delta \mathrm{Q}$SD systems development process that is driven by performance predictability concerns and is supported by a rigorous formalism (Section 5). Our formalism builds on the simple concept of quality attenuation ($\Delta \mathrm{Q}$, Section 3.3) that captures the notion of performance hazard. This helps early detection of infeasibility, thus preventing the waste of resources (financial, people, time, and systems).

$\Delta \mathrm{Q}$SD has been successfully used in a wide range of industries, including telecommunications, avionics, space and defence, and cryptocurrency. It complements other approaches that are focused primarily on functional concerns, such as functional programming or model checking.

Our formalisation of $\Delta \mathrm{Q}$SD is a part of a wider initiative both within Predictable Network Solutions and IO Global [9]. In particular, it has been applied to the development of the current iteration of the Cardano blockchain, which uses a proof-of-stake (PoS) consensus algorithm rather than the proof-of-work (PoW) approach used by most other blockchains, including Bitcoin. PoS algorithms have significant advantages over PoW, such as vastly better energy efficiency and the potential to deliver much higher performance, both in terms of processing transactions and embedding them more rapidly in the immutable chain. However, for this to work, blocks must be diffused within a predictably short time-frame across a globally distributed system with no central control so that the chain can be most efficiently extended. Only by using $\Delta \mathrm{Q}$SD was the Cardano engineering team able to untangle this knot to deliver a secure and efficient system.

$\Delta \mathrm{Q}$SD is based on taking the observable outcomes of a system as the central point of focus (Section 3.1), capturing the causal dependencies between outcomes in the form of outcome diagrams (Section 3.2). The formalism also describes the process of refining outcome diagrams (Definition 7) as part of a system design process. The formal specification of a system serves as a basis for different analyses such as timeliness (Section 5.3) and behaviour under load (Section 5.4). Although we have illustrated the $\Delta \mathrm{Q}$SD paradigm in the context of design refinement, the aim is that these aspects should permeate throughout the complete system development life-cycle.

7.1. Takeaways for System Designers

Let us summarise the main insights of the $\Delta \mathrm{Q}$SD paradigm for the system designer. The main new concept is focus on performance as determined by observations, which are captured using outcome diagrams. Designing with outcome diagrams allows problems to be discovered early on in the design process, which saves time and reduces cost. We are working on tools and documentation to disseminate the $\Delta \mathrm{Q}$SD paradigm in the system design community.

7.1.1. Outcome Diagrams

The outcome diagram defines a system in terms of what is observable from the outside (of the (sub)system under consideration), whereas traditional approaches such as UML (discussed in Section 3.5.1) all describe what is inside the system. A major advantage of this approach is that it avoids making decisions prematurely on how the system should be built. Outcome diagrams allow infeasibility to be discovered early on, avoiding costly dead ends and reducing time-to-market. On the other hand, all these advantages do not come for free. The main difficulty of using $\Delta \mathrm{Q}$SD is psychological: some decisions on the actual system structure have to be “kept in the air” for long periods as the designer works with outcome diagrams. This can conflict with the natural urge to make decisions at the earliest opportunity and the often-imposed requirement to demonstrate ‘progress’. Quantifying design risks is rarely understood as progress, although this is often the most valuable part of the entire design process. Outcome diagrams provide a framework for ‘rigidly defined areas of doubt and uncertainty’ [48], enabling such value to be evidenced.

7.1.2. Design Example

Figure 19 compares $\Delta \mathrm{Q}$SD with a traditional approach. The figure shows a design tree. Each nonleaf node corresponds to one design decision. The design starts at the root and continues down the tree until it reaches a leaf node, which corresponds to a completely designed system. The subtree outlined on the left contains all designs where decision $D_x$ took the leftmost branch. In our case, all these designs are infeasible. In $\Delta \mathrm{Q}$SD, this fact would be detected immediately after the $D_x$ decision is made by observing that the quality attenuation required from any subsequent refinement is infeasibly small, for instance less than the time taken for signals to move between components of the distributed system. Using an approach based on refining the system’s structure, such as a UML-based approach, would require specifying much more of the system before this fact became evident. In many cases, it can only be seen by actually building the system and checking that it cannot satisfy the requirements. With $\Delta \mathrm{Q}$SD, the cost of designing and building all these infeasible systems is saved. This example summarises the actual experience of Predictable Network Solutions (PNSol) in many industrial projects.

7.1.3. Recommendations

We recommend that you think about how the two main concepts of $\Delta \mathrm{Q}$SD, outcomes and quality attenuation, can apply to your own work. Try to express one of your own designs in terms of the outcomes that a user sees without making any decisions about how the system is built. Instead of describing the system structure, as UML does, try to think only of externally visible outcomes. The blockchain example of Section 4 gives a realistic example of how this is done. Note that in practice, we expect that a software tool would do all the tedious bookkeeping needed to keep track of the outcome diagrams.

To design a system, start from the outcomes that the user expects, and work your way in from there. A primary outcome, such as a request–reply, can be divided into smaller outcomes. Bigger outcomes decompose into smaller ones, either by sequencing small outcomes, by creating a choice between small outcomes, or by synchronising on small outcomes. Eventually, you get to primitive outcomes that can be directly provided by components, such as networks, servers, or databases. At any time, you can combine the quality attenuation of small outcomes to get the quality attenuation of a bigger outcome. This means that you can start answering questions immediately, even if the system is only partially designed. The main question is, is the system feasible? In other words, is there a probability close to 1 that the reply returns with an acceptable delay? For cutting-edge systems, the answer to this question might be ‘no’. In that case, you need to step back and build an alternative outcome decomposition.

7.2. Limitations of the $\Delta \mathrm{Q}$SD Paradigm

There are two main limitations of the work that has been described here.

• Contextuality vs. Compositionality:As a performance modelling tool, $\Delta \mathrm{Q}$SD deliberately trades detail in exchange for compositionality. The highest level of detail is provided by timed traces of a real system or a discrete event simulation thereof. A level of abstraction is provided by the use of generator functions [49], which obscure some details such as data-dependency but retain the local temporal context. Representing behaviour using random variables removes the temporal context, treating aspects of the system as Markovian. Thus, the $\Delta \mathrm{Q}$SD paradigm is most applicable to systems that execute many independent instances of the same action, such as diffusing blocks, streaming video frames, or responding to web requests. For systems that engage in long sequences of highly dependent actions, it may only deliver bounding estimates.
• Non-linearity: In many systems, resource sharing may introduce a relationship between load and $\Delta \mathrm{Q}$, which can be incorporated in to the analysis. An obvious example is a simple queue (which is ubiquitous in networks), where the delay/loss is a function of the applied load. However, where system behaviour introduces a further relationship between $\Delta \mathrm{Q}$ and load, for example due to timeouts and retries, the coupling becomes non-linear. In this case, a satisfactory performance analysis requires iterating to a fixed point, which may not be forthcoming. Failure to find a fixed point can be considered a warning that the performance of the system may be unstable.

7.3. Future Work

The $\Delta \mathrm{Q}$SD paradigm has been developed for over 30 years by a small group of people in and around PNSol, and it has shown its value in large-scale industrial projects. It has matured enough that it should be more widely known. Unfortunately, applying it today requires a high level of commitment and effort, because there is no tool support and little documentation. The ultimate goal of our work is to make it usable with much less effort; this paper takes the first step by defining a formal framework for outcome diagrams. Ideally, the system designer will mostly need domain expertise to apply $\Delta \mathrm{Q}$SD and very little expertise in the paradigm itself. To achieve this goal, we are working towards building tools to handle most of the details of creating outcome diagrams and computing quality attenuation.

The immediate next step after this paper is a tutorial on $\Delta \mathrm{Q}$SD given at the HiPEAC conference in June 2022 [50]. This tutorial will give a broad introduction to the use of $\Delta \mathrm{Q}$SD through a variety of practical examples that come from PNSol’s experience. That will help the adaptation of $\Delta \mathrm{Q}$SD by other practitioners and therefore will help us with further tuning of the $\Delta \mathrm{Q}$SD tool we are currently developing.

Future work will also include the development of new analyses for non-ephemeral resources and for dynamic loads as well as an extension to non-linear systems in which the load and timeliness are coupled. In parallel, we plan to use our formalism as an intermediate step to better teaching and dissemination of $\Delta \mathrm{Q}$SD.

We will build additional tools that will enable us to track the key observables/outcomes from the design into the implementation so that they can support ongoing system design and development throughout the system development life-cycle. Given appropriate tools, it would become feasible to systematically articulate the benefits of the paradigm, for instance by comparing various metrics between design projects that do or do not use it, such as the time/budget to compete the project, number of major design changes, etc. This line of research would require new collaborators with expertise in social science disciplines.

The wider $\Delta \mathrm{Q}$ framework is also under active development within the International Broadband Forum [51] as a means of characterising quality attenuation associated with networks.