Tumor–Stroma Ratio in Colorectal Cancer—Comparison between Human Estimation and Automated Assessment
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Segmentation Dataset with Pixel-Wise Annotations
2.1.2. Survey Dataset
2.2. Segmentation Methods
2.3. Training
2.4. Evaluation Protocols
2.4.1. Pixel-Wise Evaluation of Segmentation Approaches
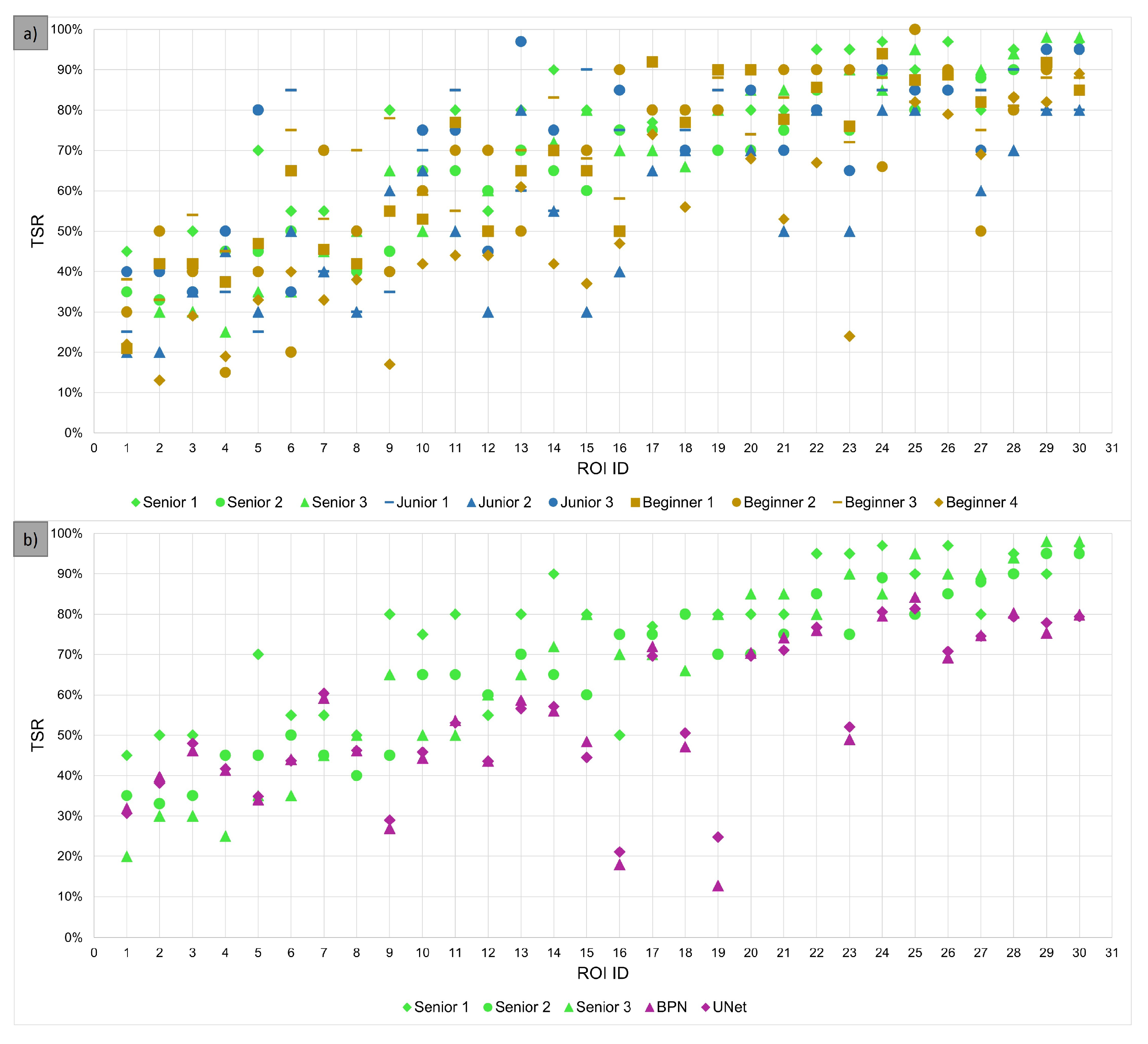
2.4.2. Comparison between Human Estimation and Automated TSR Assessment
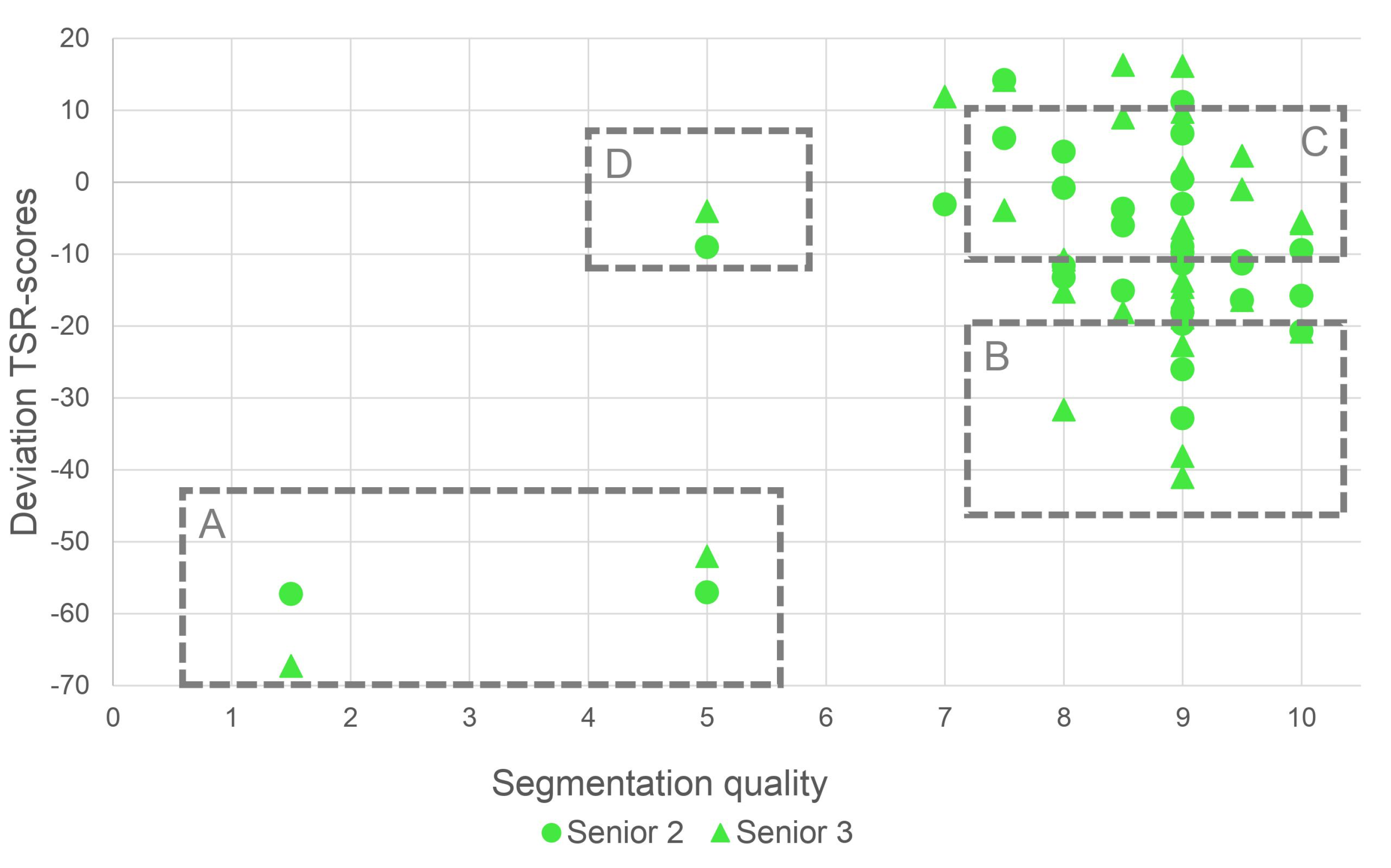
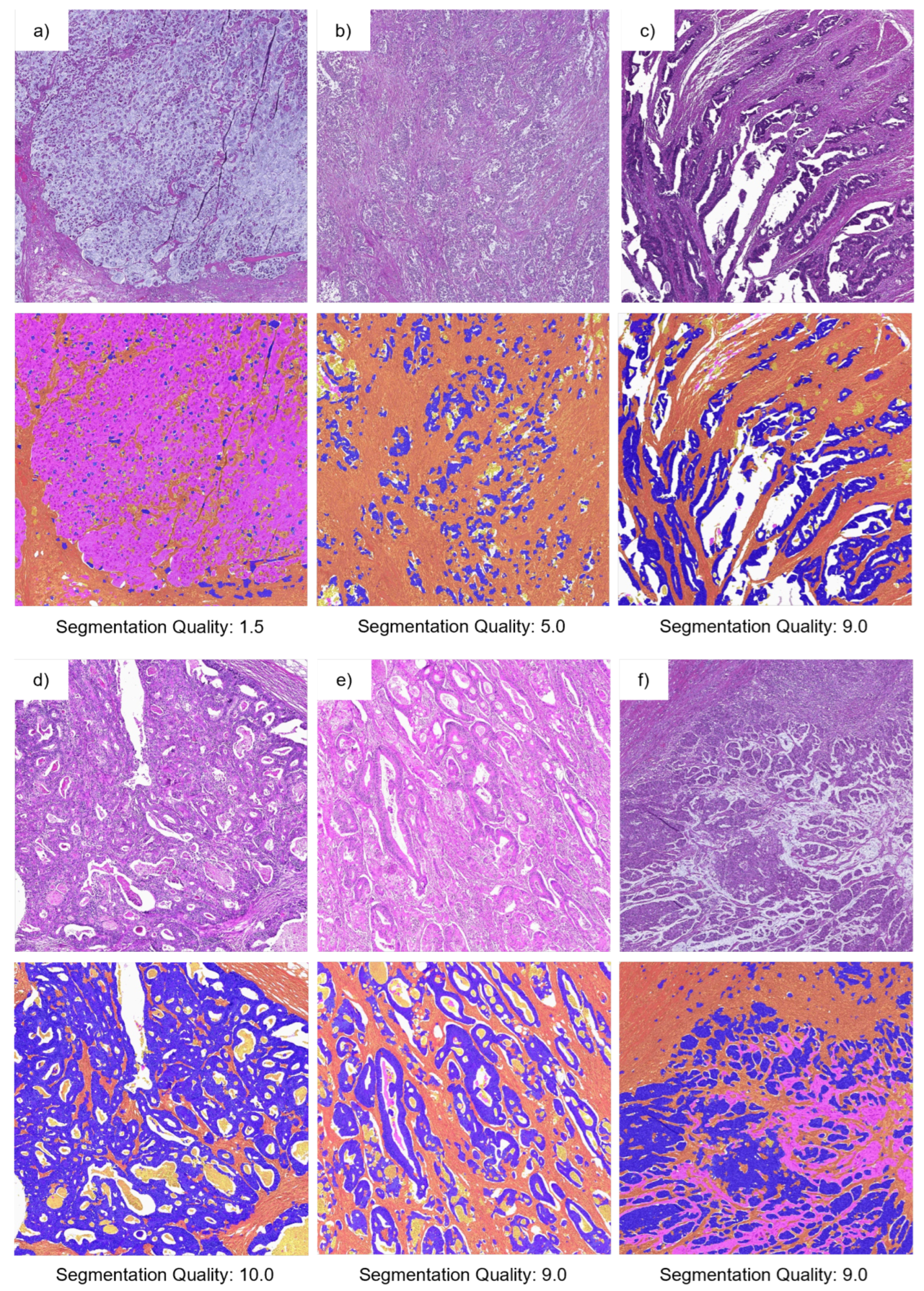
2.4.3. Survey 2—Assessment of Segmentation Quality
3. Results and Discussion
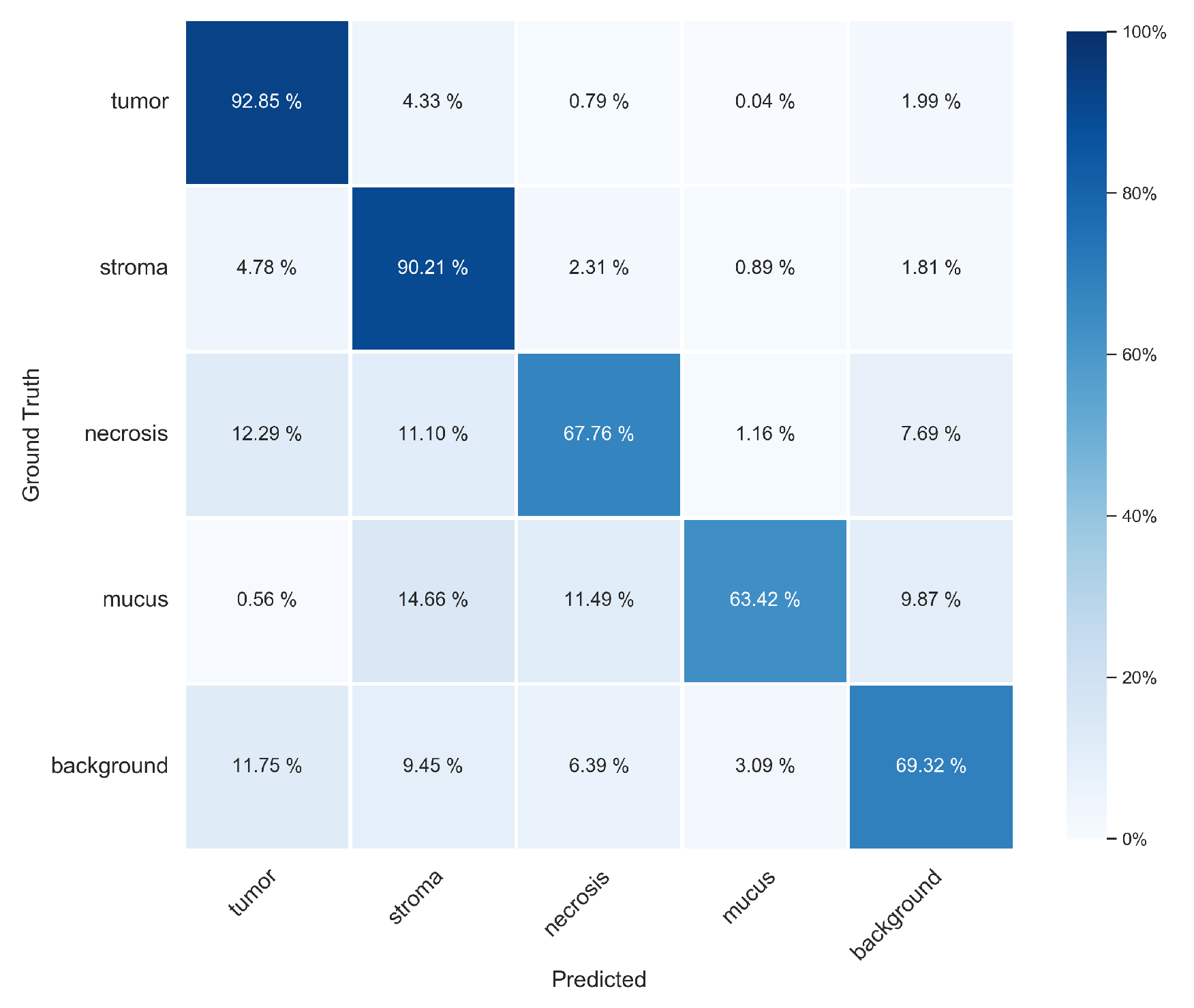
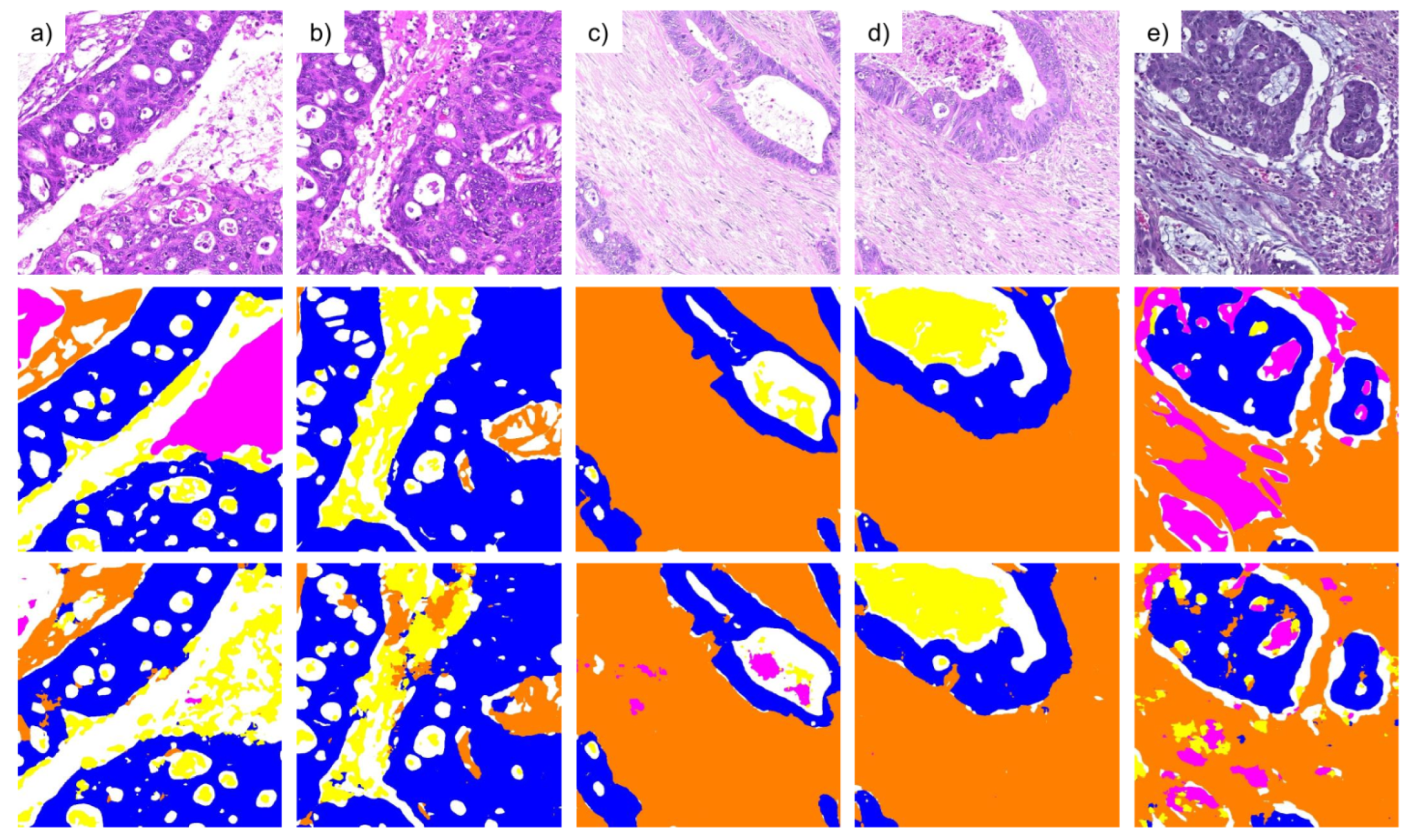
3.1. Pixel-Wise Segmentation
3.2. Evaluation of TSR Assessment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | artifical intelligence |
| BPN | basic prototype network |
| CI | confidence interval |
| CNN | convolutional neural network |
| DAB | diaminobenzidine |
| GAN | generative adversarial network |
| H&E | hematoxylin and eosin |
| ICC | intraclass correlation |
| IoU | intersection over union |
| m.e. | most experienced |
| PANet | prototype alignment network |
| ROI | region of interest |
| SVM | support vector machine |
| TMA | tissue microarray |
| TME | tumor microenvironment |
| TSR | tumor–stroma ratio |
| WSI | whole slide image |
Appendix A. Additional Information for U-Net Structure
Appendix B. Additional Information about the Surveys

Appendix C. Evaluation Metrics
| Predicted | |||
|---|---|---|---|
| P | N | ||
| Actual | P | TP | FN |
| N | FP | TN | |
Appendix D. Additional Results of Pixel-Wise Evaluation on Segmentation Test Set
| Class | BPN (Tiling A) | U-Net (Tiling A) | BPN (Tiling B) | U-Net (Tiling B) |
|---|---|---|---|---|
| tumor | 0.914 ± 0.016 | 0.918 ± 0.011 | 0.925 ± 0.014 | 0.929 ± 0.009 |
| stroma | 0.897 ± 0.006 | 0.897 ± 0.005 | 0.910 ± 0.009 | 0.902 ± 0.004 |
| necrosis | 0.648 ± 0.034 | 0.655 ± 0.062 | 0.682 ± 0.027 | 0.678 ± 0.062 |
| mucus | 0.582 ± 0.100 | 0.618 ± 0.033 | 0.525 ± 0.115 | 0.634 ± 0.029 |
| background | 0.701 ± 0.014 | 0.689 ± 0.028 | 0.710 ± 0.012 | 0.693 ± 0.028 |
| overall | 0.748 ± 0.014 | 0.755 ± 0.003 | 0.751 ± 0.021 | 0.767 ± 0.003 |
| Class | BPN (Tiling A) | U-Net (Tiling A) | BPN (Tiling B) | U-Net (Tiling B) |
|---|---|---|---|---|
| tumor | 0.912 ± 0.006 | 0.914 ± 0.004 | 0.917 ± 0.006 | 0.918 ± 0.003 |
| stroma | 0.866 ± 0.021 | 0.870 ± 0.010 | 0.881 ± 0.020 | 0.886 ± 0.008 |
| necrosis | 0.620 ± 0.017 | 0.601 ± 0.046 | 0.631 ± 0.018 | 0.611 ± 0.044 |
| mucus | 0.792 ± 0.033 | 0.797 ± 0.010 | 0.848 ± 0.046 | 0.811 ± 0.011 |
| background | 0.731 ± 0.015 | 0.746 ± 0.026 | 0.727 ± 0.017 | 0.749 ± 0.025 |
| overall | 0.784 ± 0.009 | 0.785 ± 0.007 | 0.801 ± 0.003 | 0.795 ± 0.007 |
| Class | BPN (Tiling A) | U-Net (Tiling A) | BPN (Tiling B) | U-Net (Tiling B) |
|---|---|---|---|---|
| tumor | 0.788 ± 0.019 | 0.791 ± 0.010 | 0.810 ± 0.012 | 0.808 ± 0.010 |
| stroma | 0.840 ± 0.010 | 0.845 ± 0.007 | 0.854 ± 0.007 | 0.858 ± 0.006 |
| necrosis | 0.464 ± 0.021 | 0.452 ± 0.009 | 0.487 ± 0.014 | 0.469 ± 0.009 |
| mucus | 0.499 ± 0.066 | 0.533 ± 0.023 | 0.472 ± 0.076 | 0.553 ± 0.022 |
| background | 0.557 ± 0.005 | 0.557 ± 0.005 | 0.560 ± 0.005 | 0.562 ± 0.006 |
| overall | 0.629 ± 0.007 | 0.635 ± 0.004 | 0.637 ± 0.017 | 0.650 ± 0.003 |
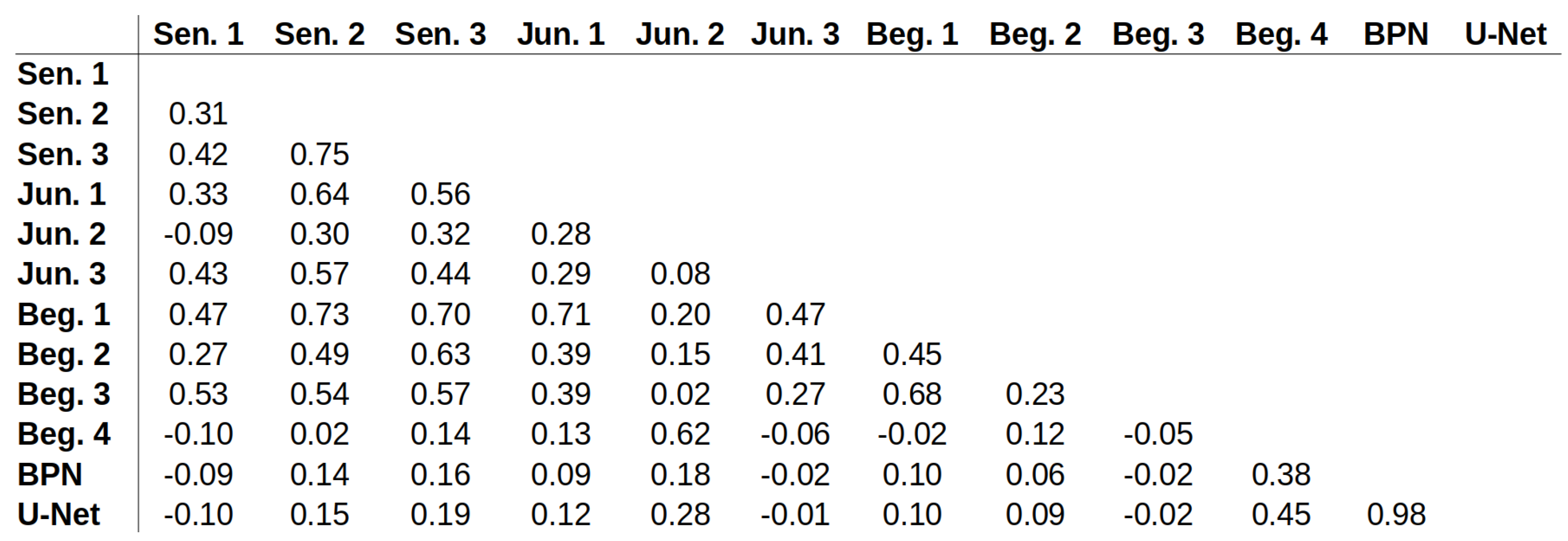
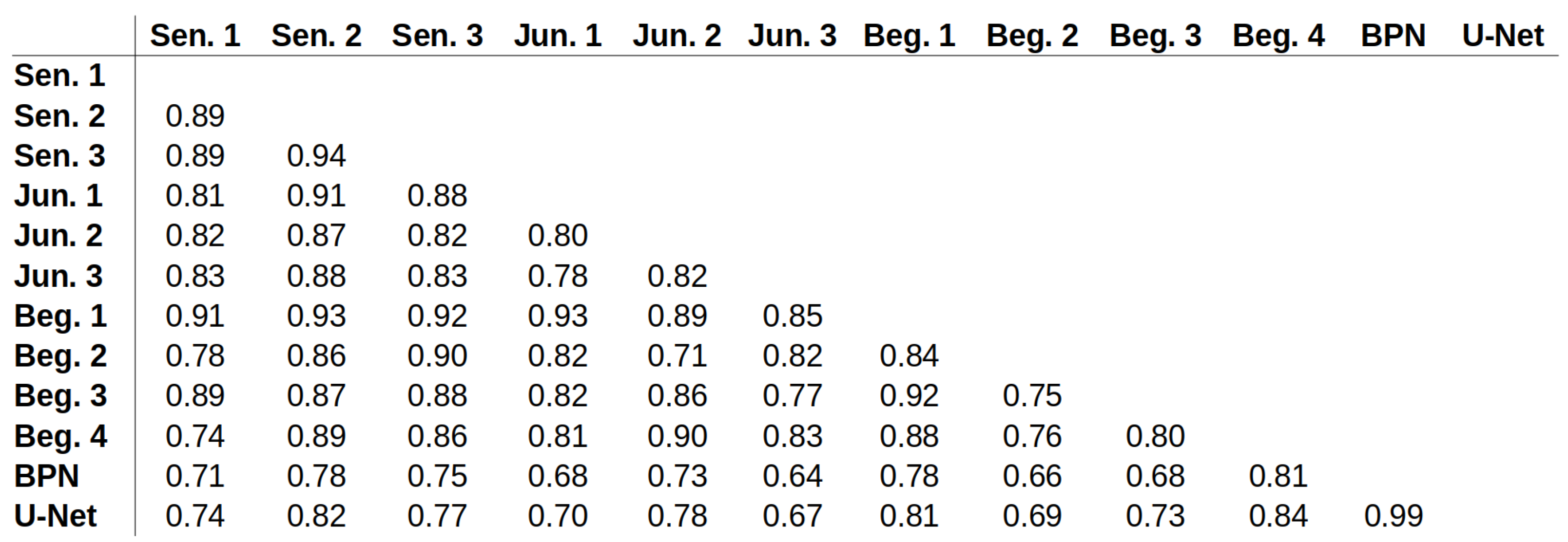
Appendix E. ICC Values for All Possible Pairs

References
- Mesker, W.E.; Junggeburt, J.M.C.; Szuhai, K.; de Heer, P.; Morreau, H.; Tanke, H.J.; Tollenaar, R.A.E.M. The carcinoma–stromal ratio of colon carcinoma is an independent factor for survival compared to lymph node status and tumor stage. Anal. Cell. Pathol. 2007, 29, 387–398. [Google Scholar] [CrossRef] [PubMed]
- West, N.P.; Dattani, M.; McShane, P.; Hutchins, G.; Grabsch, J.; Mueller, W.; Treanor, D.; Quirke, P.; Grabsch, H. The proportion of tumour cells is an independent predictor for survival in colorectal cancer patients. Br. J. Cancer 2010, 102, 1519–1523. [Google Scholar] [CrossRef] [PubMed]
- Huijbers, A.; Tollenaar, R.A.E.M.; v Pelt, G.W.; Zeestraten, E.C.M.; Dutton, S.; McConkey, C.C.; Domingo, E.; Smit, V.T.H.B.M.; Midgley, R.; Warren, B.F.; et al. The proportion of tumor-stroma as a strong prognosticator for stage II and III colon cancer patients: Validation in the VICTOR trial. Ann. Oncol. 2013, 24, 179–185. [Google Scholar] [CrossRef]
- Park, J.H.; Richards, C.H.; McMillan, D.C.; Horgan, P.G.; Roxburgh, C.S.D. The relationship between tumour stroma percentage, the tumour microenvironment and survival in patients with primary operable colorectal cancer. Ann. Oncol. 2014, 25, 644–651. [Google Scholar] [CrossRef] [PubMed]
- Wright, A.; Magee, D.; Quirke, P.; Treanor, D.E. Towards automatic patient selection for chemotherapy in colorectal cancer trials. In Proceedings of the Medical Imaging 2014: Digital Pathology. SPIE, San Diego, CA, USA, 15–20 February 2014; Volume 9041, pp. 58–65. [Google Scholar] [CrossRef]
- Scheer, R.; Baidoshvili, A.; Zoidze, S.; Elferink, M.A.G.; Berkel, A.E.M.; Klaase, J.M.; van Diest, P.J. Tumor-stroma ratio as prognostic factor for survival in rectal adenocarcinoma: A retrospective cohort study. World J. Gastrointest. Oncol. 2017, 9, 466–474. [Google Scholar] [CrossRef]
- van Pelt, G.W.; Sandberg, T.P.; Morreau, H.; Gelderblom, H.; van Krieken, J.H.J.M.; Tollenaar, R.A.E.M.; Mesker, W.E. The tumour-stroma ratio in colon cancer: The biological role and its prognostic impact. Histopathology 2018, 73, 197–206. [Google Scholar] [CrossRef]
- Geessink, O.G.F.; Baidoshvili, A.; Klaase, J.M.; Ehteshami Bejnordi, B.; Litjens, G.J.S.; van Pelt, G.W.; Mesker, W.E.; Nagtegaal, I.D.; Ciompi, F.; van der Laak, J.A.W.M. Computer aided quantification of intratumoral stroma yields an independent prognosticator in rectal cancer. Cell. Oncol. 2019, 42, 331–341. [Google Scholar] [CrossRef]
- Zhao, K.; Li, Z.; Yao, S.; Wang, Y.; Wu, X.; Xu, Z.; Wu, L.; Huang, Y.; Liang, C.; Liu, Z. Artificial intelligence quantified tumour-stroma ratio is an independent predictor for overall survival in resectable colorectal cancer. EBioMedicine 2020, 61, 103054. [Google Scholar] [CrossRef]
- Jiang, D.; Hveem, T.S.; Glaire, M.; Church, D.N.; Kerr, D.J.; Yang, L.; Danielsen, H.E. Automated assessment of CD8+ T-lymphocytes and stroma fractions complement conventional staging of colorectal cancer. EBioMedicine 2021, 71, 103547. [Google Scholar] [CrossRef]
- Smit, M.A.; van Pelt, G.W.; Terpstra, V.; Putter, H.; Tollenaar, R.A.E.M.; Mesker, W.E.; van Krieken, J.H.J.M. Tumour-stroma ratio outperforms tumour budding as biomarker in colon cancer: A cohort study. Int. J. Color. Dis. 2021, 36, 2729–2737. [Google Scholar] [CrossRef]
- Abbet, C.; Studer, L.; Zlobec, I.; Thiran, J.P. Toward Automatic Tumor-Stroma Ratio Assessment for Survival Analysis in Colorectal Cancer. Medical Imaging with Deep Learning MIDL 2022 Short Papers. 2022. Available online: https://openreview.net/forum?id=PMQZGFtItHJ (accessed on 2 March 2023).
- Yang, J.; Ye, H.; Fan, X.; Li, Y.; Wu, X.; Zhao, M.; Hu, Q.; Ye, Y.; Wu, L.; Li, Z.; et al. Artificial intelligence for quantifying immune infiltrates interacting with stroma in colorectal cancer. J. Transl. Med. 2022, 20, 451. [Google Scholar] [CrossRef]
- Smit, M.A.; Ciompi, F.; Bokhorst, J.M.; van Pelt, G.W.; Geessink, O.G.F.; Putter, H.; Tollenaar, R.A.E.M.; van Krieken, J.H.J.M.; Mesker, W.E.; van der Laak, J.A.W.M. Deep learning based tumor–stroma ratio scoring in colon cancer correlates with microscopic assessment. J. Pathol. Inform. 2023, 14, 100191. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, H.; Zhao, R.; Zhang, H.; Liu, C.; Song, Y. Tumor-stroma Ratio is An Independent Prognostic Factor of Non-small Cell Lung Cancer. Chin. J. Lung Cancer 2013, 16, 191–196. [Google Scholar]
- Zhang, T.; Xu, J.; Shen, H.; Dong, W.; Ni, Y.; Du, J. Tumor-stroma ratio is an independent predictor for survival in NSCLC. Int. J. Clin. Exp. Pathol. 2015, 8, 11348–11355. [Google Scholar]
- Ichikawa, T.; Aokage, K.; Sugano, M.; Miyoshi, T.; Kojima, M.; Fujii, S.; Kuwata, T.; Ochiai, A.; Suzuki, K.; Tsuboi, M.; et al. The ratio of cancer cells to stroma within the invasive area is a histologic prognostic parameter of lung adenocarcinoma. Lung Cancer 2018, 118, 30–35. [Google Scholar] [CrossRef]
- Lv, Z.; Cai, X.; Weng, X.; Xiao, H.; Du, C.; Cheng, J.; Zhou, L.; Xie, H.; Sun, K.; Wu, J.; et al. Tumor–stroma ratio is a prognostic factor for survival in hepatocellular carcinoma patients after liver resection or transplantation. Surgery 2015, 158, 142–150. [Google Scholar] [CrossRef]
- Moorman, A.M.; Vink, R.; Heijmans, H.J.; van der Palen, J.; Kouwenhoven, E.A. The prognostic value of tumour-stroma ratio in triple-negative breast cancer. Eur. J. Surg. Oncol. (EJSO) 2012, 38, 307–313. [Google Scholar] [CrossRef]
- Gujam, F.J.A.; Edwards, J.; Mohammed, Z.M.A.; Going, J.J.; McMillan, D.C. The relationship between the tumour stroma percentage, clinicopathological characteristics and outcome in patients with operable ductal breast cancer. Br. J. Cancer 2014, 111, 157–165. [Google Scholar] [CrossRef]
- Roeke, T.; Sobral-Leite, M.; Dekker, T.J.A.; Wesseling, J.; Smit, V.T.H.B.M.; Tollenaar, R.A.E.M.; Schmidt, M.K.; Mesker, W.E. The prognostic value of the tumour-stroma ratio in primary operable invasive cancer of the breast: A validation study. Breast Cancer Res. Treat. 2017, 166, 435–445. [Google Scholar] [CrossRef]
- Millar, E.K.; Browne, L.H.; Beretov, J.; Lee, K.; Lynch, J.; Swarbrick, A.; Graham, P.H. Tumour Stroma Ratio Assessment Using Digital Image Analysis Predicts Survival in Triple Negative and Luminal Breast Cancer. Cancers 2020, 12, 3749. [Google Scholar] [CrossRef]
- Hagenaars, S.C.; Vangangelt, K.M.H.; Van Pelt, G.W.; Karancsi, Z.; Tollenaar, R.A.E.M.; Green, A.R.; Rakha, E.A.; Kulka, J.; Mesker, W.E. Standardization of the tumor-stroma ratio scoring method for breast cancer research. Breast Cancer Res. Treat. 2022, 193, 545–553. [Google Scholar] [CrossRef] [PubMed]
- Linder, N.; Konsti, J.; Turkki, R.; Rahtu, E.; Lundin, M.; Nordling, S.; Haglund, C.; Ahonen, T.; Pietikäinen, M.; Lundin, J. Identification of tumor epithelium and stroma in tissue microarrays using texture analysis. Diagn. Pathol. 2012, 7, 22. [Google Scholar] [CrossRef] [PubMed]
- Bianconi, F.; Álvarez Larrán, A.; Fernández, A. Discrimination between tumour epithelium and stroma via perception-based features. Neurocomputing 2015, 154, 119–126. [Google Scholar] [CrossRef]
- Geessink, O.G.F.; Baidoshvili, A.; Freling, G.; Klaase, J.M.; Slump, C.H.; Heijden, F.V.D. Toward automatic segmentation and quantification of tumor and stroma in whole-slide images of H and E stained rectal carcinomas. In Proceedings of the Medical Imaging 2015: Digital Pathology. SPIE, Orlando, FL, USA, 21–26 February 2015; Volume 9420, pp. 85–91. [Google Scholar] [CrossRef]
- Hacking, S.M.; Wu, D.; Alexis, C.; Nasim, M. A Novel Superpixel Approach to the Tumoral Microenvironment in Colorectal Cancer. J. Pathol. Inform. 2022, 13, 100009. [Google Scholar] [CrossRef]
- Hong, Y.; Heo, Y.J.; Kim, B.; Lee, D.; Ahn, S.; Ha, S.Y.; Sohn, I.; Kim, K.M. Deep learning-based virtual cytokeratin staining of gastric carcinomas to measure tumor–stroma ratio. Sci. Rep. 2021, 11, 19255. [Google Scholar] [CrossRef]
- Abbet, C.; Studer, L.; Fischer, A.; Dawson, H.; Zlobec, I.; Bozorgtabar, B.; Thiran, J.P. Self-Rule to Multi-Adapt: Generalized Multi-source Feature Learning Using Unsupervised Domain Adaptation for Colorectal Cancer Tissue Detection. arXiv 2021, arXiv:2108.09178. [Google Scholar] [CrossRef]
- Wang, K.; Liew, J.H.; Zou, Y.; Zhou, D.; Feng, J. PANet: Few-Shot Image Semantic Segmentation with Prototype Alignment. arXiv 2019, arXiv:1908.06391. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Liu, X.; Song, L.; Liu, S.; Zhang, Y. A Review of Deep-Learning-Based Medical Image Segmentation Methods. Sustainability 2021, 13, 1224. [Google Scholar] [CrossRef]
- TensorFlow Developers. TensorFlow (v2.3.0). Zenodo. Available online: https://zenodo.org/record/7764425 (accessed on 2 March 2023).
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. arXiv 2018, arXiv:1801.04381. [Google Scholar]
- Kenyon-Dean, K.; Cianflone, A.; Page-Caccia, L.; Rabusseau, G.; Cheung, J.C.K.; Precup, D. Clustering-Oriented Representation Learning with Attractive-Repulsive Loss. arXiv 2018, arXiv:1812.07627. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kuritcyn, P.; Geppert, C.I.; Eckstein, M.; Hartmann, A.; Wittenberg, T.; Dexl, J.; Baghdadlian, S.; Hartmann, D.; Perrin, D.; Bruns, V.; et al. Robust Slide Cartography in Colon Cancer Histology. In Bildverarbeitung Für Die Medizin 2021; Informatik aktuell; Palm, C., Deserno, T.M., Handels, H., Maier, A., Maier-Hein, K., Tolxdorff, T., Eds.; Springer Fachmedien: Wiesbaden, Germany, 2021; pp. 229–234. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef]


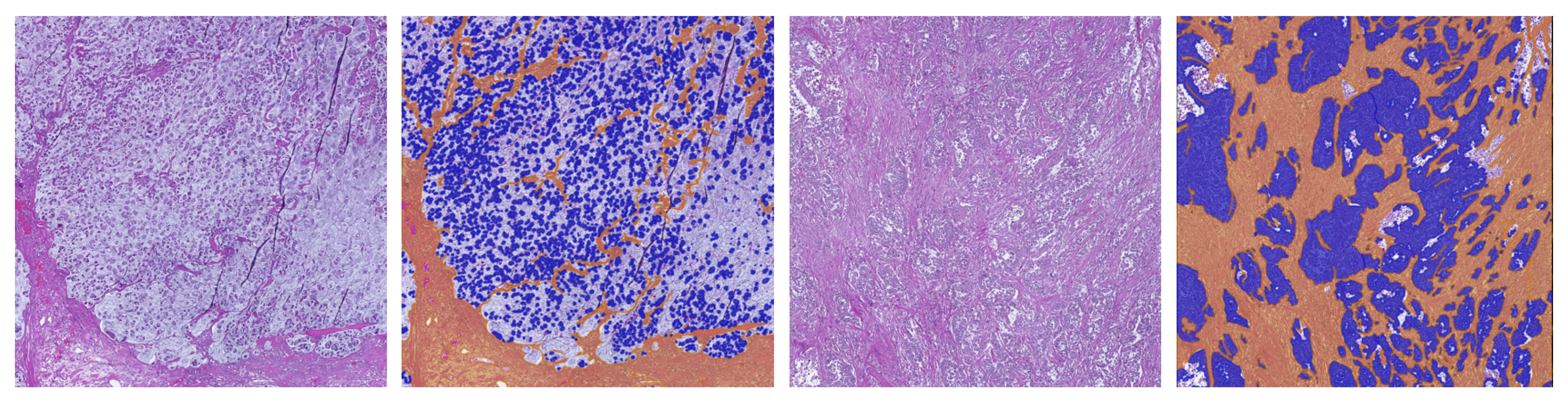
| Dataset | # Tumor | # Stroma | # Necrosis | # Mucus | # Background | # Artifact |
|---|---|---|---|---|---|---|
| training | 306,215,439 | 226,924,661 | 36,776,447 | 33,136,244 | 77,120,642 | 3,289,067 |
| validation | 67,367,966 | 47,092,974 | 11,588,088 | 10,367,879 | 29,945,593 | 0 |
| test | 86,969,626 | 71,515,442 | 10,713,472 | 9,694,276 | 20,507,721 | 3,691,963 |
| Metric | BPN (Tiling A) | U-Net (Tiling A) | BPN (Tiling B) | U-Net (Tiling B) |
|---|---|---|---|---|
| accuracy | 0.856 ± 0.007 | 0.858 ± 0.004 | 0.865 ± 0.005 | 0.867 ± 0.004 |
| precision | 0.784 ± 0.009 | 0.785 ± 0.007 | 0.801 ± 0.003 | 0.795 ± 0.007 |
| recall | 0.748 ± 0.014 | 0.755 ± 0.003 | 0.751 ± 0.021 | 0.767 ± 0.003 |
| IoU | 0.629 ± 0.007 | 0.635 ± 0.004 | 0.637 ± 0.017 | 0.650 ± 0.003 |
| F score | 0.761 ± 0.011 | 0.766 ± 0.003 | 0.765 ± 0.016 | 0.777 ± 0.003 |
| Class | BPN (Tiling A) | U-Net (Tiling A) | BPN (Tiling B) | U-Net (Tiling B) |
|---|---|---|---|---|
| tumor | 0.913 ± 0.006 | 0.916 ± 0.004 | 0.921 ± 0.004 | 0.923 ± 0.004 |
| stroma | 0.881 ± 0.012 | 0.883 ± 0.007 | 0.895 ± 0.007 | 0.894 ± 0.006 |
| necrosis | 0.634 ± 0.020 | 0.622 ± 0.008 | 0.655 ± 0.013 | 0.638 ± 0.009 |
| mucus | 0.663 ± 0.061 | 0.695 ± 0.020 | 0.638 ± 0.069 | 0.712 ± 0.019 |
| background | 0.715 ± 0.004 | 0.715 ± 0.004 | 0.718 ± 0.004 | 0.719 ± 0.005 |
| overall | 0.761 ± 0.011 | 0.766 ± 0.003 | 0.765 ± 0.016 | 0.777 ± 0.003 |
| ROI ID | Manual | m.e. Observers | BPN | U-Net |
|---|---|---|---|---|
| 16 | 47.6% | 72.5% | 18.0% | 21.1% |
| 19 | 41.8% | 75.0% | 12.7% | 24.8% |
| ROI ID | m.e. Observers | BPN | U-Net |
|---|---|---|---|
| 16 | 24.9 pp | −29.6 pp | −26.5 pp |
| 19 | 33.2 pp | −29.1 pp | −17.0 pp |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Firmbach, D.; Benz, M.; Kuritcyn, P.; Bruns, V.; Lang-Schwarz, C.; Stuebs, F.A.; Merkel, S.; Leikauf, L.-S.; Braunschweig, A.-L.; Oldenburger, A.; et al. Tumor–Stroma Ratio in Colorectal Cancer—Comparison between Human Estimation and Automated Assessment. Cancers 2023, 15, 2675. https://doi.org/10.3390/cancers15102675
Firmbach D, Benz M, Kuritcyn P, Bruns V, Lang-Schwarz C, Stuebs FA, Merkel S, Leikauf L-S, Braunschweig A-L, Oldenburger A, et al. Tumor–Stroma Ratio in Colorectal Cancer—Comparison between Human Estimation and Automated Assessment. Cancers. 2023; 15(10):2675. https://doi.org/10.3390/cancers15102675
Chicago/Turabian StyleFirmbach, Daniel, Michaela Benz, Petr Kuritcyn, Volker Bruns, Corinna Lang-Schwarz, Frederik A. Stuebs, Susanne Merkel, Leah-Sophie Leikauf, Anna-Lea Braunschweig, Angelika Oldenburger, and et al. 2023. "Tumor–Stroma Ratio in Colorectal Cancer—Comparison between Human Estimation and Automated Assessment" Cancers 15, no. 10: 2675. https://doi.org/10.3390/cancers15102675
APA StyleFirmbach, D., Benz, M., Kuritcyn, P., Bruns, V., Lang-Schwarz, C., Stuebs, F. A., Merkel, S., Leikauf, L.-S., Braunschweig, A.-L., Oldenburger, A., Gloßner, L., Abele, N., Eck, C., Matek, C., Hartmann, A., & Geppert, C. I. (2023). Tumor–Stroma Ratio in Colorectal Cancer—Comparison between Human Estimation and Automated Assessment. Cancers, 15(10), 2675. https://doi.org/10.3390/cancers15102675









