1. Introduction
The use of acoustic forces is an established technique for manipulating and sorting cells [
1,
2,
3], micro-particles and micro-droplets in lab-on-a-chip applications [
4]. Applications exploit the interaction of the suspended solid particles with the acoustic field, such as acoustic radiation force and streaming, to exert control on their dynamics [
4] and measure their elastic properties [
3]. The acoustic manipulation of microbubbles (MBs) is a more recent application [
5,
6], which builds on the success of coated microbubbles as a contrast agent in ultrasound imaging [
7] and focuses on their use in drug delivery [
8,
9] and bio-sensing applications [
10]. Microstreaming generated from the oscillations of uncoated microbubbles (acoustically, thermally or chemically actuated) has been used for localised flow control, leading to dynamic switching in microfluidic chips [
11,
12], microswimmers’ propulsion [
13,
14] and localised probing of cell properties [
15,
16]. In these applications, microbubbles are potentially more effective than particles because their deformation can be controlled by an external agent, but they are often simply treated as particles with a higher compressibility.
According to theory [
17,
18], however, the behaviour of microbubbles is frequency-dependent: uncoated microbubbles in a watery solution would behave according to classical Gor’kov theory [
19] only when excited below their acoustic resonance. In these conditions, the forces are similar to the ones acting on solid particles, but opposite in sign [
20,
21,
22]. In the presence of a standing wave, MBs would therefore move towards antinodes when solid particles of similar size would move towards nodes [
19]. Above resonance, the sign of the force changes, and bubbles move to nodes, just like solid particles of a similar size [
5,
6]. In addition, the response of microbubbles in an acoustofluidic device depends on their number concentration: ultrasound-activated interactions between bubbles and surrounding objects (e.g., other bubbles) depend on inter-bubble distance and are predicted to be stronger than for particles of equivalent diameter [
17], leading to concentration-dependent scattering [
23]. Finally, the presence of a coating on the shell of bubbles leads to pressure-dependent phenomena, i.e., onset of oscillations, buckling and rupture [
24,
25,
26]. All these phenomena need to be quantified for the optimisation of applications based on acoustically-driven microbubble dynamics.
This study presents a set of experiments using commercially-available polymer-coated MBs, highlighting the dependence of microbubble’s compressibility on excitation frequency, pressure and number concentration. Experiments are conducted in a well-known acoustofluidic manifold (described in [
27]), at increasing acoustic driving pressures and two different number concentrations. First, we look at isolated bubbles in their motion towards an “aggregation site” (i.e., the closest acoustic antinode, in our experimental conditions), under the action of radiation forces (primary Bjerknes forces). In this way, we obtain a value of the effective acoustic pressure
acting on the bubbles, as a function of the driving voltage at two microbubble concentrations. Second, we track pairs of bubbles joining into a single entity (i.e., a “doublet”) before proceeding further towards the aggregation site and following the example of Garcia-Sabatè et al. [
18], we use these events to measure bubble-bubble interactions (i.e., secondary Bjerknes forces) perpendicular to the direction of motion. Third, we observe doublets aggregating into linear structures, perpendicular to the direction of motion of the bubbles (“ripples”), and discuss their separation using recent [
17] and historical [
28,
29] theories, to estimate the nature of the interaction between bubbles in the direction of motion. In doing so, we show that the forces acting on the bubbles depend on the acoustic pressure, but not as expected by particle-based theories [
17], which assume a purely elastic behaviour. In particular, we show evidence of a threshold pressure, above which phenomena classically attributed to bubble-bubble interactions (secondary Bjerknes forces [
17]) can be observed. We propose a correction to the acoustic contrast factor to account for secondary Bjerknes forces and summarise our findings in a dynamical measurement of the compressibility of coated microbubbles: a key parameter for the uptake of microbubble-based therapies [
8] and sensing applications [
15,
16]. Thanks to a direct estimation of key shell parameters—obtained by milling and compressing a selection of bubbles under a Focussed Ion Beam Scanning Electron Microscope (FIB-SEM)—we discuss our results in terms of the onset of volume oscillations [
25,
30] and of buckling [
26].
2. Materials and Methods
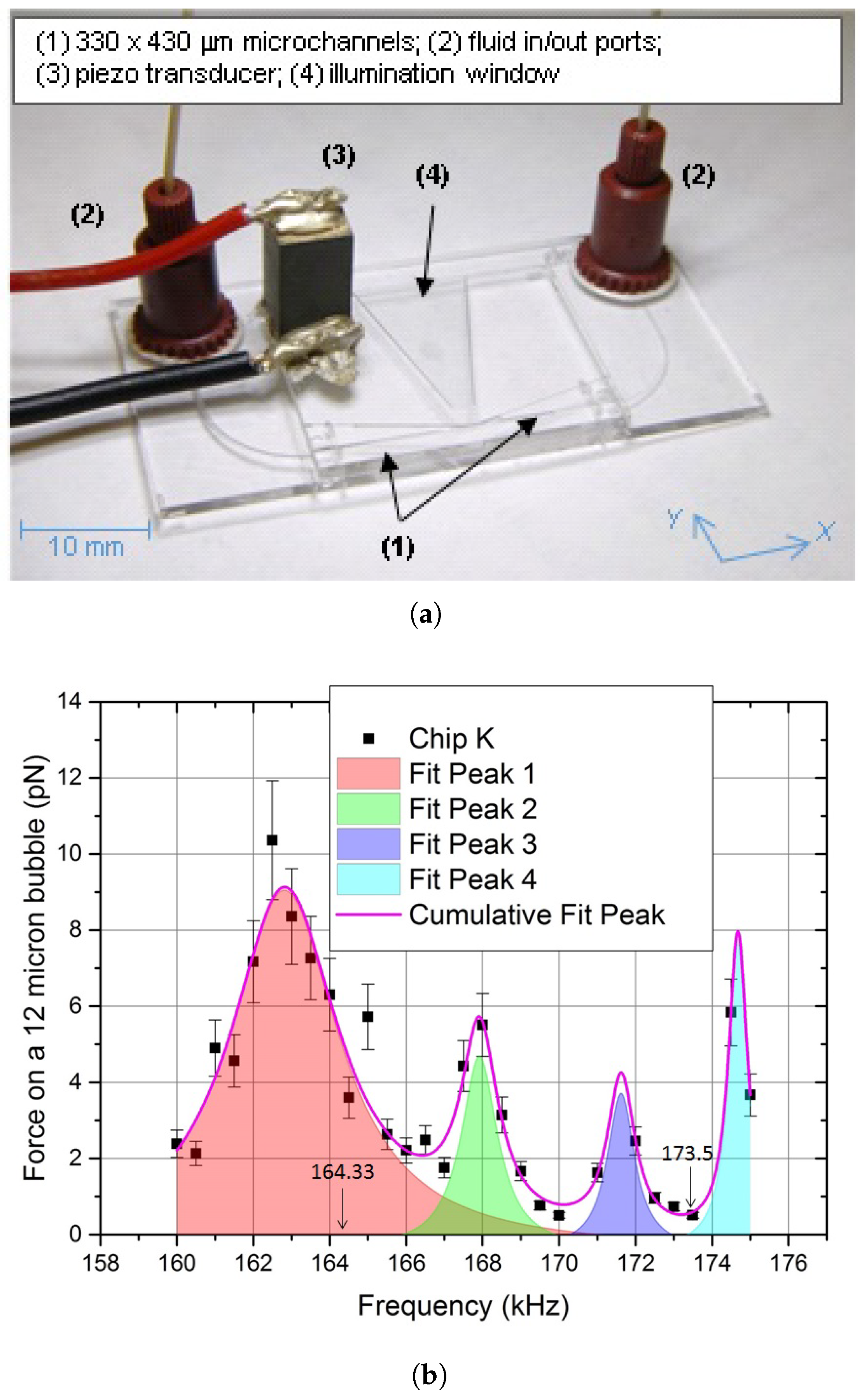
Experiments were conducted in a glass microfluidic chip (W: 25 mm, H: 2 mm, L: 20 mm), designed at the National Physical Laboratory (NPL) and manufactured by Dolomite Microfluidics (Royston, UK). The microfluidic chip (see [
27] for full details) presents a K-shaped manifold of etched microchannels (330
× 430
section, with a 100
-wide flat surface on the top and bottom of each channel) and is mounted on a glass base (W: 40 mm, H: 1 mm, L: 25 mm), which provides fluidic connection to the in/out ports. A trapezoidal window provides for lateral illumination of the central area (see
Figure 1a). The thickness of the polished flat surface above the trapping region was 0.17 mm [
31]. The K-shaped geometry has been chosen to facilitate future studies, where the two inclined channels will be used for monitoring acoustic emission from trapped bubbles.
The acoustic field was generated using a 5.9 mm × 5.9 mm × 13 mm Lead Zirconate Titanate (PZT) transducer (Morgan Ceramics Ltd., Southampton, UK) with a nominal resonance (in air) of ∼164 kHz, bonded onto the device’s top surface using conductive epoxy (CircuitWorks CW2400, Farnell, Leeds, United Kingdom). A sinusoidal voltage in the range of 160–180 kHz was used to drive the PZT transducer, after being amplified using a chain formed by a signal generator (Agilent 33250A, Agilent Technologies, Santa Clara, CA, USA), a power amplifier (E&I, Model A300, Electronics & Innovation, Rochester, NY, USA) and a 1:25 step-up matching impedance transformer.
As shown in
Figure 1b, which reports the force spectrum for a typical realisation of the microchip, we found the force on a 12
diameter Expancel
bubble to depend on frequency, due to the presence of different acoustic resonances [
27]. The frequency of 164.33 kHz (highlighted in
Figure 1b) was however the one where aggregation in the central area was repeatedly observed in different realisations of the chip: we consequently used this frequency for most of this study.
The acoustic pressure in this device has been accurately characterised (both spatially and as a function of the driving voltage) in previous studies [
27] providing, at 164.33 kHz, a calibration coefficient of
Pa
(peak pressure, 1 standard deviation) for input voltages up to 85 mV
(i.e., input peak pressures up to 4.1 kPa). Direct force measurements in the central area of the main microfluidic channel confirm the sinusoidal nature of the acoustic field at this frequency, with an antinode in the centre [
27].
The maximum power registered by the power amplifier during these experiments was 7 W, far below the amplifier’s rated specifications: therefore the amplifier chain was assumed to be working linearly. A maximum temperature increase of 1.5 C was observed on the surface of the chip (using a thin-film thermocouple) during tests (i.e., with the field ON), but the amount of vibrational energy transmitted to the main channel does not suggest localised heating. After each experiment, the temperature was allowed to return to its initial value. For this study, then, we assumed the fluid temperature to be constant and equal to the ambient value of C (experiments were run in a temperature-controlled room).
Similarly, since a maximum change of 0.3% in the speed of sound has been observed in the presence of Expancel
concentrations of
bubbles/mL at MHz frequencies [
23], we consider the speed of sound unaffected by the bubbles in this work. Under these assumptions, we consider the driving acoustic field in the microfluidic device,
, unperturbed by the presence of the bubbles.
2.1. Microbubble Characterisation
In this study, we use different number concentrations of commercially-available polymeric-shelled bubbles (Expancel
WU-20; gas: iso-butane; coating: acrylic copolymer, CAS 38742-70-0; diameter: 6–20
; manufactured by Akzo Nobel, Amsterdam, NL, USA). Polymer-coated Expancel
microbubbles were expanded by leaving them for 10 min in boiled water, mixed with a 0.08 M solution of sodium dodecyl sulfate (SDS) and injected into a microfluidic chip (see
Section 2) using a 1-mL syringe, before closing the open sides of the channels with Vaseline
. In the experiments, we injected a diluted sample of Expancel
microbubbles into the chip and switched on the acoustic standing wave, causing the bubbles to move towards an aggregation point (see the
Supplementary Material for a movie).
Once in the chip, we recorded Expancel
dynamics through a CCD camera (Model DCU223M, Thorlabs Ltd., Ely, UK) and an InfiniProbe TS-160 objective (Infinity, Franklin, TN, USA) in a brightfield microscopy setup. We calibrated the images using a 400-
NPL graticule (National Physical Laboratory, Teddington, UK) and used a basic thresholding method in ImageJ (Fiji distribution [
32]) to establish the diameter of each monitored bubble, thus allowing a measurement of their size distribution after expansion directly in the chip (measured mode diameter: 10.1
, measured average diameter: 12.4
, 10% percentile: 8.1
, 90% percentile: 18.1
). An uncertainty of
was assigned to this method, due to pixel resolution [
27]. We chose to leave the microbubble sample as close to the commercial one as possible, and therefore, no further preparation of the bubbles (e.g., sieving, to reduce the width of their size distribution) was conducted. We used camera images also to assess number concentrations, in the range of
–
bubbles/mL, by counting the bubbles appearing in the videos, as described by Grishenkov et al. [
33]. In the experiments, we selected two different bubble concentrations: one where we expect interactions to be detectable (
bubbles/mL, according to [
23]) and one approximatively three-times lower, i.e.,
bubbles/mL.
At the start of this work, we estimated the resonance frequency
of a given polymer-coated microbubble using the linearised Hoff model [
22]:
where
is the equilibrium radius of the bubble,
is the liquid density,
is the ratio of the specific heats of the gas inside the bubble,
is the hydrostatic pressure,
is the surface tension at the shell-liquid interface and
is the elasticity parameter of the shell. In the case of a polymer-coated bubble, Hoff et al. [
22] proposed to use for
the expression for incompressible flat sheets:
with
and
respectively the Young’s modulus and Poisson’s ratio of the material in the shell and
its thickness. Using for the shell typical properties from the literature (
101 kPa,
1.07, Young’s modulus:
GPa, Poisson’s ratio
0.3, shell thickness
3 nm [
34,
35]) and
for a 0.08 M water-SDS solution [
36], the resonant frequency for the range of Expancel
diameters utilised in this study was calculated to be above 1 MHz; see Equation (
1). It was therefore not surprising to see Expancel
bubbles moving towards antinodes at the frequencies used in this study, in the range 160–180 kHz (see also
Appendix C).
2.2. Primary Bjerknes Forces
In the experiments with isolated bubbles, run at 164.33 kHz and aimed at measuring the forces acting on isolated bubbles as a function of driving pressure (i.e., primary Bjerknes forces), we injected a diluted sample of Expancel
microbubbles into the chip and switched on the acoustic standing wave, causing the bubbles to move towards an aggregation point (see
Supplementary Movie).
We selected at least 5 different bubbles for each experimental condition (defined by frequency and unperturbed acoustic pressure
) and recorded their trajectories using the MTrackJ plugin in ImageJ [
37]. Selected bubbles were isolated (i.e., at least 5 particle diameters from another bubble) and far (i.e., at least 20 bubble diameters) from the centre of the aggregation area. As the voltage was increased, it was necessary to take more repeats due to the presence of acoustic streaming, in the form of vortices detaching from the junction between the two “legs” of the K-shaped manifold. For each movie, the coordinate system was set at the centre of the aggregation point. Trajectories were fitted using a least-squares method, imposing a balance between the radiation force
and the drag
. Having assumed a constant value for the acoustic contrast factor (
, see below), this left us with a single fitting parameter
that we defined as the “effective” pressure: a sum of the input pressure
and of the pressure scattered by the other bubbles [
19,
27,
38]. Good agreement to the fits (i.e.,
) was obtained in all cases. Unless explicitly stated otherwise, the value of
assigned to each experimental condition (i.e.,
f: driving frequency;
: input acoustic pressure;
: number concentration) was eventually a weighted average over the analysed trajectories (each corresponding to a different bubble diameter). This method is well established in the literature when particles are involved [
4] and has been extended, by Memoli et al. [
27], to Expancel
microbubbles of diameter
at low number concentrations and input pressures below 1.5 kPa. [
27].
In this work, we used for
the classical expression from the Gor’kov model [
17,
19], but modified to take into account the resonant behaviour of the bubbles [
20,
21].
In the simple case of a spherical particle in a sinusoidal standing wave
, in the Rayleigh regime, this approach gives (primary Bjerknes force):
where
is the “effective” acoustic pressure (sum of input acoustic pressure and scattered pressure),
is the input acoustic pressure (not affected by the presence of the MBs at the concentrations used in this study),
a is the particle radius,
k is the wave number,
is the ratio between the compressibilities of the particle (
) and the liquid (
),
is the ratio of their densities,
is the speed of sound in the liquid medium,
is the dampening coefficient for volume oscillations,
is the frequency of the driving acoustic field and
is also known as the acoustophoretic contrast factor (here calculated for a spherical particle). The change of sign implicit in Equation (
2) was confirmed by the results of Rabaud et al. [
39] and Bernassau et al. [
6]: these authors also looked at the acoustic forces acting on confined bubbles, but used MBs with dimensions larger than the resonance radius (
), which therefore moved towards nodes of the field.
We used for
the classical expression due to Stokes:
, where
a is the bubble radius,
is the viscosity of the liquid and
is the bubble velocity [
40,
41]. For bubbles moving in surfactant-water solutions, this formula is valid in non-pure water when the Reynolds number is smaller than 0.1 [
42]: a condition that was always met in our experiments. Rabaud et al. [
39] showed, however, that it is necessary to correct the drag force to account for the presence of the walls of the microfluidic system: for bubbles always in contact with the walls, these authors proposed an additive correction proportional to
for
(
, where
L is the size of the microchannel). A more complex expression for the increased drag can be found in the classical text by Clift et al. [
40], who for low Reynolds numbers and
proposed as the leading term
. Under similar conditions, [
38] proposed a leading correction
. The particular case of the interaction of bubbles with the walls of an acoustically-resonant pipe has been explored by Leighton [
43], who showed an effect on the inertia and a different damping for bubbles moving, resulting in a change in their resonant frequency. In the experiments presented here, the additive correction to
due to the walls (for the range of diameters considered) was estimated to be
for all theories and was therefore neglected.
Finally, in order to use
as a single fitting parameter, we assumed the acoustic contrast factor in Equation (
2) to be a known constant. In particular, we used
for an uncoated spherical bubble of iso-butane in water (at
C, speed of sound in iso-butane:
, density: 2.65
, viscosity:
[
44], to be compared with
of air and
of polystyrene).
Before fitting, we checked that the critical diameter above which the dynamics is radiation-dominated [
38] was lower than the diameters used in this study (it was equal to 0.02
). Inertial effects due to streaming-induced velocities were therefore neglected.
2.3. Secondary Bjerknes Forces
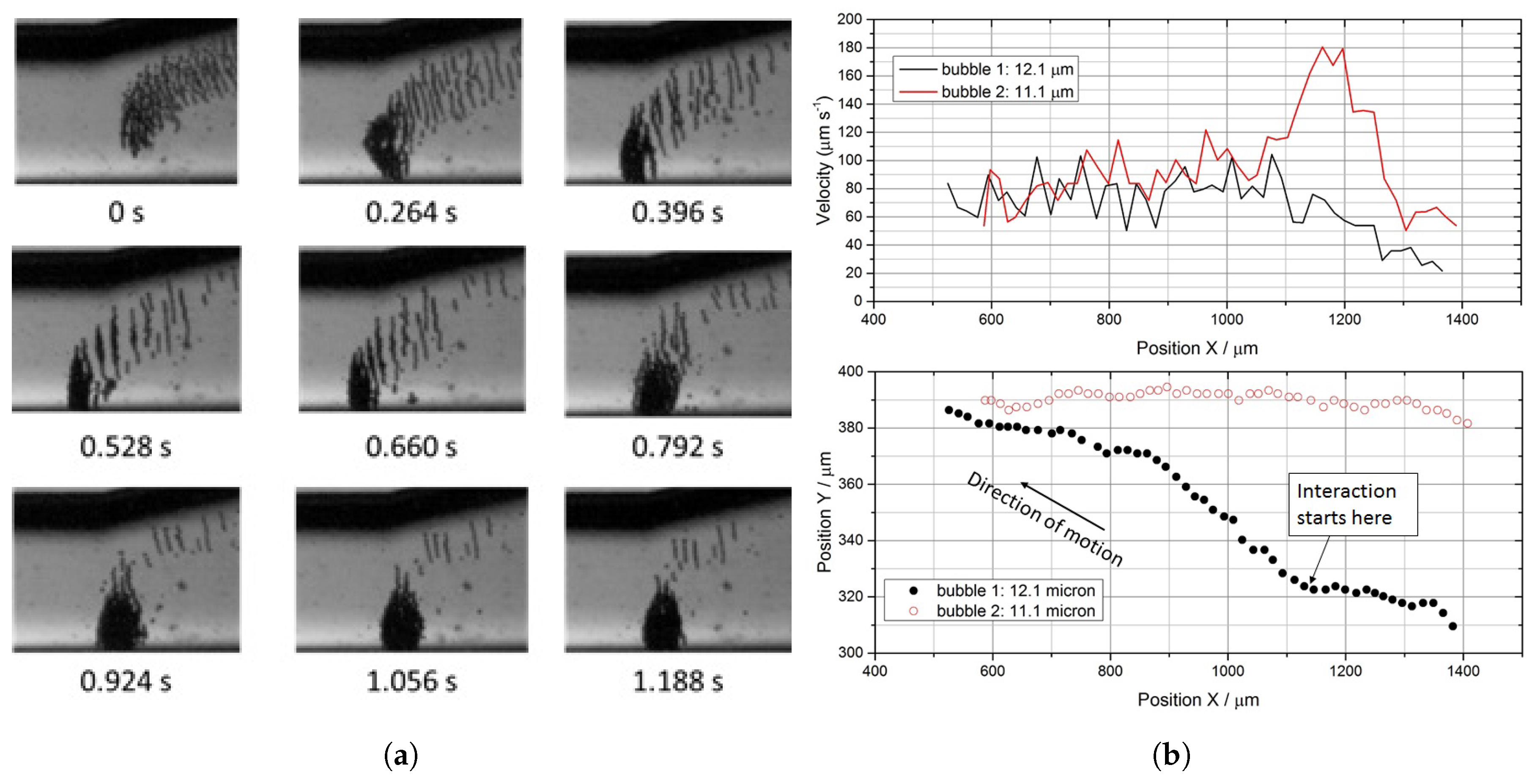
For the experiments with multiple bubbles, aimed at determining the relative weight of bubble-bubble interactions (i.e., secondary Bjerknes forces) on bubble dynamics, we kept analysing a trajectory even when the relative bubble was no longer “isolated”, i.e., after the presence of other bubbles altered the path. We conducted two types of experiments:
At the single frequency of 164.33 kHz, but varying the input acoustic pressure
, we monitored the occurrence of “pairing”, defined as an event in which two previously isolated bubbles of similar size started interacting before joining into a single item (i.e., a “doublet”) and continuing to travel together towards the aggregation point. These events have been used by [
18] to measure interactions between particles, perpendicular to the direction of motion.
In the range of 160–180 kHz, but at the fixed input voltage of 40 mV
, we observed the formation of lines of bubbles (“ripples”) perpendicular to the direction of motion. The formation of similar structures for particles has been used since the 19th Century to estimate the interaction forces acting in the direction of motion [
28,
29,
45].
Self-aggregation into sub-wavelength structures has been observed for microbubbles [
5,
6,
9,
39] but, so far, always at frequencies above their resonance (i.e., when they move towards nodes). In particular, Rabaud et al. [
5] observed the formation of structures they called “acoustic crystals” (using 20–50
-diameter bubbles within 25-
channels at 70 and 220 kHz), while Bernassau et al. [
6] observed at 4 MHz the formation of hexagonal shapes in a heptagonal cell using microspheres, emulsions and lipid-coated microbubbles (Sonovue
: mean diameter 3
, with 95% of the bubbles smaller than 10
). Phospholipid-shelled microbubbles (diameters 1–10
, measured resonance: 3.8 MHz) were also studied by Raiton et al. [
9], who reported their accumulation in a low acoustic pressure region at 7 MHz. In all these studies, the geometry of the acoustic pressure and its absolute value were not simultaneously controlled, and this did not allow rheological studies on the shell or the quantitative analysis of bubble-bubble interactions reported here.
Here, we base our analysis on the analytical expressions for secondary Bjerknes forces proposed by Silva and Bruus [
17], who modelled the interaction between small spherical particles suspended in an ideal fluid and an external acoustic wave, building on previous results [
21,
46]. In particular, in
Table 1, we report the results of their analysis (up to the first scattering order) under conditions relevant for this study: bubbles or particles aggregating in a standing wave, when the inter-particle distance
is much smaller than the wavelength (
, i.e., in the Rayleigh limit) and the driving frequency is much smaller than the resonance frequency of the bubbles. In
Table 1,
is the inter-particle distance in the direction of motion,
is the inter-particle distance in the transverse plane,
k is the wave number and
and
are the compressibility and density factors.
According to the analysis in
Table 1:
for bubbles, the forces are attractive in both directions and , with the same multiplying coefficient for interactions in the direction of motion and perpendicular to it;
for particles, forces are repulsive in the direction of motion and attractive in the transverse plane, in both directions, but with a different multiplying coefficient;
the forces on particles depend on the density ratios , while the forces on microbubbles depend on the ratio of compressibilities and on the driving frequency.
Garbin et al. [
47] used optical tweezers to position bubbles of different diameters at a known separation before exciting them with an acoustic pulse, using a high speed camera to monitor their translation. These authors show that the role of the unsteady component of the drag (the “history force”) is crucial for a correct description of the instantaneous translation of coated microbubbles subject to acoustic pulses, but mainly at the start of the motion. As our measurements will be done when the motion of the bubbles is already established, we will neglect this correction.
2.4. The Role of Shell Parameters
In the case of phospholipid-coated bubbles, Emmer et al. [
25] showed that the linear oscillator model behind Equation (
1) is only valid above a threshold pressure, which they related to the onset of volume oscillations, highlighting how smaller bubbles have a larger threshold. According to Doinikov and Bouakaz [
30], this behaviour would be due to the shear stress
of the phospholipid as a material: before oscillations start, the acoustic pressure would need to overcome the value:
where
is the equilibrium radius of the bubble and
is the average thickness of the shell. At a fixed driving acoustic pressure, then, only the largest microbubbles would oscillate: the number of oscillating bubbles would increase with pressure.
The need to explain experimental results (e.g., the asymmetric response of the diameter to repeated cycles of compression/expansion) introduced for phospholipid-coated MBs more complex models [
24,
26], similar to the ones used for spherical shells in continuum mechanics, adding to the picture two threshold pressures: one for buckling and one for break-up. According to these descriptions, polymer-coated bubbles would maintain a spherical shell at low deflations (elastic state, with the elasticity parameter
given by the flat sheet formula), but would buckle into spherical caps as the pressure overcomes a threshold given by [
48]:
where
is the equilibrium radius of the bubble and
is a coefficient of proportionality. As the driving pressure is further increased, axial symmetry would break through polygonal deformation of the depression, until the pressure is enough to rupture the shell.
For thin-shelled spheres subject to uniform load, the most used coefficient of proportionality in Equation (
4) is
: an expression attributed to Zoelly [
49,
50]. It is however known that the presence of axis-symmetric dimple imperfections may reduce the experimental value to approximately 15–20% of the theoretical value for a ”perfect” shell [
50,
51] i.e., one without imperfections.
The first attempt to estimate shell parameters (and therefore, the threshold pressures determining the different dynamical regimes) is by Gorce et al. [
52], who used attenuation and scattering measurements from suspensions of microbubbles. Such measurements, however, may not be valid for predicting the behaviour of each individual microbubble with its specific size and shell thickness. At the single-bubble level, Acoustic Force Microscopy (AFM) has been used to measure the elastic properties of lipid-coated microbubbles with different shell architectures attached to a functionalised substrate [
53,
54,
55], giving Young’s moduli of ∼10 MPa (i.e., much smaller than the values in [
34,
35]). It has been argued, however, that bubbles attached to a surface may not respond as they would during sonication [
56].
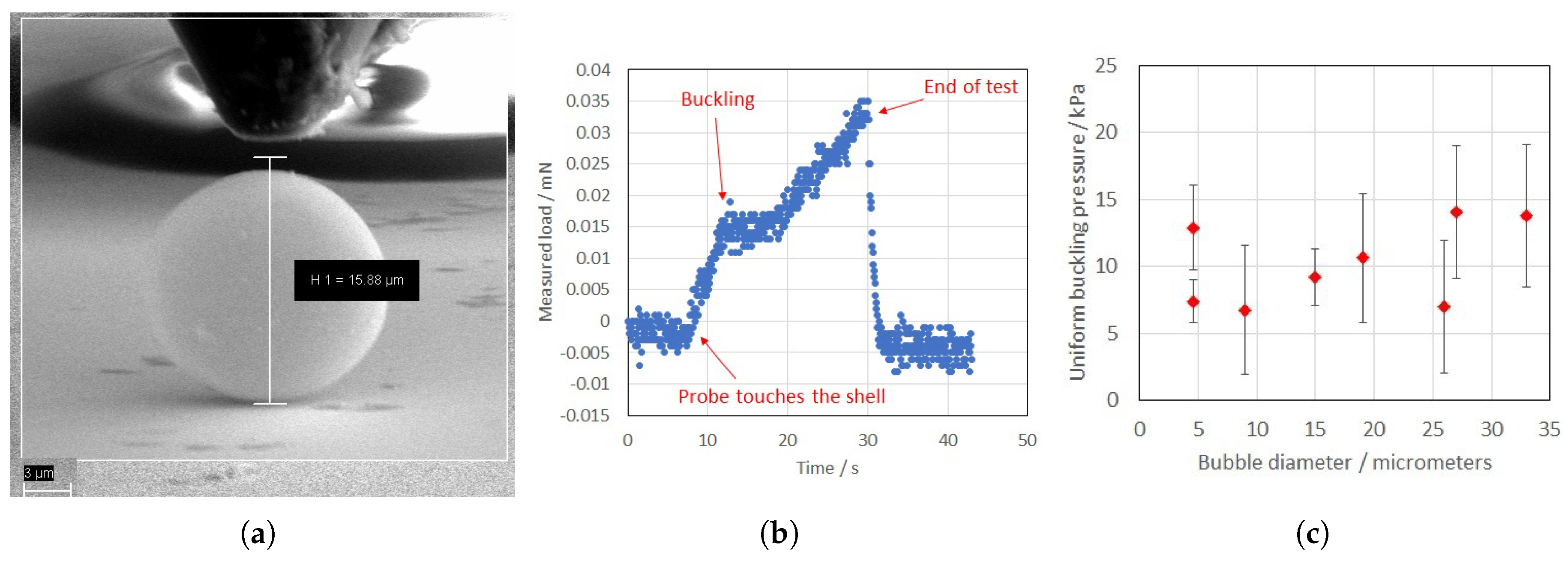
Given this uncertainty, during this study, we decided to obtain a direct estimate of shell thickness and buckling pressure, using an Auriga Focussed Ion Beam Scanning Electron Microscope (Zeiss, Cambridge, UK). First, Expancel bubbles were milled to reveal the average thickness/radius ratio for the sample microbubbles. For this measurement, we deposited a small droplet of the Expancel/SDS solution on an aluminium stub and allowed the water to evaporate. The collection of bubbles left on the stub were then examined using a 2-kV electron beam: an intensity sufficiently low to avoid the need for a conductive coating. A range of ion beam currents was tested to determine the optimal setting at which a section could be cut through the thin shell of the MBs, without causing excessive distortion or obvious damage to the shell itself. A 30-kV/50-pA ion beam was found optimum for this procedure.
To estimate the buckling pressure, we then used a 5 -diameter flat tip nano-indenter (ASMEC UNAT-SEM2) and observed the compression behaviour of Expancel bubbles on a silicon substrate. The indenter was operated in situ inside the Carl Zeiss Auriga 60 FIB-SEM (see above); the stage was tilted to and sample surface imaged at using the SEM, at an accelerating voltage of 10 kV. The indenter was positioned manually, centrally and approximately 2 above each bubble, with a maximum displacement defined depending on the diameter of the bubble. Bubble diameters were measured only in the horizontal axis to avoid inaccuracies due to image drift and image tilt. The displacement rate of the tests was optimised at 250 nm/s, which was slow enough to record the progress of the test with SEM imaging in real time. Load, displacement, time data and a movie were acquired for each bubble.
4. Discussion
In this work, we monitored the dynamics of Expancel
bubbles, as they aggregated in the well-characterised acoustic field of an acoustofluidic chip. First, we observed a difference between the pressures obtained by bubble tracking (
) and the input pressures (
) measured by other methods, which becomes evident for input voltages above 35 mV
(corresponding to pressures above 1.7 kPa and concentrations of the order of
bubbles/mL). Above this threshold, we repeatedly observed the formation of doublets, the appearance of ripples during trap formation and a pronounced dependence on bubble number concentration: all phenomena previously observed with particles and classically attributed to the presence of secondary Bjerknes forces, due to volume oscillations. We also observed a dependence of the force per unit volume on bubble diameter and, above the threshold, a change in the law that describes the mutual distance between ripples: effects not clearly explained by the description of secondary Bjerknes forces for solid particles. Having excluded the role of non-linearity in the E&Iamplifier or minor changes of temperature in the glass chip (see
Section 2), we investigate in this section other potential causes to explain our observations.
Since the data in
Figure 2a are averaged over bubble diameters far from their resonance, the weighting factor in Equation (
2) can be considered constant, leaving an effect that depends on the number concentration and therefore on the average bubble-bubble distance. At low concentrations, we explain this effect with the presence of secondary Bjerknes forces. With a derivation similar to the one in Robinson [
45], we consider three bubbles/particles moving towards the aggregation point, positioned on a line at distances
,
x and
from the aggregation. We calculate the force on the central one by inserting the expressions for
and
from
Table 1 in the force balance utilised to analyse particles/bubble tracks and obtain:
where
s is the coordinate along the direction of motion (
at the aggregation point) and
t is the coordinate perpendicular to it. The second term on the RHS of Equations (
6) and (
7) represents the contribution to the velocity, respectively for particles and bubbles, due to the bubble/particles preceding and following the selected one, both at distance
along the direction of motion.
Equations (
6) and (
7) show that, when
and
, the presence of secondary Bjerknes forces can be described by adding a term
to the standard acoustic contrast factor: for the same fixed input pressure
, interacting bubbles would experience forces greater than the ones acting on solid particles with the same
and number concentration. Assuming as average inter-bubble distance the Wigner–Seitz radius
where
n is the number concentration, the expected additive correction to the acoustic contrast factor of a 10-
diameter bubble at 164.33 kHz is
for
bubbles/mL and
for
bubbles/mL.
We confirmed the validity of this result by fitting a line to the averaged data at
bubbles/mL in
Figure 2a: a least-squares fit gives a coefficient of
(1 standard deviation) with an
and a value of
. When passing to
bubbles/mL, however, the trend in
Figure 2a is far from linear: other factors need to be taken into account.
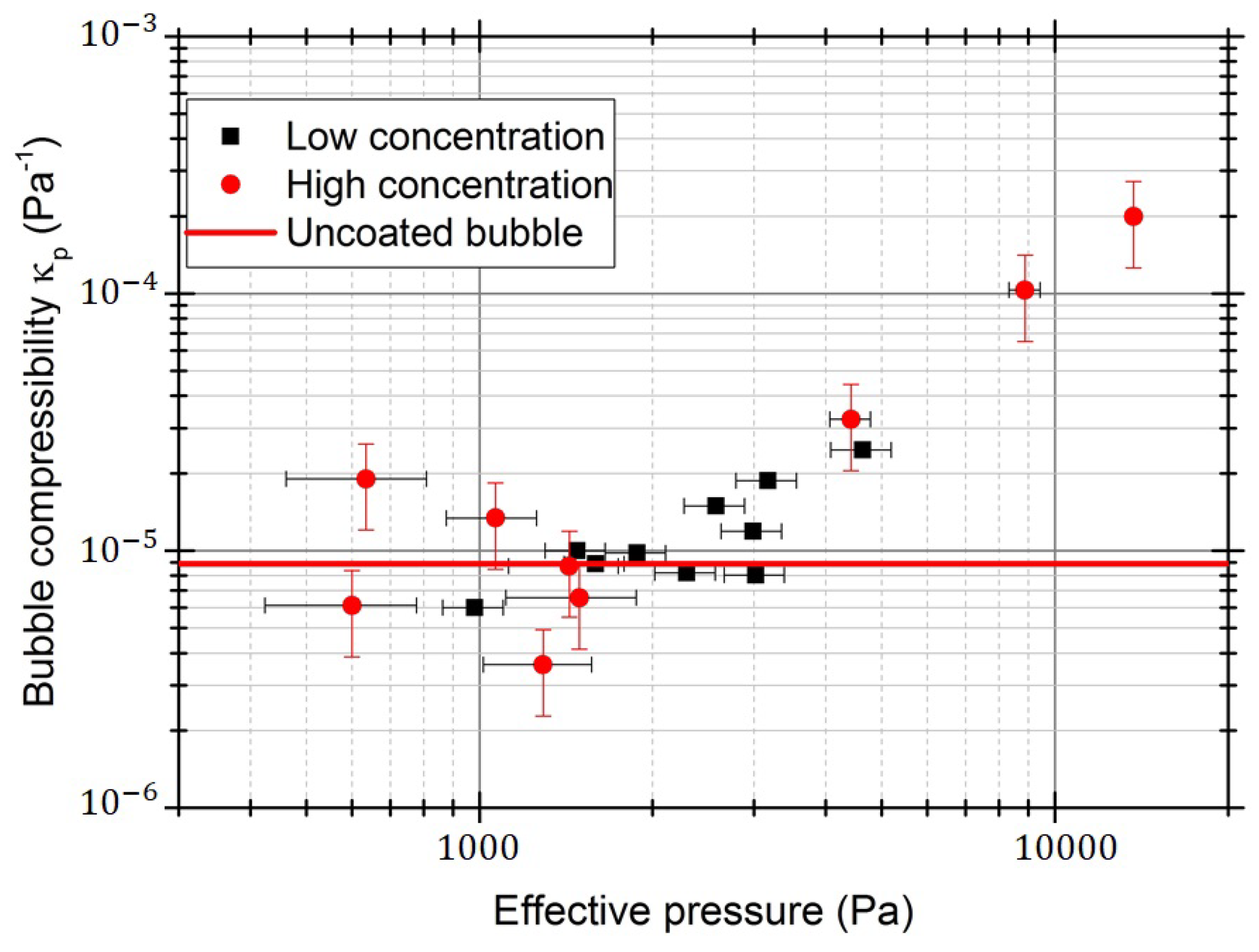
In order to estimate the effect of the shell, we use the observed trajectories to measure microbubble compressibility, as in [
3], after correcting
for the effect of interactions
. In
Figure 7, we report the values of
as a function of the measured pressure from the data in
Figure 2a. Also reported is the compressibility of an uncoated bubble (i.e., only made of iso-butane, with
at 20
C). In this way, we account for the dependence on concentration by noting that secondary Bjerknes forces modify the acoustic pressure locally acting on the bubbles: compressibility should be related not to
, but to the effective pressure
from
Figure 2a.
Figure 7, which presents compressibility
as a function of effective pressure, allows the threshold to be estimated between 1.7 ± 0.5 kPa and 2.0 ± 0.3 kPa (164.33 kHz).
The observed (quadratic) trend with increasing pressure is not compatible with the onset of oscillations, as described by Emmer et al. [
25] and Doinikov and Bouakaz [
30], but instead agrees with the models of shell compressibility based on Hooke’s law [
41,
49], which account for buckling. Paul et al. [
59], in particular, proposes near the transition to buckling a quadratic dependence of the radial compression rate
, where
is the equilibrium radius of the bubble. For pressures above the threshold for the onset of oscillations, where the radial compression rate increases linearly with pressure [
25], this would correspond to a quadratic dependence on pressure.
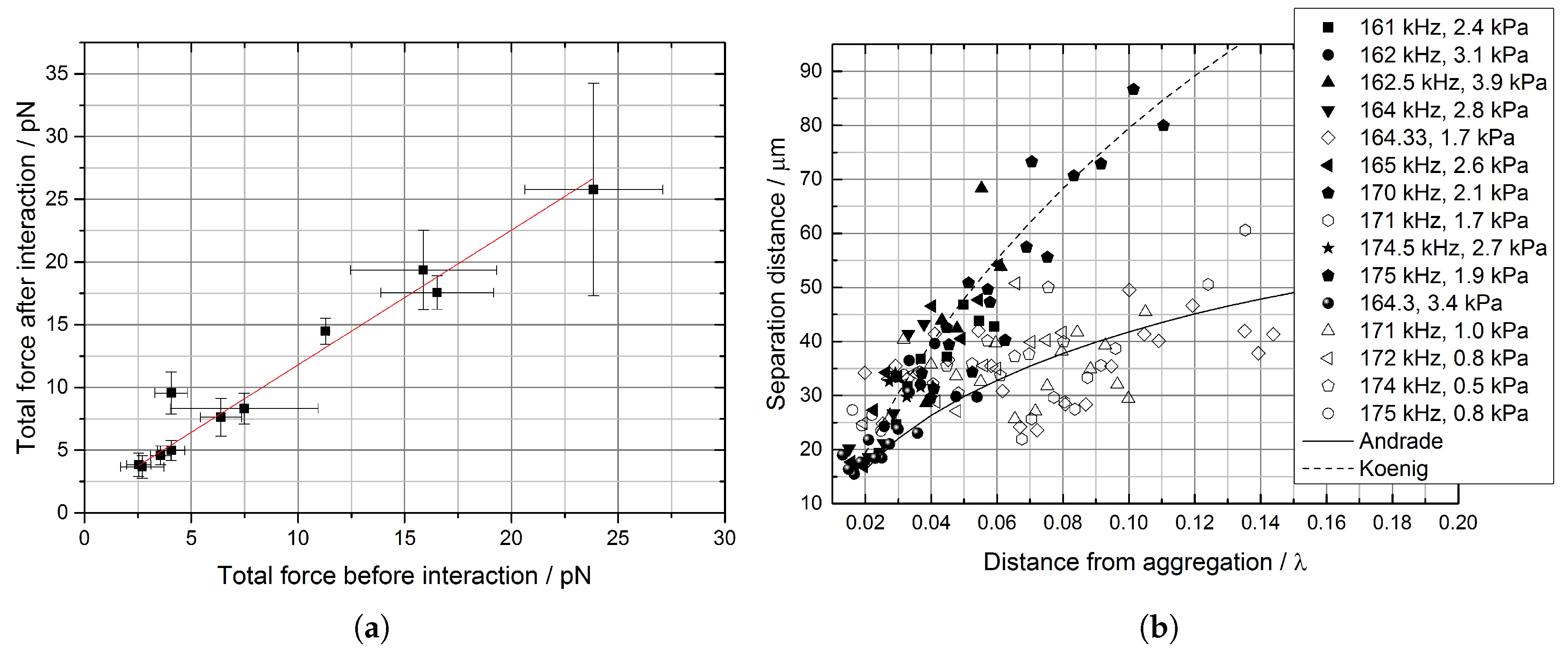
The different behaviour observed in
Figure 4b, for a similar threshold pressure of 1.7 kPa, confirms the interpretation of this dynamical change as the onset of buckling. We already highlighted that all the data following da C. Andrade’s correlation are relative to acoustic pressures below
kPa, while the ones following Robinson’s relation are relative to pressures above
kPa. Looking back at the original studies by these authors, we notice that they propose two different mechanisms of interaction. According to da C. Andrade, the formation of lines perpendicular to the direction of motion in an air-filled Kundt tube is due to the “circulation of air between two particles, due to the vibration of the involved dust particles” [
29]. da C. Andrade highlighted this circulation with careful imaging and noted that while “at small distances a vortex system is formed around two particles, pushing them together, at larger distances the two particles tend to repel each other, so that each can form its own vortex system”. In modern terms, da C. Andrade is attributing separation to the presence of acoustically-driven fluid movement between the particles (e.g., like the one caused by repeated buckling). Koenig’s description [
45], instead, aligns with the description of secondary Bjerknes forces: interactions between elastic particles that are either attractive or repulsive in nature. This difference in description, if extendible to coated microbubbles, would indicate a different interaction method as the bubbles move through the threshold. Further studies will look at different types and sizes of bubbles, in order to establish a clearer explanation.
It is however expected that this effect will be stronger for lipid-coated microbubbles, which start buckling at very low pressures [
26]: with a threshold in the kPa region, MBs subject to the typical pressures used in diagnostics would always buckle. This is a crucial observation, as buckling causes an increase in the sub-harmonic emission during sonication [
24,
26] that, properly calibrated (e.g., having a precise value for
), could be used for localised blood pressure measurements [
60]. In this sense, experiments with phospholipid-coated MBs [
61] have found a sub-harmonic increase of 17 dB, when using an external (static) pressure of 60 mmHg (i.e.,
kPa).
We also observed that microbubbles tend to aggregate into sub-wavelength structures as their number concentration increases (above
bubbles/mL, in this study). This may also happen in medical applications, where concentrations of the order of
bubbles/mL are typically used [
23], but the presence of such phenomena is typically neglected.
With the incremental number of attempts of using MBs for therapeutic applications, experimentation on MBs has moved to novel manufacturing methods (e.g., [
62,
63,
64]) and/or formulations [
65,
66]. In this context, knowing microbubbles’ behaviour near
and their compressibility as pressure increases (i.e., the coefficient for the quadratic dependence afterwards) may help practitioners to distinguish how a specific MB responds to sonication, even at higher pressures. Not all the bubble formulations may be equally effective under each delivery method. While some delivery mechanisms rely on the bubble carrier being destroyed, others depend in fact on the drug being propelled through the blood vessel walls [
8]: a mechanism still poorly understood, dominated by non-linear oscillations [
67], where buckling may have a significant impact. It is however in techniques like sonoporation [
68] or sonothrombolysis [
69] that differences between buckled/unbuckled bubbles may be determinant. Not only because these techniques are often used at frequencies far from the bubble resonance and relatively lower acoustic pressures (i.e., closer to the experimental conditions used here), but because in these methods the microstreaming induced by buckling or the presence of microstructures may have a directional effect not accounted for so far [
70].
The microchip used in this study offers a privileged environment to optimise delivery parameters and/or to understand better the biophysical phenomena underpinning microbubble-mediated drug delivery with different potential vectors, but like other “in vitro” set-ups [
71], it is still far from the environmental conditions microbubbles experience in a patient. Future studies will consider simple upgrades, like adding a flow rate and/or changing the operating temperatures, and more complex ones, like functionalising the glass walls with more tissue-relevant substrata. In parallel, we will look at ways to incorporate characterisation setups (like ours) into existing microfluidic-based systems for microbubble production, for in situ quality assurance.
5. Conclusions
In this work, we have measured the primary and secondary Bjerknes forces acting on polymer-coated microbubbles in an acoustofluidic chip, excited below (“to the red of”) their resonance. Due to the presence of the shell, we observed that coated microbubbles cannot be simply treated as particles in such an environment, but that they exhibit a clear threshold in their compressibility as pressure is increased. Thanks to experiments at different number concentrations of the bubbles in the chip, benchmarked by measurements under an electron scanning microscope, we provide evidence for this threshold to be identified as the onset of buckling. We conclude that the presence of the shell does not influence Bjerknes forces before buckling starts, i.e., below the buckling threshold, bubbles in aqueous fluids can be treated as particles with a negative acoustic contrast factor, neglecting their shell. This simple result may be useful to other researchers, conducting acoustofluidic experiments with bubbles, elastic particles or shelled vesicles (e.g., liposomes).
In acoustofluidic applications, where oscillating bubbles are used for acoustically-driven microflow control [
11,
13], our results show that local microstreaming may be enhanced by the presence of buckling, after the threshold (
Section 3.3). Off-resonance, actuation may even be triggered by modifying the amplitude of the driving acoustic pressure, instead its frequency, with cycles of hysteresis across the buckling threshold. Long-lasting coated bubbles, like the ones suggested by Bertin et al. [
13], may therefore be better placed to exploit these effects.
In the medical context, where lipid-coated microbubbles are used for diagnostic and (incrementally) for therapeutic applications, our methods may lead to precise measurements of the compressibility of different bubble vectors, each manufactured with a different method, helping practitioners in choosing the “right bubble” for a specific drug delivery task. In the long term, measurements like the ones presented in this study may reduce the duration of clinical studies, by providing a standardised test for comparing novel microbubble formulations with already approved ones.
In this study, we used a direct estimate of the shell thickness and of the onset of buckling to determine the elastic properties of the material in the shell. If the latter are known, as is the case for the lipids typically going on the shell of medical microbubbles, precise knowledge of the buckling pressure may be linked to the average shell thickness, and therefore to the average payload of a bubble: a key measurement underpinning “dose” planning during microbubble-based treatments and the taste experience for bubbles in food [
72].