A Study on the Transient Process of Contact-Mode Triboelectric Nanogenerators
Abstract
1. Introduction
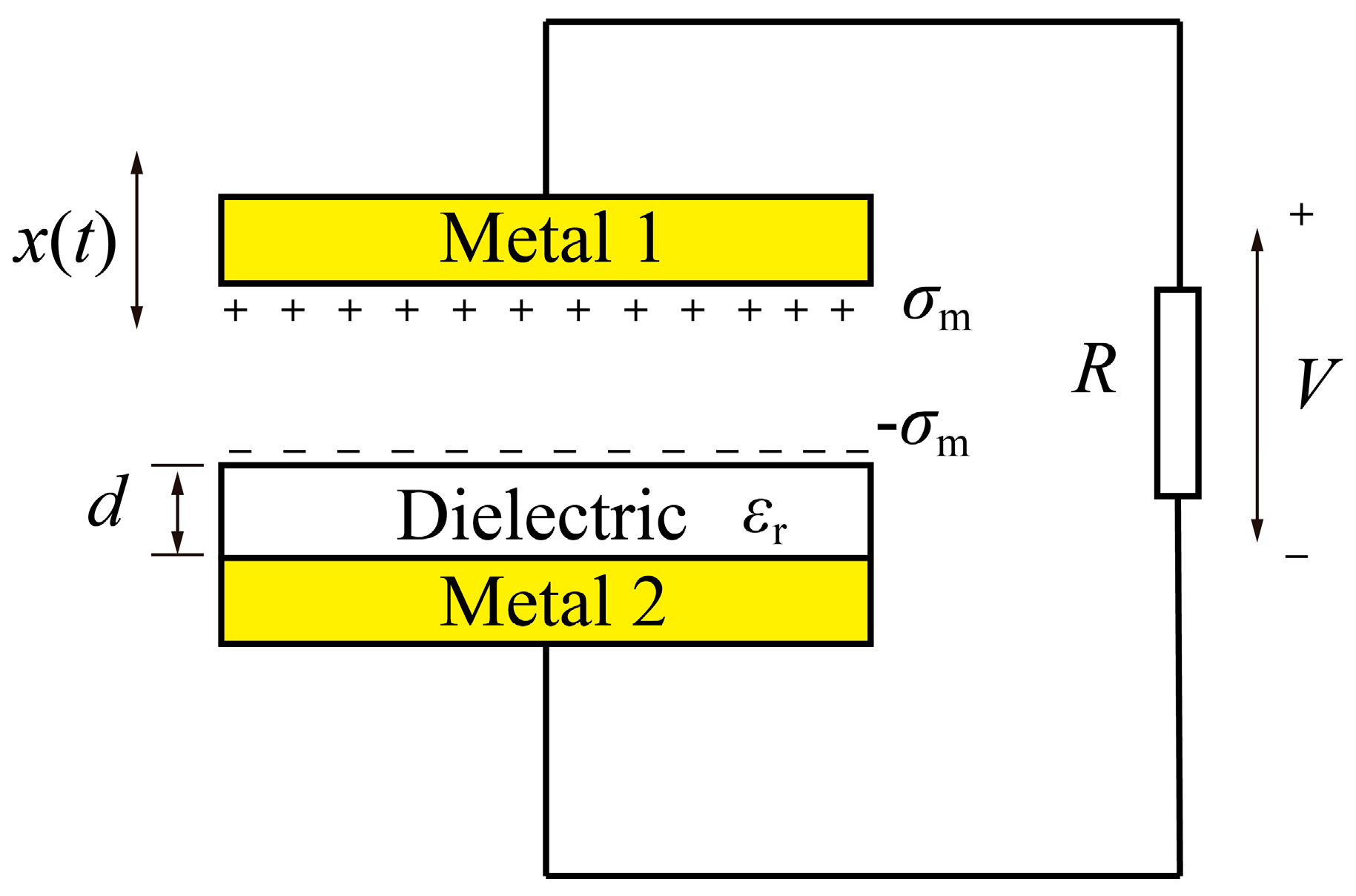
2. Theoretical Basis
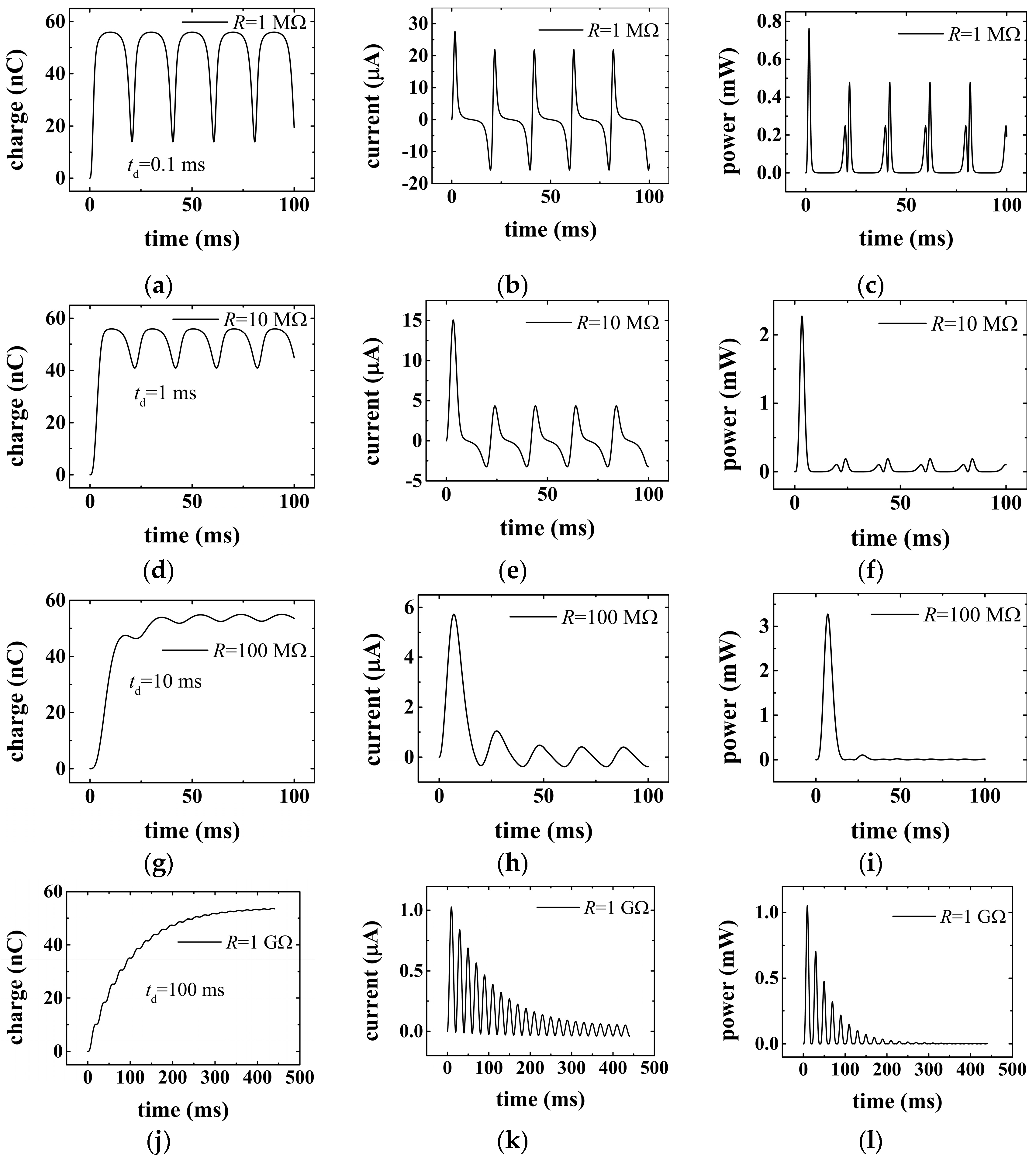
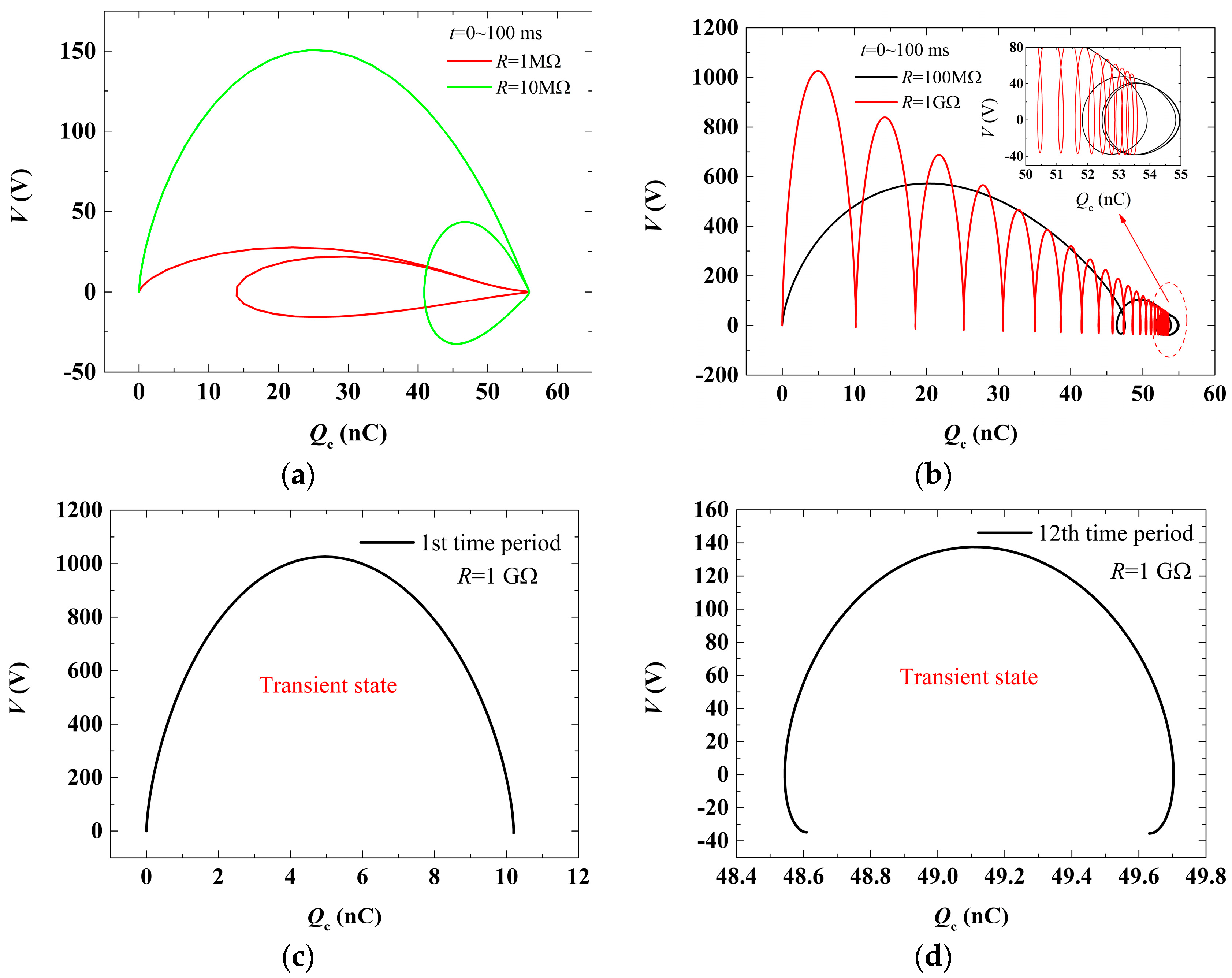
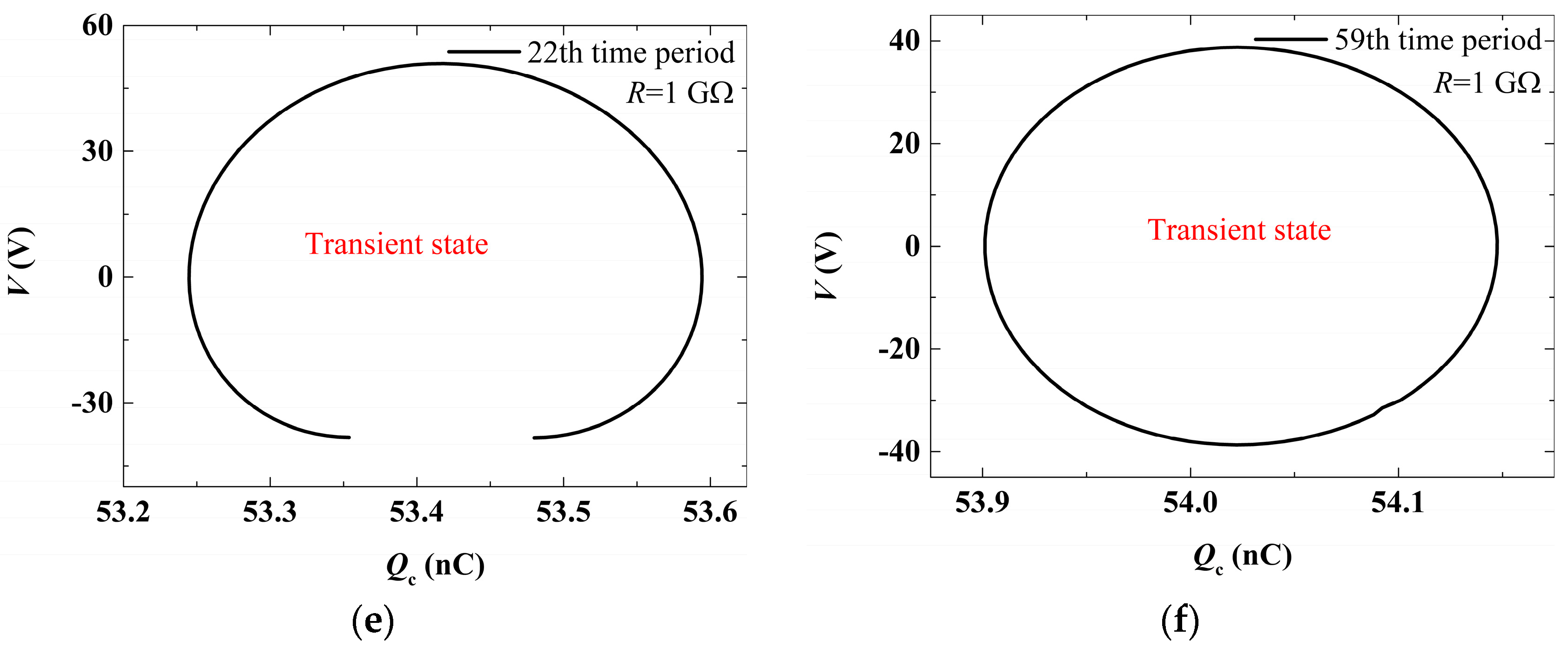
3. Results and Discussion
4. Experimental Verification and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
References
- Shi, Z.; Zhang, Y.; Gu, J.; Liu, B.; Fu, H.; Liang, H.; Ji, J. Triboelectric Nanogenerators: State of the Art. Sensors 2024, 24, 4298. [Google Scholar] [CrossRef]
- Choi, D.; Lee, Y.; Lin, Z.-H.; Cho, S.; Kim, M.; Ao, C.K.; Soh, S.; Sohn, C.; Jeong, C.K.; Lee, J.; et al. Recent Advances in Triboelectric Nanogenerators: From Technological Progress to Commercial Applications. ACS Nano 2023, 17, 11087–11219. [Google Scholar] [CrossRef]
- Cao, C.; Li, Z.; Shen, F.; Zhang, Q.; Gong, Y.; Guo, H.; Peng, Y.; Wang, Z.L. Progress in Techniques for Improving the Output Performance of Triboelectric Nanogenerators. Energy Environ. Sci. 2024, 17, 885–924. [Google Scholar] [CrossRef]
- Pan, C.; Cao, L.N.Y.; Meng, J.; Jia, L.; Hu, W.; Wang, Z.L.; Pu, X. Field Effect Nanogenerator Operated by Sliding Gates. Energy Environ. Sci. 2024, 17, 1132–1140. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.; Dai, Y.; Zhao, Z.; Wang, A.; Zhang, T.; Wang, Z.L. Achieving Ultrahigh Triboelectric Charge Density for Efficient Energy Harvesting. Nat. Commun. 2017, 8, 88. [Google Scholar] [CrossRef]
- Jiao, P.; Wang, Z.L.; Alavi, A.H. Maximizing Triboelectric Nanogenerators by Physics-Informed AI Inverse Design. Adv. Mater. 2024, 36, 2308505. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, S.; Liu, Q.; Bai, Y.; Jiang, T.; Guo, B.; Liu, C.; Wang, Z.L.; Luo, D. Self-Powered Carbon-Neutral System. Cell Rep. Phys. Sci. 2024, 5, 101871. [Google Scholar] [CrossRef]
- Gao, Y.; He, L.; Liu, D.; Zhang, J.; Zhou, L.; Wang, Z.L.; Wang, J. Spontaneously Established Reverse Electric Field to Enhance the Performance of Triboelectric Nanogenerators via Improving Coulombic Efficiency. Nat. Commun. 2024, 15, 4167. [Google Scholar] [CrossRef]
- Tao, X.; Chen, X.; Wang, Z.L. Design and Synthesis of Triboelectric Polymers for High Performance Triboelectric Nanogenerators. Energy Environ. Sci. 2023, 16, 3654–3678. [Google Scholar] [CrossRef]
- Niu, J.; Hu, R.; Li, M.; Zhang, L.; Xu, B.; Zhang, Y.; Luo, Y.; Ding, J.; Duan, Q. A Novel Triboelectric–Electromagnetic Hybrid Generator with a Multi-Layered Structure for Wind Energy Harvesting and Wind Vector Monitoring. Micromachines 2025, 16, 795. [Google Scholar] [CrossRef]
- Yang, S.; Klinkov, V.; Grozova, N.; Shalnova, S.; Larionova, T.; Tolochko, O.; Klimova-Korsmik, O. Nanostructures and Nanomaterials Integrated into Triboelectric Nanogenerators. Micromachines 2025, 16, 403. [Google Scholar] [CrossRef]
- Niu, S.; Wang, S.; Lin, L.; Liu, Y.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical Study of Contact-Mode Triboelectric Nanogenerators as an Effective Power Source. Energy Environ. Sci. 2013, 6, 3576. [Google Scholar] [CrossRef]
- Peng, J.; Kang, S.D.; Snyder, G.J. Optimization Principles and the Figure of Merit for Triboelectric Generators. Sci. Adv. 2017, 3, eaap8576. [Google Scholar] [CrossRef]
- Deane, J.H.B.; Dharmasena, R.D.I.G.; Gentile, G. Power Computation for the Triboelectric Nanogenerator. Nano Energy 2018, 54, 39–49. [Google Scholar] [CrossRef]
- Liu, W.; Shi, J. A Dynamics Model of Triboelectric Nanogenerator Transducers. Nano Energy 2021, 89, 106479. [Google Scholar] [CrossRef]
- Dharmasena, R.D.I.G.; Jayawardena, K.D.G.I.; Mills, C.A.; Deane, J.H.B.; Anguita, J.V.; Dorey, R.A.; Silva, S.R.P. Triboelectric Nanogenerators: Providing a Fundamental Framework. Energy Environ. Sci. 2017, 10, 1801–1811. [Google Scholar] [CrossRef]
- Dharmasena, R.D.I.G.; Deane, J.H.B.; Silva, S.R.P. Nature of Power Generation and Output Optimization Criteria for Triboelectric Nanogenerators. Adv. Energy Mater. 2018, 8, 1802190. [Google Scholar] [CrossRef]
- Dharmasena, R.D.I.G.; Jayawardena, K.D.G.I.; Mills, C.A.; Dorey, R.A.; Silva, S.R.P. A Unified Theoretical Model for Triboelectric Nanogenerators. Nano Energy 2018, 48, 391–400. [Google Scholar] [CrossRef]
- Lu, M.; Yin, W.; Peyton, A.; Qu, Z.; Meng, X.; Xie, Y.; Zhao, P.; Luo, J.; Zhao, Q.; Tao, Y.; et al. A Model for the Triboelectric Nanogenerator with Inductive Load and Its Energy Boost Potential. Nano Energy 2019, 63, 103883. [Google Scholar] [CrossRef]
- Shao, J.; Willatzen, M.; Shi, Y.; Wang, Z.L. 3D Mathematical Model of Contact-Separation and Single-Electrode Mode Triboelectric Nanogenerators. Nano Energy 2019, 60, 630–640. [Google Scholar] [CrossRef]
- Shao, J.; Liu, D.; Willatzen, M.; Wang, Z.L. Three-Dimensional Modeling of Alternating Current Triboelectric Nanogenerator in the Linear Sliding Mode. Appl. Phys. Rev. 2020, 7, 011405. [Google Scholar] [CrossRef]
- Guo, X.; Shao, J.; Willatzen, M.; Yang, Y.; Wang, Z.L. Three-Dimensional Mathematical Modelling and Dynamic Analysis of Freestanding Triboelectric Nanogenerators. J. Phys. D Appl. Phys. 2022, 55, 345501. [Google Scholar] [CrossRef]
- Shao, J.; Willatzen, M.; Wang, Z.L. Theoretical Modeling of Triboelectric Nanogenerators (TENGs). J. Appl. Phys. 2020, 128, 111101. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Dielectric thickness d | 125 |
| Relative dielectric permittivity | 3.4 |
| Area size S | 58 cm2 |
| Triboelectric charge density | 10 μC/m2 |
| Maximum displacement xm | 1 mm |
| Motion frequency f | 50 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Luo, H.; Zhang, R.; Ye, S.; Wei, H.; Zeng, Z.; Liu, F.; Zhou, G. A Study on the Transient Process of Contact-Mode Triboelectric Nanogenerators. Micromachines 2025, 16, 1070. https://doi.org/10.3390/mi16091070
Zhang S, Luo H, Zhang R, Ye S, Wei H, Zeng Z, Liu F, Zhou G. A Study on the Transient Process of Contact-Mode Triboelectric Nanogenerators. Micromachines. 2025; 16(9):1070. https://doi.org/10.3390/mi16091070
Chicago/Turabian StyleZhang, Shengyao, Hongchun Luo, Ru Zhang, Shun Ye, Haoyu Wei, Zhiqiang Zeng, Futi Liu, and Guiyu Zhou. 2025. "A Study on the Transient Process of Contact-Mode Triboelectric Nanogenerators" Micromachines 16, no. 9: 1070. https://doi.org/10.3390/mi16091070
APA StyleZhang, S., Luo, H., Zhang, R., Ye, S., Wei, H., Zeng, Z., Liu, F., & Zhou, G. (2025). A Study on the Transient Process of Contact-Mode Triboelectric Nanogenerators. Micromachines, 16(9), 1070. https://doi.org/10.3390/mi16091070







