Investigation of Scribing Parameters’ Influence on the Tomography and Crack Initiation of OLED Display Panels for Circular Structures
Abstract
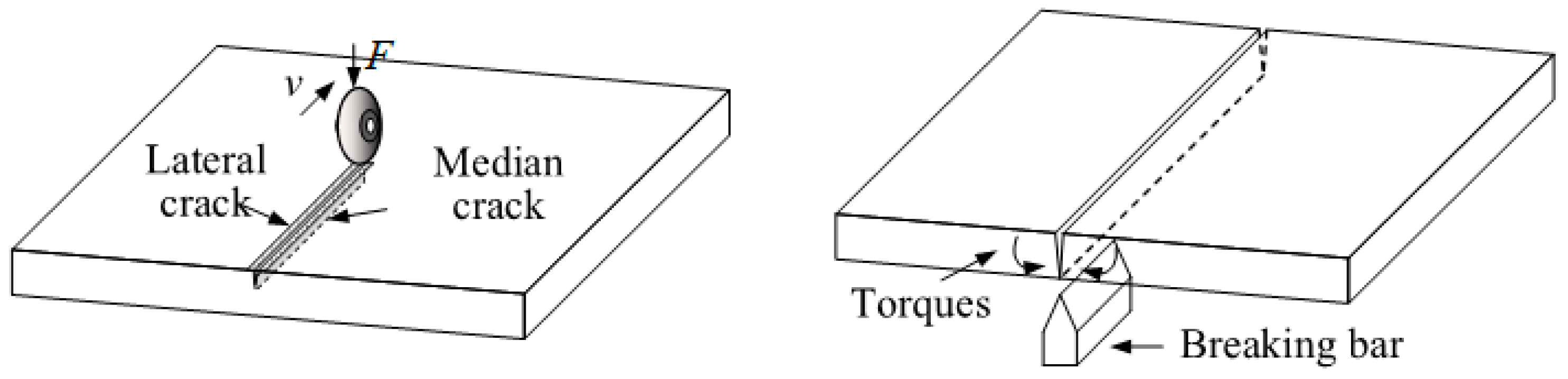
1. Introduction
2. Experimental Design and Setup
2.1. Experimental Design Method
2.2. Experimental Equipment and Materials
2.2.1. Construction of Scoring-Wheel Cutting Experimental Platform
2.2.2. Experimental Materials
2.3. Preparation of Display Panel Samples
2.4. Surface Quality Characterization
2.4.1. Morphology Characterization
2.4.2. Roughness Characterization
2.4.3. Hardness Characterization
3. Experimental Results and Analysis
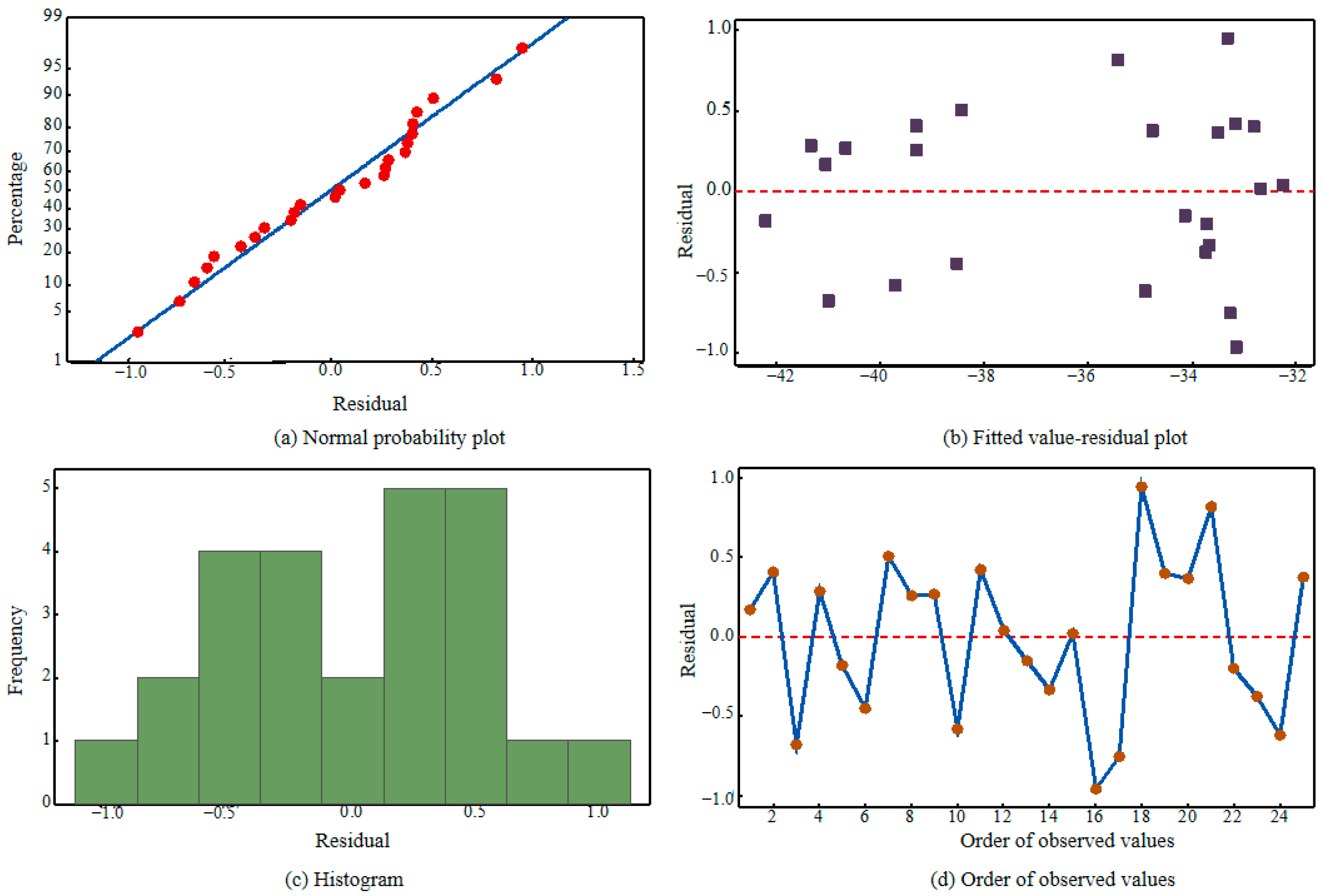
3.1. Analysis of Signal-to-Noise Ratio Response Table
3.2. Analysis of Variance for Signal-to-Noise Ratio
3.3. Estimation of Signal-to-Noise Ratio Model Coefficients
4. Determination of Parameter Combination Based on Morphological Characteristics
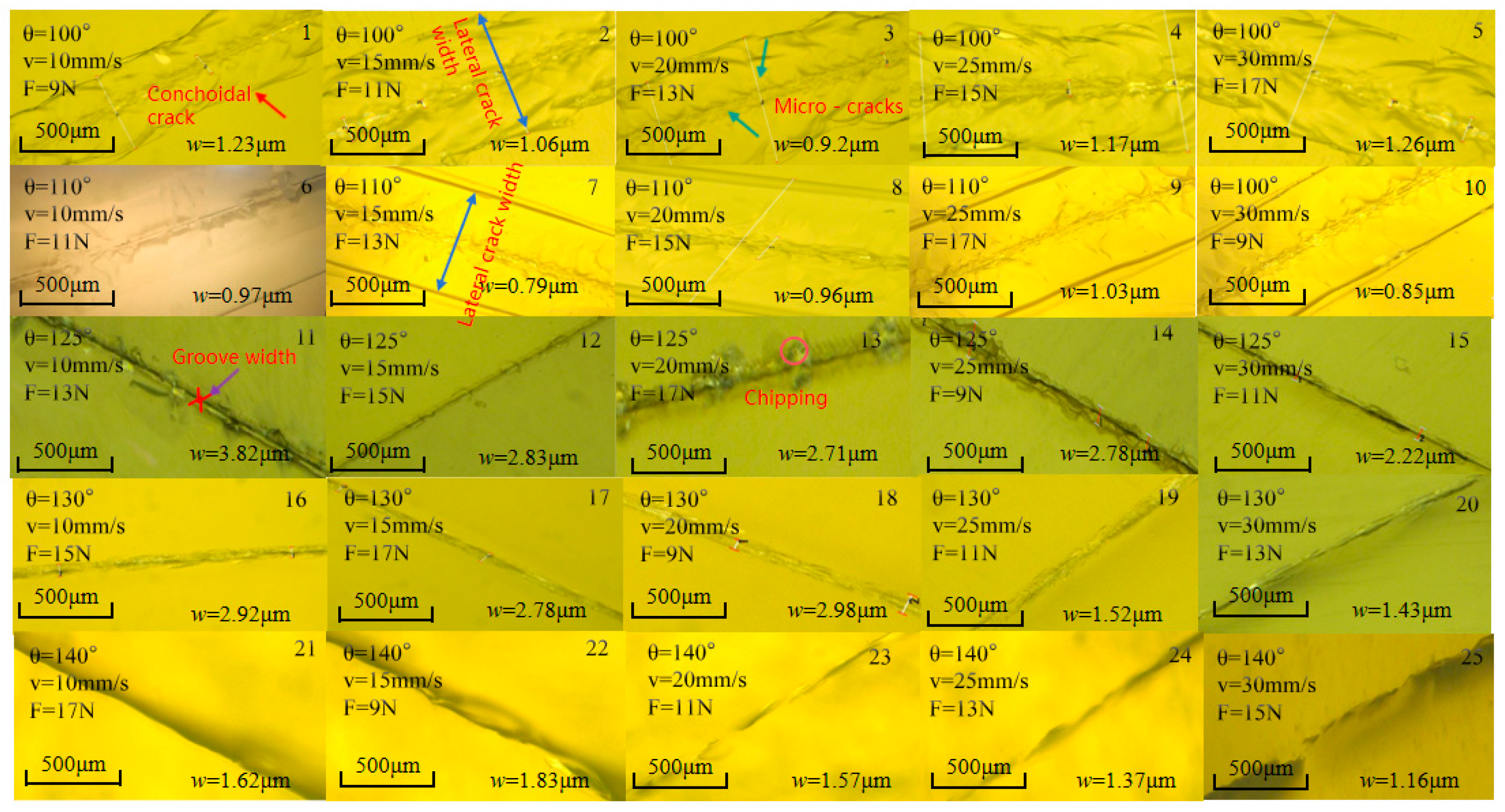
4.1. Determination of Cutter Wheel Angle
4.2. Determination of Cutting Speed
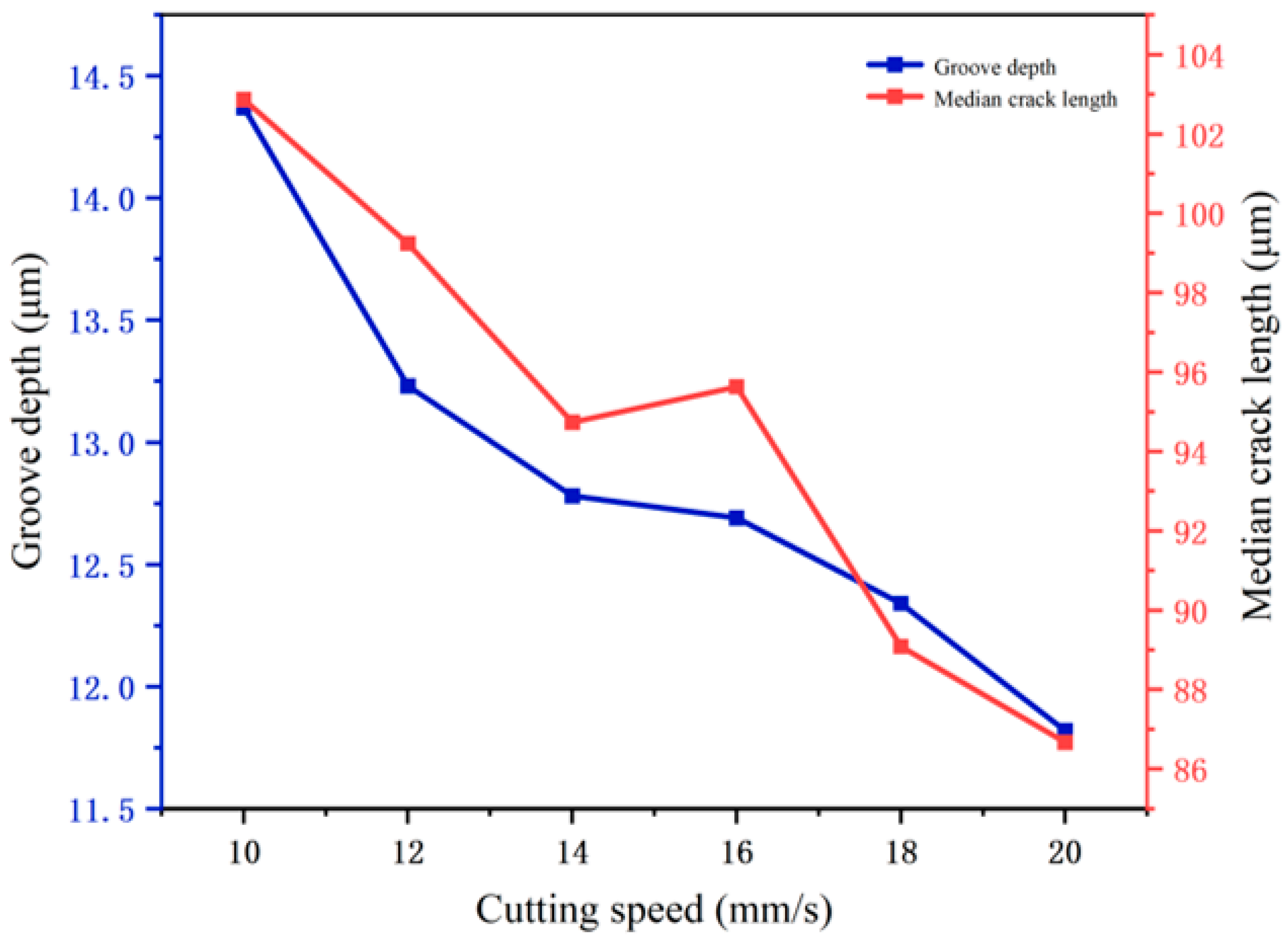
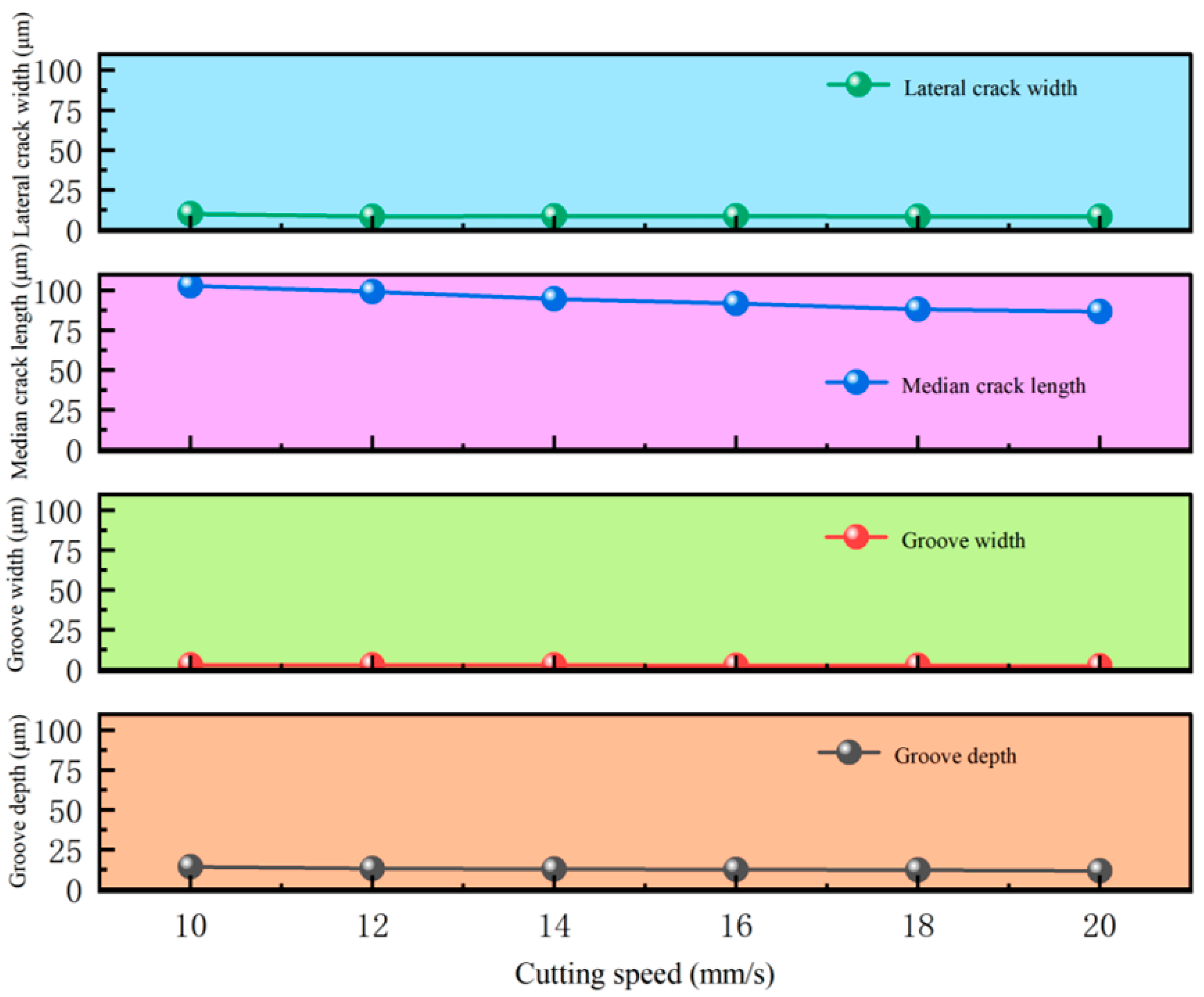
4.2.1. Influence of Cutting Speed on Cutting Surface Morphology and Transverse Cracks
4.2.2. Influence of Cutting Speed on Cross-Sectional Morphology and Median Cracks
5. Verification of Optimal Parameter Combination
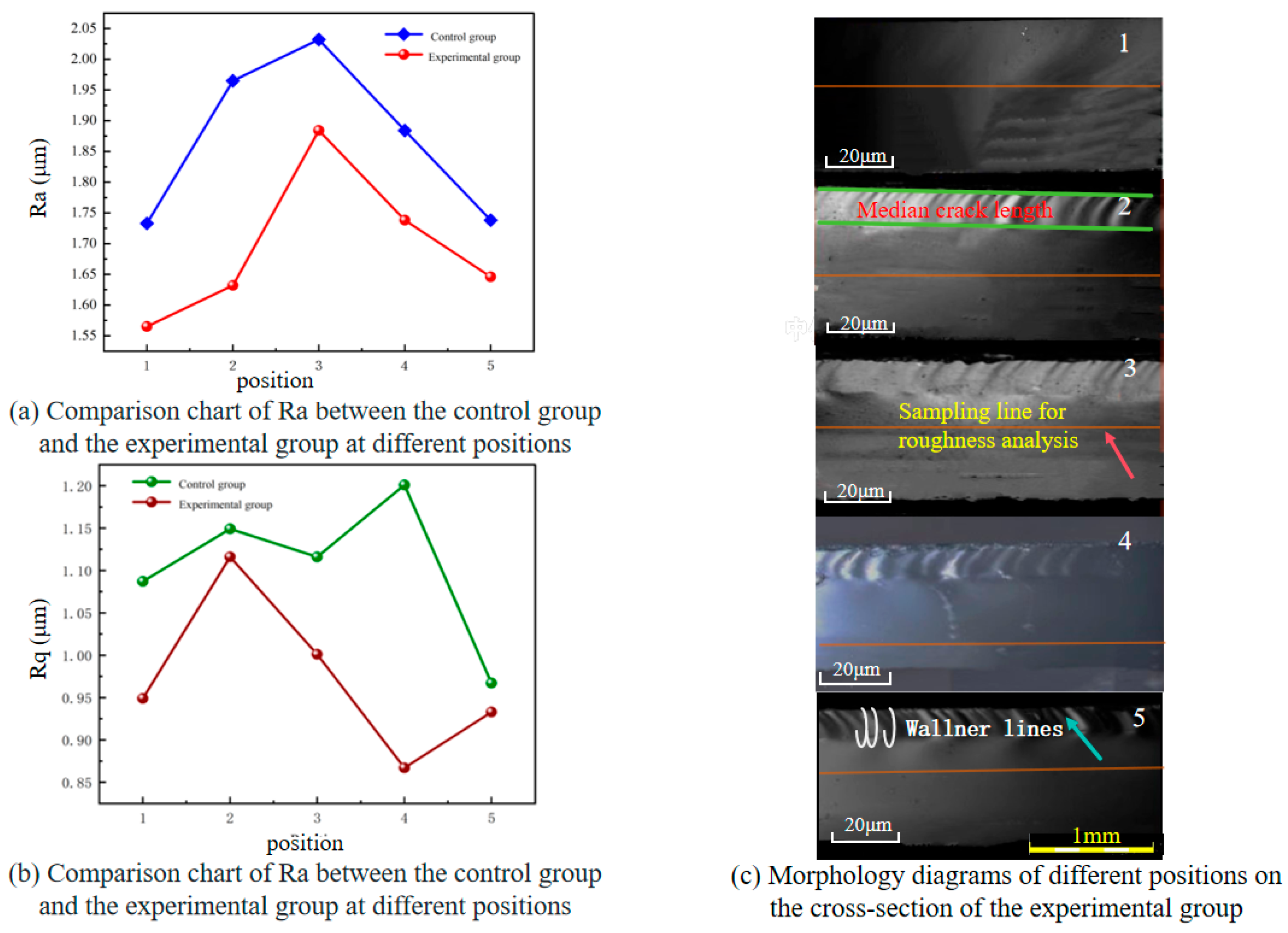
5.1. Roughness Analysis
5.2. Hardness Testing
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Liu, J.Y.; Zhao, Y.D.; Cao, Y.C. Recent advancements of high efficient donor–acceptor type blue small molecule applied for OLEDs. Mater. Today 2017, 20, 258–266. [Google Scholar] [CrossRef]
- Liu, J. The application of organic materials used in OLED display. Results Opt. 2025, 21, 100856. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, Z.; Qiu, X.; Sun, J.; Zhao, Z. Low-Temperature Gas Cooling Correction Trajectory Offset Technology of Laser-Induced Thermal Crack Propagation for Asymmetric Linear Cutting Glass. Processes 2023, 11, 1493. [Google Scholar] [CrossRef]
- Zhao, C.; Ding, Y.; Yang, L.; Wang, Y.; Wang, Z. Cutting the Closed Curve Shape Inside Glass with Laser Induced Thermal-Crack Propagation. In Advanced Laser Technology and Application, Proceedings of the 9th Applied Optics and Photonics China (AOPC 2020), Beijing, China, 30 November–2 December 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11562, pp. 298–303. [Google Scholar]
- Dornfeld, D.; Min, S.; Takeuchi, Y. Recent Advances in Mechanical Micromachining. CIRP Ann. 2006, 55, 745–768. [Google Scholar] [CrossRef]
- Sarkisov, P.D.; Smirnov, M.I.; Spiridonov, Y.A.; Karapetyan, A.R. Effect of residual stresses in float-glass on cutting quality. Glass Ceram. 2012, 69, 149–152. [Google Scholar] [CrossRef]
- Tsai, C.H.; Huang, B.W. Diamond scribing and laser breaking for LCD glass substrates. J. Mater. Process. Technol. 2007, 198, 350–358. [Google Scholar] [CrossRef]
- Khatak, P. Laser cutting technique: A literature review. Mater. Today Proc. 2022, 56, 2484–2489. [Google Scholar]
- Zhimalov, A.B.; Solinov, V.F.; Kondratenko, V.S.; Kaplina, T.V. Laser cutting of float glass during production. Glass Ceram. 2006, 63, 319–321. [Google Scholar] [CrossRef]
- Xiong, L.; An, Y.; Zhang, L.; Tang, C.; Zhang, T.; Zuo, A.; Gao, W. Highly Efficient Cutting of Quartz Glass with Low Roughness and Minor Chipping Using Bessel Laser Beams. Photonics 2025, 12, 162. [Google Scholar] [CrossRef]
- Ikawa, N.; Donaldson, R.; Komanduri, R.; König, W.; Aachen, T.; McKeown, P.; Moriwaki, T.; Stowers, I. Ultraprecision Metal Cutting—The Past, the Present and the Future. CIRP Ann. 1991, 40, 587–594. [Google Scholar] [CrossRef]
- Kim, J.; Park, S.; Lee, J. Optimization of scribing parameters for glass substrates using orthogonal array and analysis of variance. J. Mater. Process. Technol. 2016, 231, 220–227. [Google Scholar]
- Cheng, H.C.; Li, K.H.; Shih, C.Y.; Chen, W.H. Characterization of the Flexural Strength and Fatigue Life of Ultrathin Glass After Dicing. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 2213–2221. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, F.H.; Li, Y.L. Effect of Optimized Scribing and Breaking Conditions on Cleland Module Process for TFT-LCD Glass Substrates. Adv. Disp. 2006, 9, 43–46. [Google Scholar]
- Xuedan, P.; Bing-hua, S.; Jun-wen, X.; Li-li, W. Study of the Influence of Cutting Parameters on LCD Machining Quality. Infrared 2018, 39, 30–35. [Google Scholar]
- Luo, S.Y.; Tsai, Y.Y.; Chen, C.H. Studies on cut-off grinding of BK7 optical glass using thin diamond wheels. J. Mater. Process. Technol. 2006, 173, 321–329. [Google Scholar] [CrossRef]
- Li, J.S.; Guo, B.F.; Zhang, B.D. Problems and Their Solutions in Cutting Process for Liquid Crystal Glass Substrate. Glass Enamel Ophthalmic Opt. 2020, 48, 19–21+24. [Google Scholar]
- Swain, M.V.; Metras, J.C.; Guillemet, C.G. A deformation and fracture mechanics approach to the scoring and breaking of glass. J. Non-Cryst. Solids 1980, 38, 445–450. [Google Scholar] [CrossRef]
- Pan, C.T.; Hsieh, C.C.; Su, C.Y.; Liu, Z.S. Study of cutting quality for TFT-LCD glass substrate. Int. J. Adv. Manuf. Technol. 2008, 39, 1071–1079. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Zhang, J. Experimental investigation on crack formation mechanism in ultra-thin glass cutting. Ceram. Int. 2019, 45, 17774–17782. [Google Scholar]
- Ono, T.; Tanaka, K. Effect of scribe-wheel dimensions on the cutting of AMLCD glass substrate. J. Soc. Inf. Disp. 2001, 9, 87–94. [Google Scholar] [CrossRef]
- Hasegawa, R.; Matsusaka, S.; Hidai, H.; Chiba, A.; Morita, N.; Onuma, T. In-process estimation of fracture surface morphology during wheel scribing of a glass sheet by high-speed photoelastic observation. Precis. Eng. 2017, 48, 164–171. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Li, Y. Finite element analysis of crack propagation in glass cutting with a diamond wheel. Int. J. Adv. Manuf. Technol. 2018, 96, 3977–3985. [Google Scholar]
- Murakami, K.; Matsusaka, S.; Itoh, S.; Hidai, H.; Kitaichi, M. Effect of bottom deformation on median crack repropagation after wheel scribing in glass. Int. J. Appl. Glass Sci. 2025, 16, e16686. [Google Scholar] [CrossRef]
- Li, D.; Li, J.; Kong, H.; Guo, J.; Huang, L.; Liu, Y. Investigation of Ultra-Thin Glass Scribing Mechanism. Coatings 2025, 15, 275. [Google Scholar] [CrossRef]
- Chang, B.P.; Chan, W.H.; Zamri, M.H.; Md Akil, H.; Chuah, H.G. Investigating the Effects of Operational Factors on Wear Properties of Heat-Treated Pultruded Kenaf Fiber-Reinforced Polyester Composites using Taguchi Method. J. Nat. Fibers 2019, 16, 702–717. [Google Scholar] [CrossRef]
- Khoshaim, A.B.; Elsheikh, A.H.; Moustafa, E.B.; Basha, M.; Showaib, E.A. Experimental investigation on laser cutting of PMMA sheets: Effects of process factors on kerf characteristics. J. Mater. Res. Technol. 2021, 11, 235–246. [Google Scholar] [CrossRef]
- Moradi, M.; Moghadam, M.K.; Shamsborhan, M.; Beiranvand, Z.M.; Rasouli, A.; Vahdati, M.; Bakhtiari, A.; Bodaghi, M. Simulation, statistical modeling, and optimization of CO2 laser cutting process of polycarbonate sheets. Optik 2021, 225, 164932. [Google Scholar] [CrossRef]
- Luo, Y.; Xie, X.; Zhang, Z.; Li, Z.; Huang, Y. Ultrafast laser composite cutting ultra-thin glass. Opt. Commun. 2024, 555, 130224. [Google Scholar] [CrossRef]









| Levels | Factors | ||
|---|---|---|---|
| A (°) | B (mm/s) | C (N) | |
| 1 | 100 | 10 | 9 |
| 2 | 110 | 15 | 11 |
| 3 | 125 | 20 | 13 |
| 4 | 130 | 25 | 15 |
| 5 | 140 | 30 | 17 |
| Serial Number | A (°) | B (mm/s) | C (N) |
|---|---|---|---|
| 1 | 100 | 10 | 9 |
| 2 | 100 | 15 | 11 |
| 3 | 100 | 20 | 13 |
| 4 | 100 | 25 | 15 |
| 5 | 100 | 30 | 17 |
| 6 | 110 | 10 | 11 |
| 7 | 110 | 15 | 13 |
| 8 | 110 | 20 | 15 |
| 9 | 110 | 25 | 17 |
| 10 | 110 | 30 | 9 |
| 11 | 125 | 10 | 13 |
| 12 | 125 | 15 | 15 |
| 13 | 125 | 20 | 17 |
| 14 | 125 | 25 | 9 |
| 15 | 125 | 30 | 11 |
| 16 | 130 | 10 | 15 |
| 17 | 130 | 15 | 17 |
| 18 | 130 | 20 | 9 |
| 19 | 130 | 25 | 11 |
| 20 | 130 | 30 | 13 |
| 21 | 140 | 10 | 17 |
| 22 | 140 | 15 | 9 |
| 23 | 140 | 20 | 11 |
| 24 | 140 | 25 | 13 |
| 25 | 140 | 30 | 15 |
| Instrument Name | Instrument Model | Manufacturer | City | Country |
|---|---|---|---|---|
| Ultrasonic cleaner | KQ2200E | Kunshan Ultrasonic Instrument Co., Ltd. | Kunshan | China |
| Laser confocal microscope | OLS5000 | Olympus Corporation | Tokyo | Japan |
| Touch screen microhardness tester | HVST-1000Z | Shanghai Taiming Optical Instrument Co., Ltd. | Shanghai | China |
| Super-depth-of-field microscope | VH-Z500R | Keyence Corporation | Osaka | Japan |
| Component | Fe2O3 | Al2O3 | MgO | CaO | Na2O + K2O | SiO2 |
|---|---|---|---|---|---|---|
| Content | 0.1 ± 0.02 | 1 ± 0.5 | 4 ± 0.5 | 13.5 ± 0.5 | 8.1 ± 0.4 | 72 ± 0.5 |
| Serial Number | A (°) | B (mm/s) | C (N) | h (µm) | w (µm) | l (µm) | d (µm) |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 10 | 9 | 14.38 | 1.23 | 136.58 | 173.52 |
| 2 | 100 | 15 | 11 | 15.57 | 1.06 | 111.55 | 135.36 |
| 3 | 100 | 20 | 13 | 17.43 | 0.92 | 128.69 | 204.84 |
| 4 | 100 | 25 | 15 | 15.87 | 1.17 | 118.18 | 191.52 |
| 5 | 100 | 30 | 17 | 11.58 | 1.26 | 130.63 | 228.24 |
| 6 | 110 | 10 | 11 | 15.52 | 0.97 | 98.48 | 146.88 |
| 7 | 110 | 15 | 13 | 16.12 | 0.79 | 104.27 | 117.36 |
| 8 | 110 | 20 | 15 | 16.63 | 0.96 | 107.43 | 142.56 |
| 9 | 110 | 25 | 17 | 22.73 | 1.03 | 123.13 | 167.72 |
| 10 | 110 | 30 | 9 | 16.64 | 0.85 | 125.73 | 163.36 |
| 11 | 125 | 10 | 13 | 12.75 | 3.32 | 85.12 | 9.56 |
| 12 | 125 | 15 | 15 | 14.34 | 2.83 | 80.12 | 5.28 |
| 13 | 125 | 20 | 17 | 13.67 | 2.71 | 102.46 | 6.34 |
| 14 | 125 | 25 | 9 | 16.31 | 2.78 | 98.53 | 7.61 |
| 15 | 125 | 30 | 11 | 13.48 | 2.22 | 84.32 | 8.73 |
| 16 | 130 | 10 | 15 | 15.37 | 2.92 | 99.86 | 9.87 |
| 17 | 130 | 15 | 17 | 12.93 | 2.78 | 99.24 | 8.23 |
| 18 | 130 | 20 | 9 | 12.38 | 2.98 | 81.73 | 8.41 |
| 19 | 130 | 25 | 11 | 10.06 | 2.52 | 82.34 | 9.35 |
| 20 | 130 | 30 | 13 | 9.58 | 2.43 | 89.78 | 8.78 |
| 21 | 140 | 10 | 17 | 12.62 | 3.12 | 105.32 | 16.75 |
| 22 | 140 | 15 | 9 | 10.67 | 3.34 | 97.46 | 14.57 |
| 23 | 140 | 20 | 11 | 12.85 | 3.46 | 99.32 | 15.87 |
| 24 | 140 | 25 | 13 | 11.71 | 3.49 | 117.45 | 17.32 |
| 25 | 140 | 30 | 15 | 13.61 | 3.66 | 102.12 | 18.08 |
| Level | A | B | C |
|---|---|---|---|
| 1 | −40.98 | −36.26 | −36.29 |
| 2 | −39.33 | −35.40 | −35.41 |
| 3 | −33.18 | −36.30 | −36.20 |
| 4 | −33.21 | −36.67 | −36.16 |
| 5 | −34.50 | −36.57 | −37.14 |
| Delta | 7.80 | 1.28 | 1.73 |
| Ranking | 1 | 3 | 2 |
| Source | Free Degree | Seq SS | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|---|
| A | 4 | 267.706 | 267.706 | 66.9265 | 132.39 | 0.000 |
| B | 4 | 5.066 | 5.066 | 1.2664 | 2.51 | 0.098 |
| C | 4 | 7.553 | 7.553 | 1.8881 | 3.73 | 0.034 |
| Residual error | 12 | 6.066 | 6.066 | 0.5055 | - | - |
| Total | 24 | 286.391 | - | - | - | - |
| Item | Coefficient | Coefficient Standard Error | T | p |
|---|---|---|---|---|
| constant | −36.2391 | 0.1422 | −254.841 | 0.000 |
| A1 | −4.7371 | 0.2844 | −16.656 | 0.000 |
| A2 | −3.0895 | 0.2844 | −10.863 | 0.000 |
| A3 | 3.0613 | 0.2844 | 10.764 | 0.000 |
| A4 | 3.0273 | 0.2844 | 10.644 | 0.000 |
| B1 | −0.0199 | 0.2844 | −0.070 | 0.945 |
| B2 | 0.8436 | 0.2844 | 2.966 | 0.012 |
| B3 | −0.0594 | 0.2844 | −0.209 | 0.838 |
| B4 | −0.4346 | 0.2844 | −1.528 | 0.152 |
| C1 | −0.0508 | 0.2844 | −0.179 | 0.861 |
| C2 | 0.8323 | 0.2844 | 2.926 | 0.013 |
| C3 | 0.0381 | 0.2844 | 0.134 | 0.896 |
| C4 | 0.0791 | 0.2844 | 0.278 | 0.786 |
| S = 0.7110, R-Sq = 97.9%, R-Sq (adjustment) = 95.8% | ||||
| Serial Number | C (mm/s) | h (µm) | w (µm) | l (µm) | d (µm) |
|---|---|---|---|---|---|
| 1 | 10 | 14.37 | 3.02 | 102.86 | 9.87 |
| 2 | 12 | 13.23 | 2.88 | 99.24 | 8.23 |
| 3 | 14 | 12.78 | 2.98 | 94.73 | 8.41 |
| 4 | 16 | 12.69 | 2.73 | 91.63 | 8.39 |
| 5 | 18 | 12.34 | 2.64 | 88.08 | 8.17 |
| 6 | 20 | 11.82 | 2.32 | 86.67 | 8.27 |
| Position | Control Group | Experimental Group | ||||
|---|---|---|---|---|---|---|
| Ra (µm) | Rq (µm) | Rt (µm) | Ra (µm) | Rq (µm) | Rt (µm) | |
| 1 | 1.733 | 1.087 | 10.878 | 1.565 | 0.949 | 9.564 |
| 2 | 1.965 | 1.149 | 10.564 | 1.632 | 1.116 | 8.954 |
| 3 | 2.032 | 1.116 | 10.954 | 1.884 | 1.001 | 11.306 |
| 4 | 1.884 | 1.201 | 11.306 | 1.738 | 0.867 | 10.821 |
| 5 | 1.738 | 0.967 | 12.021 | 1.646 | 0.933 | 9.933 |
| Mean value | 1.870 | 1.104 | 11.145 | 1.693 | 0.973 | 10.116 |
| Standard deviation | 0.127 | 0.092 | 0.503 | 0.125 | 0.097 | 0.893 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, H.; Zhu, X.; Li, G.; Liu, Y. Investigation of Scribing Parameters’ Influence on the Tomography and Crack Initiation of OLED Display Panels for Circular Structures. Micromachines 2025, 16, 1071. https://doi.org/10.3390/mi16091071
Kong H, Zhu X, Li G, Liu Y. Investigation of Scribing Parameters’ Influence on the Tomography and Crack Initiation of OLED Display Panels for Circular Structures. Micromachines. 2025; 16(9):1071. https://doi.org/10.3390/mi16091071
Chicago/Turabian StyleKong, Huaye, Xijing Zhu, Guohong Li, and Yao Liu. 2025. "Investigation of Scribing Parameters’ Influence on the Tomography and Crack Initiation of OLED Display Panels for Circular Structures" Micromachines 16, no. 9: 1071. https://doi.org/10.3390/mi16091071
APA StyleKong, H., Zhu, X., Li, G., & Liu, Y. (2025). Investigation of Scribing Parameters’ Influence on the Tomography and Crack Initiation of OLED Display Panels for Circular Structures. Micromachines, 16(9), 1071. https://doi.org/10.3390/mi16091071







