Design and Research of Superimposed Force Sensor
Abstract
1. Introduction
2. Scheme Design and Simulation Analysis
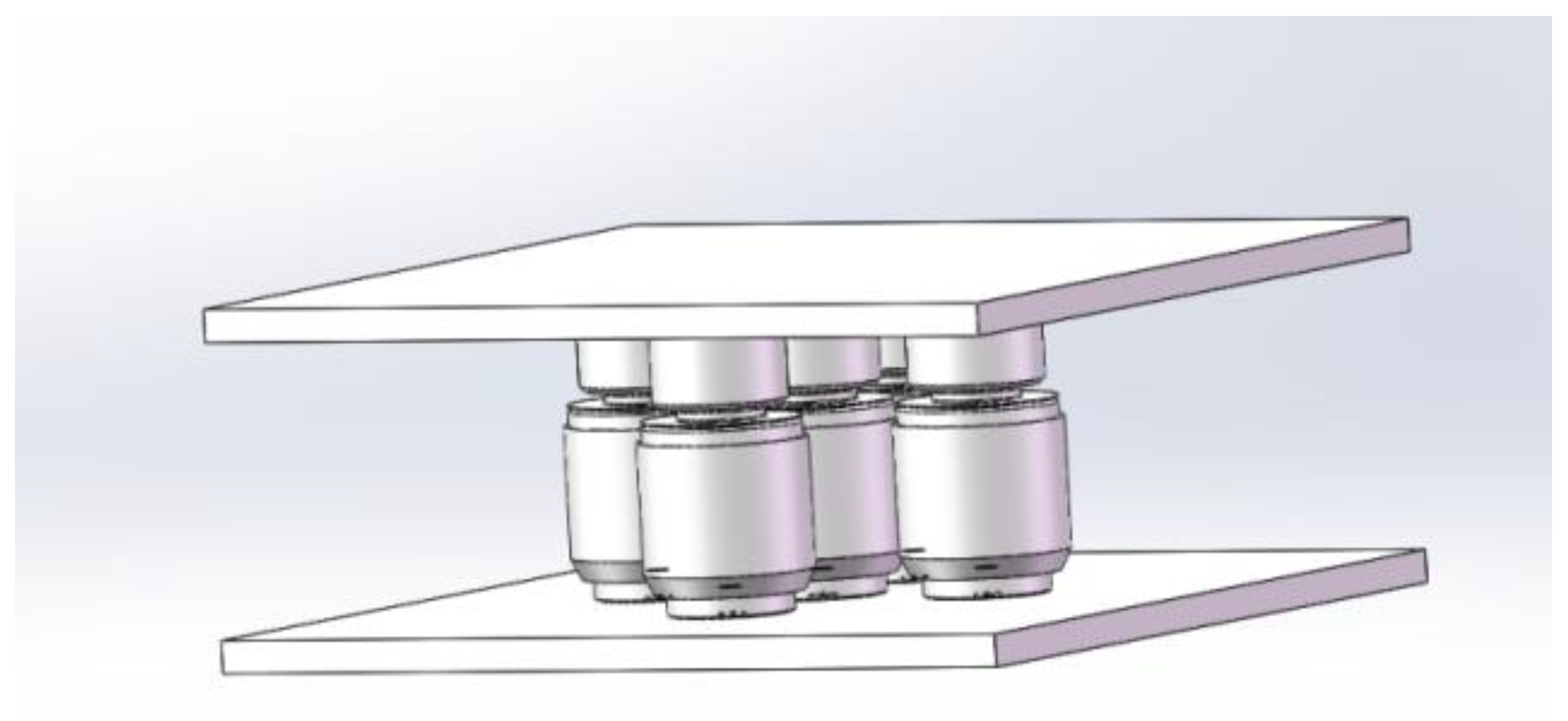
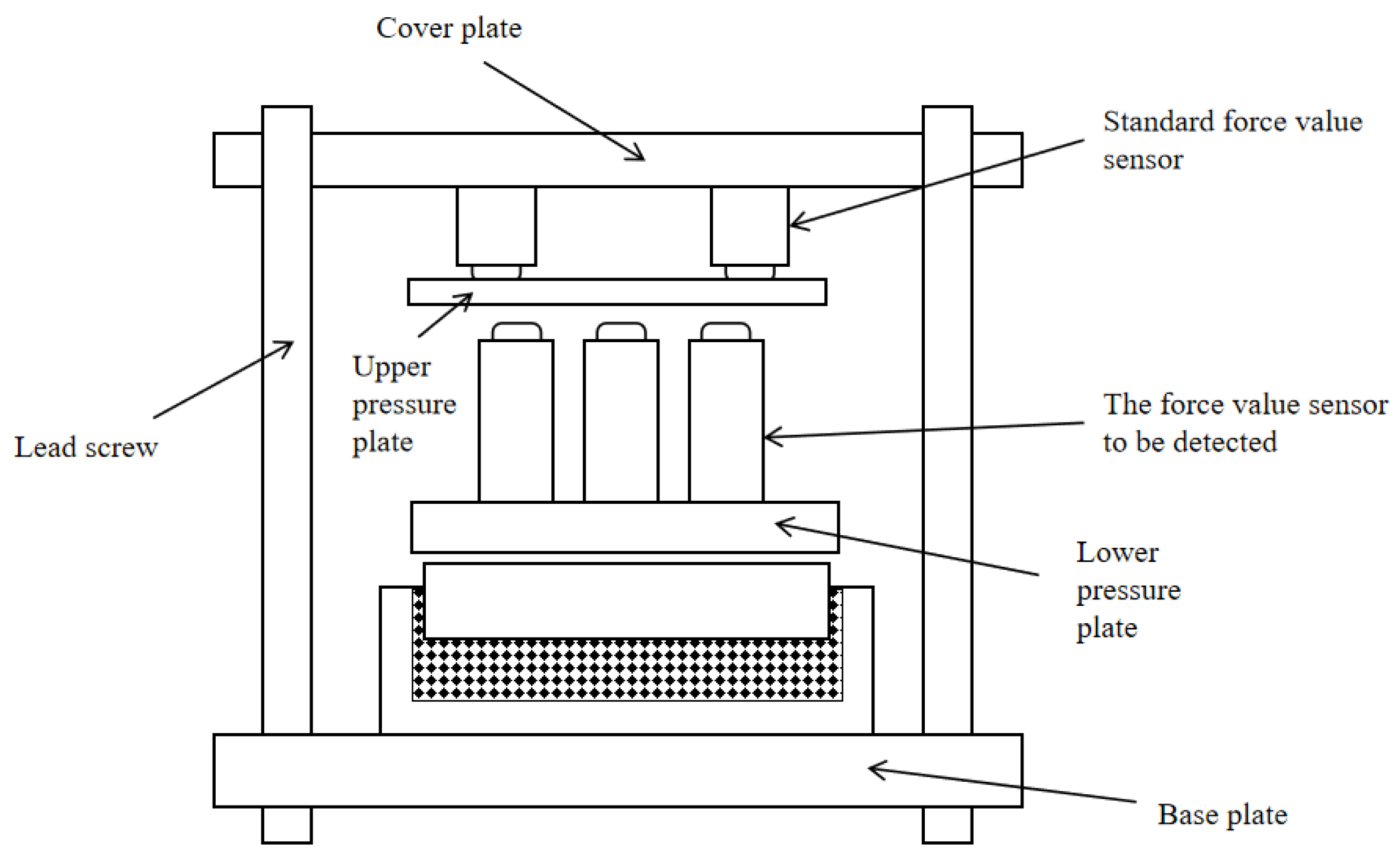
2.1. Design of Scheme
2.2. Three-Dimensional Model Construction
2.3. Finite Element Simulation Preprocessing
2.4. Material Properties and Boundary Conditions
3. Results
3.1. Total Deformation
3.2. Y-Direction Stress
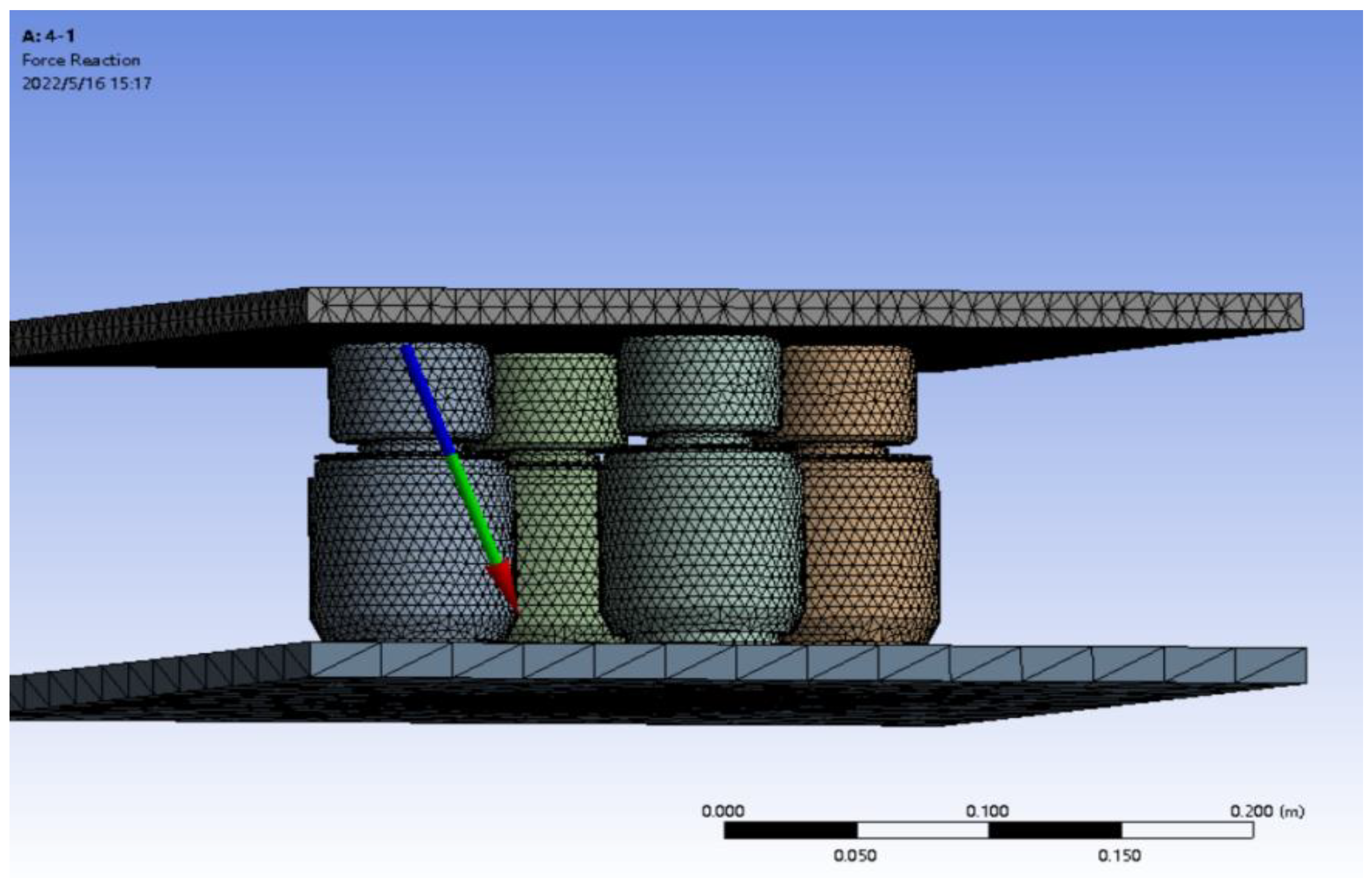
3.3. Force Value
4. Discussion
5. Conclusions
- (1)
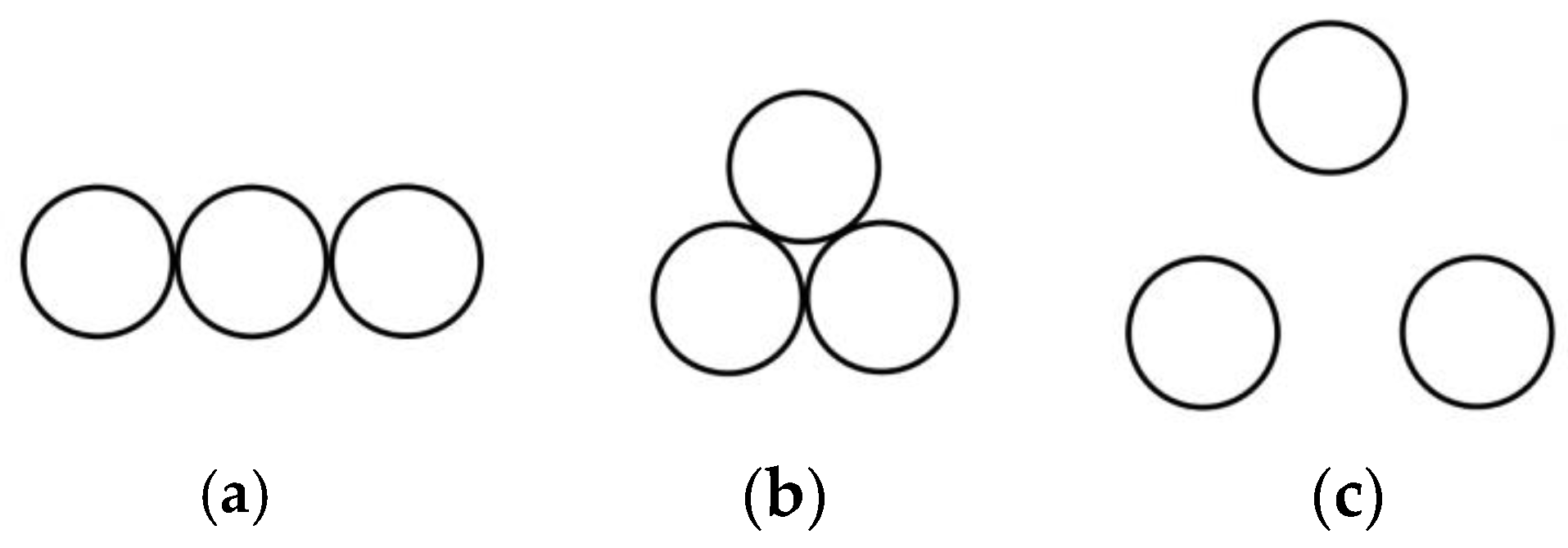
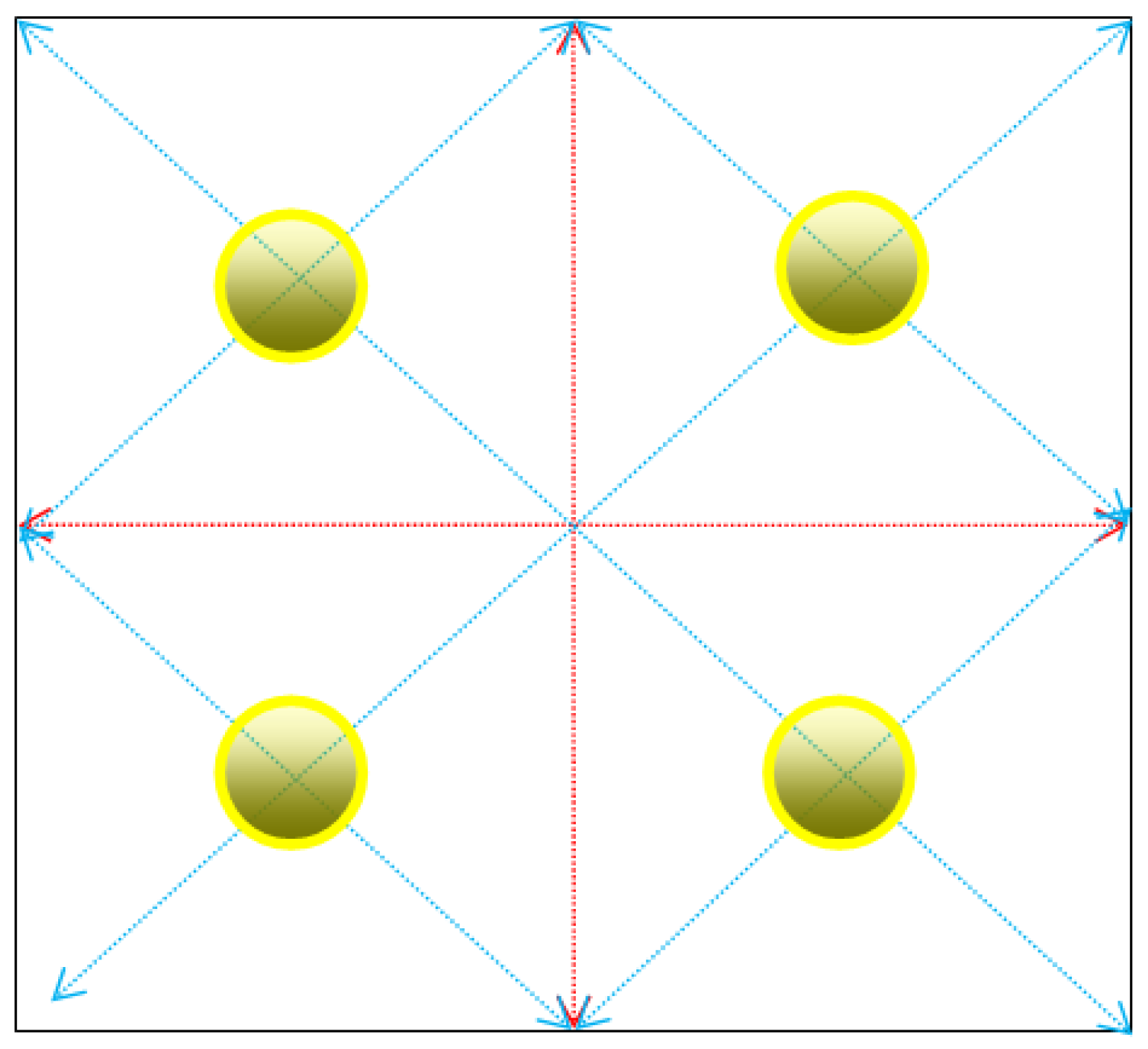
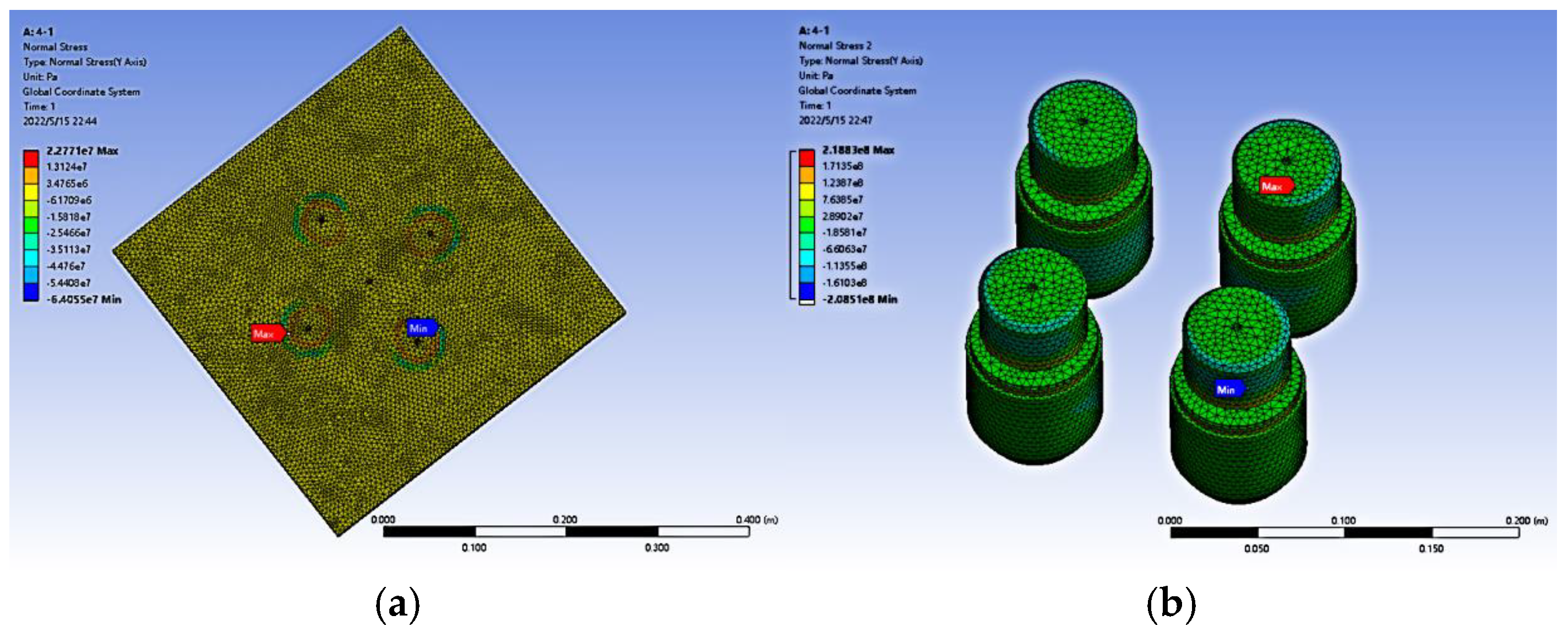
- In the superimposed force measurement model, the layout of sensors should be spaced at certain intervals, and the entire chassis should be utilized as much as possible to reduce the deformation of the pressure-bearing plate under force, improve the stability of the overall equipment, and reduce the error caused by deformation when measuring the force value. Among them, when the three sensors are placed in a “Pin font” shape, the total deformation of the pressure-bearing plate is the smallest, which is 0.42848 mm. The position is located at the top corner of the upper pressure-bearing plate, while the center position of the lower chassis is the minimum deformation position of the entire model.
- (2)
- The stress of the superimposed force measurement model is mainly concentrated at the contact surface between the lower end face of the upper pressure-bearing plate and the upper end face of the sensor. Among them, when the three sensors are placed in a “Pin font” shape, the stress is the smallest, with a magnitude of 20.358 MPa, which is less than the yield strength of structural steel and meets the safety requirements.
- (3)
- The error between the total force value of each superimposed sensor in the Y direction and the applied force value is controlled within one ten-thousandth to one ten-thousandth. The error does not change significantly with the number and layout of sensors and remains within an acceptable range.
- (4)
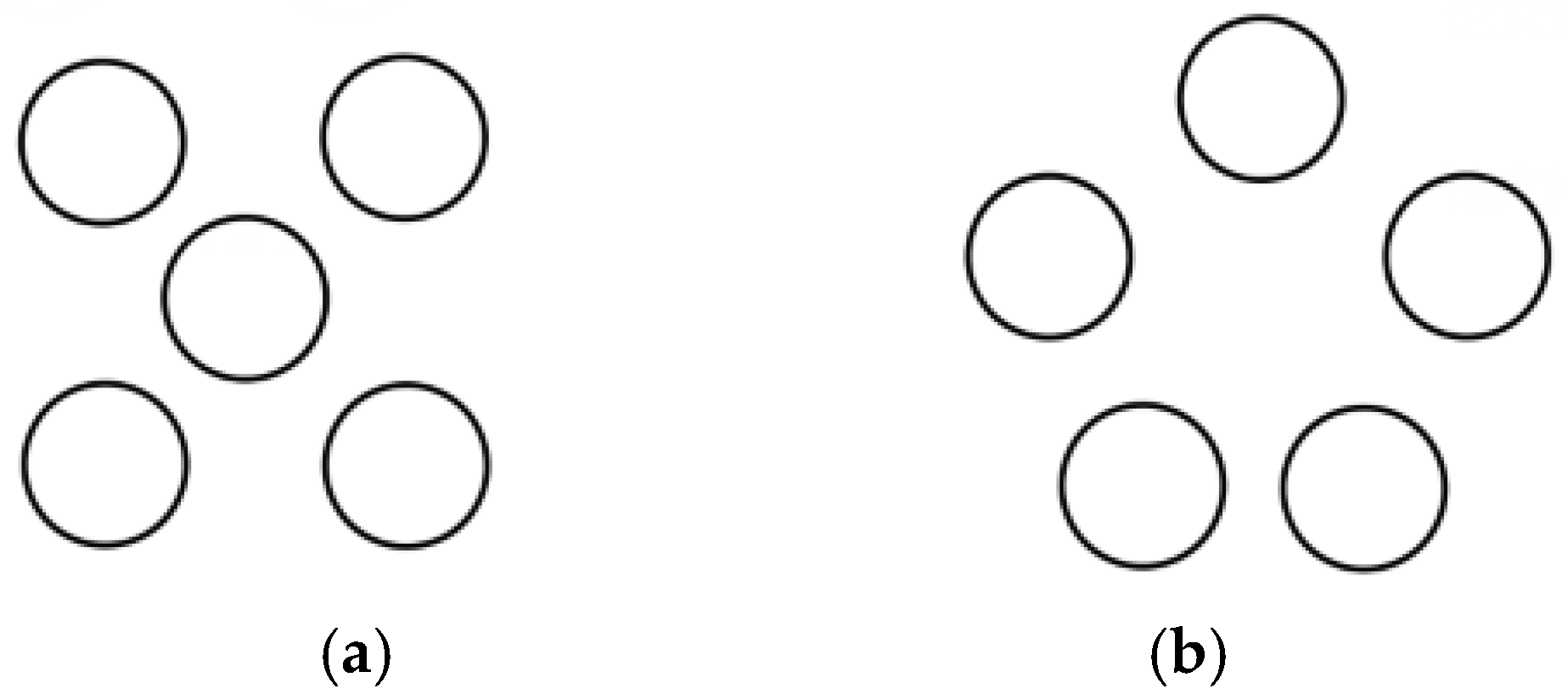
- When the three sensors are arranged in a “Pin font” shape for the test, the sum of the forces measured by each sensor differs from the theoretical parallel value by only a few ten-thousandths of the indicated value of the force standard machine. This error will not fluctuate greatly with the increase in the test force value, meeting the corresponding requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Wang, Y.; Hu, X. Review on the Development of Force Standard Machine. Metrol. Test. Technol. 2020, 47, 61–63. [Google Scholar] [CrossRef]
- Hasegawa, A.; Hayashi, T. Calibration and measurement capability evaluation for 1 MN hydraulic force standard machine newly installed at NMIJ. Eng. Res. Express 2024, 6, 025427. [Google Scholar] [CrossRef]
- Schwind, D.; Eller, M.; Krusemark, O. A new deadweight force standard machine for classifying C6 load cells under temperature conditions. Meas. Sens. 2025, 38, 101333. [Google Scholar] [CrossRef]
- Isaac, N.M.; David, I.B. A proposal of an evaluation method for hydraulic standard force machine. Meas. Sens. 2021, 18, 100319. [Google Scholar]
- Zhang, Z.X.; Liu, X.H.; Zhang, Q.M. Verification and Characteristics of Superimposed Force Standard Machine. Equip. Manag. Maint. 2024, 6, 47–50. [Google Scholar] [CrossRef]
- Zhang, H.; Tao, Z.; Xin, L.; Qian, L.; Qi, S. Research and discussion on traceability of force values for large force standard machines. Meas. Sens. 2025, 38, 101372. [Google Scholar] [CrossRef]
- Liu, T. Some Understanding and Thoughts on the Current Situation of Superimposed Force Standard Machines. Stand. Metrol. Instrum. 2019, 4, 44–45+48. [Google Scholar]
- Zheng, H.; Wang, P.; Li, S.X.; Wei, S.L.; Zhang, T. Research on Reference Standard Technology of Superimposed Force Standard Machine. Metrol. Test. Technol. 2020, 47, 25–26+30. [Google Scholar] [CrossRef]
- Baumgarten, S.; Kahmann, H.; Röske, D. Metrological characterization of a 2 kN · m torque standard machine for superposition with axial forces up to 1 MN. Metrologia 2016, 53, 1165–1176. [Google Scholar] [CrossRef]
- Yu, Y.L.; Kang, Z.Y.; Hu, X.Y. A New Type of superimposed force Standard Machine. Shanghai Metrol. Test. 2017, 44, 23–25. [Google Scholar]
- Yang, M.K.; Zhang, W.Q. Control Method of Hydraulic System for Superimposed Force Standard Machine. Instrum. Technol. 2019, 10, 32–34. [Google Scholar] [CrossRef]
- Hai, D.; Zhao, W.M.; Liu, Q.H. Development of 20 MN Superimposed Force Standard Machine. Ind. Metrol. 2017, 27 (Suppl. 2), 55–57. [Google Scholar]
- Wang, X.R. Frame Structure Design and Optimization of 60MN Superimposed Force Standard Device. Qual. Tech. Superv. Res. 2014, 4, 32–36. [Google Scholar] [CrossRef]
- Huang, A.Y.; Liu, S.X. Research on Force Value Transmission System of Compound Force Standard Machine. Digit. Manuf. Sci. 2025, 23, 11–15+42. [Google Scholar]
- Wang, Y.Y.; Wang, S.A.; Li, W.Z. Technical Transformation of 1MN Superimposed Force Standard Machine. Metrol. Technol. 2015, 1, 42–44. [Google Scholar]
- Han, J. Development of a New Type of Superimposed Compound Force Standard Machine. Eng. Exp. 2019, 59, 80–81. [Google Scholar]
- Ngo, H.H.; Lalin, V.V.; Lalina, I.I. The Idea of a “Loop Fragment” of the Finite Element Force Method in the Loop Resultant Method for Static Structural Analysis. Mater. Proc. 2024, 18, 3. [Google Scholar]
- Luo, X.; Xue, D.; Yan, R.; Han, C.; Tao, Z.C.; Li, S.S. Design of a Wide-Range Superimposed Force Standard Machine. Metrol. Technol. 2019, 1, 17–19. [Google Scholar]
- Zhang, W. Characteristics and Verification of Superimposed Force Standard Machine. Metrol. Technol. 2018, 9, 42–45+67. [Google Scholar]
- Lees, A.S.; Kelly, R.B. Railway formation design by elasto-plastic FEM mechanistic-empirical approach. Transp. Geotech. 2023, 39, 100955. [Google Scholar] [CrossRef]
- Osman, S.M.; Khaled, K.M. Proposal for improving force testing machines calibration standards. Measurement 2019, 146, 643–652. [Google Scholar] [CrossRef]
- Aydemir, B.; Vatan, C.; Dizdar, H. Comparison of force standard machines in the range of 100 kN and 1000 kN. Metrologia 2020, 57, 07006. [Google Scholar] [CrossRef]






| Materials | Density | Tensile Yield Strength | Compressive Yield Strength | Tensile Strength Limit |
|---|---|---|---|---|
| Structural steel | 7850 kg × m3 | 250 MPa | 250 MPa | 460 MPa |
| Number of Sensors | Placement Method | Maximum Deformation | Location |
|---|---|---|---|
| 3 | Single font | / | / |
| 3 | Tight circle | 0.53148 mm | Top corner |
| 3 | “Pin font” | 0.42848 mm | Top corner |
| 4 | Tight square | 0.62565 mm | Top corner |
| 4 | Sparse square | 0.45199 mm | Top corner |
| 4 | “3 + 1” | 0.54681 mm | Top corner |
| 5 | “4 + 1” | 0.57020 mm | Top corner |
| 5 | Sparse ring | 0.60385 mm | Top corner |
| Number of Sensors | Placement Method | Upper Bearing Plate | Maximum Stress | Upper End Face of the Sensor | Maximum Stress |
|---|---|---|---|---|---|
| 3 | Single font | / | / | / | / |
| 3 | Tight circle | Contact surface | 21.450 MPa | Contact surface | 21.451 MPa |
| 3 | “Pin font” | Contact surface | 20.358 MPa | Contact surface | 20.352 MPa |
| 4 | Tight square | Contact surface | 33.891 MPa | Contact surface | 33.281 MPa |
| 4 | Sparse square | Contact surface | 22.771 MPa | Contact surface | 22.765 MPa |
| 4 | “3 + 1” | Contact surface | 25.835 MPa | Contact surface | 25.835 MPa |
| 5 | “4 + 1” | Contact surface | 29.744 MPa | Contact surface | 29.744 MPa |
| 5 | Sparse ring | Contact surface | 32.513 MPa | Contact surface | 32.548 MPa |
| Arrangement Mode | The First Component | Second Component | The Third Component | Force Sum | Error |
|---|---|---|---|---|---|
| Single font | / | / | / | / | / |
| Tight circle | 10,008.2 N | 9993.1 N | 9998.9 N | 30,000.2 N | 6.6678 × 10−6 |
| “Pin font” | 10,004.3 N | 9997.3 N | 9998.5 N | 30,000.1 N | 3.333 × 10−6 |
| Arrangement Mode | The First Component | Second Component | The Third Component | The Fourth Component | Force Sum | Error |
|---|---|---|---|---|---|---|
| Tight square | 10,015 N | 9986.5 N | 10,008 N | 9992.3 N | 40,001.8 N | 4.5 × 10−5 |
| Sparse square | 10,010 N | 9989.8 N | 10,012 N | 9988.4 N | 40,000.2 N | 5.0 × 10−6 |
| “3 + 1” placement | 10,000.5 N | 10,004.6 N | 9994.2 N | 10,000.1 N | 39,999.4 N | 1.5 × 10−5 |
| Arrangement Mode | The First | Second | The Third | The Fourth | The Fifth | Force Sum | Error |
|---|---|---|---|---|---|---|---|
| “4 + 1” | 10,000.8 N | 9988.4 N | 10,012 N | 9994.2 N | 10,006.7 N | 50,002.1 N | 4.2 × 10−5 |
| Sparse ring | 10,005.2 N | 10,003.7 N | 9995.6 N | 10,001.9 N | 9992.6 N | 49,999.0 N | 2.0 × 10−5 |
| Force Standard Machine (kN) | 31715918 (kN) | 52043494 (kN) | 52043493 (kN) | Actual Parallel (kN) | Theoretical Parallel (kN) | Error |
|---|---|---|---|---|---|---|
| 3 | 0.9690 | 1.0548 | 0.9768 | 3.0006 | / | / |
| 6 | 1.9445 | 2.0772 | 1.9776 | 5.9993 | 5.9959 | 0.06% |
| 9 | 2.9473 | 3.0960 | 2.9575 | 9.0008 | 8.9957 | 0.06% |
| 12 | 3.9590 | 4.1610 | 3.8773 | 11.9973 | 11.9938 | 0.03% |
| 15 | 4.9705 | 5.2264 | 4.7997 | 14.9966 | 14.9922 | 0.03% |
| 18 | 5.9808 | 6.2914 | 5.7241 | 17.9963 | 17.9912 | 0.03% |
| 21 | 6.9859 | 7.3634 | 6.6473 | 20.9966 | 21.001 | −0.02% |
| 24 | 7.9894 | 8.4310 | 7.5758 | 23.9962 | 24.0114 | −0.06% |
| 27 | 8.9929 | 9.4980 | 8.5051 | 26.996 | 27.0038 | −0.03% |
| 30 | 9.9959 | 10.5647 | 9.4364 | 29.997 | 29.9966 | 0.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Shao, J.; Xu, Y.; He, Z.; Liu, S. Design and Research of Superimposed Force Sensor. Micromachines 2025, 16, 1069. https://doi.org/10.3390/mi16091069
Wu G, Shao J, Xu Y, He Z, Liu S. Design and Research of Superimposed Force Sensor. Micromachines. 2025; 16(9):1069. https://doi.org/10.3390/mi16091069
Chicago/Turabian StyleWu, Genshang, Jinggan Shao, Yicun Xu, Zhanshu He, and Shifei Liu. 2025. "Design and Research of Superimposed Force Sensor" Micromachines 16, no. 9: 1069. https://doi.org/10.3390/mi16091069
APA StyleWu, G., Shao, J., Xu, Y., He, Z., & Liu, S. (2025). Design and Research of Superimposed Force Sensor. Micromachines, 16(9), 1069. https://doi.org/10.3390/mi16091069







