A 90–100 GHz SiGe BiCMOS 6-Bit Digital Phase Shifter with a Coupler-Based 180° Unit for Phased Arrays
Abstract
1. Introduction
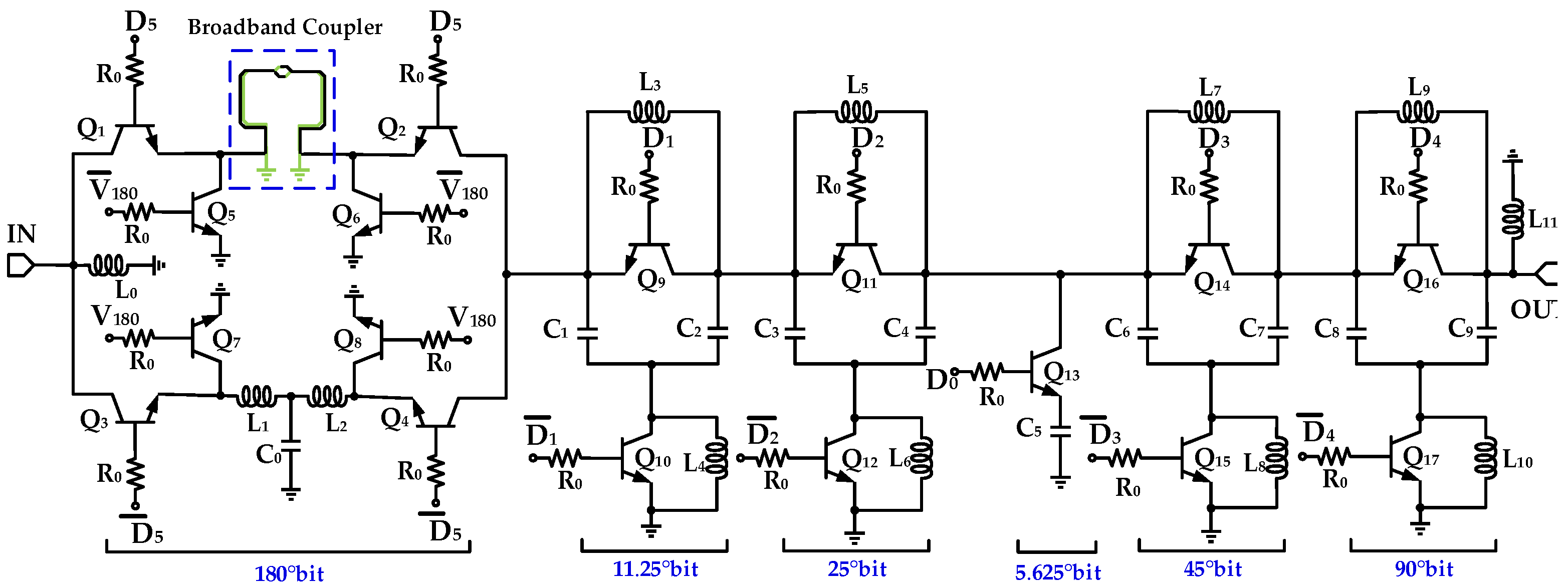
2. 180° Phase Shifter with a Broadband Coupler
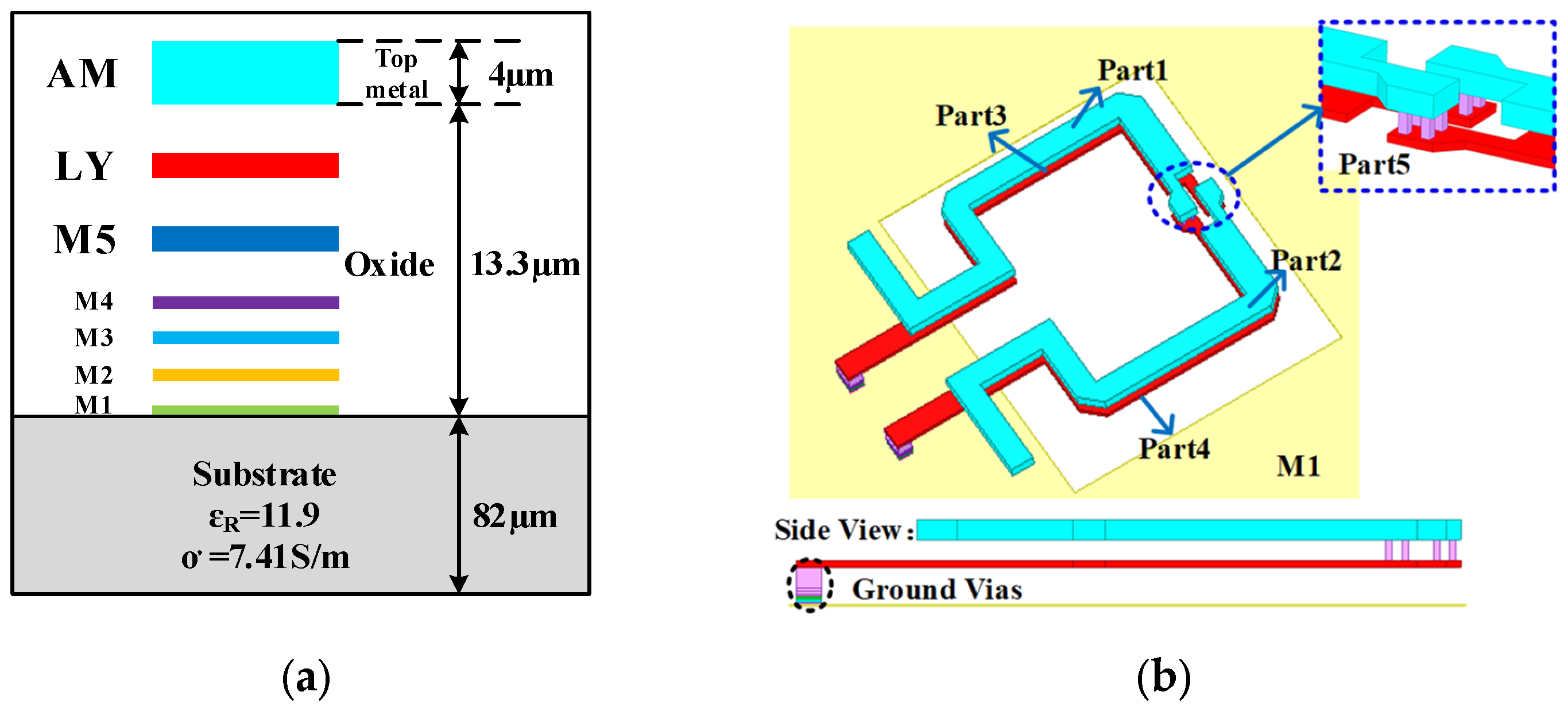
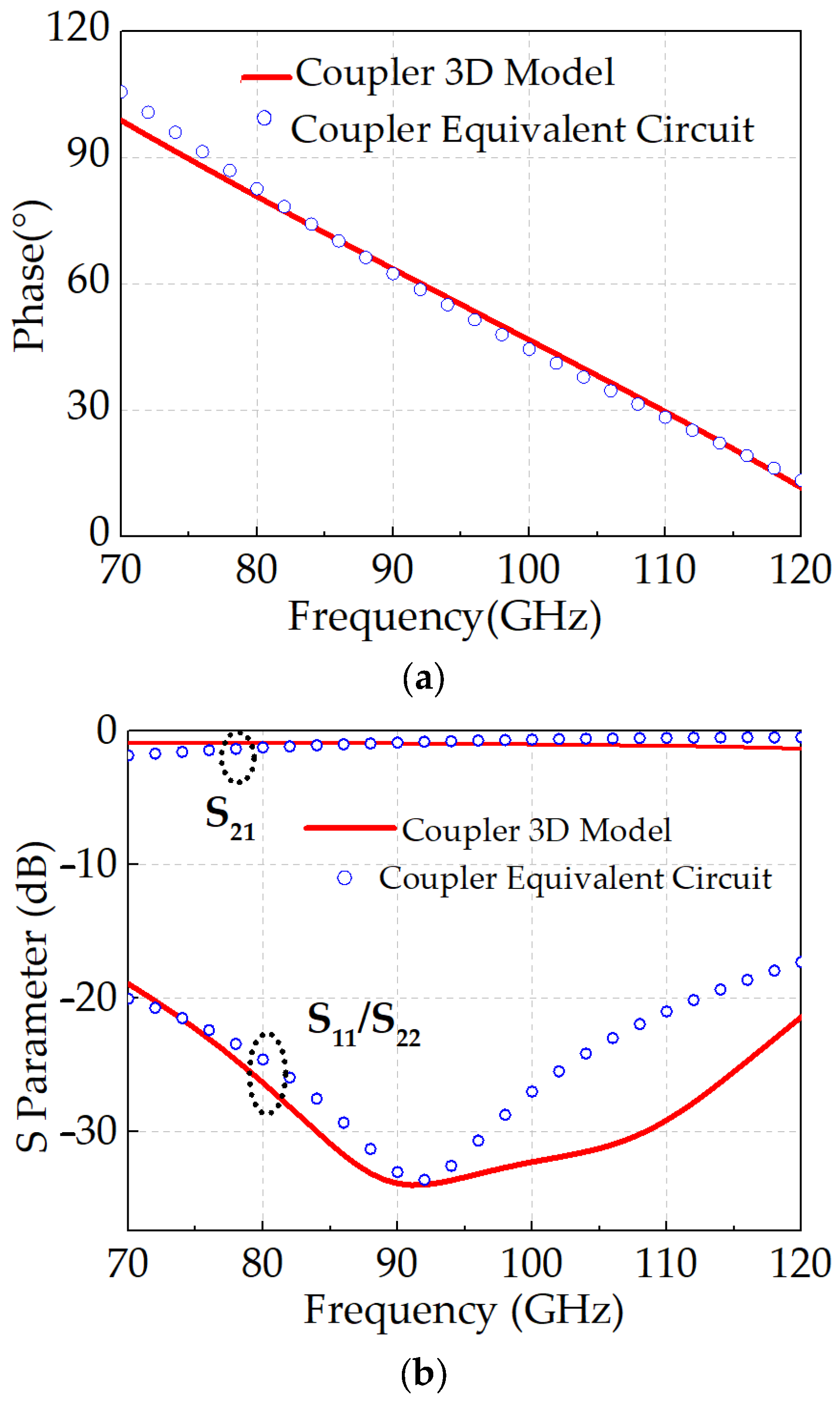
2.1. A. Design of Broadband Coupler
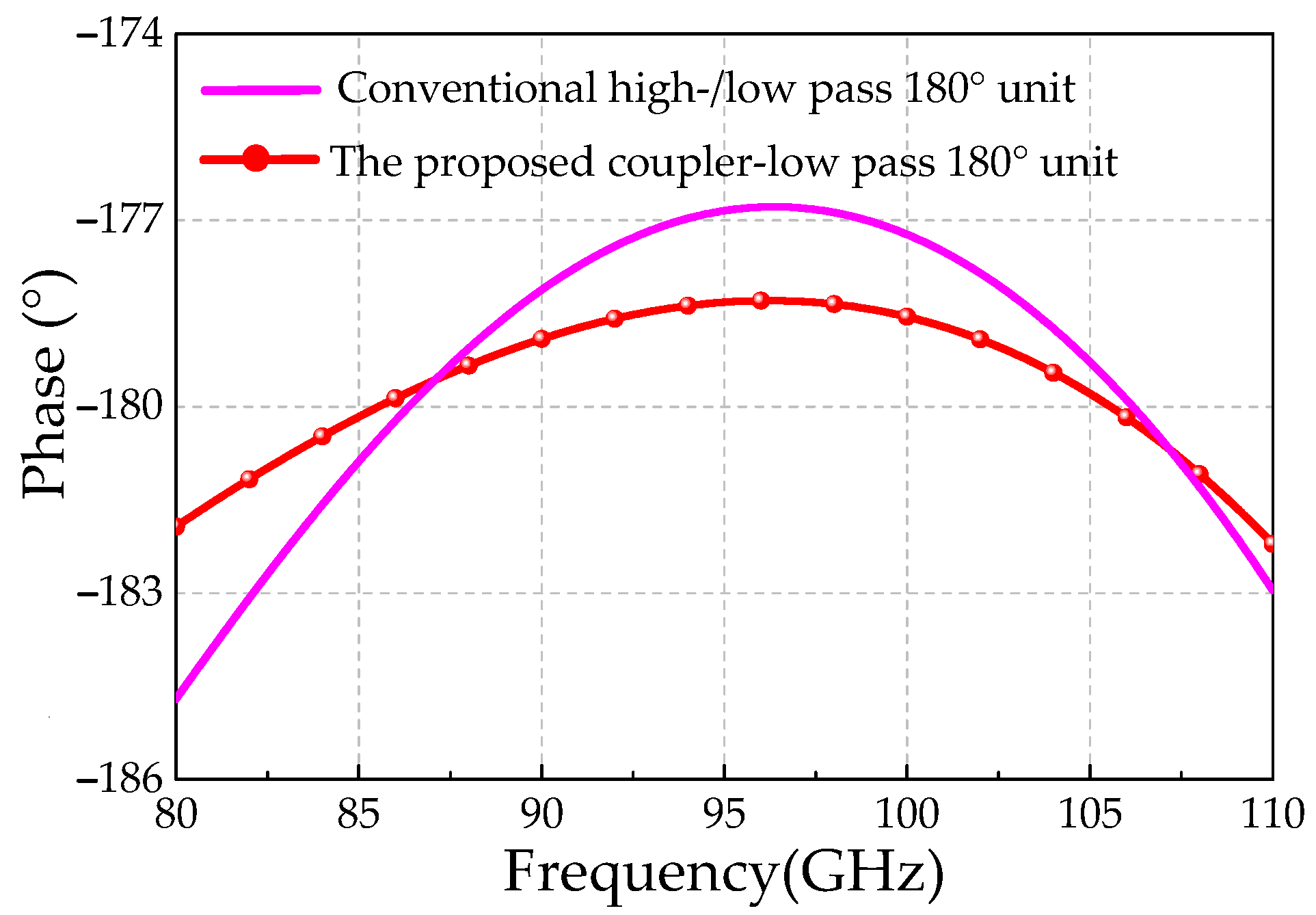
2.2. B. Analysis of a Coupler-Based Low-Pass 180° Phase Shifter Unit
3. W-Band 6-Bit Digital Phase Shifter Implementation
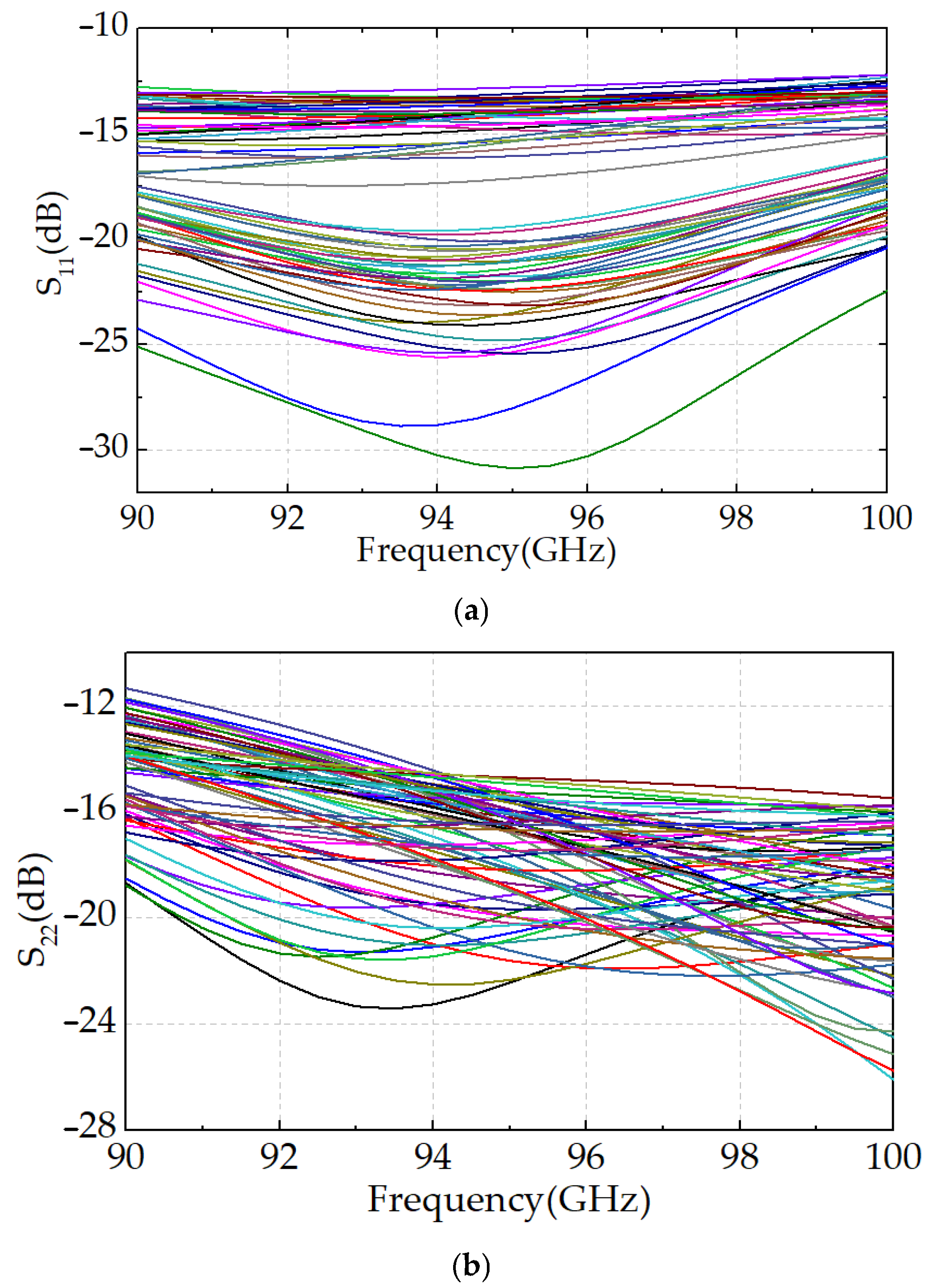
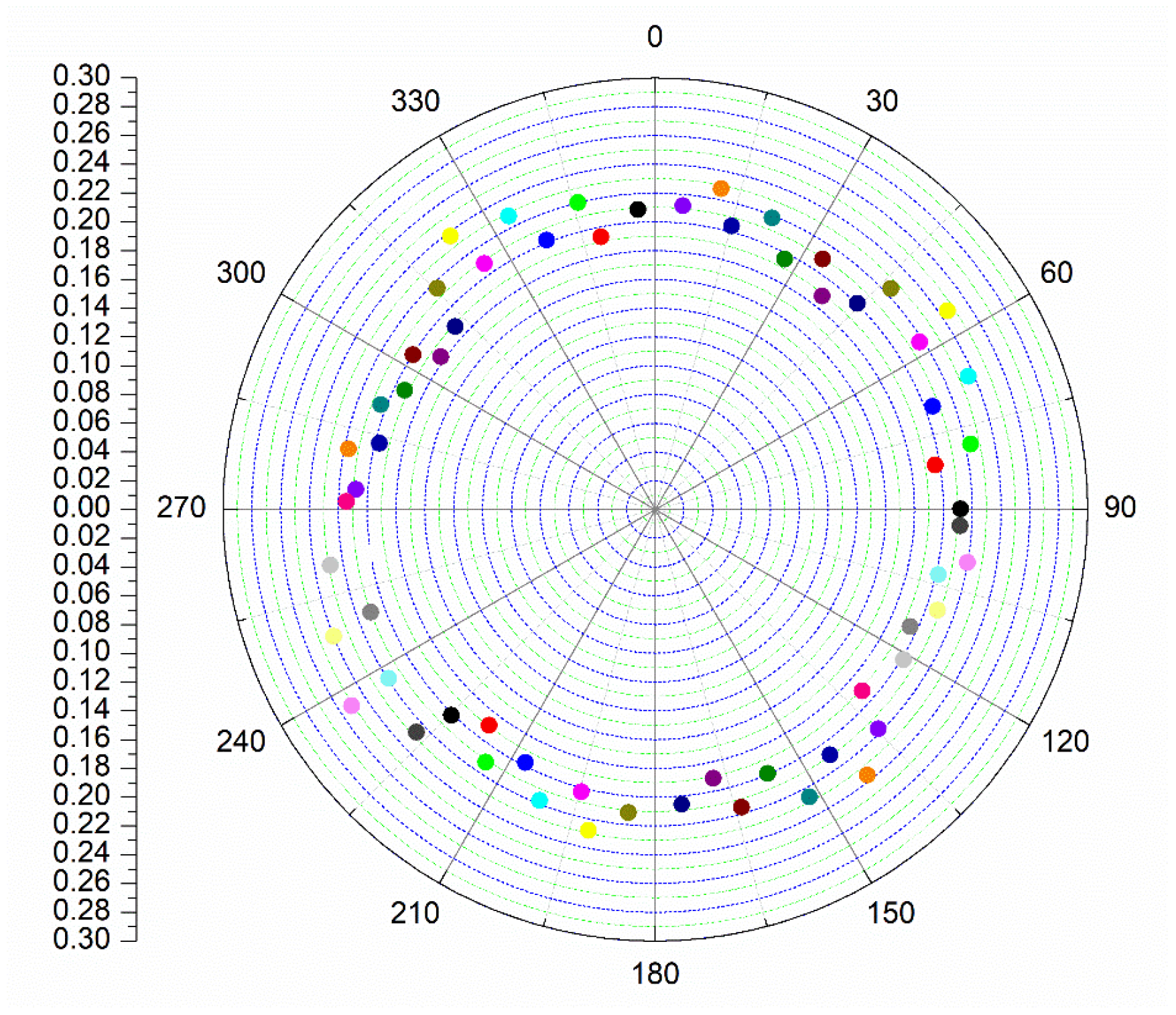
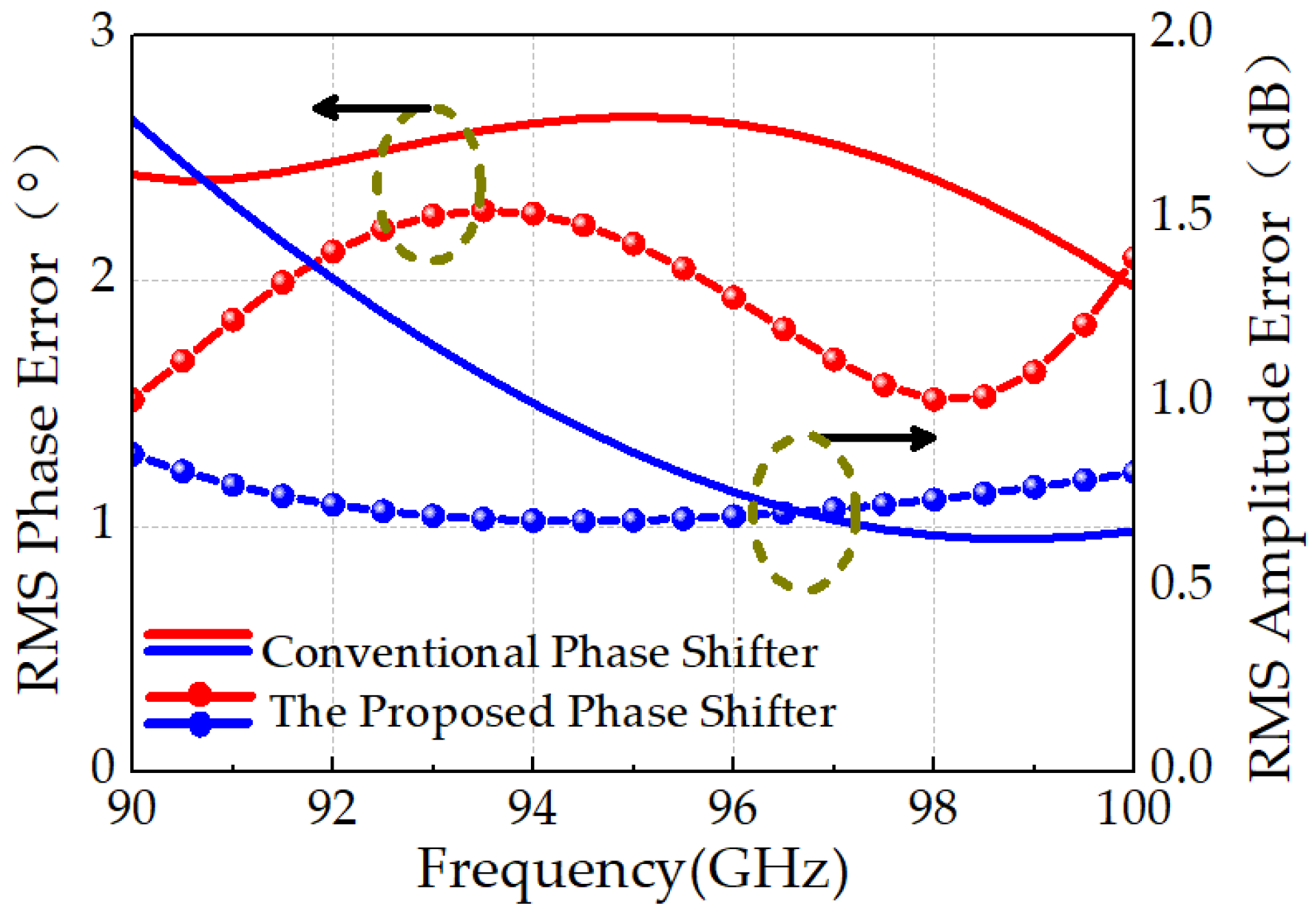
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, D.; Yu, P.; Jiang, S.; Gao, W.; He, P.; Liu, H. W-band CMOS beamforming ICs and integrated phased-array antennas with 20+ Gb/s data rates. Sci. China Inf. Sci. 2024, 67, 212301. [Google Scholar] [CrossRef]
- Huang, Y.S.; Ni, D.X.; Zhou, L.; Zhao, Z.; Zhang, C.R.; Wang, S.; Xie, Y.; Liu, R.Q.; Mao, J.F. A 1T2R heterogeneously integrated phased-array FMCW radar transceiver with AMC-based antenna in package in the W-band. IEEE Trans. Microw. Theory Tech. 2023, 72, 3772–3787. [Google Scholar] [CrossRef]
- Li, H.B.; Chen, J.X.; Hou, D.B.; Hong, W. A W-Band 6-Bit Phase Shifter with 7 dB Gain and 1.35° RMS Phase 375 Error in 130 nm SiGe BiCMOS. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 1839–1843. [Google Scholar]
- Natarajan, A.; Valdes-Garcia, A.; Sadhu, B.; Reynolds, S.K.; Parker, B.D. W-Band Dual-Polarization Phased-Array Transceiver Front-End in SiGe BiCMOS. IEEE Trans. Microw. Theory Tech. 2015, 63, 1989–2002. [Google Scholar] [CrossRef]
- Yishay, R.B.; Elad, D. E-band reflection-type phase shifter with uniform insertion loss. In Proceedings of the 2018 IEEE 18th Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems (SiRF), Anaheim, CA, USA, 14–17 January 2018; pp. 75–78. [Google Scholar]
- Guan, P.; Jia, H.; Deng, W.; Dong, S.; Huang, X.; Wang, Z.; Chi, B. A 33.5–37.5-GHz Four-Element Phased-Array Transceiver Front-End with Hybrid Architecture Phase Shifters and Gain Controllers. IEEE Trans. Microw. Theory Tech. 2023, 71, 4129–4143. [Google Scholar] [CrossRef]
- Ma, W.; Zou, P.; Bai, L.; Chen, K. A Low-Loss and Full-360° Reflection-Type Phase Shifter for WLAN Wireless Backhaul Applications. IEEE Access 2023, 11, 138850–138855. [Google Scholar] [CrossRef]
- Smirnova, K.; van der Heijden, M.; Leenaerts, D.; Ulusoy, A.Ç. 90–100 GHz 6-Bit Blixer-Based Active Phase Shifter in SiGe BiC-386 MOS. In Proceedings of the 2025 IEEE 24th Topical Meeting on Silicon Monolithic Integrated Circuits in RF Systems 2025, San Juan, PR, USA, 19–22 January 2025; pp. 26–29. [Google Scholar]
- Smirnova, K.; van der Heijden, M.; Yang, X.; Giannakidis, K.; Leenaerts, D.; Ulusoy, A.Ç. W-Band 6-Bit Active Phase Shifter Using Differential Lange Coupler in SiGe BiCMOS. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 1035–1038. [Google Scholar] [CrossRef]
- Montaseri, M.H.; Singh, S.P.; Jokinen, M.; Rahkonen, T.; Leinonen, M.E.; Pärssinen, A. A 270–330 GHz Vector Modulator Phase Shifter in 130 nm SiGe 390 BiCMOS. In Proceedings of the IEEE European Microwave Integrated Circuits Conference 2021, London, UK, 3–4 April 2022; pp. 309–312. [Google Scholar]
- Lee, H.-S.; Min, B.-W. W-Band CMOS 4-Bit Phase Shifter for High Power and Phase Compression Points. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 1–5. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, Y.; Wang, R.; Zhang, Q.; Zhao, C.; Liu, H.; Wu, Y.; Kang, K. A 90–100 GHz Passive Phase Shifter with Transistor-Based Capacitor-loaded Technique. In Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications, Guangzhou, China, 12–14 December 2022; pp. 1–3. [Google Scholar]
- Li, J.X.; Meng, F.Y.; Ma, K.X. A 220 GHz 5-Bit Differential Passive Phase Shifter in 0.13-μm SiGe BiCMOS. In Proceedings of the 397 IEEE International Workshop on Electromagnetics: Applications and Student Innovation Competition, Guangzhou, China, 7–9 November 2021; pp. 1–3. [Google Scholar]
- Lin, Y.-H.; Wang, H. A low phase and gain error passive phase shifter in 90 nm CMOS for 60 GHz phase array system application. In Proceedings of the IEEE MTT-S International Microwave Symposium, San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Sayginer, M.; Rebeiz, G.M. A 94–96 GHz phased-array receive front-end with 5-bit phase control and 5 dB noise figure in 32 nm CMOS SOI. In Proceedings of the IEEE MTT-S International Microwave Symposium (IMS), Honolulu, HI, USA, 4–9 June 2017; pp. 768–770. [Google Scholar]
- Afroz, S.; Koh, K.-J. W-Band (92–100 GHz) Phased-Array Receive Channel with Quadrature-Hybrid-Based Vector Modulator. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2070–2082. [Google Scholar] [CrossRef]
- Sayginer, M.; Rebeiz, G.M. A W-Band LNA/Phase Shifter with 5-dB NF and 24-mW Power Consumption in 32-nm CMOS SOI. IEEE Trans. Microw. Theory Tech. 2018, 66, 1973–1982. [Google Scholar] [CrossRef]
- Song, Z.; Yu, Y.; Zhao, C.; Zhang, X.; Zhu, J.; Guo, J.; Liu, H.; Wu, Y.; Kang, K. A 94 GHz FMCW Radar Transceiver with 17 dBm Output Power and 6.25 dB NF in 65 nm CMOS. In Proceedings of the IEEE MMT-S International Microwave Symposium, Denver, CO, USA, 19–24 June 2022; pp. 1009–1012. [Google Scholar]
- Morton, M.A.; Comeau, J.P.; Cressler, J.D.; Mitchell, M.; Papapolymerou, J. Sources of Phase Error and Design Considerations for Silicon-Based Monolithic High-Pass/Low-Pass Microwave Phase Shifters. IEEE Trans. Microw. Theory Tech. 2006, 54, 4032–4040. [Google Scholar] [CrossRef]
- Byeon, C.W.; Park, C.S. A Low-Loss Compact 60-GHz Phase Shifter in 65-nm CMOS. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 663–665. [Google Scholar] [CrossRef]
- Song, I.S.; Yoon, G.; Park, C.S. A Highly Integrated 1-Bit Phase Shifter Based on High-Pass/Low-Pass Structure. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 523–525. [Google Scholar] [CrossRef]
- Lim, J.T.; Song, J.H.; Kim, J.H.; Baek, M.S.; Park, C.; Kim, C.Y. Low Insertion Loss CMOS Phase Shifter for Wireless Power Transfer System. IEEE Microw. Wirel. Technol. Lett. 2024, 34, 49–52. [Google Scholar] [CrossRef]
- Chen, L.; Bai, Y.; Xing, X. Performance of high-/low-pass phase shifter in broadband. In Proceedings of the IEEE International Conference on Ultra-Wideband, Nanjing, China, 20–23 September 2010; pp. 1–4. [Google Scholar]
- Şengül, M.; Çakmak, G.; Özdemir, R. Phase Shifting Properties of High-Pass and Low-Pass Mixed-Element Two-Ports. IEEE Trans. Circuits Syst. II Express Brief 2021, 68, 1208–1212. [Google Scholar]
- Luo, J.; He, J.; Apriyana, A.; Feng, G.; Huang, Q. A D-band SPST switch using parallel-stripline swap with defected ground structure. IEICE Electron. Express 2017, 14, 20171104. [Google Scholar] [CrossRef][Green Version]
- Luo, J.; Peng, Y.; Cheng, Q. A 10 to 15 GHz Digital Step Attenuator with Robust Temperature Tolerance Across −55 °C to 125 °C. IEEE Trans. Circuits Syst. II Express Briefs 2025, 72, 653–657. [Google Scholar] [CrossRef]








| L1 | L2 | L3 | L4 | L5 |
| 120 pH | 115 pH | 92 pH | 92 pH | 15 pH |
| L6 | L7 | L8 | L9 | R1 |
| 38 pH | 39 pH | 44 pH | 43 pH | 2.4 ohm |
| R2 | C1 | C2 | C3 | K12, K34 |
| 2.4 ohm | 24.9 fF | 2.7 fF | 12.8 fF | 0.77 |
| Q1,2,3,4 (W/L) | Q5,6,7,8 (W/L) | Q9 (W/L) | Q10 (W/L) | Q11 (W/L) | Q12 (W/L) |
| 120 nm/8 µm | 120 nm/1 µm | 120 nm/4 µm | 120 nm/17 µm | 120 nm/2.5 µm | 120 nm/12 µm |
| Q13 (W/L) | Q14 (W/L) | Q15 (W/L) | Q16 (W/L) | Q17 (W/L) | R0 |
| 120 nm/3 µm | 120 nm/6 µm | 120 nm/18 µm | 120 nm/4 µm | 120 nm/6 µm | 5.7 k ohm |
| L0 | L1 | L2 | L3 | L4 | L5 |
| 75 pH | 63 pH | 20 pH | 65 pH | 36 pH | 72 pH |
| L6 | L7 | L8 | L9 | L10 | L11 |
| 45 pH | 77 pH | 70 pH | 85 pH | 70 pH | 65 pH |
| C0 | C1,2 | C3,4 | C5 | C6,7 | C8,9 |
| 9 fF | 5 fF | 6 fF | 5 fF | 13 fF | 17 fF |
| [14] | [11] | [12] | [16] | [15] | ★ This Work | |
|---|---|---|---|---|---|---|
| Process | 90 nm CMOS | 65 nm CMOS | 65 nm CMOS | 130 nm BiCMOS | 32 nm CMOS SOI | 130 nm BiCMOS |
| Frequency (GHz) | 57~66 | 75~85 | 90~100 | 92~100 | 94~96 | 90~100 |
| Insertion Loss (dB) | 16~19 | 22~27 | 16~20 | 23~26 | 17~18 | 12~15.5 |
| Phase Range (°)/Bits | 360/4 | 360/4 | 360/6 | 360/5 | 360/5 | 360/6 |
| RMS phase error (°) | <5 | <11.25 | <11 | <5 | <6 | <2.3 |
| RMS amplitude error (dB) | <0.5 | <1.4 | N/A | <1.8 | <1 | <0.9 |
| Chip Size (mm2) | 0.17 | 0.12 | 0.19 | 0.85 | 0.7 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, H.; Zhang, H.; Pu, Y.; Wang, C.; Li, B.; Tang, X.; Zeng, X.; Luo, J. A 90–100 GHz SiGe BiCMOS 6-Bit Digital Phase Shifter with a Coupler-Based 180° Unit for Phased Arrays. Micromachines 2025, 16, 1056. https://doi.org/10.3390/mi16091056
Shen H, Zhang H, Pu Y, Wang C, Li B, Tang X, Zeng X, Luo J. A 90–100 GHz SiGe BiCMOS 6-Bit Digital Phase Shifter with a Coupler-Based 180° Unit for Phased Arrays. Micromachines. 2025; 16(9):1056. https://doi.org/10.3390/mi16091056
Chicago/Turabian StyleShen, Hongchang, Hongyun Zhang, Yuqian Pu, Chong Wang, Bing Li, Xusheng Tang, Xinxi Zeng, and Jiang Luo. 2025. "A 90–100 GHz SiGe BiCMOS 6-Bit Digital Phase Shifter with a Coupler-Based 180° Unit for Phased Arrays" Micromachines 16, no. 9: 1056. https://doi.org/10.3390/mi16091056
APA StyleShen, H., Zhang, H., Pu, Y., Wang, C., Li, B., Tang, X., Zeng, X., & Luo, J. (2025). A 90–100 GHz SiGe BiCMOS 6-Bit Digital Phase Shifter with a Coupler-Based 180° Unit for Phased Arrays. Micromachines, 16(9), 1056. https://doi.org/10.3390/mi16091056





