Design and Fabrication of Air-Coupled CMUT for Non-Contact Temperature Measurement Applications
Abstract
1. Introduction
2. Device Design and Fabrication
2.1. Device Parameters
2.2. Finite Element Simulation
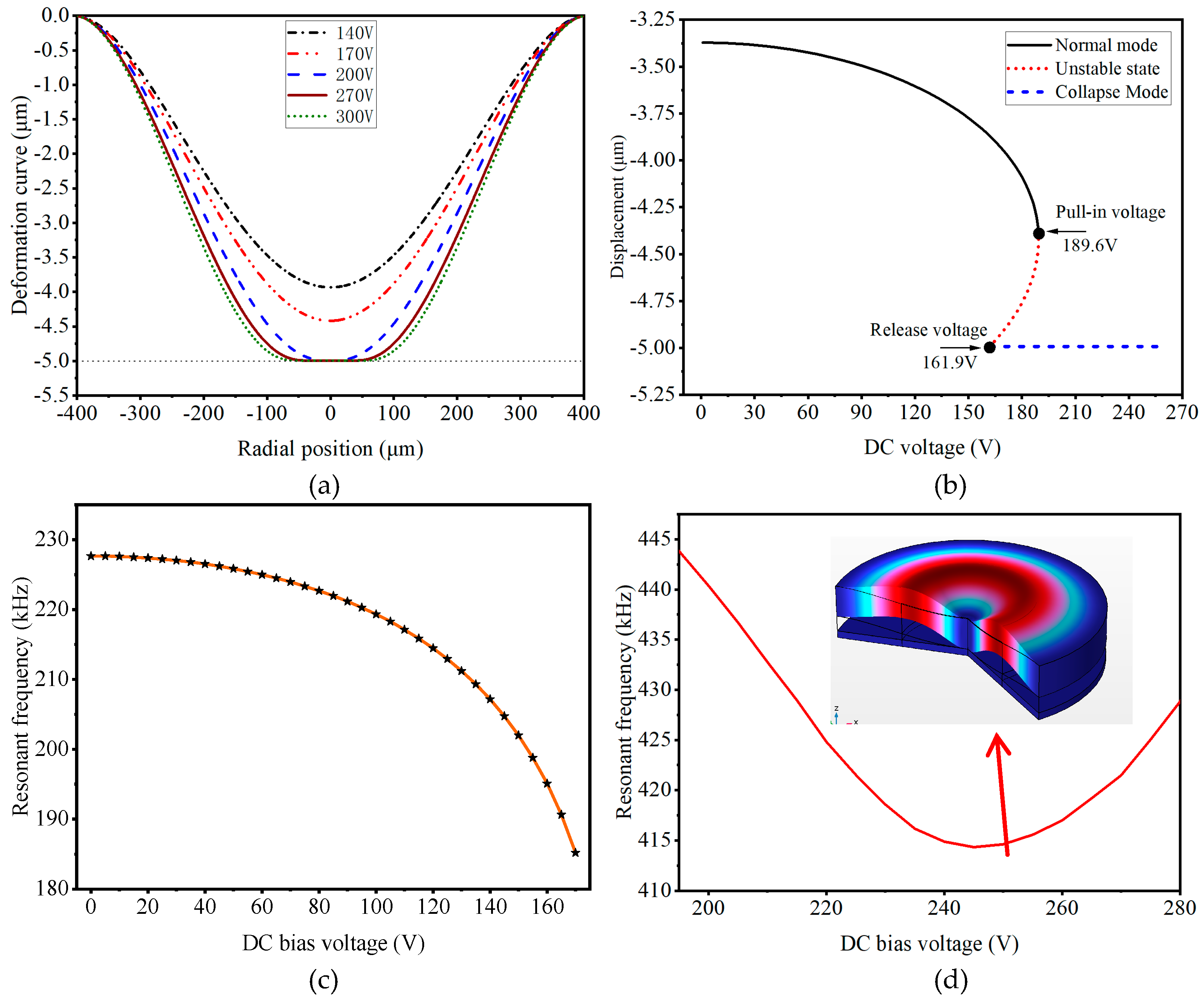
2.2.1. Pull-in Characteristics Analysis
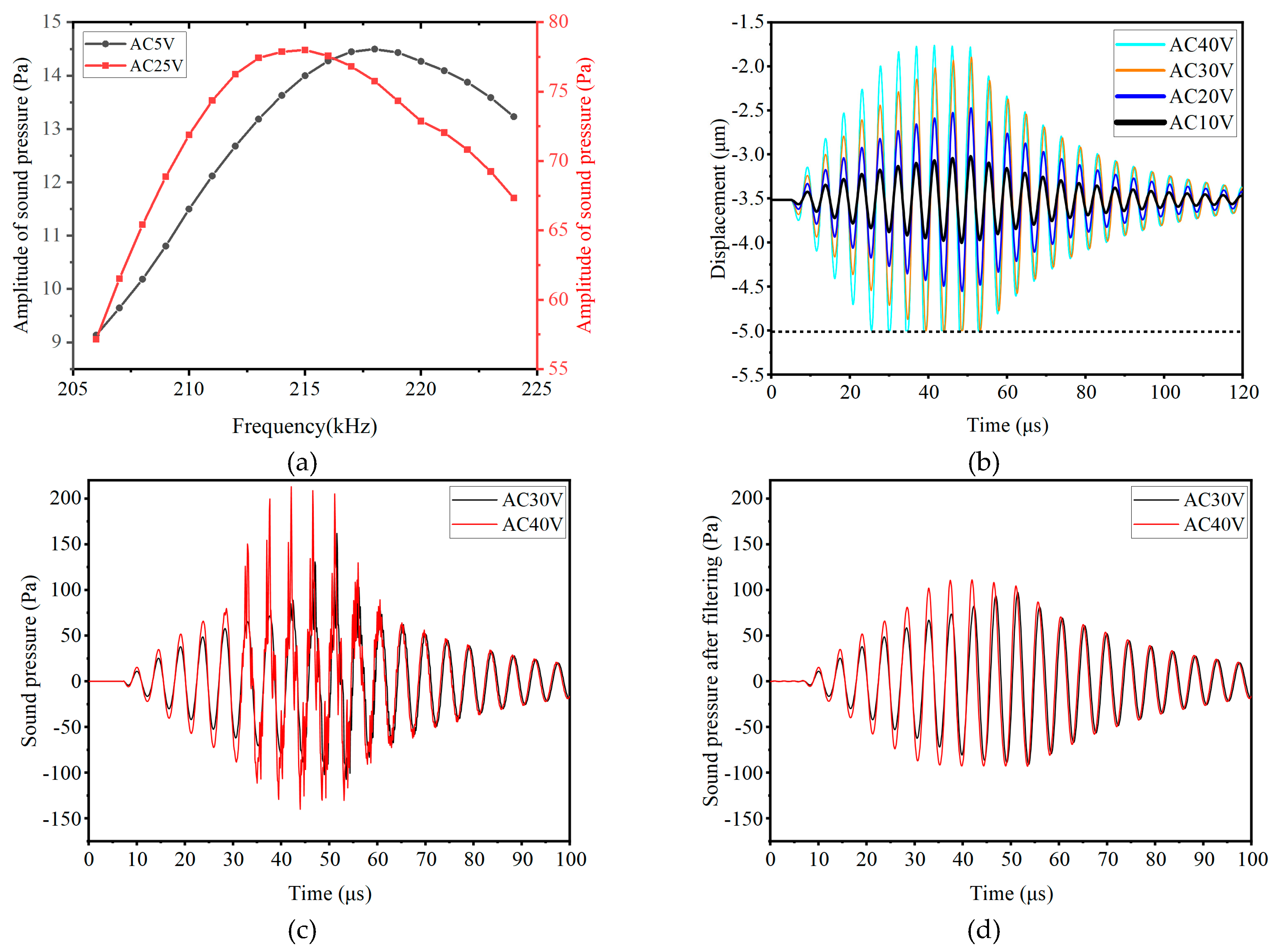
2.2.2. Response Characteristic Analysis
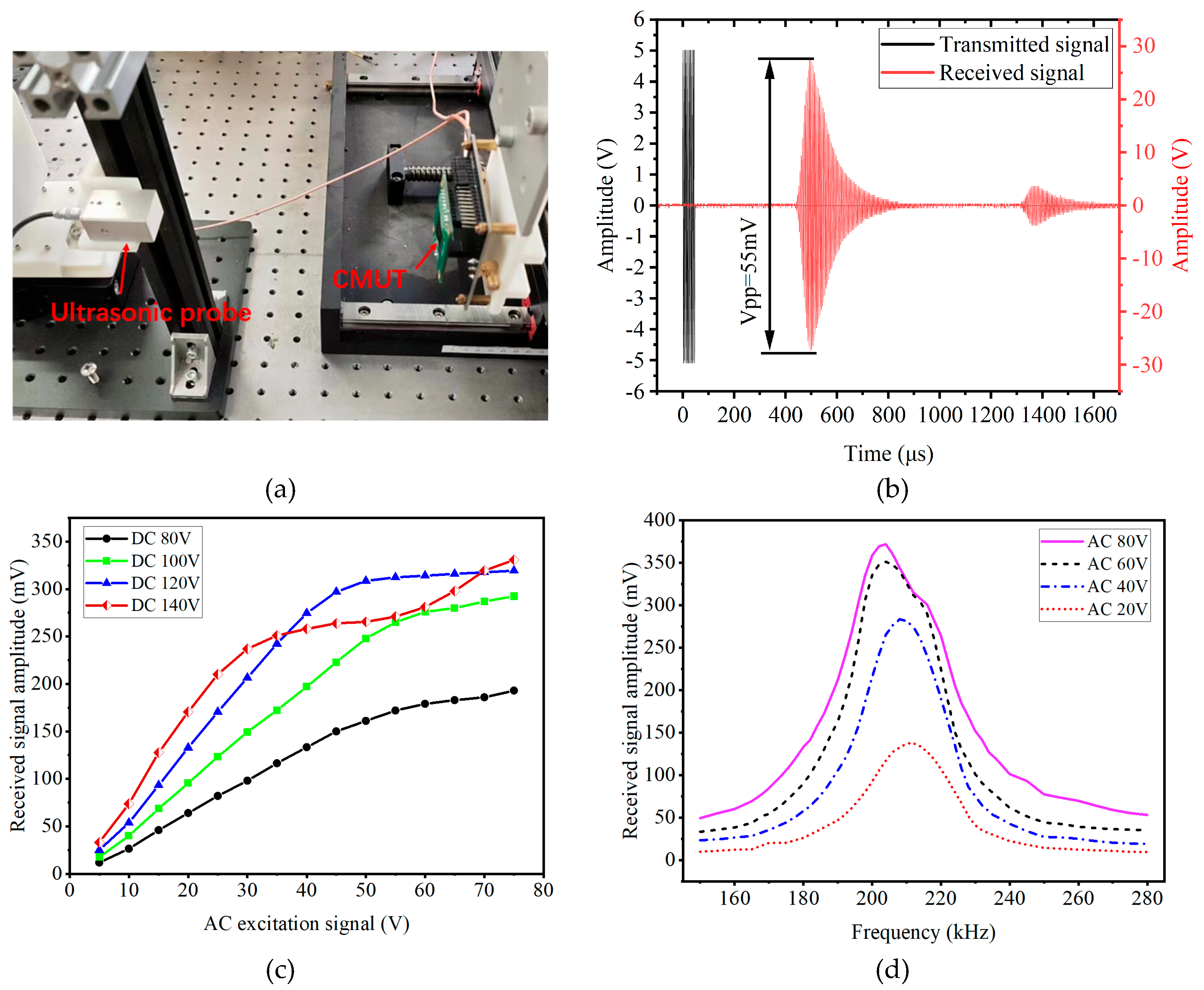
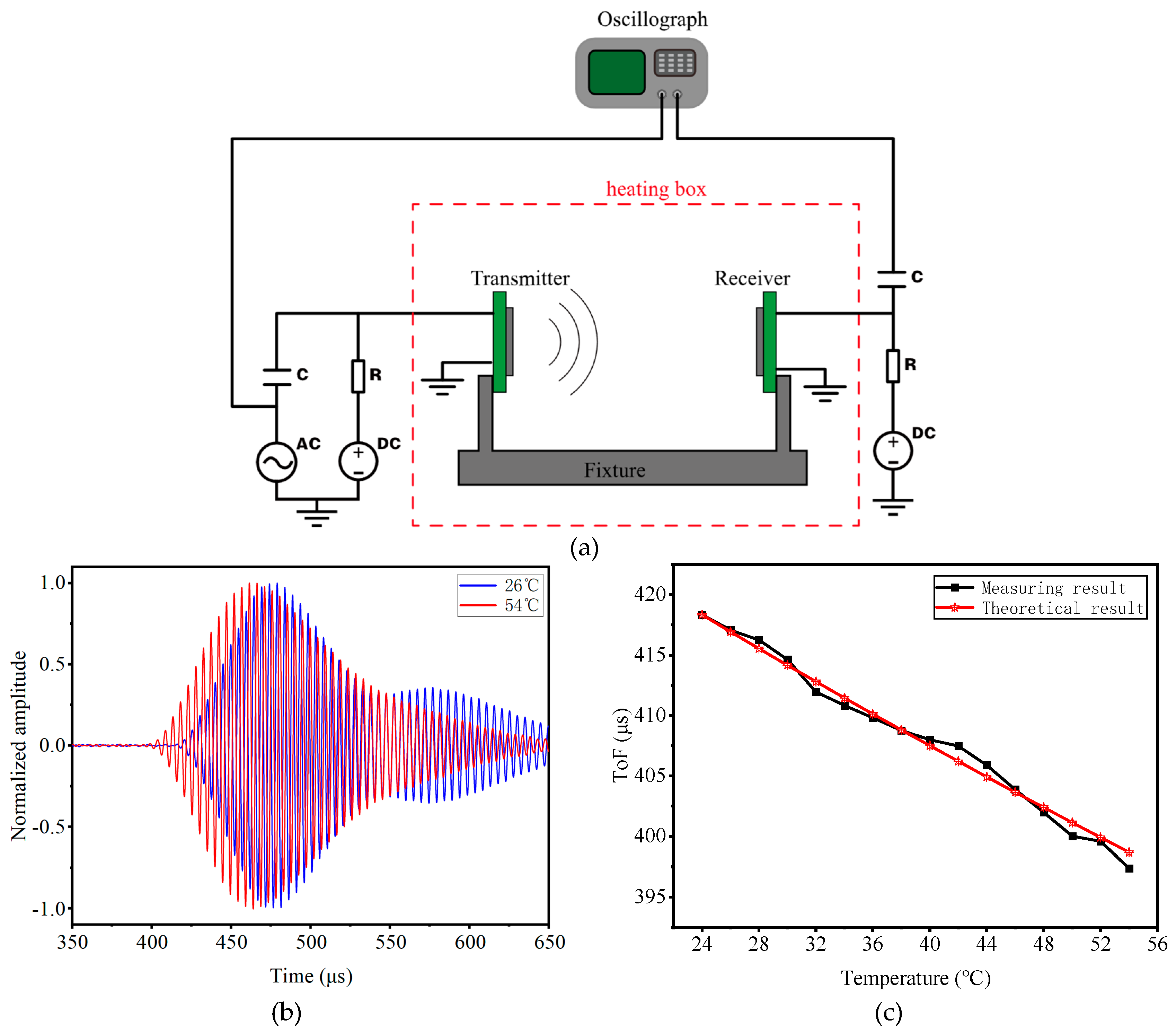
2.3. Device Testing
2.3.1. Topography Measurement
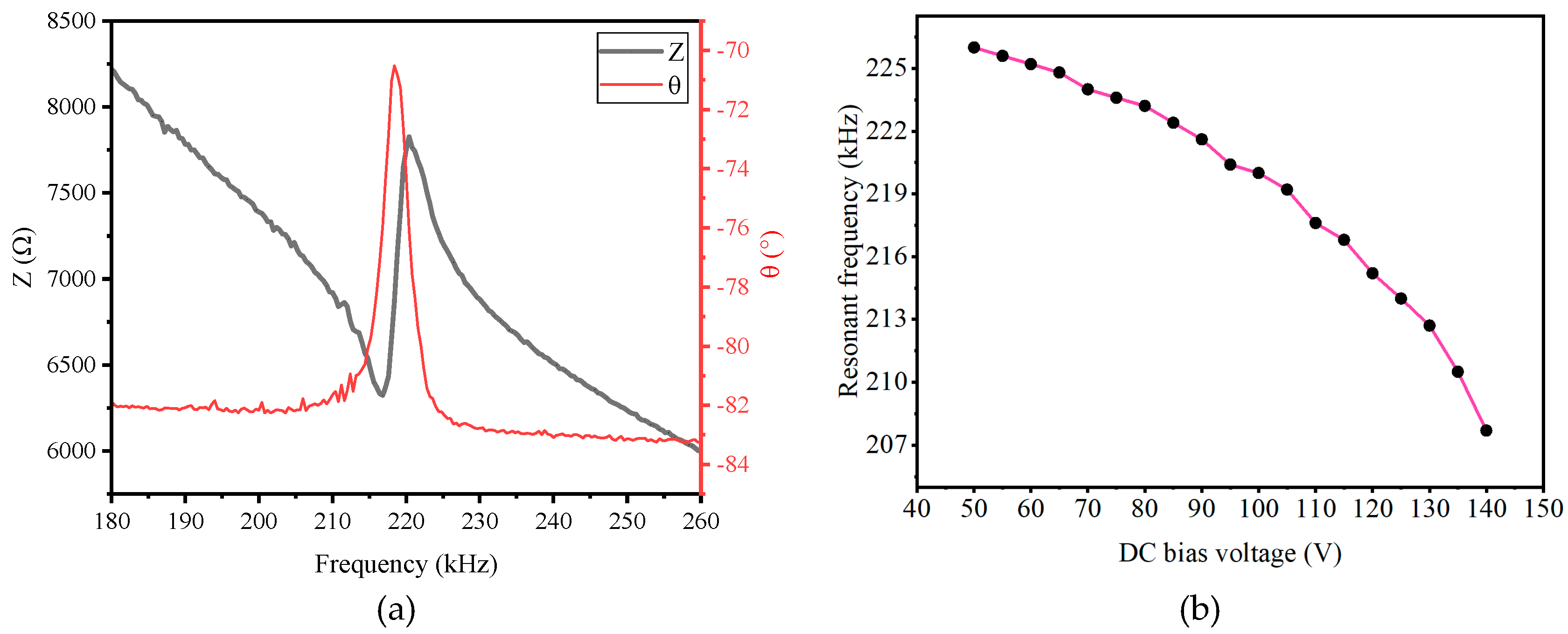
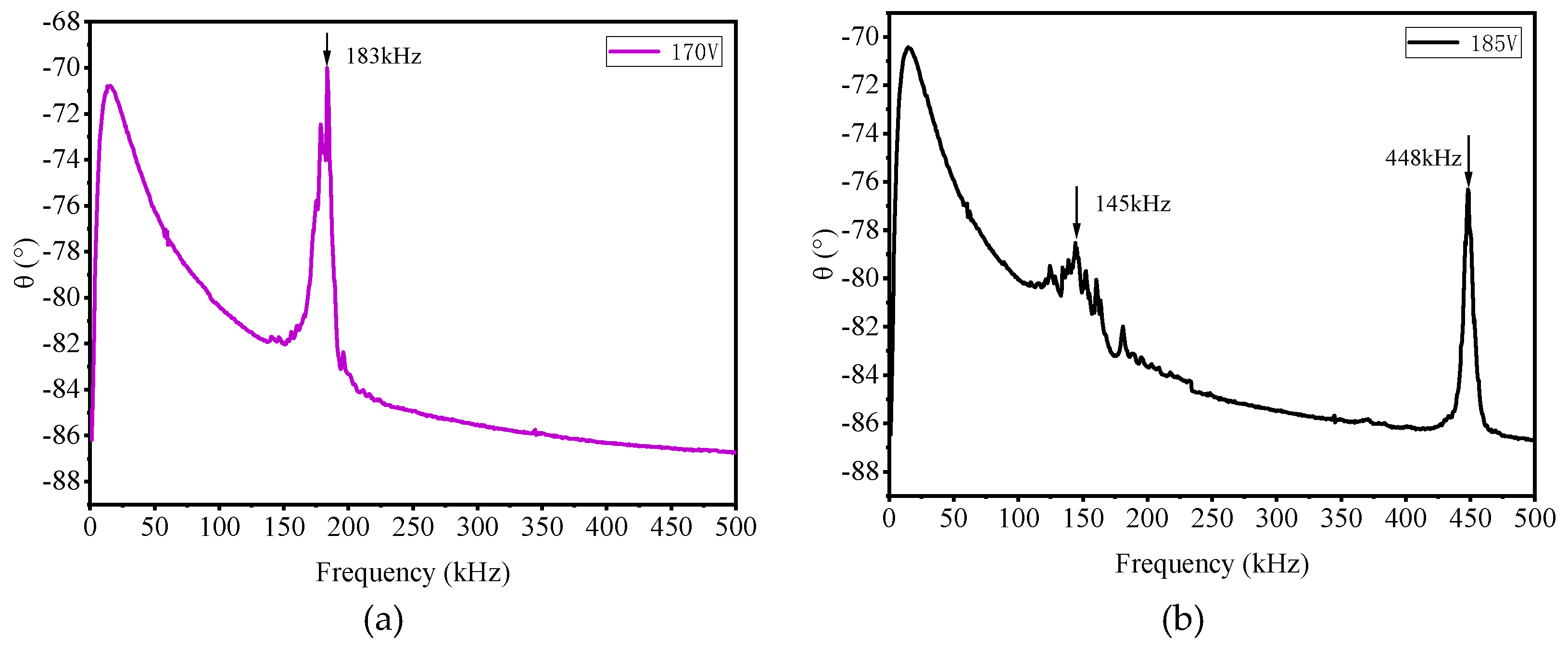
2.3.2. Impedance Test
2.3.3. Pull-in Voltage Test
2.3.4. Transmitting Characteristics Testing
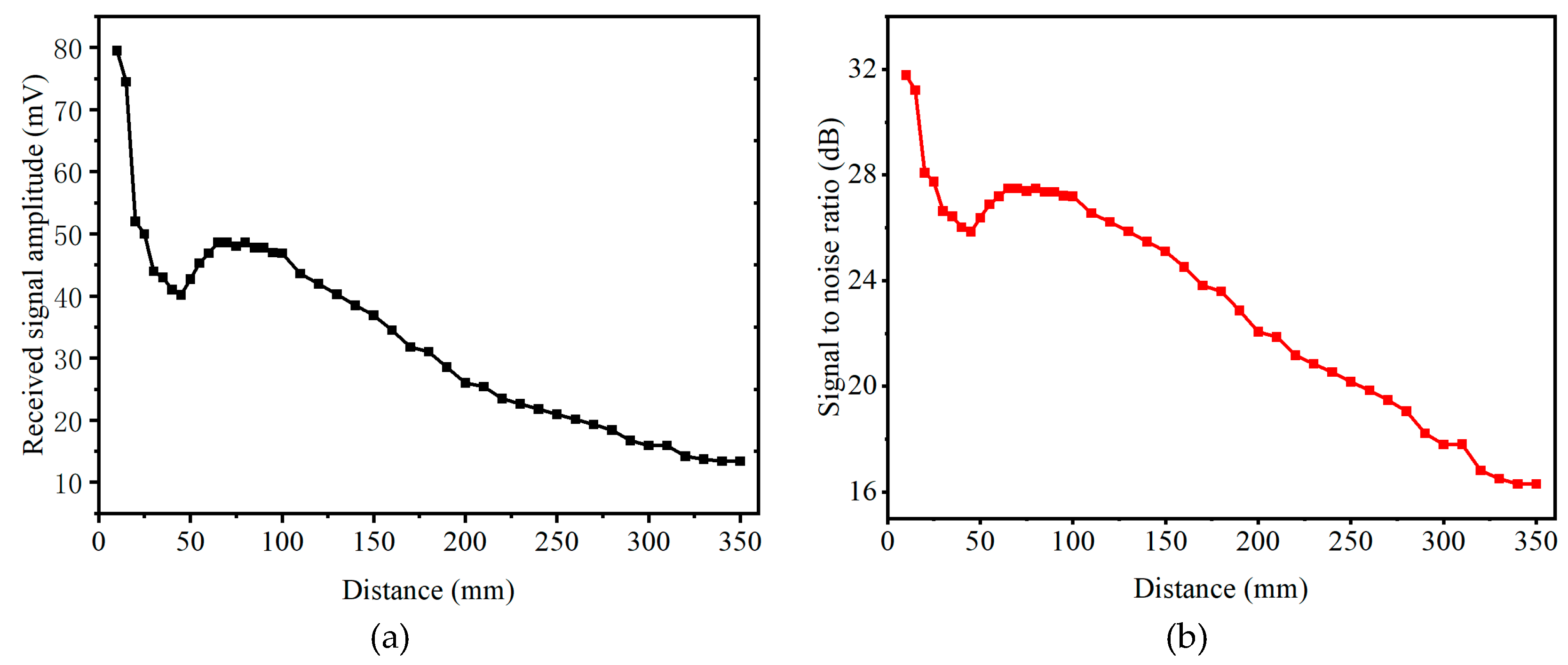
2.3.5. Transmission Distance Testing
3. CMUT Temperature Measurement Method
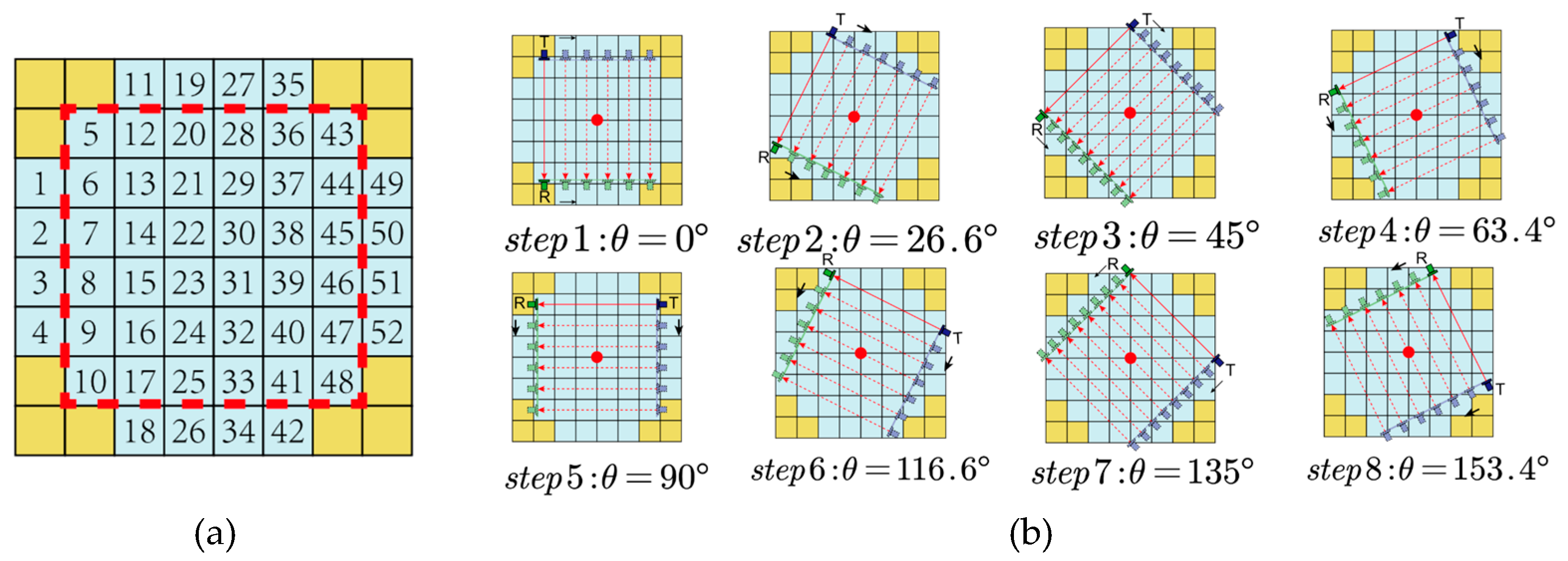
- Step 1: Grid division. The measurement area is divided into grids with uniform temperature distribution within each grid based on the measurement scenario and resolution. The more grids there are, the higher the resolution, but the required number of sound paths will also increase, corresponding to a larger computational load. Therefore, it is necessary to select the appropriate number of grids according to the imaging requirements. When setting sound paths, it is necessary to ensure that all sound paths cover the entire grid area as much as possible. And it is necessary to ensure that the sound path does not overlap with the boundary of the grid. Taking into account factors such as complexity of the reconstruction algorithm and experimental feasibility, the measured areas were divided into a 6 × 6 grid as shown in Figure 9a. Among them, the yellow grid is the non-measurement grid, the blue grid containing numbers is the measurement grid, and the grid with red dashed boxes is the reconstruction area.
- Step 2: Scanning scheme. This article uses two sets of CMUT transducers to obtain acoustic projection data from different orientations through a scanning motion that combines mechanical translation and rotation. Figure 9b shows the scanning scheme. Linear scanning was performed on 8 different angle directions, resulting in a total of 58 paths. There were 52 paths in the blue grid area, and the number of sound paths was greater than the number of grids. The sound wave reception signals on the sound path at different positions were obtained by receiving the CMUT chip.
- Step 3: Temperature field reconstruction. Obtain the received signal flight time of all sound paths through cross-correlation and other time delay estimation algorithms. Due to the uniform temperature distribution of each grid, the flight time of a single path can be rewritten as Formula (3).
4. Experiment Validation
4.1. Uniform Temperature Field
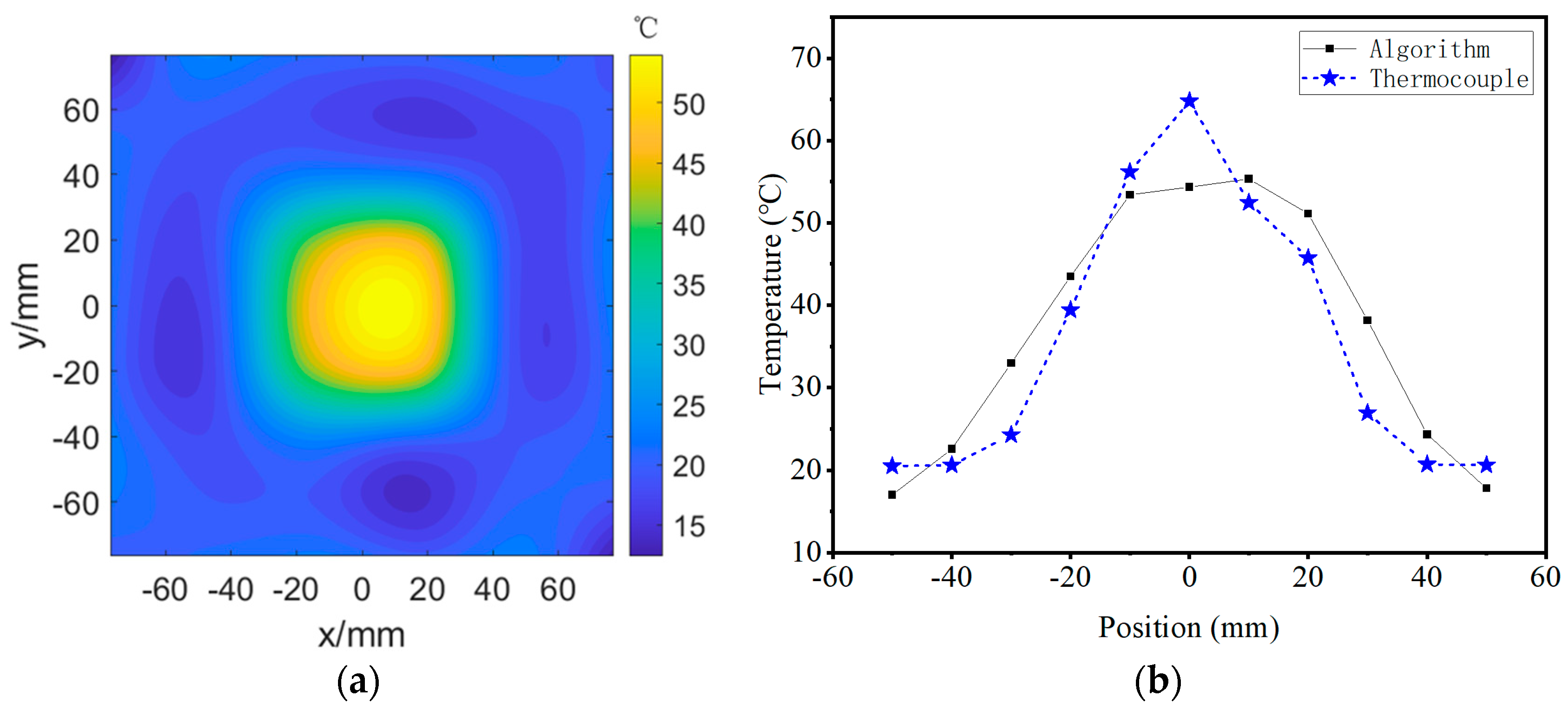
4.2. Scanning of Temperature Field Cross-Section
4.3. Temperature Field Reconstruction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dew, E.B.; Kashani, I.A.; Maadi, M. Outperforming piezoelectric ultrasonics with high-reliability single-membrane CMUT array elements. Microsyst. Nanoeng. 2022, 8, 59. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Lee, W.; Kang, W. Review of piezoelectric micromachined ultrasonic transducers and their applications. J. Micromech. Microeng. 2017, 27, 113001. [Google Scholar] [CrossRef]
- Chimenti, D. Review of air-coupled ultrasonic materials characterization. Ultrasonics 2014, 54, 1804–1816. [Google Scholar] [CrossRef] [PubMed]
- Capineri, L.; Bulletti, A. Ultrasonic guided-waves sensors and integrated structural health monitoring systems for impact detection and localization: A review. Sensors 2021, 21, 2929. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liang, D.; Wang, Z. Fabrication and characterization of a wideband low-frequency CMUT array for air-coupled imaging. IEEE Sens. J. 2020, 20, 14090–14100. [Google Scholar] [CrossRef]
- Chen, X.; Xu, J.; Chen, H. High-accuracy ultrasonic rangefinders via pMUTs arrays using multi-frequency continuous waves. J. Microelectromech. Syst. 2019, 28, 634–642. [Google Scholar] [CrossRef]
- Bui, G.T.; Jiang, Y.T.; Pang, D.C. Two capacitive micro-machined ultrasonic transducers for wind speed measurement. Sensors 2016, 16, 814. [Google Scholar] [CrossRef] [PubMed]
- Voldán, M.; Husník, L. Simple single transducer ultrasonic thermometer using electrostatic actuator. Appl. Acoust. 2019, 148, 448–456. [Google Scholar] [CrossRef]
- Iglesias, H.L.; Shanmugam, P.; Michaud, J.F. Discrimination of Binary Gas Mixture Using CMUT Based Sound Attenuation Spectrum Gas Sensor. In Electrochemical Society Meeting Abstracts 239; The Electrochemical Society, Inc.: Pennington, NJ, USA, 2021; p. 1592. [Google Scholar]
- Dokhanchi, N.S.; Othmani, C.; Arnold, J. Indoor air temperature measurements using ultrasonic travel-time tomography. Appl. Acoust. 2024, 218, 109894. [Google Scholar] [CrossRef]
- Schwarz, M.; Zagar, B.G. Ultrasonic measurement and methods for reconstruction of temperature fields for the use in bioreactors. tm-Tech. Mess. 2022, 89, 556–565. [Google Scholar] [CrossRef]
- Wei, Y.; Liang, H.; Wang, G. Ultrasonic thermometric measurement system for solid rocket combustion chambers. Ultrasonics 2021, 113, 106361. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Lin, S.; Hong, X. Reconstructing Underwater Temperature Spatial Distribution Using Ultrasound Tomography. IEEE Access 2021, 9, 103670–103676. [Google Scholar] [CrossRef]
- Dong, H.; Qian, S.; Tan, Q. Temperature Measurement Using Passive Harmonics during High Intensity Focused Ultrasound Exposures in Porcine Tissue. Acta Phys. Pol. A 2018, 134, 524–528. [Google Scholar] [CrossRef]
- Abhishek, S.; John, G.; Eric, D. Noninvasive acoustic temperature tomography in multiphase materials. NDT E Int. 2025, 156, 103444. [Google Scholar] [CrossRef]
- Hu, L.; Zuo, P.; Sun, Z. Non-contact subsurface thermography for high-temperature metallic structures using laser ultrasound and wave-equation-based inversion. Mech. Syst. Signal Process. 2023, 197, 110378. [Google Scholar] [CrossRef]
- Gan, T.H.; Hutchins, D.A. Air-coupled ultrasonic tomographic imaging of high-temperature flames. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2003, 50, 1214–1218. [Google Scholar] [CrossRef] [PubMed]
- Holstein, P.; Raabe, A.; Müller, R. Acoustic tomography on the basis of travel-time measurement. Meas. Sci. Technol. 2004, 15, 1420. [Google Scholar] [CrossRef]
- Wright, W.M.; Ingleby, P.; O’sullivan, I.J. Air-coupled through-transmission fan-beam tomography using divergent capacitive ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 2384–2394. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.; Pala, S.; Liang, Y. Non-Contact Surface Temperature Sensing Based on a Single Bimorph pMUTs Array. In Proceedings of the 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), Vancouver, BC, Canada, 18–22 January 2020; pp. 861–864. [Google Scholar]
- Schwarz, M.; Zagar, B.G. Reconstruction of temperature fields from ultrasonic travel time measurements. In Proceedings of the 2021 IEEE International Ultrasonics Symposium (IUS), Virtual, 11–16 September 2021; pp. 1–4. [Google Scholar]
- Zhao, L.; Zhou, X.; Dong, C. Ultrasonic thermometry algorithm based on inverse quadratic function. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2020, 68, 1876–1884. [Google Scholar] [CrossRef] [PubMed]
- Sarafianou, M.; Goh, D.J.; Choong, D.S.W. A Time-of-Flight (ToF) estimation algorithm for ranging using Sili-con-On-Nothing pMUTs. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022; pp. 1–4. [Google Scholar]
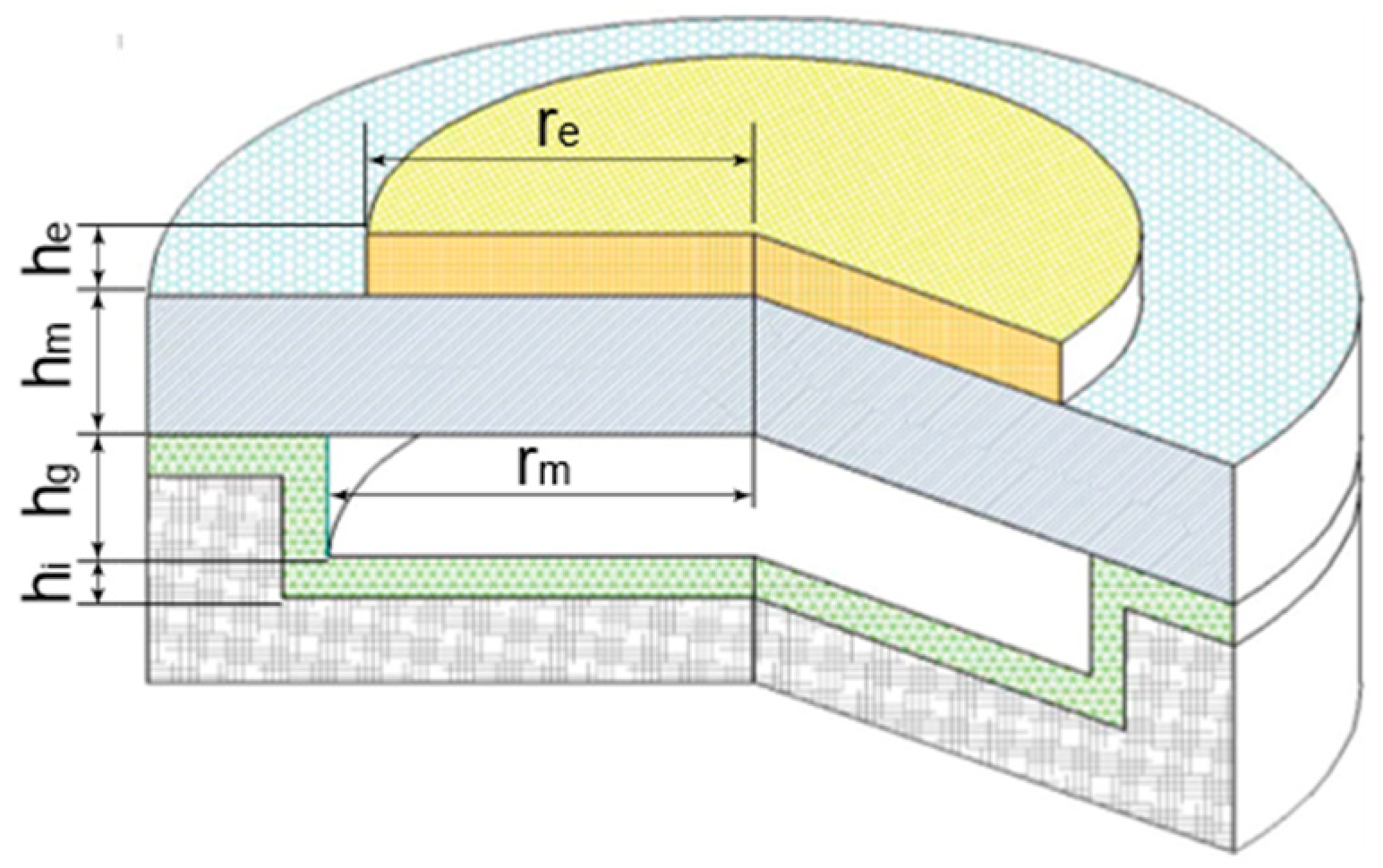


| Parameter | Value/um |
|---|---|
| Membrane radius, rm | 400 |
| Membrane thickness, hm | 10 |
| Insulating layer thickness, hi | 2.2 |
| Cavity depth, hg | 5 |
| Metal electrode diameter, re | 200 |
| Metal electrode thickness, he | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rui, X.; Ma, Y.; He, C.; Zhang, C.; Wang, Z.; Zhang, H. Design and Fabrication of Air-Coupled CMUT for Non-Contact Temperature Measurement Applications. Micromachines 2025, 16, 1008. https://doi.org/10.3390/mi16091008
Rui X, Ma Y, He C, Zhang C, Wang Z, Zhang H. Design and Fabrication of Air-Coupled CMUT for Non-Contact Temperature Measurement Applications. Micromachines. 2025; 16(9):1008. https://doi.org/10.3390/mi16091008
Chicago/Turabian StyleRui, Xiaobo, Yongshuai Ma, Chenghao He, Chi Zhang, Zhuochen Wang, and Hui Zhang. 2025. "Design and Fabrication of Air-Coupled CMUT for Non-Contact Temperature Measurement Applications" Micromachines 16, no. 9: 1008. https://doi.org/10.3390/mi16091008
APA StyleRui, X., Ma, Y., He, C., Zhang, C., Wang, Z., & Zhang, H. (2025). Design and Fabrication of Air-Coupled CMUT for Non-Contact Temperature Measurement Applications. Micromachines, 16(9), 1008. https://doi.org/10.3390/mi16091008







