Development of MEMS Airflow Volumetric Flow Sensing System with Single Piezoelectric Micromachined Ultrasonic Transducer (PMUT) Array
Abstract
1. Introduction
2. Measurement Principle
2.1. The Method
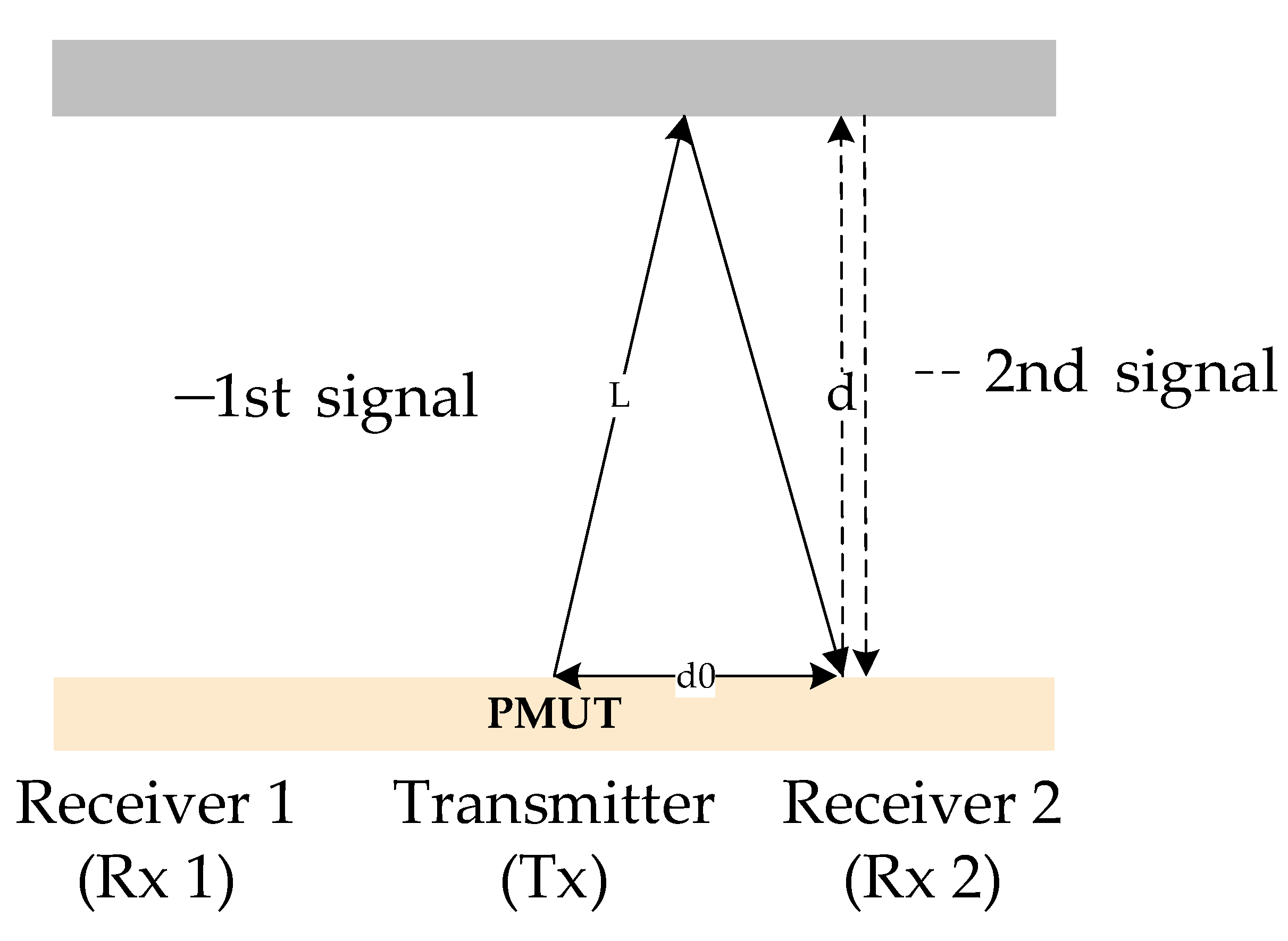
2.2. Differential Time of Flight Measurement
- (1)
- Use the cross-correlation method to calculate Rxy[m] (Equation (10)) and find the index point M for the maximum value.
- (2)
- Find Rxy[M], Rxy[M − 1], Rxy[M + 1], cosine interpolation of the three points to derive the offsets δ [20], (Equations (11)–(13)).
- (3)
- Calculate the final dTof using the offset, M, and sample rate fs (Equation (14)).
3. The Design of PMUT Array
4. Experiment and Discussion
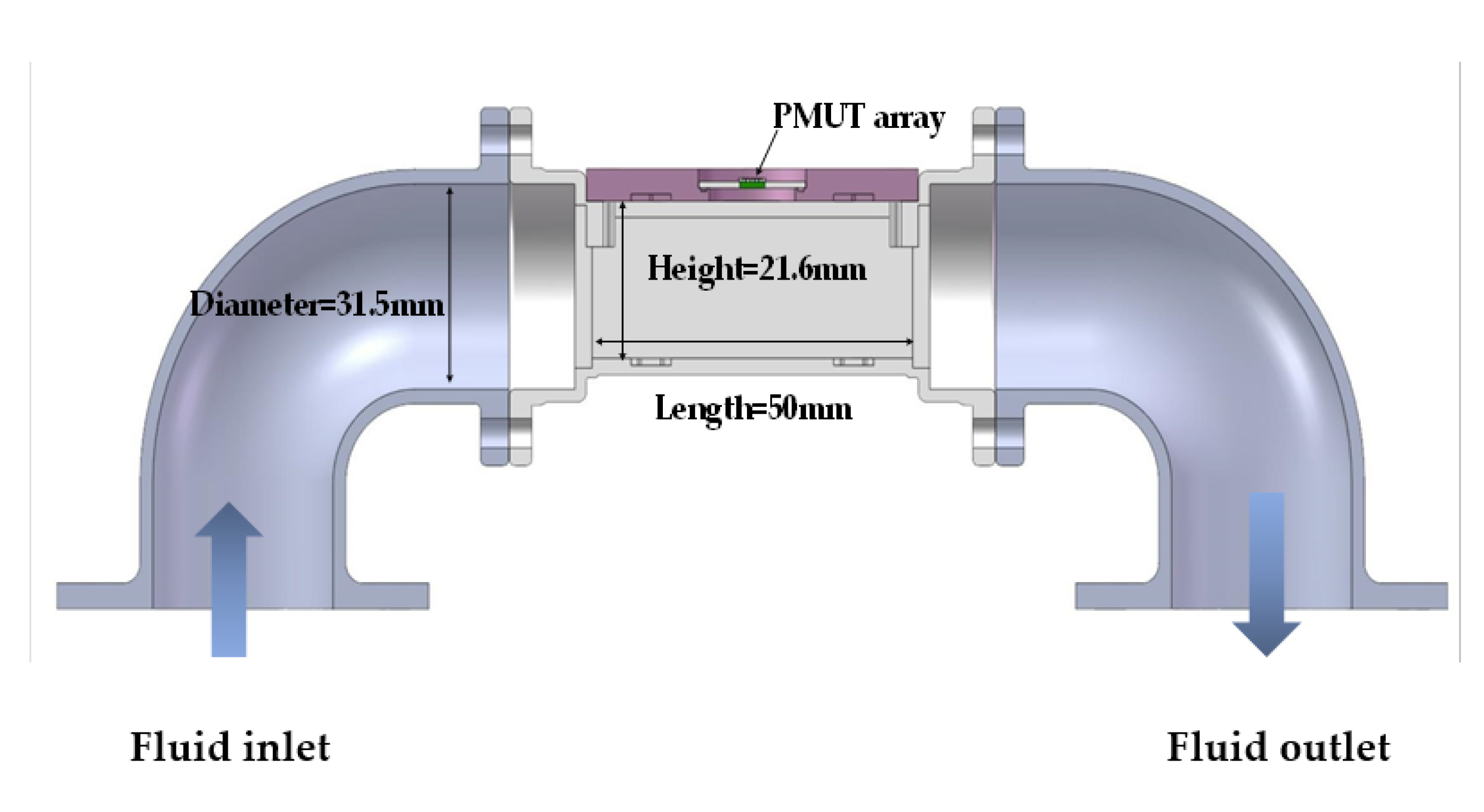
4.1. Experimental Setup
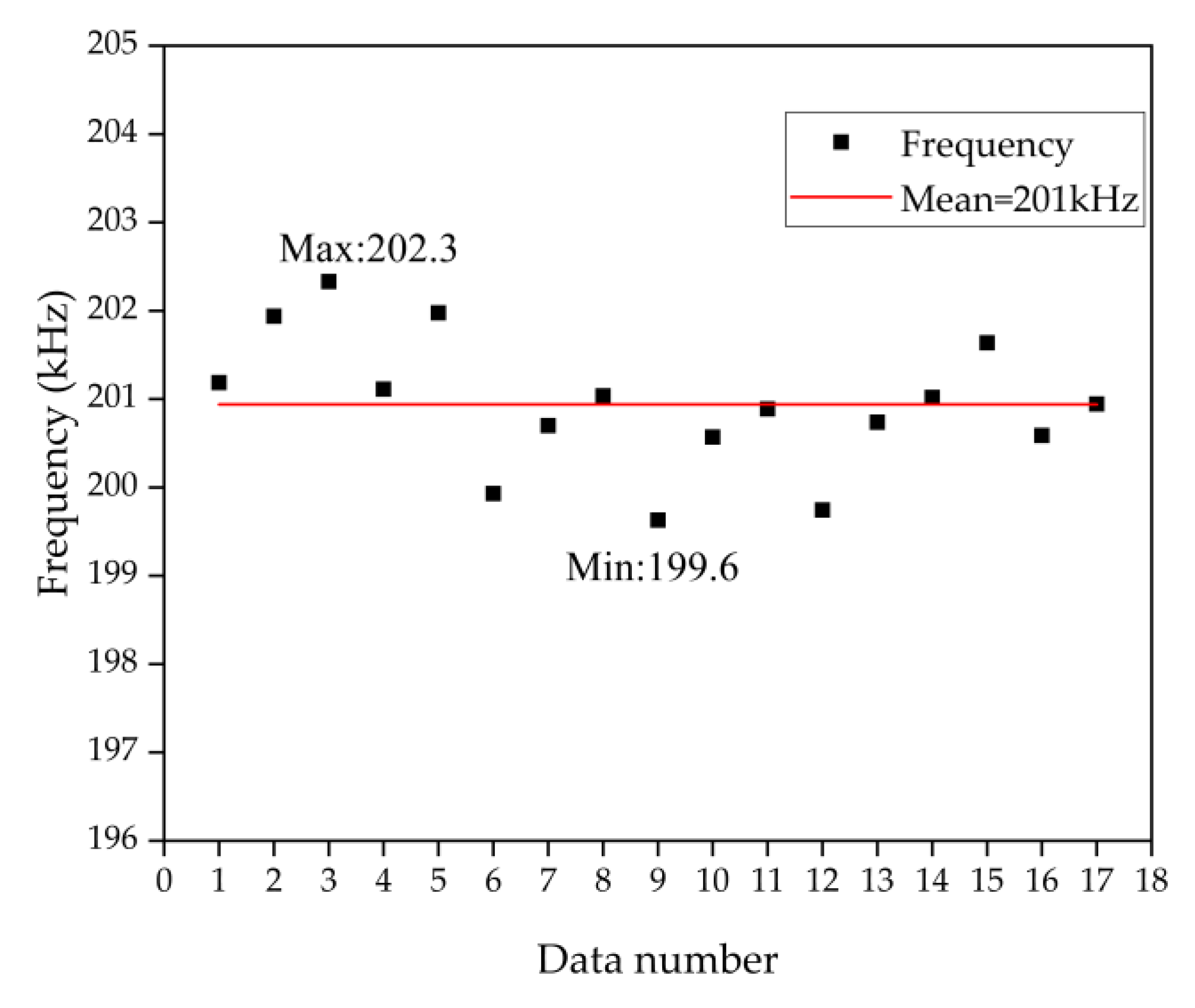
4.2. Auto-Calibration Technique
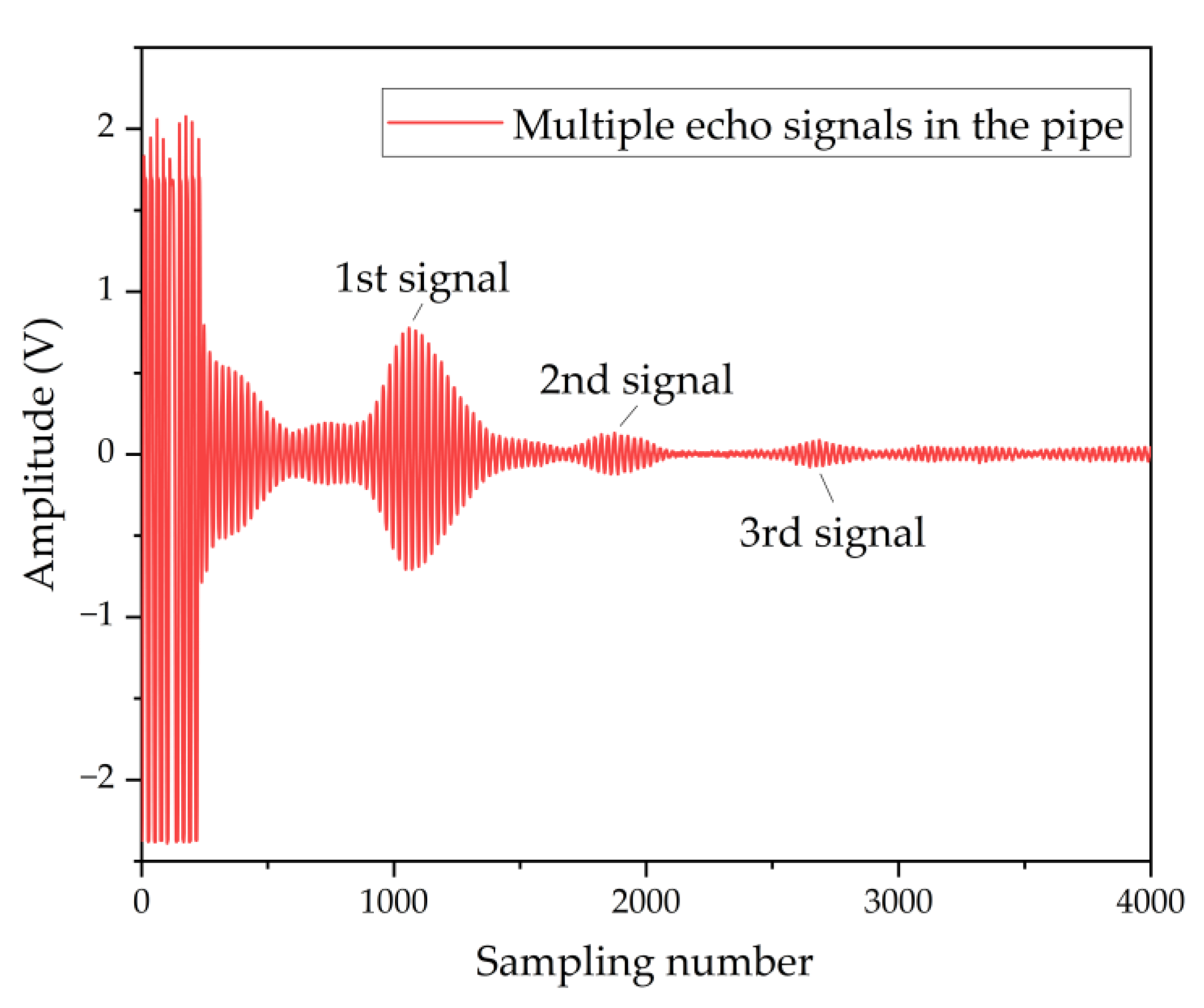
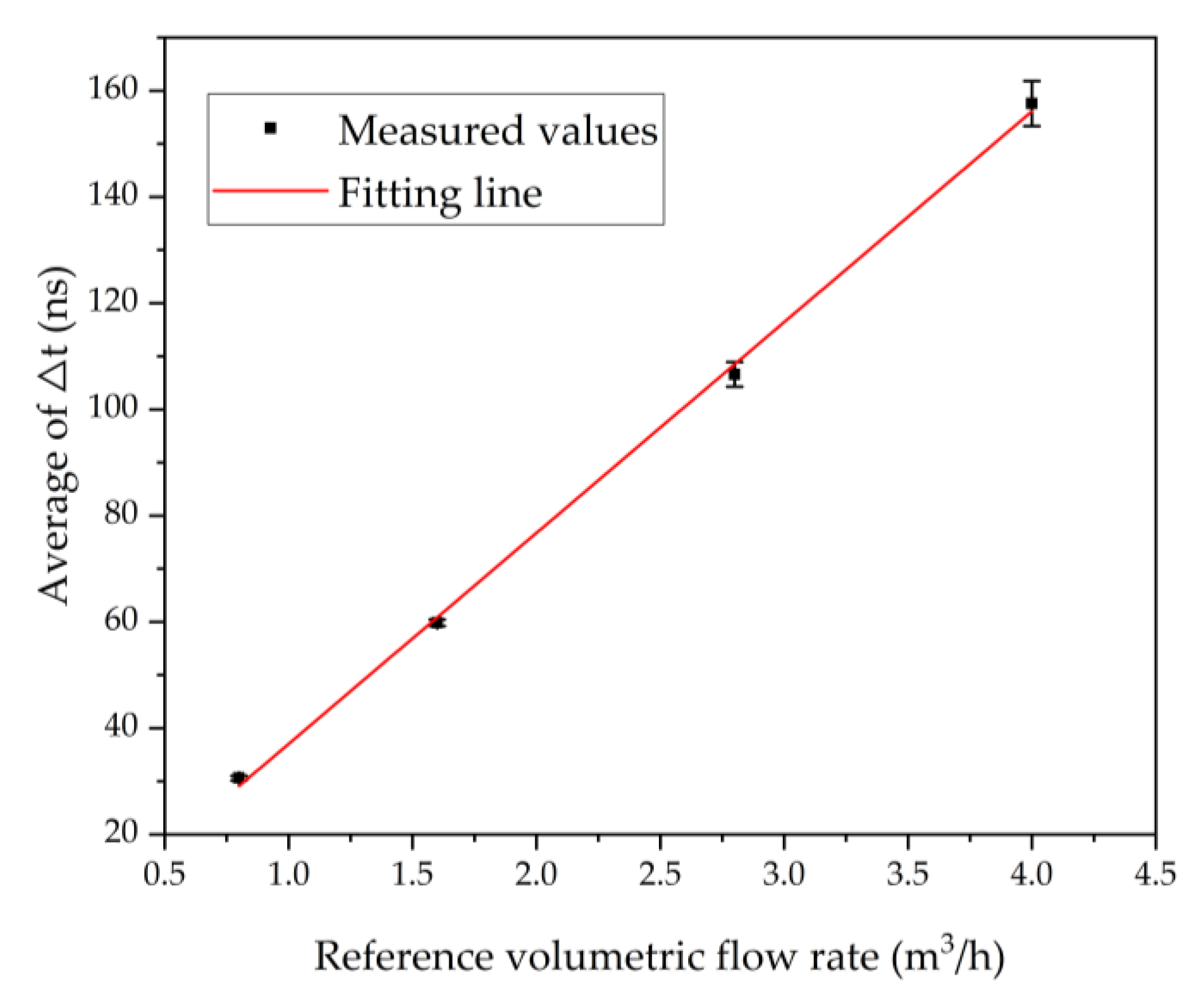
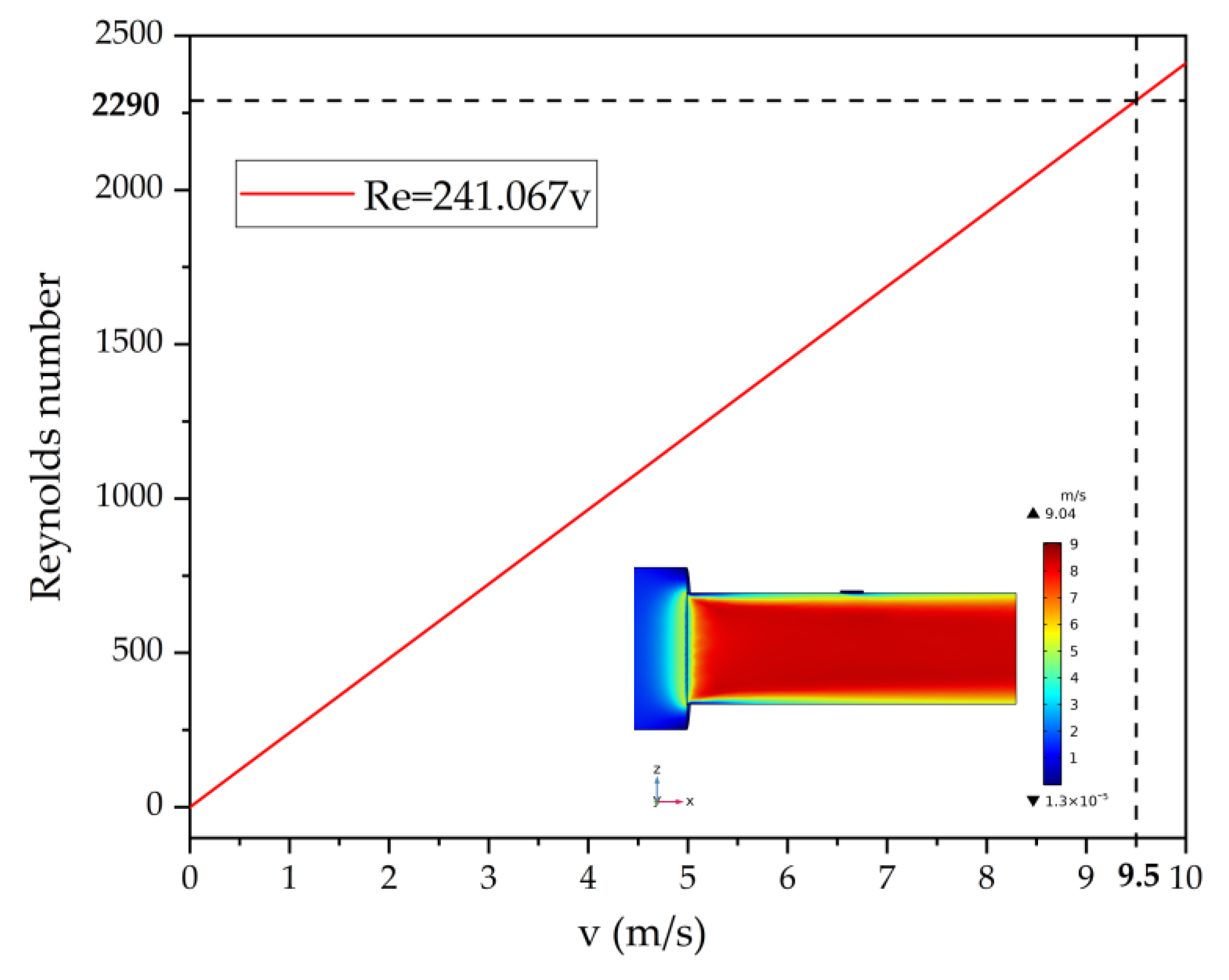
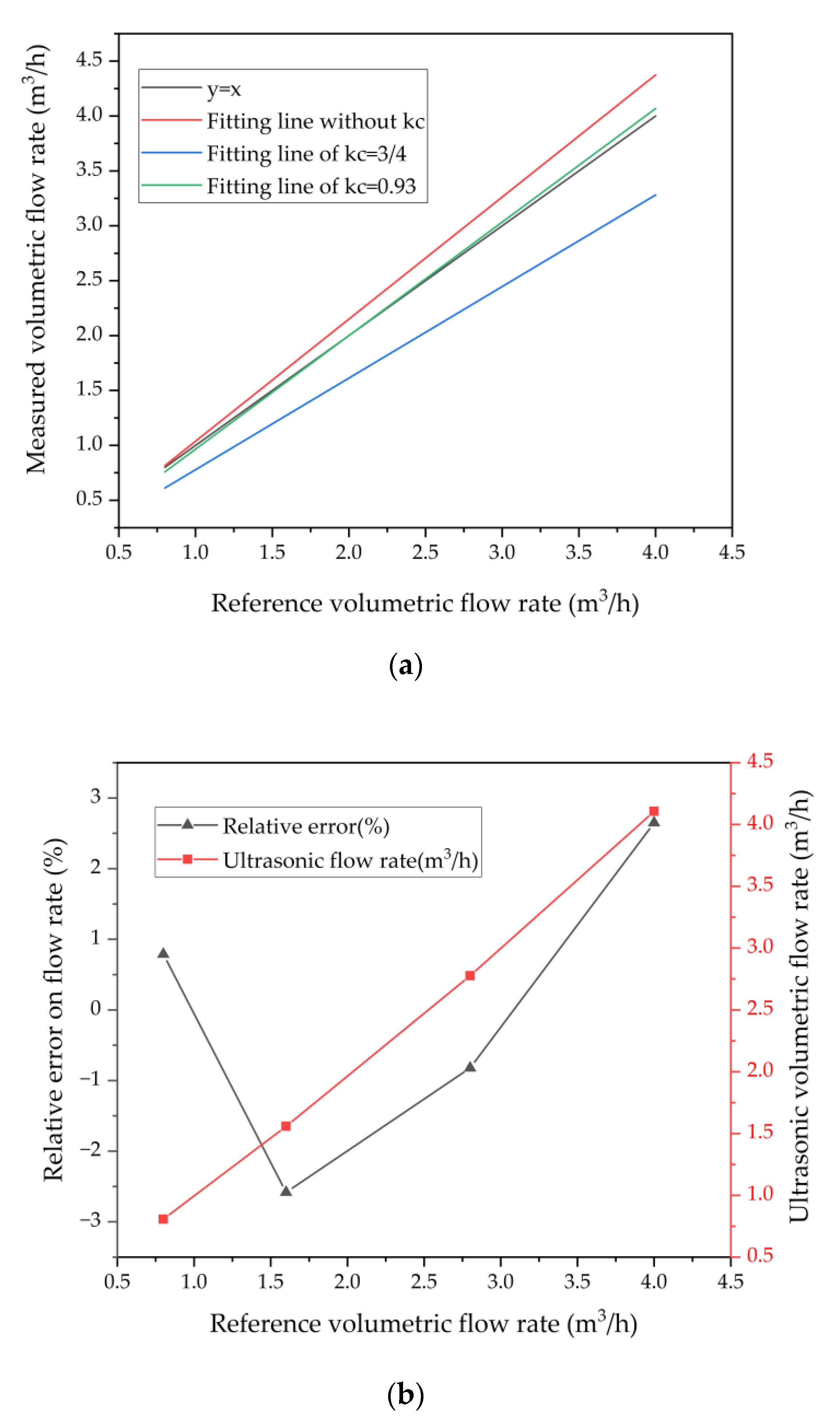
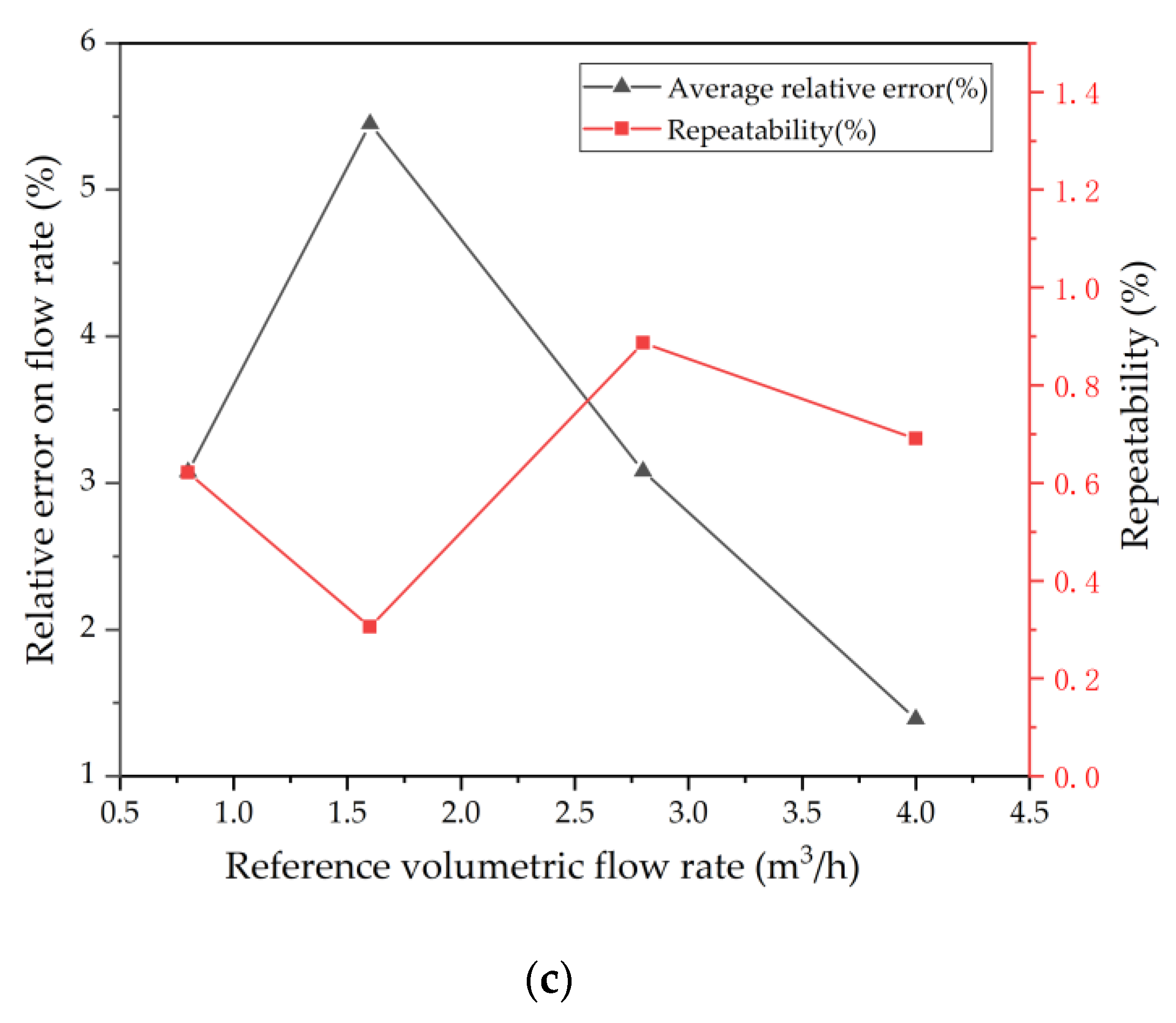
4.3. Flow Measurement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gu, Y.-F.; Zhao, Y.; Lv, R.-Q.; Yang, Y. Theory and Structure of a Modified Optical Fiber Turbine Flowmeter. Flow Meas. Instrum. 2016, 50, 178–184. [Google Scholar] [CrossRef]
- Venugopal, A.; Agrawal, A.; Prabhu, S.V. Review on Vortex Flowmeter-Designer Perspective. Sens. Actuators A Phys. 2011, 170, 8–23. [Google Scholar] [CrossRef]
- Sarbu, G.C. Modern Water Flowmeters: Differential Pressure Flowmeters. In Proceedings of the 2016 International Conference and Exposition on Electrical and Power Engineering (EPE), Iasi, Romania, 20–22 October 2016; pp. 609–616. [Google Scholar] [CrossRef]
- Lynnworth, L.C.; Liu, Y. Ultrasonic Flowmeters: Half-Century Progress Report, 1955–2005. Ultrasonics 2006, 44, e1371–e1378. [Google Scholar] [CrossRef] [PubMed]
- Rajita, G.; Mandal, N. Review on Transit Time Ultrasonic Flowmeter. In Proceedings of the 2016 2nd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 28–30 January 2016; pp. 88–92. [Google Scholar] [CrossRef]
- Dantas, R.G.; Costa, E.T. Ultrasonic Pulsed Doppler Blood Flowmeter for Use in Extracorporeal Circulation. Artif. Organs 2000, 24, 198–201. [Google Scholar] [CrossRef]
- Coulthard, J. Ultrasonic Cross-Correlation Flowmeters. In Proceedings of the IEE Colloquium on Ultrasound in the Process Industry, London, UK, 23–23 September 1993; pp. 7/1–7/3. [Google Scholar]
- Drenthen, J.G.; De Boer, G. The Manufacturing of Ultrasonic Gas Flow Meters. Flow Meas. Instrum. 2001, 12, 89–99. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, C.; Lin, J. Effects of Velocity Profiles on Measuring Accuracy of Transit-Time Ultrasonic Flowmeter. Appl. Sci. 2019, 9, 1648. [Google Scholar] [CrossRef]
- Chen, X.; Liu, C.; Yang, D.; Liu, X.; Hu, L.; Xie, J. Highly Accurate Airflow Volumetric Flowmeters via PMUTs Arrays Based on Transit Time. J. Microelectromech. Syst. 2019, 28, 707–716. [Google Scholar] [CrossRef]
- Bui, G.T.; Jiang, Y.T.; Pang, D.C. Two Capacitive Micro-Machined Ultrasonic Transducers for Wind Speed Measurement. Sensors 2016, 16, 814. [Google Scholar] [CrossRef]
- Eovino, B.E.; Liang, Y.; Akhbari, S.; Lin, L. A Single-Chip Flow Sensor Based on Bimorph PMUTs with Differential Readout Capabilities. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 1084–1087. [Google Scholar] [CrossRef]
- Caronti, A.; Caliano, G.; Carotenuto, R.; Savoia, A.; Pappalardo, M.; Cianci, E.; Foglietti, V. Capacitive Micromachined Ultrasonic Transducer (CMUT) Arrays for Medical Imaging. Microelectron. J. 2006, 37, 770–777. [Google Scholar] [CrossRef]
- Salim, M.S.; Abd Malek, M.F.; Heng, R.B.W.; Juni, K.M.; Sabri, N. Capacitive Micromachined Ultrasonic Transducers: Technology and Application. J. Med. Ultrasound 2012, 20, 8–31. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, W.; Tong, Z.; Zhang, S.; Gu, Y.; Wu, G.; Tovstopyat, A.; Sun, C.; Lou, L. A Novel Transfer Function Based Ring-down Suppression System for Pmuts. Sensors 2021, 21, 6414. [Google Scholar] [CrossRef] [PubMed]
- Akhbari, S.; Sammoura, F.; Eovino, B.; Yang, C.; Lin, L. Bimorph Piezoelectric Micromachined Ultrasonic Transducers. J. Microelectromech. Syst. 2016, 25, 326–336. [Google Scholar] [CrossRef]
- Kreczmer, B. Connections between Object Classification Criteria Using an Ultrasonic Bi-Sonar System. Int. J. Appl. Math. Comput. Sci. 2016, 26, 123–132. [Google Scholar] [CrossRef]
- Li, L.; Zheng, X.; Gao, Y.; Hu, Z.; Zhao, J.; Tian, S.; Wu, Y.; Qiao, Y. Experimental and Numerical Analysis of a Novel Flow Conditioner for Accuracy Improvement of Ultrasonic Gas Flowmeters. IEEE Sens. J. 2022, 22, 4197–4206. [Google Scholar] [CrossRef]
- Lei, Z.; He, K.; Huang, Q.; Bao, Z.; Li, X. Numerical Study on Supercritical Heat Transfer of N-Decane during Pyrolysis in Rectangular Tubes. Appl. Therm. Eng. 2020, 170, 115002. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Cheng, C.H.; Liu, D.G.; Le, M.H. A Fast Cross-Correlation Combined with Interpolation Algorithms for the LiDAR Working in the High Background Noise. Electronics 2022, 11, 985. [Google Scholar] [CrossRef]
- Brassier, P.; Hosten, B.; Vulovic, F. High-Frequency Transducers and Correlation Method to Enhance Ultrasonic Gas Flow Metering. Flow Meas. Instrum. 2001, 12, 201–211. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Le, X.; Wang, Y.; Wu, C.; Xie, J. Reducing Ring-down Time of PMUTs with Phase Shift of Driving Waveform. Sens. Actuators A Phys. 2018, 281, 100–107. [Google Scholar] [CrossRef]
- Pala, S.; Shao, Z.; Peng, Y.; Lin, L. Improved Ring-Down Time and Axial Resolution of PMUTs via a Phase-Shift Excitation Scheme. In Proceedings of the 2021 IEEE 34th International Conference on Micro Electro Mechanical Systems (MEMS), Gainesville, FL, USA, 25–29 January 2021; pp. 390–393. [Google Scholar] [CrossRef]
- He, L.M.; Xu, W.J.; Liu, W.J.; Wang, X.B.; Zhou, J.; Ren, J.Y. Performance and Crosstalk Evaluation of 2-D Array Piezoelectric Micromachined Ultrasonic Transducer with 3-D Finite Element Simulation. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019; pp. 792–795. [Google Scholar] [CrossRef]
- Thao, P.N. Development of Linear PMUT Array with Low Mechanical Crosstalk Toward Ultrasonography Applications. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021; pp. 659–662. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, B.; Li, X.; Liu, D.; Wang, Y.; Huang, Z. A Model-Based Hybrid Ultrasonic Gas Flowmeter. IEEE Sens. J. 2018, 18, 4443–4452. [Google Scholar] [CrossRef]

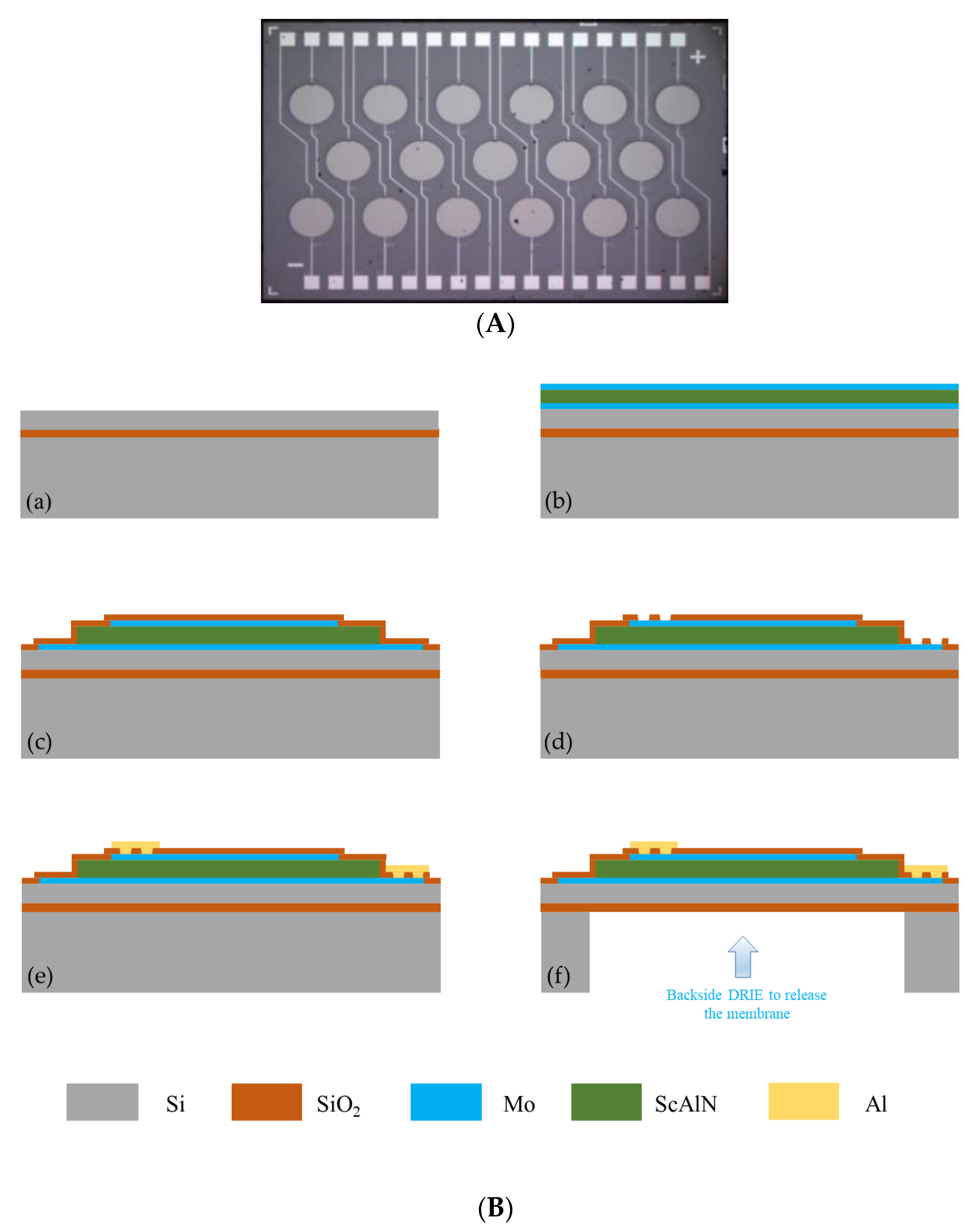





| Material | Top Mo | ScAlN | Bottom Mo | Si | SiO2 | Cavity |
|---|---|---|---|---|---|---|
| Radius (µm) | 234 | 300 | ||||
| Thickness | 0.15 | 1 | 0.2 | 4 | 1 | 400 |
| No. | Reference Flowmeter (m3/h)_Q2 | Ultrasonic Flowmeter (m3/h)_Q1 | Q2:Q1 | Q1 × 0.93 | Relative Error |
|---|---|---|---|---|---|
| 1 | 0.8 | 0.867 | 0.92272203 | 0.80631 | 0.78875 |
| 2 | 1.6 | 1.676 | 0.954653938 | 1.55868 | −2.5825 |
| 3 | 2.8 | 2.986 | 0.93770931 | 2.77698 | −0.822142857 |
| 4 | 4 | 4.415 | 0.906002265 | 4.10595 | 2.64875 |
| This Work | Ref. [10] | Ref. [12] | Ref. [11] | |
|---|---|---|---|---|
| Frequency | 201 kHz | 980 kHz | 730 kHz | 200 kHz |
| Transducers | A PMUT array | Two PMUT arrays | A PMUT array | A CMUT array |
| Pipe’s shape | Rectangular | Circular | Only baffle | Only baffle |
| Pipe’s height | 21.6 mm | 10 mm | 4 cm | 10 mm |
| Flow rate/Velocity | 4 m3/h (~9 m/s) | 0.56 m3/h | 5 m/s | 10 m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiu, X.; Yang, H.; Ji, M.; Lv, H.; Zhang, S. Development of MEMS Airflow Volumetric Flow Sensing System with Single Piezoelectric Micromachined Ultrasonic Transducer (PMUT) Array. Micromachines 2022, 13, 1979. https://doi.org/10.3390/mi13111979
Xiu X, Yang H, Ji M, Lv H, Zhang S. Development of MEMS Airflow Volumetric Flow Sensing System with Single Piezoelectric Micromachined Ultrasonic Transducer (PMUT) Array. Micromachines. 2022; 13(11):1979. https://doi.org/10.3390/mi13111979
Chicago/Turabian StyleXiu, Xueying, Haolin Yang, Meilin Ji, Haochen Lv, and Songsong Zhang. 2022. "Development of MEMS Airflow Volumetric Flow Sensing System with Single Piezoelectric Micromachined Ultrasonic Transducer (PMUT) Array" Micromachines 13, no. 11: 1979. https://doi.org/10.3390/mi13111979
APA StyleXiu, X., Yang, H., Ji, M., Lv, H., & Zhang, S. (2022). Development of MEMS Airflow Volumetric Flow Sensing System with Single Piezoelectric Micromachined Ultrasonic Transducer (PMUT) Array. Micromachines, 13(11), 1979. https://doi.org/10.3390/mi13111979





