A Non-Invasive Physiological Control System of a Rotary Blood Pump Based on Preload Sensitivity: Use of Frank–Starling-Like Mechanism
Abstract
1. Introduction
2. Methodology
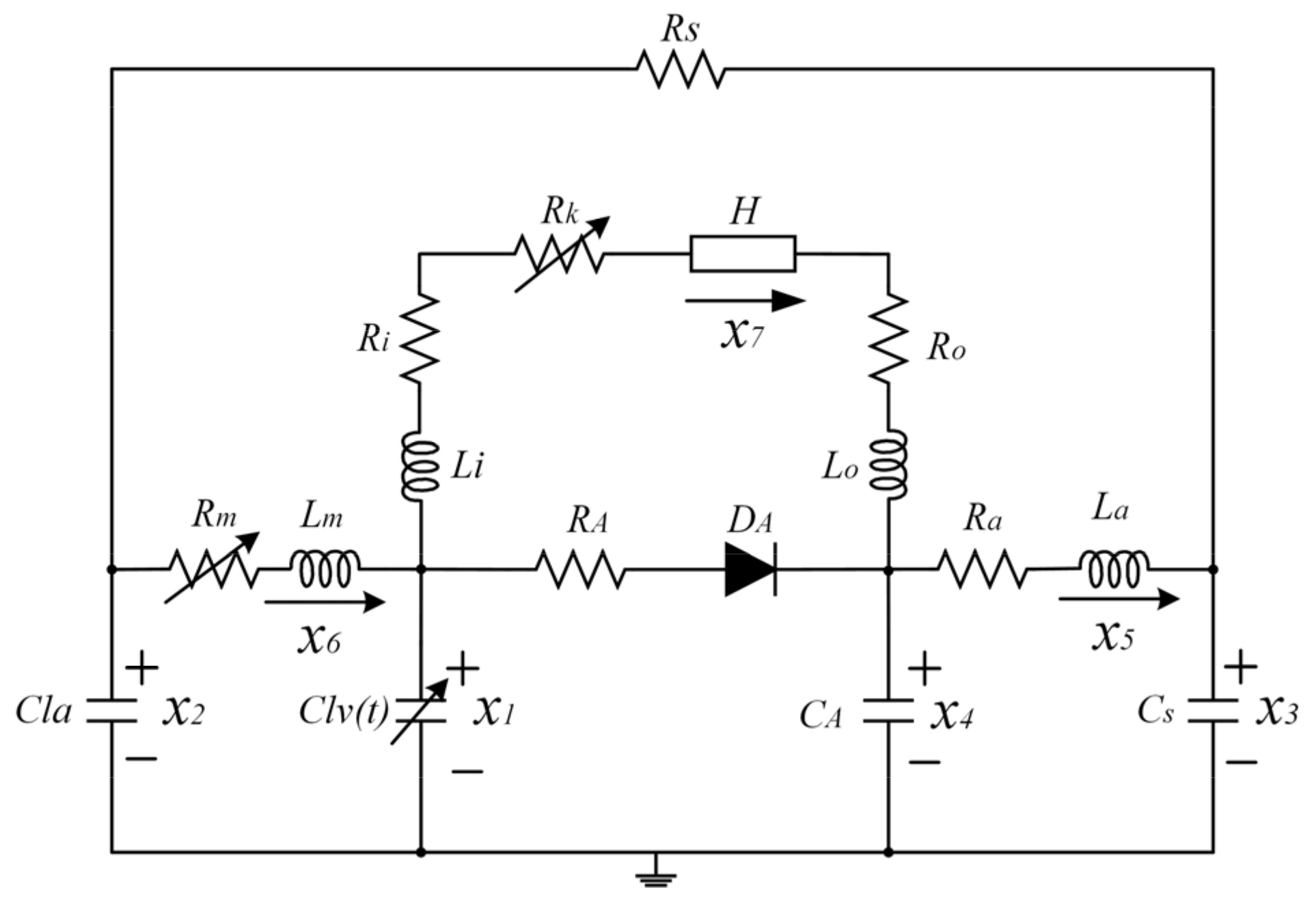
2.1. Mock Circulation Loop (MCL)
2.2. Control Strategy
2.2.1. Estimate Average Pump Flow
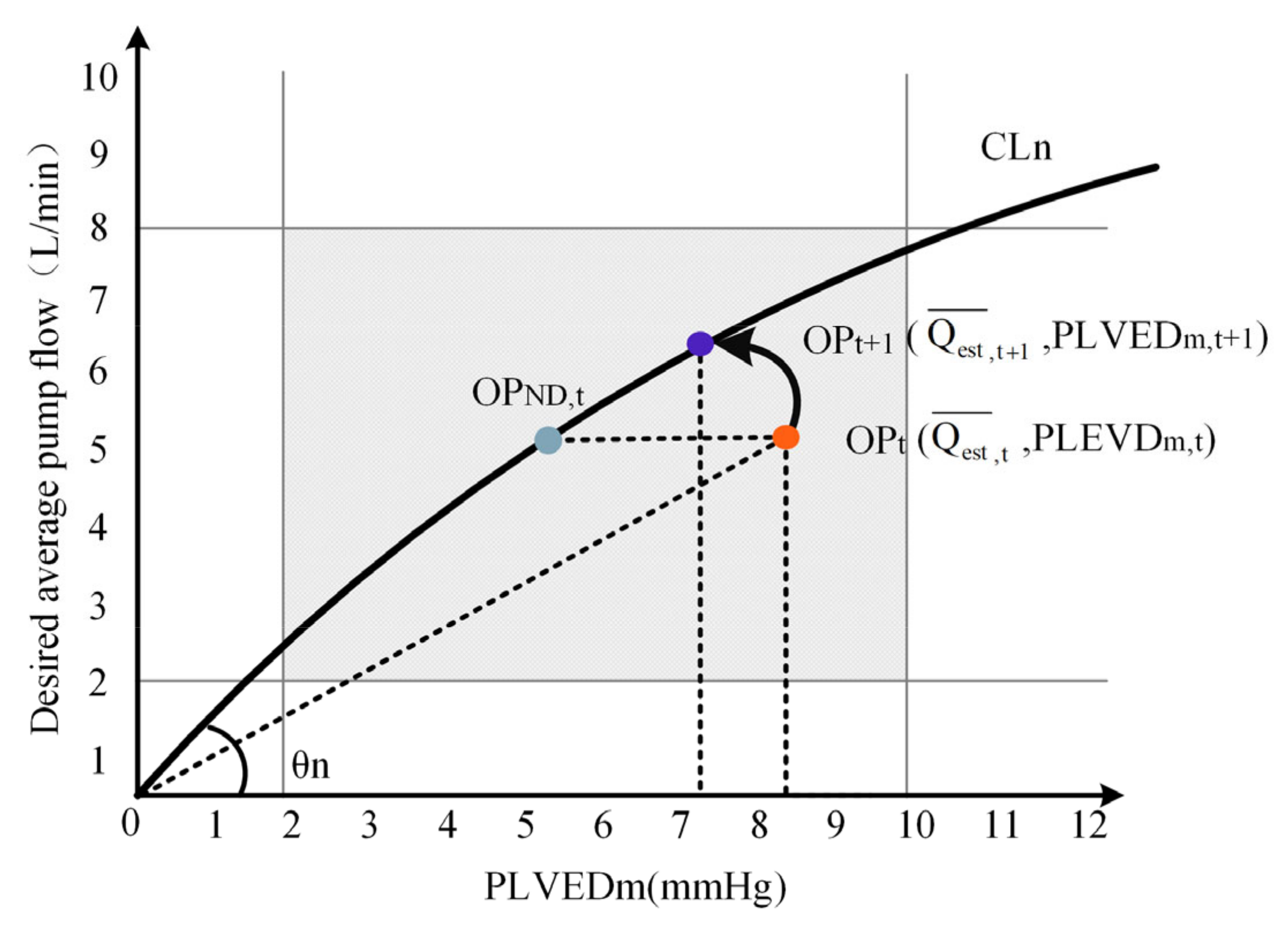
2.2.2. Calculate the Desired Average Pump Flow
2.2.3. Motor Speed Control
2.3. Parameters Setting for Physiological States
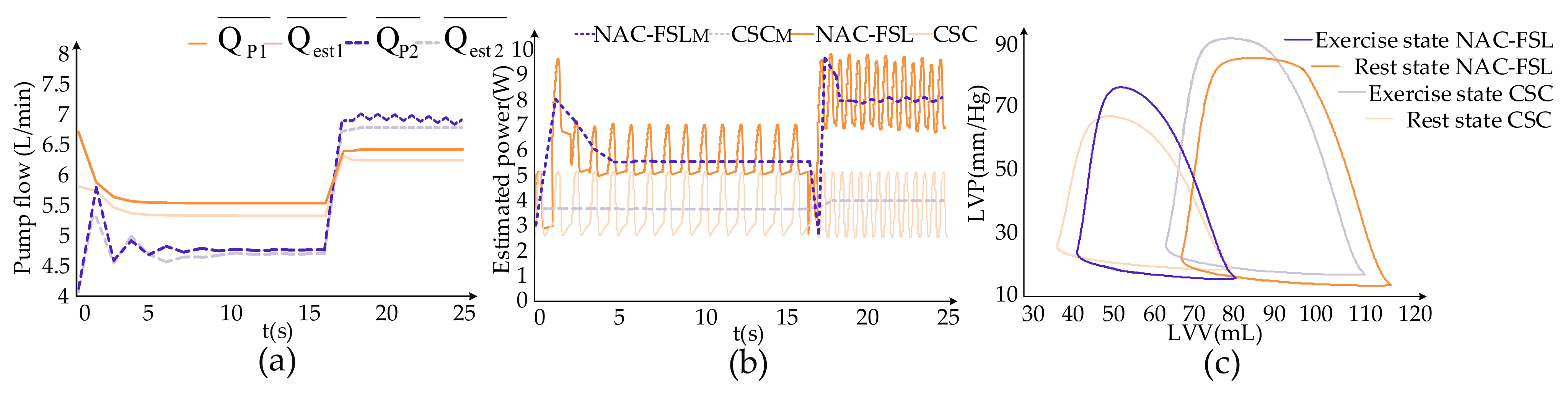
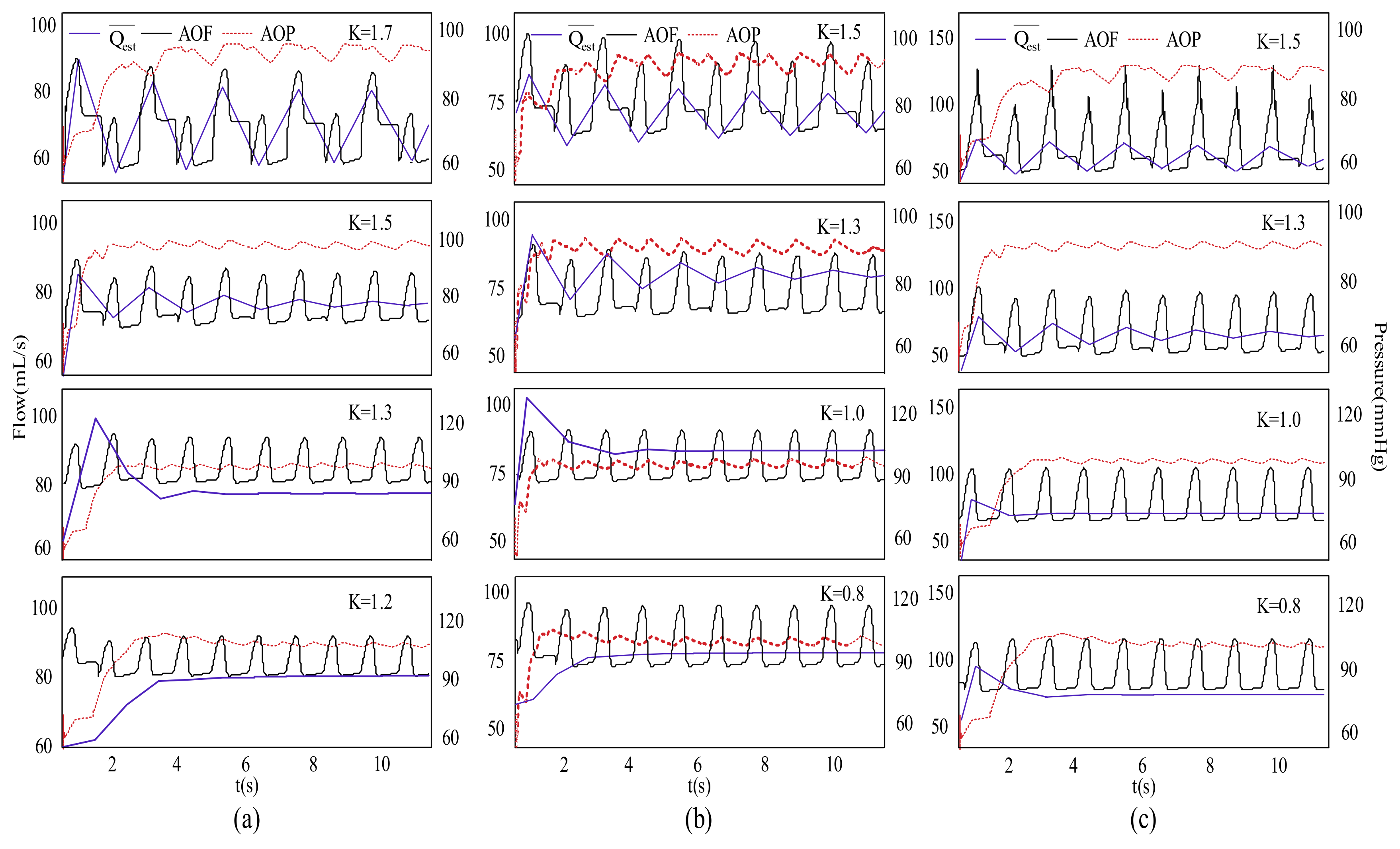
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, Y.; Gu, K.; Gao, B.; Liu, Y. Hemodynamic influence of cardiovascular system in intra-aorta pump. J. Beijing Univ. Technol. 2013, 39, 629–633. [Google Scholar]
- Shi, L.; Huo, C.; Liu, J. Observation and nursing of complications of mechanical assisted treatment after cardiac surgery. Chin. J. Mod. Nurs. 2013, 19, 1684–1686. [Google Scholar]
- Salamonsen, R.F.; Mason, D.G.; Ayre, P.J. Response of rotary blood pumps to changes in preload and afterload at a fixed speed setting are unphysiological when compared with the natural heart. J. Artif. Organs 2011, 35, E47–E53. [Google Scholar] [CrossRef] [PubMed]
- AlOmari, A.-H.H.; Savkin, A.V.; Stevens, M.; Mason, D.G.; Timms, D.L.; Salamonsen, R.F.; Lovell, N.H. Developments in control systems for rotary left ventricular assist devices for heart failure patients: A review. J. Physiol. Meas. 2012, 34, R1–R27. [Google Scholar] [CrossRef] [PubMed]
- Stevens, M.C.; Gaddum, N.R.; Pearcy, M.; Meboldt, M.; Schmid, D.M. Frank-starling control of a left ventricular assist device. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 1335–1338. [Google Scholar]
- Petrou, A.; Ochsner, G.; Amacher, R.; Pergantis, P.; Rebholz, M.; Meboldt, M.; Daners, M.S. A Physiological controller for turbodynamic ventricular assist devices based on left ventricular systolic pressure. J. Artif. Organs 2016, 40, 842–855. [Google Scholar] [CrossRef] [PubMed]
- Cordeiroa, T.D.; Sousaa, D.L.; Cestari, I.A.; Lima, A.M.N. A physiological control system for ECG-synchronized pulsatile pediatric ventricular assist devices. J. Biomed. Signal Process. Control. 2020, 57, 101752. [Google Scholar] [CrossRef]
- Fetanat, M.; Stevens, M.; Hayward, C.; Lovell, N.H. A physiological control system for an implantable heart pump that accommodates for interpatient and intrapatient variations. IEEE Trans. Biome. Eng. 2020, 67, 1167–1175. [Google Scholar] [CrossRef] [PubMed]
- Magkoutas, K.; Arm, P.; Meboldt, M.; Daners, M.S. Physiologic data-driven iterative learning control for left ventricular assist devices. Front. Cardiovasc. Med. 2022, 9, 922387. [Google Scholar] [CrossRef] [PubMed]
- Stephens, A.F.; Gregory, S.D.; Burrellc, A.J.C.; Silvana, M.S.; Dion, S.D.; Salamonsenc, R.F. Physiological principles of Starling-like control of rotary ventricular assist devices. Expert Rev. Med. Devices 2020, 7, 1169–1182. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Koenig, S.C.; Slaughter, M.S.; Giridharan, G.A. Suction prevention and physiologic control of continuous flow left ventricular assist devices using intrinsic pump parameters. ASAIO J. 2015, 61, 170–177. [Google Scholar] [CrossRef]
- Fu, M.; Xu, L. Computer simulation of sensorless fuzzy control of a rotary blood pump to assure normal physiology. ASAIO J. 2000, 46, 273–278. [Google Scholar] [CrossRef]
- Bakouri, M.A.; Salamonsen, R.F.; Savkin, A.V.; AlOmari, A.H. A sliding mode-based starling-like controller for implantable rotary blood pumps. Artif. Organs 2014, 38, 587–593. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Simaan, M.A. A suction detection system for rotary blood pumps based on the lagrangian support vector machine algorithm. IEEE J. Biomed. Health Inform. 2013, 17, 654–663. [Google Scholar] [CrossRef] [PubMed]
- Haddad, F.; Hunt, S.A.; Rosenthal, D.N.; Murphy, D.J. Right ventricular function in cardiovascular disease, Part I: Anatomy, Physiology, Aging, and Functional Assessment of the Right Ventricle. Circulation 2008, 117, 1436–1448. [Google Scholar] [CrossRef] [PubMed]
- Guyton, A. Circulatory Physiology: Cardiac Output and Its Regulation; W.B. Saunders Company: Philadelphia, PA, USA; London, UK, 1963; pp. 237–239. [Google Scholar]
- Wang, F.Q.; Xu, Q.; Wu, Z.H.; Wen, T.Y.; Ji, J.H.; He, Z.M. Control Study of Blood Circulation System Based on Left Heart Assist Device. J. Biomed. Eng. 2015, 33, 1075–1083. [Google Scholar]
- Faragallah, G.; Simaan, M. An engineering analysis of the aortic valve dynamics in patients with rotary Left Ventricular Assist Devices. J. Healthc. Eng. 2013, 4, 307–327. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.T.; Alomari, A.H.; Savkin, A.V.; Ayre, P.J.; Lim, E.; Salamonsen, R.F.; Rosenfeldt, F.L.; Lovell, N.H. In vivo validation of pulsatile flow and differential pressure estimation models in a left ventricular assist device. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2010, 8, 2517–2520. [Google Scholar]
- Salamonsen, R.F.; Lim, E.; Gaddum, N.; AlOmari, A.H.; Gregory, S.D.; Stevens, M.; Mason, D.G.; Fraser, J.F.; Timms, D.; Karunanithi, M.K.; et al. Theoretical foundations of a Starling-like controller for rotary blood pumps. Artif. Organs. 2012, 36, 787–796. [Google Scholar] [CrossRef] [PubMed]
- Gaddum, N.R.; Stevens, M.; Lim, E.; Fraser, J.; Lovell, N.; Mason, D. Starling-like flow control of a left ventricular assist device: In vitro validation. Artif. Organs 2014, 38, E46–E56. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Value | Physiological Meaning |
|---|---|---|
| f cell7 row 1 cell8 row 1 | 10.06 | constant |
| g cell6 row 2 cell7 row 2 cell8 row 2 | 6.5-HCT × 3.25 × 10−2 | Linearly related values to HCT |
| h cell6 row 3 cell7 row 3 cell8 row 3 | HCT × 4.67 × 10−3–0.557 | Linearly related values to HCT |
| i | 0.009-HCT × 2.90 × 10−4 | Linearly related values to HCT |
| j | 0.0105 | constant |
| k | 5.5 | constant |
| ρ | 13,600 | reference liquid density (kg/m3) |
| g | 9.8 | gravity acceleration (m/s2) |
| η | 100% | efficiency of electrical power to hydraulic power |
| β | 9.9025 × 10−7 | pump parameter (mmHg/rpm2) |
| Parameter | Rest State | Exercise State |
|---|---|---|
| Emax (mmHg/mL) | 1.0 | 1.0 |
| HR (bpm) | 60 | 120 |
| Rs (mmHg.s/mL) | 1.2 | 0.5 |
| Emax | K | Error | Stability | ||
|---|---|---|---|---|---|
| 0.5 | 1.0 | * | * | * | * |
| 1.2 | 5.0069 | 5.0591 | 1.68% | stable | |
| 1.3 | 4.9773 | 4.9058 | 1.44% | stable | |
| 1.5 | 4.7617 | 4.6595 | 2.15% | slight shock | |
| 1.7 | 4.3598 | 4.5163 | 3.59% | shock | |
| 1.0 | 0.5 | * | * | * | * |
| 0.8 | 5.1000 | 5.1933 | 1.87% | stable | |
| 1.0 | 4.9686 | 4.8988 | 1.2% | stable | |
| 1.3 | 4.7179 | 4.6247 | 1.4% | slight shock | |
| 1.5 | 4.3560 | 4.4967 | 3.23% | shock | |
| 1.5 | 0.4 | * | * | * | * |
| 0.8 | 4.9229 | 5.0477 | 2.24% | stable | |
| 1.0 | 4.7588 | 4.8539 | 1.99% | stable | |
| 1.3 | 4.3526 | 4.5904 | 5.46% | slight shock | |
| 1.5 | 4.0980 | 4.4797 | 9.31% | shock |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Wang, S.; Li, Z.; He, C.; Xu, F.; Jing, T. A Non-Invasive Physiological Control System of a Rotary Blood Pump Based on Preload Sensitivity: Use of Frank–Starling-Like Mechanism. Micromachines 2022, 13, 1981. https://doi.org/10.3390/mi13111981
Wang F, Wang S, Li Z, He C, Xu F, Jing T. A Non-Invasive Physiological Control System of a Rotary Blood Pump Based on Preload Sensitivity: Use of Frank–Starling-Like Mechanism. Micromachines. 2022; 13(11):1981. https://doi.org/10.3390/mi13111981
Chicago/Turabian StyleWang, Fangqun, Shaojun Wang, Zhijian Li, Chenyang He, Fan Xu, and Teng Jing. 2022. "A Non-Invasive Physiological Control System of a Rotary Blood Pump Based on Preload Sensitivity: Use of Frank–Starling-Like Mechanism" Micromachines 13, no. 11: 1981. https://doi.org/10.3390/mi13111981
APA StyleWang, F., Wang, S., Li, Z., He, C., Xu, F., & Jing, T. (2022). A Non-Invasive Physiological Control System of a Rotary Blood Pump Based on Preload Sensitivity: Use of Frank–Starling-Like Mechanism. Micromachines, 13(11), 1981. https://doi.org/10.3390/mi13111981





