Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope
Abstract
1. Introduction
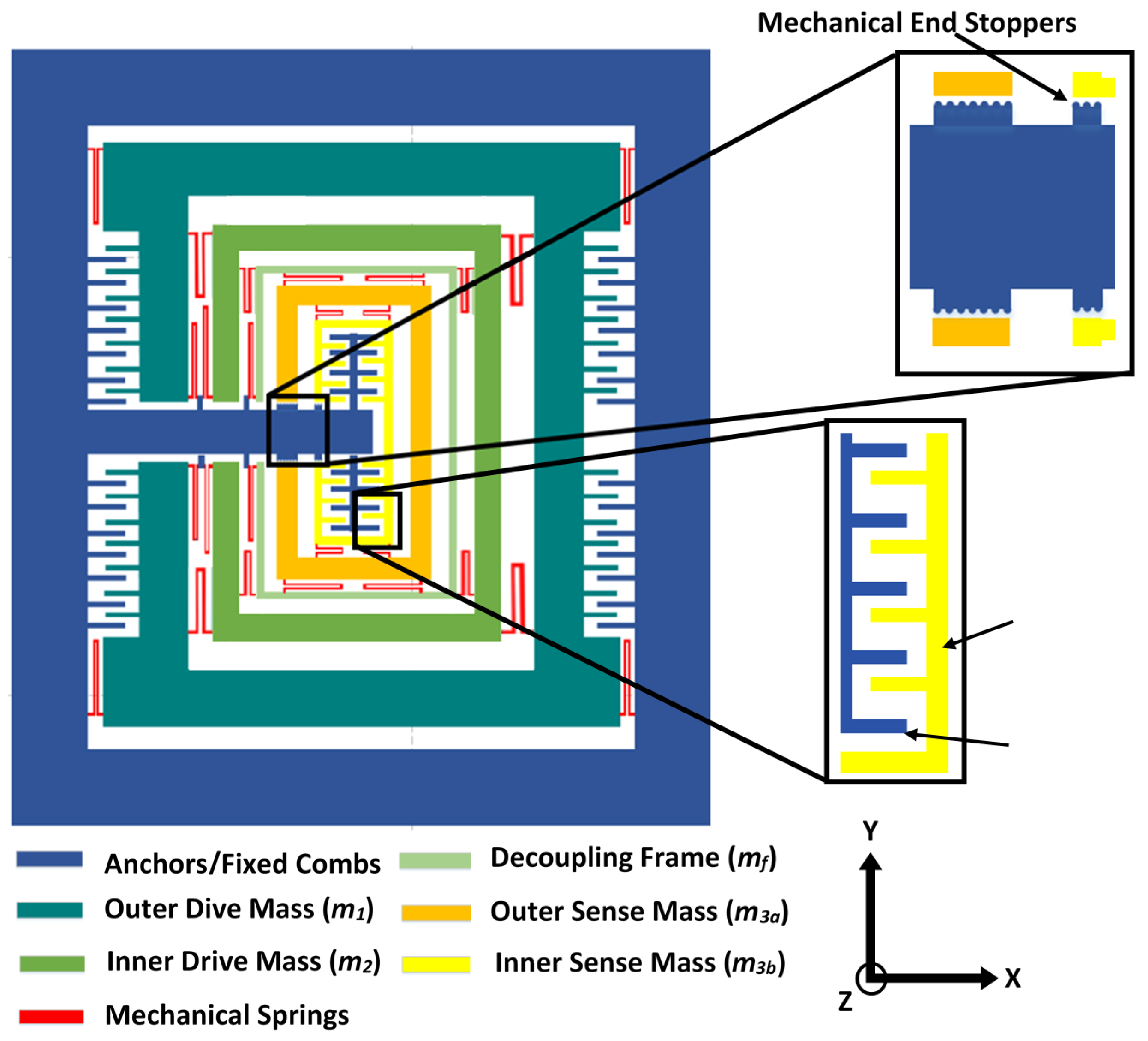
2. Structural Design of Multi-Degree of Freedom (Multi-DoF) Microelectromechanical Systems (MEMS) Gyroscope
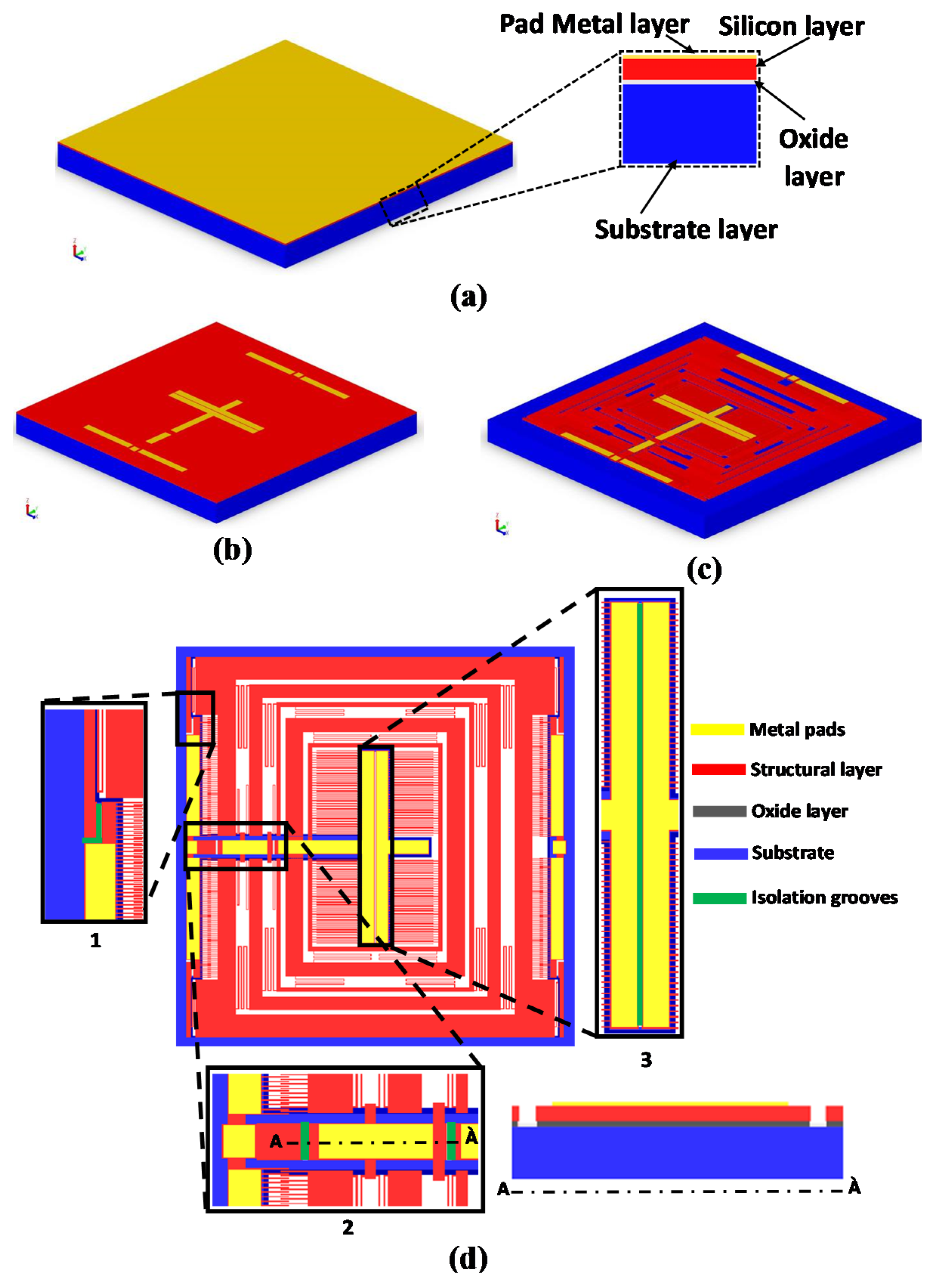
3. Microfabrication Process
- (a)
- The process starts with an SOI wafer as shown in Figure 2a. The doping of the top layer of silicon is done by depositing a phosphosilicate glass (PSG) layer and then annealing is done at 1050 °C in Argon. It is followed by the removal of the PSG layer using wet etching.
- (b)
- The lift-off process is then used to deposit the first Padmetal layer which consists of 500 nm gold stack and 20 nm chrome layer, as shown in Figure 2b.
- (c)
- To apply a second mask, a lithography technique is utilized for the patterning of the silicon layer as shown in Figure 2c.
- (d)
- To apply the TRENCH mask, substrate layer of thickness 400 µm is patterned in which lithography technique is used with successive etching through Deep Reactive Ion Etching (DRIE). The final structure is obtained by removing the buried oxide layer in the regions defined by the TRENCH mask, as shown in Figure 2d.
3.1. Microfabrication Process Limitations
3.1.1. Limitation 1
3.1.2. Limitation 2
3.1.3. Limitation 3
3.2. Process Driven Design Modifications
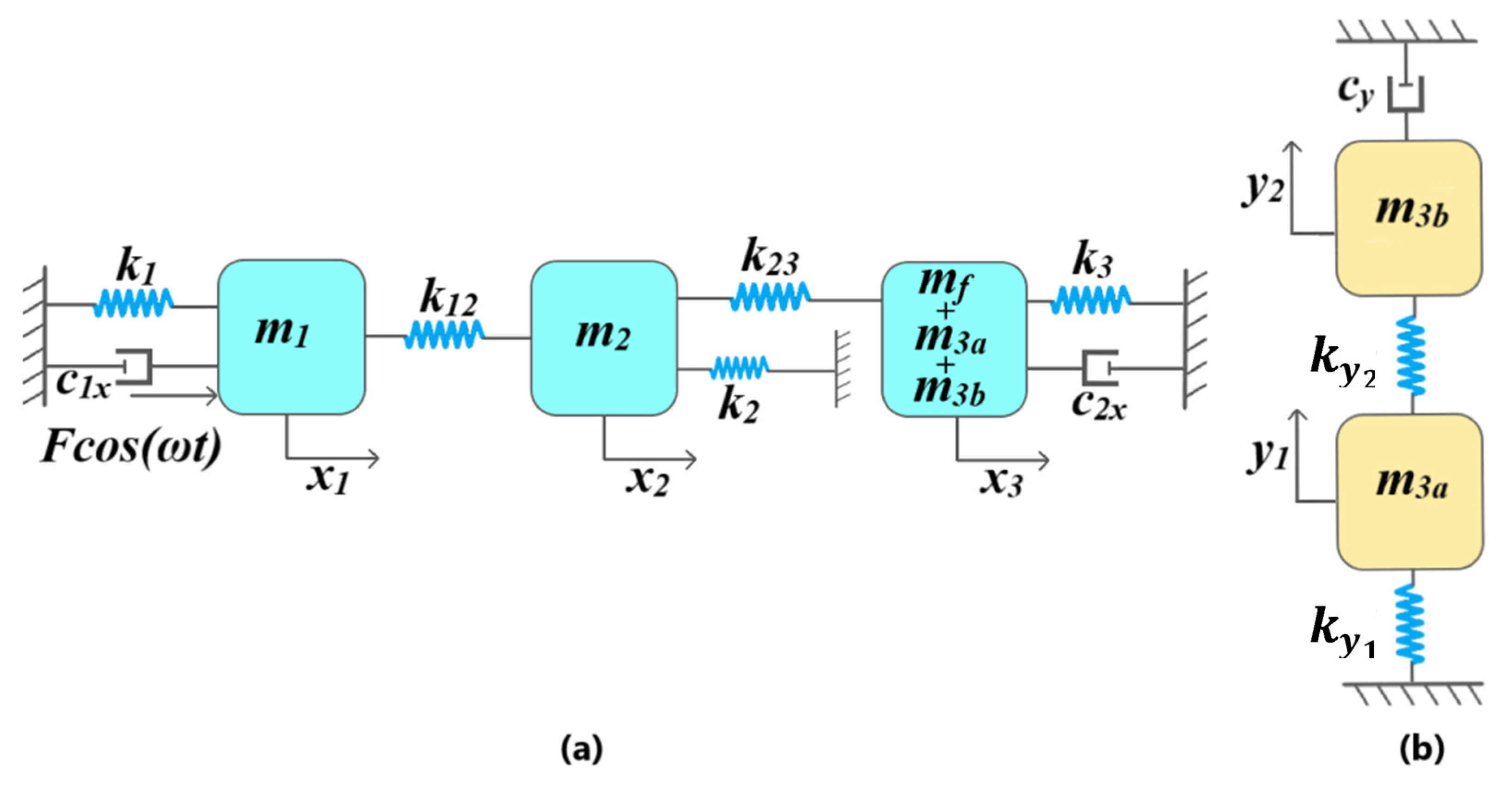
4. Analytical Modeling of the Multi-DoF MEMS Gyroscope
4.1. Equations of Motion for the Drive and Sense Mode Oscillators
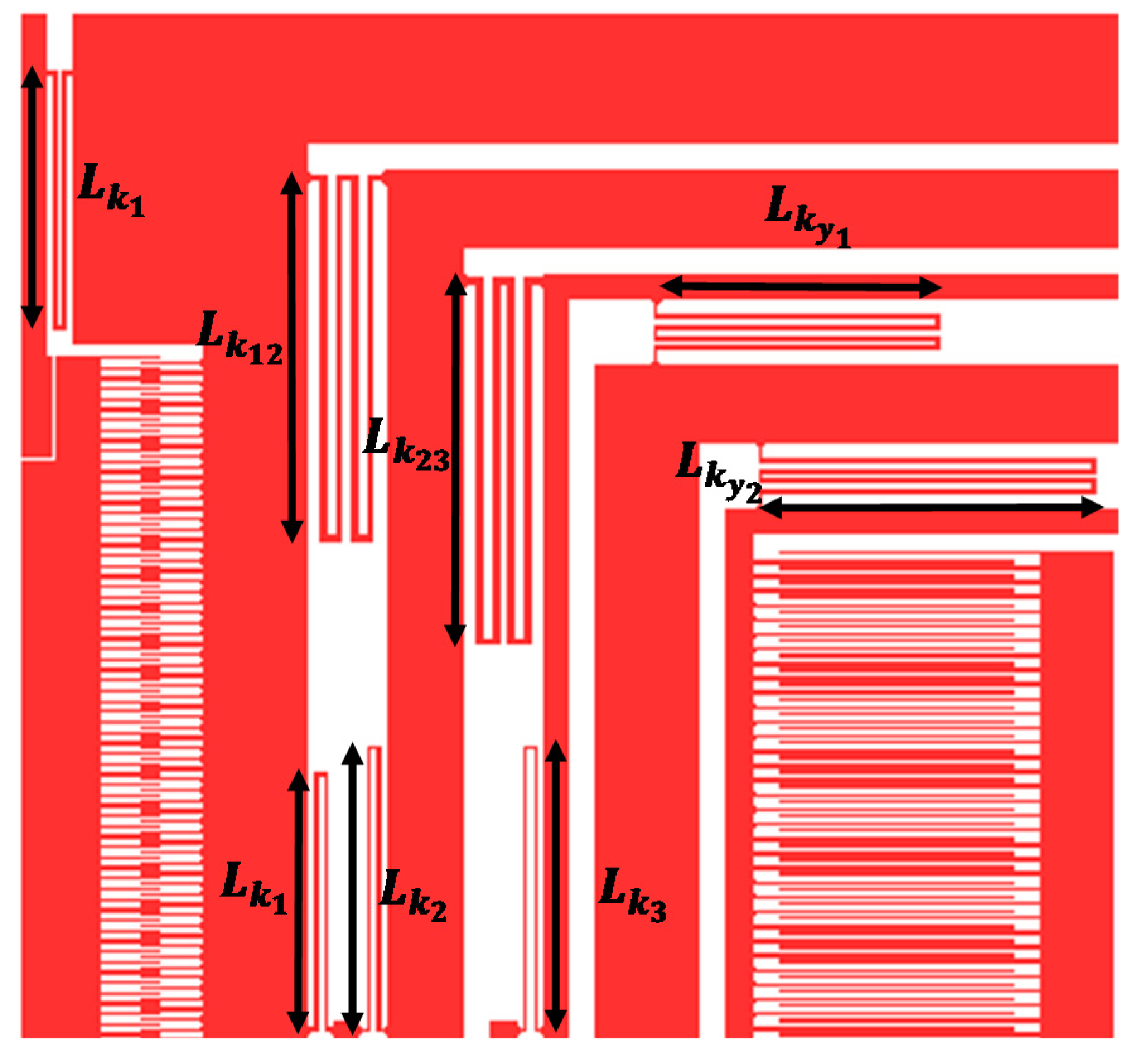
4.2. Calculation of Mechanical Stiffness
4.3. Calculation of Differential Capacitance Change
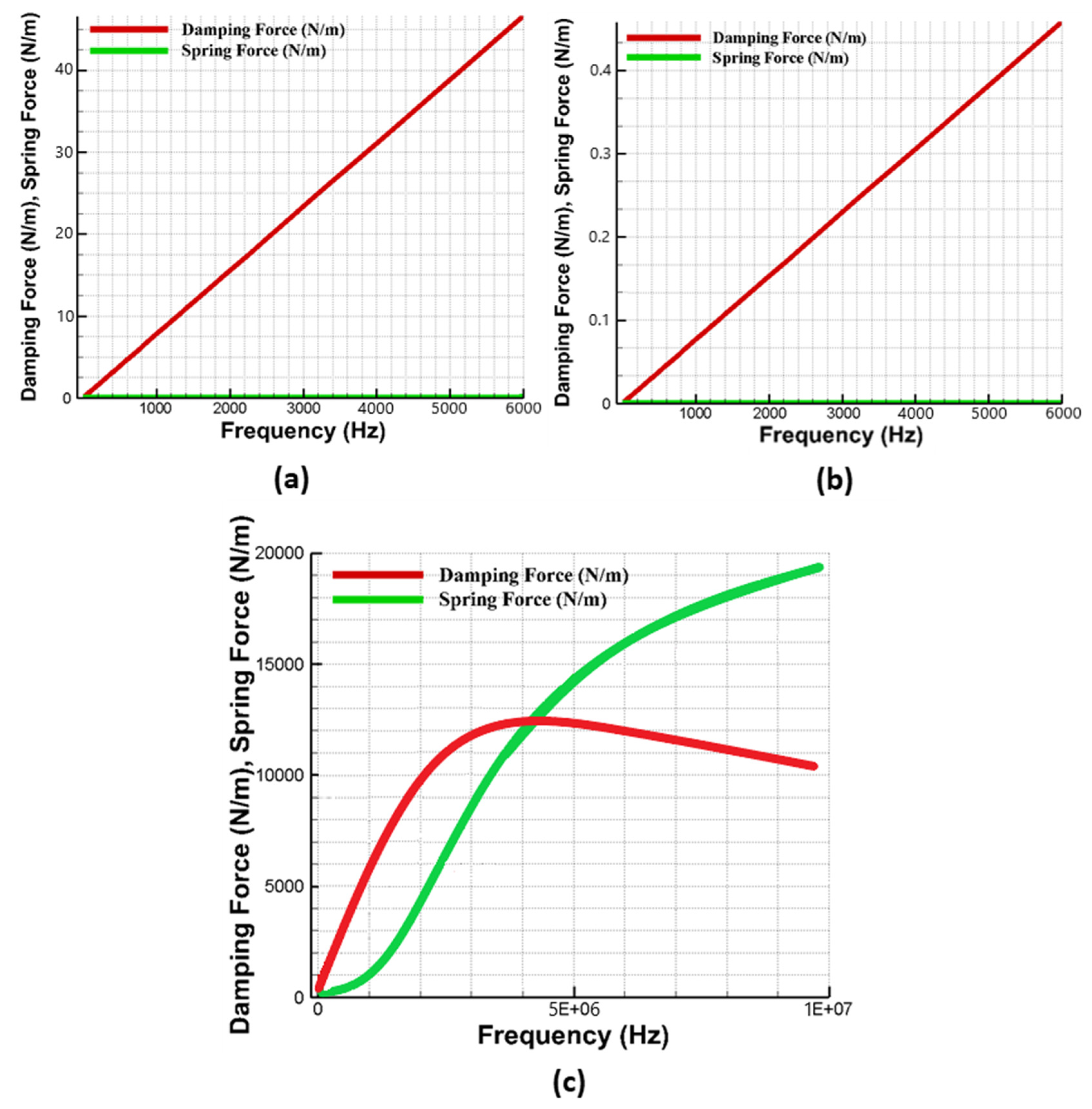
4.4. Air Damping Analysis
5. FEM Analysis for the MEMS Gyroscope
5.1. Modal Analysis
5.2. Pull-in Voltage Analysis
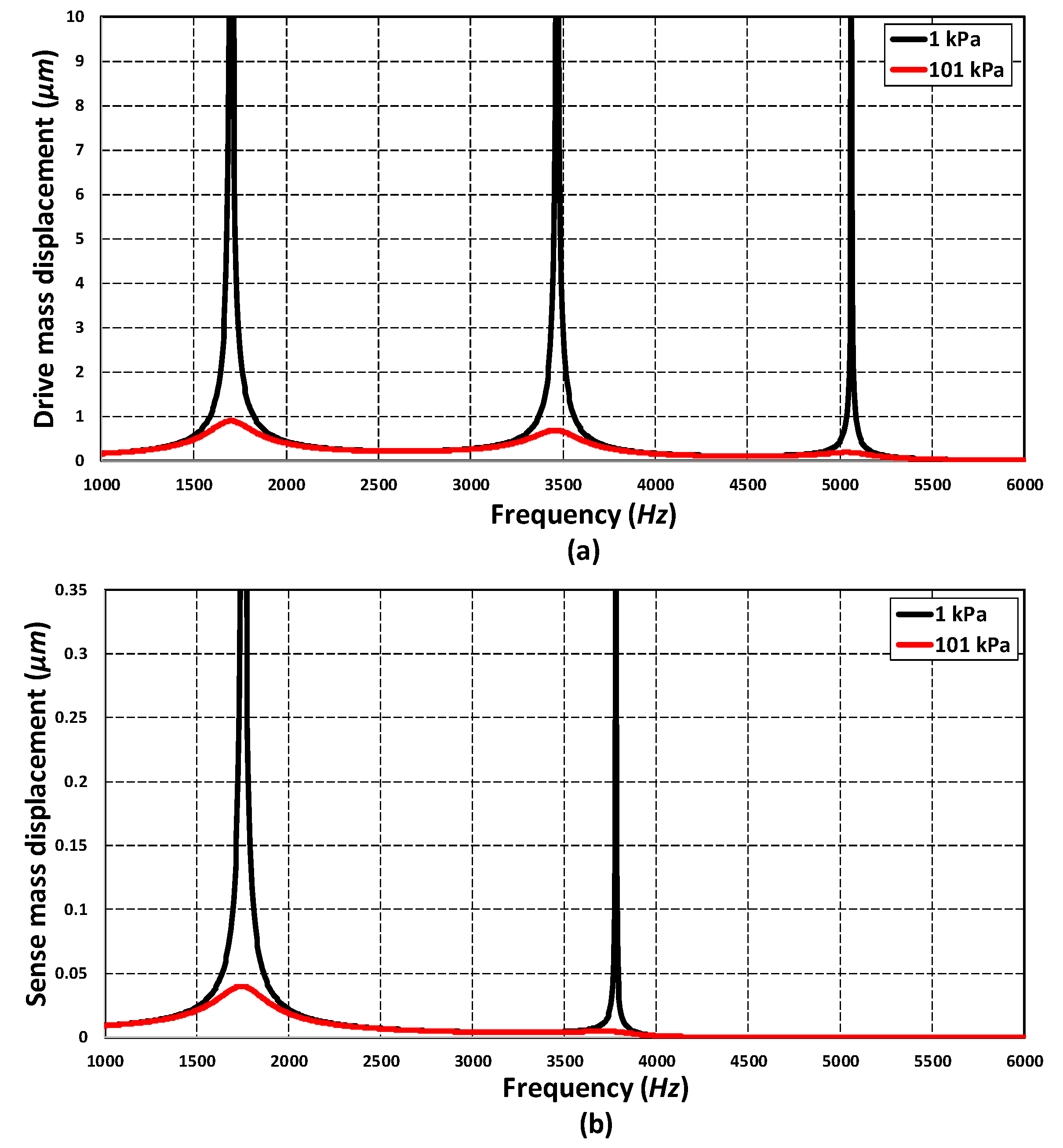
5.3. Frequency Response Analysis
5.4. Oscillation Frequency-Dependent Air Damping Analysis
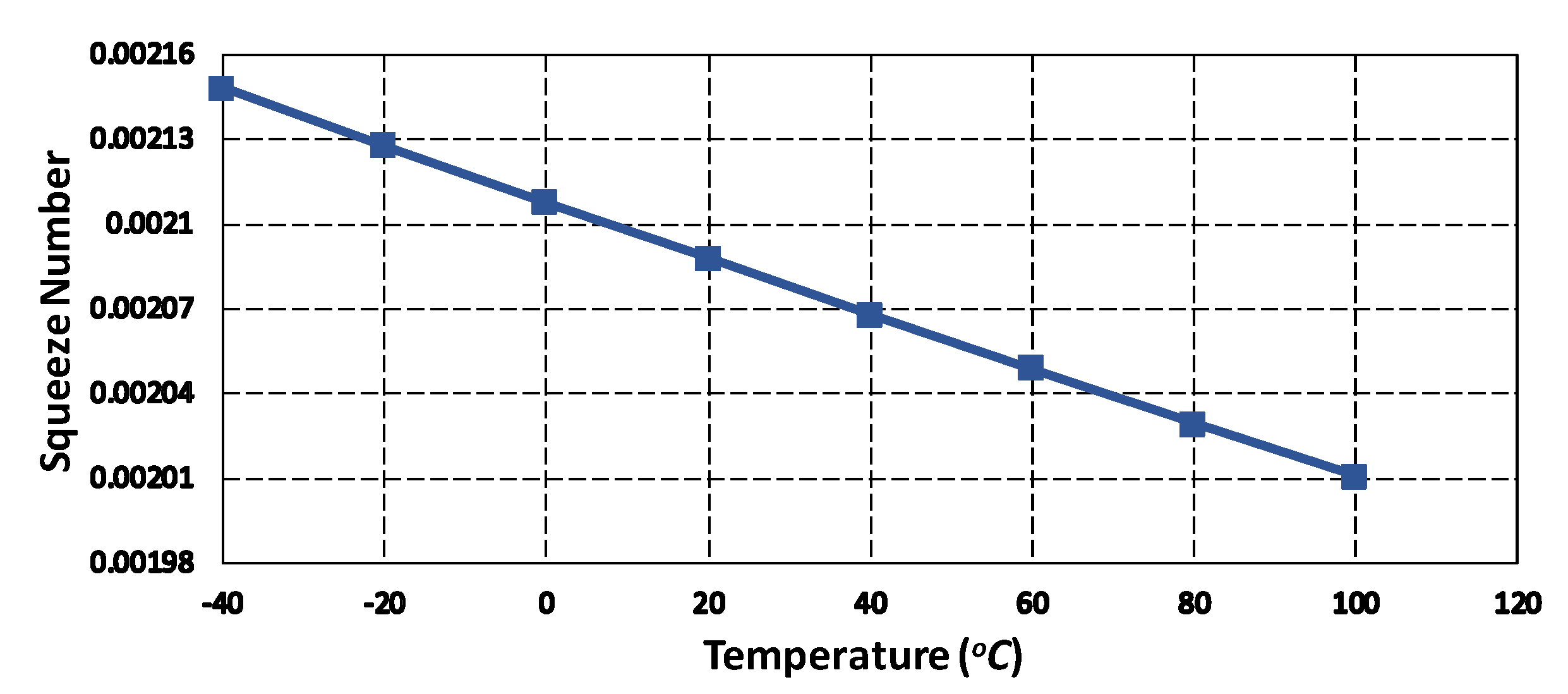
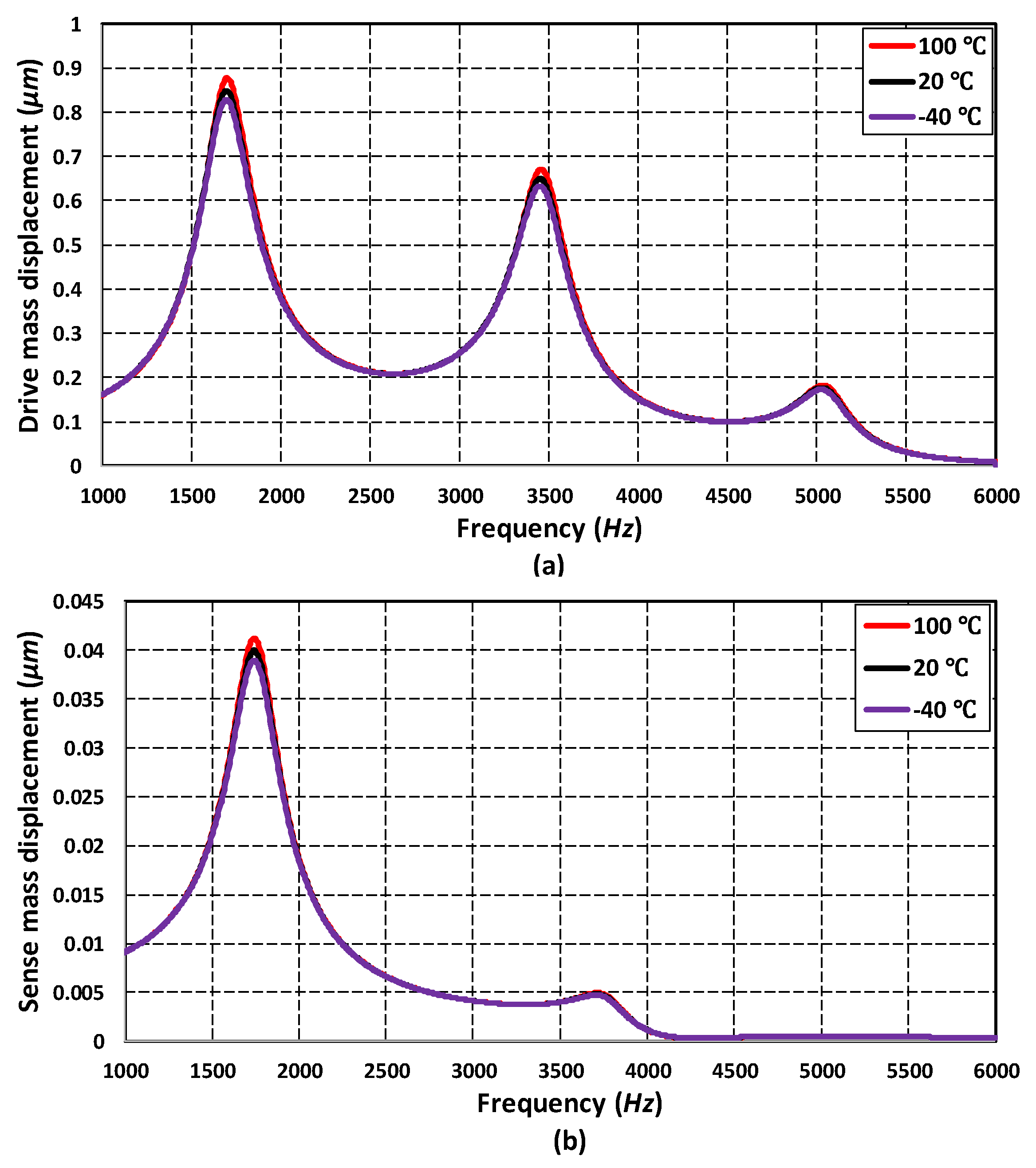
5.5. Effect of Operating Temperature and Pressure Variations on MEMS Gyroscope
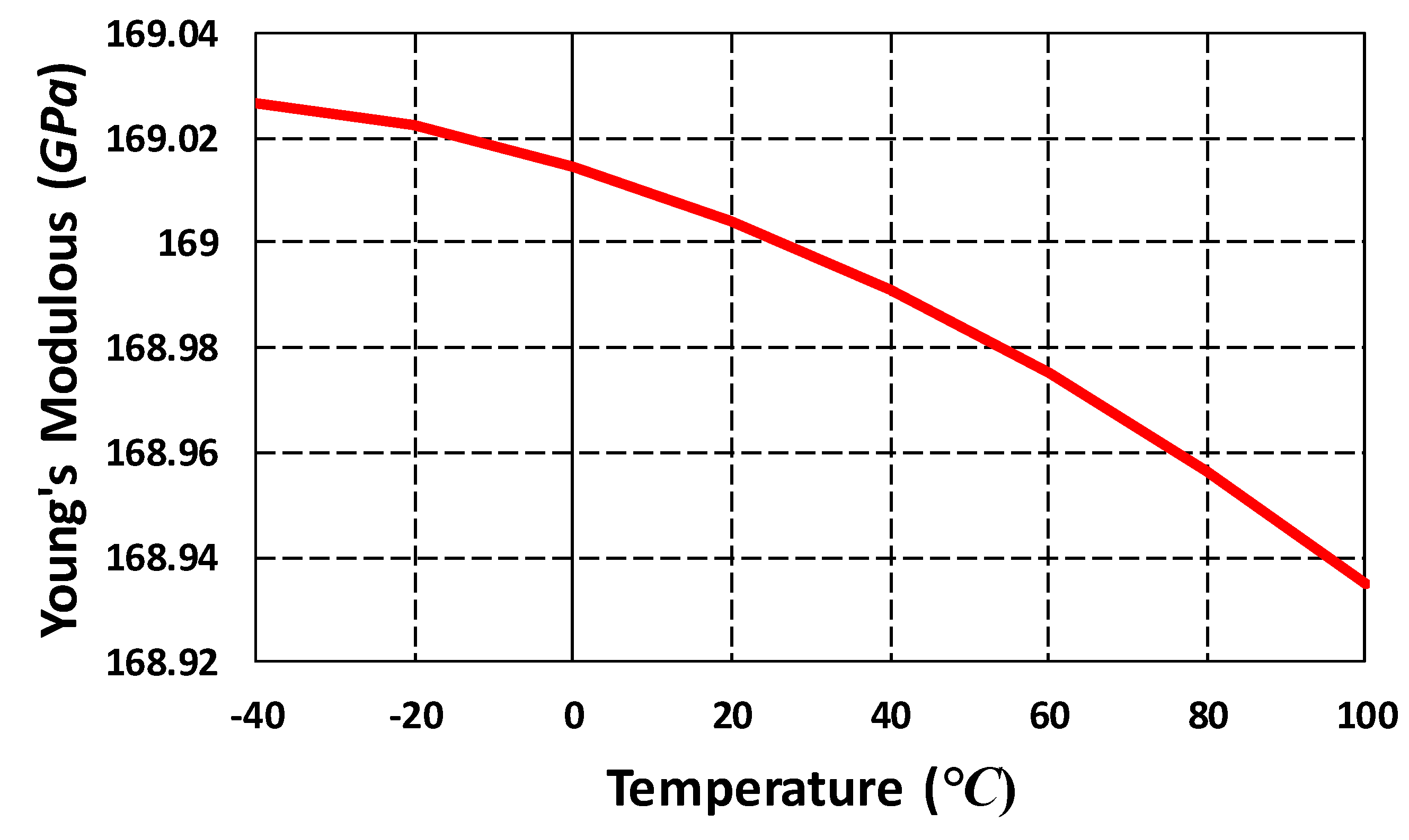
5.6. Thermal Stability Analysis of MEMS Gyroscope
5.7. Analysis of Fabrication Process Tolerances on Frequency Response
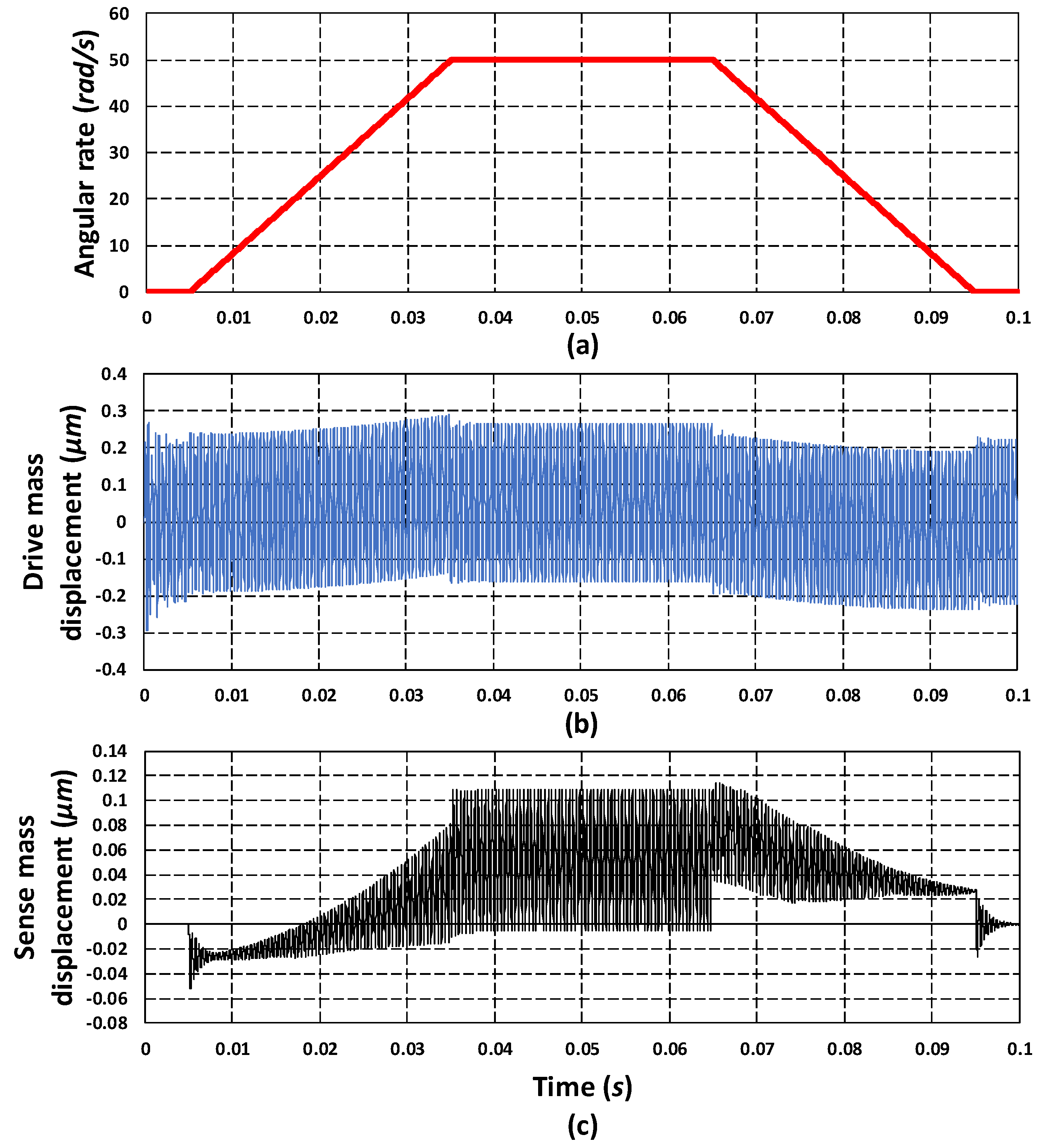
6. Sensitivity Analysis of MEMS Gyroscope
6.1. Mechanical Sensitivity Analysis
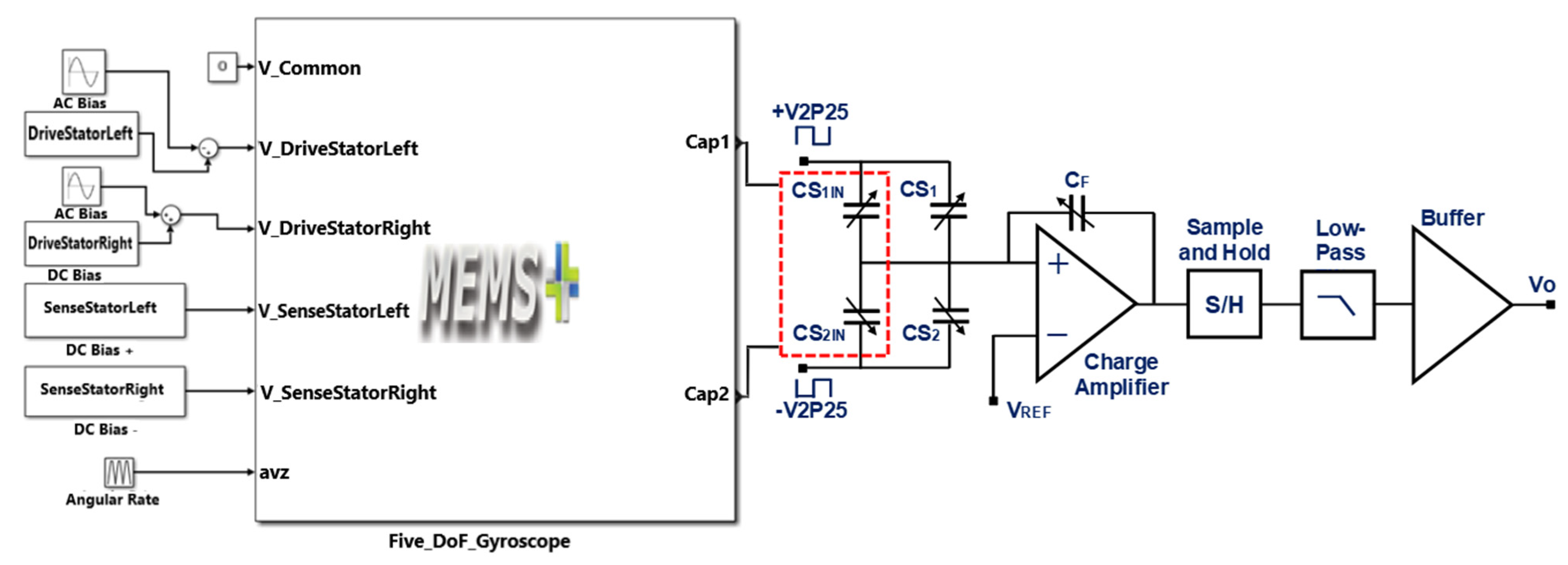
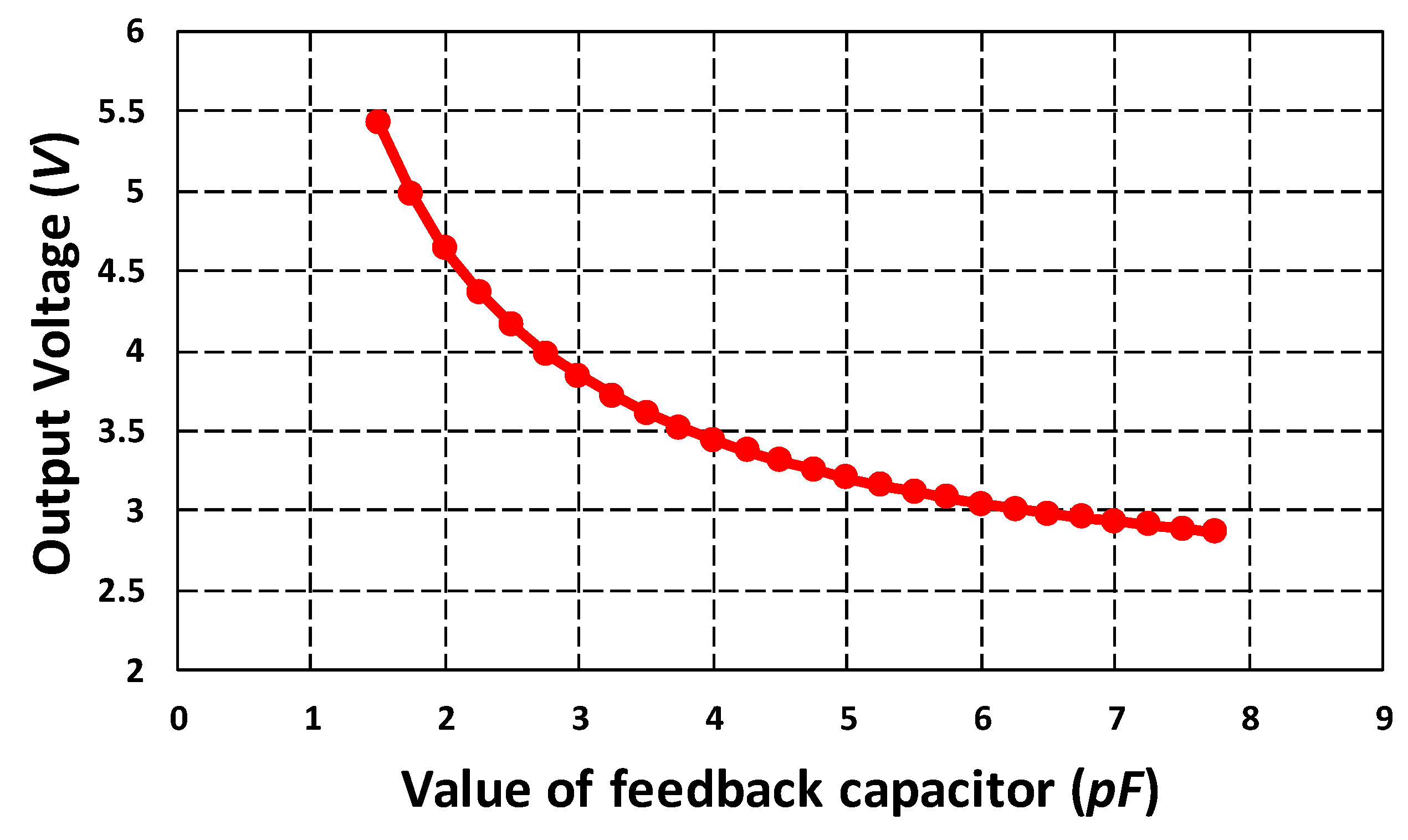
6.2. Integration of MEMS Gyroscope with Readout Electronics and Voltage Sensitivity Analysis
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, G.Q.; Chua, G.L.; Gu, Y.D. A dual-mass fully decoupled MEMS gyroscope with wide bandwidth and high linearity. Sens. Actuators A Phys. 2017, 259, 50–56. [Google Scholar] [CrossRef]
- Shakoor, R.I.; Marc, B.; Iqbal, S. Experimental evaluation of resonant frequencies with associated mode shapes and power analysis of thermally actuated vibratory microgyroscope. Microsyst. Technol. 2018, 24, 3601–3613. [Google Scholar] [CrossRef]
- Yang, J.S.; Fang, H.Y. A new ceramic tube piezoelectric gyroscope. Sens. Actuators A Phys. 2003, 107, 42–49. [Google Scholar] [CrossRef]
- Dellea, S.; Giacci, F.; Longoni, A.F.; Langfelder, G. In-plane and out-of-plane MEMS gyroscopes based on piezoresistive NEMS detection. J. Microelectromech. Syst. 2015, 24, 1817–1826. [Google Scholar] [CrossRef]
- Bochobza-Degani, O.; Seter, D.J.; Socher, E.; Nemorivsky, Y. A novel micromachined vibrating rate-gyroscope with optical sensing and electrostatic actuation. Sens. Actuators A Phys. 2000, 83, 54–60. [Google Scholar] [CrossRef]
- Chuang, W.C.; Lee, H.L.; Chang, P.Z.; Hu, Y.C. Review on the modeling of electrostatic MEMS. Sensors 2010, 10, 6149–6171. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Ha, N.S.; Nguyen, L.Q.; Chu, H.M.; Vu, H.N. Z-axis micromachined tuning fork gyroscope with low air damping. Micromachines 2017, 8, 42. [Google Scholar] [CrossRef]
- Xu, Q.; Hou, Z.; Kuang, Y.; Miao, T.; Ou, F.; Zhuo, M.; Xiao, D.; Wu, X. A Tuning Fork Gyroscope with a Polygon-Shaped Vibration Beam. Micromachines 2019, 10, 813. [Google Scholar] [CrossRef]
- He, C.; Zhao, Q.; Huang, Q.; Liu, D.; Yang, Z.; Yan, G. A MEMS vibratory gyroscope with real-time mode-matching and robust control for the sense mode. IEEE Sens. J. 2014, 15, 2069–2077. [Google Scholar] [CrossRef]
- Balachandran, G.K.; Petkov, V.P.; Mayer, T.; Balslink, T. A 3-axis gyroscope for electronic stability control with continuous self-test. IEEE J. Solid-State Circ. 2015, 51, 177–186. [Google Scholar]
- Jia, J.; Ding, X.; Gao, Y.; Li, H. Automatic Frequency tuning technology for dual-mass MEMS gyroscope based on a quadrature modulation signal. Micromachines 2018, 9, 511. [Google Scholar] [CrossRef] [PubMed]
- Dyck, C.W.; Allen, J.J.; Huber, R.J. Parallel-plate electrostatic dual-mass resonator. In Micromachined Devices and Components V; International Society for Optics and Photonics: Santa Clara, CA, USA, 1999; Volume 3876. [Google Scholar]
- Acar, C.; Shkel, A.M. Nonresonant micromachined gyroscopes with structural mode-decoupling. IEEE Sens. J. 2003, 3, 497–506. [Google Scholar] [CrossRef]
- Schofield, A.R.; Trusov, A.A.; Shkel, A.M. Effects of operational frequency scaling in multi-degree of freedom MEMS gyroscopes. IEEE Sens. J. 2008, 8, 1672–1680. [Google Scholar] [CrossRef]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Performance characterization of a new temperature-robust gain-bandwidth improved MEMS gyroscope operated in air. Sens. Actuators A Phys. 2009, 155, 16–22. [Google Scholar] [CrossRef]
- Sahin, K.; Sahin, E.; Alper, S.E.; Akin, T. A wide-bandwidth and high-sensitivity robust microgyroscope. J. Micromech. Microeng. 2009, 19, 074004. [Google Scholar] [CrossRef]
- Erismis, M. Design and modeling of a new robust multi-mass coupled-resonator family with dynamic motion amplification. Microsyst. Technol. 2013, 19, 1105–1110. [Google Scholar] [CrossRef]
- Saqib, M.; Mubasher Saleem, M.; Mazhar, N.; Awan, S.U.; Shahbaz Khan, U. Design and analysis of a high-gain and robust multi-DOF electro-thermally actuated MEMS gyroscope. Micromachines 2018, 9, 577. [Google Scholar] [CrossRef]
- Saleem, M.M.; Bazaz, S.A. Design and robustness analysis of structurally decoupled 3-DoF MEMS gyroscope in the presence of worst-case process tolerances. Microsyst. Technol. 2011, 17, 1381–1391. [Google Scholar] [CrossRef]
- Verma, P.; Khan, K.Z.; Khonina, S.N.; Kazanskiy, N.L.; Gopal, R. Ultraviolet-LIGA-based fabrication and characterization of a nonresonant drive-mode vibratory gyro/accelerometer. J. Micro-Nanolithogr. MEMS MOEMS 2016, 15, 035001. [Google Scholar] [CrossRef]
- Acar, C.; Shkel, A.M. Inherently robust micromachined gyroscopes with 2-DOF sense-mode oscillator. J. Microelectromech. Syst. 2006, 15, 380–387. [Google Scholar] [CrossRef]
- Riaz, K.; Bazaz, S.A.; Saleem, M.M.; Shakoor, R.I. Design, damping estimation and experimental characterization of decoupled 3-DoF robust MEMS gyroscope. Sens. Actuators A Phys. 2011, 172, 523–532. [Google Scholar] [CrossRef]
- Verma, P.; Shekhar, C.; Arya, S.K.; Gopal, R. New design architecture of a 3-DOF vibratory gyroscope with robust drive operation mode and implementation. Microsyst. Technol. 2015, 21, 2175–2185. [Google Scholar] [CrossRef]
- Zhu, X.H.; Chu, H.J.; Shi, Q.; Qiu, A.P.; Su, Y. Experimental study of compensation for the effect of temperature on a silicon micromachined gyroscope. Proc. Inst. Mech. Eng. Part N J. Nanoeng. Nanosyst. 2008, 222, 49–55. [Google Scholar] [CrossRef]
- Guo, Z.; Fu, P.; Liu, D.; Huang, M. Design and FEM simulation for a novel resonant silicon MEMS gyroscope with temperature compensation function. Microsyst. Technol. 2018, 24, 1453–1459. [Google Scholar] [CrossRef]
- Cui, M.; Huang, Y.; Wang, W.; Cao, H. MEMS Gyroscope Temperature Compensation Based on Drive Mode Vibration Characteristic Control. Micromachines 2019, 10, 248. [Google Scholar] [CrossRef] [PubMed]
- Dwivedi, A.; Khanna, G. Numerical simulation and modelling of a novel MEMS capacitive accelerometer based microphone for fully implantable hearing aid. Microsyst. Technol. 2019, 25, 399–411. [Google Scholar] [CrossRef]
- Cowen, A.; Hames, G.; Monk, D.; Wilcenski, S.; Hardy, B. SOIMUMPs Design Handbook (Revision 8.0.). Available online: http://www.memscap.com (accessed on 27 June 2020).
- Edalatfar, F.; Yaghootkar, B.; Qureshi, A.Q.A.; Azimi, S.; Bahreyni, B. Design, fabrication and characterization of a high performance MEMS accelerometer. IEEE Sens. J. 2016, 1–3. [Google Scholar] [CrossRef]
- Bao, M.; Yang, H. Squeeze film air damping in MEMS. Sens. Actuators A Phys. 2007, 136, 3–27. [Google Scholar] [CrossRef]
- Abdolvand, R.; Amini, B.V.; Ayazi, F. Sub-micro-gravity in-plane accelerometers with reduced capacitive gaps and extra seismic mass. J. Microelectromech. Syst. 2007, 16, 1036–1043. [Google Scholar] [CrossRef]
- Mol, L.; Rocha, L.A.; Cretu, E.; Wolffenbuttel, R.F. Squeezed film damping measurements on a parallel-plate MEMS in the free molecule regime. J. Micromech. Microeng. 2009, 19, 074021. [Google Scholar] [CrossRef]
- Syed, W.U.; Brimmo, A.; Waheed, O.; Bojesomo, A.; Ali, M.H.; Ocak, I.; Elfadel, I.A.M. Numerical modeling and validation of squeezed-film damping in vacuum-packaged industrial MEMS. J. Micromech. Microeng. 2017, 27, 075016. [Google Scholar] [CrossRef]
- Veijola, T.; Raback, P. Methods for solving gas damping problems in perforated microstructures using a 2D finite-element solver. Sensors 2007, 7, 1069–1090. [Google Scholar] [CrossRef]
- Morris, C.J.; Forster, F.K. Oscillatory flow in microchannels. Exp. Fluids 2004, 36, 928–937. [Google Scholar] [CrossRef]
- Somà, A.; Saleem, M.M.; De Pasquale, G. Effect of creep in RF MEMS static and dynamic behavior. Microsyst. Technol. 2016, 22, 1067–1078. [Google Scholar] [CrossRef]
- CoventorWare Analyzer Field Solver Reference; Coventor Inc.: Cary, NC, USA, 2018.
- Wachtman, J.B., Jr.; Tefft, W.E.; Lam, D.G., Jr.; Apstein, C.S. Exponential temperature dependence of Young’s modulus for several oxides. Phys. Rev. 1961, 122, 1754. [Google Scholar] [CrossRef]
- Gysin, U.; Rast, S.; Ruff, P.; Meyer, E.; Lee, D.W.; Vettiger, P.; Gerber, C. Temperature dependence of the force sensitivity of silicon cantilevers. Phys. Rev. B 2004, 69, 045403. [Google Scholar] [CrossRef]
- Datasheet MUCRI. MS3110 Universal Capacitive ReadoutTM IC; MicroSensors, Inc.: Costa Mesa, CA, USA, 2004. [Google Scholar]
- Bao, M.H. Micro Mechanical Transducers: Pressure Sensors, Accelerometers and Gyroscopes; Elsevier: San Diego, CA, USA, 2000. [Google Scholar]
- Apostolyuk, V. Theory and Design of Micromechanical Vibratory Gyroscopes in MEMS/NEMS; Springer: Boston, MA, USA, 2006; pp. 173–195. [Google Scholar]









| References | Structural Layer | Configuration | Device Size | Sensitivity | Bandwidth | |
|---|---|---|---|---|---|---|
| Material | Thickness (µm) | |||||
| Acar et al. [13] | Polysilicon | 2 | 2 DoF drive, 2 DoF sense | 0.7 × 0.5 mm2 | 0.72 × 10−3 µm/°/s | 23 Hz |
| Schofield et al. [14] | Silicon | 75 | 1 DoF drive, 2 DoF sense | - | 2.34 µV/(°/s) | 600 Hz |
| Trusov et al. [15] | Silicon | 50 | 1 DoF drive, 2 DoF sense | 3 × 3 mm2 | 56 µV/(°/s) | 250 Hz |
| Sahin et al. [16] | Silicon | 100 | 1 DoF drive, 2 DoF sense | 131 µV/(°/s) | 1 kHz | |
| Saqib et al. [18] | Nickel | 20 | 3 DoF drive, 1 DoF sense | 3.2 × 3 mm2 | 0.565 fF/rad/s, 0.052 × 10−3 µm/°/s | 1.2 kHz |
| Saleem et al. [19] | Nickel | 20 | 2 DoF drive, 1 DoF sense | 2.4 × 1.6 mm2 | 0.045 fF/rad/s, 0.0105 × 10−3 µm/°/s | 1.71 kHz |
| Verma et al. [20] | Nickel | 9 | 1 DoF drive, 2 DoF sense | 2 × 1.9 mm2 | - | 100 Hz |
| Acar et al. [21] | Polysilicon | 100 | 1 DoF drive, 2 DoF sense | 4 × 4 mm2 | 0.0308 mV/°/s | 50 Hz |
| Riaz et al. [22] | Nickel | 20 | 2 DoF drive, 1 DoF sense | 2.2 × 2.6 mm2 | - | 1.4 kHz |
| Verma et al. [23] | Nickel | 8 | 2 DoF drive, 1 DoF sense | 2.13 × 1.93 mm2 | - | 1 kHz |
| Parameters | Values |
|---|---|
| Overall device size | 4.2 mm × 4.2 mm |
| Structural layer thickness | 25 µm |
| Mass value of the mass | 2.5239 × 10−7 Kg |
| Mass value of the mass | 1.1203 × 10−7 Kg |
| Mass value of the decoupling frame | 3.234 × 10−8 Kg |
| Mass value of the mass | 9.8125 × 10−8 Kg |
| Mass value of the mass | 5.5343 × 10−8 Kg |
| Length of the parallel sensing plates | 500 µm |
| Width of the parallel sensing plates | 8 µm |
| Number of parallel sensing plates pair | 120 |
| Overlap length between the moving and fixed parallel sensing plates | 450 µm |
| Smaller sense gap size | 3 µm |
| Larger sense gap size | 9 µm |
| Number of drive comb pairs | 240 |
| Width of drive combs | 6 µm |
| Length of drive combs | 120 µm |
| Gap between drive combs | 3 µm |
| Mode Shape | Analytical Model (kHz) | FEM Model (kHz) |
|---|---|---|
| 1st (Drive mode) | 1.738 | 1.608 |
| 2nd (Sense mode) | 1.800 | 1.707 |
| 6th (Drive mode) | 3.507 | 3.329 |
| 7th (Sense mode) | 3.867 | 3.709 |
| 10th (Drive mode) | 4.960 | 4.822 |
| References | Structural Layer | Configuration | Device Size | Sensitivity | Bandwidth | |
|---|---|---|---|---|---|---|
| Material | Thickness (µm) | |||||
| Schofield et al. [14] | Silicon | 75 | 1 Dof drive, 2 DoF sense | - | 2.3 µV/(°/s) | 600 Hz |
| Trusov et al. [15] | Silicon | 50 | 1 Dof drive, 2 DoF sense | 3 × 3 mm2 | 56 µV/(°/s) | 250 Hz |
| Acar et al. [21] | Polysilicon | 100 | 1 Dof drive, 2 DoF sense | 4 × 4 mm2 | 0.0303 mV/(°/s) | 50 Hz |
| Saqib et al. [18] | Nickle | 20 | 3 Dof drive, 1 DoF sense | 3.2 × 3 mm2 | 0.565 fF/rad/s | 1.2 kHz |
| This work | Silicon | 25 | 3 Dof drive, 2 DoF sense | 4.2 × 4.2mm2 | 3.1 fF/rad/s, 198.9 µV/(°/s), 0.04 × 10−3 µm/(°/s) | 1.62 kHz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bukhari, S.A.R.; Saleem, M.M.; Khan, U.S.; Hamza, A.; Iqbal, J.; Shakoor, R.I. Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope. Micromachines 2020, 11, 862. https://doi.org/10.3390/mi11090862
Bukhari SAR, Saleem MM, Khan US, Hamza A, Iqbal J, Shakoor RI. Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope. Micromachines. 2020; 11(9):862. https://doi.org/10.3390/mi11090862
Chicago/Turabian StyleBukhari, Syed Ali Raza, Muhammad Mubasher Saleem, Umar Shahbaz Khan, Amir Hamza, Javaid Iqbal, and Rana Iqtidar Shakoor. 2020. "Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope" Micromachines 11, no. 9: 862. https://doi.org/10.3390/mi11090862
APA StyleBukhari, S. A. R., Saleem, M. M., Khan, U. S., Hamza, A., Iqbal, J., & Shakoor, R. I. (2020). Microfabrication Process-Driven Design, FEM Analysis and System Modeling of 3-DoF Drive Mode and 2-DoF Sense Mode Thermally Stable Non-Resonant MEMS Gyroscope. Micromachines, 11(9), 862. https://doi.org/10.3390/mi11090862





