1. Introduction
The continuous measurement of therapeutic drugs and metabolites is a strong requirement in transplantation surgery, pulmonary and critical care medicine [
1]. Drugs of interest are therapeutics with a narrow action window, which regularly pose considerable challenges in initial and ongoing dosing. These drugs are often subject to polymorphic metabolism with considerable inter- and intra-individual variability requiring therapeutic drug monitoring (TDM) [
2]. TDM, however, is regularly performed with one blood sample per dosing interval only, with trough-value (i.e., the plasma level of a pharmaceutical product) measured just before the following dosage. On the other hand, because biomarkers are typically present at very low concentrations within complex samples that contain high concentrations of background material, the methodologies need to be highly selective and accurate [
3]. Thus, a cluster of biomarker elements will emit a stronger signal than a single element of the same kind, independently of the signal type, leading to an increased reading of the sensor regardless of its accuracy [
4].
A microactuator using magnetic beads (MB) conjugated biomarkers as a driver to form clusters or to induce surface binding is a viable approach to concentrate such biomarkers, increasing the sensitivity and the specificity of the test and at the same time avoiding interference before testing [
5,
6]. The use of MB provides large surface-to-volume ratio. MB can be suitably biofunctionalized and manipulated by magnetic fields [
7,
8,
9,
10,
11], diminishing the difficulties posed by mixing at low Reynolds numbers or by the high flow resistances at small scales [
12]. Furthermore, MB are commercially available in different sizes, magnetic properties and surface coatings, making them very versatile, especially to realize integrated and miniaturized technologies based on small fluid volumes [
13,
14]. Permanent magnets (PM) are the most common to generate and control a magnetic field, however, if the microactuator working mode is based on a current flowing across planar spiral coils (resistances), the magnetic field can be modulated micromagnetically by varying the current flowing through the device [
15]. Moreover, adding permanent magnets to this setup enforces the magnetic fields by around 10 times [
16].
Electrically actuated microcoils will heat, reducing its efficiency [
17,
18] and resistive heating can be a drawback if tests need to be performed under strict temperature ranges. As a result, adapted cooling schemes may be necessary to tackle heat dissipation as the current density of the microcoils can reach thousands of A·mm
−2, and even higher values in short pulses [
19].
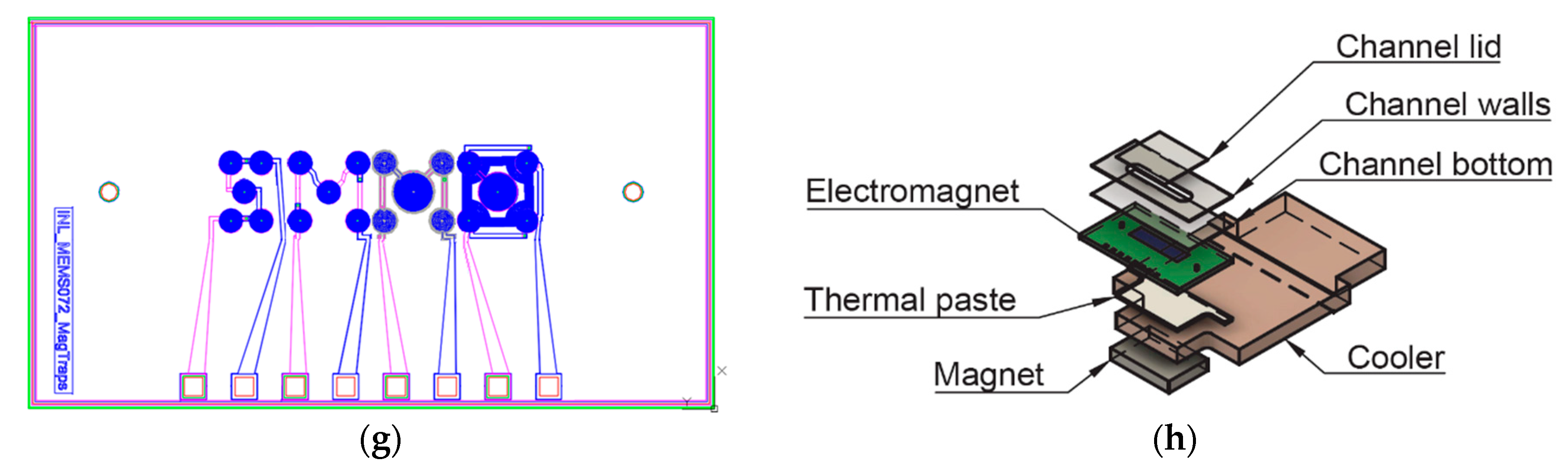
In this work we present the manipulation of magnetic beads for therapeutic drug monitoring by enclosing magnetic trapping and integrated efficient cooling. The fabrication of the microactuator allow us to direct the magnetic beads between outer coils and a central coil following the design and optimization investigated by numerical analysis. This design empowers a fast and optimized response for the manipulation of MB and consequently is foreseen to be capable of an improved dosage of the respective therapeutical drug.
3. Results and Discussion
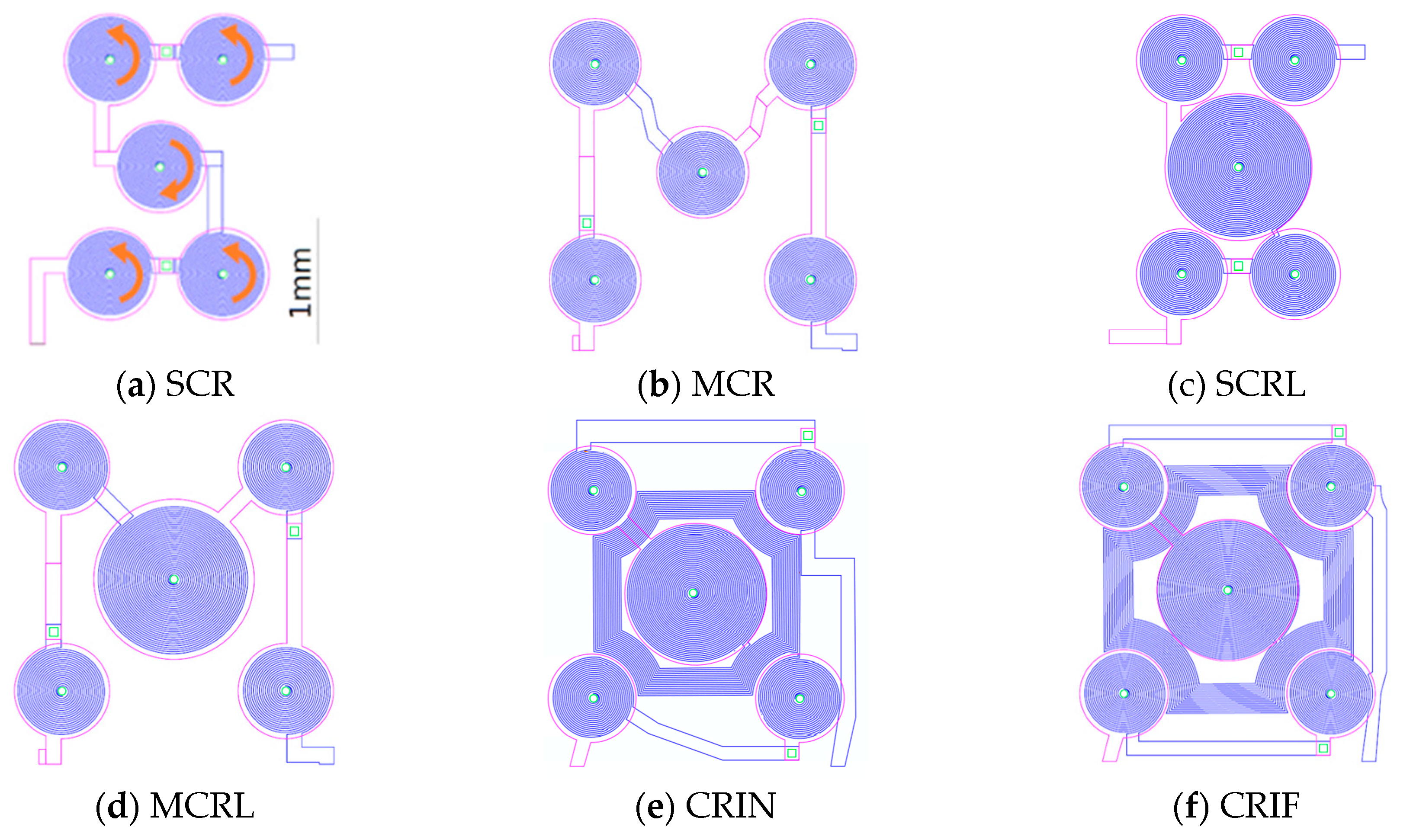
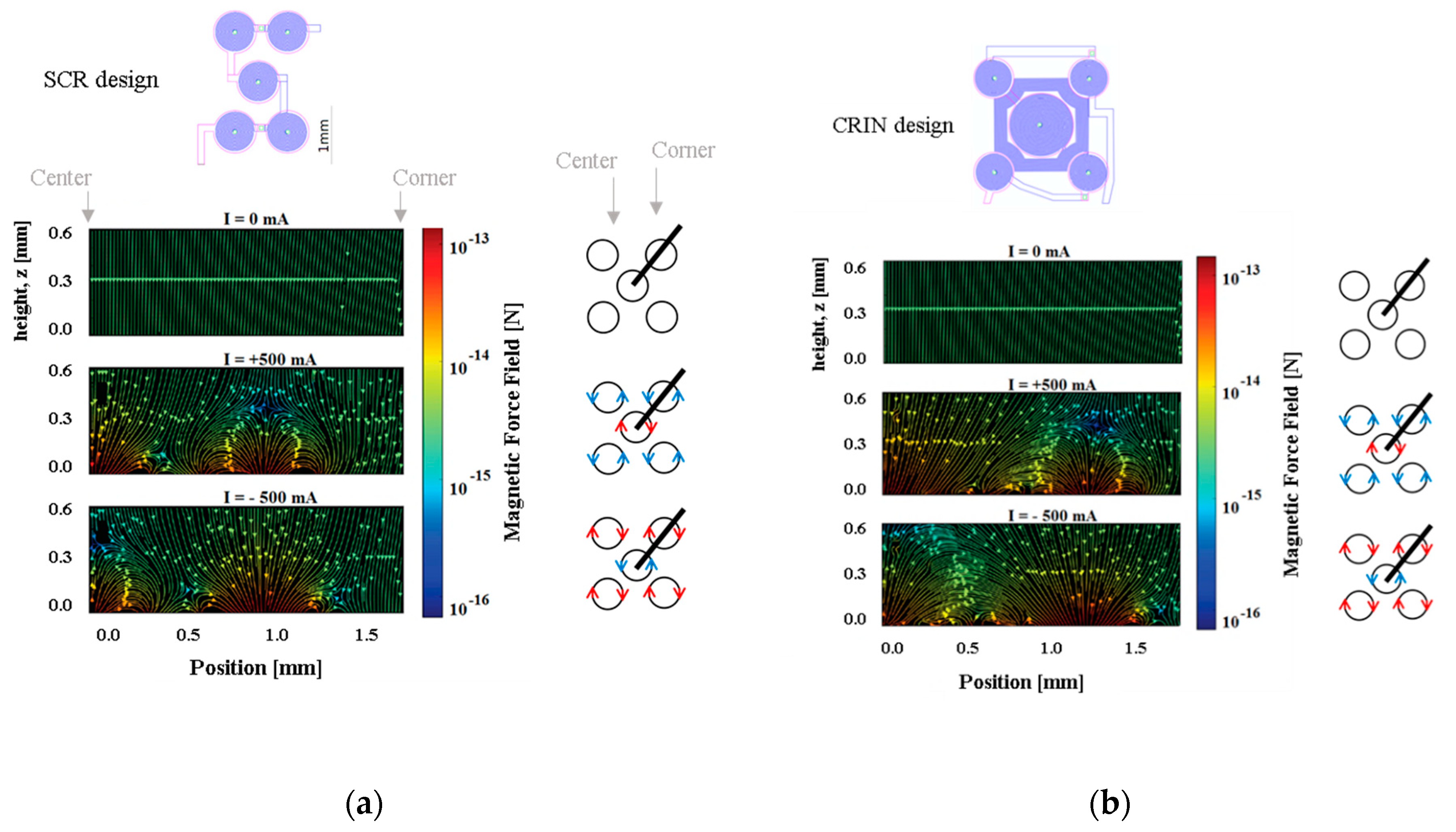
The magnetic force field was simulated for each electromagnet design and plots are presented along the diagonal between the center of the central coil and the center of one of the external coils.
Figure 6 presents the resulting magnetic force when actuating the SCR and the CRIN designs with 0 mA, +500 mA, and −500 mA starting at 0 µm from the coil surface up to 600 µm.
Considering the microfluidic channel bottom placed at a distance of 100 µm from the top of the electromagnet, the magnetic beads will move from the edge of the coils to the center, and vice-versa when actuation occurs. However, if the microchannel is placed more than 200 µm above, a region with low forces appears above the lateral coil, which reduces the efficacy of trapping. Beads sufficiently close to the bottom of the channel will be strongly attracted, relative to the rest of the force field, towards one of the sides of the current tracks, following the global pull that can be seen near the top of the plot. The separation between the channel and the electromagnet as well as the current imposed will define the strength of trapping which can be tuned for different types of real operation in immunoassays.
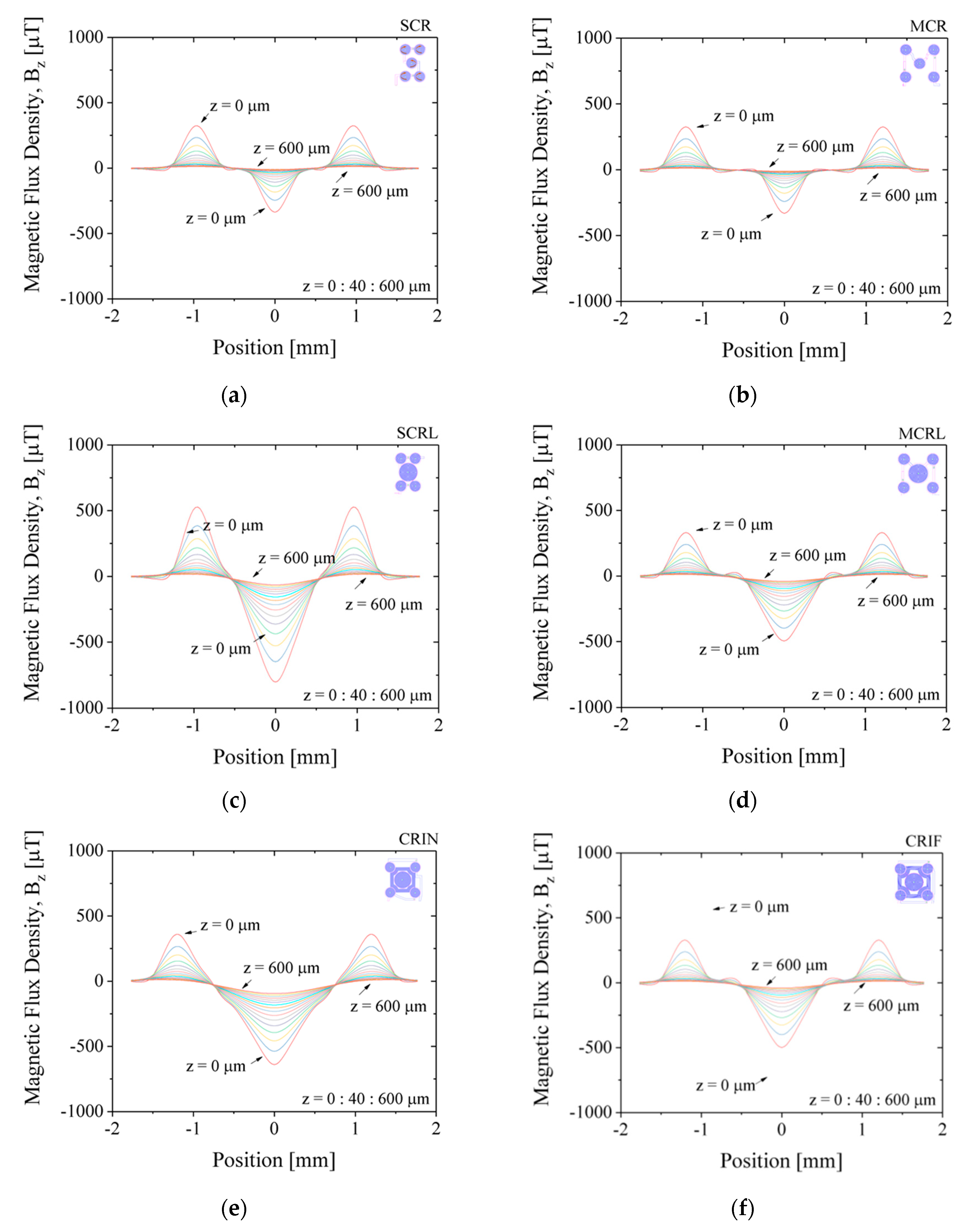
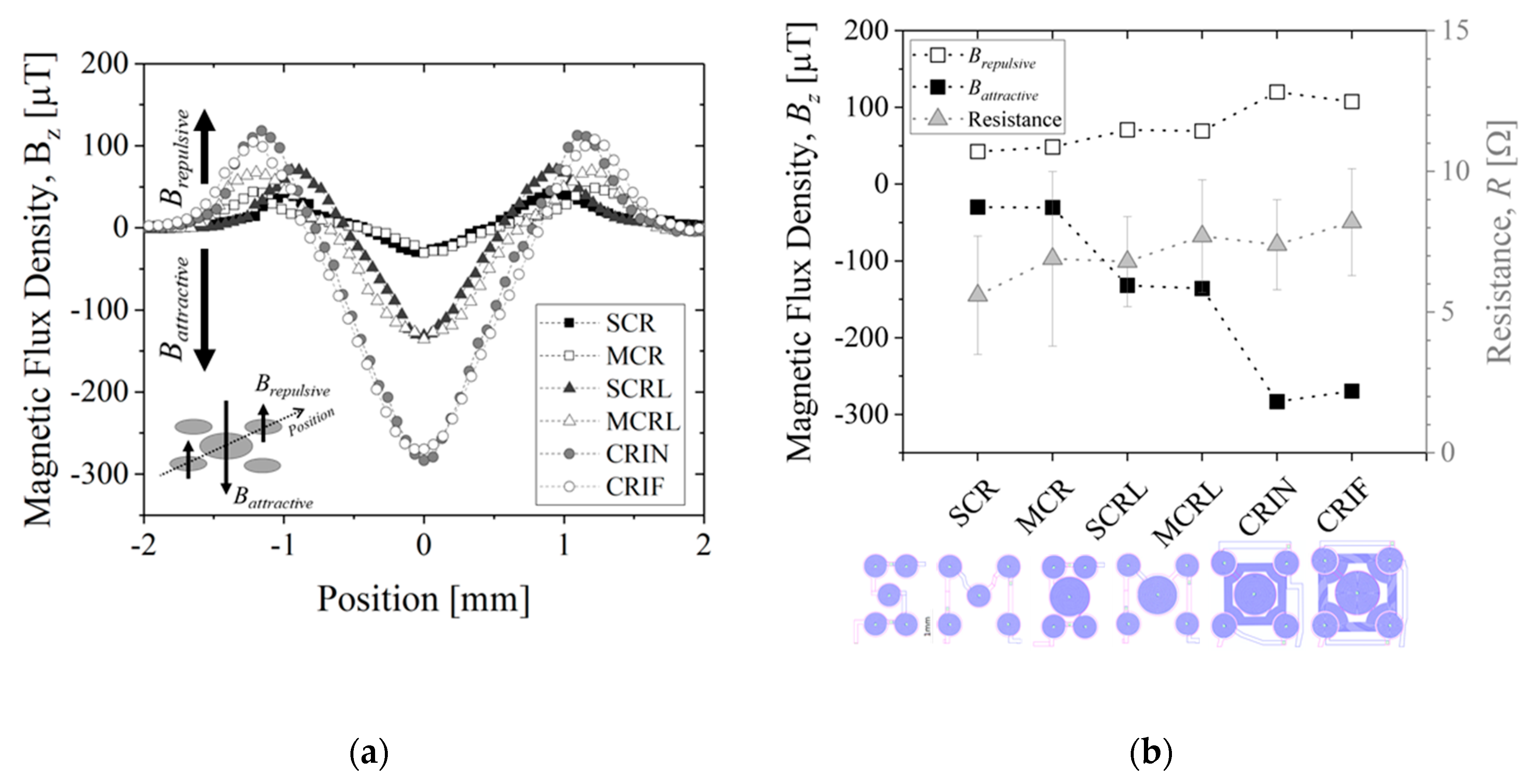
Figure 7 shows the simulated results for magnetic flux density,
Bz, along the diagonal of the chip, for z-positions varying from 0 µm (at the surface) to 600 µm away from the surface, in steps of 40 µm. The applied current is set to −30 mA. Positive values of
Bz will translate into repulsion of MB away from the surface and negative values of
Bz to attraction of MB towards the surface. The magnetic flux density,
Bz, is minimum (attraction) at the center of the coil near the surface at z-position equal to 0 µm and decreases intensity further away from the surface up to 600 µm for all configuration, as expected. MEMT with coils of equal size generate
Bz equal in the central and external coils (e.g., SCR and MCR,
Figure 7a,b) unlike larger central coils MEMT, where
Bz is always stronger in the central coil (e.g., SCRL and MCRL,
Figure 7c,d). Larger distances between central and external coils induce secondary variations of
Bz between the central and the external coils, more pronounced closer to the surface. This is clearly seen in the spacing between coils from −0.8 mm to −0.5 mm and from 0.5 mm to 0.8 mm in
Figure 7d. The secondary variations degrade the
Bz gradient and consequently the yield of MB transition between the central and the external coils. The inclusion of inter-windings was successful in the removal of these secondary variations of
Bz only for CRIN (
Figure 7e), probably enhanced by the lack of free intercoil space. This idea is reinforced by the resulting
Bz profiles obtained for CRIF (
Figure 7f), in which the larger intercoil space seems to be promoting secondary variations of
Bz. A constant
Bz gradient between coils is observed for both SCRL and CRIN MEMT (
Figure 7c,e), indicating these as preferable candidates for chip integration.
The magnetic flux density in the vertical direction,
Bz, resulting from imposing 30 mA to the MEMT was measured at 200 µm from the chip surface in a custom made magnetoresistive scanner detailed in [
21] making use of a Magnetic Tunnel Junction sensor (sensitivity −0.26 Ω·µT
−1, dimension 58.5 × 4 µm
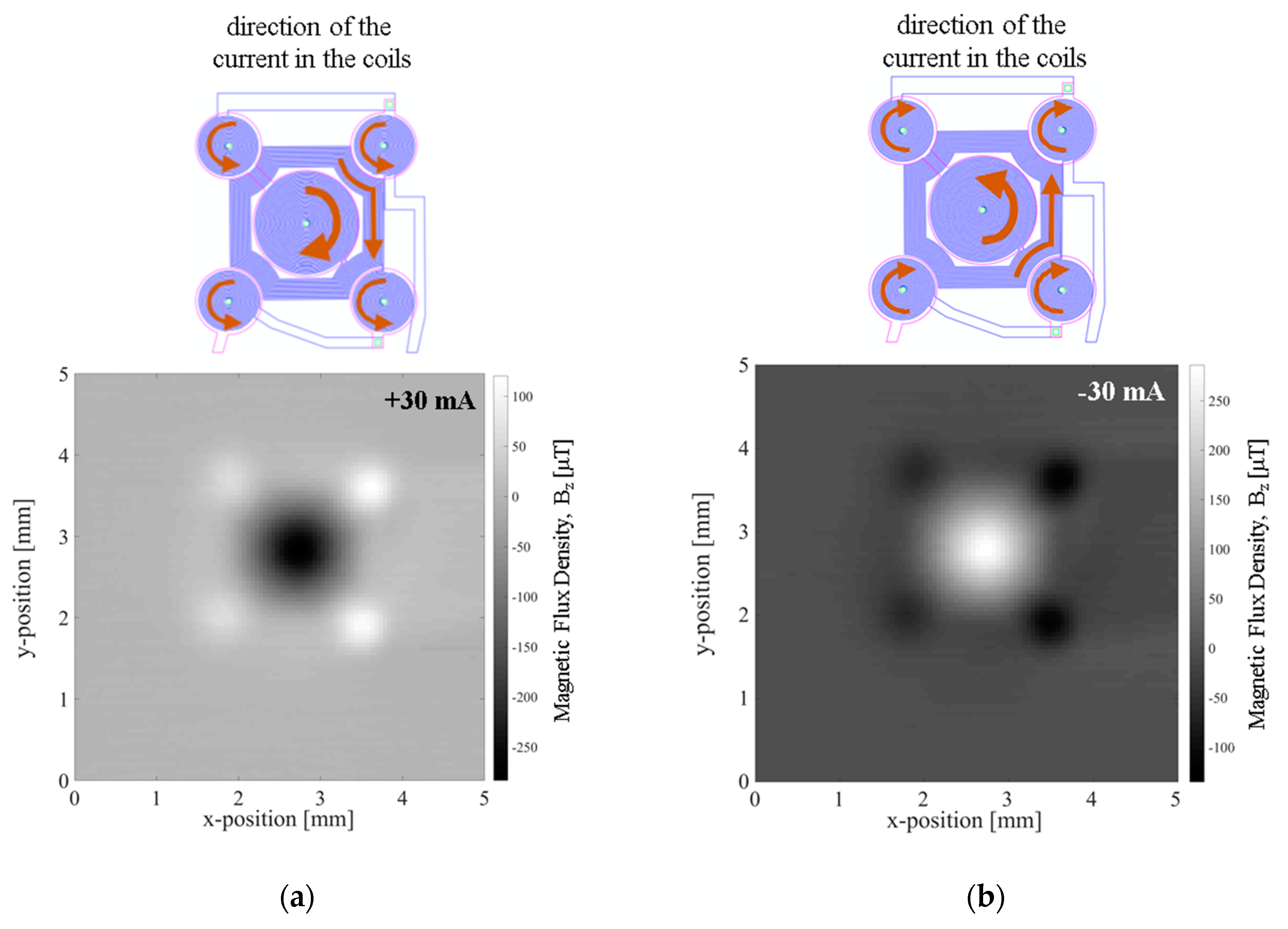
2). The magnetic scan (5 × 5 mm
2, 0.05 mm step size) shows the vertical attractive magnetic flux density of −283 µT generated in the central coil, opposing that of the external coils (120 µT) when +30 mA currents are imposed to the coil (
Figure 8a) and the system reverses when applying −30 mA (
Figure 8b).
Figure 9 shows a summary of the electromagnetic characterization of different MEMT designs when applying +30 mA measured at 200 µm from the chip surface and presented for the diagonal of the MEMT. For the configurations studied, the experimental magnetic flux density matches the simulated results qualitatively (
Figure 9a). Here, negative
Bz, relative to attractive magnetic force, becomes more negative for increasing size of central coil. Additional attraction is achieved with the inclusion of inter-windings. Vertical magnetic flux density is found independent of electrical connection configuration, as no significant differences are seen comparing SCR and MCR or SCRL and MCRL (
Figure 9b). However, when comparing the S-configuration with the M-configuration, the resistance is seen higher for the M-configuration in both cases (CR and CRL), as these have longer electrical paths.
Additionally, MEMT with larger central coils (L-large) present larger amplitudes of Bz, as well as higher Bz,maximum and lower Bz,minimum (see SCR and SCRL or MCR and MCRL) with only 1 Ω increase in system resistance. The inclusion of inter-windings (CRIN and CRIF) clearly promoted a steep increase in Bz with no significant increase in resistance.
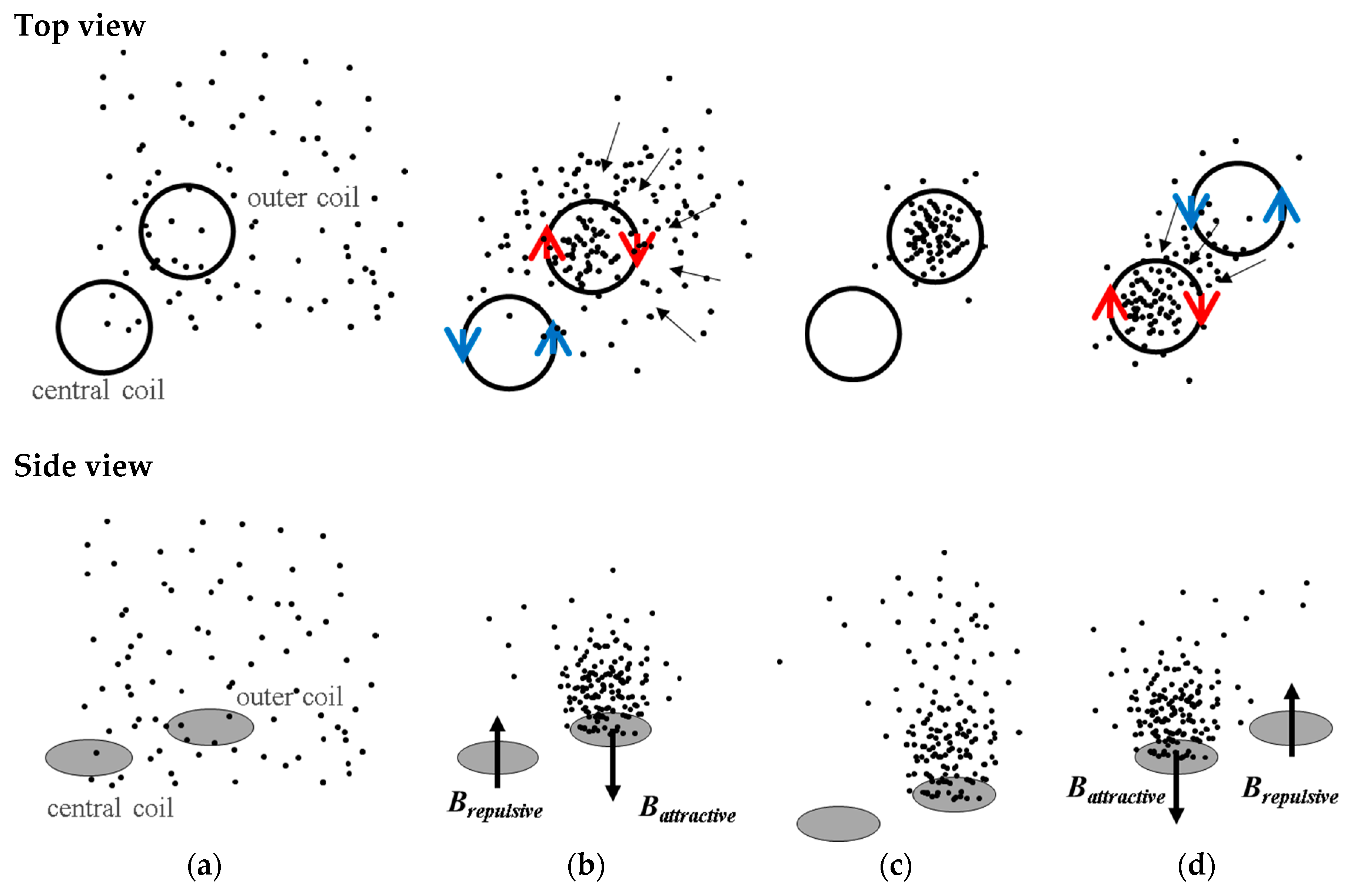
The integration of opposite magnetic behaviors in the same MEMT and instantaneous reversing of current (the transient response of the power supply is of 0.01 s) leading to rapid reverse of magnetic flux density stands favorable for particle trapping and cell attraction/repulsion. CRIN MEMT promoted the largest amplitudes in Bz while at constant gradient and was therefore chosen to proceed to further experiments.
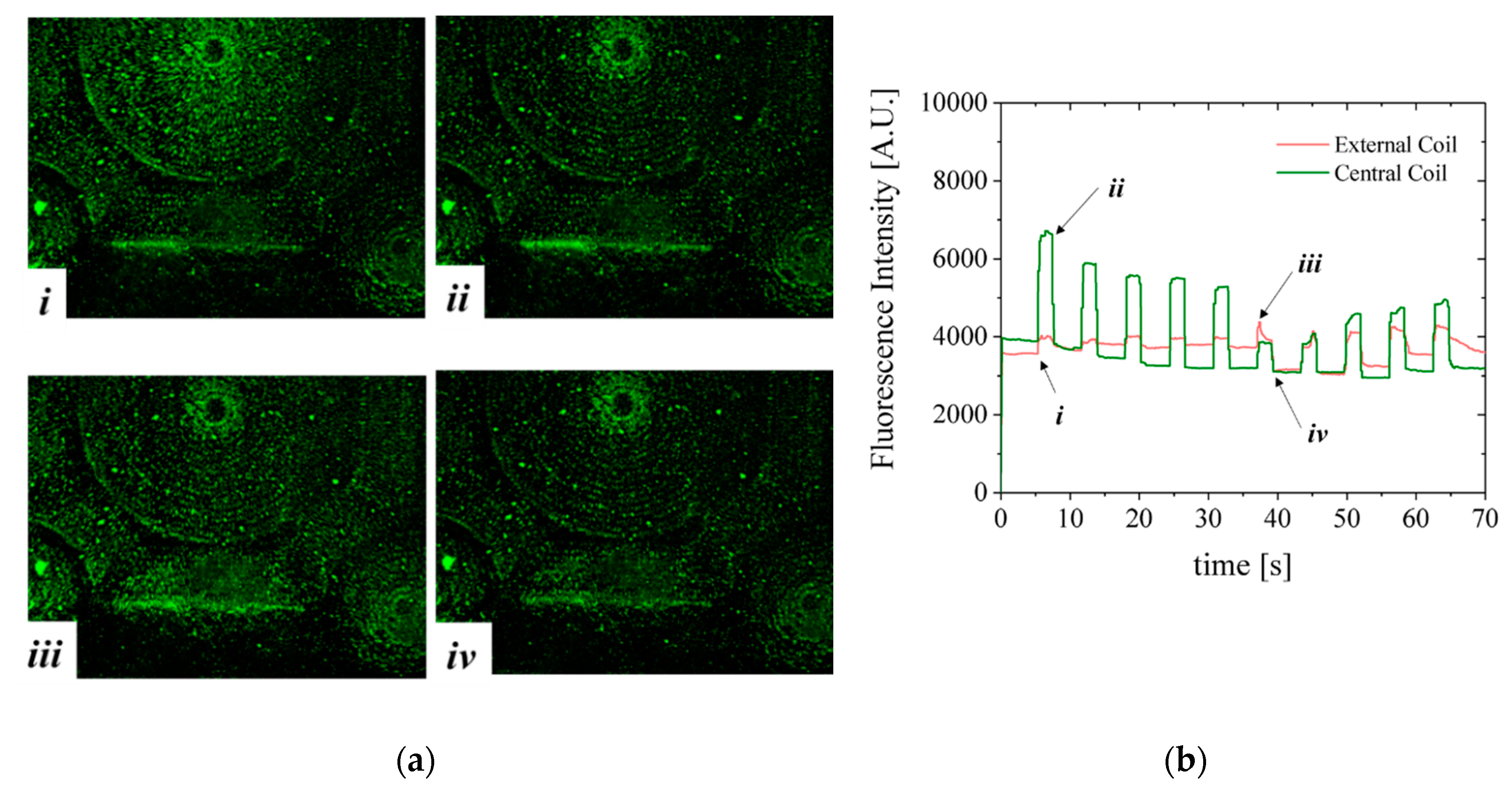
The manipulation of Estapor
© superparamagnetic fluorescent beads by the CRIN MEMT design is depicted in
Figure 10. The solution of beads is pumped through the channel. Lateral and top walls were added to the chip to obtain a microfluidic channel roughly 200 µm high, 2.5 mm wide and 10 mm long. In this configuration the MB are in direct contact with the MEMT. The MEMT is activated by running a sequence of 10 pulses of 2 s duration with current 1 A and 4 s interval. The current is inverted after the first 5 pulses. During the time of actuation, the fluorescence signal intensifies, to dim right after actuation stops.
The fluorescent nature of Estapor
® MB enabled direct observation of resulting magnetic actuation via fluorescence microscopy. The beads, once concentrated to the same area after MEMT actuation, are seen to agglomerate into larger diameter particulates and move faster in subsequent manipulations (
Figure 10a(i,iii)). When the MEMT actuation is turned off, these particulates quickly disperse (
Figure 10a(ii,iv)).
Figure 10b shows MB fluorescence intensity over time of actuation for experiment depicted in
Figure 10a. By the changes in fluorescence signal, the moments of attraction and repulsion and change in actuation signal for each position in the chip is clear. In this configuration, the beads tend to adhere to the spaces matching the shape of the MEMT tracks and agglomerate on top of those. The resulting adherence of particles to the coils after each pulse is perceived by the slight increase in the baseline of the fluorescence intensity for the external coil in the first 5 pulses and for the central coil in the last 5 pulses. The electromagnetic force directing MB away from the surface is not enough to overcome surface adhesion forces between the coil and the MB. This feature is particularly attractive to enhance surface binding in heterogeneous immunoassays in which one requires separation of bound and free labels after the biding reaction of a target substance (e.g., antigen) with the antibody [
22].
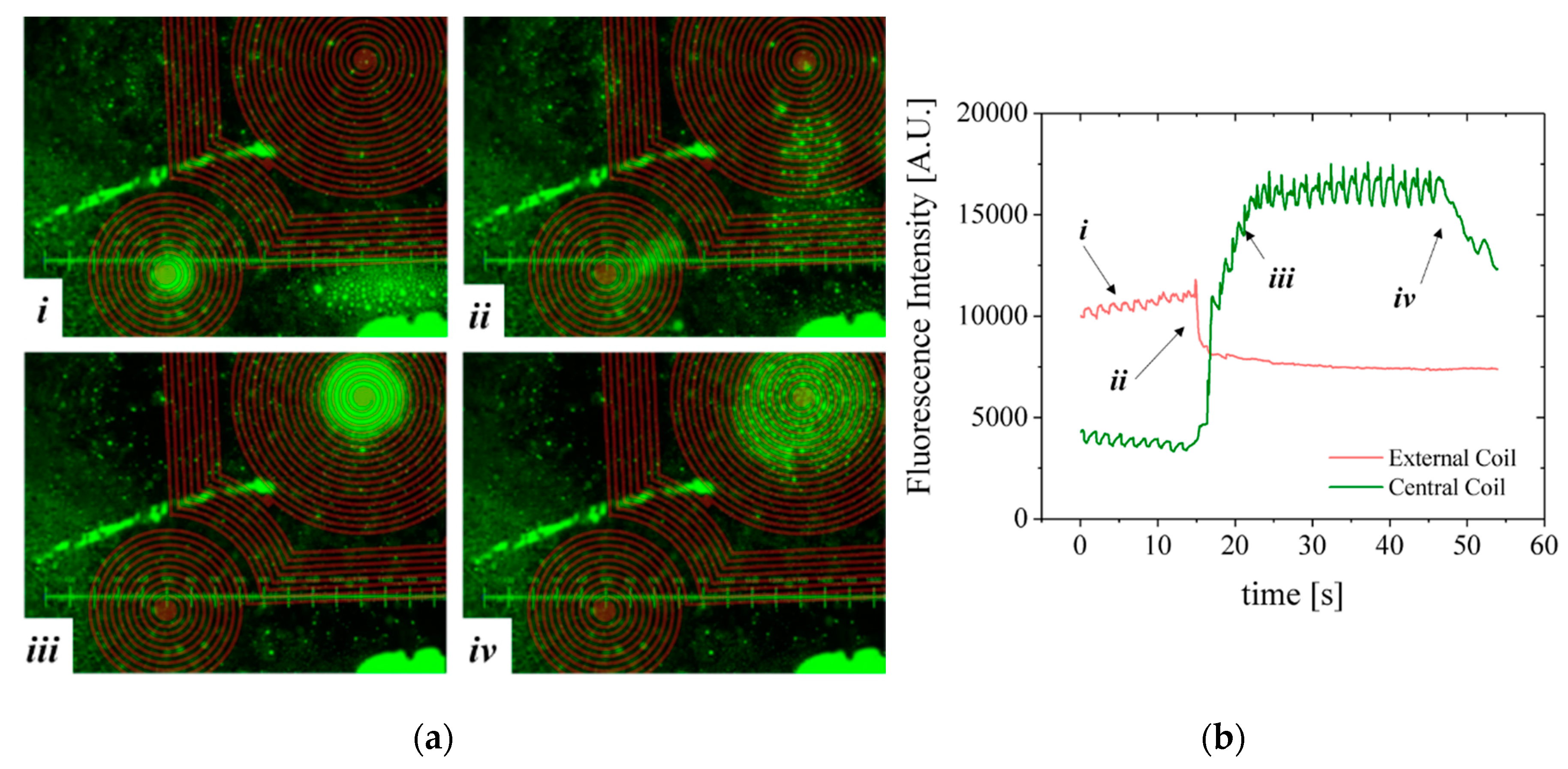
A second configuration, more favorable to homogeneous immunoassays [
23], was mounted comprising the microfluidic channel with 100 µm-thick bottom wall placed on top of the MEMT forcing the separation between the MB and the MEMT (
Figure 11). As such, images are focused from 0.2 to 0.5 mm away from the MEMT surface. Because the coils are not focused on the image, a brown CAD overlay is aligned with the MEMT tracks for easier analysis of the actuation. In this experiment, the activation is done by running a sequence of 29 pulses of 1 s duration with current 1 A and 0.5 s interval and inverting the current after the first 9 pulses.
Although the MB are subjected to lower magnetic flux densities at 100 µm from the MEMT, their distribution is uniform on top of the MEMT, preventing local agglomeration and adhesion to the chip walls (
Figure 11a), also perceived from the MB fluorescence signal (
Figure 11b). The brighter green color seen on top of the tracks, which could indicate bead—coil surface adhesion, is merely an artifice caused by the inclusion of the brown CAD overlay in this case.
During the first 9 pulses of −1 A, there is synchronous repulsion from the central coil and attraction to the external coils (i). When the current is inverted to +1 A, the fluorescence intensity inverts (ii) due to the increasing attraction of MB to the central coil and their repulsion from the external coils (iii). After the actuation sequence stops, the MB disperse (iv) due to Brownian and viscous forces. The line-type arrangement of MB remaining on the left side of the image is a result of bead-top wall surface adhesion. Effective concentration or dispersion of MB is better noticed by the variation of the base plateau after actuation pulses.
Not only did systems with inter-windings between the central and lateral coils (CRIN and CRIF) present the highest difference between
Battractive and
Brepulsive but the magnetic force generated by the inter-windings promoted the movement of the MB from coil to coil, more specifically, by being able to pull MB from the inter-winding area. This was also foreseen in simulated results (
Figure 7e) and magnetic scans of the MEMT surface (
Figure 9a) by the steep slope obtained in the inter-winding region of the CRIN and CRIF MEMT. Nonetheless, the magnetic force fields need to overcome the hydrodynamic forces and adhesion forces present in the actual functionalization of channel surfaces to become effective in the manipulation and concentration of MB.