Separation of Nano- and Microparticle Flows Using Thermophoresis in Branched Microfluidic Channels
Abstract
1. Introduction
2. Experimental Methods
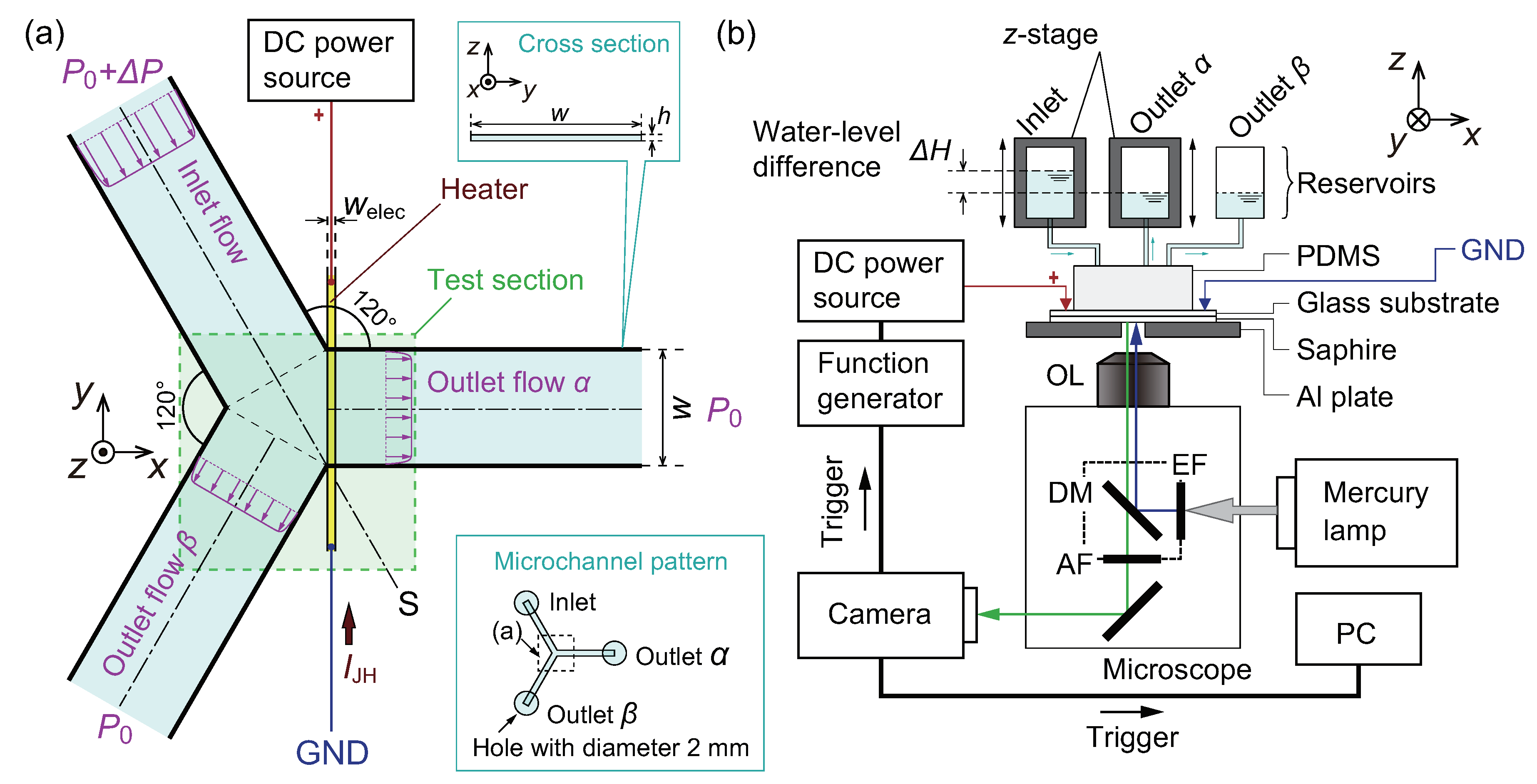
2.1. Details of Microfluidic Devices
2.1.1. Fabrication of a PDMS Block
2.1.2. Fabrication of the Electrode Pattern on the Glass Substrate
2.1.3. Bonding Process
2.2. Experimental Setup
2.3. Sample Solutions
2.4. Procedures
3. Results and Discussion
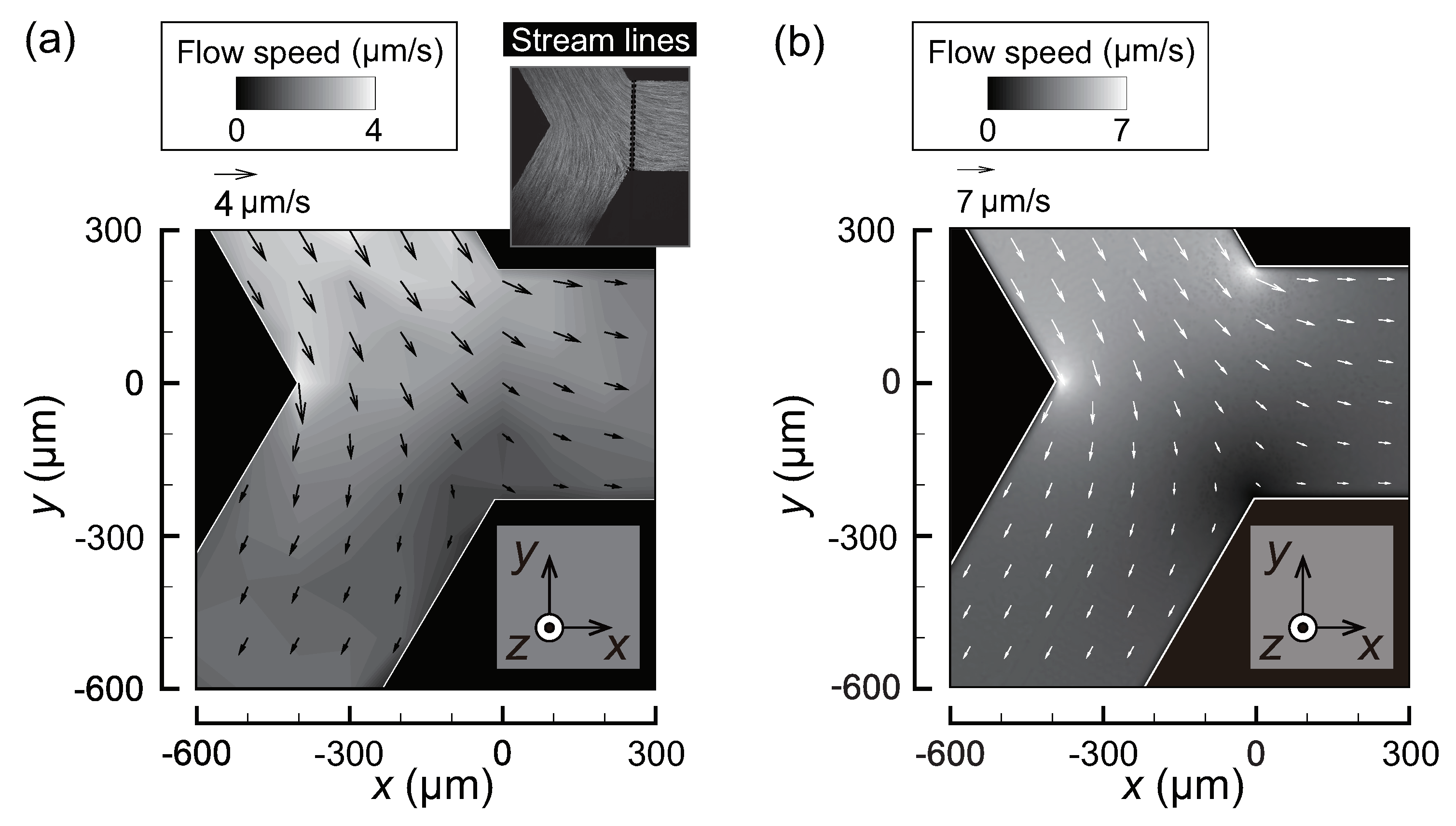
3.1. Flow Fields
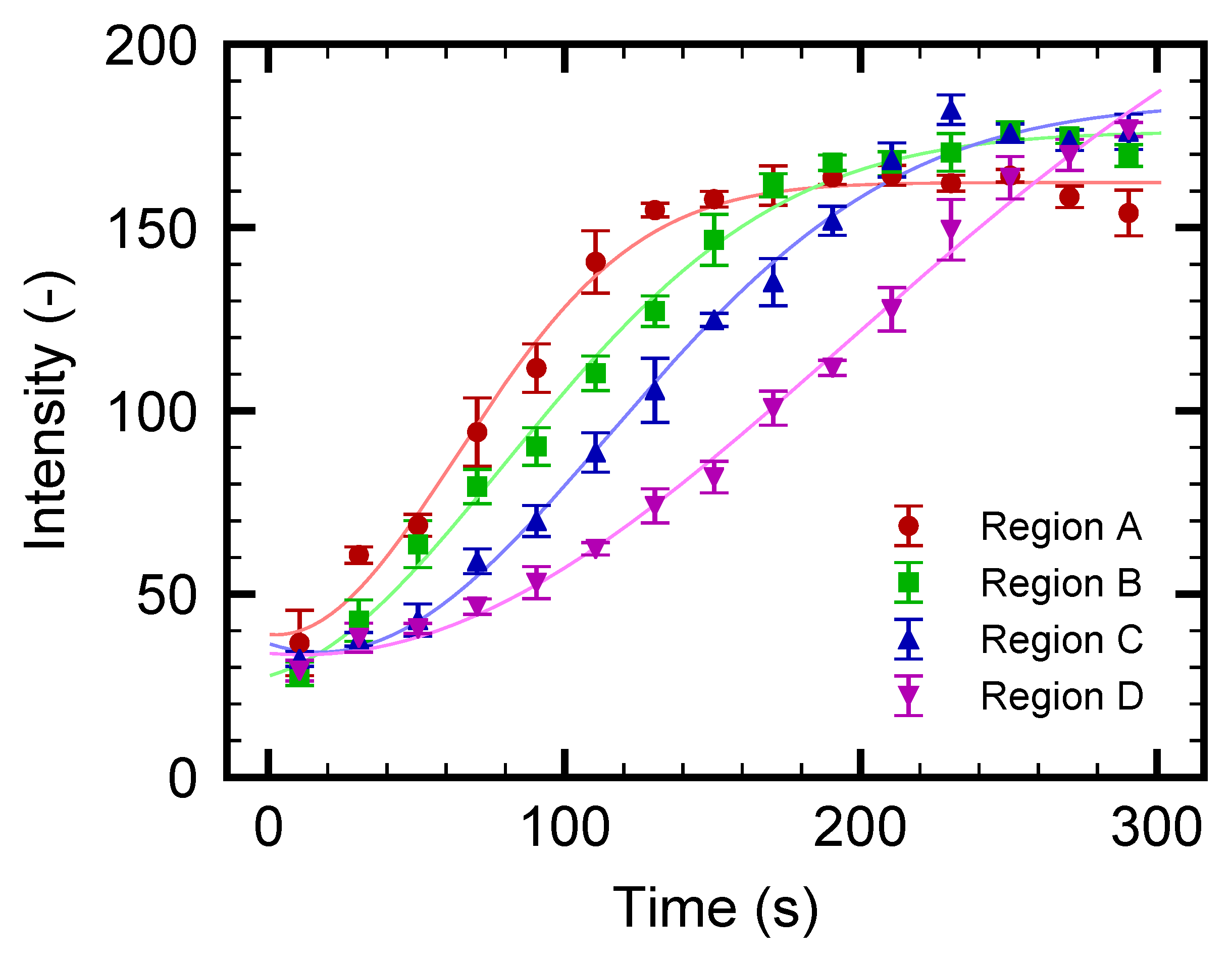
3.2. Microparticle Flow Separation
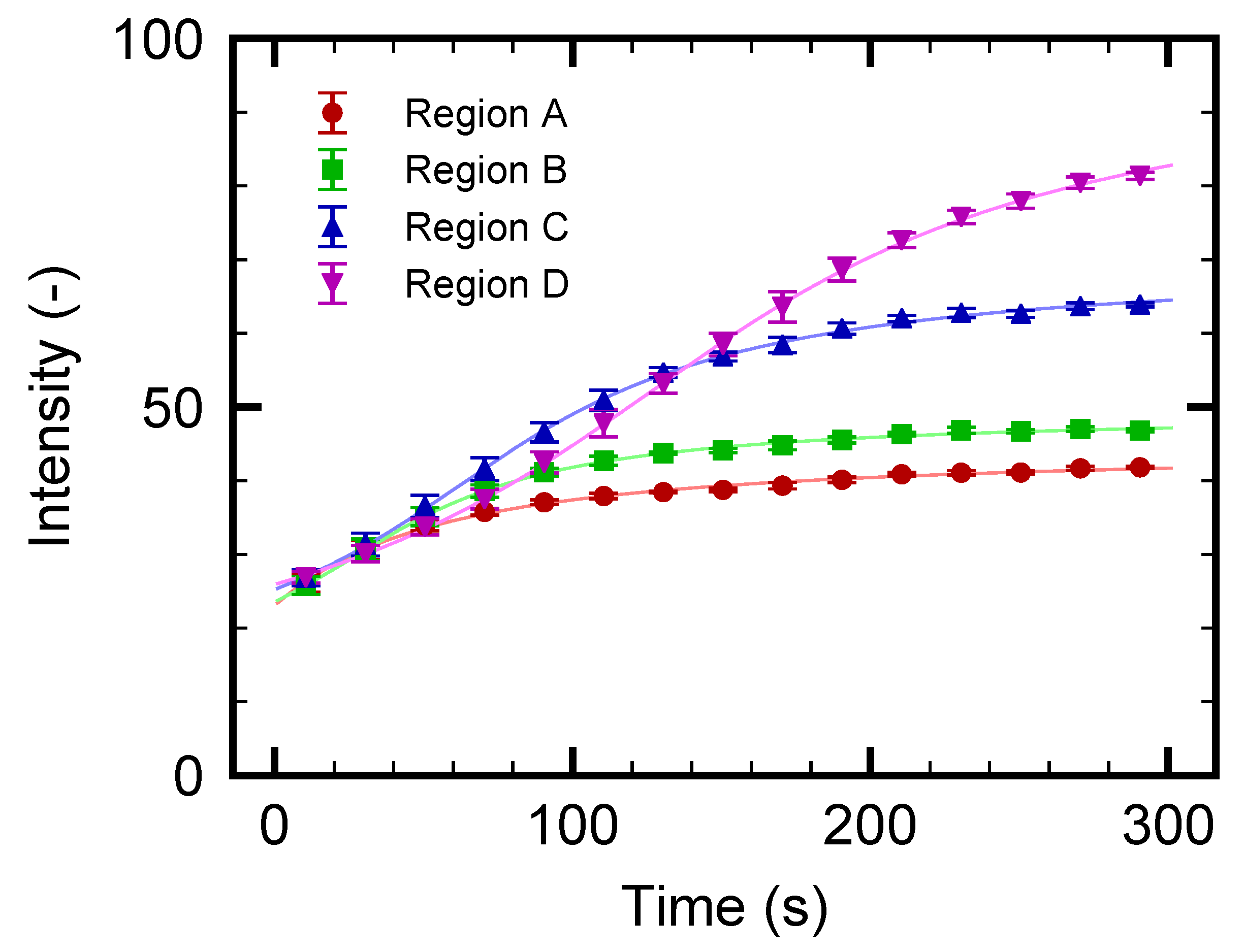
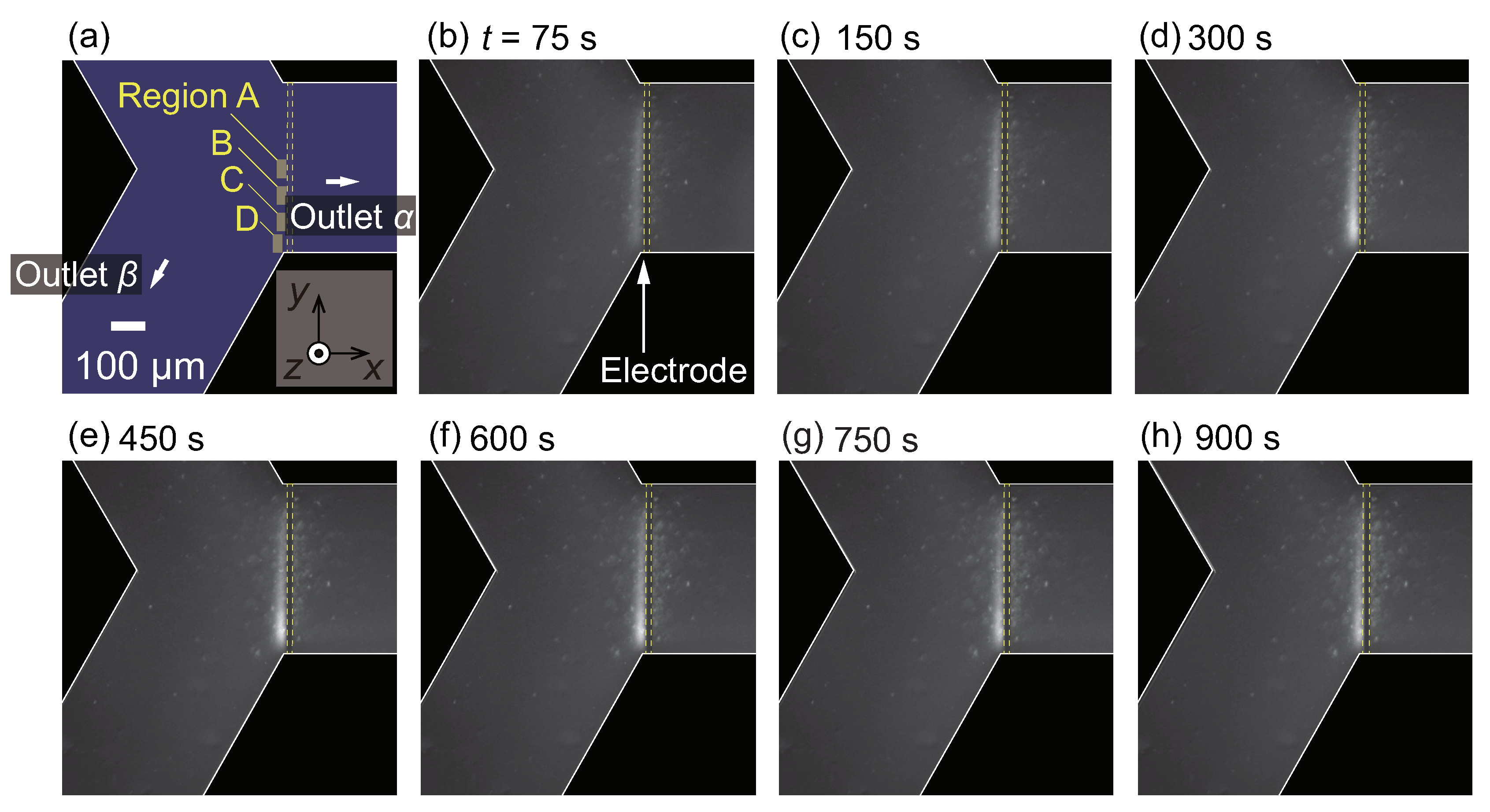
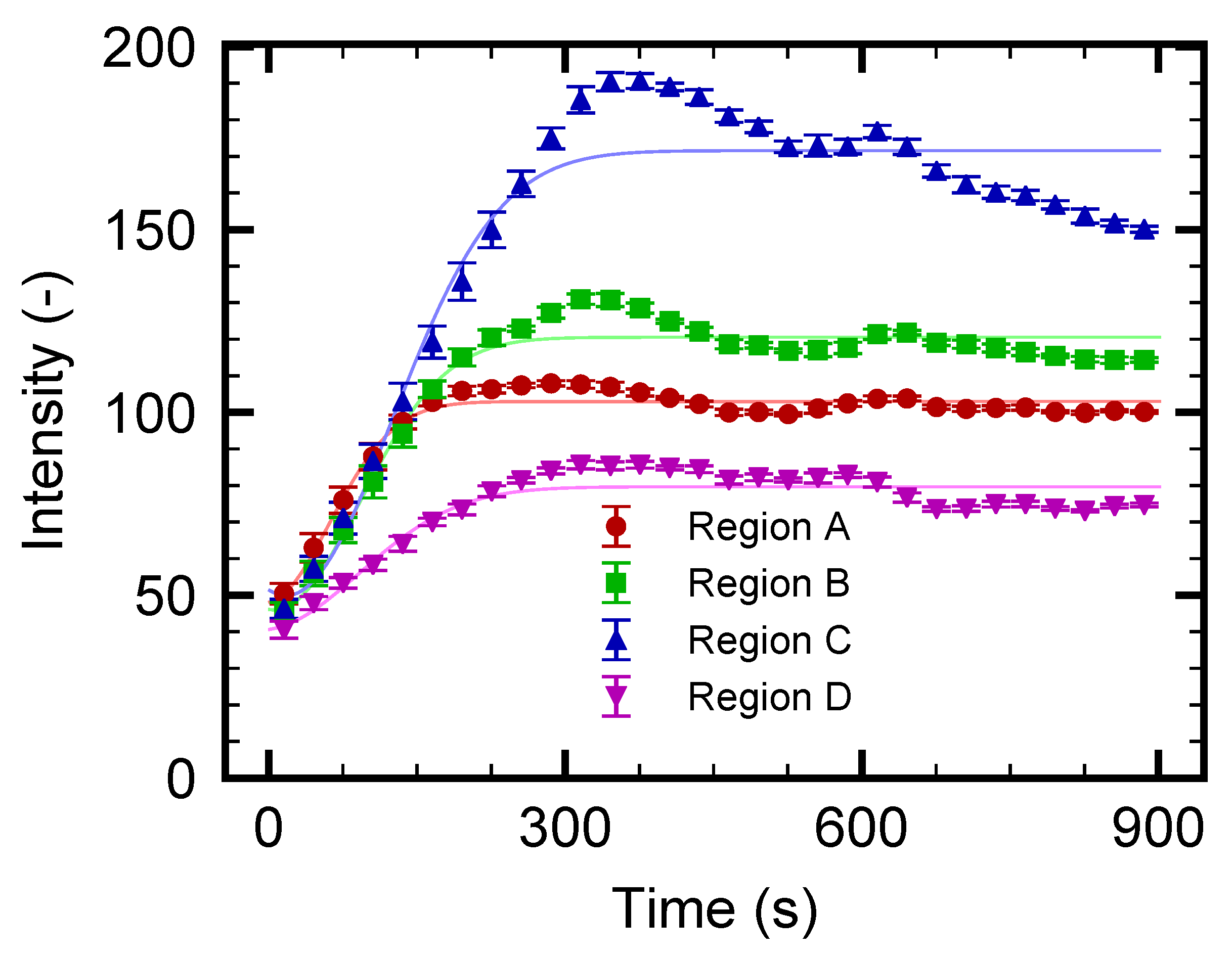
3.3. Nanoparticle Flow Separation
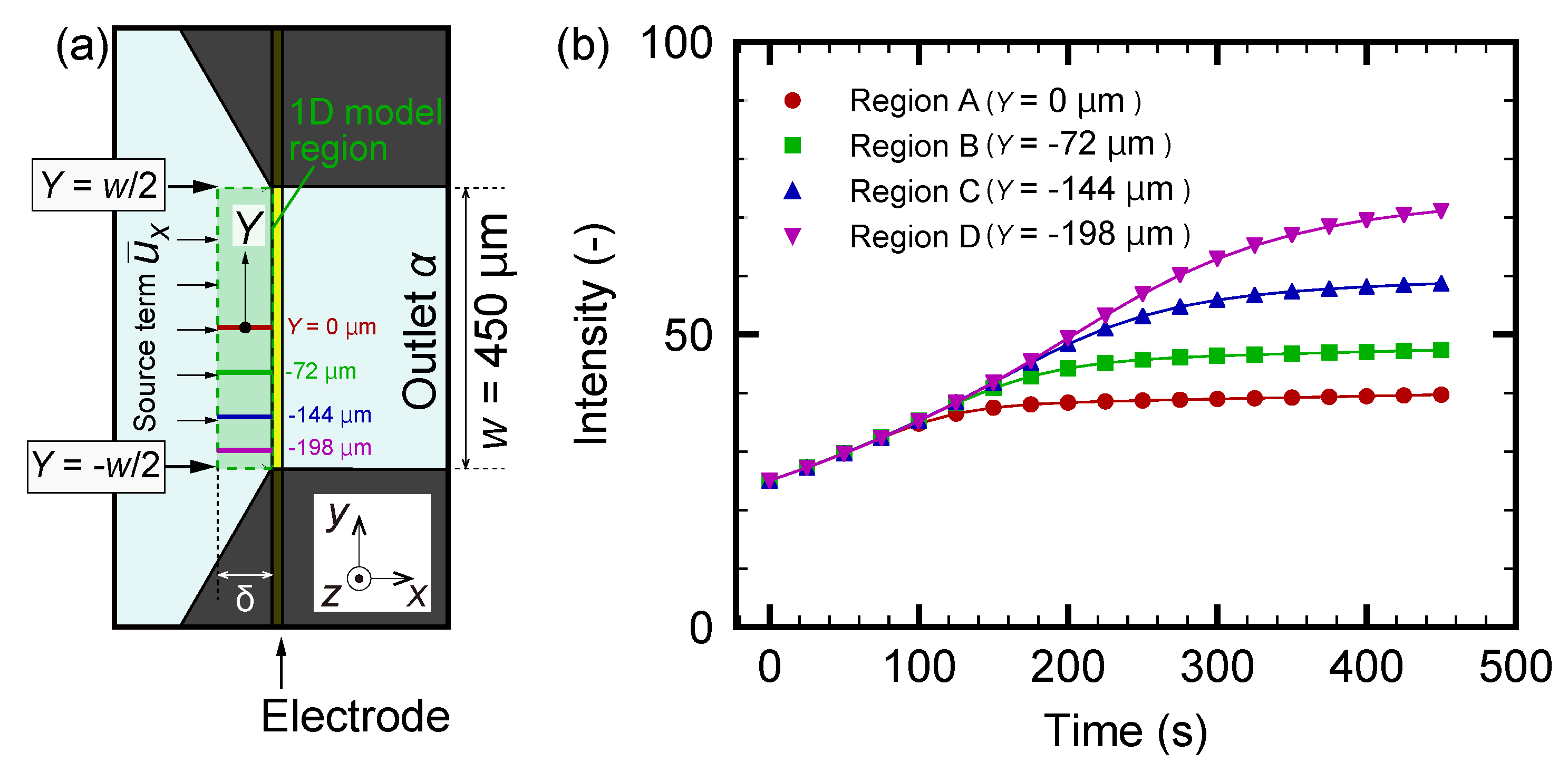
3.4. Numerical Modeling for Nanoparticle Distribution
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; FED–Volume 231/MD–Volume 66; The American Society of Mechanical Engineers: New York, NY, USA, 1995; pp. 99–105. [Google Scholar]
- Yu, W.; Xie, H. A review on nanofluids: Preparation, stability mechanisms, and applications. J. Nanomater. 2012, 2012, 435873. [Google Scholar] [CrossRef]
- Islam, M.R.; Shabani, B.; Rosengarten, G. Nanofluids to improve the performance of PEM fuel cell cooling systems: A theoretical approach. Appl. Energy 2016, 178, 660–671. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Chen, H.; Cai, H.; Deng, L. A novel fractal model for relative permeability of gas diffusion layer in proton exchange membrane fuel cell with capillary pressure effect. Fractals 2019, 27, 1950012. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Hossain, R.; Mahmud, S.; Dutta, A.; Pop, I. Energy storage system based on nanoparticle-enhanced phase change material inside porous medium. Int. J. Therm. Sci. 2015, 91, 49–58. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Trans. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Ehtesabi, H.; Ahadian, M.M.; Taghikhani, V.; Ghazanfari, M.H. Enhanced heavy oil recovery in sandstone cores using TiO2 nanofluids. Energy Fuels 2013, 28, 423–430. [Google Scholar]
- Long, G.; Xu, G. The effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Long, G.; Liu, S.; Xu, G.; Wong, S.-W.; Chen, H.; Xiao, B. A perforation-erosion model for hydraulic-fracturing applications. SPE Prod. Oper. 2018, 33, 770–783. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, X.; Wang, W.; Long, G.; Chen, H.; Kang, H.; Ren, W. A fractal model for water flow through unsaturated porous rocks. Fractals 2018, 26, 1840015. [Google Scholar] [CrossRef]
- Tsutsui, M.; Taniguchi, M.; Yokota, K.; Kawai, T. Identifying single nucleotides by tunnelling current. Nat. Nanotechnol. 2010, 5, 286. [Google Scholar] [CrossRef]
- Sackmann, E.K.; Fulton, A.L.; Beebe, D.J. The present and future role of microfluidics in biomedical research. Nature 2014, 507, 181. [Google Scholar] [CrossRef] [PubMed]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef]
- Huang, L.R.; Cox, E.C.; Austin, R.H.; Sturm, J.C. Continuous particle separation through deterministic lateral displacement. Science 2004, 304, 987–990. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef]
- Shintaku, H.; Imamura, S.; Kawano, S. Microbubble formations in MEMS-fabricated rectangular channels: A high-speed observation. Exp. Therm. Fluid Sci. 2008, 32, 1132–1140. [Google Scholar] [CrossRef]
- Kuntaegowdanahalli, S.S.; Bhagat, A.A.S.; Kumar, G.; Papautsky, I. Inertial microfluidics for continuous particle separation in spiral microchannels. Lab Chip 2009, 9, 2973–2980. [Google Scholar] [CrossRef]
- Shi, J.; Huang, H.; Stratton, Z.; Huang, Y.; Huang, T.J. Continuous particle separation in a microfluidic channel via standing surface acoustic waves (SSAW). Lab Chip 2009, 9, 3354–3359. [Google Scholar] [CrossRef]
- Qian, W.; Doi, K.; Kawano, S. Effects of polymer length and salt concentration on the transport of ssDNA in nanofluidic channels. Biophys. J. 2017, 112, 838–849. [Google Scholar] [CrossRef]
- Keyser, U.F. Controlling molecular transport through nanopores. J. R. Soc. Interface 2011, 8, 1369. [Google Scholar] [CrossRef] [PubMed]
- Uehara, S.; Shintaku, H.; Kawano, S. Electrokinetic flow dynamics of weakly aggregated λDNA confined in nanochannels. J. Fluids Eng. 2011, 133, 121203. [Google Scholar] [CrossRef]
- Sanghavi, B.J.; Varhue, W.; Chávez, J.L.; Chou, C.-F.; Swami, N.S. Electrokinetic preconcentration and detection of neuropeptides at patterned graphene-modified electrodes in a nanochannel. Anal. Chem. 2014, 86, 4120–4125. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S.; Tsutsui, M.; Theodore, H.; Yuhui, H.; Arima, A.; Tsuji, T.; Doi, K.; Kawano, S.; Taniguchi, M.; Kawai, T. Tailoring particle translocation via dielectrophoresis in pore channels. Sci. Rep. 2016, 6, 31670. [Google Scholar] [CrossRef]
- Shin, S.; Ault, J.T.; Warren, P.B.; Stone, H.A. Accumulation of colloidal particles in flow junctions induced by fluid flow and diffusiophoresis. Phys. Rev. X 2017, 7, 041038. [Google Scholar] [CrossRef]
- Prieve, D.C.; Malone, S.M.; Khair, A.S.; Stout, R.F.; Kanj, M.Y. Diffusiophoresis of charged colloidal particles in the limit of very high salinity. Proc. Natl. Acad. Sci. USA 2018. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Warren, P.B.; Stone, H.A. Cleaning by surfactant gradients: Particulate removal from porous materials and the significance of rinsing in laundry detergency. Phys. Rev. Appl. 2018, 9, 034012. [Google Scholar] [CrossRef]
- Ault, J.T.; Shin, S.; Stone, H.A. Diffusiophoresis in narrow channel flows. J. Fluid Mech. 2018, 854, 420–448. [Google Scholar] [CrossRef]
- Seki, T.; Okuzono, T.; Toyotama, A.; Yamanaka, J. Mechanism of diffusiophoresis with chemical reaction on a colloidal particle. Phys. Rev. E 2019, 99, 012608. [Google Scholar] [CrossRef]
- Piazza, R. Thermophoresis: Moving particles with thermal gradients. Soft Matter 2008, 4, 1740. [Google Scholar] [CrossRef]
- Piazza, R.; Parola, A. Thermophoresis in colloidal suspensions. J. Phys. Condens. Matter 2008, 20, 153102. [Google Scholar] [CrossRef]
- Würger, A. Thermal non-equilibrium transport in colloids. Rep. Prog. Phys. 2010, 73, 126601. [Google Scholar] [CrossRef]
- Duhr, S.; Braun, D. Why molecules move along a temperature gradient. Proc. Natl. Acad. Sci. USA 2006, 103, 19678. [Google Scholar] [CrossRef]
- Iacopini, S.; Rusconi, R.; Piazza, R. “The macromolecular tourist”: Universal temperature dependence of thermal diffusion in aqueous colloidal suspensions. Eur. Phys. J. E 2006, 19, 59. [Google Scholar] [CrossRef]
- Ning, H.; Buitenhuis, J.; Dhont, J.K.; Wiegand, S. Thermal diffusion behavior of hard-sphere suspensions. J. Chem. Phys. 2006, 125, 204911. [Google Scholar] [CrossRef]
- Vigolo, D.; Rusconi, R.; Stone, H.A.; Piazza, R. Thermophoresis: Microfluidics characterization and separation. Soft Matter 2010, 6, 3489. [Google Scholar] [CrossRef]
- Eslahian, K.A.; Majee, A.; Maskos, M.; Würger, A. Specific salt effects on thermophoresis of charged colloids. Soft Matter 2014, 10, 1931–1936. [Google Scholar] [CrossRef]
- Tsuji, T.; Kozai, K.; Ishino, H.; Kawano, S. Direct observations of thermophoresis in microfluidic systems. Micro Nano Lett. 2017, 12, 520. [Google Scholar] [CrossRef]
- Lin, L.; Wang, M.; Peng, X.; Lissek, E.N.; Mao, Z.; Scarabelli, L.; Adkins, E.; Coskun, S.; Unalan, H.E.; Korgel, B.A.; et al. Opto-thermoelectric nanotweezers. Nat. Photonics 2018, 12, 195. [Google Scholar] [CrossRef]
- Jiang, H.-R.; Wada, H.; Yoshinaga, N.; Sano, M. Manipulation of colloids by a nonequilibrium depletion force in a temperature gradient. Phys. Rev. Lett. 2009, 102, 208301. [Google Scholar] [CrossRef]
- Maeda, Y.T.; Tlusty, T.; Libchaber, A. Effects of long DNA folding and small RNA stem–loop in thermophoresis. Proc. Natl. Acad. Sci. USA 2012, 109, 17972. [Google Scholar] [CrossRef] [PubMed]
- Wienken, C.J.; Baaske, P.; Rothbauer, U.; Braun, D.; Duhr, S. Protein-binding assays in biological liquids using microscale thermophoresis. Nat. Commun. 2010, 1, 100. [Google Scholar] [CrossRef]
- Seidel, S.A.I.; Wienken, C.J.; Geissler, S.; Jerabek-Willemsen, M.; Duhr, S.; Reiter, A.; Trauner, D.; Braun, D.; Baaske, P. Label-free microscale thermophoresis discriminates sites and affinity of protein–ligand binding. Angew. Chem. Int. Edit. 2012, 51, 10656. [Google Scholar] [CrossRef]
- Burelbach, J.; Zupkauskas, M.; Lamboll, R.; Lan, Y.; Eiser, E. Colloidal motion under the action of a thermophoretic force. J. Chem. Phys. 2017, 147, 094906. [Google Scholar] [CrossRef]
- Burelbach, J.; Brückner, D.B.; Frenkel, D.; Eiser, E. Thermophoretic forces on a mesoscopic scale. Soft Matter 2018, 14, 7446–7454. [Google Scholar] [CrossRef]
- Burelbach, J.; Frenkel, D.; Pagonabarraga, I.; Eiser, E. A unified description of colloidal thermophoresis. Eur. Phys. J. E 2018, 41, 7. [Google Scholar]
- Tsuji, T.; Saita, S.; Kawano, S. Thermophoresis of a Brownian particle driven by inhomogeneous thermal fluctuation. Physica A 2018, 493, 467. [Google Scholar] [CrossRef]
- Galliéro, G.; Volz, S. Thermodiffusion in model nanofluids by molecular dynamics simulations. J. Chem. Phys. 2008, 128, 064505. [Google Scholar] [CrossRef] [PubMed]
- Lüsebrink, D.; Yang, M.; Ripoll, M. Thermophoresis of colloids by mesoscale simulations. J. Phys. Condens. Matter 2012, 24, 284132. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tsuji, T.; Iseki, H.; Hanasaki, I.; Kawano, S. Molecular dynamics study of force acting on a model nano particle immersed in fluid with temperature gradient: Effect of interaction potential. AIP Conf. Proc. 2016, 1786, 110003. [Google Scholar]
- Tsuji, T.; Iseki, H.; Hanasaki, I.; Kawano, S. Negative thermophoresis of nanoparticles interacting with fluids through a purely-repulsive potential. J. Phys. Condens. Matter 2017, 29, 475101. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, T.; Saita, S.; Kawano, S. Dynamic pattern formation of microparticles in a uniform flow by an on-chip thermophoretic separation device. Phys. Rev. Appl. 2018, 9, 024035. [Google Scholar] [CrossRef]
- Tsuji, T.; Sasai, Y.; Kawano, S. Thermophoresithermophoretic manipulation of micro- and nanoparticle flow through a sudden contraction in a microchannel with near-infrared laser irradiation. Phys. Rev. Appl. 2018, 10, 044005. [Google Scholar] [CrossRef]
- Briggs, J.A.G.; Grünewald, K.; Glass, B.; Förster, F.; Kräusslich, H.-G.; Fuller, S.D. The mechanism of HIV-1 core assembly: Insights from three-dimensional reconstructions of authentic virions. Structure 2006, 14, 15. [Google Scholar] [CrossRef]
- Bouvier, N.M.; Palese, P. The biology of influenza viruses. Vaccine 2008, 26, D49. [Google Scholar] [CrossRef]
- Kawaguchi, C.; Noda, T.; Tsutsui, M.; Taniguchi, M.; Kawano, S.; Kawai, T. Electrical detection of single pollen allergen particles using electrode-embedded microchannels. J. Phys. Condens. Matter 2012, 24, 164202. [Google Scholar] [CrossRef]
- Bruus, H. Theoretical Microfluidics; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Mäki, A.-J.; Hemmilä, S.; Hirvonen, J.; Girish, N.N.; Kreutzer, J.; Hyttinen, J.; Kallio, P. Modeling and experimental characterization of pressure drop in gravity-driven microfluidic systems. J. Fluids Eng. 2015, 137, 021105. [Google Scholar] [CrossRef]
- Kestin, J.; Sokolov, M.; Wakeham, W.A. Viscosity of liquid water in the range −8 ∘C to 150 ∘C. J. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar] [CrossRef]
- Abu-Nada, E. Numerical prediction of entropy generation in separated flows. Entropy 2005, 7, 234–252. [Google Scholar] [CrossRef]
- Pour, M.S.; Nassab, S.G. Numerical investigation of forced laminar convection flow of nanofluids over a backward facing step under bleeding condition. J. Mech. 2012, 28, N7–N12. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuji, T.; Matsumoto, Y.; Kugimiya, R.; Doi, K.; Kawano, S. Separation of Nano- and Microparticle Flows Using Thermophoresis in Branched Microfluidic Channels. Micromachines 2019, 10, 321. https://doi.org/10.3390/mi10050321
Tsuji T, Matsumoto Y, Kugimiya R, Doi K, Kawano S. Separation of Nano- and Microparticle Flows Using Thermophoresis in Branched Microfluidic Channels. Micromachines. 2019; 10(5):321. https://doi.org/10.3390/mi10050321
Chicago/Turabian StyleTsuji, Tetsuro, Yuki Matsumoto, Ryo Kugimiya, Kentaro Doi, and Satoyuki Kawano. 2019. "Separation of Nano- and Microparticle Flows Using Thermophoresis in Branched Microfluidic Channels" Micromachines 10, no. 5: 321. https://doi.org/10.3390/mi10050321
APA StyleTsuji, T., Matsumoto, Y., Kugimiya, R., Doi, K., & Kawano, S. (2019). Separation of Nano- and Microparticle Flows Using Thermophoresis in Branched Microfluidic Channels. Micromachines, 10(5), 321. https://doi.org/10.3390/mi10050321




