Design Guidelines for Thermally Driven Micropumps of Different Architectures Based on Target Applications via Kinetic Modeling and Simulations
Abstract
1. Introduction
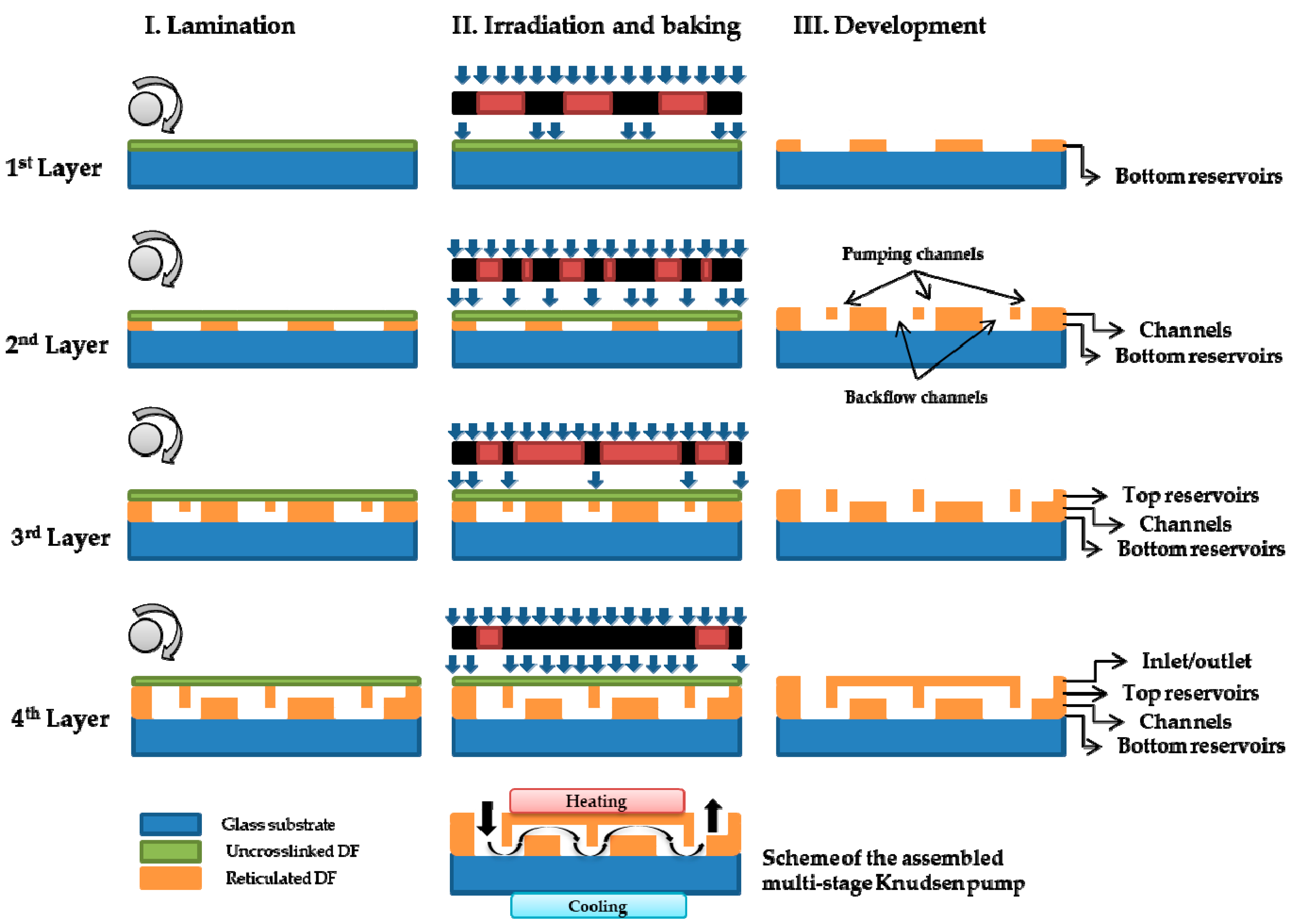
2. Proposed Pump Designs, Manufacturing Materials, and Fabrication Process
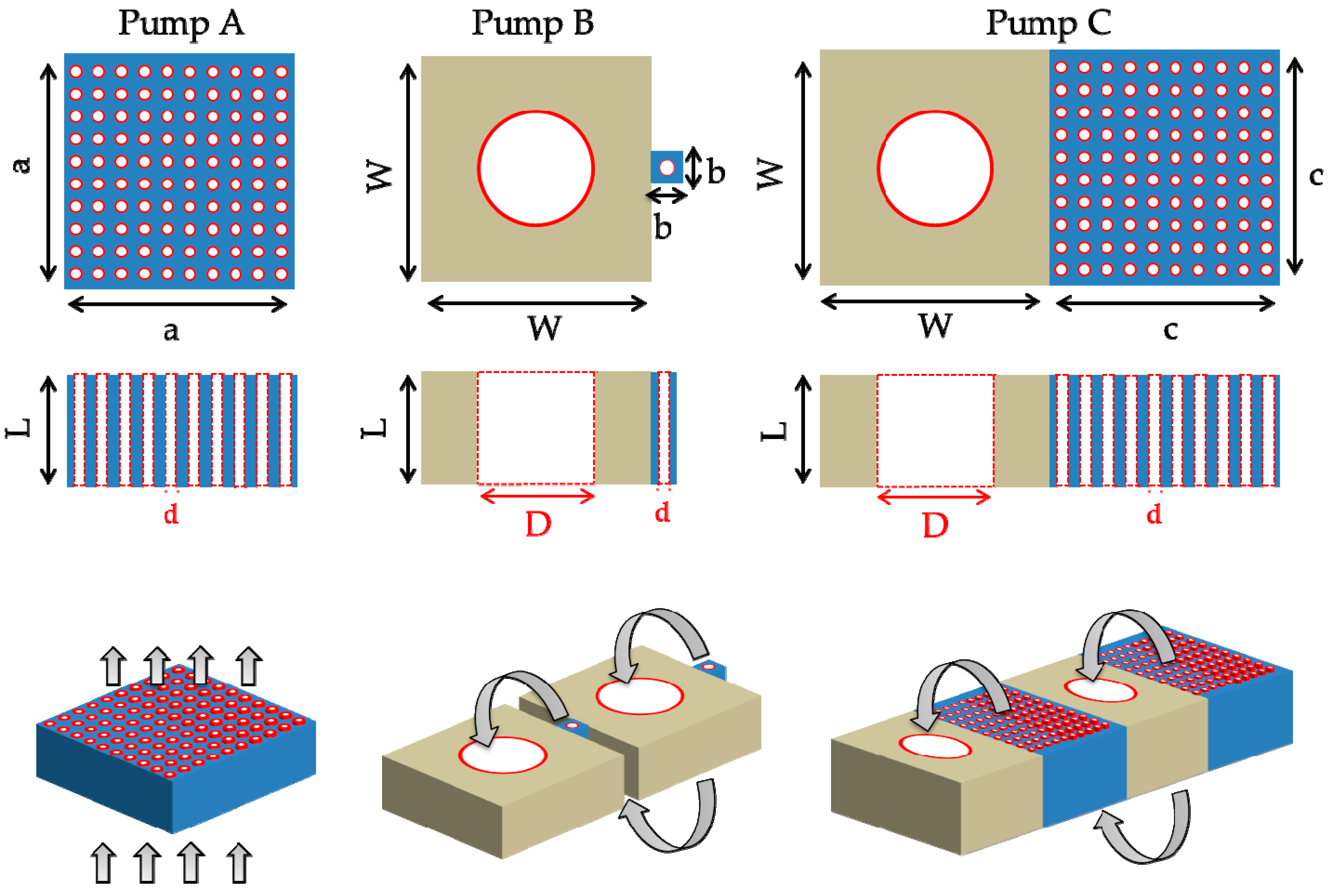
- Pump A consists of an array of multiple parallel narrow microchannels in one single pumping stage to achieve high mass flow rate () performance. The layout area is with parallel narrow microchannels of diameter and length .
- Pump B consists of a multistage system where each stage is formed by one single narrow pumping microchannel followed by one wide channel (where the reduced counter thermal transpiration flow will appear) to achieve high pressure difference () performance. The layout area is . The diameter of the narrow and wide channels are and , respectively, and the length of both channels is .
- Pump C combines the two previous designs. More specifically, it consists of a multistage system and each stage is formed by an array of parallel narrow pumping microchannels, followed by one wide channel where the reduced counter thermal transpiration flow will appear. This design provides high and performances, due to the multi-stage cascade system and to the multiple narrow microchannels per stage, respectively. The layout area is . The diameter of the narrow and wide channels are and , respectively, while the length of all channels is .
3. Kinetic Modeling
4. Results and Discussion
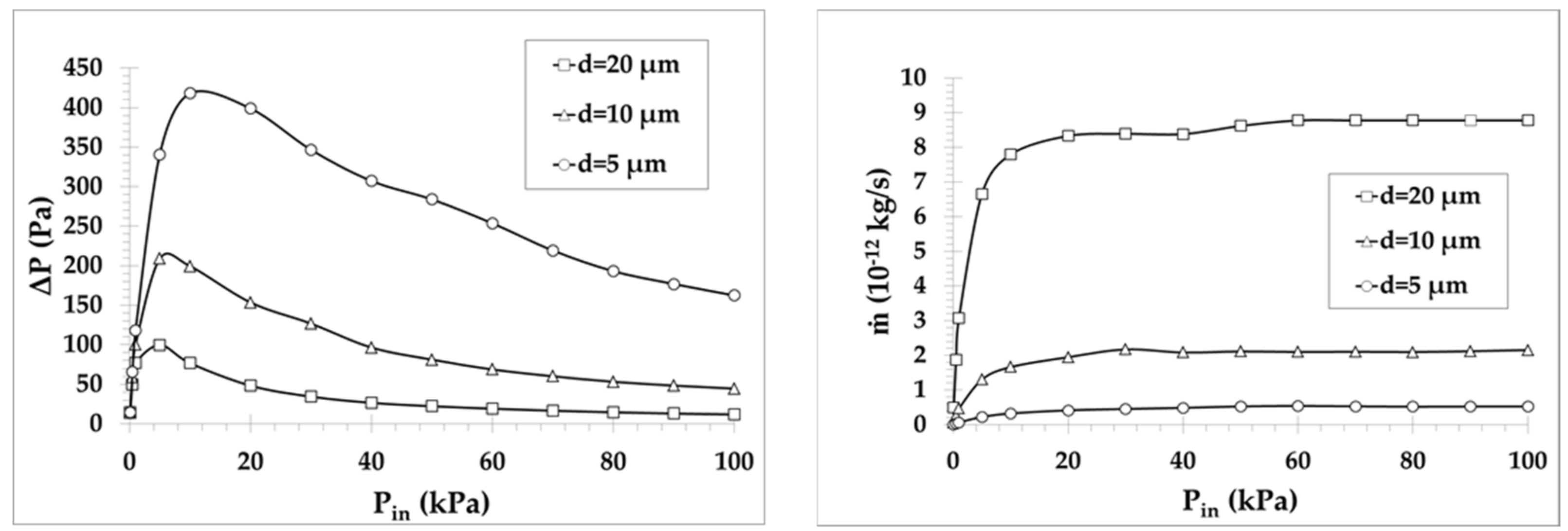
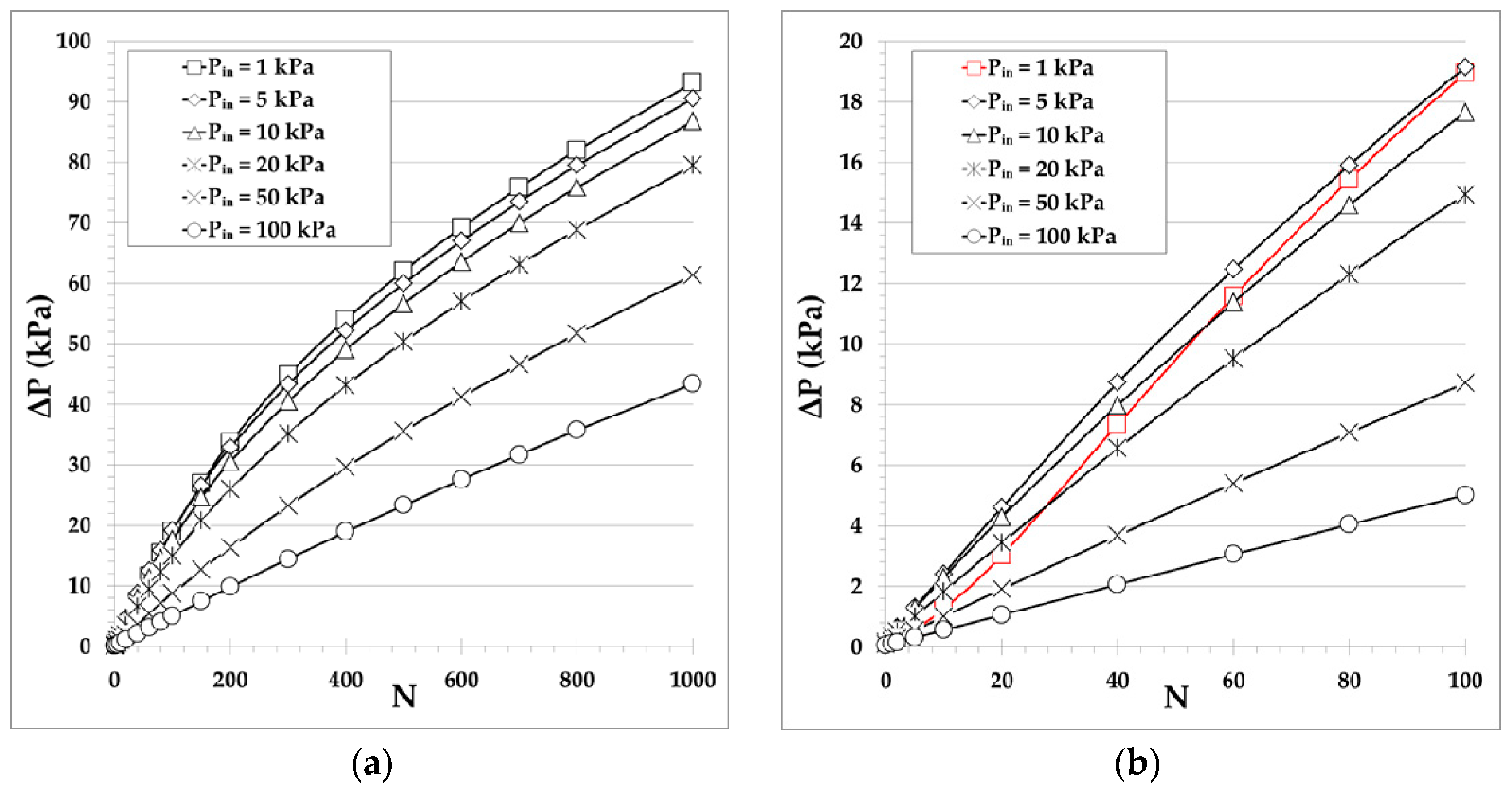
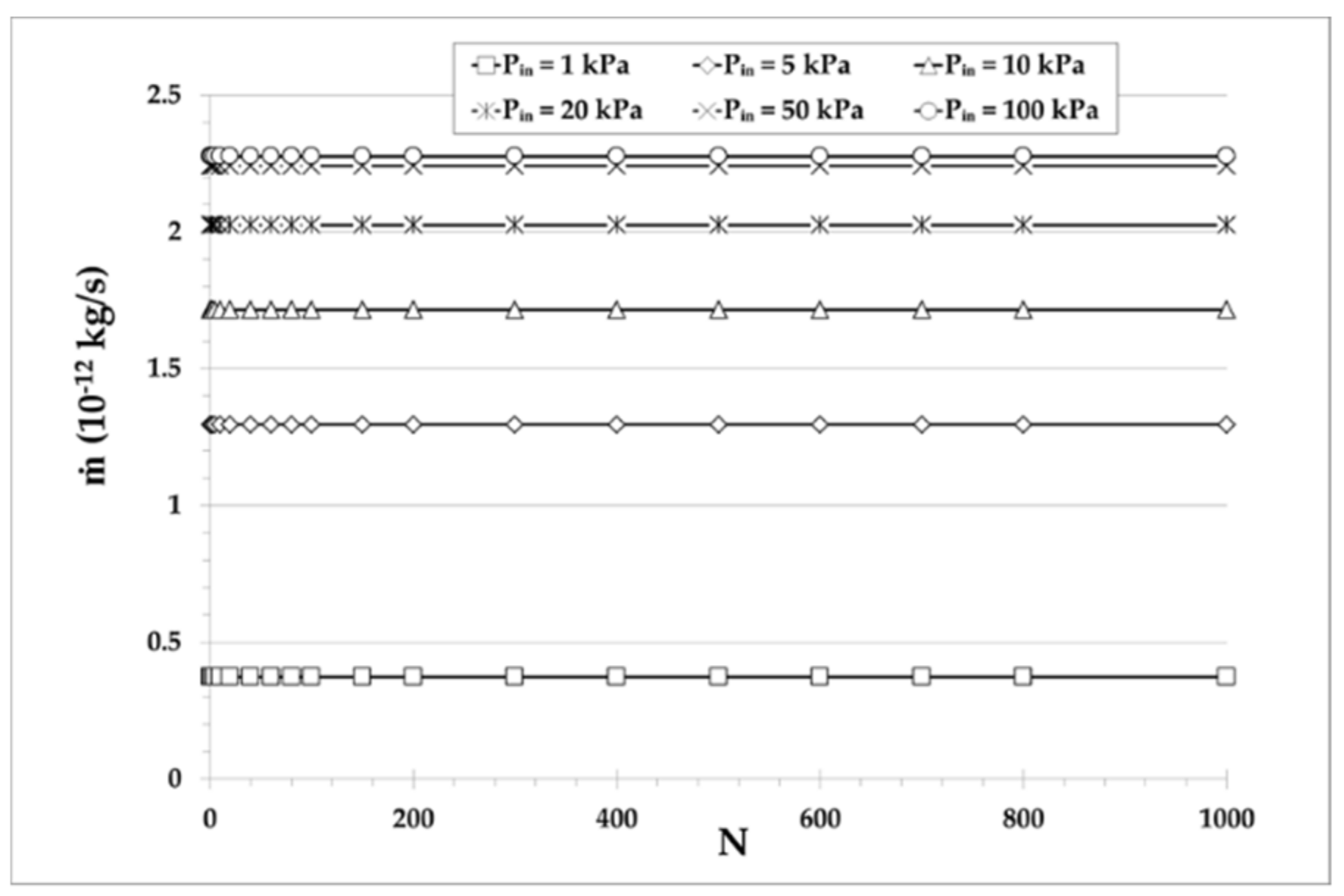
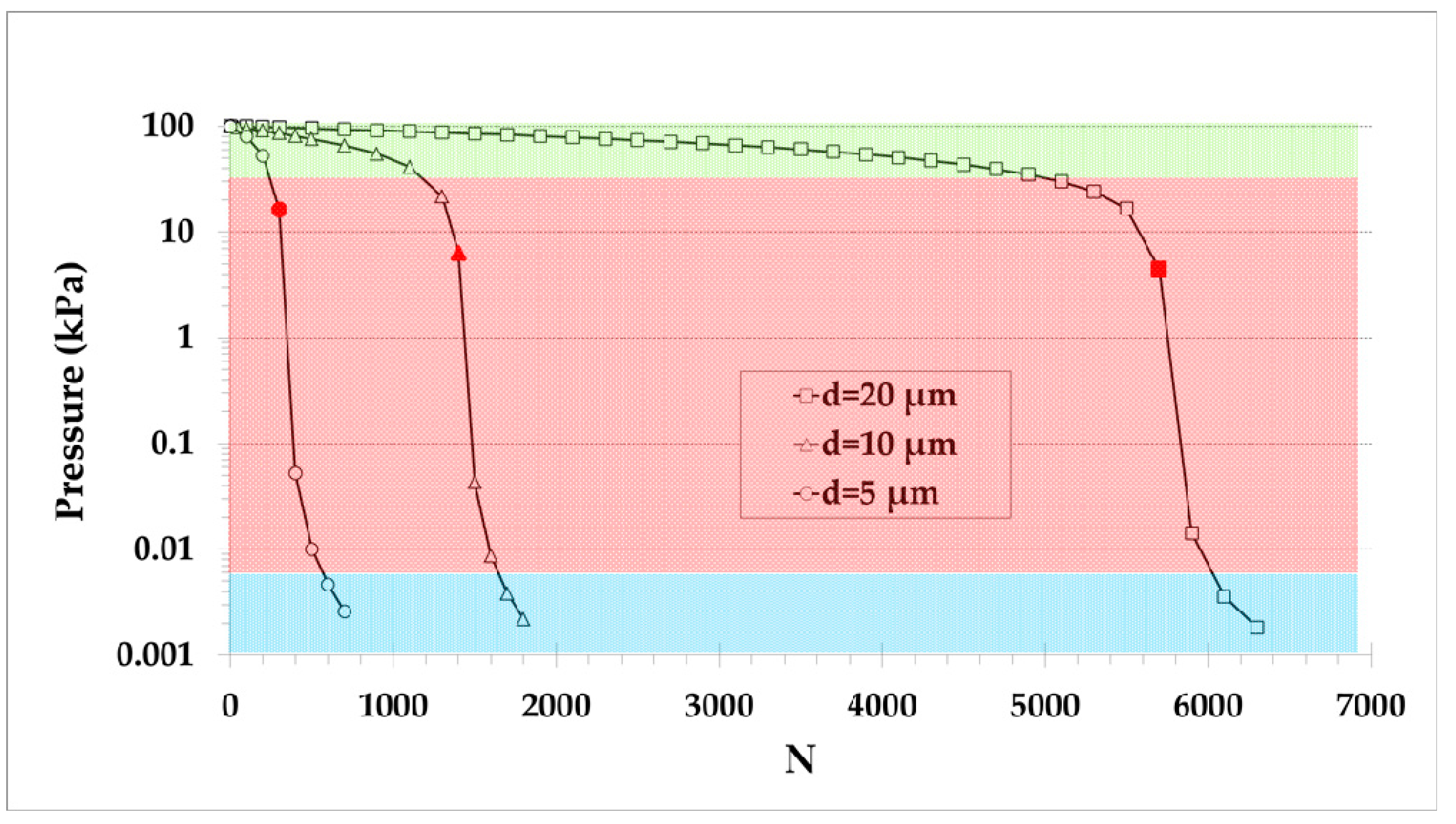
4.1. Pump A: One Pumping Stage with Multiple Parallel Microchannels
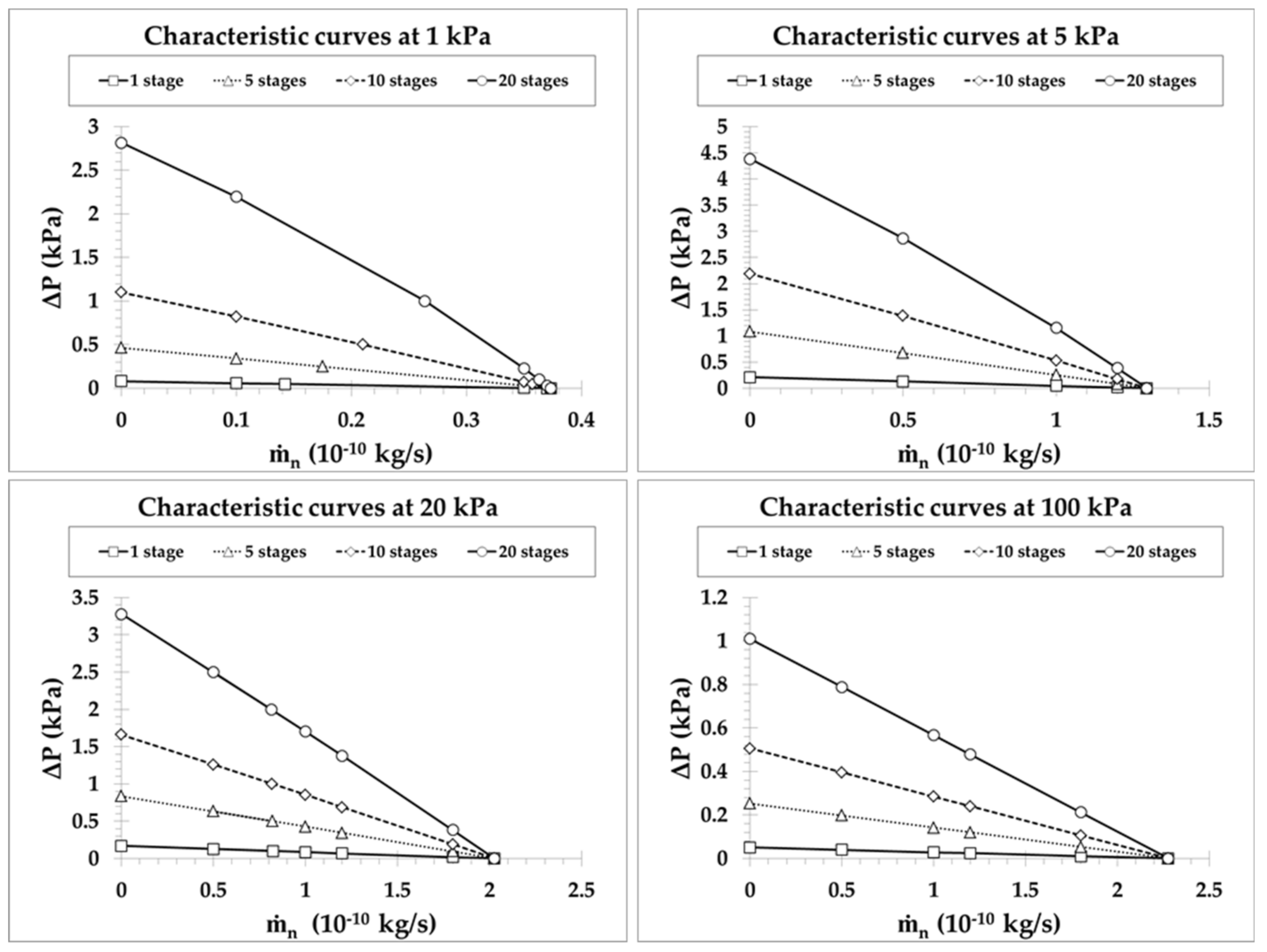
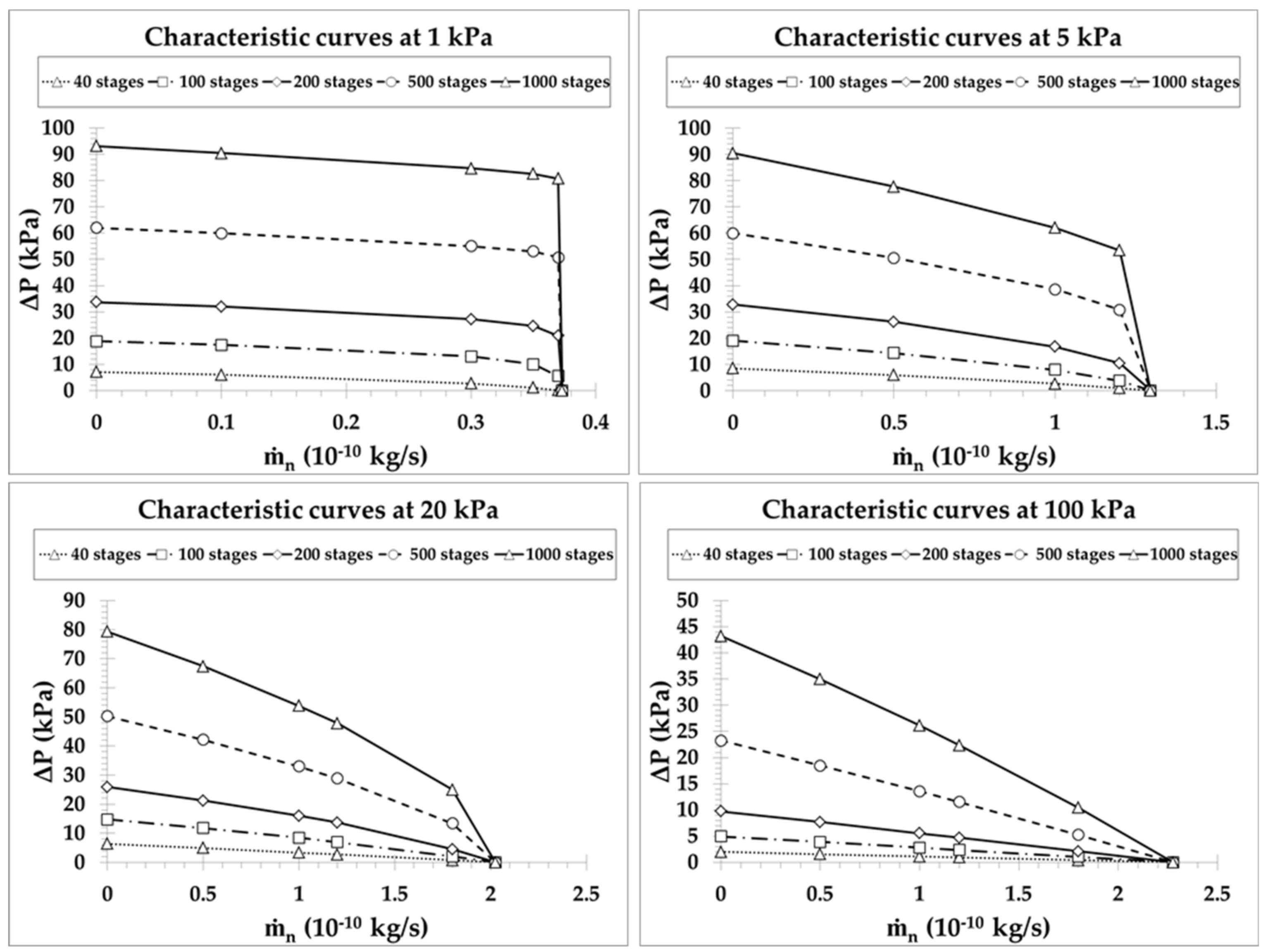
4.2. Pump B: Multistage Pumping with One Narrow and One Large Channel Per Stage
4.3. Pump C: Multistage Pumping with Multiple Parallel Microchannels Per Stage
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Tabulated Results of the Kinetic Coefficients
| δ | 0.0005 | 0.001 | 0.005 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 |
| GP | 1.5023 | 1.5008 | 1.4904 | 1.4800 | 1.4636 | 1.4514 | 1.4418 | 1.4339 |
| GT | 0.7502 | 0.7486 | 0.7366 | 0.7243 | 0.7042 | 0.6884 | 0.6752 | 0.6637 |
| δ | 0.06 | 0.07 | 0.08 | 0.09 | 0.1 | 0.2 | 0.3 | 0.4 |
| GP | 1.4273 | 1.4217 | 1.4168 | 1.4127 | 1.4101 | 1.3911 | 1.3876 | 1.3920 |
| GT | 0.6536 | 0.6444 | 0.6359 | 0.6281 | 0.6210 | 0.5675 | 0.5303 | 0.5015 |
| δ | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 1.2 | 1.4 |
| GP | 1.4011 | 1.4130 | 1.4270 | 1.4425 | 1.4592 | 1.4758 | 1.5158 | 1.5550 |
| GT | 0.4779 | 0.4576 | 0.4367 | 0.4237 | 0.4092 | 0.3959 | 0.3721 | 0.3514 |
| δ | 1.6 | 1.8 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
| GP | 1.5956 | 1.6373 | 1.6799 | 1.9014 | 2.1315 | 2.3666 | 2.6049 | 2.8455 |
| GT | 0.3330 | 0.3165 | 0.3016 | 0.2439 | 0.2042 | 0.1752 | 0.1531 | 0.1359 |
| δ | 8.0 | 9.0 | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | |
| GP | 3.0878 | 3.3314 | 3.5749 | 6.0492 | 8.5392 | 11.0360 | 13.4950 | |
| GT | 0.1220 | 0.1106 | 0.1014 | 0.05426 | 0.03685 | 0.02785 | 0.02212 |
References
- Schomburg, W.K.; Vollmer, J.; Bustgens, B.; Fahrenberg, J.; Hein, H.; Menz, W. Microfluidic components in LIGA technique. J. Micromech. Microeng. 1994, 4, 186–191. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, 35–64. [Google Scholar] [CrossRef]
- Maxwell, J.C. On stresses in rarefied gases arising from inequalities of temperature. Proc. R. Soc. Lond. 1878, 27, 304–308. [Google Scholar]
- Reynolds, O. XVIII. On certain dimensional properties of matter in the gaseous state. Philos. Trans. R. Soc. Lond. Ser. A 1879, 170, 727–845. [Google Scholar]
- Knudsen, M. Eine Revision der gleichgewichtsbedingung der gase. Thermische Molekularströmung. Ann. Phys. 1909, 336, 205–229. [Google Scholar] [CrossRef]
- Knudsen, M. Thermischer molekulardruck der gase in Röhren. Ann. Phys. 1910, 338, 1435–1448. [Google Scholar] [CrossRef]
- Sone, Y.; Waniguchi, Y.; Aoki, K. One-way flow of a rarefied gas induced in a channel with a periodic temperature distribution. Phys. Fluids 1996, 8, 2227–2235. [Google Scholar] [CrossRef]
- Sone, Y. Molecular Gas Dynamics: Theory, Techniques, and Applications; Birkhäuser: Basel, Switzerland, 2007; ISBN 9780817643454. [Google Scholar]
- Aoki, K.; Mieussens, L.; Takata, S.; Degond, P.; Nishioka, M.; Takata, S. Numerical Simulation of a Knudsen Pump Using the Effect of Curvature of the Channel; Global Science Press: Hong Kong, China, 2007. [Google Scholar]
- Aoki, K.; Takata, S.; Kugimoto, K. Diffusion approximation for the knudsen compressor composed of circular tubes. AIP Conf. Proc. 2008, 953–958. [Google Scholar] [CrossRef]
- Colin, S. Single-Phase Gas Flow in Microchannels. In Heat Transfer and Fluid Flow in Minichannels and Microchannels; Elsevier: Amsterdam, The Netherlands, 2014; pp. 11–102. [Google Scholar]
- Aoki, K.; Degond, P.; Takata, S.; Yoshida, H. Diffusion models for Knudsen compressors. Phys. Fluids 2007, 19, 117103. [Google Scholar] [CrossRef]
- Li, X.; Oehrlein, G.S.; Schaepkens, M.; Ellefson, R.E.; Frees, L.C. Spatially resolved mass spectrometric sampling of inductively coupled plasmas using a movable sampling orifice. J. Vac. Sci. Technol. A 2003, 21, 1971–1977. [Google Scholar] [CrossRef]
- Hamad, F.; Khulbe, K.C.; Matsuura, T. Comparison of gas separation performance and morphology of homogeneous and composite PPO membranes. J. Membr. Sci. 2005, 256, 29–37. [Google Scholar] [CrossRef]
- McNamara, S.; Gianchandani, Y.B. On-chip vacuum generated by a micromachined Knudsen pump. J. Microelectromech. Syst. 2005, 14, 741–746. [Google Scholar] [CrossRef]
- Gupta, N.K.; Gianchandani, Y.B. Porous ceramics for multistage Knudsen micropumps-modeling approach and experimental evaluation. J. Micromech. Microeng. 2011, 21, 095029. [Google Scholar] [CrossRef]
- Vargo, S.E. Initial results from the first MEMS fabricated thermal transpiration-driven vacuum pump. AIP Conf. Proc. 2001, 585, 502–509. [Google Scholar]
- Gupta, N.K.; An, S.; Gianchandani, Y.B. A Si-micromachined 48-stage Knudsen pump for on-chip vacuum. J. Micromech. Microeng. 2012, 22, 105026. [Google Scholar] [CrossRef]
- An, S.; Gupta, N.K.; Gianchandani, Y.B. A Si-Micromachined 162-stage two-part knudsen pump for on-chip vacuum. J. Microelectromech. Syst. 2014, 23, 406–416. [Google Scholar] [CrossRef]
- Qin, Y.; An, S.; Gianchandani, Y.B. Arrayed architectures for multi-stage Si-micromachined high-flow Knudsen pumps. J. Micromech. Microeng. 2015, 25, 115026. [Google Scholar] [CrossRef]
- Qin, Y.; Gianchandani, Y.B. A fully electronic microfabricated gas chromatograph with complementary capacitive detectors for indoor pollutants. Microsyst. Nanoeng. 2016, 2, 15049. [Google Scholar] [CrossRef]
- Cheng, Q.; Qin, Y.; Gianchandani, Y.B. A Bidirectional Knudsen Pump with Superior Thermal Management for Micro-Gas Chromatography Applications. In Proceedings of the IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 167–170. [Google Scholar]
- Courson, R.; Cargou, S.; Conédéra, V.; Fouet, M.; Blatché, M.-C.; Serpentini, C.L.; Gué, A.-M. Low-cost multilevel microchannel lab on chip: DF-1000 series dry film photoresist as a promising enabler. RSC Adv. 2014, 4, 54847–54853. [Google Scholar] [CrossRef]
- Sharipov, F. Rarefied gas flow through a long tube at any temperature ratio. J. Vac. Sci. Technol. A 1996, 14, 2627–2635. [Google Scholar] [CrossRef]
- Sharipov, F.; Seleznev, V. Data on Internal Rarefied Gas Flows. J. Phys. Chem. Ref. Data 1998, 27, 657–706. [Google Scholar] [CrossRef]
- Sharipov, F. Non-isothermal gas flow through rectangular microchannels. J. Micromech. Microeng. 1999, 9, 394–401. [Google Scholar] [CrossRef]
- Sharipov, F.; Bertoldo, G. Rarefied gas flow through a long tube of variable radius. J. Vac. Sci. Technol. A 2005, 23, 531–533. [Google Scholar] [CrossRef]
- Graur, I.; Sharipov, F. Non-isothermal flow of rarefied gas through a long pipe with elliptic cross section. Microfluid. Nanofluid. 2009, 6, 267–275. [Google Scholar] [CrossRef]
- Ritos, K.; Lihnaropoulos, Y.; Naris, S.; Valougeorgis, D. Pressure- and temperature-driven flow through triangular and trapezoidal microchannels. Heat Transf. Eng. 2011, 32, 1101–1107. [Google Scholar] [CrossRef]
- Tatsios, G.; Lopez Quesada, G.; Rojas-Cardenas, M.; Baldas, L.; Colin, S.; Valougeorgis, D. Computational investigation and parametrization of the pumping effect in temperature-driven flows through long tapered channels. Microfluid. Nanofluid. 2017, 21, 99. [Google Scholar] [CrossRef]
- Pantazis, S.; Valougeorgis, D.; Sharipov, F. End corrections for rarefied gas flows through circular tubes of finite length. Vacuum 2014, 101, 306–312. [Google Scholar] [CrossRef]
- Valougeorgis, D.; Vasileiadis, N.; Titarev, V. Validity range of linear kinetic modeling in rarefied pressure driven single gas flows through circular capillaries. Eur. J. Mech. B Fluids 2017, 64, 2–7. [Google Scholar] [CrossRef]
- Naris, S.; Valougeorgis, D.; Kalempa, D.; Sharipov, F. Flow of gaseous mixtures through rectangular microchannels driven by pressure, temperature, and concentration gradients. Phys. Fluids 2005, 17, 100607. [Google Scholar] [CrossRef]
- Rojas Cardenas, M.; Graur, I.; Perrier, P.; Meolans, J.G. Thermal transpiration flow: A circular cross-section microtube submitted to a temperature gradient. Phys. Fluids 2011, 23, 031702. [Google Scholar] [CrossRef]
- Rojas-Cárdenas, M.; Perrier, P.; Graur, I.; Méolans, J.G. Time-dependent experimental analysis of a thermal transpiration rarefied gas flow. Phys. Fluids 2013, 25, 72001. [Google Scholar] [CrossRef]
- Sharipov, F. Data on the velocity slip and temperature jump on a gas-solid interface. J. Phys. Chem. Ref. Data 2011, 40, 023101. [Google Scholar] [CrossRef]
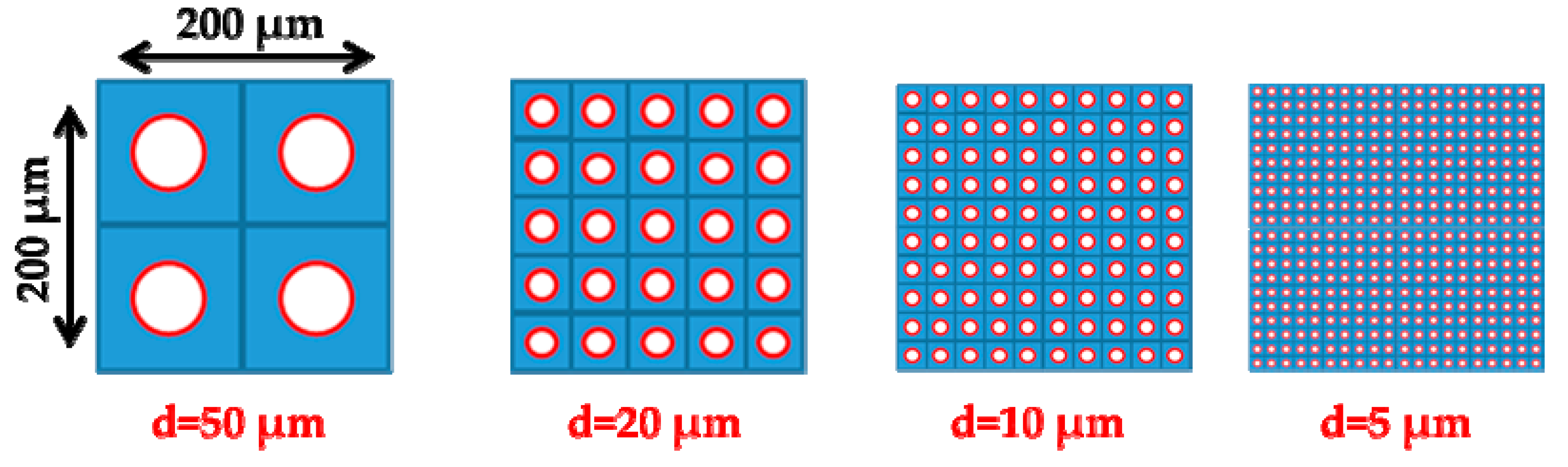

| Total Layout Area a × a (μm × μm) | Microchannel Diameter d (μm) | Number n of Parallel Microchannels |
|---|---|---|
| 200 × 200 | 50 | 4 |
| 200 × 200 | 20 | 25 |
| 200 × 200 | 10 | 100 |
| 200 × 200 | 5 | 400 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López Quesada, G.; Tatsios, G.; Valougeorgis, D.; Rojas-Cárdenas, M.; Baldas, L.; Barrot, C.; Colin, S. Design Guidelines for Thermally Driven Micropumps of Different Architectures Based on Target Applications via Kinetic Modeling and Simulations. Micromachines 2019, 10, 249. https://doi.org/10.3390/mi10040249
López Quesada G, Tatsios G, Valougeorgis D, Rojas-Cárdenas M, Baldas L, Barrot C, Colin S. Design Guidelines for Thermally Driven Micropumps of Different Architectures Based on Target Applications via Kinetic Modeling and Simulations. Micromachines. 2019; 10(4):249. https://doi.org/10.3390/mi10040249
Chicago/Turabian StyleLópez Quesada, Guillermo, Giorgos Tatsios, Dimitris Valougeorgis, Marcos Rojas-Cárdenas, Lucien Baldas, Christine Barrot, and Stéphane Colin. 2019. "Design Guidelines for Thermally Driven Micropumps of Different Architectures Based on Target Applications via Kinetic Modeling and Simulations" Micromachines 10, no. 4: 249. https://doi.org/10.3390/mi10040249
APA StyleLópez Quesada, G., Tatsios, G., Valougeorgis, D., Rojas-Cárdenas, M., Baldas, L., Barrot, C., & Colin, S. (2019). Design Guidelines for Thermally Driven Micropumps of Different Architectures Based on Target Applications via Kinetic Modeling and Simulations. Micromachines, 10(4), 249. https://doi.org/10.3390/mi10040249







