Mechanophenotyping of B16 Melanoma Cell Variants for the Assessment of the Efficacy of (-)-Epigallocatechin Gallate Treatment Using a Tapered Microfluidic Device
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Sample
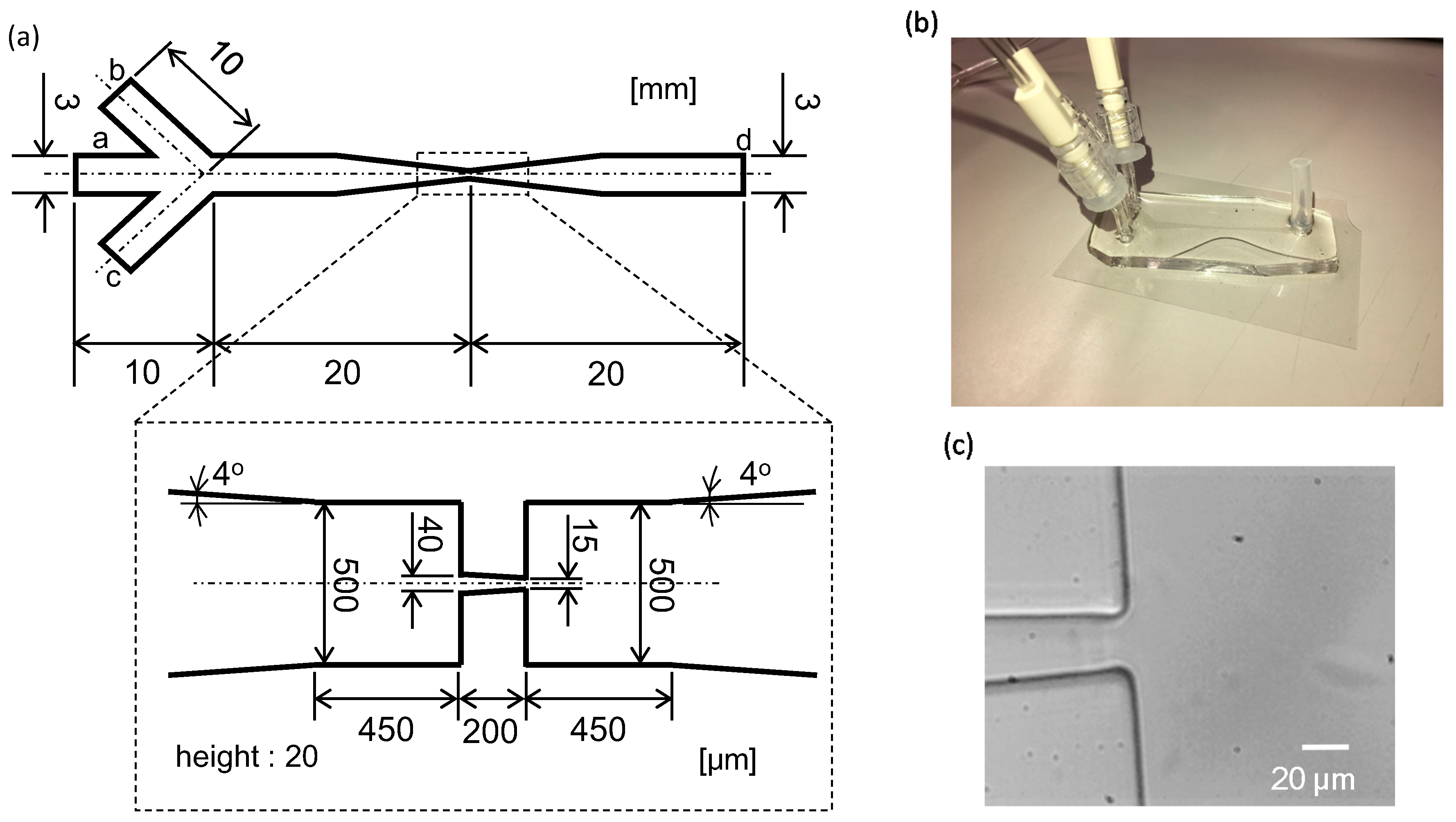
2.2. Microflow Channel
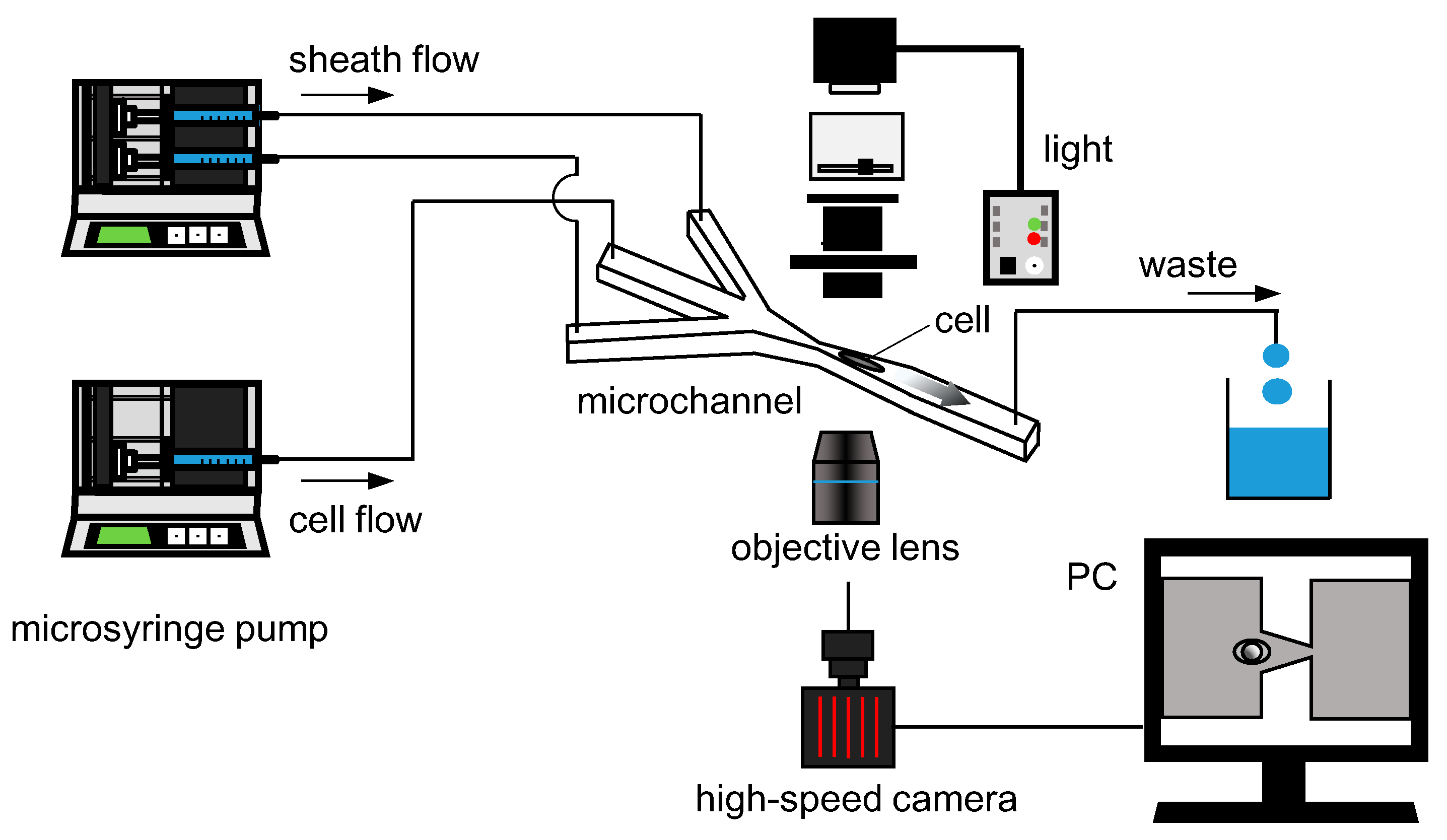
2.3. Experimental Setup
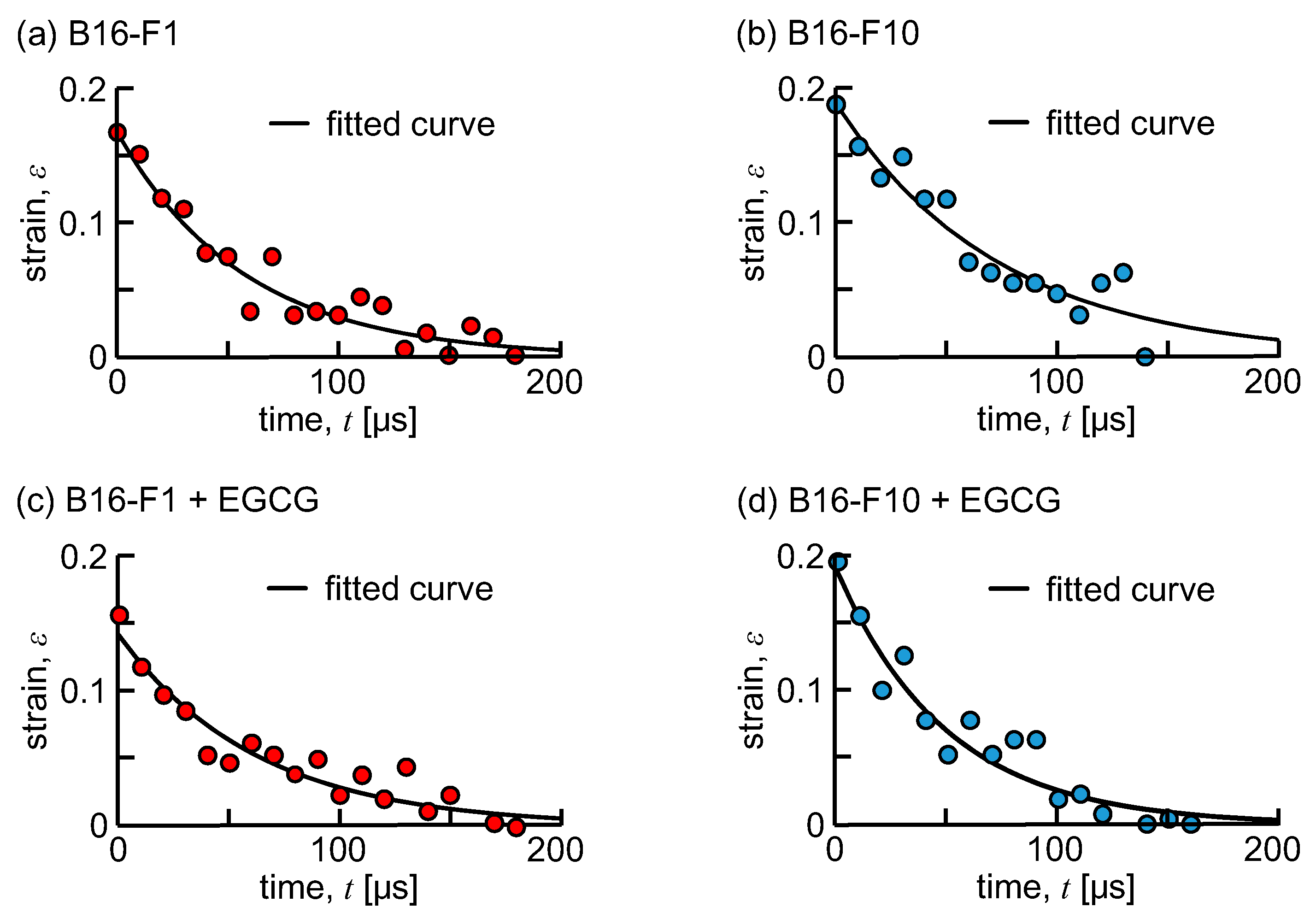
2.4. Mechanical Characterization of a Cell
2.5. EGCG Treatment
2.6. Staining
2.7. Statistical Method
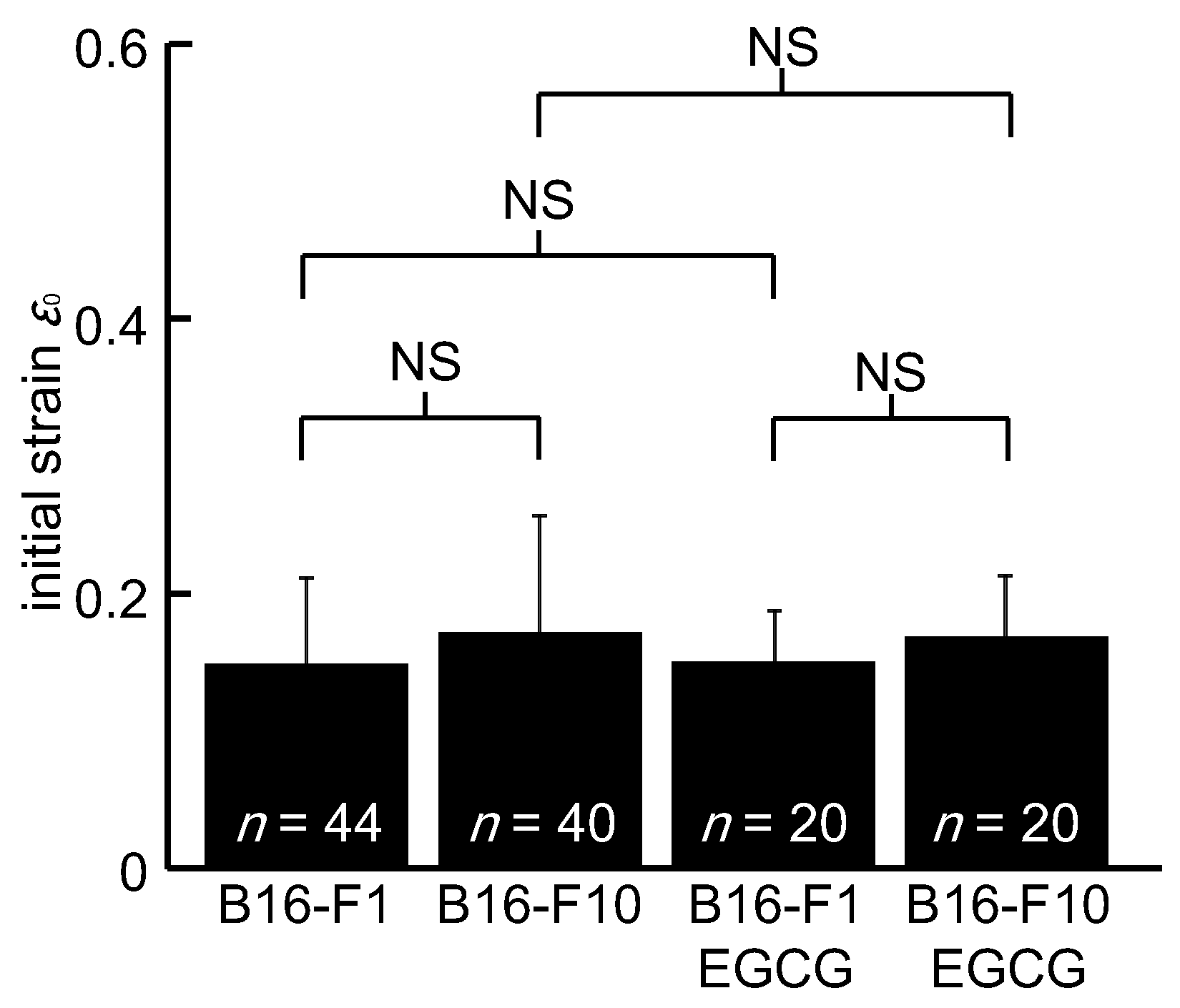
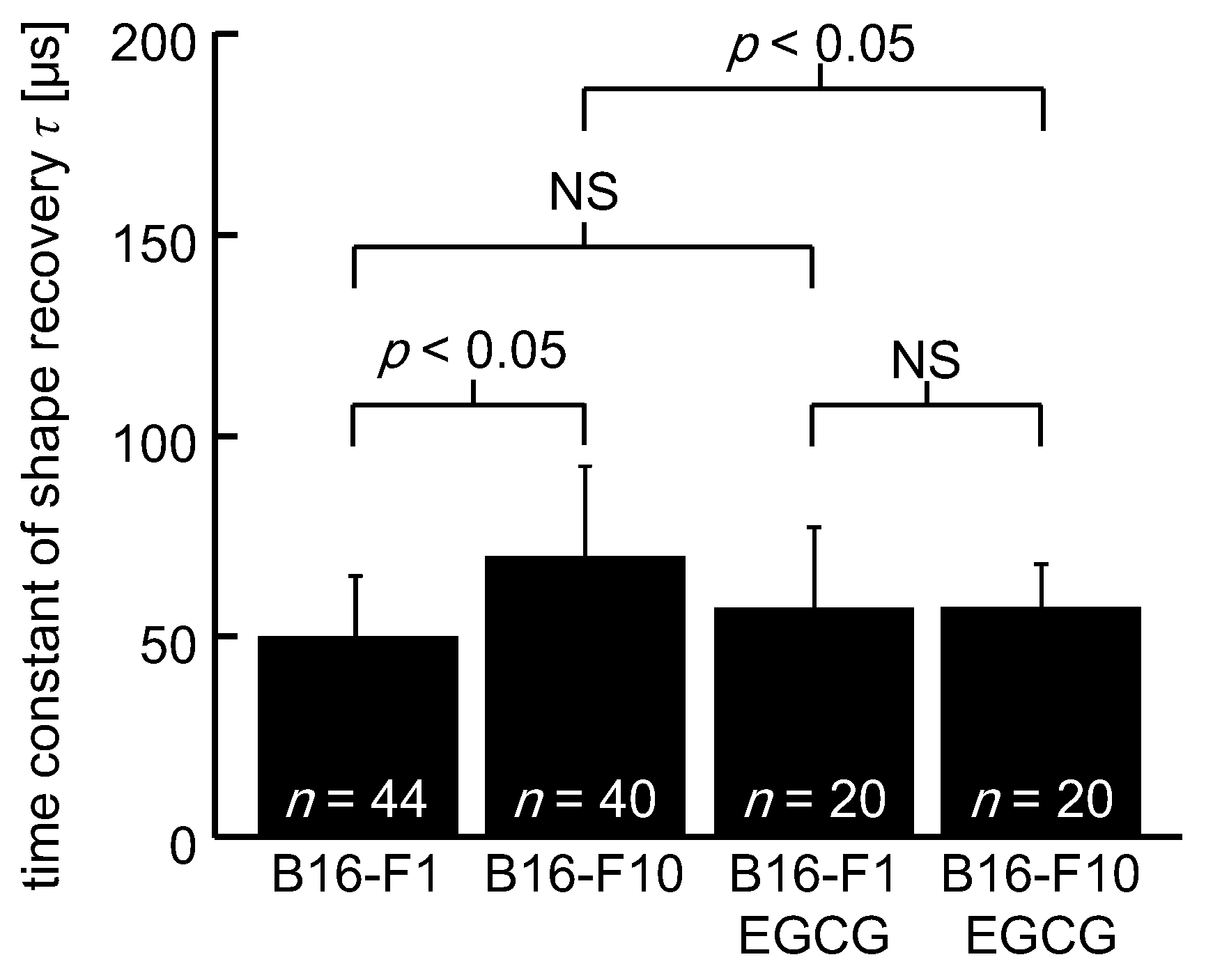
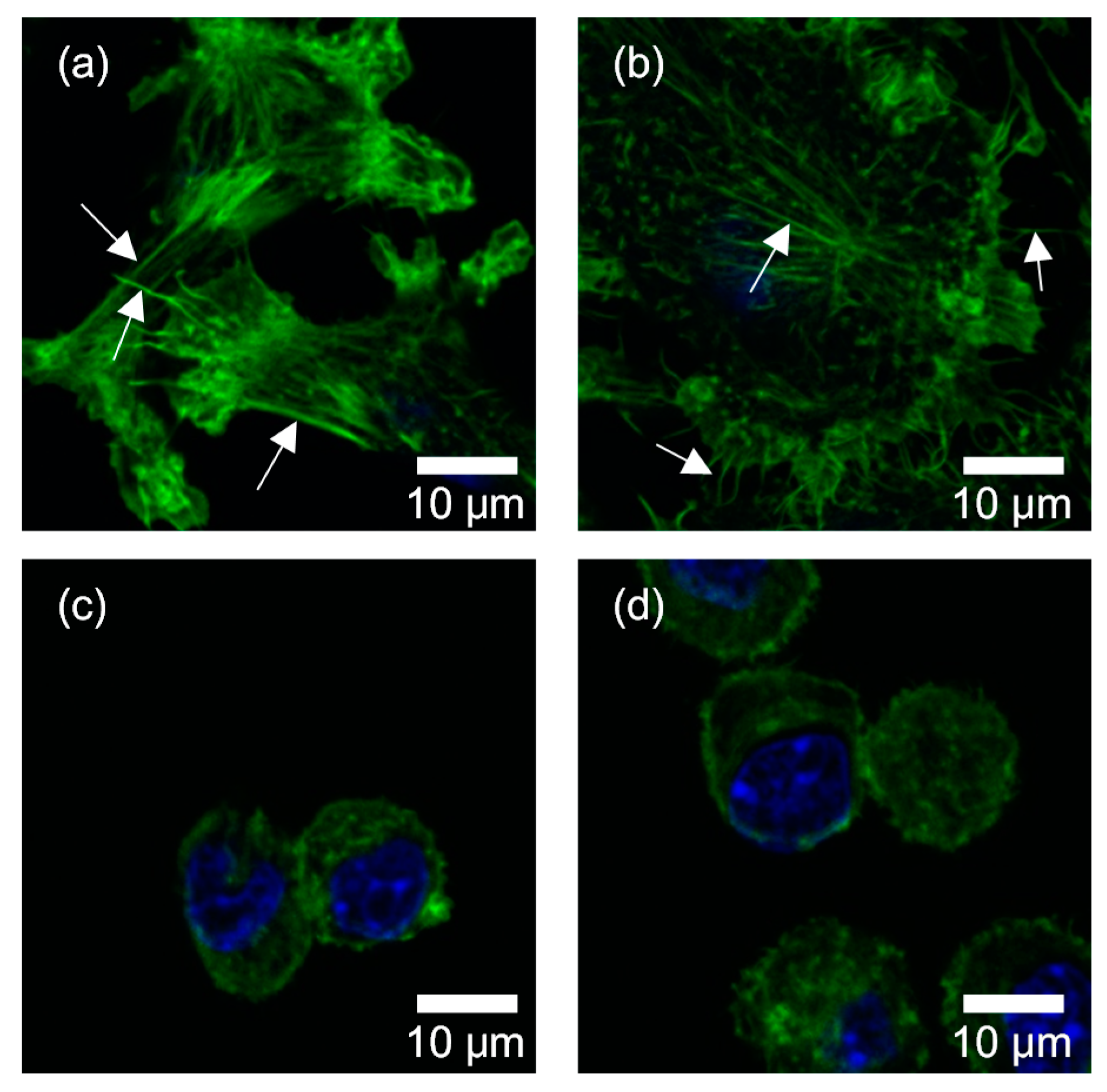
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Orr, F.W.; Wang, H.H.; Lafrenie, R.M.; Scherbarth, S.; Nance, D.M. Interactions between cancer cells and the endothelium in metastasis. J. Pathol. 2000, 190, 310–329. [Google Scholar] [CrossRef]
- Eger, A.; Mikulits, W. Models of epithelial–mesenchymal transition. Drug Dis. Today Dis. Models 2005, 2, 57–63. [Google Scholar] [CrossRef]
- Chambers, A.F.; Groom, A.C.; MacDonald, I.C. Dissemination and growth of cancer cells in metastatic sites. Nat. Rev. Cancer 2002, 2, 563–572. [Google Scholar] [CrossRef]
- Alibert, C.; Goud, B.; Manneville, J.B. Are cancer cells really softer than normal cells? Biol. Cell 2017, 109, 167–189. [Google Scholar] [CrossRef]
- Jonietz, E. Mechanics: The forces of cancer. Nature 2012, 491, S56–S57. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic force microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef]
- Hochmuth, R.M. Micropipette aspiration of living cells. J. Biomech. 2000, 33, 15–22. [Google Scholar] [CrossRef]
- Cross, S.E.; Jin, Y.S.; Rao, J.Y.; Gimzewski, J.K. Nanomechanical analysis of cells from cancer patients. Nat. Nanotechnol. 2007, 2, 780–783. [Google Scholar] [CrossRef] [PubMed]
- Suresh, S. Nanomedicine: Elastic clues in cancer detection. Nat. Nanotechnol. 2007, 2, 748–749. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, K.; Soc, J.R. Optical tweezers for single cells. J. R. Soc. Interface 2008, 5, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Remmerbach, T.W.; Wottawah, F.; Dietrich, J.; Lincoln, B.; Wittekind, C.; Guck, J. Oral cancer diagnosis by mechanical phenotyping. Cancer Res. 2009, 69, 1728–1732. [Google Scholar] [CrossRef]
- Swaminathan, V.; Mythereye, K.; O’Brien, E.T.; Berchuck, A.; Blobe, G.C.; Superfine, R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell line. Cancer Res. 2011, 71, 5075–5080. [Google Scholar] [CrossRef] [PubMed]
- Plodinec, M.; Loparic, M.; Monnier, C.A.; Obermann, E.C.; Zanetti-Dallenbach, R.; Oertle, P.; Hyotyla, J.T.; Aebi, U.; Bentires-Alj, M.; Lim, R.Y.H.; et al. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 2012, 7, 757–765. [Google Scholar] [CrossRef]
- Watanabe, T.; Kuramochi, H.; Takahashi, A.; Imai, K.; Katsuta, N.; Nakayama, T.; Fujiki, H.; Suganuma, M. Higher cell stiffness indicating lower metastatic potential in B16 melanoma cell variants and in (-)-epigallocatechin gallate-treated cells. J. Cancer Res. Clin. Oncol. 2012, 138, 859–866. [Google Scholar] [CrossRef]
- Hayashi, K.; Iwata, M. Stiffness of cancer cells measured with an AFM indentation method. J. Mech. Behav. Biomed. Mater. 2015, 49, 105–111. [Google Scholar] [CrossRef]
- Darling, E.M.; Di Carlo, D. High-throughput assessment of cellular mechanical properties. Annu. Rev. Biomed. Eng. 2015, 17, 35–62. [Google Scholar] [CrossRef]
- Chaudhuri, P.K.; Low, B.C.; Lim, C.T. Mechanobiology of tumor growth. Chem. Rev. 2018, 118, 6499–6515. [Google Scholar] [CrossRef] [PubMed]
- Bento, D.; Rodrigues, R.O.; Faustino, V.; Pinho, D.; Fernandes, C.S.; Pereira, A.I.; Garcia, V.; Miranda, J.M.; Lima, R. Deformation of red blood cells, air bubbles, and droplets in microfluidic devices: Flow visualizations and measurements. Micromachines 2018, 9, 151. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.J.; Yobas, L.; Lee, G.Y.H.; Ong, C.N.; Lim, C.T. Microdevice for the isolation and enumeration of cancer cells from blood. Biomed. Microdevices 2009, 11, 883–892. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Sun, Y. Microfluidic approaches for cancer cell detection, characterization, and separation. Lab Chip 2012, 12, 1753–1767. [Google Scholar] [CrossRef]
- Ma, Y.H.V.; Middleton, K.; You, L.; Sun, Y. A review of microfluidic approaches for investigating cancer extravasation during metastasis. Microsys. Nanoeng. 2018, 4, 17104. [Google Scholar] [CrossRef]
- Hou, H.W.; Warkiani, M.E.; Khoo, B.L.; Li, Z.R.; Soo, R.A.; Tan, D.S.W.; Lim, W.T.; Han, J.; Bhagat, A.A.S.; Lim, C.T. Isolation and retrieval of circulating tumor cells using centrifugal forces. Sci. Rep. 2013, 3, 1259. [Google Scholar] [CrossRef]
- Khoo, B.L.; Warkiani, M.E.; Tan, D.S.W.; Bhagat, A.A.S.; Irwin, D.; Lau, D.P.; Lim, A.S.T.; Lim, K.H.; Krisna, S.S.; Lim, W.T.; et al. Clinical validation of an ultra high-throughput spiral microfluidics for the detection and enrichment of viable circulating tumor cells. PLoS ONE 2014, 9, e99409. [Google Scholar] [CrossRef]
- Tse, H.T.; Gossett, D.R.; Moon, Y.S.; Masaeli, M.; Sohsman, M.; Ying, Y.; Mislick, K.; Adams, R.P.; Rao, J.; Di Carlo, D. Quantitative diagnosis of malignant pleural effusions by single-cell mechanophenotyping. Sci. Transl. Med. 2013, 5, 212ra163. [Google Scholar] [CrossRef]
- Gossett, D.R.; Henry, T.K.; Lee, S.A.; Ying, Y.; Lindgrenc, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Carlo, D.D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar] [CrossRef]
- Taniguchi, S.; Fujiki, H.; Kobayashi, H.; Go, H.; Miyado, K.; Sadano, H.; Shimokawa, R. Effect of (-)-epigallocatechin gallate; the main constituent of green tea; on lung metastasis with mouse B16 melanoma cell lines. Cancer Lett. 1992, 65, 51–54. [Google Scholar] [CrossRef]
- Kuzuhara, T.; Sei, Y.; Yamaguchi, K.; Suganuma, M.; Fujiki, H. DNA and RNA as new binding targets of green tea catechins. J. Biol. Chem. 2006, 281, 17446–17456. [Google Scholar] [CrossRef]
- Sah, J.F.; Balasubramanian, S.; Eckert, R.L.; Rorke, E.A. Epigallocatechin-3-gallate inhibits epidermal growth factor receptor signaling pathway. Evidence for direct inhibition of ERK1/2 and AKT kinases. J. Biol. Chem. 2004, 279, 12755–12762. [Google Scholar] [CrossRef] [PubMed]
- Rawangkan, A.; Wongsirisin, P.; Namiki, K.; Iida, K.; Kobayashi, Y.; Shimizu, Y.; Fujiki, H.; Suganuma, M. Green tea catechin is an alternative immune checkpoint inhibitor that inhibits PD-L1 expression and lung tumor growth. Molecules 2018, 23, 2071. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, H.; Nagayama, M.; Tanaka, T.; Furusawa, M.; Kashimata, M.; Takeuchi, H. Membrane-rigidifying effects of anti-cancer dietary factors. Biofactors 2002, 16, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.Y.; Wu, C.C.; Hsu, H.Y.; Chuang, H.Y.; Huang, S.Y.; Tsai, C.H.; Chang, Y.; Tsao, G.S.W.; Chen, C.L.; Chen, J.Y. EGCG inhibits proliferation, invasiveness and tumor growth by up-regulation of adhesion molecules, suppression of gelatinases activity, and induction of apoptosis in nasopharyngeal carcinoma cells. Int. J. Mol. Sci. 2015, 16, 2530–2558. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, A.; Watanabe, T.; Mondal, A.; Suzuki, K.; Kururu-Kanno, M.; Li, Z.; Yamazaki, T.; Fujiki, H.; Suganuma, M. Mechanism-based inhabitation of cancer metastasis with (-)-epigallocatechin gallate. Biochem. Biophys. Res. Commun. 2014, 443, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Fidler, I.J. Selection of successive tumour lines for metastasis. Nat. New Biol. 1973, 242, 148–149. [Google Scholar] [CrossRef] [PubMed]
- Poste, G.; Doll, J.; Hart, I.R.; Fidler, I.J. In vitro selection of murine B16 melanoma variants with enhanced tissue-invasive properties. Cancer Res. 1980, 40, 1636–1644. [Google Scholar] [PubMed]
- Nakamura, K.; Yoshikawa, N.; Yamaguchi, Y.; Kagota, S.; Shinozuka, K.; Kunitomo, M. Characterization of mouse melanoma cell lines by their mortal malignancy using an experimental metastatic model. Life Sci. 2002, 70, 791–798. [Google Scholar] [CrossRef]
- Lee, S.S.; Yim, Y.; Ahn, K.H.; Lee, S.J. Extensional flow-based assessment of red blood cell deformability using hyperbolic converging microchannel. Biomed. Microdevices 2009, 11, 1021–1027. [Google Scholar] [CrossRef]
- Yaginuma, T.; Oliveira, M.S.N.; Lima, R.; Ishikawa, T.; Yamaguchi, T. Human red blood cell behavior under homogeneous extensional flow in a hyperbolic-shaped microchannel. Biomicrofluidics 2013, 7, 054110. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, R.O.; Lopes, R.; Pinho, D.; Pereira, A.I.; Garcia, V.; Gassmann, S.; Sousa, P.C.; Lima, R. In vitro blood flow and cell-free layer in hyperbolic microchannels: Visualizations and measurements. BioChip J. 2016, 10, 9–15. [Google Scholar] [CrossRef]
- TruongVo, T.N.; Kennedy, R.M.; Chen, H.; Chen, A.; Berndt, A.; Agarwal, M.; Zhu, L.; Nakshatri, H.; Wallace, J.; Na, S. Microfluidic channel for characterizing normal and breast cancer cells. J. Micromech. Microeng. 2017, 27, 035017. [Google Scholar] [CrossRef]
- Yoshizawa, S.; Horiuchi, T.; Fujiki, H.; Yoshida, T.; Okuda, T.; Sugimura, T. Antitumor promoter activity of (-)-epigallocatechin gallate, the main constituent of “tannin” in green tea. Phytother. Res. 1987, 1, 44–47. [Google Scholar] [CrossRef]
- Fujita, Y.; Yamane, T.; Tanaka, M.; Kuwata, K.; Okuzumi, J.; Takahashi, T.; Fujiki, H.; Okuda, T. Inhibitory effect of (-)-epigallocatechin gallate on carcinogenesis with IV-ethyl-IV’-nitro-N-nitrosoguanidine in mouse duodenum. Jpn. J. Cancer Res. 1989, 80, 503–505. [Google Scholar] [CrossRef]
- Bettuzzi, S.; Brausi, M.; Rizzi, F.; Castagnetti, G.; Peracchia, G.; Corti, A. Chemoprevention of human prostate cancer by oral administration of green tea catechins in volunteers with highgrade prostate intraepithelial neoplasia: A preliminary report from a one-year proof-of-principle study. Cancer Res. 2006, 66, 1234–1240. [Google Scholar] [CrossRef]
- Tsao, A.S.; Liu, D.; Martin, J.; Tang, X.M.; Lee, J.J.; El-Naggar, A.K.; Wistuba, I.; Culotta, K.S.; Mao, L.; Gillenwater, A.; et al. Phase II randomized, placebocontrolled trial of green tea extract in patients with high-risk oral premalignant lesions. Cancer Prev. Res. 2009, 2, 931–941. [Google Scholar] [CrossRef] [PubMed]
- Singh, B.N.; Shankar, S.; Srivastava, R.K. Green tea catechin, epigallocatechin-3-gallate (EGCG): Mechanisms, perspectives and clinical applications. Biochem. Pharmacol. 2011, 82, 1807–1821. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.S.; Wang, X. Green tea and cancer prevention. Nutr. Cancer 2010, 62, 931–937. [Google Scholar] [CrossRef]
- Fujiki, H.; Okuda, T. (−)-Epigallocatechin gallate. Drugs Future 1992, 17, 462–464. [Google Scholar] [CrossRef]
- Raj, A.; Dixit, M.; Doble, M.; Sen, A.K. A combined experimental and theoretical approach towards mechanophenotyping of biological cells using a constricted microchannel. Lab Chip 2017, 17, 3704–3716. [Google Scholar] [CrossRef]
- Zhou, J.; Papautsky, I. Fundamentals of inertial focusing in microchannels. Lab Chip 2013, 13, 1121–1132. [Google Scholar] [CrossRef]
- Masaeli, M.; Sollier, E.; Amini, H.; Mao, W.; Camacho, K.; Doshi, N.; Mitragotri, S.; Alexeev, A.; Di Carlo, D. Continuous inertial focusing and separation of particles by shape. Phys. Rev. X 2012, 2, 031017. [Google Scholar] [CrossRef]
- Peeters, E.A.G.; Bouten, C.V.C.; Oomens, C.W.J.; Bader, D.L.; Snoeckx, L.H.E.H.; Baajiens, F.P.T. Anisotropic, three-dimensional deformation of single attached cells under compression. Ann. Biomed. Eng. 2004, 32, 1443–1452. [Google Scholar] [CrossRef]
- Hu, S.; Eberhard, L.; Chen, J.; Love, J.L.; Butler, J.P.; Fredberg, J.J.; Whitesides, G.M.; Wang, N. Mechanical anisotropy of adherent cells probed by a three-dimensional magnetic twisting device. Am. J. Physiol. Cell Physiol. 2004, 287, C1184–C1191. [Google Scholar] [CrossRef]
- Kumar, S.; Mexwell, I.Z.; Heisterkamp, A.; Polte, T.R.; Lele, T.P.; Salanga, M.; Mazur, E.; Ingber, D.E. Viscoelastic retraction of single living stress fibers and its imoact on cell shape, cytoskeletal organization, and extracellular matrix mechanics. Biophys. J. 2006, 90, 3762–3773. [Google Scholar] [CrossRef] [PubMed]
- Titushkin, I.; Cho, M. Modulation of cellular mechanics during osteongenic differentiation of human mesenchymal stem cells. Biophys. J. 2007, 93, 3693–3702. [Google Scholar] [CrossRef] [PubMed]
- Sadano, H.; Shimokawa-Kuroki, R.; Taniguchi, S. Intracellular localization and biochemical function of variant β-Actin, which inhibits metastasis of B16 melanoma. Cancer Res. 1994, 85, 735–743. [Google Scholar] [CrossRef]
- Zhou, J.; Giridhar, P.V.; Kasper, S.; Papautsky, I. Modulation of rotation-induced lift force for cell filtration in a low aspect ratio microchannel. Biomicrofluidics 2014, 8, 044112. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, F.; Du, J.; Shu, W.; Feng, H.; Xu, X.; Cheng, Y. Rapid isolation of cancer cells using microfluidic deterministic lateral displacement structure. Biomicrofluidics 2013, 7, 0011801. [Google Scholar] [CrossRef]
- Du, G.; Fang, Q.; den Toonder, J.M.J. Microfluidics for cell-based high throughput screening platformsd—A review. Anal. Chim. Acta 2016, 903, 36–50. [Google Scholar] [CrossRef]
- Jiang, J.; Zhao, H.; Shu, W.; Tian, J.; Huang, Y.; Song, Y.; Wang, R.; Li, E.; Slamon, D.; Hou, D.; et al. An integrated microfluidic device for rapid and high-sensitivity analysis of circulating tumor cells. Sci. Rep. 2017, 7, 42612. [Google Scholar] [CrossRef] [PubMed]
- Nivedita, N.; Garg, N.; Lee, A.P.; Papautsky, I. A high throughput microfluidic platform for size-selective enrichment of cell populations in tissue and blood samples. Analyst 2017, 142, 2558–2569. [Google Scholar] [CrossRef]
- Tajikawa, T. Quantitative evaluation of erythrocyte deformability by using micro-visualization technique—Measurement of time constant of shape recovery process as a visco-elastic specification of each blood cells. J. Vis. Soc. Jpn. 2014, 34, 16–21. (In Japanese) [Google Scholar]
- Kohri, S.; Kato, Y.; Tajikawa, T.; Yamamoto, Y.; Bando, K. Measurement of erythrocyte deformability by uniaxial stretching—Measurement of apparent Young’s modulus and time constant of shape recovering. Trans. Jpn. Soc. Med. Biol. Eng. 2015, 53, 1–7. (In Japanese) [Google Scholar]
- Raj, A.; Sen, A.K. Entry and passage behavior of biological cells in a constricted compliant microchannel. R. Soc. Chem. 2018, 8, 20884–20893. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakamura, M.; Ono, D.; Sugita, S. Mechanophenotyping of B16 Melanoma Cell Variants for the Assessment of the Efficacy of (-)-Epigallocatechin Gallate Treatment Using a Tapered Microfluidic Device. Micromachines 2019, 10, 207. https://doi.org/10.3390/mi10030207
Nakamura M, Ono D, Sugita S. Mechanophenotyping of B16 Melanoma Cell Variants for the Assessment of the Efficacy of (-)-Epigallocatechin Gallate Treatment Using a Tapered Microfluidic Device. Micromachines. 2019; 10(3):207. https://doi.org/10.3390/mi10030207
Chicago/Turabian StyleNakamura, Masanori, Daichi Ono, and Shukei Sugita. 2019. "Mechanophenotyping of B16 Melanoma Cell Variants for the Assessment of the Efficacy of (-)-Epigallocatechin Gallate Treatment Using a Tapered Microfluidic Device" Micromachines 10, no. 3: 207. https://doi.org/10.3390/mi10030207
APA StyleNakamura, M., Ono, D., & Sugita, S. (2019). Mechanophenotyping of B16 Melanoma Cell Variants for the Assessment of the Efficacy of (-)-Epigallocatechin Gallate Treatment Using a Tapered Microfluidic Device. Micromachines, 10(3), 207. https://doi.org/10.3390/mi10030207



