Interactive Effects of Rarefaction and Surface Roughness on Aerodynamic Lubrication of Microbearings
Abstract
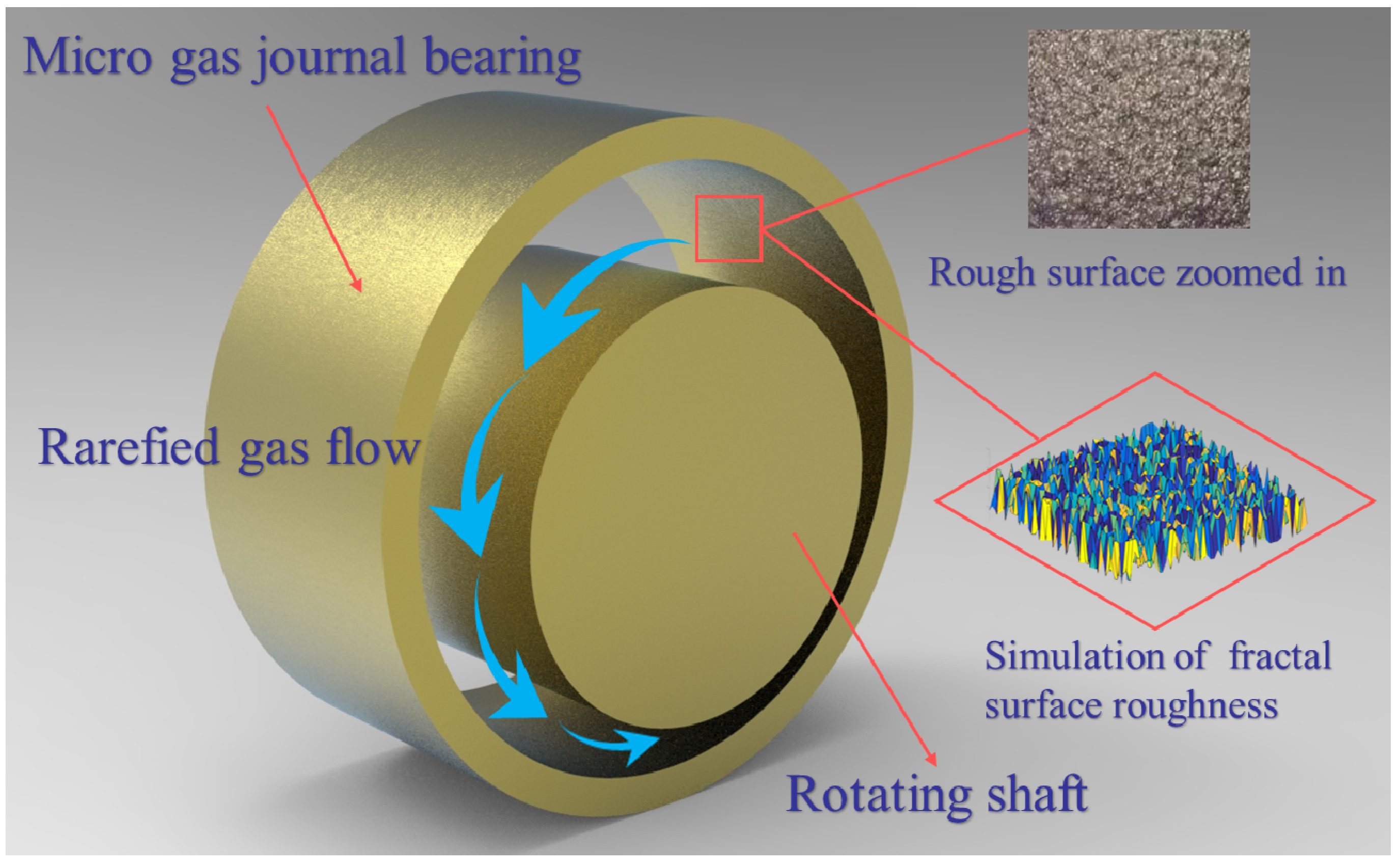
:1. Introduction
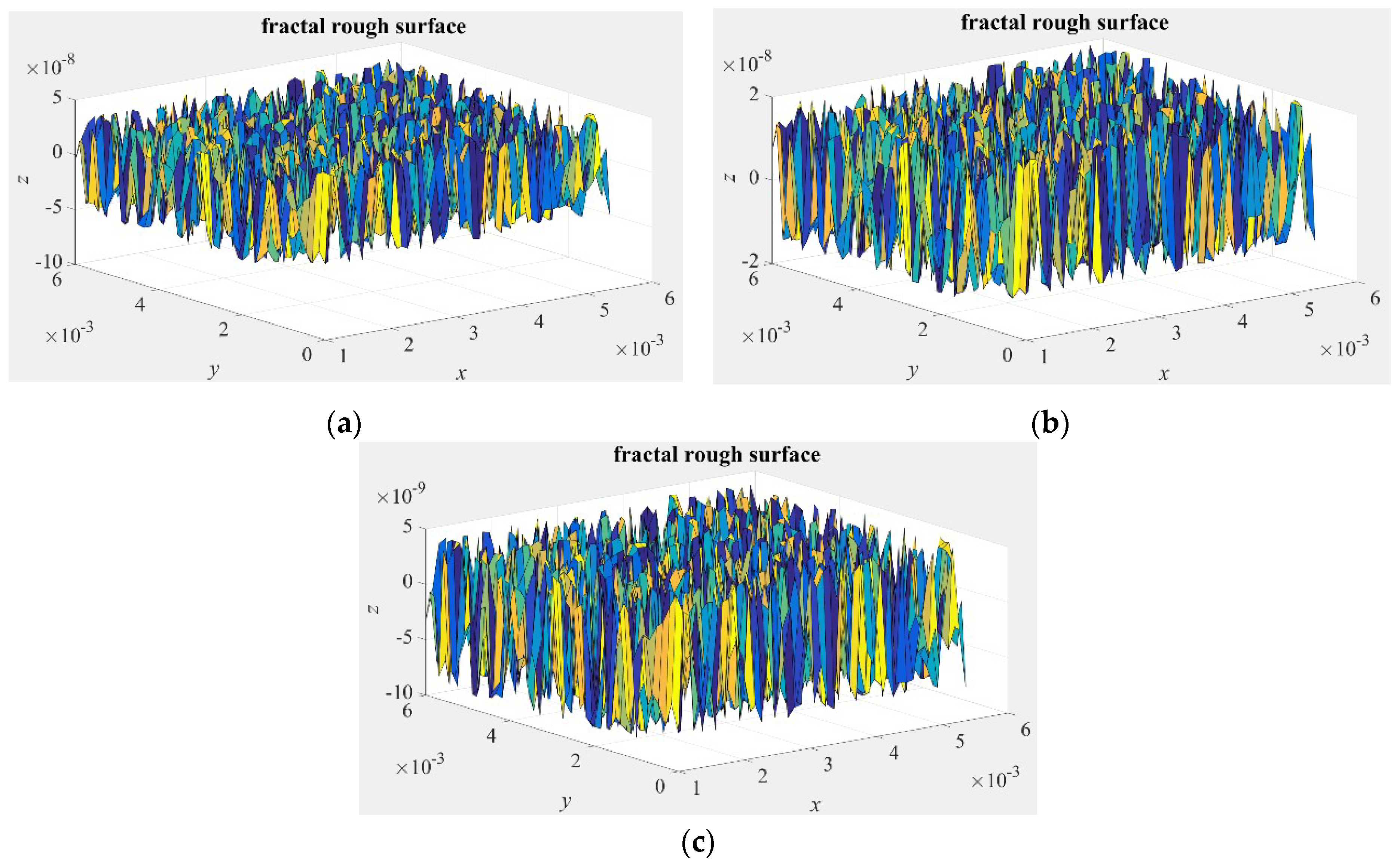
2. Characterization of Fractal Rough Surface
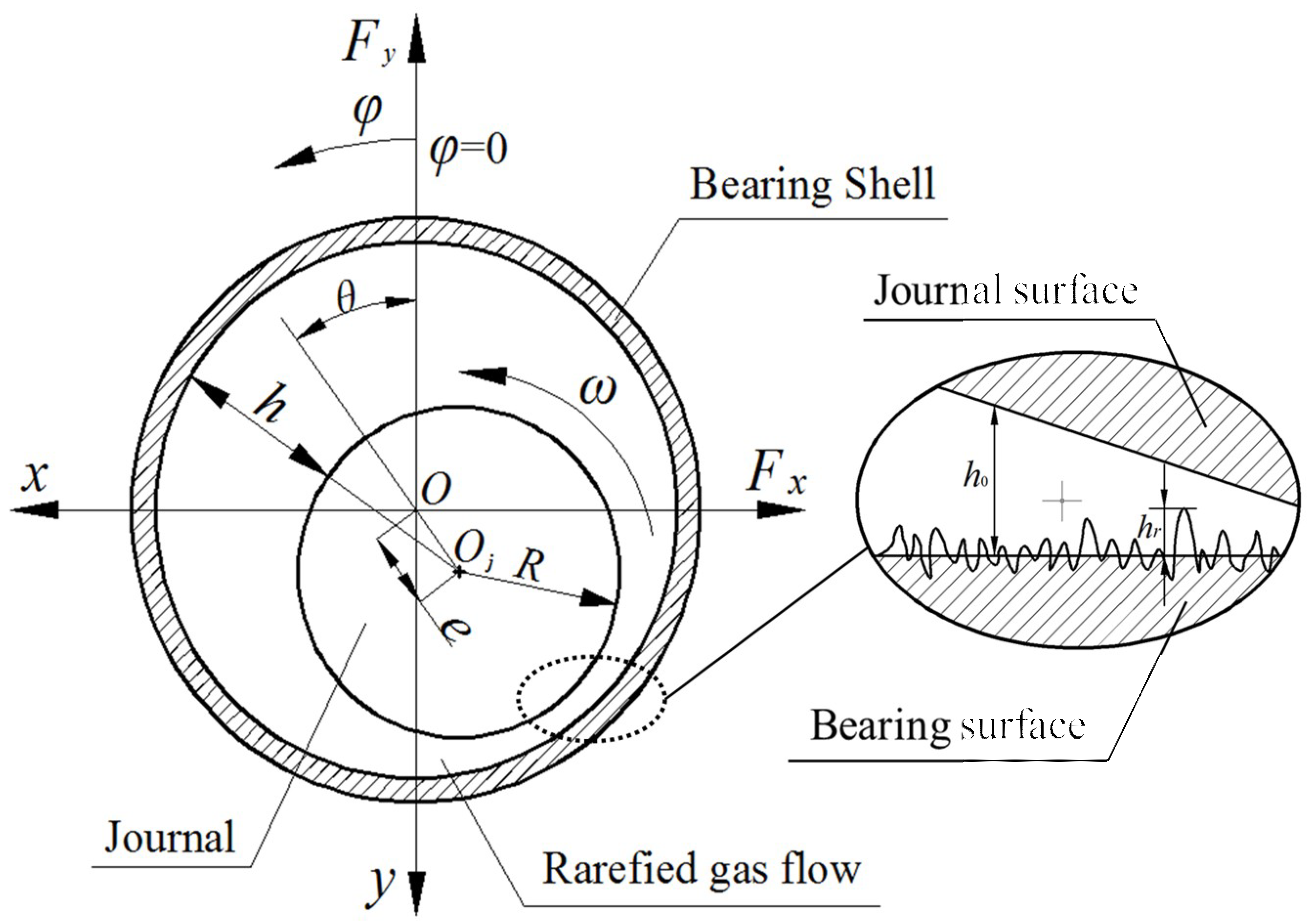
3. Numerical Model and Solution Method
4. Results and Discussion
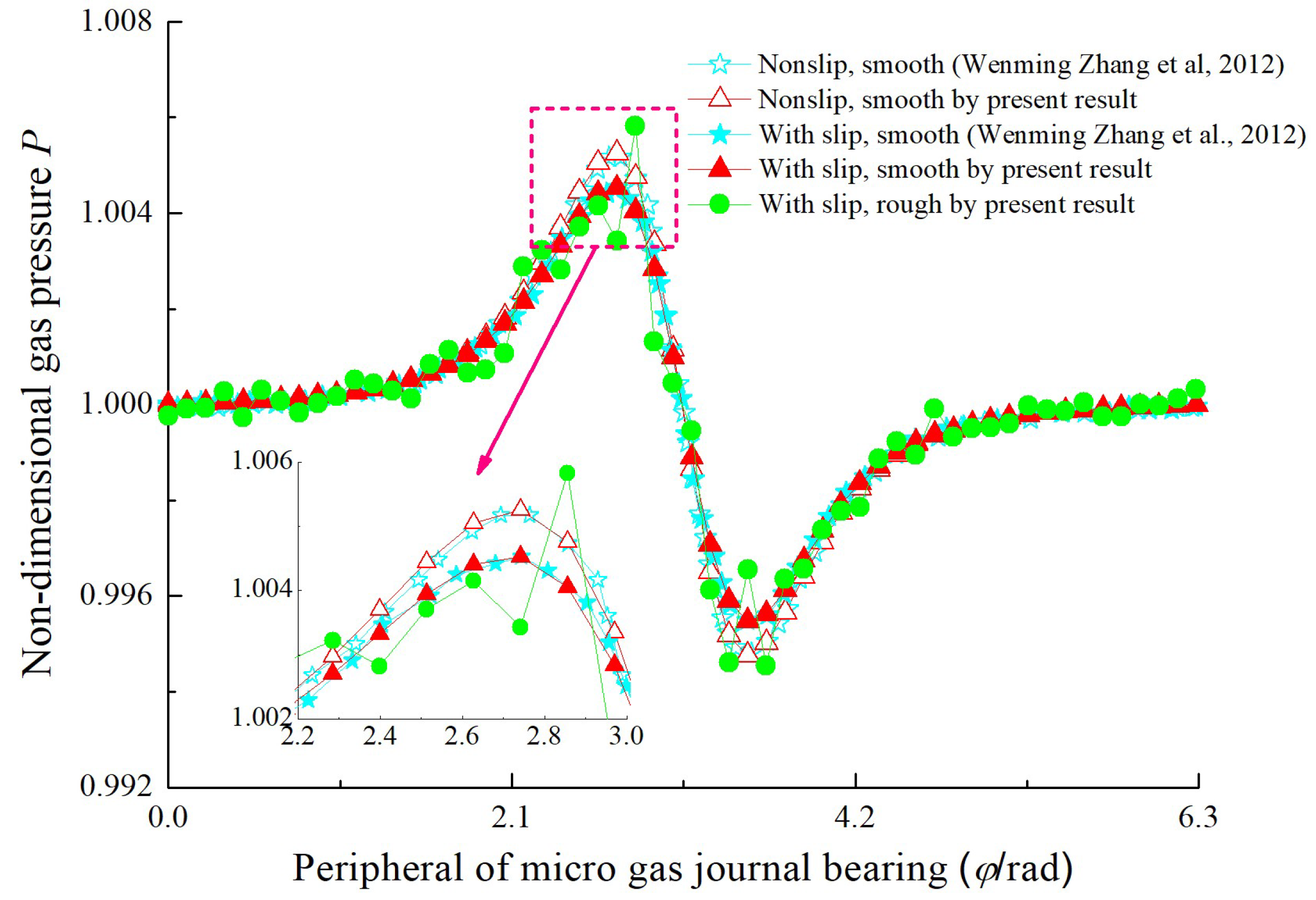
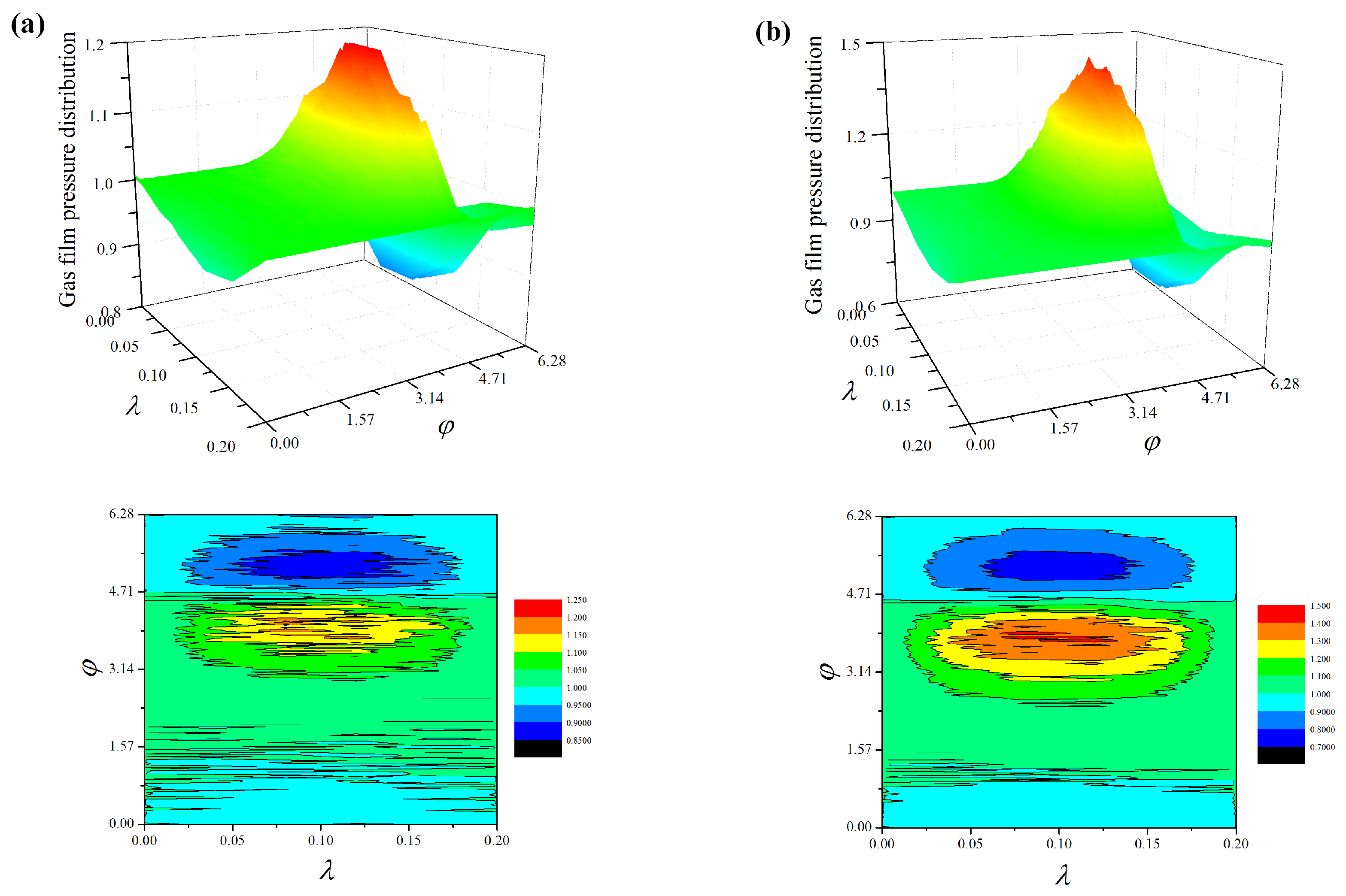
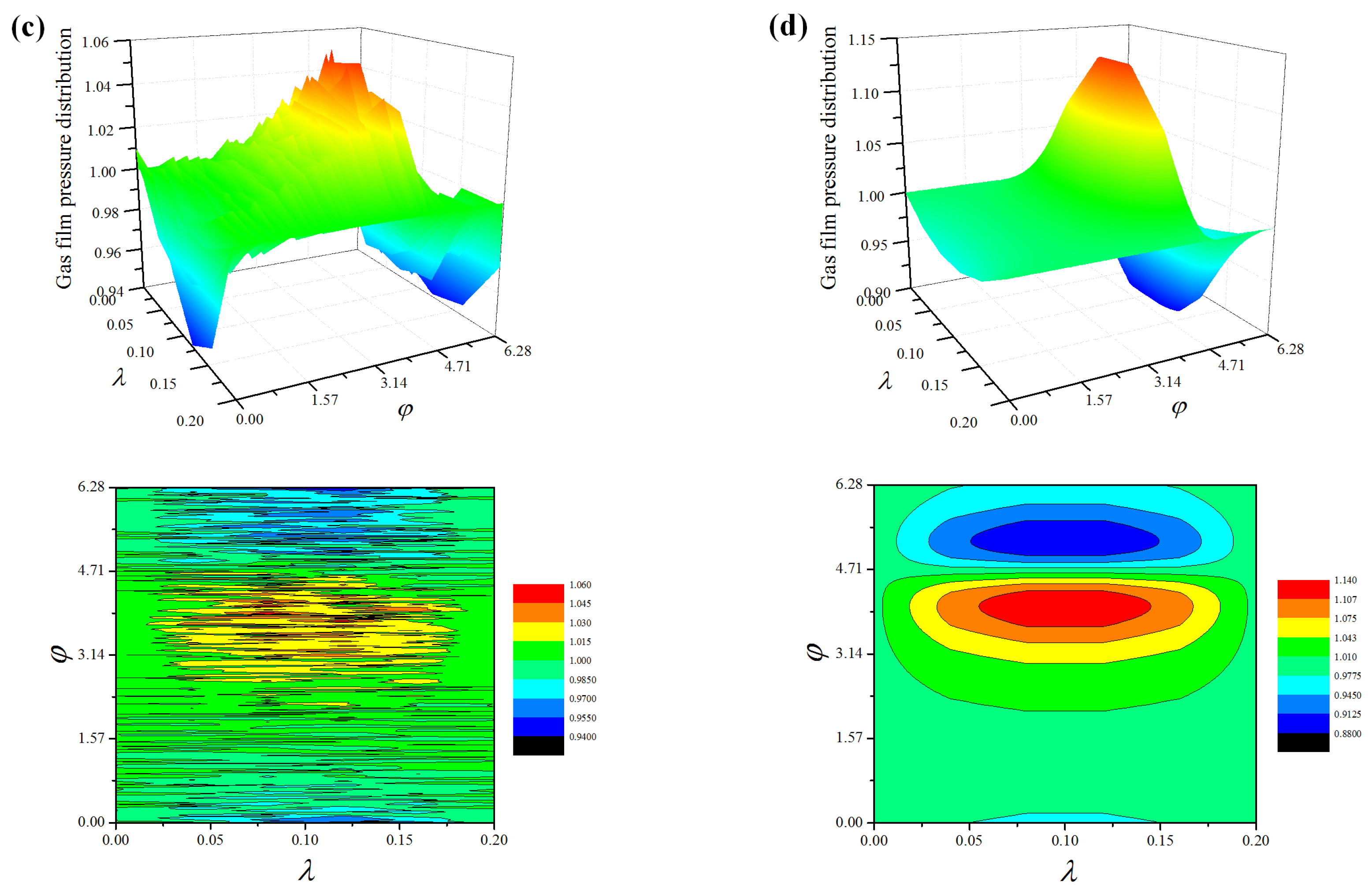
4.1. Steady-State Film Pressure
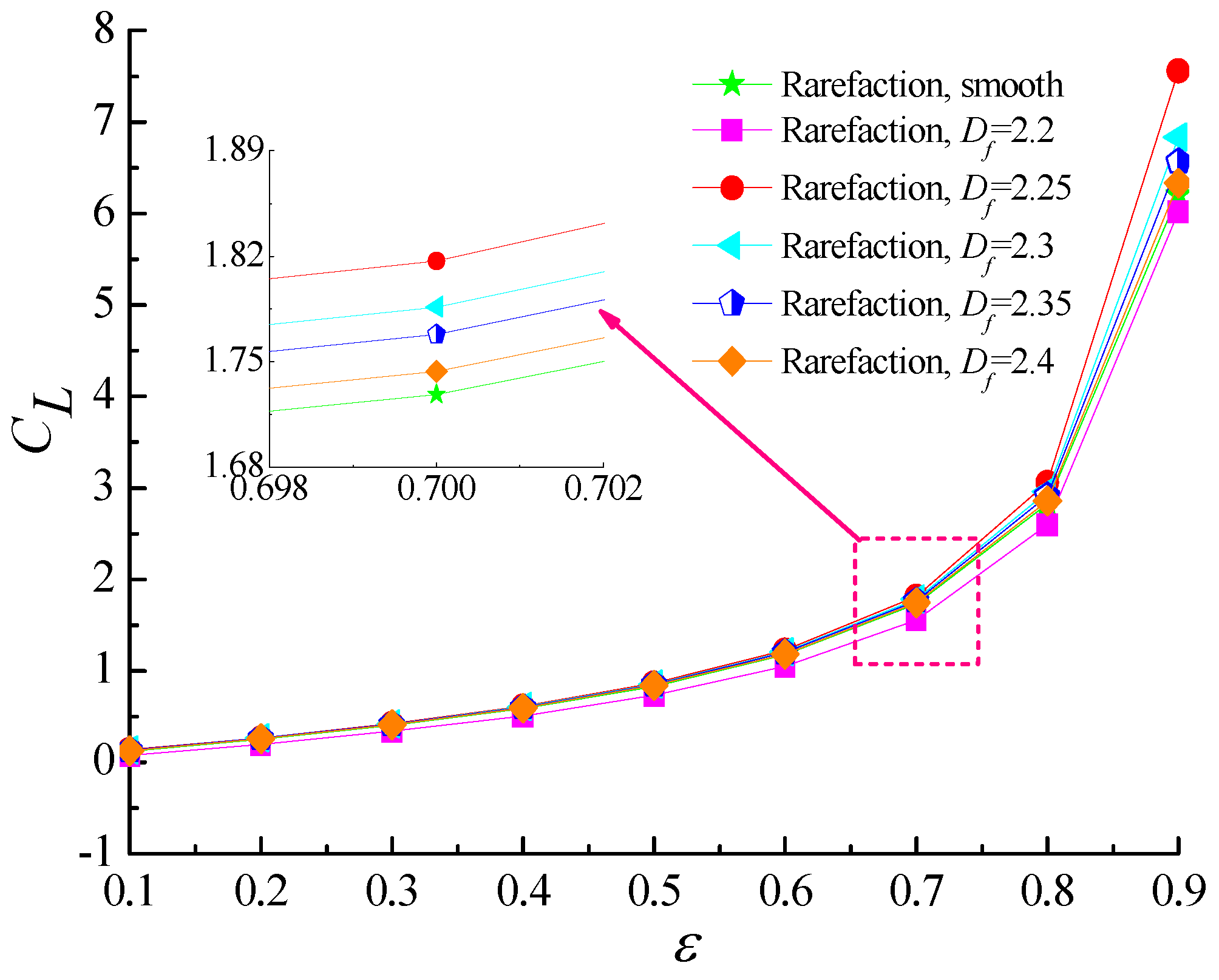
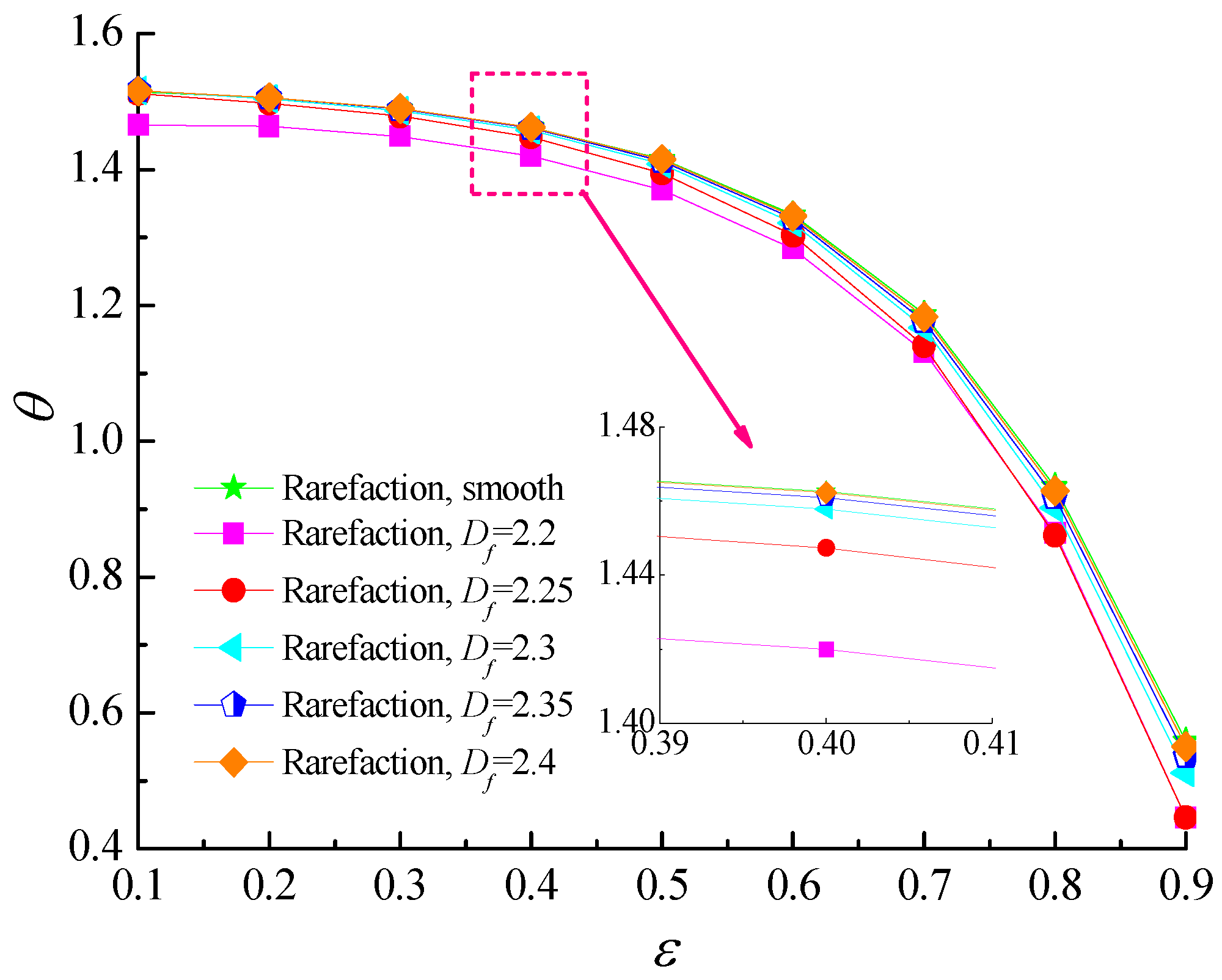
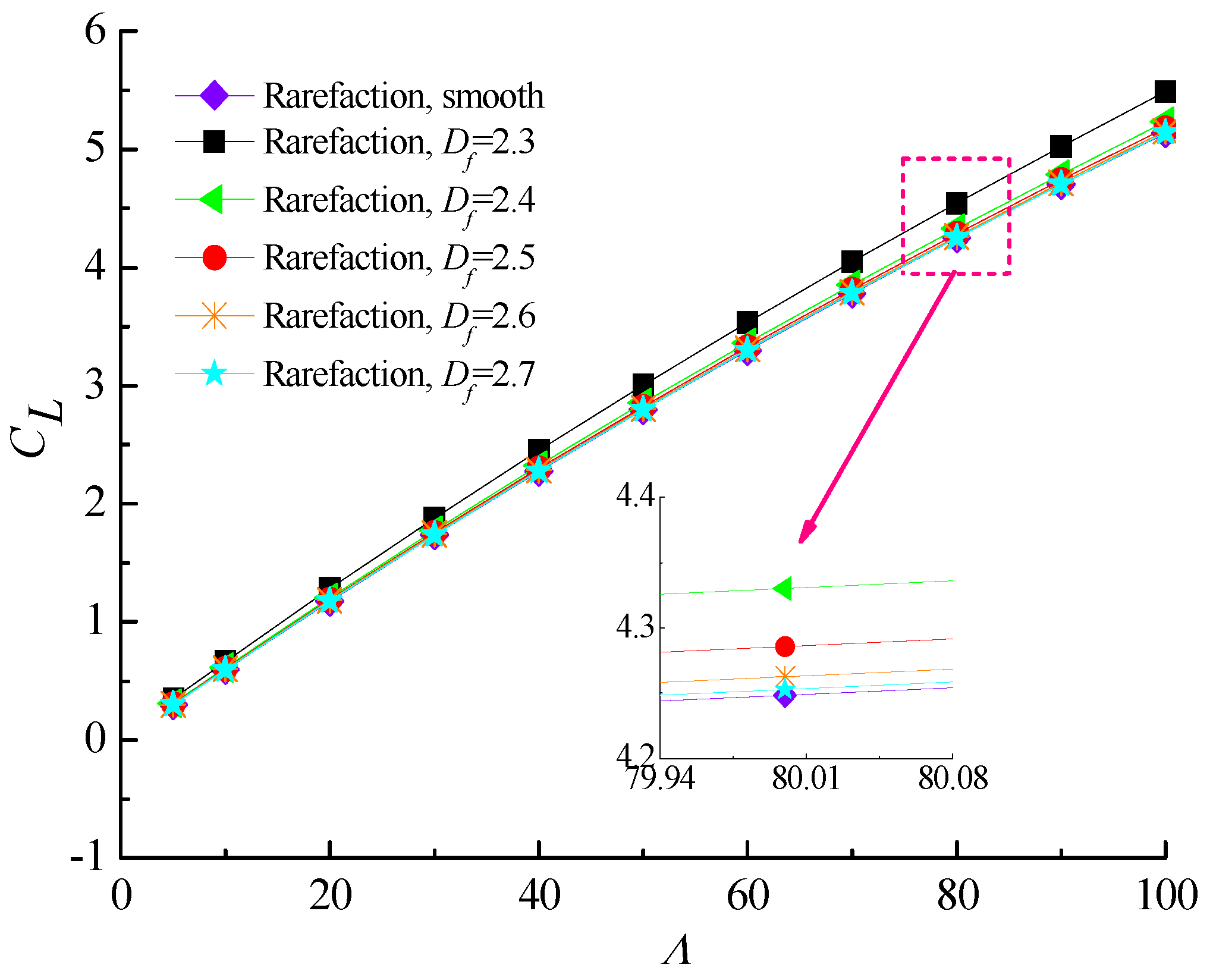
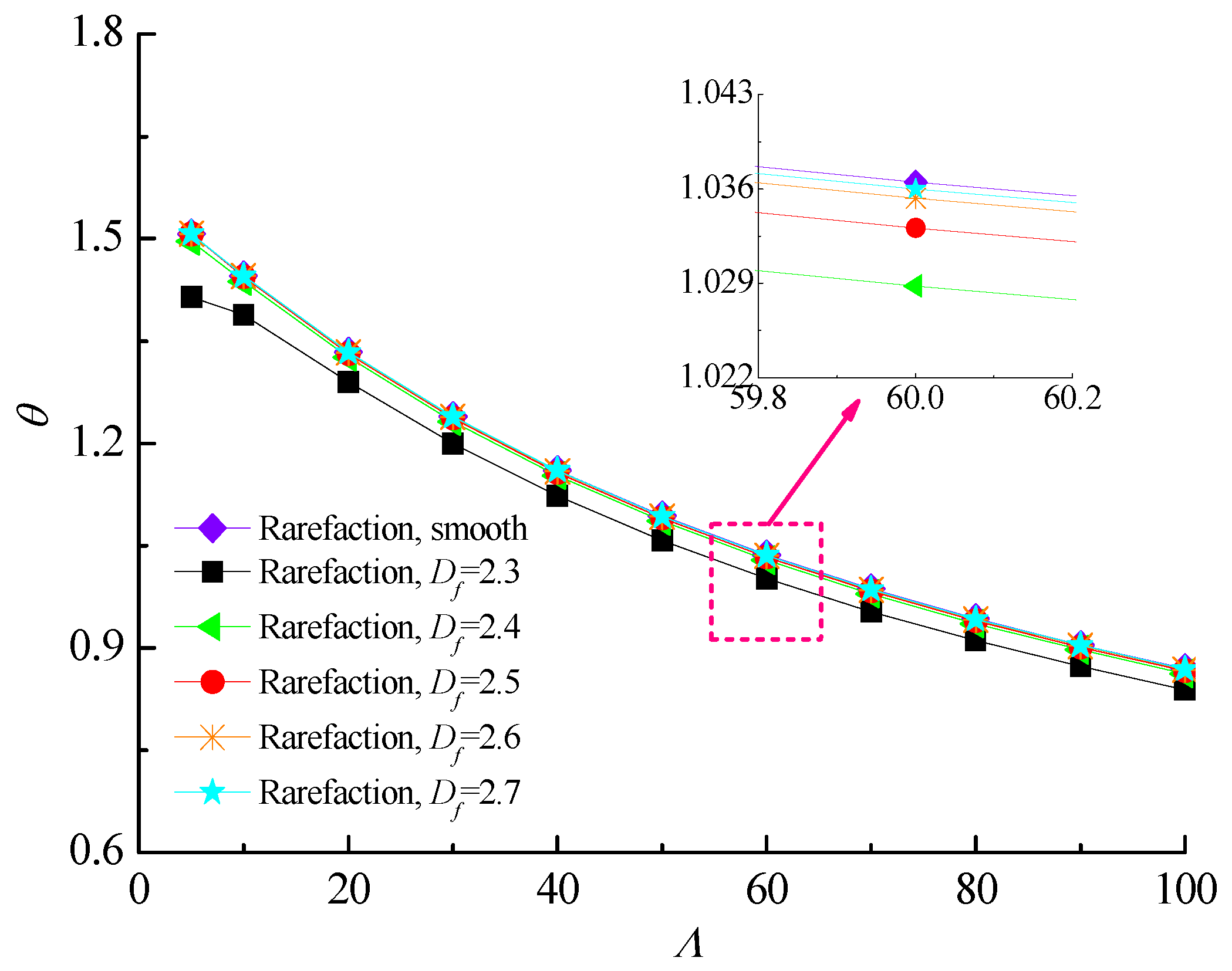
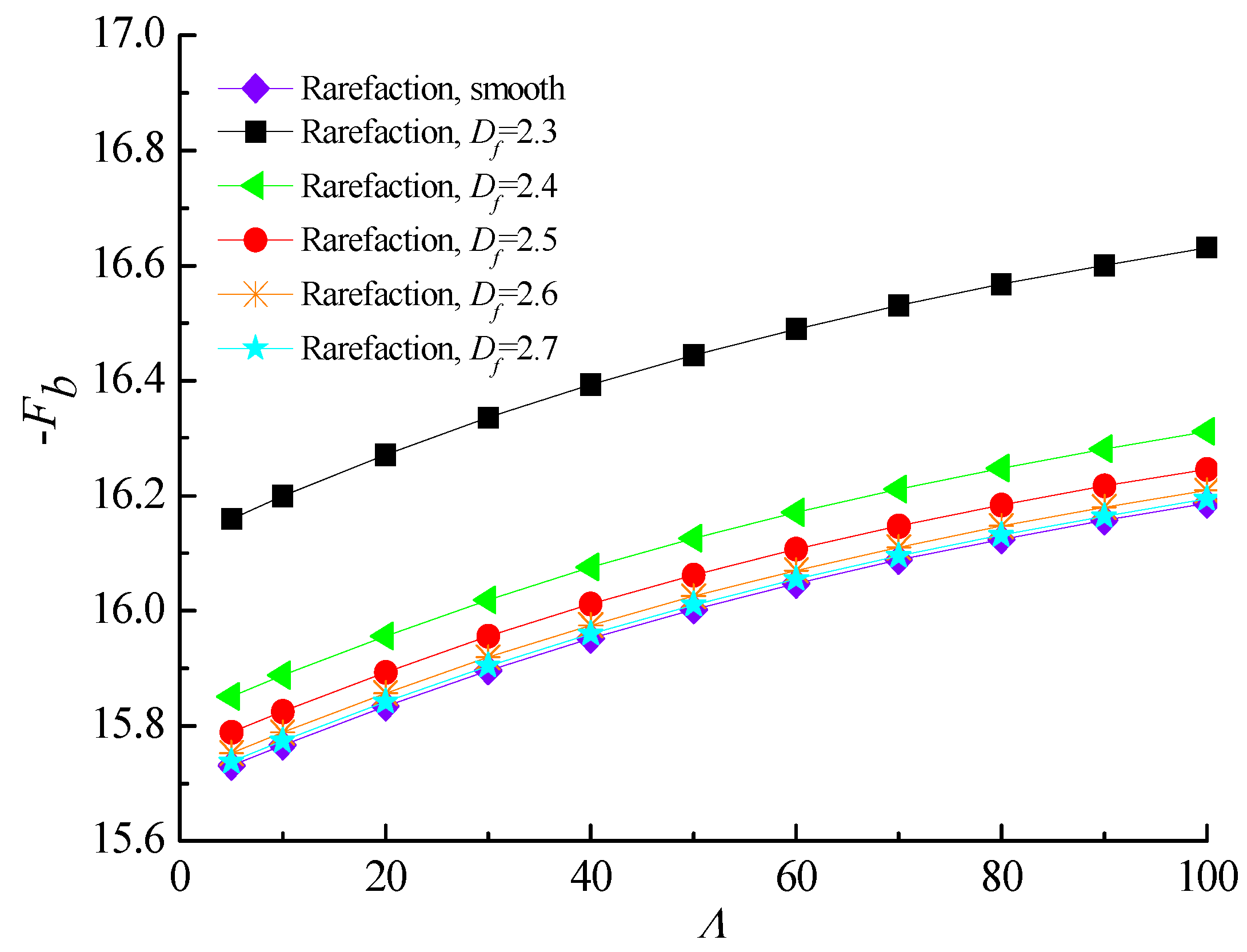
4.2. Load-Carry Capacity and Friction Coefficient
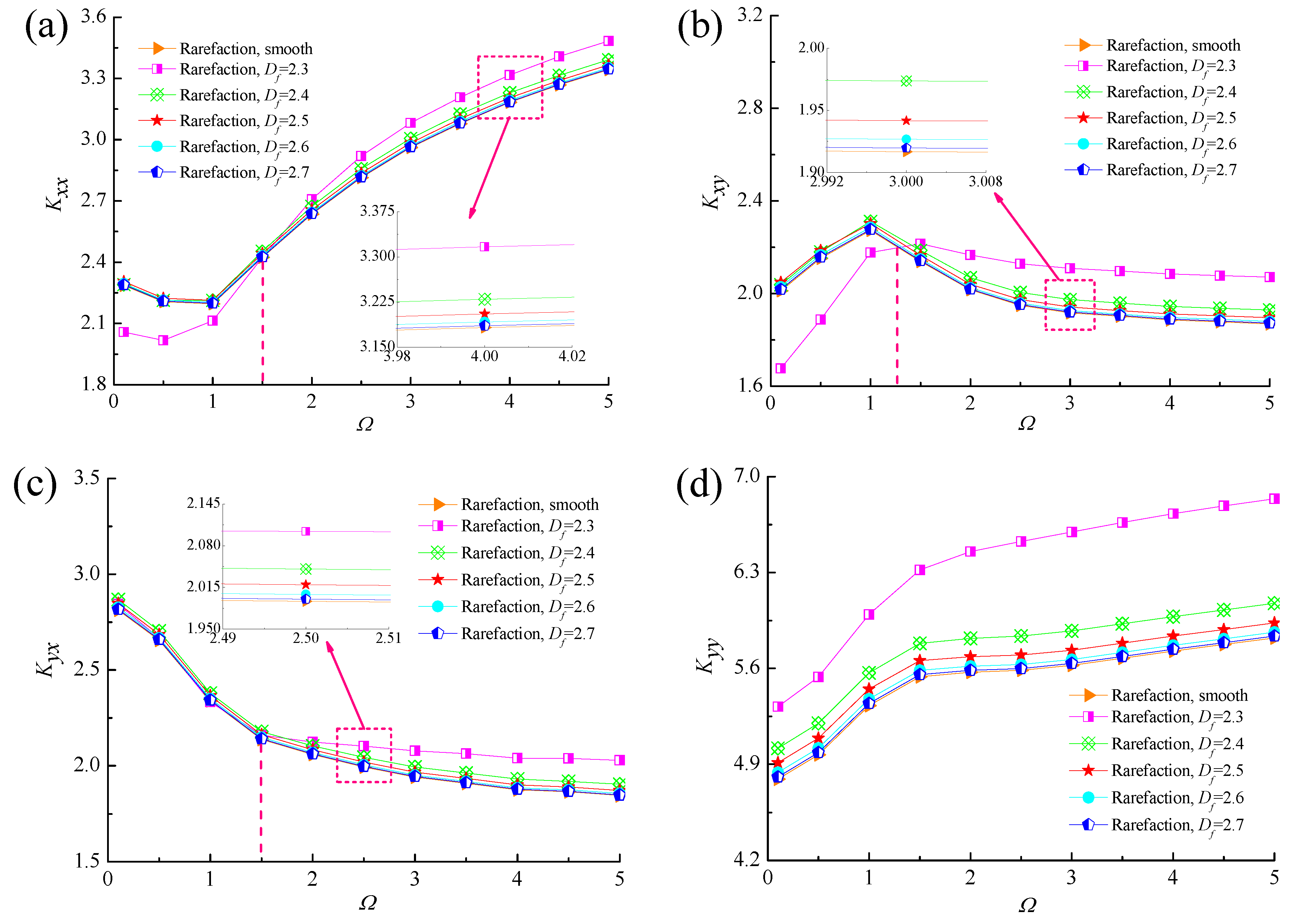
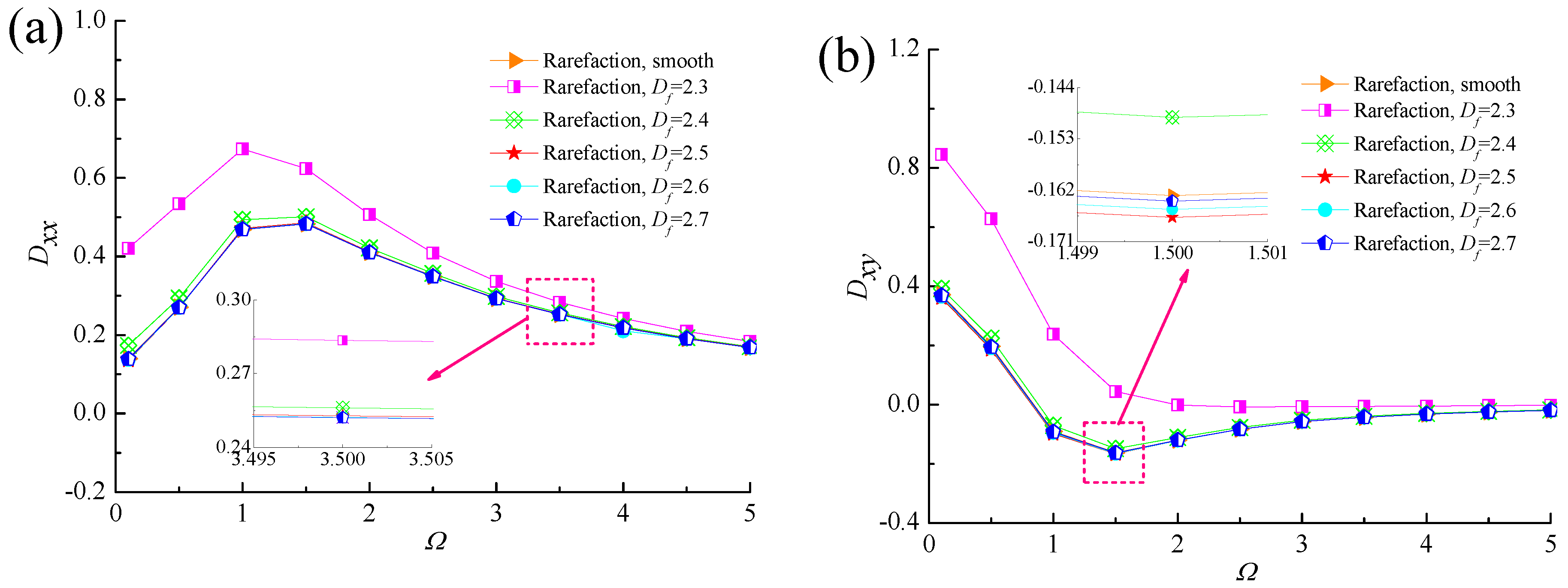
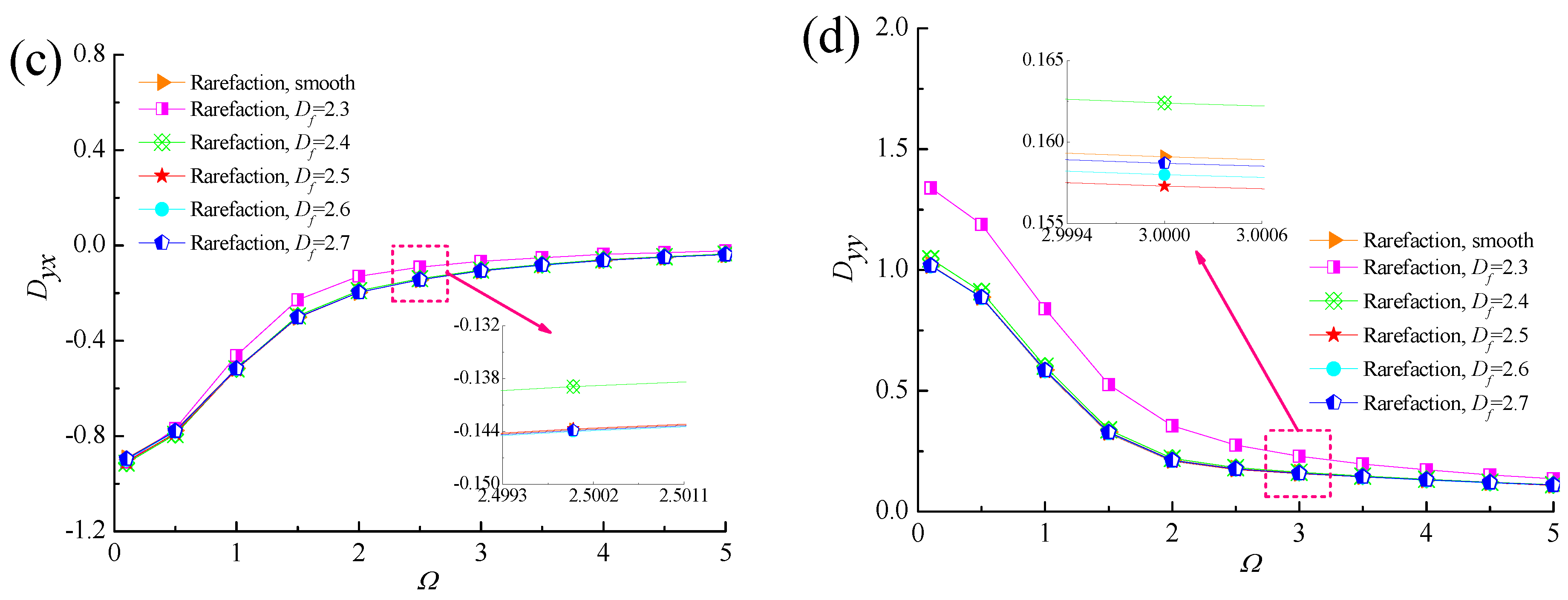
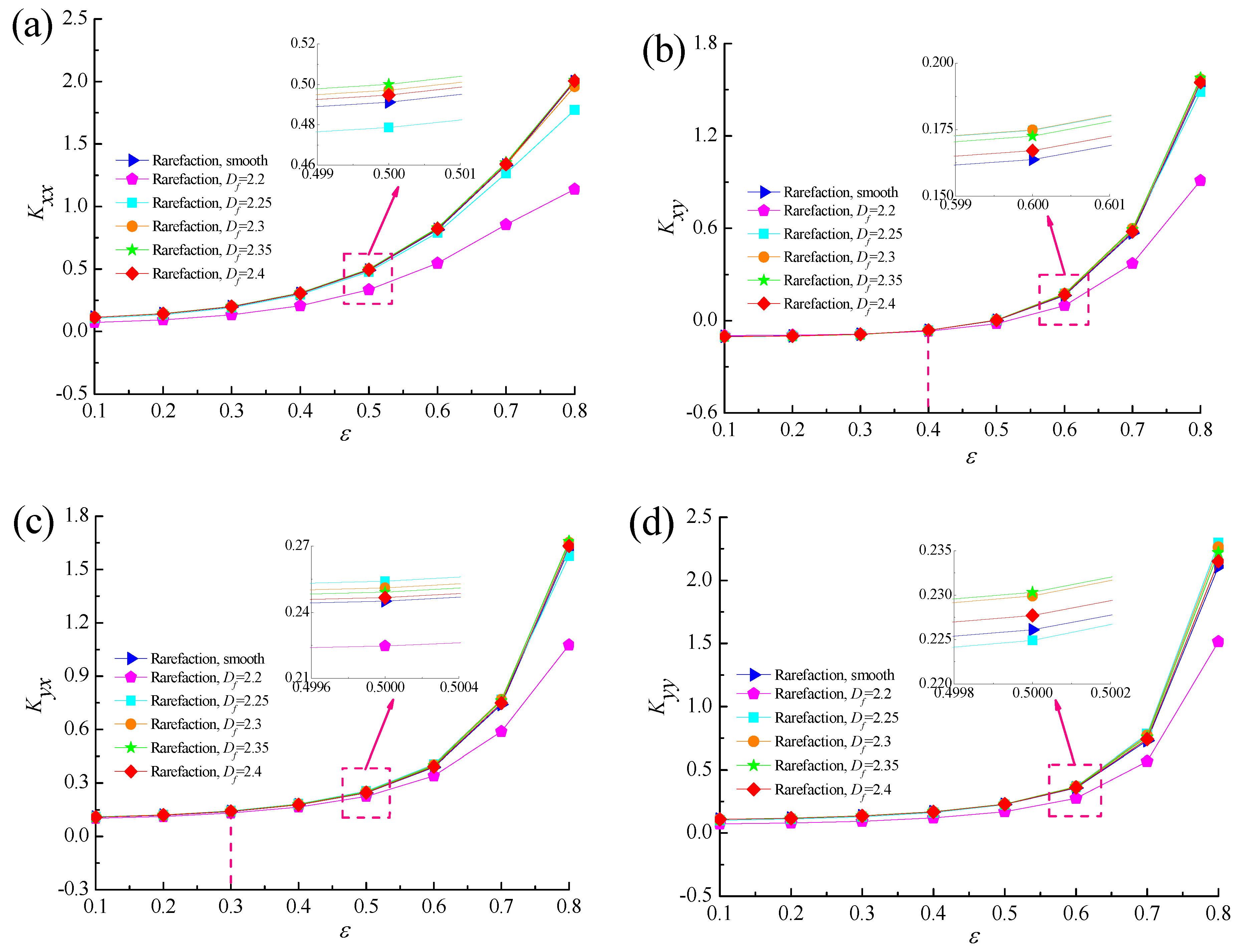
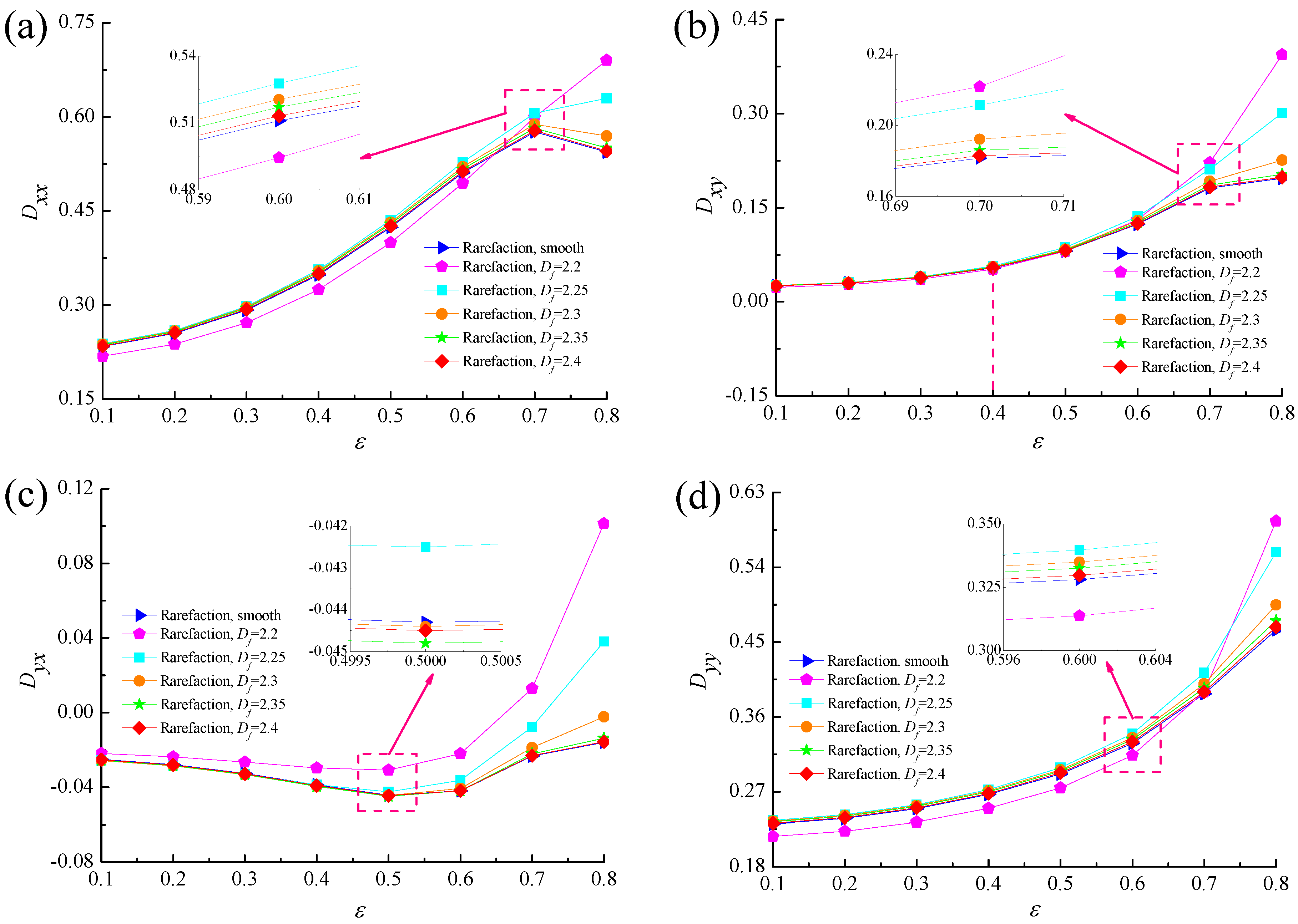
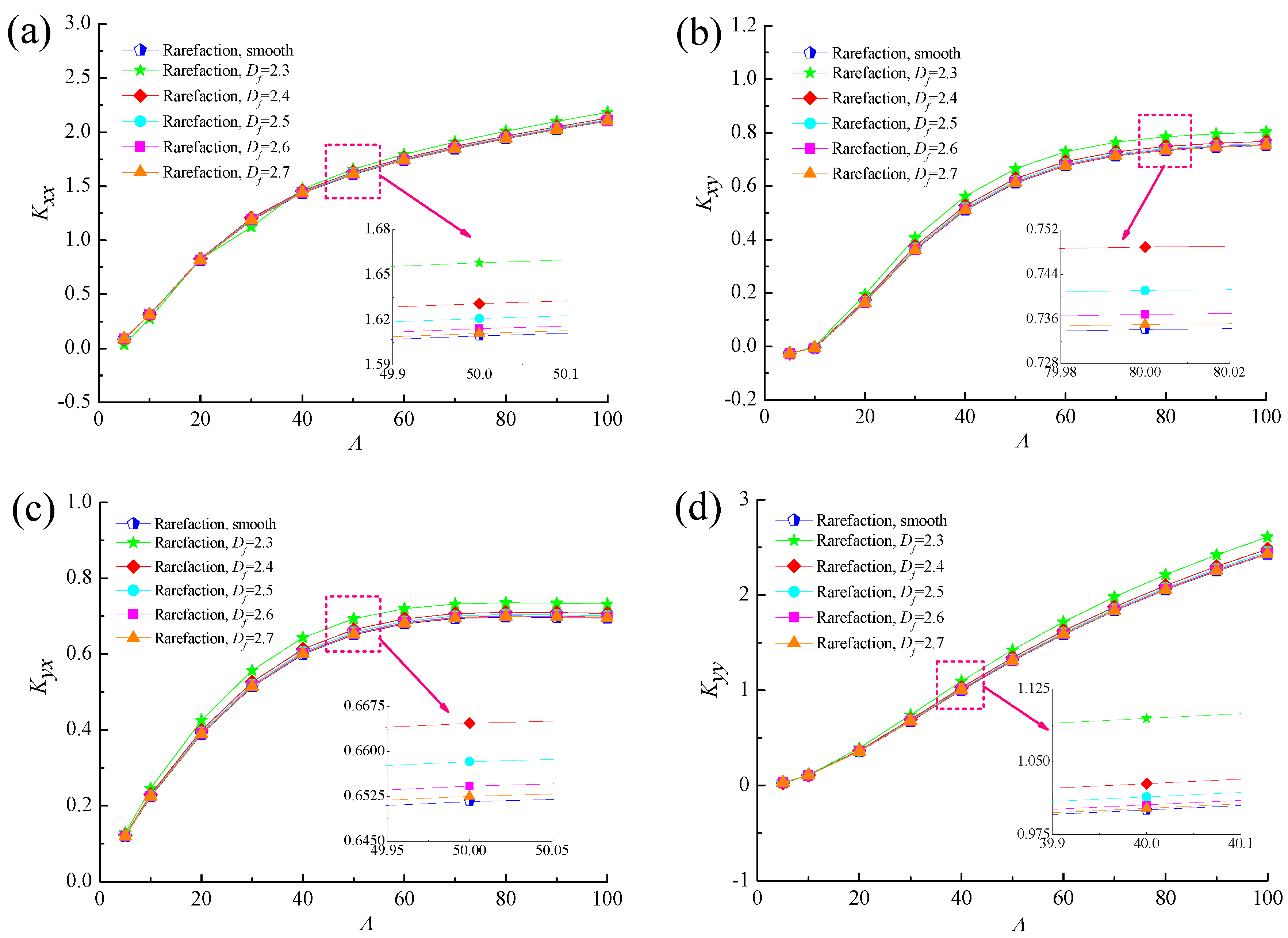
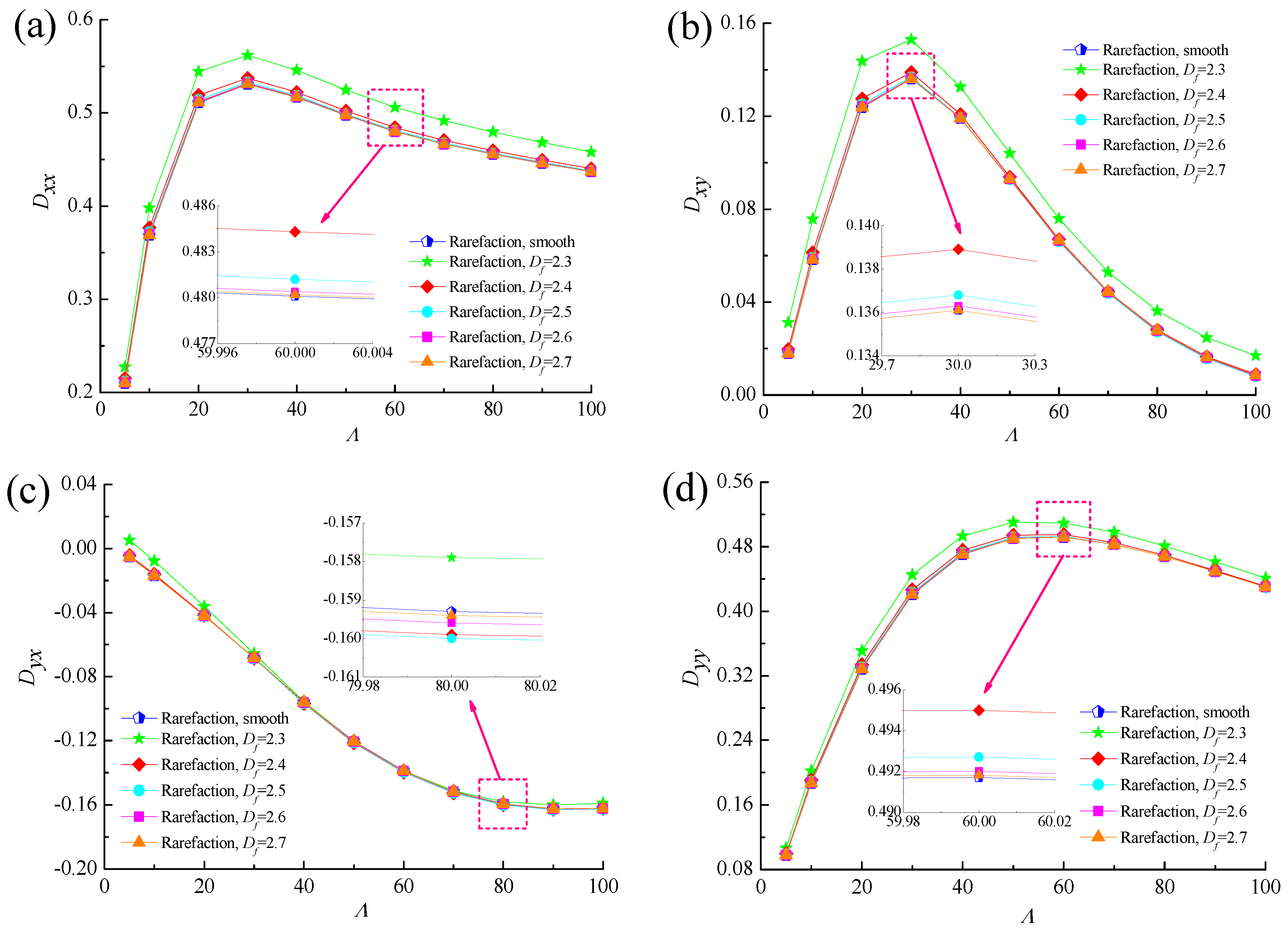
4.3. Dynamic Stiffness and Damping Coefficients
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prakash, J.; Sinha, P. Lubrication theory for micropolar fluids and its application to a journal bearing. Int. J. Eng. Sci. 1975, 13, 217–232. [Google Scholar] [CrossRef]
- Lee, Y.B.; Kwak, H.D.; Kim, C.H.; Jang, G.H. Analysis of Gas-Lubricated Bearings with a Coupled Boundary Effect for Micro Gas Turbine. ASLE Trans. 2001, 44, 685–691. [Google Scholar] [CrossRef]
- Piekos, E.S.; Breuer, K.S. Manufacturing Effects in Microfabricated Gas Bearings: Axially Varying Clearance. J. Tribol. 2002, 124, 815. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Koo, J. Computational Analysis of Wall Roughness Effects for Liquid Flow in Micro-Conduits. J. Fluids Eng. 2004, 126, 1–9. [Google Scholar] [CrossRef]
- Kim, D.; Lee, S.; Bryant, M.D.; Ling, F.F. Hydrodynamic Performance of Gas Microbearings. J. Tribol. 2004, 126, 711–718. [Google Scholar] [CrossRef]
- Zhe, W.; Tong, Y.; Wang, Y. Promoting effect of silicon particles on gas-diffusion-reaction system: In-situ synthesis of AlN in Al-Si materials. J. Alloys Compd. 2017, 735, 13–25. [Google Scholar]
- Zhe, W.; Wang, Y. Impact of convection-diffusion and flow-path interactions on the dynamic evolution of microstructure: Arc erosion behavior of Ag-SnO2 contact materials. J. Alloys Compd. 2019, 774, 1046–1058. [Google Scholar]
- Burgdorfer, A. The influence of the molecular mean free path on the performance of hydrodynamic gas lubricated bearings. Trans. ASME 1959, 88, 94. [Google Scholar]
- Hsia, Y.T.; Domoto, G.A.; Hsia, Y.T.; Domoto, G.A. An Experimental Investigation of Molecular Rarefaction Effects in Gas Lubricated Bearings at Ultra-Low Clearances. J. Tribol. 1983, 105, 120–130. [Google Scholar] [CrossRef]
- Mitsuya, Y. Modified Reynolds Equation for Ultra-Thin Film Gas Lubrication Using 1.5 Order Slip-Flow Model and Considering Surface Accommodation Coefficient. Trans. Jpn. Soc. Mech. Eng. 1992, 58, 3341–3346. [Google Scholar] [CrossRef]
- Fukui, S.; Kaneko, R. A Database for Interpolation of Poiseuille Flow Rates for High Knudsen Number Lubrication Problems. ASME J. Tribol. 1990, 112, 78–83. [Google Scholar] [CrossRef]
- Fukui, S.; Kaneko, R. Analysis of Ultra-Thin Gas Film Lubrication Based on Linearized Boltzmann Equation: First Report—Derivation of a Generalized Lubrication Equation Including Thermal Creep Flow. J. Tribol. 1988, 110, 253–261. [Google Scholar] [CrossRef]
- Christensen, H.; Tonder, K. The Hydrodynamic Lubrication of Rough Bearing Surfaces of Finite Width. J. Tribol. 1971, 93, 324. [Google Scholar] [CrossRef]
- Christensen, H.; Tonder, K. The Hydrodynamic Lubrication of Rough Journal Bearings. Trans. ASME 1973, 95, 166. [Google Scholar] [CrossRef]
- Patir, N. A numerical procedure for random generation of rough surfaces. Wear 1978, 47, 263–277. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of Average Flow Model to Lubrication Between Rough Sliding Surfaces. Trans. ASME 1979, 101, 220. [Google Scholar] [CrossRef]
- Tripp, J.H. Surface Roughness Effects in Hydrodynamic Lubrication: The Flow Factor Method. J. Lubr. Technol. 1983, 105, 458–465. [Google Scholar] [CrossRef]
- White, J.W.; Raad, P.E.; Tabrizi, A.H.; Ketkar, S.P.; Prabhu, P.P. A Numerical Study of Surface Roughness Effects on Ultra-Thin Gas Films. J. Tribol. 1986, 108, 171. [Google Scholar] [CrossRef]
- Li, W.L.; Weng, C.; Hwang, C.C. Effects of roughness orientations on thin film lubrication of a magnetic recording system. J. Phys. D Appl. Phys. 1995, 28, 1011. [Google Scholar] [CrossRef]
- Turaga, R.; Sekhar, A.S.; Majumdar, B.C. The effect of roughness parameter on the performance of hydrodynamic journal bearings with rough surfaces. Tribol. Int. 1999, 32, 231–236. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Siddangouda, A. Effect of surface roughness on the hydrodynamic lubrication of porous step-slider bearings with couple stress fluids. Tribol. Int. 2007, 40, 780–793. [Google Scholar] [CrossRef]
- Zhang, W.M.; Meng, G.; Wei, K.X. Numerical Prediction of Surface Roughness Effect on Slip Flow in Gas-Lubricated Journal Microbearings. Tribol. Trans. 2012, 55, 71–76. [Google Scholar] [CrossRef]
- Zhang, W.M.; Meng, G.; Peng, Z.K. Gaseous slip flow in micro-bearings with random rough surface. Int. J. Mech. Sci. 2013, 68, 105–113. [Google Scholar] [CrossRef]
- Lin, J.R.; Hung, T.C.; Chou, T.L.; Liang, L.J. Effects of surface roughness and non-Newtonian micropolar fluids on dynamic characteristics of wide plane slider bearings. Tribol. Int. 2013, 66, 150–156. [Google Scholar] [CrossRef]
- Jao, H.C.; Chang, K.M.; Chu, L.M.; Li, W.L. A Modified Average Reynolds Equation for Rough Bearings With Anisotropic Slip. J. Tribol. 2016, 138, 011702. [Google Scholar] [CrossRef]
- Kalavathi, G.K.; Dinesh, P.A.; Gururajan, K. Influence of roughness on porous finite journal bearing with heterogeneous slip/no-slip surface. Tribol. Int. 2016, 102, 174–181. [Google Scholar] [CrossRef]
- Quiñonez, A.F.; Morales-Espejel, G.E. Surface roughness effects in hydrodynamic bearings. Tribol. Int. 2016, 98, 212–219. [Google Scholar] [CrossRef]
- Wang, X.; Qiao, X.; Ming, H.; Zhang, L.; Peng, Z. Effects of journal rotation and surface waviness on the dynamic performance of aerostatic journal bearings. Tribol. Int. 2017, 112, 1–9. [Google Scholar] [CrossRef]
- Mandelbrot, B. How long is the coast of britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.C.; Fung, R.F.; Yang, R.F.; Weng, C.I.; Li, W.L. A new modified Reynolds equation for ultrathin film gas lubrication. IEEE Trans. Magn. 1996, 32, 344–347. [Google Scholar] [CrossRef]
- Duwensee, M. Numerical and Experimental Investigations of the Head/Disk Interface. Ph.D. Thesis, The University of California, San Diego, CA, USA, 2007. [Google Scholar]
- Yang, L.; Li, H.; Yu, L. Dynamic stiffness and damping coefficients of aerodynamic tilting-pad journal bearings. Tribol. Int. 2007, 40, 1399–1410. [Google Scholar]
- Yang, L.; Qi, S.; Yu, L. Analysis on Dynamic Performance of Hydrodynamic Tilting-Pad Gas Bearings Using Partial Derivative Method. J. Tribol. 2009, 131, 011703. [Google Scholar]
- Lie, Y.U.; Shemiao, Q.I.; Geng, H. A generalized solution of elasto-aerodynamic lubrication for aerodynamic compliant foil bearings. Sci. China Ser. E Eng. Mater. Sci. 2005, 48, 414–429. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Yang, L.; Xu, T.; Xu, H. Interactive Effects of Rarefaction and Surface Roughness on Aerodynamic Lubrication of Microbearings. Micromachines 2019, 10, 155. https://doi.org/10.3390/mi10020155
Wu Y, Yang L, Xu T, Xu H. Interactive Effects of Rarefaction and Surface Roughness on Aerodynamic Lubrication of Microbearings. Micromachines. 2019; 10(2):155. https://doi.org/10.3390/mi10020155
Chicago/Turabian StyleWu, Yao, Lihua Yang, Tengfei Xu, and Haoliang Xu. 2019. "Interactive Effects of Rarefaction and Surface Roughness on Aerodynamic Lubrication of Microbearings" Micromachines 10, no. 2: 155. https://doi.org/10.3390/mi10020155
APA StyleWu, Y., Yang, L., Xu, T., & Xu, H. (2019). Interactive Effects of Rarefaction and Surface Roughness on Aerodynamic Lubrication of Microbearings. Micromachines, 10(2), 155. https://doi.org/10.3390/mi10020155



