A Study on the Effects of Bottom Electrode Designs on Aluminum Nitride Contour-Mode Resonators
Abstract
:1. Introduction
2. Materials and Methods
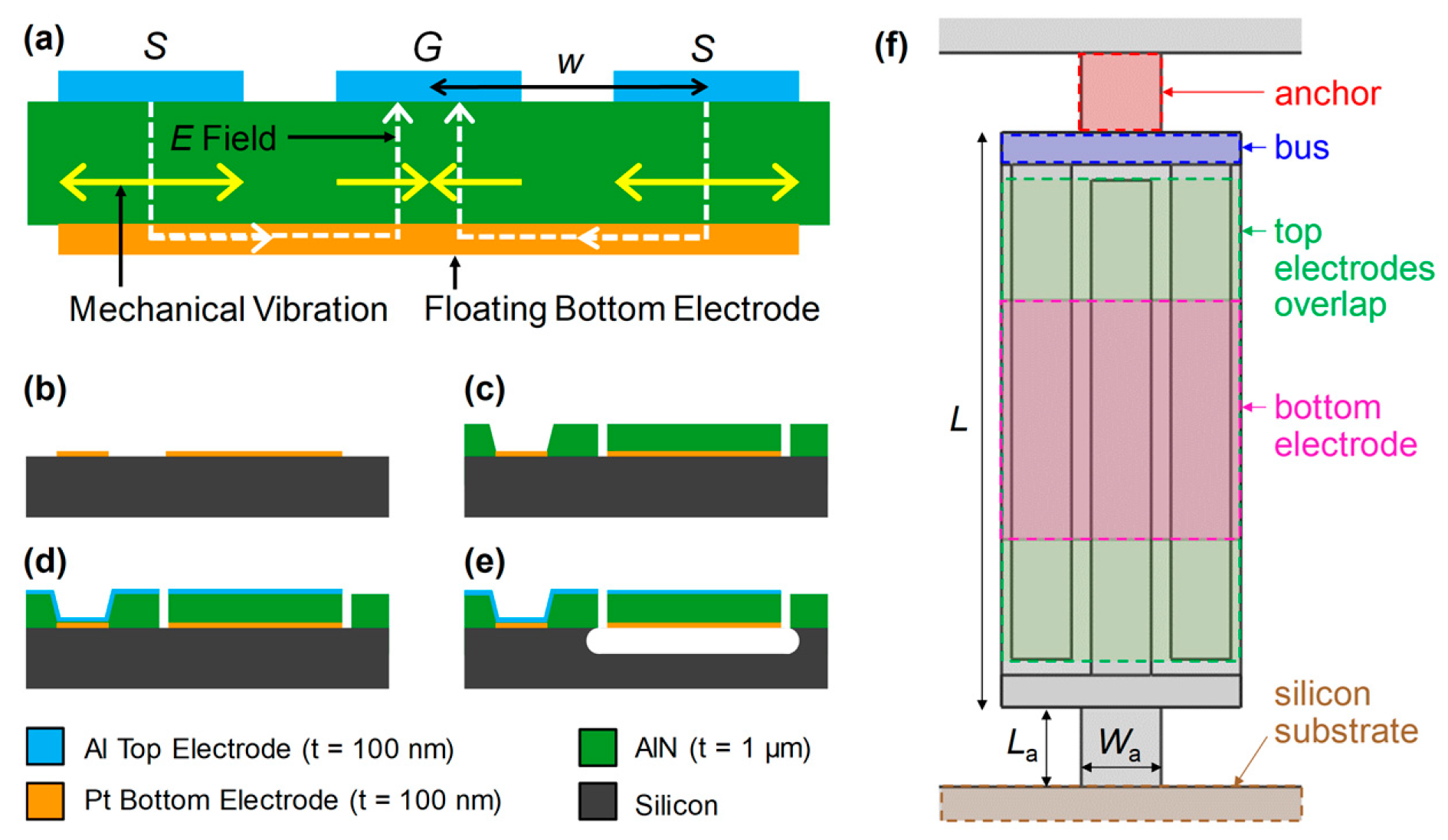
2.1. Resonator Design and Fabrication
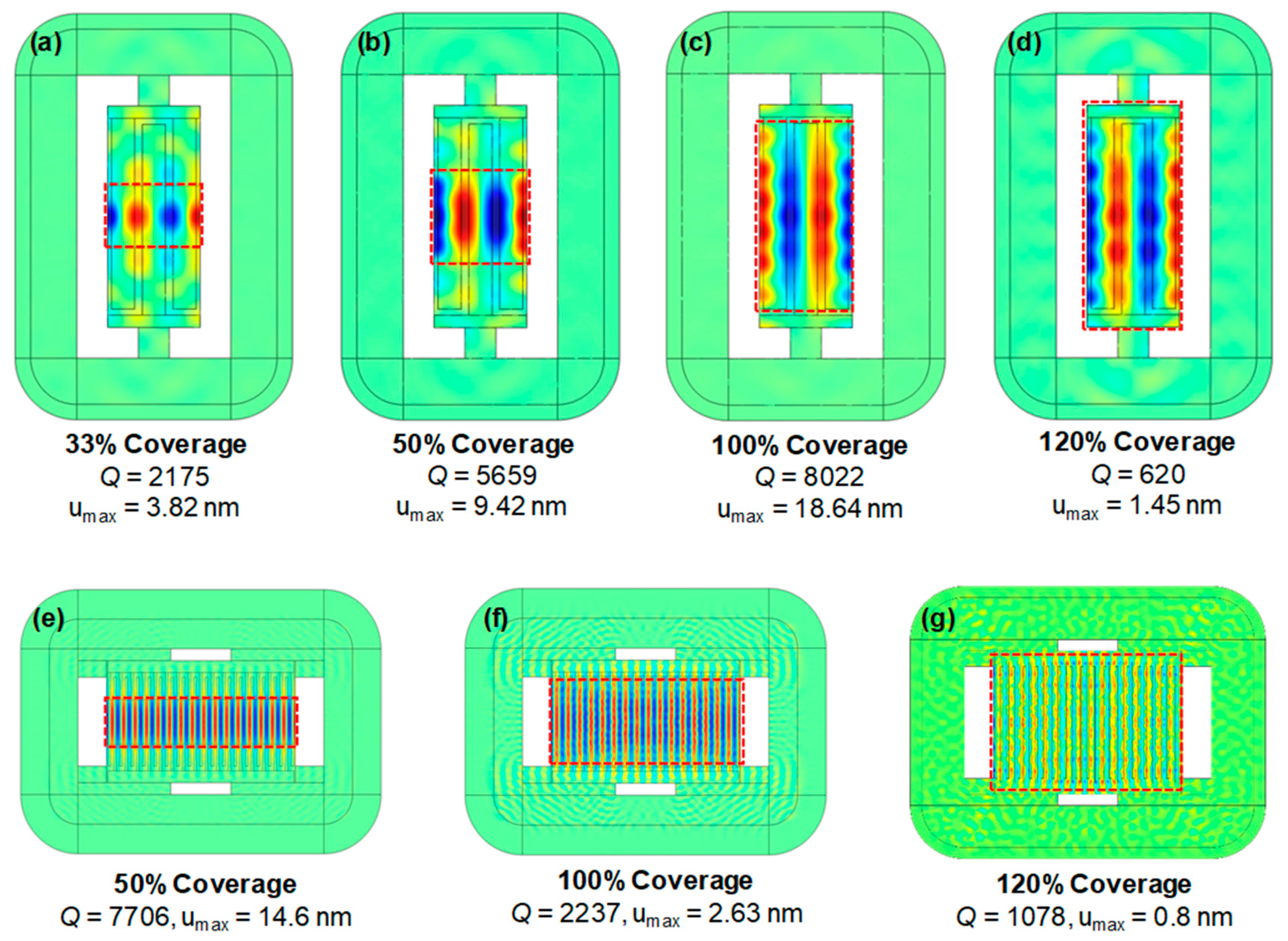
2.2. Experiment and Finite Element Analysis
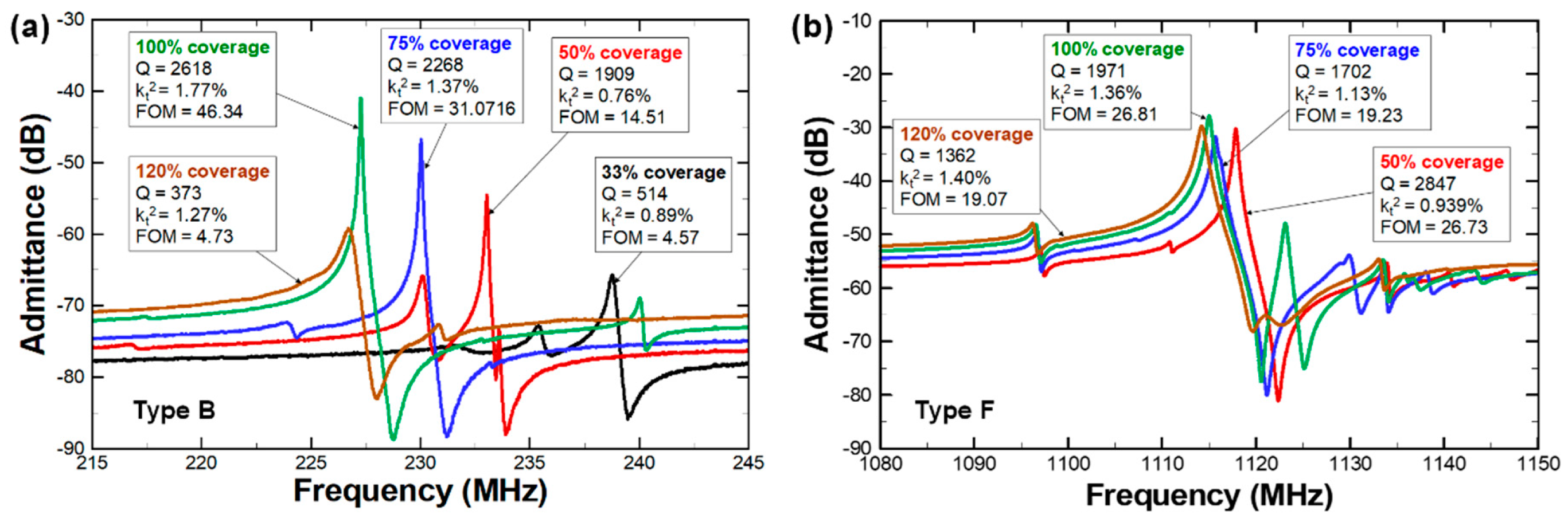
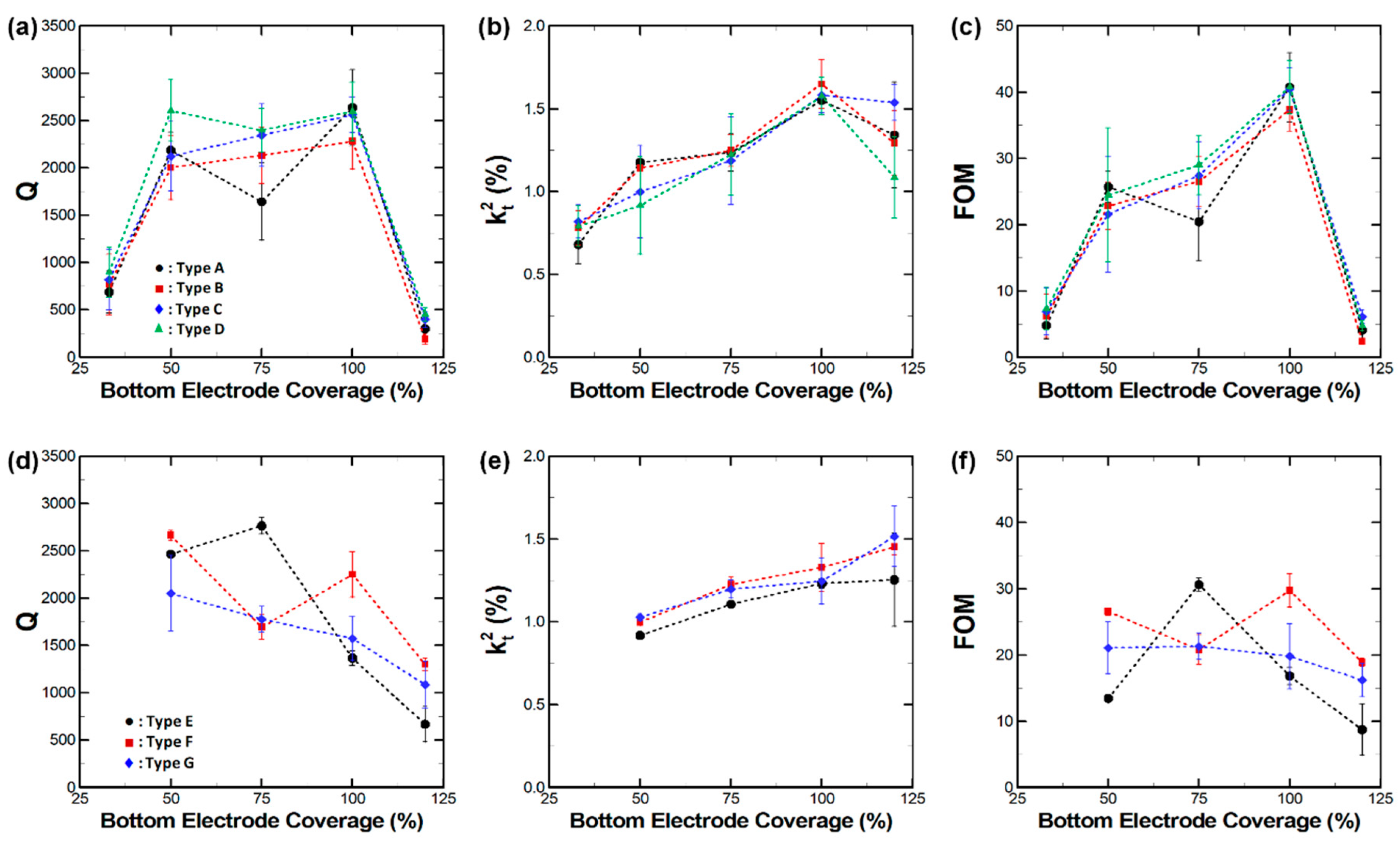
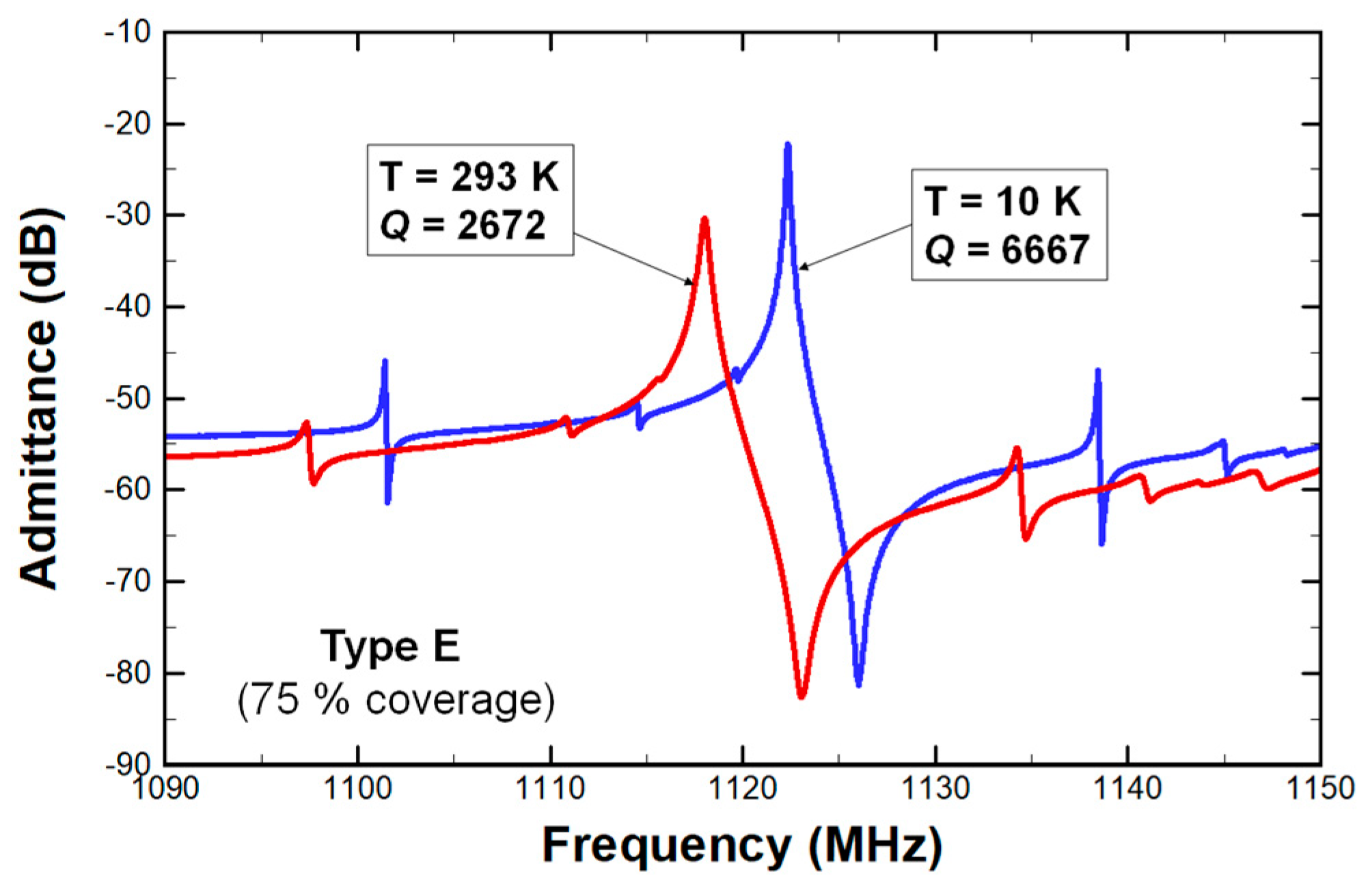
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hung, L.W.; Nguyen, C.T.C. Capacitive-Piezoelectric Transducers for High- Q Micromechanical AlN Resonators. J. Microelectromech. Syst. 2014, 24, 458–473. [Google Scholar] [CrossRef]
- Ruby, R.C.; Bradley, P.; Oshmyansky, Y.; Chien, A.; Larson, J. Thin film bulk wave acoustic resonators (FBAR) for wireless applications. In Proceedings of the 2001 IEEE Ultrasonics Symposium. Proceedings. An International Symposium, Atlanta, GA, USA, 7–10 October 2001; pp. 813–821. [Google Scholar]
- Smith, G.L.; Pulskamp, J.S.; Sanchez, L.M.; Potrepka, D.M.; Proie, R.M.; Ivanov, T.G.; Rudy, R.Q.; Nothwang, W.D.; Bedair, S.S.; Meyer, C.D. PZT-based piezoelectric MEMS technology. J. Am. Ceram. Soc. 2012, 95, 1777–1792. [Google Scholar]
- Piazza, G.; Stephanou, P.J.; Pisano, A.P. Piezoelectric aluminum nitride vibrating contour-mode MEMS resonators. J. Microelectromech. Syst. 2006, 15, 1406–1418. [Google Scholar] [CrossRef]
- Qian, Z.; Kang, S.; Rajaram, V.; Cassella, C.; McGruer, N.E.; Rinaldi, M. Zero-power infrared digitizers based on plasmonically enhanced micromechanical photoswitches. Nat. Nanotechnol. 2017, 12, 969. [Google Scholar] [CrossRef]
- Shkel, A.A.; Kim, E.S. Continuous Health Monitoring with Resonant-Microphone-Array-Based Wearable Stethoscope. IEEE Sens. J. 2019, 19, 4629–4638. [Google Scholar] [CrossRef]
- Kochhar, A.; Galanko, M.E.; Soliman, M.; Abdelsalam, H.; Colombo, L.; Lin, Y.-C.; Vidal-Álvarez, G.; Mukherjee, T.; Weldon, J.; Paramesh, J. Resonant Microelectromechanical Receiver. J. Microelectromech. Syst. 2019, 28, 327–343. [Google Scholar] [CrossRef]
- Zhu, H.; Lee, J.E.Y. AlN piezoelectric on silicon MEMS resonator with boosted Q using planar patterned phononic crystals on anchors. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 19–22 January 2015; pp. 797–800. [Google Scholar]
- Lin, C.M.; Chen, Y.Y.; Felmetsger, V.V.; Senesky, D.G.; Pisano, A.P. AlN/3C-SiC composite plate enabling high-frequency and high-Q micromechanical resonators. Adv. Mater. 2012, 24, 2722–2727. [Google Scholar] [CrossRef]
- Karabalin, R.; Matheny, M.; Feng, X.; Defaÿ, E.; Le Rhun, G.; Marcoux, C.; Hentz, S.; Andreucci, P.; Roukes, M. Piezoelectric nanoelectromechanical resonators based on aluminum nitride thin films. Appl. Phys. Lett. 2009, 95, 103111. [Google Scholar] [CrossRef] [Green Version]
- Pourkamali, S.; Hashimura, A.; Abdolvand, R.; Ho, G.K.; Erbil, A.; Ayazi, F. High-Q single crystal silicon HARPSS capacitive beam resonators with self-aligned sub-100-nm transduction gaps. J. Microelectromech. Syst. 2003, 12, 487–496. [Google Scholar]
- Lee, J.-Y.; Seshia, A. 5.4-MHz single-crystal silicon wine glass mode disk resonator with quality factor of 2 million. Sens. Actuators A-Phys. 2009, 156, 28–35. [Google Scholar] [CrossRef]
- Yunhong, H.; Meng, Z.; Guowei, H.; Chaowei, S.; Yongmei, Z.; Jin, N. A review: Aluminum nitride MEMS contour-mode resonator. J. Semicond. 2016, 37, 101001. [Google Scholar]
- Jung, S.I.; Piazza, G.; Kim, H.J. The Impact of Bottom Electrode Coverage Rate on Electromechanical Coupling and Quality Factor of AlN MEMS Contour Mode Resonators. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 917–920. [Google Scholar]
- Qiu, X.; Zhu, J.; Oiler, J.; Yu, C.; Wang, Z.; Yu, H. Film bulk acoustic-wave resonator based ultraviolet sensor. Appl. Phys. Lett. 2009, 94, 151917. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.B.; Kim, H.J.; Kim, S.G.; Hwang, C.S.; Hong, S.H.; Shin, Y.H.; Lee, N.H. Deposition of ZnO thin films by magnetron sputtering for a film bulk acoustic resonator. Thin Solid Films 2003, 435, 179–185. [Google Scholar] [CrossRef]
- Zhang, H.; Marma, M.S.; Kim, E.S.; McKenna, C.E.; Thompson, M.E. A film bulk acoustic resonator in liquid environments. J. Micromech. Microeng. 2005, 15, 1911. [Google Scholar] [CrossRef]
- Wu, X.; Zuo, C.; Zhang, M.; Van der Spiegel, J.; Piazza, G. A 47μW 204MHz AlN Contour-Mode MEMS based tunable oscillator in 65nm CMOS. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 1757–1760. [Google Scholar]
- Otis, B.P.; Rabaey, J.M. A 300 µmW 1.9 GHz CMOS oscillator utilizing micromachined resonators. In Proceedings of the 28th European Solid-State Circuits Conference, Firenze, Italy, 24–26 September 2002; pp. 151–154. [Google Scholar]
- Davis, Z.J.; Svendsen, W.; Boisen, A. Design, fabrication and testing of a novel MEMS resonator for mass sensing applications. Microelectron. Eng. 2007, 84, 1601–1605. [Google Scholar] [CrossRef]
- Vig, J.R.; Kim, Y. Noise in microelectromechanical system resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1999, 46, 1558–1565. [Google Scholar] [CrossRef]
- Sauvage, G. Phase noise in oscillators: A mathematical analysis of Leeson’s model. IEEE Trans. Instrum. Meas. 1977, 26, 408–410. [Google Scholar] [CrossRef]
- Frangi, A.; Cremonesi, M.; Jaakkola, A.; Pensala, T. Analysis of anchor and interface losses in piezoelectric MEMS resonators. Sens. Actuators A-Phys. 2013, 190, 127–135. [Google Scholar] [CrossRef]
- Segovia-Fernandez, J.; Cremonesi, M.; Cassella, C.; Frangi, A.; Piazza, G. Anchor losses in AlN contour mode resonators. J. Microelectromech. Syst. 2014, 24, 265–275. [Google Scholar] [CrossRef]
- Segovia-Fernandez, J.; Piazza, G. Thermoelastic damping in the electrodes determines $ Q $ of AlN contour mode resonators. J. Microelectromech. Syst. 2017, 26, 550–558. [Google Scholar] [CrossRef]
- Cassella, C.; Segovia-Fernandez, J.; Piazza, G. Segmented electrode excitation of aluminum nitride contour mode resonators to optimize the device figure of merit. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems, Barcelona, Spain, 16–20 June 2013; pp. 506–509. [Google Scholar]
- Giovannini, M.; Yazici, S.; Kuo, N.K.; Piazza, G. Apodization technique for spurious mode suppression in AlN contour-mode resonators. Sens. Actuators A-Phys. 2014, 206, 42–50. [Google Scholar] [CrossRef]
- Cassella, C.; Singh, N.; Soon, B.W.; Piazza, G. Quality factor dependence on the inactive regions in AlN contour-mode resonators. J. Microelectromech. Syst. 2015, 24, 1575–1582. [Google Scholar] [CrossRef]
- Kim, H.J.; Jung, S.I.; Segovia-Fernandez, J.; Piazza, G. The impact of electrode materials on 1/f noise in piezoelectric AlN contour mode resonators. AIP Adv. 2018, 8, 055009. [Google Scholar] [CrossRef]
- Ho, G.K.; Abdolvand, R.; Sivapurapu, A.; Humad, S.; Ayazi, F. Piezoelectric-on-silicon lateral bulk acoustic wave micromechanical resonators. J. Microelectromech. Syst. 2008, 17, 512–520. [Google Scholar] [CrossRef]
- Abdolvand, R.; Lavasani, H.M.; Ho, G.K.; Ayazi, F. Thin-film piezoelectric-on-silicon resonators for high-frequency reference oscillator applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 2596–2606. [Google Scholar] [CrossRef]
- Kim, H.J.; Wang, S.; Xu, C.; Laughlin, D.; Zhu, J.; Piazza, G. Piezoelectric/magnetostrictive MEMS resonant sensor array for in-plane multi-axis magnetic field detection. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 109–112. [Google Scholar]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-biased 215MHz magnetoelectric NEMS resonator for ultra-sensitive DC magnetic field detection. Sci. Rep. 2013, 3, 1985. [Google Scholar] [CrossRef]
- Rinaldi, M.; Zuniga, C.; Sinha, N.; Taheri, M.; Piazza, G.; Khamis, S.M.; Johnson, A. Gravimetric chemical sensor based on the direct integration of SWNTS on ALN Contour-Mode MEMS resonators. In Proceedings of the 2008 IEEE International Frequency Control Symposium, Honolulu, HI, USA, 18–21 May 2008; pp. 443–448. [Google Scholar]
- Qian, Z.; Hui, Y.; Liu, F.; Kar, S.; Rinaldi, M. Chemical sensing based on graphene-aluminum nitride nano plate resonators. In Proceedings of the 2015 IEEE Sensors, Bushan, Korea, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Pang, W.; Yan, L.; Zhang, H.; Yu, H.; Kim, E.S.; Tang, W.C. Femtogram mass sensing platform based on lateral extensional mode piezoelectric resonator. Appl. Phys. Lett. 2006, 88, 243503. [Google Scholar] [CrossRef]
- Chen, D.; Wang, J.J.; Xu, Y. Hydrogen sensor based on Pd-functionalized film bulk acoustic resonator. Sens. Actuators B-Chem. 2011, 159, 234–237. [Google Scholar] [CrossRef]
- Hui, Y.; Gomez-Diaz, J.S.; Qian, Z.; Alù, A.; Rinaldi, M. Plasmonic piezoelectric nanomechanical resonator for spectrally selective infrared sensing. Nat. Commun. 2016, 7, 11249. [Google Scholar] [CrossRef]


| 230 MHz CMRs | 1.1 GHz CMRs | |||||
|---|---|---|---|---|---|---|
| Type | Anchor Length (La) | Width (Wa) | Bottom Electrode Coverage | Type | Resonator Length (L) | Bottom Electrode Coverage |
| A B C D | 10 μm 10 μm 20 μm 20 μm | 10 μm 20 μm 10 μm 20 μm | 33%, 50%, 75%, 100%, 120% | G E F | 60 μm 80 μm 100 μm | 50%, 75%, 100%, 120% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, S.I.; Ryu, C.; Piazza, G.; Kim, H.J. A Study on the Effects of Bottom Electrode Designs on Aluminum Nitride Contour-Mode Resonators. Micromachines 2019, 10, 758. https://doi.org/10.3390/mi10110758
Jung SI, Ryu C, Piazza G, Kim HJ. A Study on the Effects of Bottom Electrode Designs on Aluminum Nitride Contour-Mode Resonators. Micromachines. 2019; 10(11):758. https://doi.org/10.3390/mi10110758
Chicago/Turabian StyleJung, Soon In, Chaehyun Ryu, Gianluca Piazza, and Hoe Joon Kim. 2019. "A Study on the Effects of Bottom Electrode Designs on Aluminum Nitride Contour-Mode Resonators" Micromachines 10, no. 11: 758. https://doi.org/10.3390/mi10110758
APA StyleJung, S. I., Ryu, C., Piazza, G., & Kim, H. J. (2019). A Study on the Effects of Bottom Electrode Designs on Aluminum Nitride Contour-Mode Resonators. Micromachines, 10(11), 758. https://doi.org/10.3390/mi10110758





