The Indentation-Induced Pop-in Phenomenon and Fracture Behaviors of GaP(100) Single-Crystal
Abstract
1. Introduction
2. Materials and Methods
3. Results
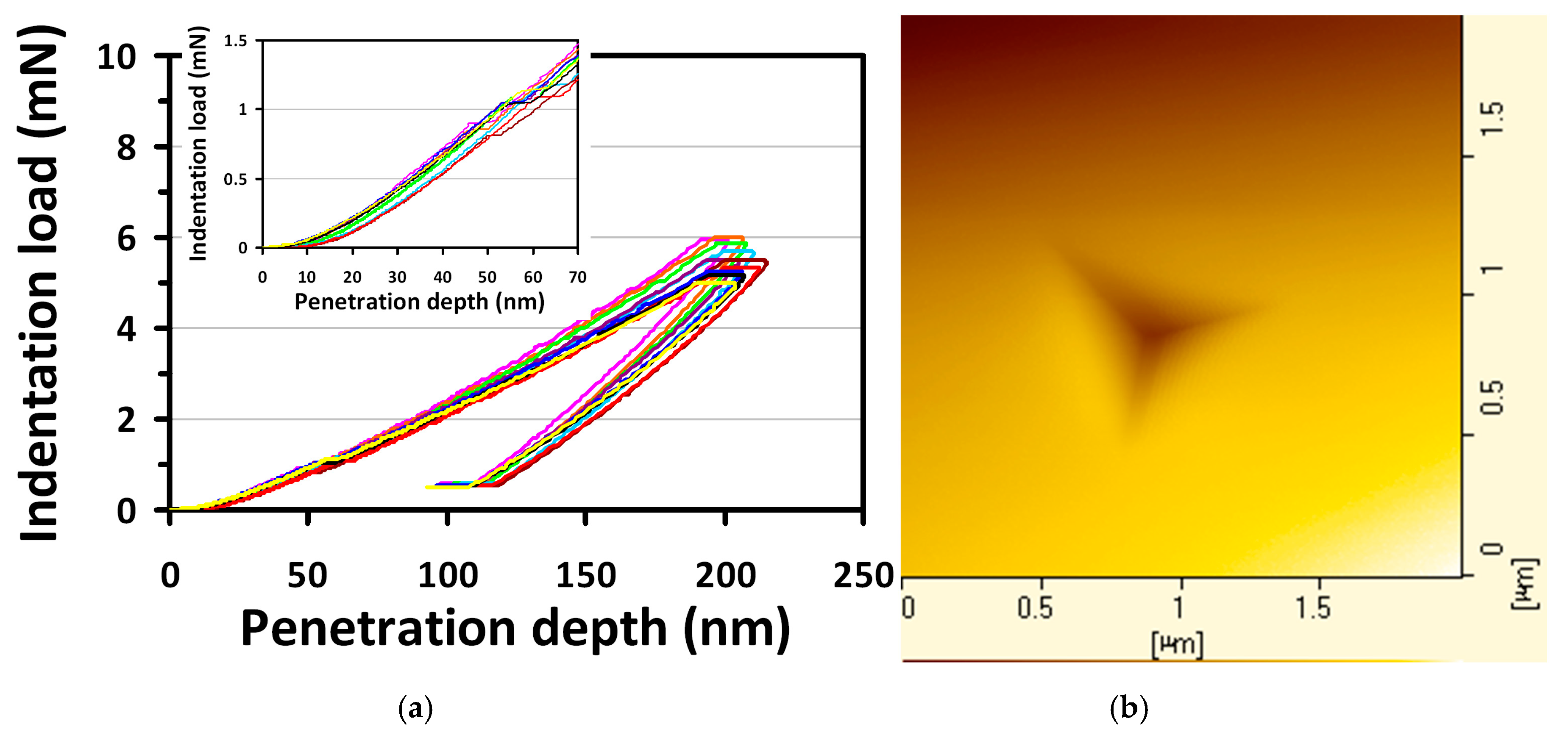
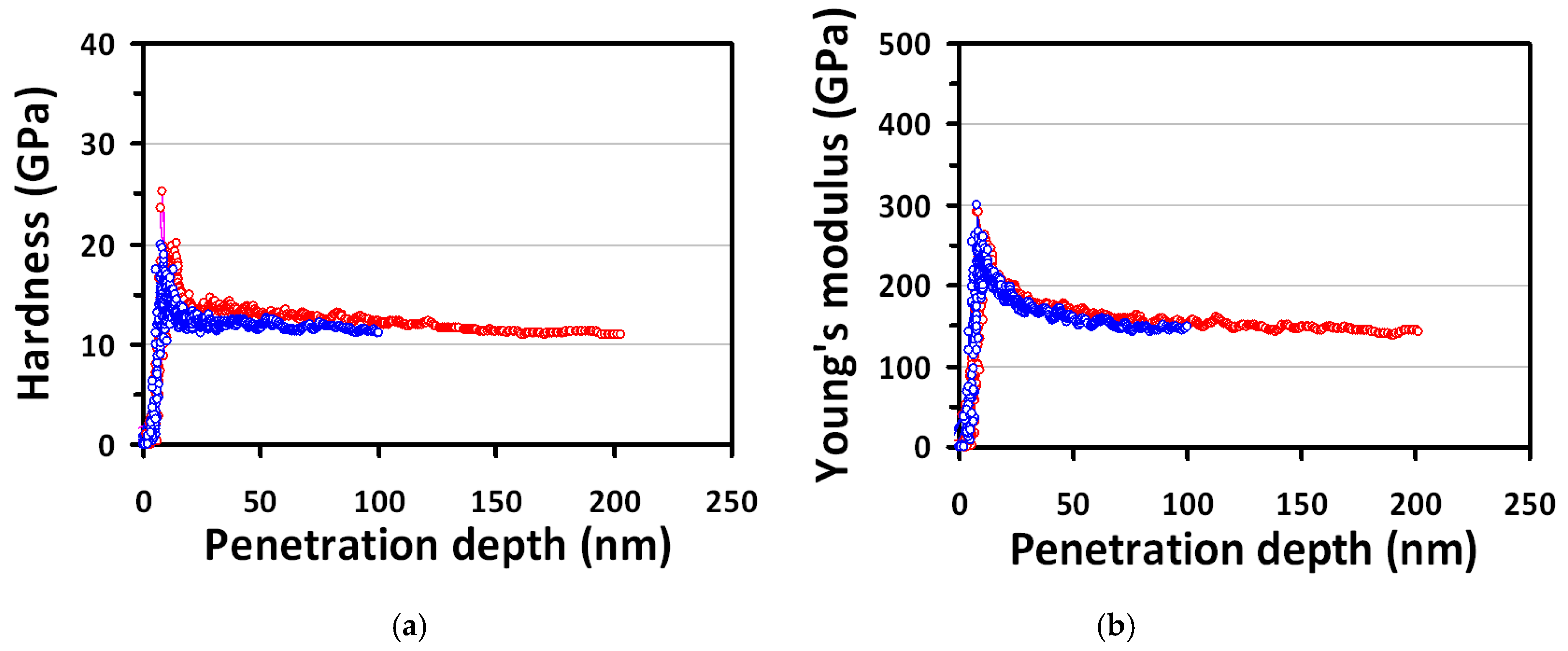
3.1. Nanoindentation
3.2. Homogeneous Dislocation Nucleation
3.3. Fracture Toughness and Fracture Energy
4. Conclusions
- From nanoindentation results, the obtained hardness and Young’s modulus of GaP(100) single crystal are 12.5 ± 1.2 GPa and 152.6 ± 12.8 GPa, respectively.
- The energetic estimation indicated that the number of dislocation loop is estimated to be in the order of 106 for the pop-in event with a critical radius of 0.95 nm.
- The KC and GC values of GaP(100) single crystal obtained from the Vickers indentation test are about 1.7 ± 0.1 MPa·m1/2 and 23.8 J·m−2, respectively.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, Q.; Ogawa, H.; Yamano, H.; Yoshida, A. Growth of InN films on GaAs(111) and GaP(111) substrates by microwave-excited metalorganic vapor-phase epitaxy. Appl. Phys. Lett. 1995, 66, 715–717. [Google Scholar] [CrossRef]
- Oishi, K.; Kobayashi, S.; Ohta, S.; Tsuboi, N.; Kaneko, F. Orientation of CuGaS2 thin films on (100) GaAs and GaP substrates. J. Cryst. Growth 1997, 177, 88–94. [Google Scholar] [CrossRef]
- Nateghi, N.; Ménard, D.; Masut, R.A. Large interface diffusion in endotaxial growth of MnP films on GaP substrates. J. Appl. Phys. 2014, 116, 133512. [Google Scholar] [CrossRef]
- Arias-Cerón, J.S.; Vilchis, H.; Hurtado-Castañeda, D.M.; Sánchez, V.M. Free standing c-GaN films grown by low-pressure metalorganic chemical vapor deposition on GaP (100) substrates. Mater. Sci. Semicond. Process. 2018, 74, 98–101. [Google Scholar] [CrossRef]
- Tao, X.; Wang, X.; Li, X.D. Nanomechanical characterization of one-step, combustion-synethesized Al4B2O9 and Al18B4O33 nanowires. Nano Lett. 2007, 7, 3172–3176. [Google Scholar] [CrossRef]
- Bao, L.; Xu, Z.H.; Li, R.; Li, X.D. Catalyst-free synthesis and structural and mechanical characterization of single crystalline Ca2B2O5 center dot H2O nanobelts and stacking faulted Ca2B2O5 nanogrooves. Nano Lett. 2010, 10, 255–262. [Google Scholar] [CrossRef]
- Sun, Z.; Liao, T.; Li, W.; Dou, Y.; Liu, K.; Jiang, L.; Kim, S.W.; Kim, J.H.; Dou, S.X. Fish-scale bio-inspired multifunctional ZnO nanostructures. NPG Asia Mater. 2015, 7, e232. [Google Scholar] [CrossRef]
- Ebenstein, D.M.; Pruitt, L.A. Nanoindentation of biological materials. Nano Today 2006, 1, 26–33. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Nanomechanical characterization of heterogeneous and hierarchial biomaterials and tissues using nanoindentation: The role of finite mixture models. Mater. Sci. Eng. C Mater. Biol. Appl. 2015, 48, 150–157. [Google Scholar] [CrossRef]
- Jian, S.R.; Le, P.H.; Luo, C.W.; Juang, J.Y. Nanomechancial and wettability properties of Bi2Te3 thin films: Effects of post-annealing. J. Appl. Phys. 2017, 121, 175302. [Google Scholar] [CrossRef]
- Martinez, G.; Ramana, C.V. Microstructure, mechanical and electrocal properties of nanocrystalline W-Mo thin films. AIP Adv. 2017, 7, 125201. [Google Scholar] [CrossRef]
- Chen, G.J.; Jian, S.R. Effects of Cu doping on the structural and nanomechanical properties of ZnO thin films. Appl. Phys. A Mater. Sci. Process. 2018, 124, 575. [Google Scholar] [CrossRef]
- Lai, H.D.; Jian, S.R.; Tuyen, L.T.C.; Le, P.H.; Luo, C.W.; Juang, J.Y. Nanoindentation of Bi2Se3 thin films. Micromachines 2018, 9, 518. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.H.; Jian, S.R.; Chen, G.J.; Cheng, H.Z.; Juang, J.Y. Annealing-driven microstructuiral evolution and its effects on the surface and nanomechanical properties of Cu-doped NiO thin films. Coatings 2019, 9, 107. [Google Scholar] [CrossRef]
- Zhang, H.; Maiti, S.; Subhash, G. Evolution of shear bands in bulk metallic glasses under dynamic loading. J. Mech. Phys. Solids 2008, 56, 21712187. [Google Scholar] [CrossRef]
- Greer, A.L.; Cheng, Y.Q.; Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R Rep. 2013, 74, 71–132. [Google Scholar] [CrossRef]
- Wang, L.; Wang, L.; Xue, Y.; Zhang, H.; Fu, H. Nnaoindentation response of laser shock peened Ti-based bulk metallic glass. AIP Adv. 2015, 5, 057156. [Google Scholar] [CrossRef]
- Bradby, J.E.; Kucheyev, S.O.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P.; Li, G.; Phillips, M.R. Indentation-induced damage in GaN epilayers. Appl. Phys. Lett. 2002, 80, 383–385. [Google Scholar] [CrossRef]
- Jian, S.R. Mechanical deformation induced in Si and GaN under Berkovich nanoindentation. Nanoscale Res. Lett. 2008, 3, 6–13. [Google Scholar] [CrossRef]
- Krimsky, E.; Jones, K.A.; Tompkins, R.P.; Rotella, P.; Ligda, J.; Schuster, B.E. Nano-indentation used to study pyramidal slip in GaN single crystals. J. Appl. Phys. 2018, 123, 065701. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Transmission electron microscopy observation of deforamtion microstructure under spherical indentation in silicon. Appl. Phys. Lett. 2000, 77, 3749–3751. [Google Scholar] [CrossRef]
- Jang Jae-il Lance, M.J.; Wen, S.; Pharr, G.M. Evidence for nanoindentation-induced phase transformations in germanium. Appl. Phys. Lett. 2005, 86, 131907. [Google Scholar] [CrossRef]
- Jian, S.R.; Chen, G.J.; Juang, J.Y. Naonindentation-induced phase transformation in (110)-oriented Si single-crystals. Curr. Opin. Solid State Mater. Sci. 2010, 14, 69–74. [Google Scholar] [CrossRef]
- Lamuta, C.; Cupolillo, A.; Politano, A.; Aliev, Z.S.; Babanly, M.B.; Chulkov, E.V.; Alfano, M.; Pagnotta, L. Nanoindentation of single-crystal Bi2Te3 topological insulators grown with the Bridgman-Stockbarger method. Phys. Status Solidi B Basic Solid State Phys. 2016, 253, 1082–1086. [Google Scholar] [CrossRef]
- Huang, J.; Xu, K.; Fan, Y.M.; Niu, M.T.; Zeng, X.H.; Wang, J.F.; Yang, H. Nanoscale anisotropic plastic deformation in single crystal GaN. Nanoscale Res. Lett. 2012, 7, 150. [Google Scholar] [CrossRef]
- Lu, J.Y.; Ren, H.; Deng, D.M.; Wang, Y.; Chen, K.J.; Lau, K.M.; Zhang, T.Y. Thermally activted pop-in and indentation size effects in GaN films. J. Phys. D Appl. Phys. 2012, 45, 085301. [Google Scholar] [CrossRef]
- Jang Jae-il Lance, M.J.; Wen, S.; Tsui, T.Y.; Pharr, G.M. Indentation-induced phase transformations in silicon: Influences of load, rate and indenter angle on the transforamtion behavior. Acta Mater. 2005, 52, 1759–1770. [Google Scholar] [CrossRef]
- Jang, J.-I.; Pharr, G.M. Influence of indenter angle on cracking in Si and Ge during nanoindentation. Acta Mater. 2008, 56, 4458–4469. [Google Scholar] [CrossRef]
- Jian, S.R. Pop-in effects and dislocation nucleation of c-plane single-crystal ZnO by Berkovich nanoindentation. J. Alloy. Compd. 2015, 644, 54–58. [Google Scholar] [CrossRef]
- Caldas, P.G.; Silva, E.M.; Prioli, R.; Huang, J.Y.; Juday, R.; Fischer, A.M.; Ponce, F.A. Plasticity and optical properties of GaN under highly localized nanoindentation stress fields. J. Appl. Phys. 2017, 121, 125105. [Google Scholar] [CrossRef]
- Chiu, Y.J.; Jian, S.R.; Liu, T.J.; Le, P.H.; Juang, J.Y. Localized deformation and fracture behaviors in InP single crystals by indentation. Micromachines 2018, 9, 611. [Google Scholar] [CrossRef] [PubMed]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Mechanical deformation on InP and GaAs by spherical indentation. Appl. Phys. Lett. 2001, 78, 3235–3237. [Google Scholar] [CrossRef]
- Jian, S.R. Cathodoluminescence rosettes in c-plane GaN films under Berkovich nanoindentation. Opt. Mater. 2013, 35, 2707–2709. [Google Scholar] [CrossRef]
- Grillo, S.E.; Ducarroir, M.; Nadal, M.; Tournié, E.; Faurie, J.P. Nanoindentation of Si, GaP, GaAs and ZnSe single crystals. J. Phys. D Appl. Phys. 2003, 36, L5–L9. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1982. [Google Scholar]
- Li, X.D.; Bhushan, B. A review of nanoindentation continuous stiffness measurement technique and its applications. Mater. Charact. 2002, 48, 11–36. [Google Scholar] [CrossRef]
- Page, T.F.; Hainsworth, S.V. Procedures for the nanoindentation testing of coated systems. In Proceedings of the International Conference Instrumented Indentation, San Diego, CA, USA, 22–23 April 1995; Smith, D.T., Ed.; Special Publication of the national Institute of Standards & Technology: Gaitherburg, MD, USA, 1995. [Google Scholar]
- Chen, J.; Bull, S.J. Relation between the ratio of elastic work to the total work of indentation and the ratio of hardness to Young’s modulus for a perfect conical tip. J. Mater. Res. 2009, 24, 590–598. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Sneddon, I.N. The relation between load and penetration in the axisymmetric Boussinseq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Adachi, S. Properties of Semiconductor Alloys: Group-IV, III-V and II-VI Semiconductors; John Wiley and Sons Ltd.: Chichester, UK, 2009. [Google Scholar]
- Jian, S.R.; Tseng, Y.C. Nanomechanical characteristics and deformation behaviors of ZnSe thin films by nanoindentation. Sci. Adv. Mater. 2014, 6, 617–622. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, L.C. Deformation mechanisms at pop-out in monocrystalline silicon under nanoindentation. Acta Mater. 2009, 57, 2148–2153. [Google Scholar] [CrossRef]
- Huston, L.Q.; Kiran, M.S.R.N.; Smillie, L.A.; Williams, J.S.; Bradby, J.E. Cold nanoindentation of germanium. Appl. Phys. Lett. 2017, 111, 021901. [Google Scholar] [CrossRef]
- Fujikane, M.; Setoyama, D.; Nagao, S.; Nowak, R.; Yamanaka, S. Nanoindentation examination of yttria-stabilized zirconia (YSZ) crystal. J. Alloy. Compd. 2007, 431, 250–255. [Google Scholar] [CrossRef]
- Wang, Q.M.; Ding, Y.; Chen, Q.; Zhao, M. Crystalline orientation dependence of nanomechanical properties of Pb(Zr0.52Ti0.48)O3 thin films. Appl. Phys. Lett. 2005, 86, 162903. [Google Scholar] [CrossRef]
- Basu, S.; Elshrief, O.A.; Coward, R.; Anasori, B.; Barsoum, M.W. Microscale deformation of (001) and (100) rutile single crystals under spherical nanoindentation. J. Mater. Res. 2012, 27, 53–63. [Google Scholar] [CrossRef]
- Taylor, C.R.; Malshe, A.P.; Salamo, G.; Prince, R.N.; Riester, L.; Cho, S.O. Characterization of ultra-low-load (mN) nanoindents in GaAs(100) using a cube corner tip. Smart Mater. Struct. 2005, 14, 963–970. [Google Scholar] [CrossRef]
- Tay, C.J.; Quan, C.; Gopal, M.; Shen, L.; Akkipeddi, R. Nanoindentation techniques in the measurement of mechanical properties of InP-based free-standing MEMS structures. J. Micromech. Microeng. 2008, 18, 025015. [Google Scholar] [CrossRef]
- Korte, S.; Farrer, I.; Clegg, W.J. Elastic and plastic properties of InxGa1−xAs. J. Phys. D Appl. Phys. 2008, 41, 205406. [Google Scholar] [CrossRef]
- Li, X.D.; Wang, X.; Xiong, Q.; Eklund, P.C. Mechanical properties of ZnS nanobelts. Nano Lett. 2005, 5, 1982–1986. [Google Scholar] [CrossRef]
- Kiran, M.S.R.N.; Kshirsagar, S.; Krishna, M.G.; Tewari, S.P. Structural, optical and nanomechanical properties of (111) oriented nanocrystalline ZnTe thin films. Eur. Phys. J. Appl. Phys. 2010, 51, 10502. [Google Scholar] [CrossRef]
- Onodera, A.; Kawi, N.; Ishizaki, K.; Spain, I.L. Semiconductor-to-metal transition in GaP under high pressure. Solid State Commun. 1974, 14, 803–806. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Yonenaga, I.; Suzuki, T. Indentation hardness of semiconductors and a scaling rule. Philos. Mag. Lett. 2002, 82, 535–542. [Google Scholar] [CrossRef]
- Chiu, Y.L.; Ngan, A.H.W. Time-dependent characteristics of incipient plasticity in nanoindentation of a Ni3Al single crystal. Acta Mater. 2002, 50, 1599–1611. [Google Scholar] [CrossRef]
- Leipner, H.S.; Lorenz, D.; Zeckzer, A.; Lei, H.; Grau, P. Nanoindentation pop-in effects in semiconductors. Phys. B Condens. Matter 2001, 308–310, 446–449. [Google Scholar] [CrossRef]
- Lorenz, D.; Zeckzer, A.; Hilpert, U.; Grau, P.; Johnson, H.; Leipner, H.S. Pop-in effects as homogeneous nucleation of dislocations during nanoindentation. Phys. Rev. B 2003, 67, 172101. [Google Scholar] [CrossRef]
- Chen, J.; Bull, S.J. Indentation fracture and toughness assessment for thin optical coatings on glass. J. Phys. Appl. Phys. 2007, 40, 5401–5417. [Google Scholar] [CrossRef]
- Niihara, K.; Morena, R.; Hasselman, D.P.H. Evaluation of KIC of brittle solids by indentation method with crack-to-indent ratios. J. Mater. Sci. Lett. 1982, 1, 13–16. [Google Scholar] [CrossRef]
- Niihara, K.; Morena, R.; Hasselman, D.P.H. A fracture mechanics analysis of indentation-induced Palmqvist crack in ceramics. J. Mater. Sci. Lett. 1983, 2, 221–223. [Google Scholar] [CrossRef]
- Harris, D.C. Materials for Infrared Windows and Domes: Properties and Performance; SPIE Optical Engineering Press: Bellingham, WA, USA, 1999. [Google Scholar]
- Rafiee, M.A.; Rafiee, J.; Srivastava, I.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Fracture and fatigue in graphene nanocomposites. Small 2010, 6, 179–183. [Google Scholar] [CrossRef]

| Materials | H (GPa) | E (GPa) |
|---|---|---|
| Single-crystal GaP(100) [#] | 12.5 ± 1.2 | 152.6 ± 12.8 |
| Single-crystal GaP [34] | 10.9 ± 0.2 (10 mN); 12.5 ± 0.2 (1 mN) | 147 ± 5 |
| Single-crystal GaAs(100) [32] | 7.5 | 97 |
| Single-crystal GaAs [34] | 8.4 ± 0.1 | 123 ± 1 |
| GaAs(100) thin films [48] | 10.62 ± 0.3 | 118.97 ± 3.81 |
| Single-crystal InP(100) [32] | 5.1 | 82 |
| InP layer [49] | 6.83 ± 0.71 | 97.1 ± 0.68 |
| InP substrate [49] | 6.41 ± 0.25 | 90.12 ± 1.59 |
| Single-crystal ZnSe [34] | 1.47 ± 0.02 | 72 ± 2 |
| ZnSe thin films [42] | 2.0 ± 0.1 | 72.6 ± 0.5 |
| Bulk InAs [50] | 5 | 69.9 |
| InAs layer [50] | 7.8 | 100 |
| Bulk ZnS [51] | 1.9 | 75 |
| ZnTe(111) thin films [52] | 4 | 70 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, Y.-J.; Jian, S.-R.; Lee, J.-W.; Juang, J.-Y. The Indentation-Induced Pop-in Phenomenon and Fracture Behaviors of GaP(100) Single-Crystal. Micromachines 2019, 10, 752. https://doi.org/10.3390/mi10110752
Chiu Y-J, Jian S-R, Lee J-W, Juang J-Y. The Indentation-Induced Pop-in Phenomenon and Fracture Behaviors of GaP(100) Single-Crystal. Micromachines. 2019; 10(11):752. https://doi.org/10.3390/mi10110752
Chicago/Turabian StyleChiu, Yi-Jui, Sheng-Rui Jian, Jyh-Wei Lee, and Jenh-Yih Juang. 2019. "The Indentation-Induced Pop-in Phenomenon and Fracture Behaviors of GaP(100) Single-Crystal" Micromachines 10, no. 11: 752. https://doi.org/10.3390/mi10110752
APA StyleChiu, Y.-J., Jian, S.-R., Lee, J.-W., & Juang, J.-Y. (2019). The Indentation-Induced Pop-in Phenomenon and Fracture Behaviors of GaP(100) Single-Crystal. Micromachines, 10(11), 752. https://doi.org/10.3390/mi10110752






