Compensating Circuit to Reduce the Impact of Wire Resistance in a Memristor Crossbar-Based Perceptron Neural Network
Abstract
1. Introduction
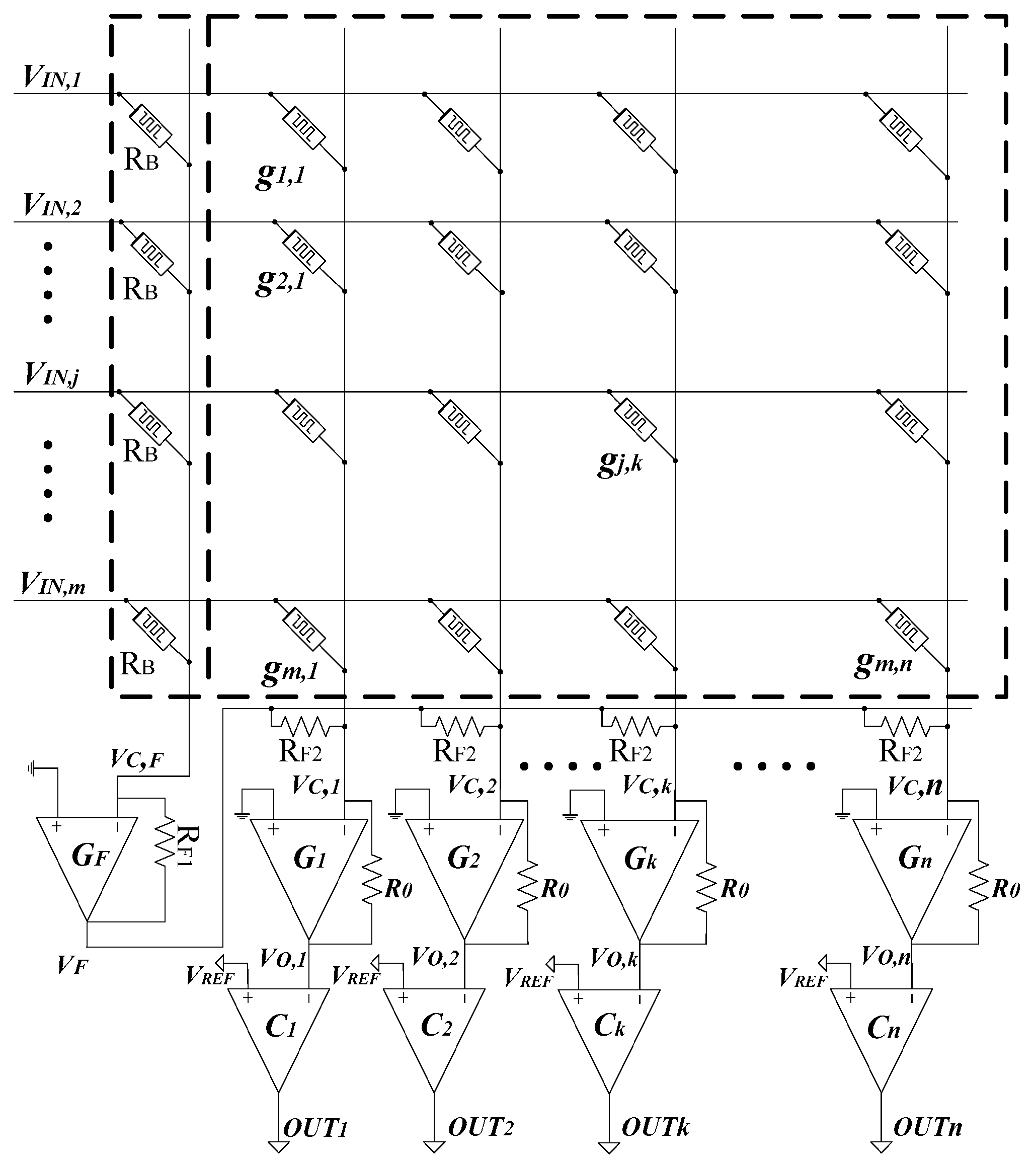
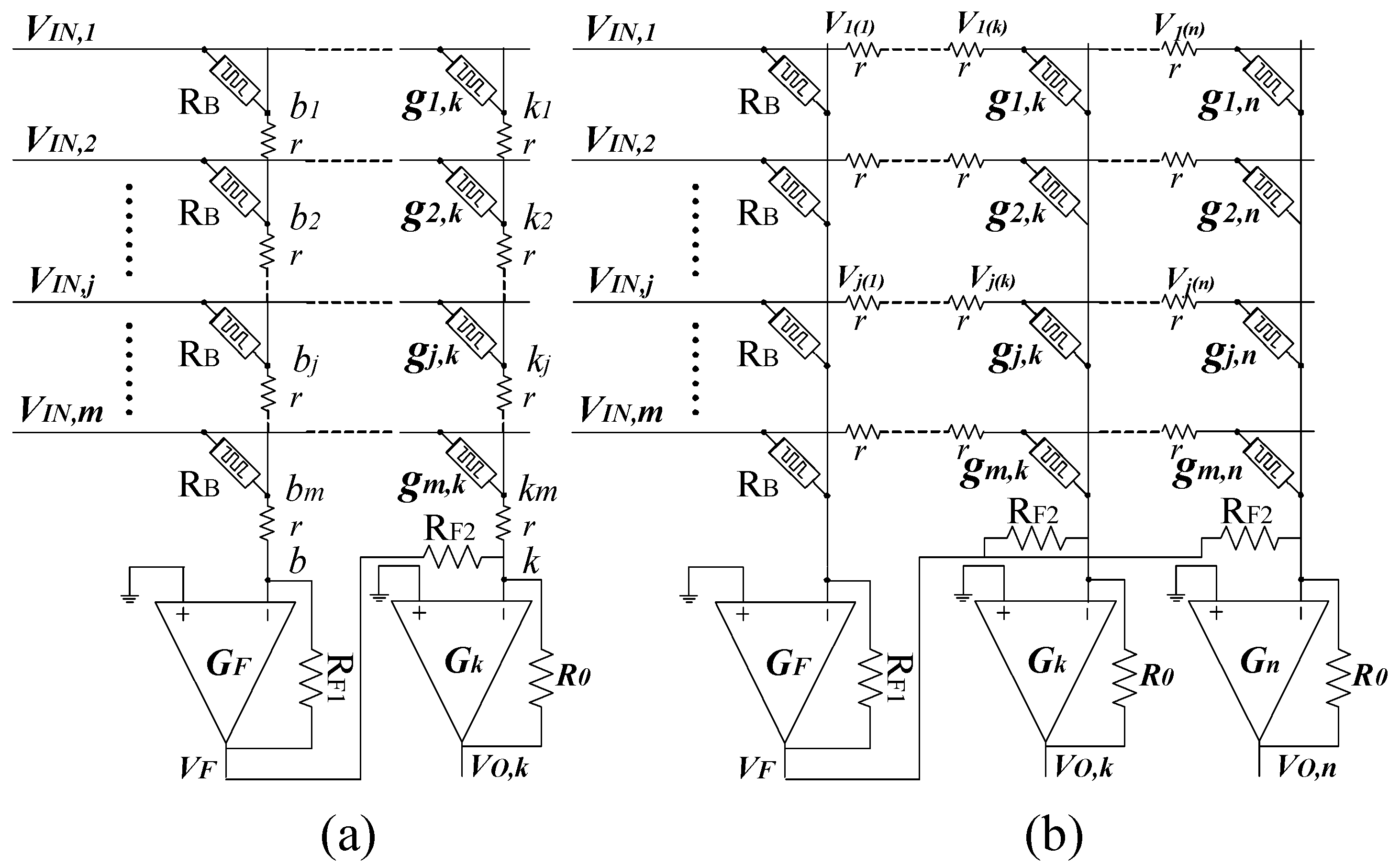
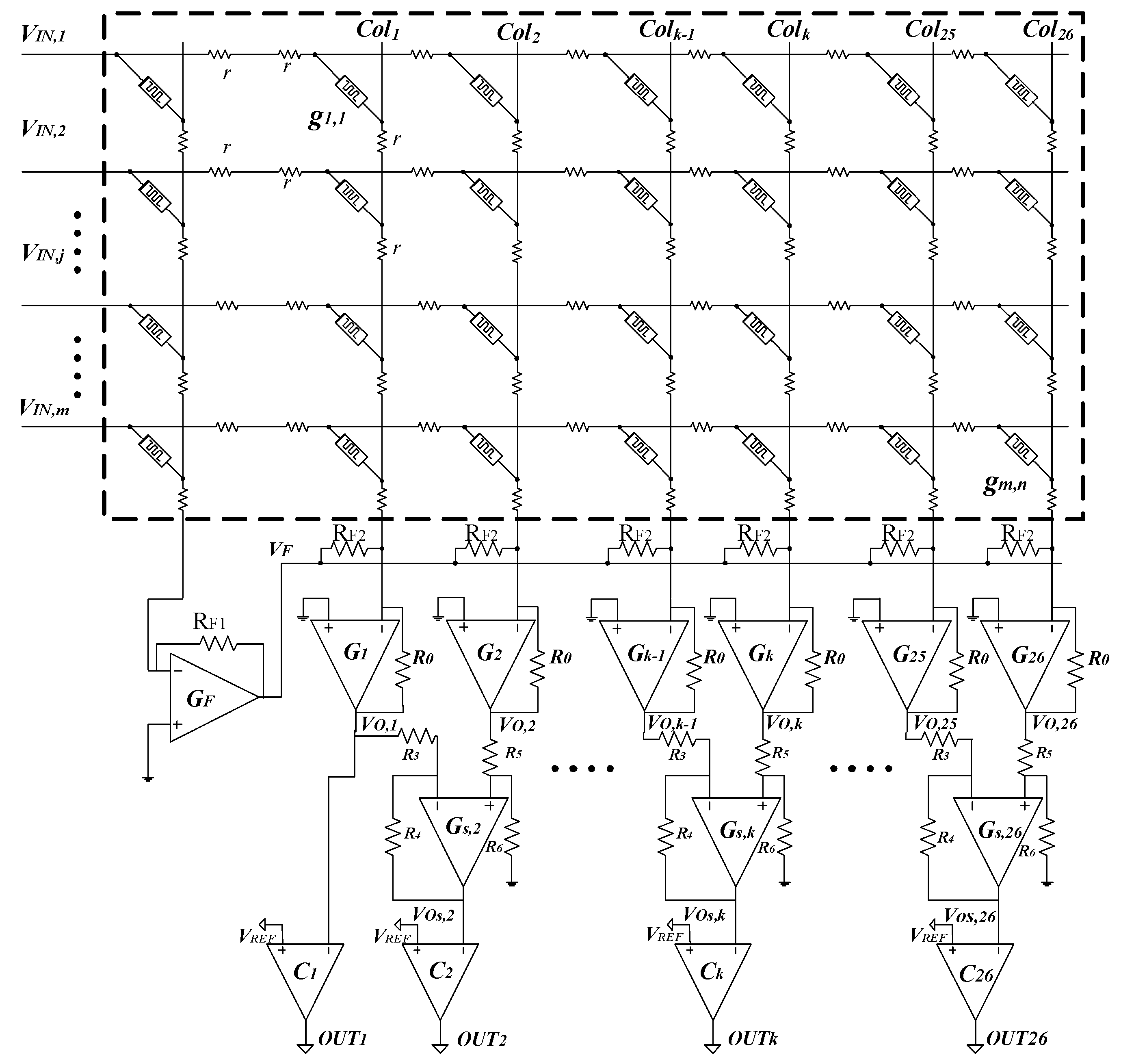
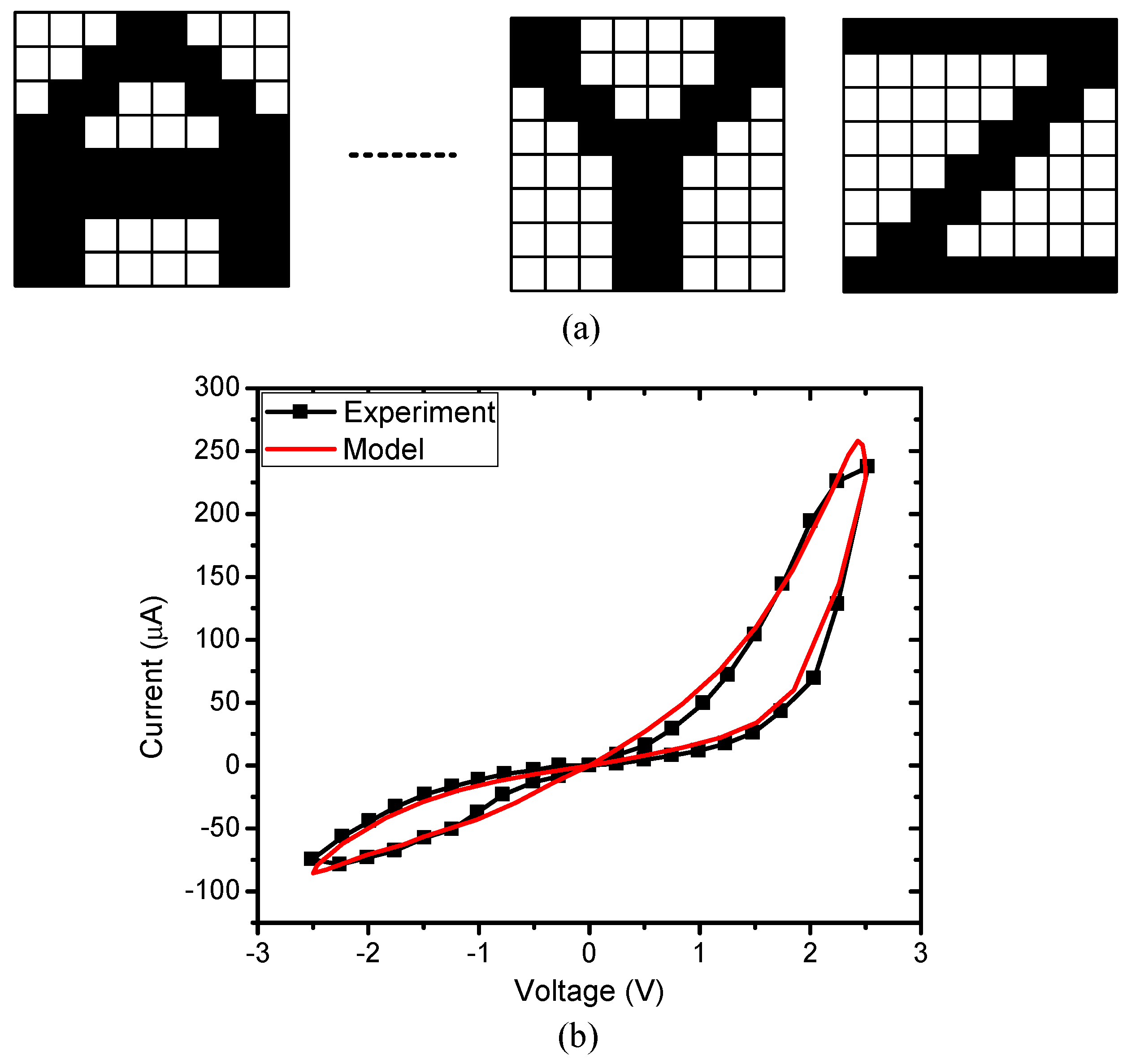
2. Materials and Methods
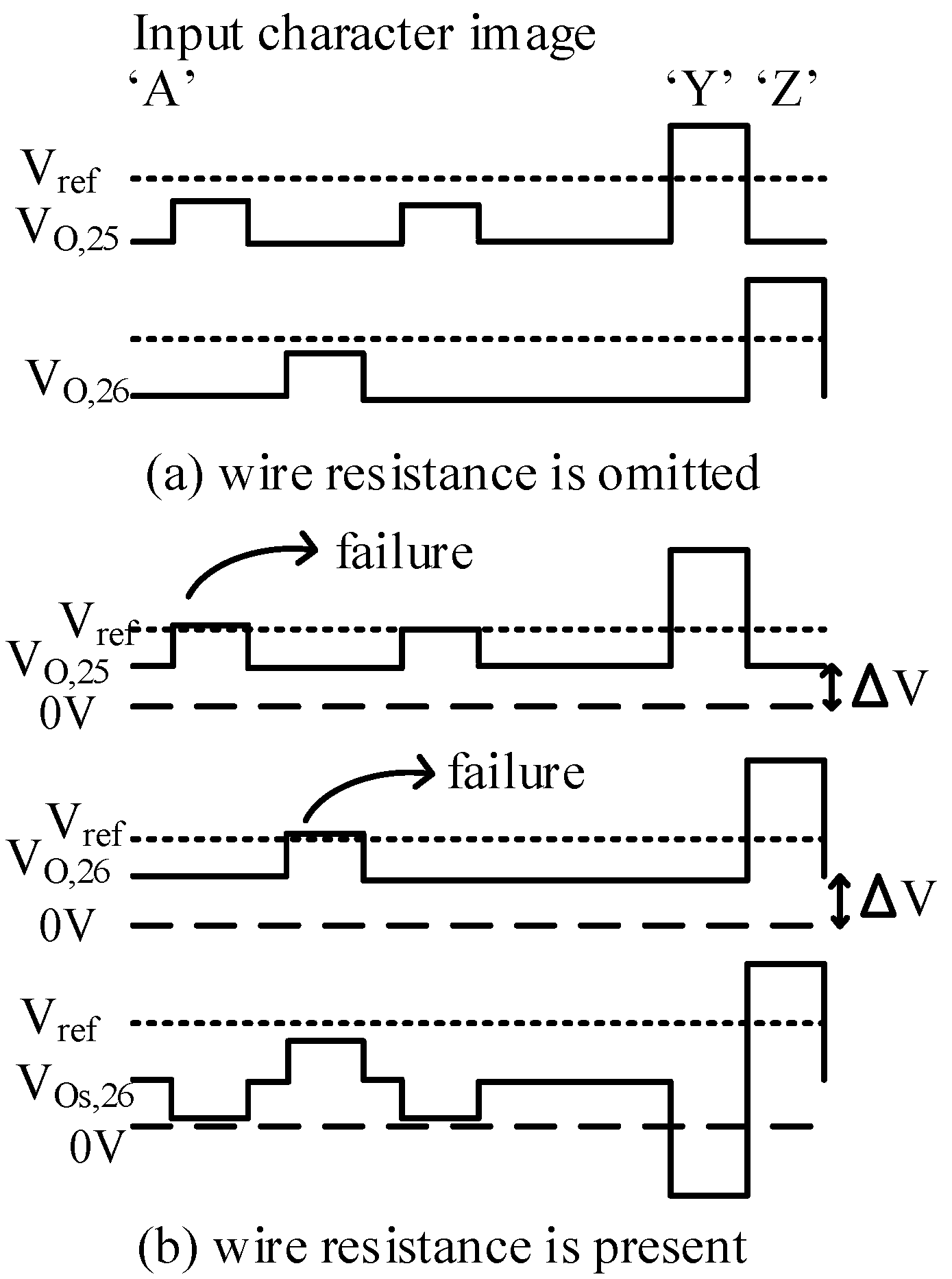
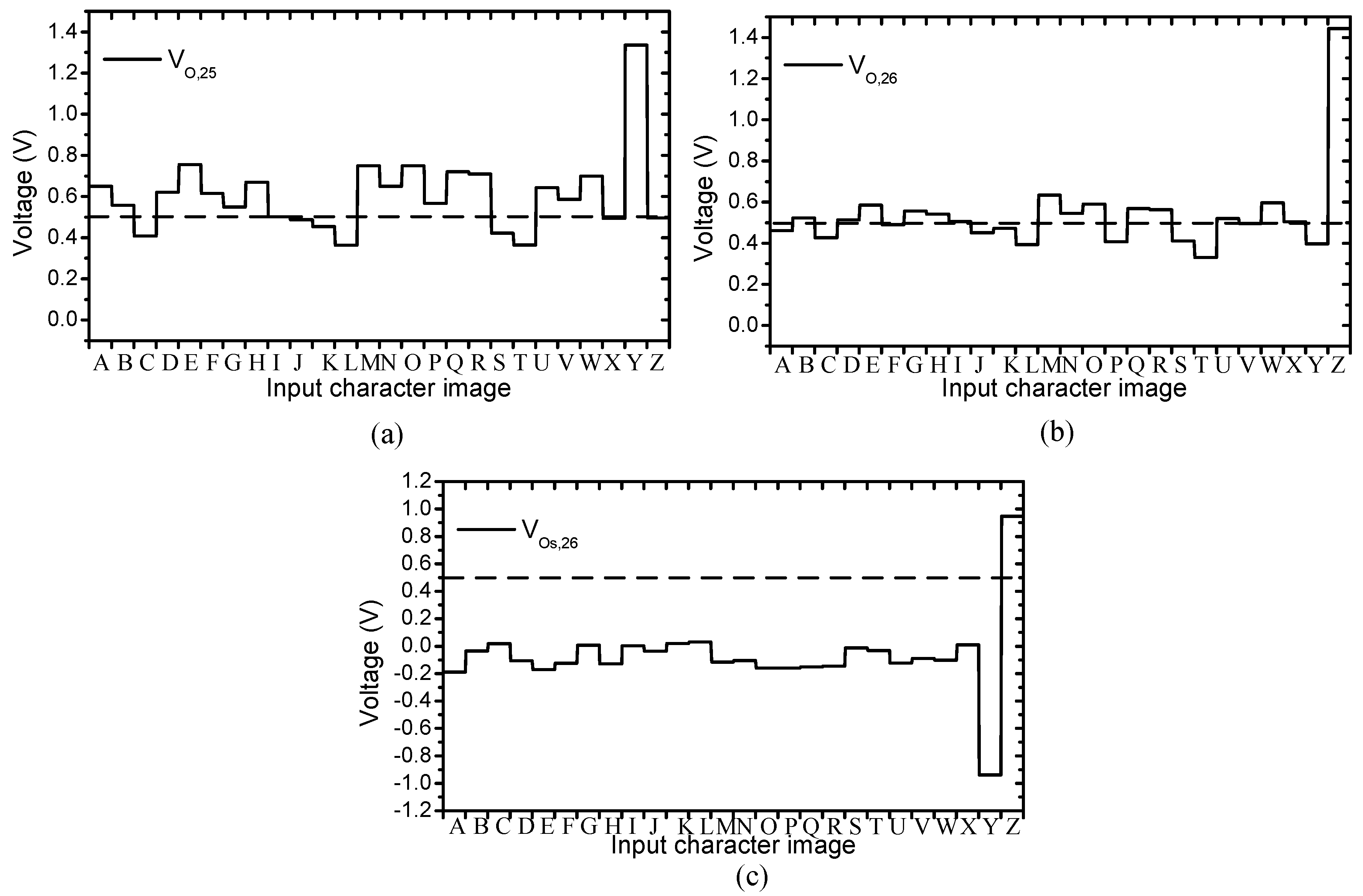
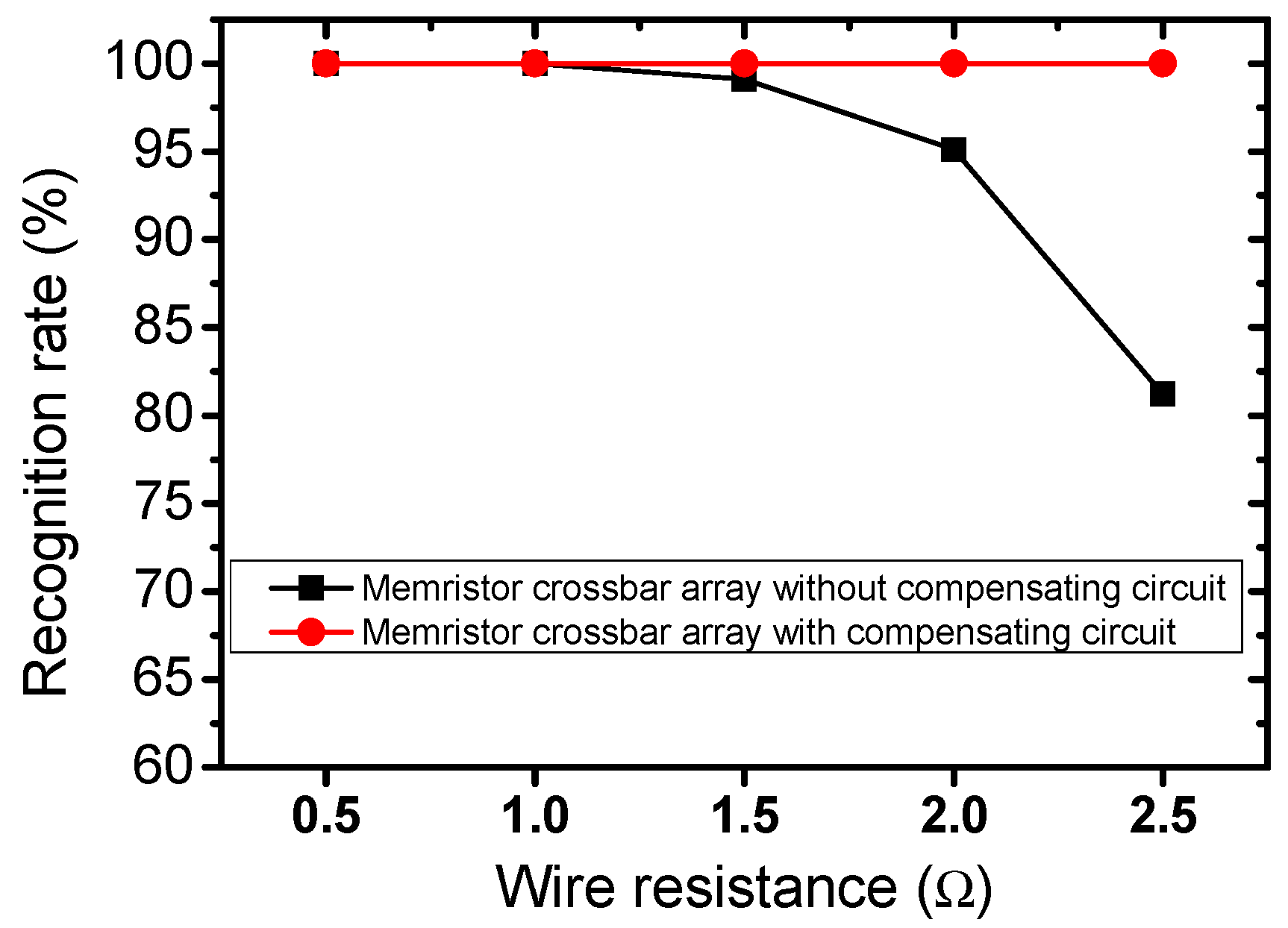
3. Results
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Mead, C. Neuromorphic electronic systems. Proc. IEEE 1990, 78, 1629–1636. [Google Scholar] [CrossRef]
- Pacheco, P.S. An Introduction to Parallel Programmin; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Mirsa, J.; Saha, I. Artificial neural networks in hardware: A survey of two decades of progress. Neurocomputing 2010, 74, 239–255. [Google Scholar]
- Himavathi, S.; Anitha, D.; Muthuramalingam, A. Feedforward neural network implementation in FPGA using layer multiplexing for effective resource utilization. IEEE Trans. Neural Netw. 2007, 18, 880–888. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Du, L.; Gu, X.; Du, J.; Wang, X.S.; Hu, B.; Jiang, M.; Chen, X.; Su, J.; Iye, S.S.; et al. An analog neural network computing engine using CMOS-compatible charge-trap-transistor (CTT). IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2018, 38, 1811–1819. [Google Scholar] [CrossRef]
- Kawaguchia, M.; Ishiib, N.; Umeno, M. Analog neural circuit and hardware design of deep learning model. Procedia Comput. Sci. 2015, 60, 976–985. [Google Scholar] [CrossRef]
- Wang, F.; Li, Y.X. Analog Circuit Design Automation Using Neural Network-Based Two-Level Genetic Programming. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006. [Google Scholar]
- Shima, T.; Kimura, T.; Kamatani, Y.; Itakura, T.; Fujita, Y.; Iida, T. Neuro chips with on-chip back-propagation and/or Hebbian learning. IEEE J. Solid-State Circuits 1992, 27, 1868–1875. [Google Scholar] [CrossRef]
- Solomon, P.M. Device innovation and material challenges at the limit of CMOS technology. Annu. Rev. Mater. Sci. 2000, 30, 681–697. [Google Scholar] [CrossRef]
- Brđanin, T.P.; Dokić, B. Strained silicon layer in CMOS technology. Electronics 2014, 18, 63–69. [Google Scholar]
- Kügeler, C.; Meier, M.; Rosezin, R.; Gilles, S.; Waser, R. High density 3D memory architecture based on the resistive switching effect. Solid State Electron. 2009, 53, 1287–1292. [Google Scholar] [CrossRef]
- Chua, L.O. Memristor—The missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Sinder, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.H.; Chang, T.; Ebong, I.; Bhadviya, B.B.; Mazumder, P.; Lu, W. Nanoscale memristor device as synapse in neuromorphic systems. Nano Letters 2010, 10, 1297–1301. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Li, H.; Pino, R.E. Memristor-based synapse design and training scheme for neuromorphic computing architecture. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–5. [Google Scholar]
- Kim, H.; Sad, M.P.; Yang, C.; Roska, T.; Chua, L.O. Neural synapse weighting with a pulse-based memristor circuit. IEEE Trans. Circuit Syst. 2012, 59, 148–158. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Yang, C.; Kim, H.; Chua, L.O. Memristor bridge synapse-based neural network and its learning. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1426–1435. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.C.; Li, H.; Zhang, W.; Pino, R.E. The 3-D stacking bipolar RRAM for high density. IEEE Trans. Nanotechnol. 2012, 11, 948–956. [Google Scholar] [CrossRef]
- Liang, J.; Wong, H.S.P. Cross-point memristor array without cell selector—Device characteristics and data storage pattern dependencies. IEEE Trans. Electron. Device 2010, 57, 2531–2538. [Google Scholar] [CrossRef]
- Hu, M.; Li, H.; Wu, Q.; Rose, G.S.; Chen, Y. Memristor crossbar based hardware realization of BSB recall function. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, Australia, 10–15 June 2012; pp. 1–7. [Google Scholar]
- Truong, S.N.; Min, K.S. New memristor-based crossbar array architecture with 50-% area reduction and 48-% power saving for matrix-vector multiplication of analog neuromorphic computing. J. Semicond. Technol. Sci. 2014, 14, 356–363. [Google Scholar] [CrossRef]
- Soudry, D.; Castro, D.D.; Gal, A.; Kolodny, A.; Kvatinsky, S. Memristor-Based Multilayer Neural Networks with Online Gradient Descent Training. IEEE Trans. Neural Netw. Learn. Syst. 2015, 36, 2048–2421. [Google Scholar] [CrossRef]
- Wang, L.; Shen, Y.; Yin, Q.; Zhang, G. Adaptive synchronization of memristor-based neural networks with time-varying delays. IEEE Trans. Neural Netw. Learn Syst. 2014, 26, 2033–2042. [Google Scholar] [CrossRef]
- Linn, E.; Rosezin, R.; Kügeler, C.; Waser, R. Complementary resistive switches for passive nanocrossbar memories. Nature Mater. 2010, 9, 403–406. [Google Scholar] [CrossRef]
- Shin, S.H.; Byeon, S.D.; Song, J.S.; Truong, S.N.; Mo, H.S.; Kim, D.J.; Min, K.S. Dynamic reference scheme with improved read voltage margin for compensating cell-position and back ground-pattern dependencies in pure memristor array. J. Semicond. Technol. Sci. 2015, 15, 685–694. [Google Scholar] [CrossRef]
- Levisse, A.; Royer, P.; Giraud, B.; Noel, J.P.; Moreau, M.; Portal, J.M. Architecture, design and technology guidelines for crosspoint memories. In Proceedings of the 2017 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Newport, RI, USA, 25–26 July 2017. [Google Scholar]
- Giraud, B.; Makosiej, A.; Boumchedda, R.; Gupta, N.; Levisse, A.; Vianello, E.; Noel, J.-P. Advanced memory solutions for emerging circuits and systems. In Proceedings of the 2017 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 2–6 December 2017. [Google Scholar]
- Truong, S.N.; Pham, K.V.; Yang, W.; Shin, S.; Pedrotti, K.; Min, K.S. New pulse amplitude modulation for fine tuning of memristor synapses. Mircoelectron. J. 2016, 55, 162–168. [Google Scholar] [CrossRef]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E.; Rogers, S. A memristor device model. IEEE Electron Device Lett. 2011, 32, 1436–1438. [Google Scholar] [CrossRef]
- Spectre® Circuit Simulator User Guide. Available online: https://www.ee.columbia.edu/~harish/uploads/2/6/9/2/26925901/spectre_reference.pdf (accessed on 1 October 2019).
- International Technology Roadmap for Semiconductors. 2007. Available online: https://www.semiconductors.org/wp-content/uploads/2018/08/2007Interconnect.pdf (accessed on 1 October 2019).
- Kim, S.; Zhou, J.; Lu, W.D. Crossbar RRAM arrays: Selector device requirements during wire operation. IEEE Trans. Electron. Devices 2014, 61, 2820–2826. [Google Scholar]
- Schindler, G.; Steinlesberger, G.; Engelhardt, M.; Steinhögl, W. Electrical characterization of copper interconnects with end-of-roadmap feature sizes. Solid State Electron. 2003, 47, 1233–1236. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organization and Associative Memory. In Information Sciences; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Li, C.; Belkin, D.; Li, Y.; Yan, P.; Hu, M.; Ge, N.; Jiang, H.; Montgomery, E.; Lin, P.; Wang, Z.; et al. Efficient and self-adaptive in-situ learning in multilayer memristor neural networks. Nat. Commun. 2018, 9, 2385. [Google Scholar] [CrossRef]
- Caravelli, F.; Carbajal, J.P. Memristors for the curious outsider. Technologies 2018, 6, 118. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truong, S.N. Compensating Circuit to Reduce the Impact of Wire Resistance in a Memristor Crossbar-Based Perceptron Neural Network. Micromachines 2019, 10, 671. https://doi.org/10.3390/mi10100671
Truong SN. Compensating Circuit to Reduce the Impact of Wire Resistance in a Memristor Crossbar-Based Perceptron Neural Network. Micromachines. 2019; 10(10):671. https://doi.org/10.3390/mi10100671
Chicago/Turabian StyleTruong, Son Ngoc. 2019. "Compensating Circuit to Reduce the Impact of Wire Resistance in a Memristor Crossbar-Based Perceptron Neural Network" Micromachines 10, no. 10: 671. https://doi.org/10.3390/mi10100671
APA StyleTruong, S. N. (2019). Compensating Circuit to Reduce the Impact of Wire Resistance in a Memristor Crossbar-Based Perceptron Neural Network. Micromachines, 10(10), 671. https://doi.org/10.3390/mi10100671




