Comparison of the Electrical Response of Cu and Ag Ion-Conducting SDC Memristors Over the Temperature Range 6 K to 300 K
Abstract
:1. Introduction
2. Materials and Methods
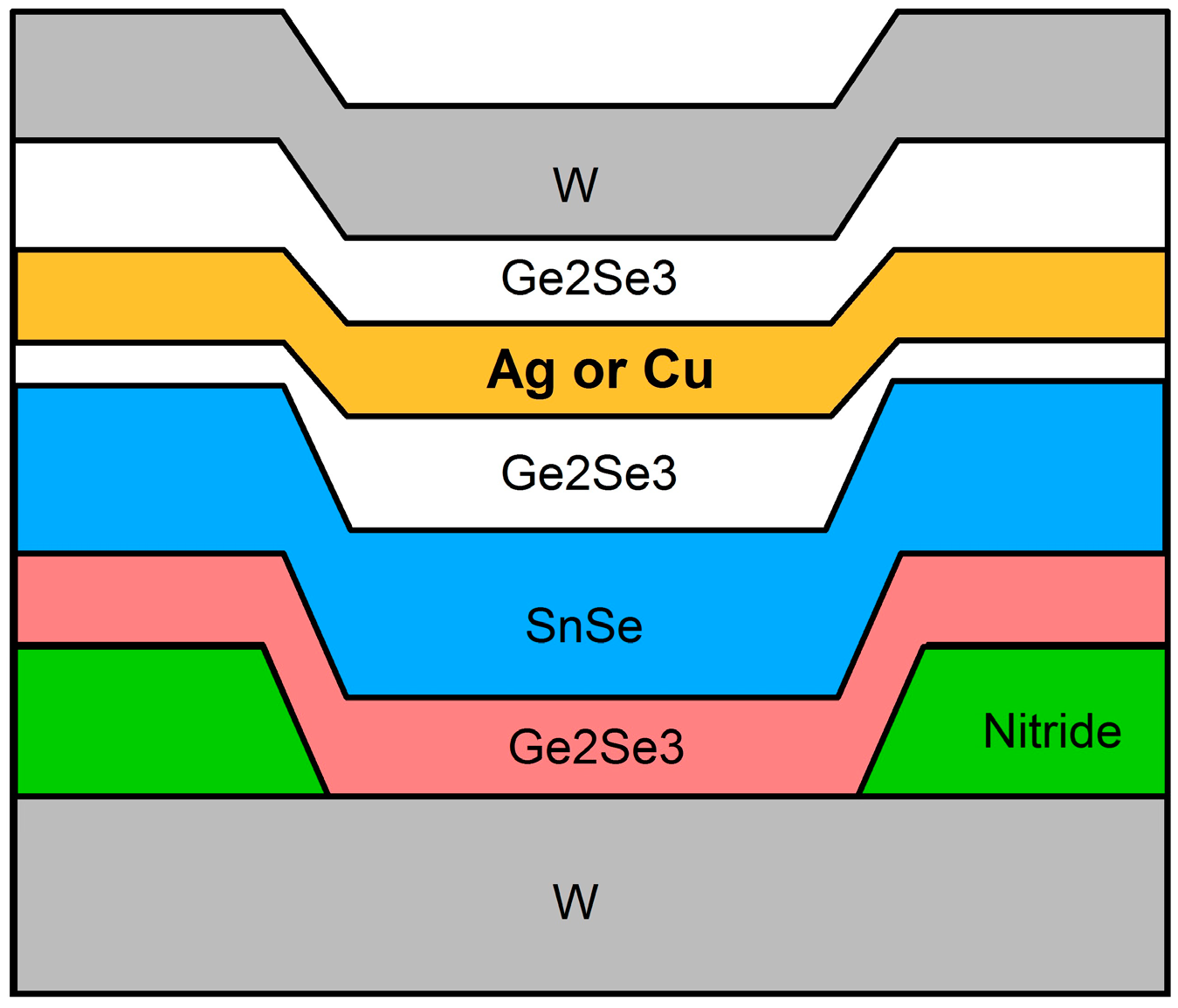
2.1. Device Structure and Fabrication
2.2. Electrical Measurements
3. Results
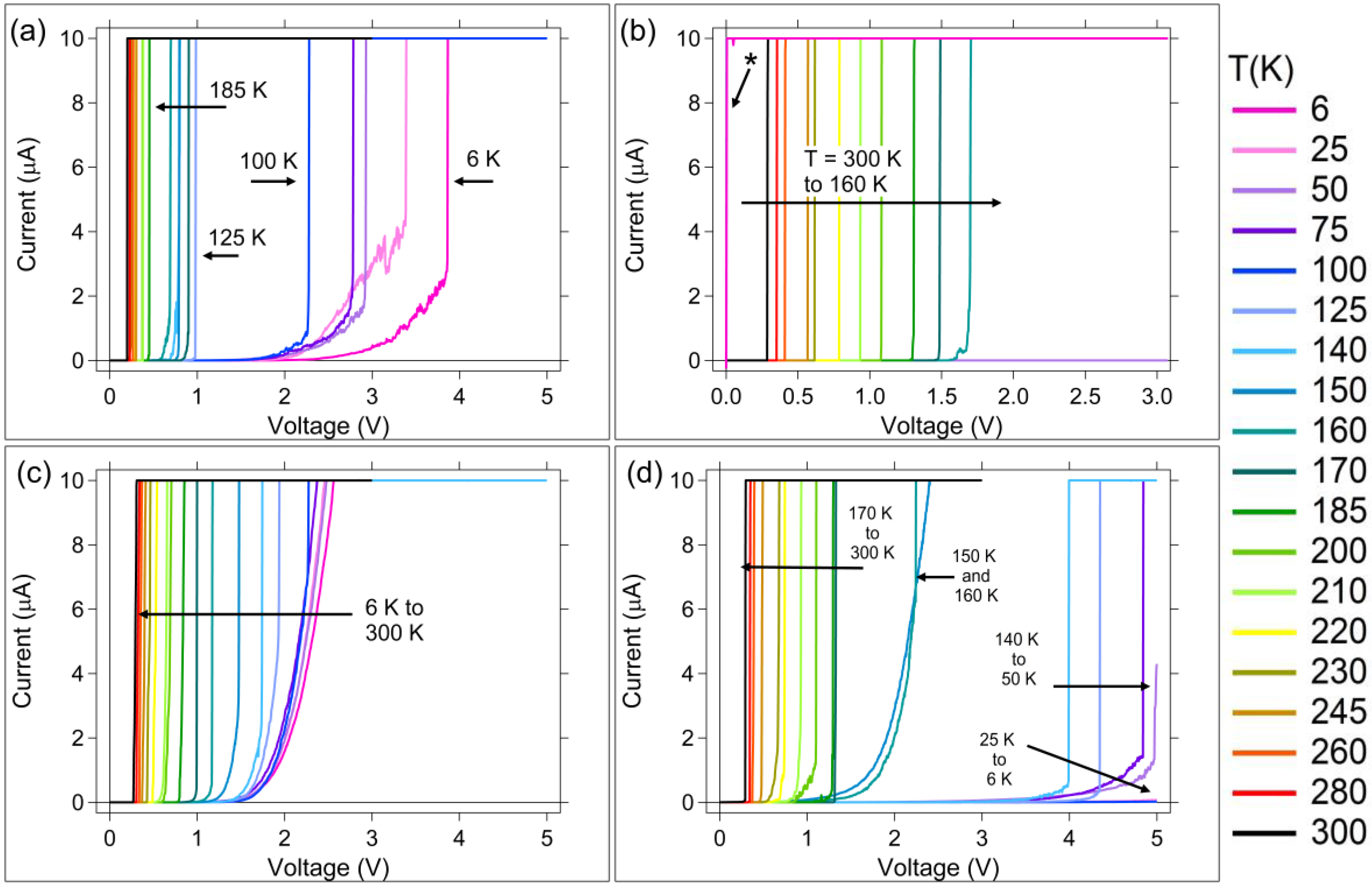
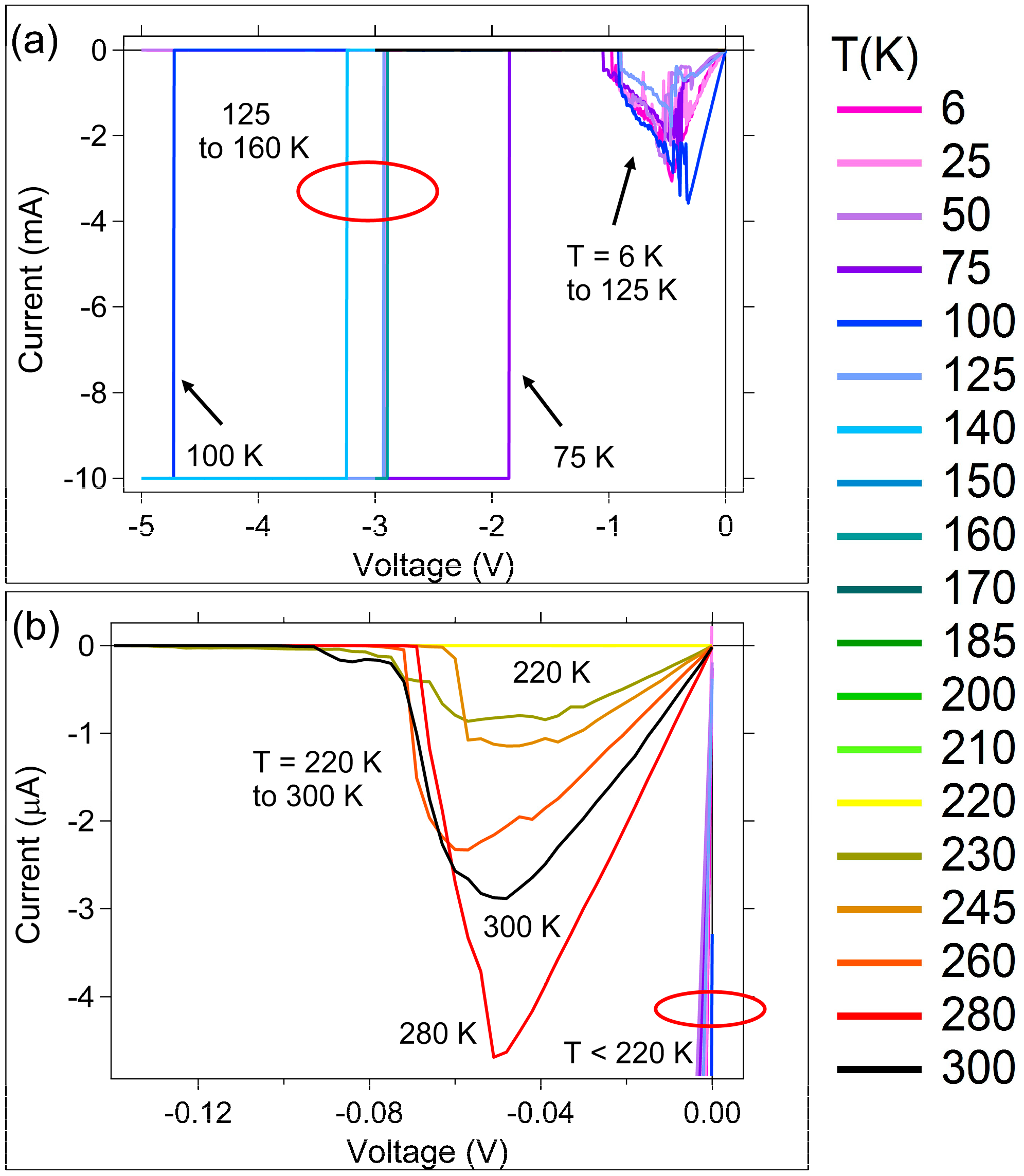
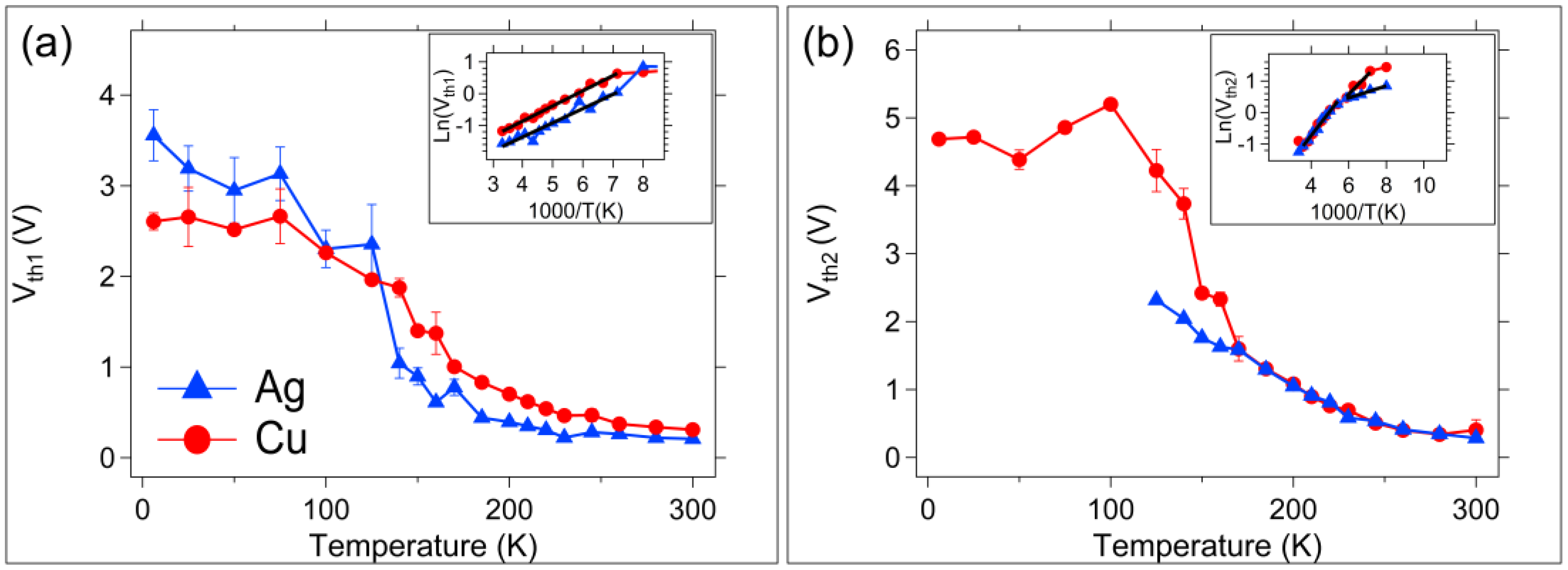
3.1. DC (Quasi-Static) Measurements
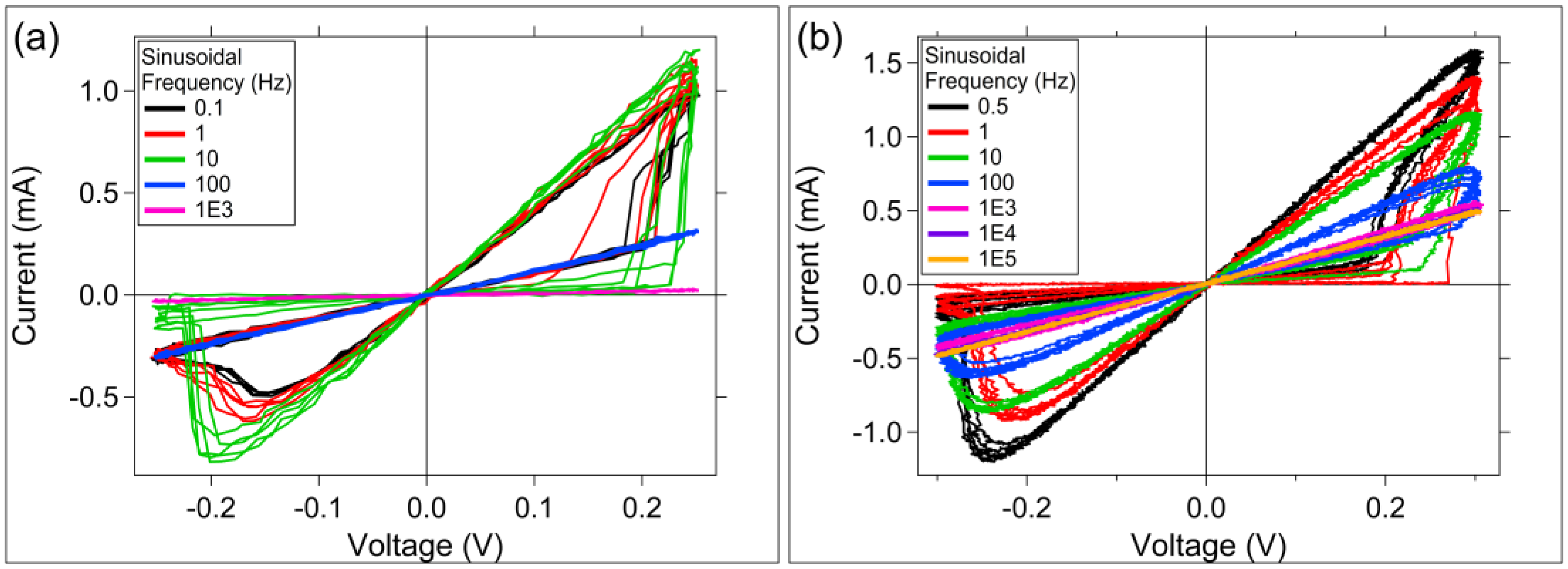
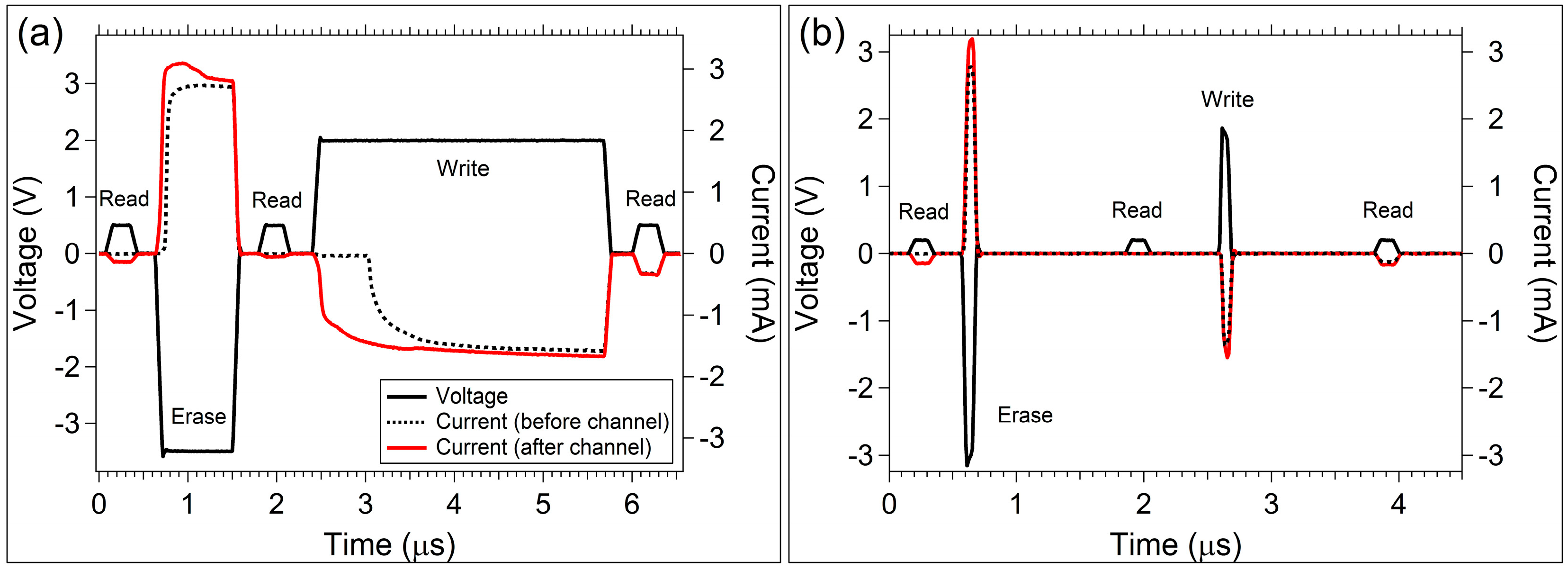
3.2. Sinusoidal Excitation and Pulsed Response
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Valov, I.; Waser, R.; Jameson, J.R.; Kozicki, M.N. Electrochemical metallization memories-fundamentals, applications, prospects. Nanotechnology 2011, 22, 254003. [Google Scholar] [CrossRef] [PubMed]
- Waser, R.; Ielmini, D.; Akinaga, H.; Shima, H.; Wong, H.-S.P.; Yang, J.J.; Yu, S. Introduction to nanoionics elements for information technology. In Resistive Switching; Ielmini, D., Waser, R., Eds.; Wiley-VCH: Weinheim, Germany, 2016; pp. 1–29. [Google Scholar]
- Zidan, M.A.; Chen, A.; Indiveri, G.; Lu, W.D. Memristive computing devices and applications. J. Electroceram. 2017. [Google Scholar] [CrossRef]
- Waser, R.; Dittmann, R.; Menzel, S.; Noll, T. Introduction to new memory paradigms: Memristive phenomena and neuromorphic applications. Faraday Discuss. 2019, 213, 11–27. [Google Scholar] [CrossRef] [PubMed]
- Menzel, S.; Tappertzhofen, S.; Waser, R.; Valov, I. Switching Kinetics of Electrochemical Metallization Memory Cells. Phys. Chem. Chem. Phys. 2013, 15, 6945–6952. [Google Scholar] [CrossRef] [PubMed]
- Campbell, K.A. Self-Directed Channel Memristor for High Temperature Operation. Microelectron. J. 2017, 59, 10–14. [Google Scholar] [CrossRef]
- Campbell, K.A. Self-Directed Channel Memristor: Operational Dependence on the Metal-Chalcogenide Layer. In Handbook of Memristor Networks; Springer: New York, NY, USA, 2019; p. 38. [Google Scholar]
- Rajendran, B.; Alibart, F. Neuromorphic computing based on emerging memory technologies. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 198–211. [Google Scholar] [CrossRef]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Van den Hurk, J.; Havel, V.; Linn, E.; Waser, R.; Valov, I. Ag/GeSx/Pt-based complementary resistive switches for hybrid CMOS/ nanoelectronic logic and memory architectures. Sci. Rep. 2013, 3, 2856. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Chamele, N.; Gonzalez-Velo, Y.; Barnaby, H.J.; Kozicki, M.N. Low-temperature characterization of Cu-Cu: Silica-based programmable metallization cell. IEEE Electron Device Lett. 2017, 38, 1244–1247. [Google Scholar] [CrossRef]
- Kozicki, M.N.; Barnaby, H.J. Conductive bridging random access memory-materials, devices and applications. Semicond. Sci. Technol. 2016, 31, 113001. [Google Scholar] [CrossRef]
- Mahalanabis, D.; Barnaby, H.J.; Gonzalez-Velo, Y.; Kozicki, M.N.; Vrudhula, S.; Dandamudi, P. Incremental resistance programming of programmable metallization cells for use as electronic synapses. Solid-State Electron. 2014, 100, 39–44. [Google Scholar] [CrossRef]
- Campbell, K.A.; Drake, K.T.; Barney Smith, E.H. Pulse shape and timing dependence on the spike-timing dependent plasticity response of ion-conducting memristors as synapses. Front. Bioeng. Biotechnol. 2016, 4, 97. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Minghui, Y.; Zhang, T.; Cai, Y.; Wang, Y.B.; Yang, Y.; Huang, R. Engineering incremental resistive switching in TaOx based memristors for brain-inspired computing. Nanoscale 2016, 8, 14015–14022. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.Q.; Xu, H.Y.; Li, X.H.; Yu, H.; Liu, Y.C.; Zhu, X.J. Synaptic learning and memory functions achieved using oxygen ion migration/diffusion in an amorphous InGaZnO memristor. Adv. Funct. Mater. 2012, 22, 2759–2765. [Google Scholar] [CrossRef]
- Pickett, M.D.; Medeiros-Ribeiro, G.; Williams, R.S. A scalable neuristor built with Mott memristors. Nat. Mater. 2013, 12, 114–117. [Google Scholar] [CrossRef] [PubMed]
- Mahalanabis, D.; Sivaraj, M.; Chen, W.; Shah, S.; Barnaby, H. Demonstration of spike timing dependent plasticity in CBRAM devices with silicon neurons. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016. [Google Scholar] [CrossRef]
- Gaba, S.; Sheridan, P.; Zhou, J.; Choi, S.; Lu, W. Stochastic memristive devices for computing and neuromorphic applications. Nanoscale 2013, 5, 5872–5878. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Edwards, A.H.; Barnaby, H.J.; Campbell, K.A.; Kozicki, M.N.; Liu, W.; Marinella, M.J. Reconfigurable memristive device technologies. Proc. IEEE 2015, 103, 1004–1033. [Google Scholar] [CrossRef]
- Arita, M.; Ohno, Y.; Murakami, Y.; Takamizawa, K.; Tsurumaki-Fukuchi, A.; Takahashi, Y. Microstructural transitions in resistive random access memory composed of molybdenum oxide with copper during switching cycles. Nanoscale 2016, 8, 14754–14766. [Google Scholar] [CrossRef]
- Schindler, C.; Valov, I.; Waser, R. Faradaic currents during electroforming of resistively switching Ag-Ge-Se type electrochemical metallization memory cells. Phys. Chem. Chem. Phys. 2009, 11, 5974–5979. [Google Scholar] [CrossRef]
- Jameson, J.R.; Gilbert, N.; Koushan, F.; Saenz, J.; Wang, J.; Hollmer, S.; Kozicki, M. Effects of cooperative ionic motion on programming kinetics of conductive-bridge memory cells. Appl. Phys. Lett. 2012, 100, 023505. [Google Scholar] [CrossRef]
- Jameson, J.R.; Gilbert, N.; Koushan, F.; Saenz, J.; Wang, J.; Hollmer, S.; Kozicki, M.; Derhacobian, N. Quantized conductance in Ag/GeS2/W conductive-bridge memory cells. IEEE Electron Device Lett. 2012, 33, 257–259. [Google Scholar] [CrossRef]
- Kozicki, M.N.; Mitkova, M. Mass transport in chalcogenide electrolyte films–materials and applications. J. Non-Cryst. Solids 2006, 352, 567–577. [Google Scholar] [CrossRef]
- Wang, F.; Dunn, W.P.; Jain, M.; De Leo, C.; Vickers, N. The effects of active layer thickness on programmable metallization cell based on Ag-Ge-S. Solid-State Electron. 2011, 61, 33–37. [Google Scholar] [CrossRef]
- Kamalanathan, D.; Russo, U.; Ielmini, D.; Kozicki, M.N. Voltage-driven on-off transition and tradeoff with program and erase current in programmable metallization cell (PMC) memory. IEEE Electron Device Lett. 2009, 30, 553–555. [Google Scholar] [CrossRef]
- Mitkova, M.; Kozicki, M.N. Silver incorporation in Ge-Se glasses used in programmable metallization cell devices. J. Non-Cryst. Solids 2002, 299, 1023–1027. [Google Scholar] [CrossRef]
- Kamalanathan, D.; Akhavan, A.; Kozicki, M.N. Low voltage cycling of programmable metallization cell memory devices. Nanotechnology 2011, 22, 254017. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Mitkova, M.; Georgiev, D.G.; Mamedov, S.; Boolchand, P. Macroscopic phase separation of Se-rich (x<1/3) ternary Agy(GexSe1−x)1−y glasses. J. Phys. Condens. Matter 2003, 15, S1573–S1584. [Google Scholar]
- Lee, D.; Oukassi, S.; Molas, G.; Carabasse, C.; Salot, R.; Perniola, L. Memory and energy storage dual operation in chalcogenide-based CBRAM. IEEE Electron Dev. Soc. 2017, 5, 283–287. [Google Scholar] [CrossRef]
- Song, M.-J.; Kwon, K.-H.; Park, J.-G. Electro-forming and electro-breaking of nanoscale Ag filaments for conductive-bridging random-access memory cell using Ag-doped polymer-electrolyte between Pt electrodes. Sci. Rep. 2017, 7, 3065. [Google Scholar] [CrossRef]
- Jeon, Y.-R.; Abbas, Y.; Sokolov, A.S.; Kim, S.; Ku, B.; Choi, C. Study of in situ silver migration in amorphous boron nitride CBRAM device. ACS Appl. Mater. Interfaces 2019, 11, 23320–23336. [Google Scholar] [CrossRef]
- Valov, I.; Tsuruoka, T. Effects of moisture and redox reactions in VCM and ECM resistive switching memories. J. Phys. D Appl. Phys. 2018, 51, 413001. [Google Scholar] [CrossRef]
- Li, P.; Wang, Q.; Deng, G.; Guo, X.; Jiang, W.; Liu, H.; Li, F.; Thanh, N.T.K. A new insight into the thermodynamical criterion for the preparation of semiconductor and metal nanocrystals using a polymerized complexing method. Phys. Chem. Chem. Phys. 2017, 19, 24742–24751. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yalon, E.; Kalaev, D.; Gavrilov, A.; Cohen, S.; Riess, I.; Ritter, D. Detection of the conductive filament growth direction in resistive memories. In Proceedings of the 72nd Device Research Conference, Santa Barbara, CA, USA, 22–25 June 2014; pp. 299–300. [Google Scholar]
- Celano, U.; Goux, L.; Belmonte, A.; Opsomer, K.; Franquet, A.; Schulze, A.; Detavernier, C.; Richard, O.; Bender, H.; Jurczak, M.; et al. Three-dimensional observation of the conductive filament in nanoscaled resistive memory devices. Nano Lett. 2014, 14, 2401–2406. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Li, X.; Xu, H.; Wang, Z.; Ding, W.; Liu, W.; Ma, J.; Liu, Y. Improved uniformity and endurance through suppression of filament overgrowth in electrochemical metallization memory with AgInSbTe buffer layer. Electron Dev. Soc. 2018, 6, 714–720. [Google Scholar] [CrossRef]
- Shaban, M.; Kholidy, I.; Ahmed, G.M.; Negem, M.; El-Salam, H.M.A. Cyclic voltammetry growth and characterization of Sn-Ag alloys of different nanomorphologies and compositions for efficient hydrogen evolution in alkaline solutions. RSC Adv. 2019, 9, 22389–22400. [Google Scholar] [CrossRef]
- Walsh, F.C.; Low, C.T.J. Composite, multi-layer and three-dimensional substrate supported tin based electrodeposits from methanesulfonic acid. Trans. Inst. Met. Finish. 2016, 94, 152–158. [Google Scholar] [CrossRef]
- Chua, L. Everything you wish to know about memristors but are afraid to ask. Radioengineering 2015, 24, 331–368. [Google Scholar] [CrossRef]
- Chiang, T.-H.; Wager, J.F. Electronic conduction mechanisms in insulators. IEEE Trans. Electron Dev. 2018, 64, 223–230. [Google Scholar] [CrossRef]
- Bychkov, E. Superionic and ion-conducting chalcogenide glasses: Transport regimes and structural features. Sol. Stat. Ion. 2009, 180, 510–516. [Google Scholar] [CrossRef]
- Chiu, F.-C. A review on conduction mechanisms in dielectric films. Adv. Mater. Sci. Eng. 2014, 578168. [Google Scholar] [CrossRef]
- Jo, H.; Kim, M.-W.; Hong, W.-K. Voltage sweep direction-dependent metal-insulator transition in a single-crystalline VO2 nanobeam embedded in a insulating layer. J. Alloy. Compd. 2017, 720, 445–450. [Google Scholar] [CrossRef]

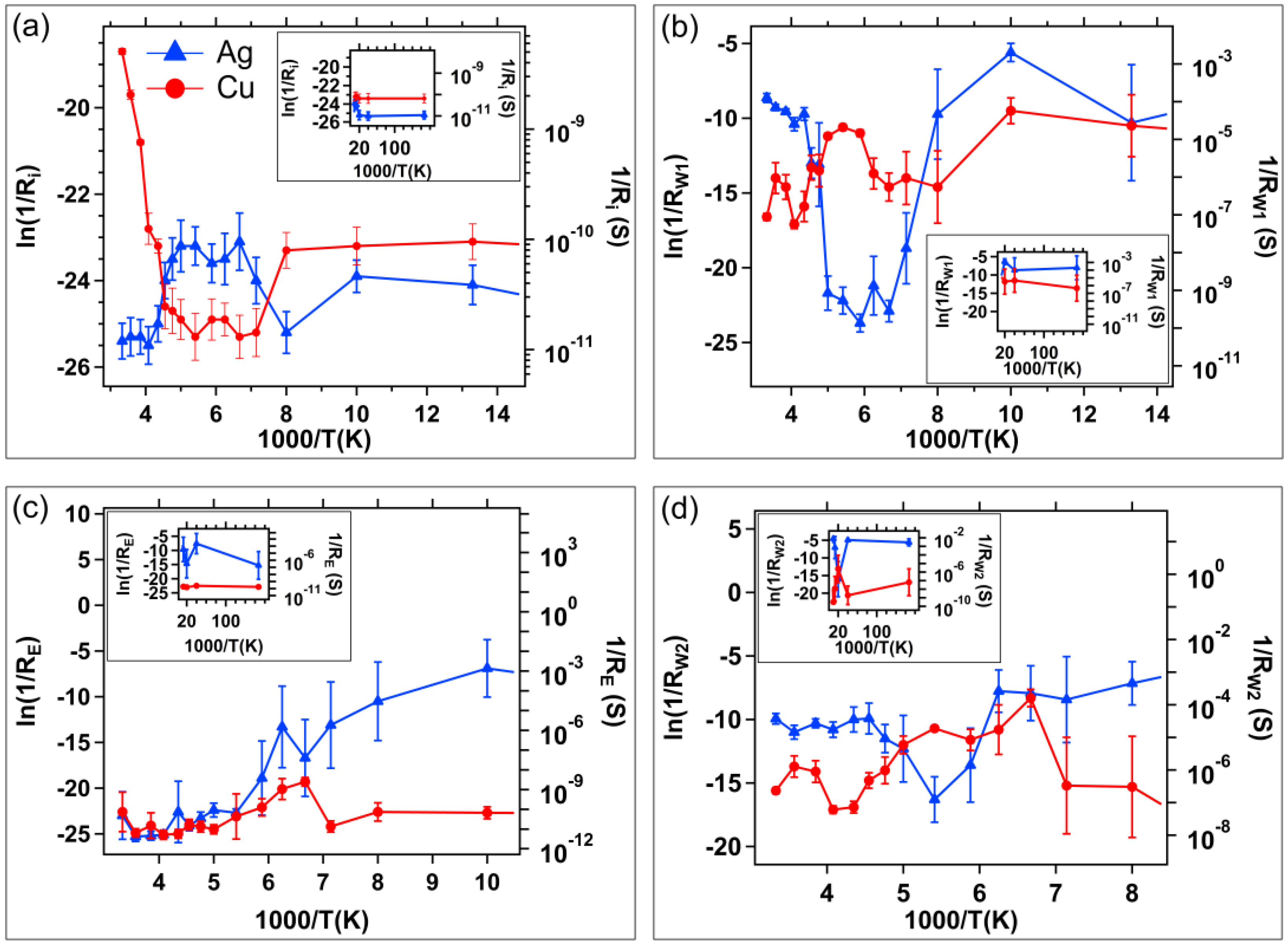
| Resistance | Resistance Measurement Sweep |
|---|---|
| Initial, Ri | +20 mV on Write 1 |
| First Write, RW1 | −20 mV on Erase |
| Erased, RE | +20 mV on Write 2 |
| Second Write, RW2 | +20 mV on Read |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drake, K.; Lu, T.; Majumdar, M.K.H.; Campbell, K.A. Comparison of the Electrical Response of Cu and Ag Ion-Conducting SDC Memristors Over the Temperature Range 6 K to 300 K. Micromachines 2019, 10, 663. https://doi.org/10.3390/mi10100663
Drake K, Lu T, Majumdar MKH, Campbell KA. Comparison of the Electrical Response of Cu and Ag Ion-Conducting SDC Memristors Over the Temperature Range 6 K to 300 K. Micromachines. 2019; 10(10):663. https://doi.org/10.3390/mi10100663
Chicago/Turabian StyleDrake, Kolton, Tonglin Lu, Md. Kamrul H. Majumdar, and Kristy A. Campbell. 2019. "Comparison of the Electrical Response of Cu and Ag Ion-Conducting SDC Memristors Over the Temperature Range 6 K to 300 K" Micromachines 10, no. 10: 663. https://doi.org/10.3390/mi10100663
APA StyleDrake, K., Lu, T., Majumdar, M. K. H., & Campbell, K. A. (2019). Comparison of the Electrical Response of Cu and Ag Ion-Conducting SDC Memristors Over the Temperature Range 6 K to 300 K. Micromachines, 10(10), 663. https://doi.org/10.3390/mi10100663






