Vibration Induced Transport of Enclosed Droplets
Abstract
:1. Introduction
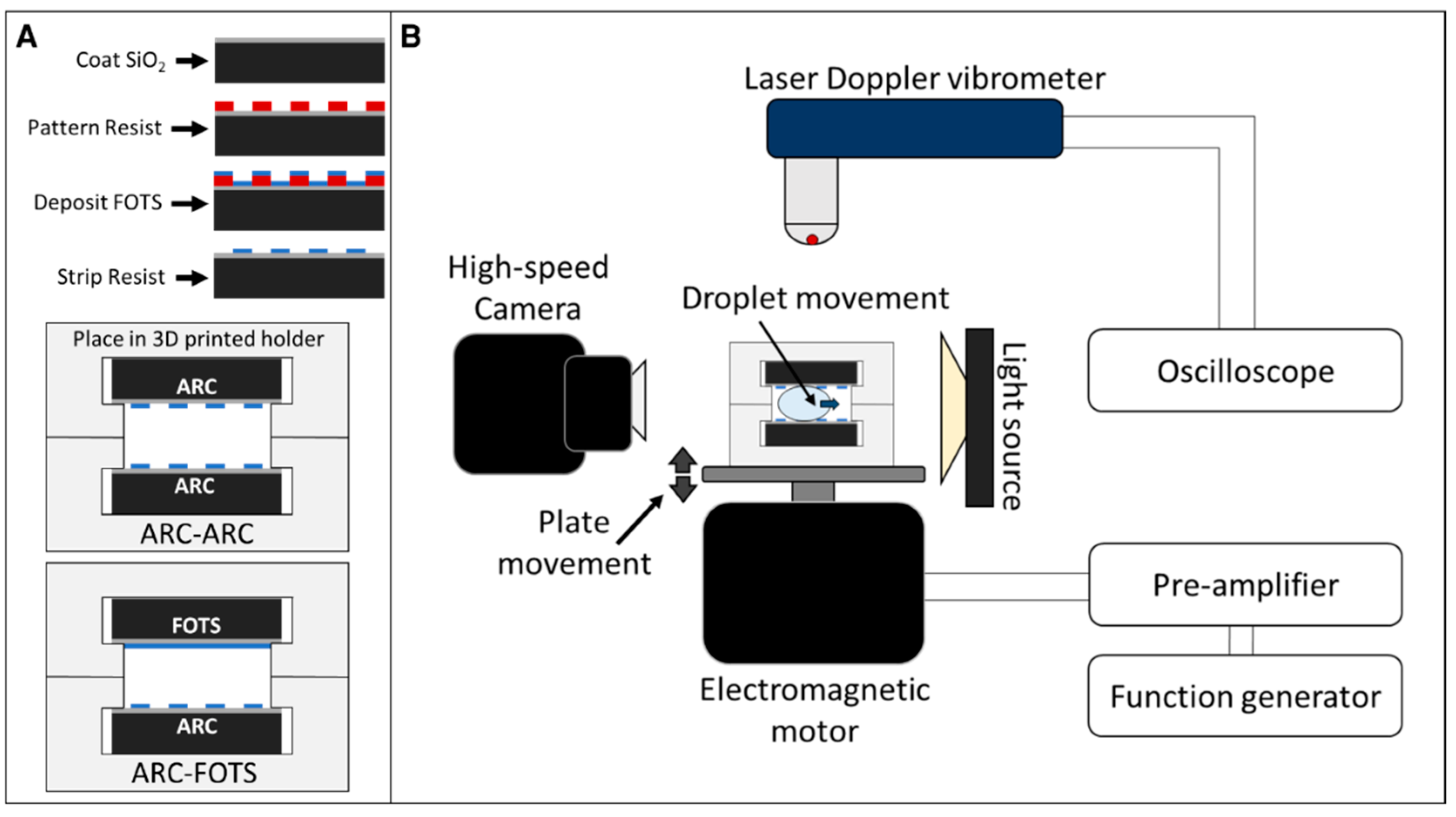
2. Materials and Methods
3. Results
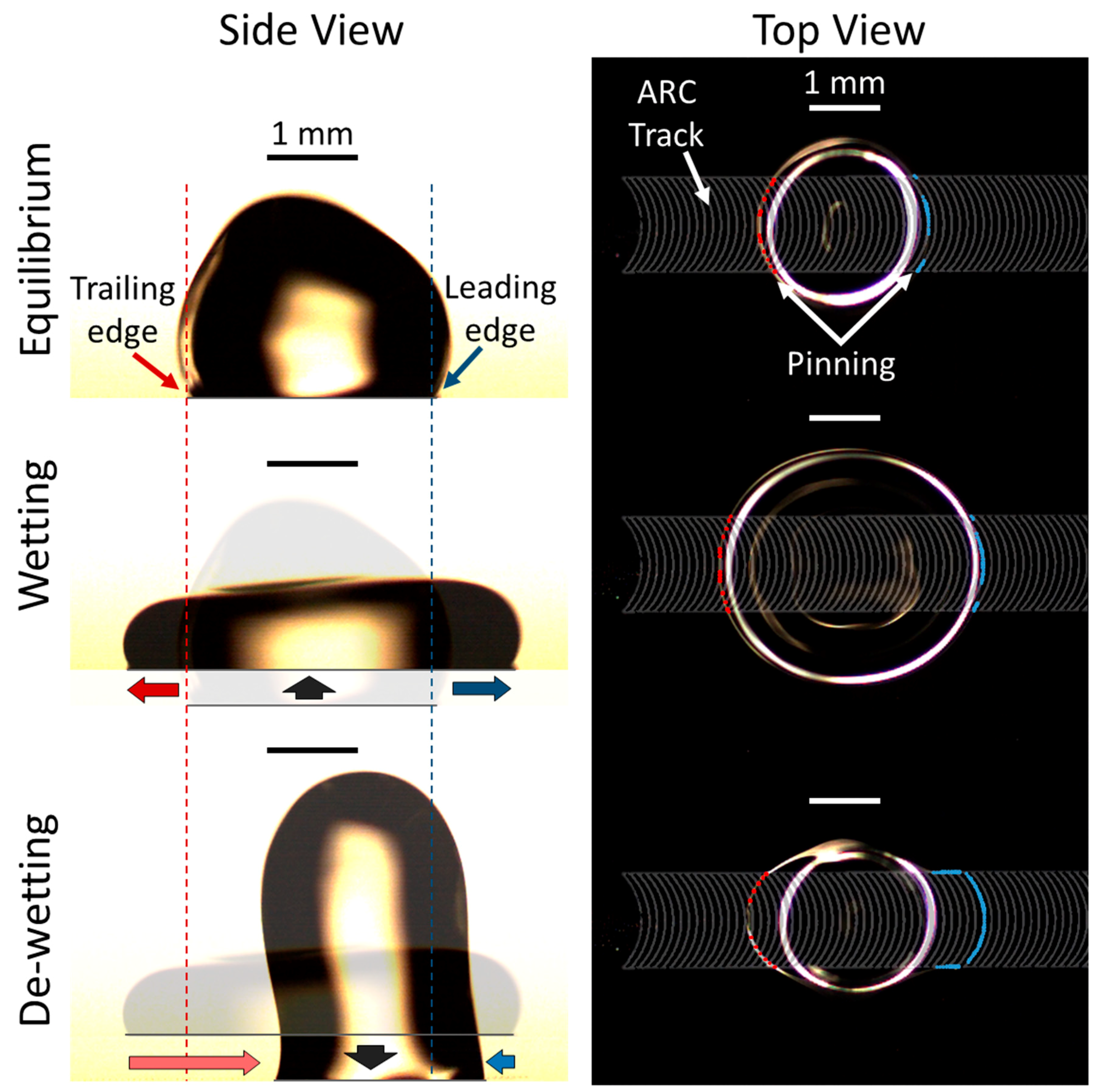
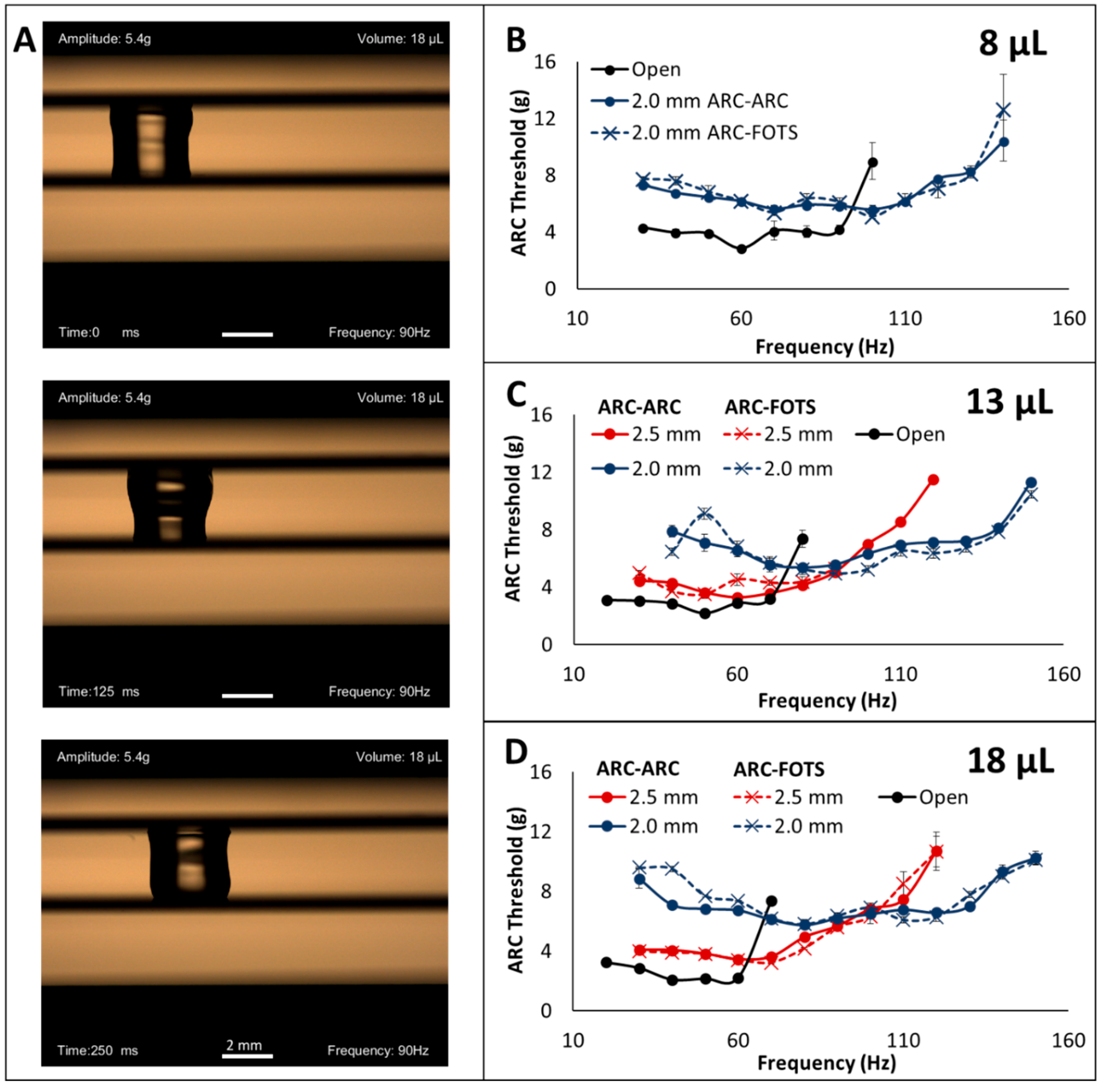
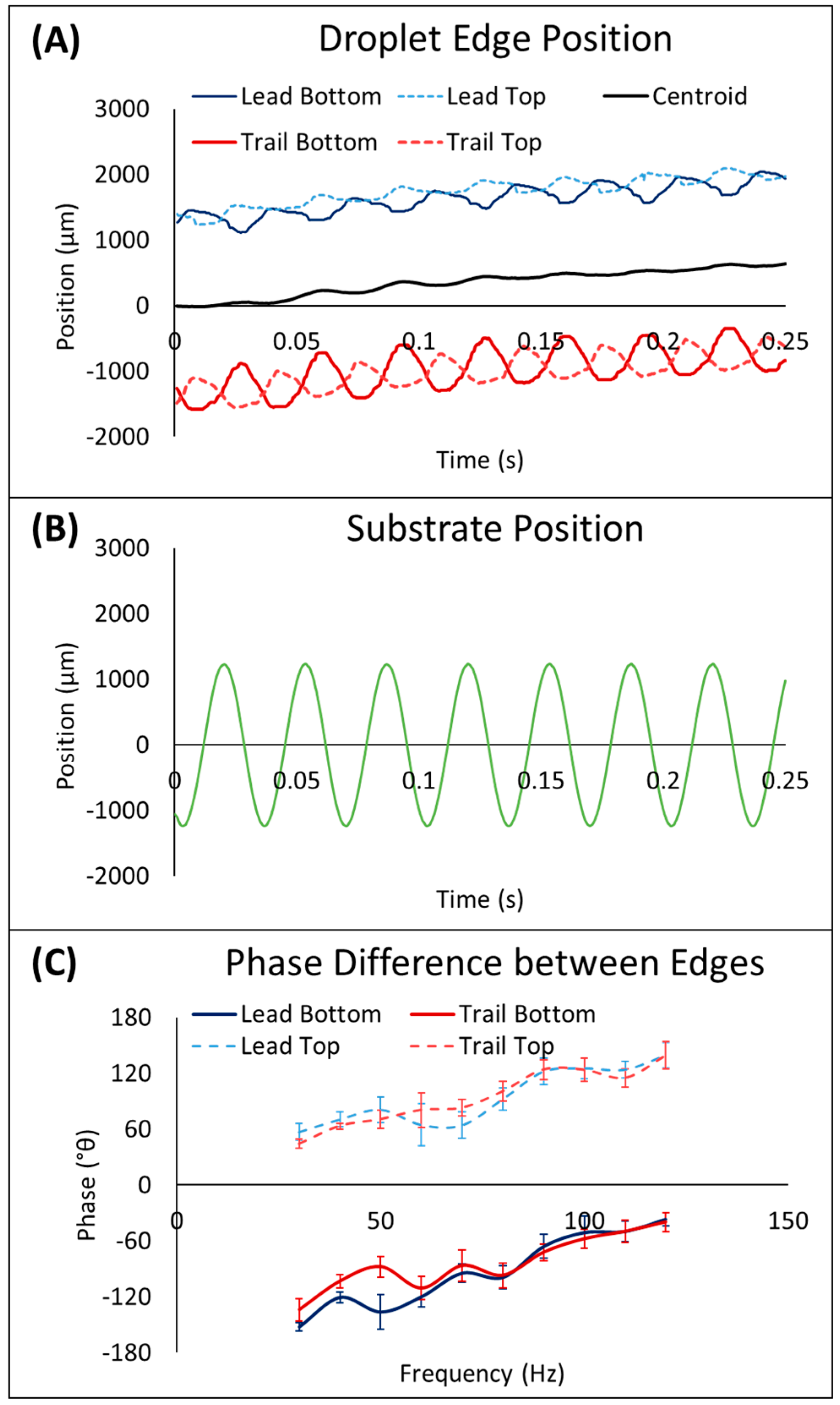
3.1. Effects of Top Plate Enclosure on Droplet Transport
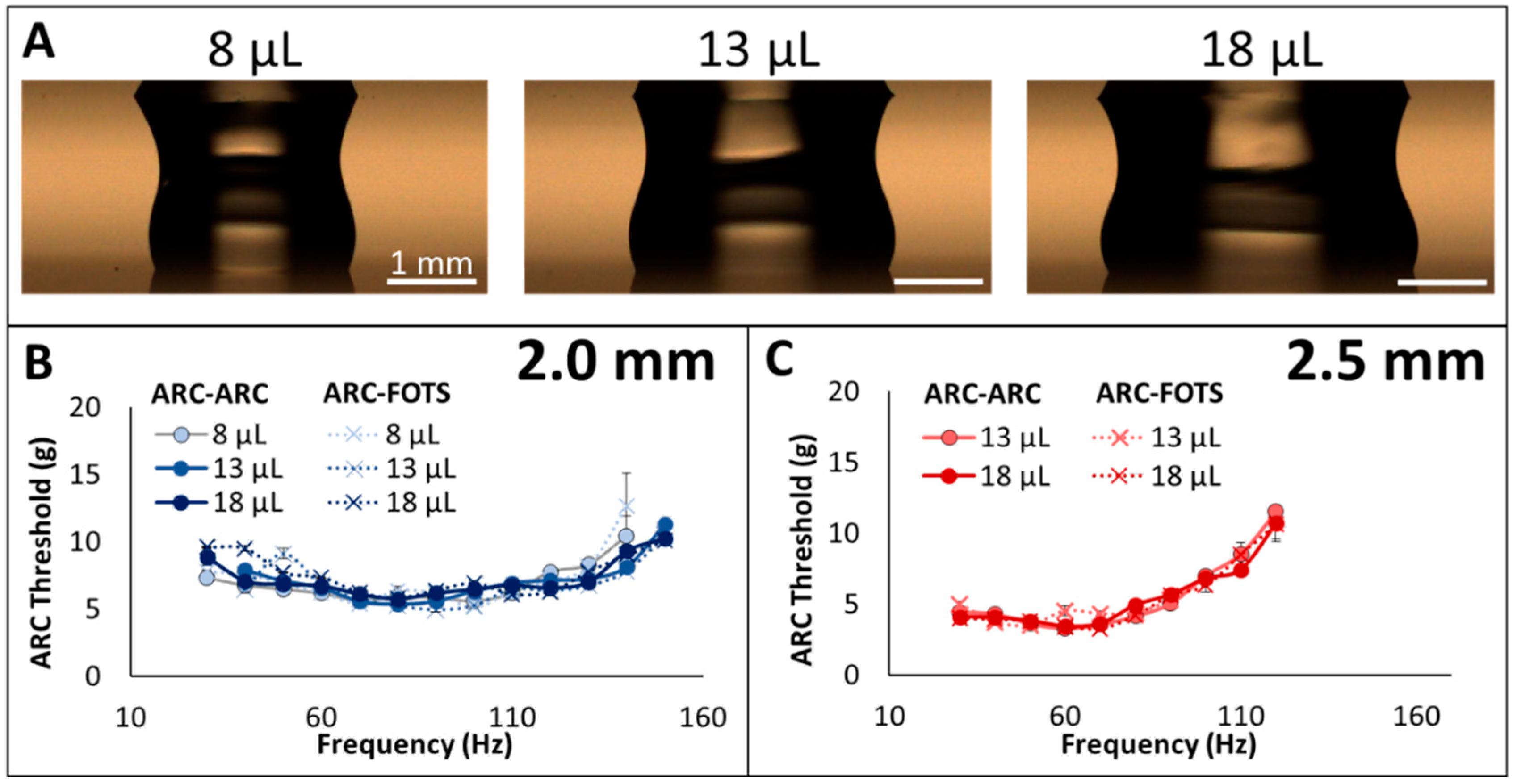
3.2. Length Scale Normalization
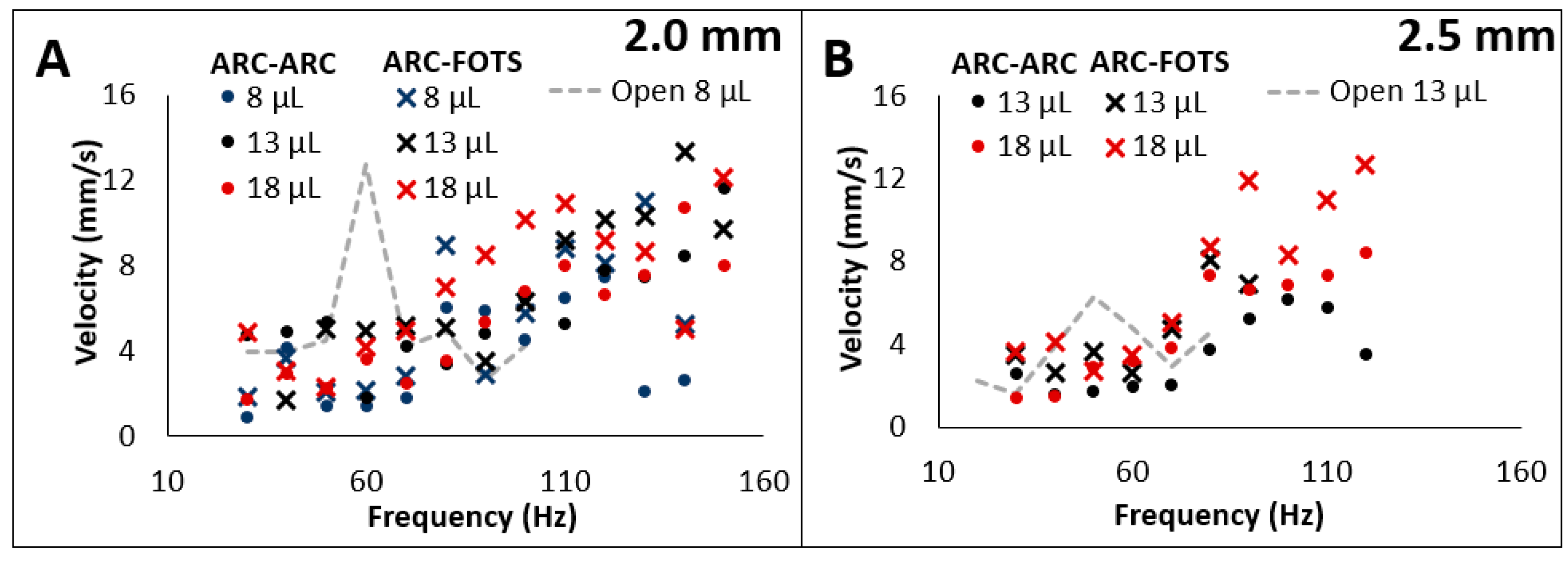
3.3. Transport Velocity of Enclosed Droplets
4. Discussion and Conclusion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perez, M.; Brechet, Y.; Salvo, L.; Papoular, M.; Suery, M. Oscillation of liquid drops under gravity: Influence of shape on the resonance frequency. Europhys. Lett. 1999, 47, 189. [Google Scholar] [CrossRef]
- Vukasinovic, B.; Smith, M.K.; Glezer, A. Dynamics of a sessile drop in forced vibration. J. Fluid Mech. 2007, 587, 395–423. [Google Scholar] [CrossRef]
- Sharp, J.S. Resonant properties of sessile droplets; contact angle dependence of the resonant frequency and width in glycerol/water mixtures. Soft Matter 2011, 8, 399–407. [Google Scholar] [CrossRef]
- Sharp, J.S.; Farmer, D.J.; Kelly, J. Contact angle dependence of the resonant frequency of sessile water droplets. Langmuir 2011, 27, 9367–9371. [Google Scholar] [CrossRef] [PubMed]
- Mettu, S.; Chaudhury, M.K. Vibration spectroscopy of a sessile drop and its contact line. Langmuir 2012, 28, 14100–14106. [Google Scholar] [CrossRef] [PubMed]
- Noblin, X.; Buguin, A.; Brochard-Wyart, F. Vibrated sessile drops: Transition between pinned and mobile contact line oscillations. Eur. Phys. J. E 2004, 14, 395–404. [Google Scholar] [CrossRef] [PubMed]
- Noblin, X.; Buguin, A.; Brochard-Wyart, F. Vibrations of sessile drops. Eur. Phys. J. Spec. Top. 2009, 166, 7–10. [Google Scholar] [CrossRef]
- Buguin, A.; Brochard, F.; De Gennes, P.-G. Motions induced by asymmetric vibrations. Eur. Phys. J. E 2006, 19, 31–36. [Google Scholar] [CrossRef]
- Mettu, S.; Chaudhury, M.K. Motion of liquid drops on surfaces induced by asymmetric vibration: Role of contact angle hysteresis. Langmuir 2011, 27, 10327–10333. [Google Scholar] [CrossRef]
- Daniel, S.; Chaudhury, M.K. Rectified motion of liquid drops on gradient surfaces induced by vibration. Langmuir 2002, 18, 3404–3407. [Google Scholar] [CrossRef]
- Daniel, S.; Sircar, S.; Gliem, J.; Chaudhury, M.K. Ratcheting motion of liquid drops on gradient surfaces. Langmuir 2004, 20, 4085–4092. [Google Scholar] [CrossRef] [PubMed]
- Shastry, A.; Case, M.J.; Böhringer, K.F. Directing Droplets Using Microstructured Surfaces. Langmuir 2006, 22, 6161–6167. [Google Scholar] [CrossRef] [PubMed]
- Daniel, S.; Chaudhury, M.K.; De Gennes, P.-G. Vibration-actuated drop motion on surfaces for batch microfluidic processes. Langmuir 2005, 21, 4240–4248. [Google Scholar] [CrossRef] [PubMed]
- Holmes, H.R.; Böhringer, K.F. Transporting droplets through surface anisotropy. Microsyst. Nanoeng. 2015, 1, 15022. [Google Scholar] [CrossRef]
- Demirel, M.C. Emergent properties of spatially organized poly(p-xylylene) films fabricated by vapor deposition. Colloids Surf. Physicochem. Eng. Asp. 2008, 321, 121–124. [Google Scholar] [CrossRef]
- Malvadkar, N.A.; Hancock, M.J.; Sekeroglu, K.; Dressick, W.J.; Demirel, M.C. An engineered anisotropic nanofilm with unidirectional wetting properties. Nat. Mater. 2010, 9, 1023–1028. [Google Scholar] [CrossRef] [PubMed]
- Agapov, R.L.; Boreyko, J.B.; Briggs, D.P.; Srijanto, B.R.; Retterer, S.T.; Collier, C.P.; Lavrik, N.V. Length scale selects directionality of droplets on vibrating pillar ratchet. Adv. Mater. Interfaces 2014, 1. [Google Scholar] [CrossRef]
- Duncombe, T.A.; Parsons, J.F.; Böhringer, K.F. Directed drop transport rectified from orthogonal vibrations via a flat wetting barrier ratchet. Langmuir 2012, 28, 13765–13770. [Google Scholar] [CrossRef]
- Duncombe, T.A.; Erdem, E.Y.; Shastry, A.; Baskaran, R.; Böhringer, K.F. Controlling liquid drops with texture ratchets. Adv. Mater. 2012, 24, 1545–1550. [Google Scholar] [CrossRef]
- Lin, T.-H.; Yao, D.-J. Applications of EWOD Systems for DNA Reaction and Analysis. J. Adhes. Sci. Technol. 2012, 26, 1789–1804. [Google Scholar] [CrossRef]
- Zhu, L.; Feng, Y.; Ye, X.; Feng, J.; Wu, Y.; Zhou, Z. An ELISA chip based on an EWOD microfluidic platform. J. Adhes. Sci. Technol. 2012, 26, 2113–2124. [Google Scholar] [CrossRef]
- Dong, Y.; Holmes, H.R.; Böhringer, K.F. Converting vertical vibration of anisotropic ratchet conveyors into horizontal droplet motion. Langmuir 2017, 33, 10745–10752. [Google Scholar] [CrossRef] [PubMed]
- Holmes, H.R.; Gomez, A.E.; Böhringer, K.F. Enabling Droplet Functionality on Anisotropic Ratchet Conveyors. Micromachines 2017, 8, 363. [Google Scholar] [CrossRef] [PubMed]
- Duncombe, T.A.; Kumemura, M.; Fujita, H.; Böhringer, K.F. Integrating EWOD with surface ratchets for active droplet transport and sorting. In Proceedings of the 2009 IEEE 22nd International Conference on Micro Electro Mechanical Systems, Sorrento, Italy, 25–29 January 2009; pp. 531–534. [Google Scholar]
- Holmes, H.R.; Böhringer, K.F. Transport velocity of droplets on ratchet conveyors. Adv. Colloid Interface Sci. 2017. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holmes, H.R.; Böhringer, K.F. Vibration Induced Transport of Enclosed Droplets. Micromachines 2019, 10, 69. https://doi.org/10.3390/mi10010069
Holmes HR, Böhringer KF. Vibration Induced Transport of Enclosed Droplets. Micromachines. 2019; 10(1):69. https://doi.org/10.3390/mi10010069
Chicago/Turabian StyleHolmes, Hal R., and Karl F. Böhringer. 2019. "Vibration Induced Transport of Enclosed Droplets" Micromachines 10, no. 1: 69. https://doi.org/10.3390/mi10010069
APA StyleHolmes, H. R., & Böhringer, K. F. (2019). Vibration Induced Transport of Enclosed Droplets. Micromachines, 10(1), 69. https://doi.org/10.3390/mi10010069




