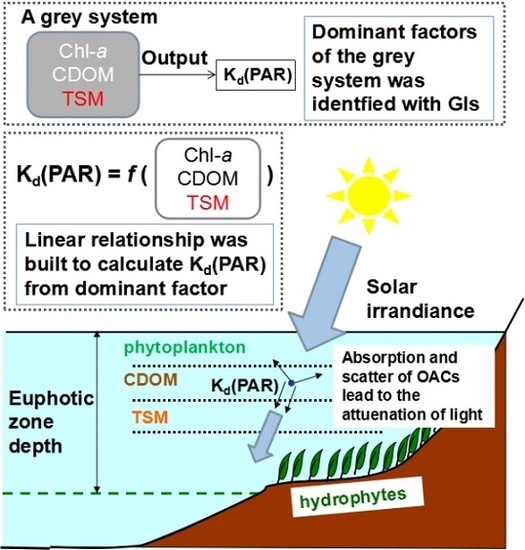
Spatial Distribution of Diffuse Attenuation of Photosynthetic Active Radiation and Its Main Regulating Factors in Inland Waters of Northeast China
Abstract
:1. Introduction
2. Materials and Methodologies
2.1. Study Area
2.2. In Situ Data Collection and Analysis
2.3. Water Quality Parameters
2.4. Grey Incidences (GIs) Analysis
2.5. Linear Regression between Kd(PAR) and OACs
2.6. Relationship between Kd(PAR) and SDD
3. Results and Discussion
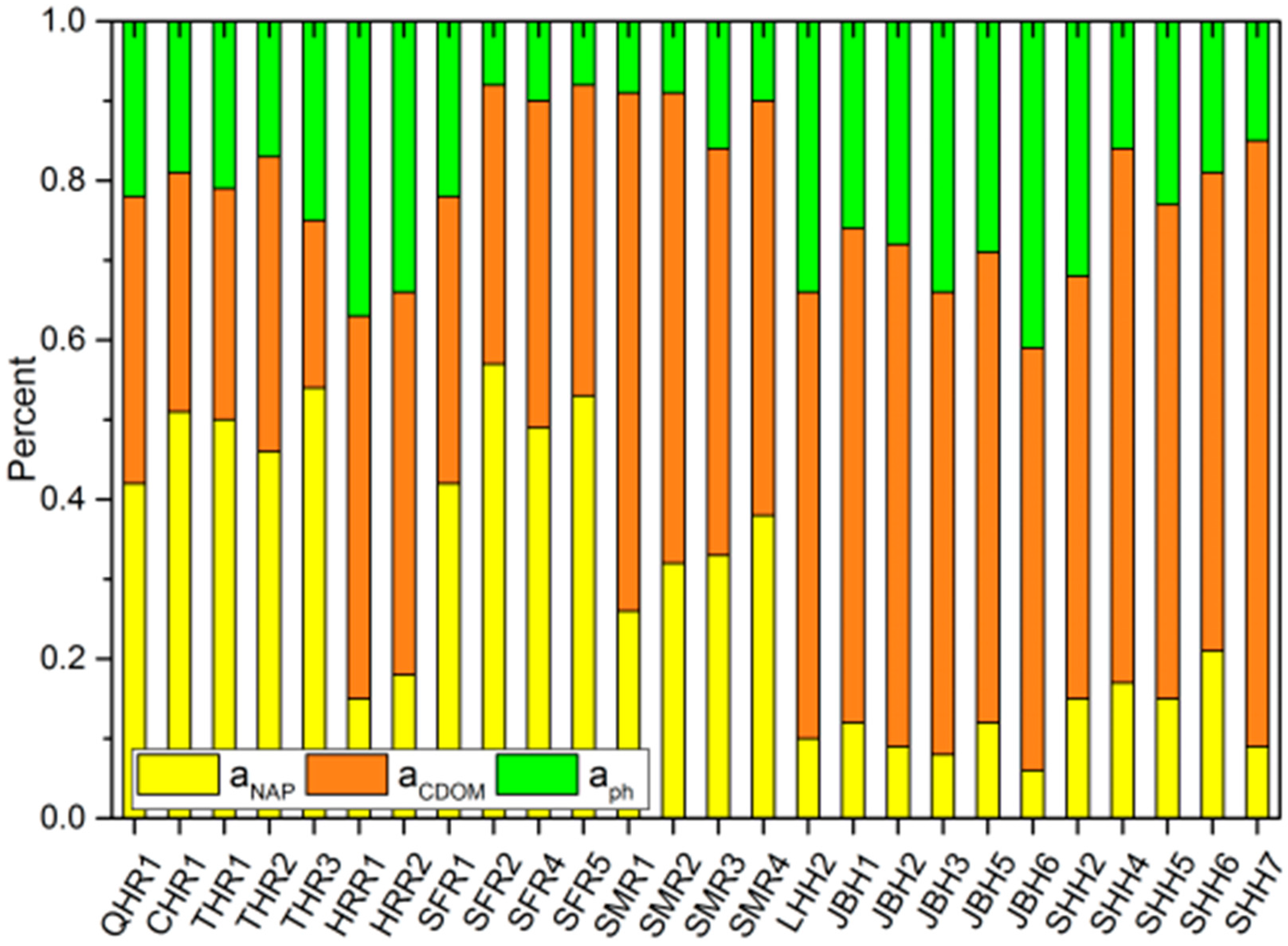
3.1. Water Quality Characteristics
3.2. Spatial Distribution of Kd(PAR)
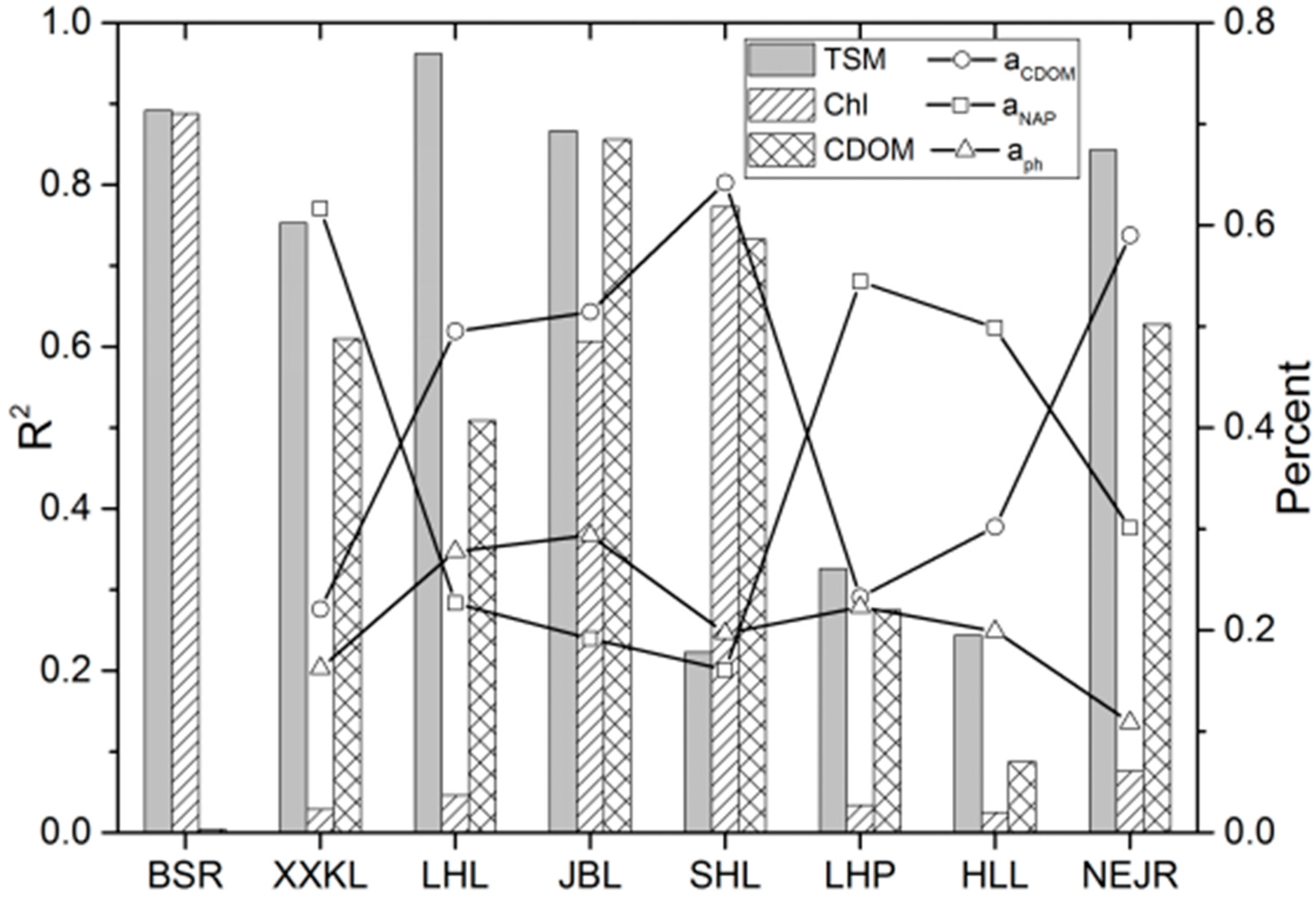
3.3. Grey Incidences between Kd(PAR) and OACs
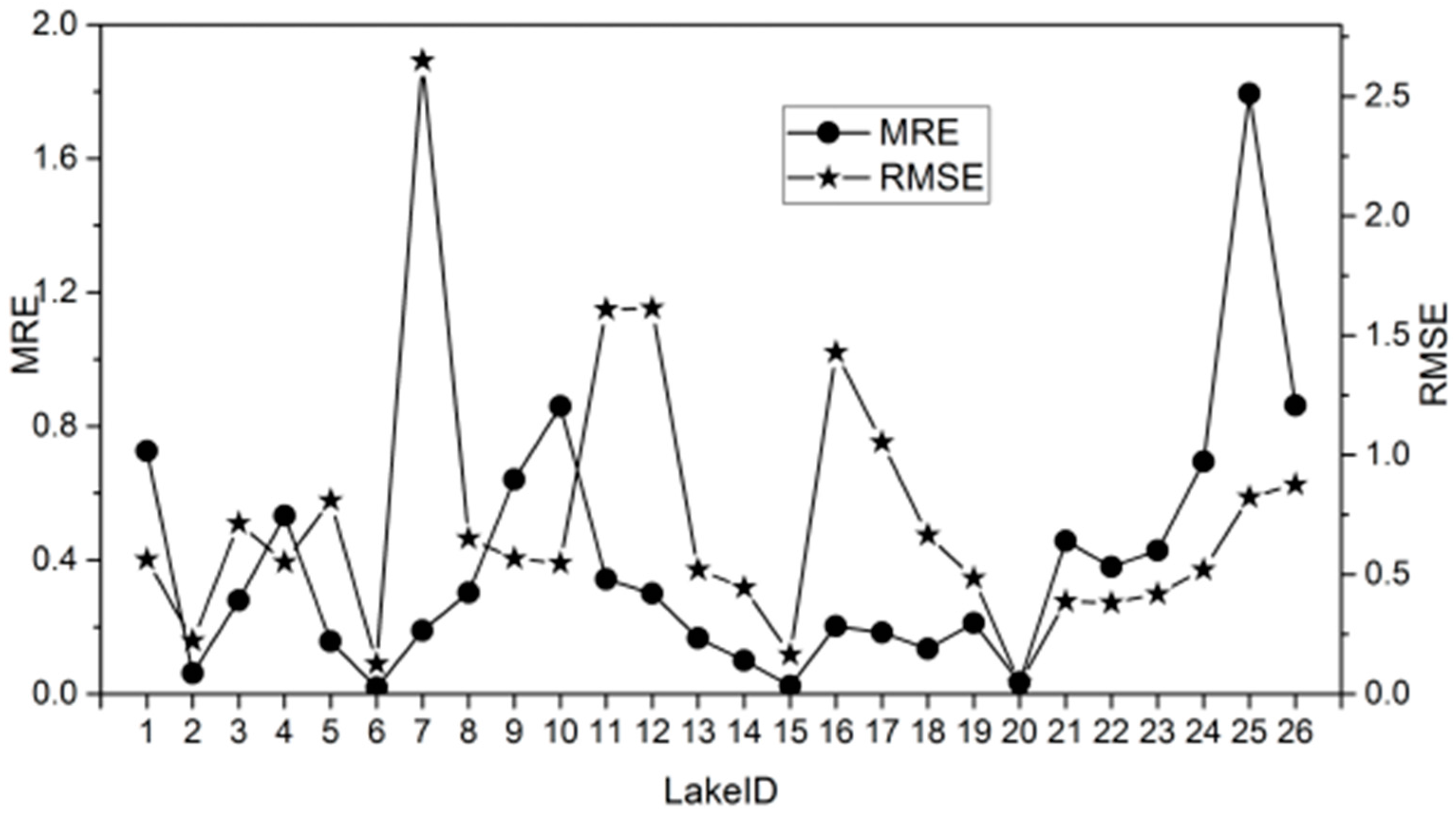
3.4. Kd(PAR) Model Calibration and Validation
3.5. Spatial Transferability
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lund-Hansen, L.C. Diffuse attenuation coefficients Kd(PAR) at the estuarine North Sea-Baltic Sea transition: Time-series, partitioning, absorption, and scattering. Estuar. Coast. Shelf Sci. 2004, 61, 251–259. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Zhang, B.; Ma, R.H.; Feng, S.; Le, C.F. Optically active substances and their contributions to the underwater light climate in Lake Taihu, a large shallow lake in China. Fundam. Appl. Limnol. Arch. Hydrobiol. 2007, 170, 11–19. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. A consumer’s guide to phytoplankton primary productivity models. Limnol. Oceanogr. 1997, 42, 1479–1491. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems; Cambridge University Press: New York, NY, USA, 1994. [Google Scholar]
- Chang, G.C.; Dickey, T.D. Coastal ocean optical influences on solar transmission and radiant heating rate. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Qin, B.Q.; Hu, W.P.; Wang, S.M.; Chen, Y.W.; Chen, W.M. Temporal-spatial variations of euphotic depth of typical lake regions in Lake Taihu and its ecological environmental significance. Sci. China Ser. D 2006, 49, 431–442. [Google Scholar] [CrossRef]
- Holmes, R.W. The Secchi disk in turbid coastal zones. Limnol. Oceanogr. 1970, 15, 688–694. [Google Scholar] [CrossRef]
- Shang, S.L.; Lee, Z.P.; Wei, G.M. Characterization of MODIS-derived euphotic zone depth: Results for the China Sea. Remote Sens. Environ. 2011, 115, 180–186. [Google Scholar] [CrossRef]
- Devlin, M.J.; Barry, J.; Mills, D.K.; Gowen, R.J.; Foden, J.; Sivyer, D.; Tett, P. Relationships between suspended particulate material, light attenuation and Secchi depth in UK marine waters. Estuar. Coast. Shelf Sci. 2008, 79, 429–439. [Google Scholar] [CrossRef]
- Devlin, M.J.; Barry, J.; Mills, D.K.; Gowen, R.J.; Foden, J.; Sivyer, D.; Greenwood, N.; Pearce, D.; Tett, P. Estimating the diffuse attenuation coefficient from optically active constituents in UK marine waters. Estuar. Coast. Shelf Sci. 2009, 82, 73–83. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.L.; Liu, X.H.; Wang, M.Z.; Qin, B.Q. Remote sensing of diffuse attenuation coefficient of photosynthetically active radiation in Lake Taihu using MERIS data. Remote Sens. Environ. 2014, 140, 365–377. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Zhang, Y.L.; Zha, Y.; Shi, K.; Zhou, Y.Q.; Li, Y.L. Estimation of diffuse attenuation coefficient of photosynthetically active radiation in Xin’anjiang Reservoir based on Landsat 8 data. Chin. J. Environ. Sci. 2015, 36, 4420–4429, (In Chinese with English Abstract). [Google Scholar]
- Mueller, J.L. SeaWiFS algorithm for the diffuse attenuation coefficient, Kd(490), using water-leaving radiances at 490 and 555 nm. SeaWiFS Postlaunch calibration and validation analyses, part. Med. Today 2000, 5, 16–29. [Google Scholar]
- Chen, J.; Cui, T.W.; Tang, J.W.; Song, Q.J. Remote sensing of diffuse attenuation coefficient using MODIS imagery of turbid coastal waters: A case study in Bohai Sea. Remote Sens. Environ. 2014, 140, 78–93. [Google Scholar] [CrossRef]
- Majozi, N.P.; Salama, M.S.; Bernard, S.; Harper, D.M.; Habte, M.G. Remote sensing of euphotic depth in shallow tropical inland waters of Lake Naivasha using MERIS data. Remote Sens. Environ. 2014, 148, 178–189. [Google Scholar] [CrossRef]
- Ramon, D.; Jolivet, D.; Tan, J.; Frouin, R. Estimating photosynthetically available radiation at the ocean surface for primary production (3P Project): Modeling, evaluation, and application to global MERIS imagery. Proc. SPIE 2016. [Google Scholar] [CrossRef]
- Frouin, R.; McPherson, J. Estimating photosynthetically available radiation at the ocean surface from GOCI data. Ocean Sci. J. 2012, 47, 313–321. [Google Scholar] [CrossRef]
- Doron, M.; Babin, M.; Mangin, A.; Hembise, O. Estimation of light penetration, and horizontal and vertical visibility in oceanic and coastal waters from surface reflectance. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Lee, Z.P.; Weidemann, A.; Kindle, J.; Arnone, R.; Carder, K.L.; Davis, C. Euphotic zone depth: Its derivation and implication to ocean color remote sensing. J. Geophys. Res. Oceans 2007, 112. [Google Scholar] [CrossRef]
- Son, S.H.; Wang, M.H. Diffuse attenuation coefficient of the photosynthetically available radiation Kd (PAR) for global open ocean and coastal waters. Remote Sens. Environ. 2015, 159, 250–258. [Google Scholar] [CrossRef]
- Alikas, K.; Kratzer, S.; Reinart, A.; Kauer, T.; Paavel, B. Robust remote sensing algorithms to derive the diffuse attenuation coefficient for lakes and coastal waters. Limnol. Oceanogr. Methods 2015, 13, 402–415. [Google Scholar] [CrossRef]
- Austin, R.W.; Petzold, T.J. The Determination of the Diffuse Attenuation Coefficient of Sea Water Using the Coastal Zone Color Scanner; Springer: New York, NY, USA, 1981. [Google Scholar]
- Mueller, J.L.; Trees, C.C. Revised SeaWiFS prelaunch algorithm for diffuse attenuation coefficient K (490). Case Stud. SeaWiFS Calibration Valid. 1997, 41, 18–21. [Google Scholar]
- Zhang, T.L.; Fell, F. An empirical algorithm for determining the diffuse attenuation coefficient Kd in clear and turbid waters from spectral remote sensing reflectance. Limnol. Oceanogr. Methods 2007, 5, 457–462. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Liu, X.H.; Yin, Y.; Wang, M.Z.; Qin, B.Q. A simple optical model to estimate diffuse attenuation coefficient of photosynthetically active radiation in an extremely turbid lake from surface reflectance. Opt. Express 2012, 20, 20482–20493. [Google Scholar] [CrossRef] [PubMed]
- Phlips, E.J.; Aldridge, F.J.; Schelske, C.L.; Crisman, T.L. Relationships between light availability, chlorophyll a, and tripton in a large, shallow subtropical lake. Limnol. Oceanogr. 1995, 40, 416–421. [Google Scholar] [CrossRef]
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Shi, Z.Q.; Zhang, Y.L.; Yin, Y.; Liu, X.H. Characterization of the underwater light field and the affecting factors in Bosten Lake in summer. Acta Sci. Circumst. 2012, 32, 2969–2977, (In Chinese with English Abstract). [Google Scholar]
- Kratzer, S.; Hakansson, B.; Sahlin, C. Assessing Secchi and photic zone depth in the Baltic Sea from satellite data. AMBIO J. Hum. Environ. 2003, 32, 577–585. [Google Scholar] [CrossRef]
- Li, Y.L.; Zhang, Y.L.; Liu, M.L. Calculation and retrieval of euphotic depth of Lake Taihu by remote sensing. J. Lake Sci. 2009, 21, 165–172, (In Chinese with English Abstract). [Google Scholar]
- Qu, M.Y.; Cai, Q.H.; Shen, H.L.; Li, B. Variation and influencing factors of euphotic depth in Danjiangkou reservoir in different hydrological periods. Resour. Environ. Yangtze Basin 2014, 23, 53–59, (In Chinese with English Abstract). [Google Scholar]
- Pierson, D.C.; Kratzer, S.; Strömbeck, N.; Håkansson, B. Relationship between the attenuation of downwelling irradiance at 490 nm with the attenuation of PAR (400 nm–700 nm) in the Baltic Sea. Remote Sens. Environ. 2008, 112, 668–680. [Google Scholar] [CrossRef]
- Tan, J.; Cherkauer, K.A.; Chaubey, I. Using hyperspectral data to quantify water-quality parameters in the Wabash River and its tributaries, Indiana. Int. J. Remote Sens. 2015, 36, 5466–5484. [Google Scholar] [CrossRef]
- Tan, J.; Cherkauer, K.A.; Chaubey, I. Developing a comprehensive spectral-biogeochemical database of midwestern rivers for water quality retrieval using remote sensing data: A case study of the Wabash River and its tributary, Indiana. Remote Sens. 2016, 8, 517. [Google Scholar] [CrossRef]
- Li, N.; Liu, J.P.; Wang, Z.M. Dynamics and driving force of lake changes in northeast China during 2000–2010. J. Lake Sci. 2014, 26, 545–551, (In Chinese with English Abstract). [Google Scholar]
- Wang, S.M.; Dou, H.S. (Eds.) Chinese Lake Catalogue; Science Press: Beijing, China, 1998. (In Chinese)
- Duan, H.T.; Ma, R.H.; Zhang, Y.L.; Zhang, B. Remote-sensing assessment of regional inland lake water clarity in northeast China. Limnology 2009, 10, 135–141. [Google Scholar] [CrossRef]
- Song, K.S.; Zang, S.Y.; Zhao, Y.; Li, L.; Du, J.; Zhang, N.N.; Wang, X.D.; Shao, T.T.; Guan, Y.; Liu, L. Spatiotemporal characterization of dissolved carbon for inland waters in semi-humid/semi-arid region, China. Hydrol. Earth Syst. Sci. 2013, 17, 4269–4281. [Google Scholar] [CrossRef]
- Wen, Z.D.; Song, K.S.; Zhao, Y.; Du, J.; Ma, J.H. Influence of environmental factors on spectral characteristic of chromophoric dissolved organic matter (CDOM) in Inner Mongolia Plateau, China. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 5895–5929. [Google Scholar] [CrossRef]
- Zhao, Y.; Song, K.; Wen, Z.D.; Li, L.; Zang, S.Y.; Shao, T.T.; Li, S.J.; Du, J. Seasonal characterization of CDOM for lakes in semiarid regions of Northeast China using excitation–emission matrix fluorescence and parallel factor analysis (EEM–PARAFAC). Biogeosciences 2016, 13, 1635–1645. [Google Scholar] [CrossRef]
- Mao, D.H.; Wang, Z.M.; Wu, C.; Song, K.S.; Ren, C.Y. Examining forest net primary productivity dynamics and driving forces in northeastern China during 1982–2010. Chin. Geogr. Sci. 2014, 24, 631–646. [Google Scholar] [CrossRef]
- Song, K.S.; Wang, Z.M.; Blackwell, J.; Zhang, B.; Li, F.; Zhang, Y.Z.; Jiang, G.J. Water quality monitoring using Landsat Themate Mapper data with empirical algorithms in Chagan Lake, China. J. Appl. Remote Sens. 2011, 5, 053506. [Google Scholar] [CrossRef]
- Song, K.S.; Li, L.; Tedesco, L.P.; Li, S.; Duan, H.T.; Liu, D.W.; Hall, B.E.; Du, J.; Li, Z.C.; Shi, K.; et al. Remote estimation of chlorophyll—A in turbid inland waters: Three-band model versus GA-PLS model. Remote Sens. Environ. 2013, 136, 342–357. [Google Scholar] [CrossRef]
- Jeffrey, S.W.; Humphrey, G.F. New spectrophotometric equations for determining chlorophylls a, b, c1 and c2 in higher plants, algae and natural phytoplankton. Biochem. Physiol. Pflanz. 1975, 167, 191–194. [Google Scholar]
- Bricaud, A.; Morel, A.; Prieur, L. Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnol. Oceanogr. 1981, 26, 43–53. [Google Scholar] [CrossRef]
- Miller, R.L.; Belz, M.; Del Castillo, C.; Trzaska, R. Determining CDOM absorption spectra in diverse coastal environments using a multiple pathlength, liquid core waveguide system. Cont. Shelf Res. 2002, 22, 1301–1310. [Google Scholar] [CrossRef]
- Shao, T.T.; Song, K.S.; Du, J.; Zhao, Y.; Liu, Z.M.; Zhang, B. Seasonal Variations of CDOM Optical Properties in Rivers across the Liaohe Delta. Wetlands 2016, 36, 181–192. [Google Scholar] [CrossRef]
- Xu, J.P.; Li, F.; Zhang, B.; Song, K.S.; Wang, Z.M.; Liu, D.W.; Zhang, G.X. Estimation of chlorophyll—A concentration using field spectral data: A case study in inland Case-II waters, North China. Environ. Monit. Assess. 2009, 158, 105–116. [Google Scholar] [CrossRef] [PubMed]
- Cao, M.X.; Dang, Y.G.; Mi, C.M. An improvement on calculation of absolute degree of grey incidence. In Proceedings of the 2006 IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 8–11 October 2006.
- Jin, X.L.; Du, J.; Liu, H.J.; Wang, Z.M.; Song, K.S. Remote estimation of soil organic matter content in the Sanjiang Plain, Northest China: The optimal band algorithm versus the GRA-ANN model. Agric. For. Meteorol. 2016, 218, 250–260. [Google Scholar] [CrossRef]
- Deng, J.L. Basic Methods of Gray System; Science and Technology University of Central China Press: Wuhan, China, 1987. (In Chinese) [Google Scholar]
- Liu, S.F.; Cai, H.; Cao, Y.; Yang, Y.J. Advance in grey incidence analysis modelling. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Anchorage, Alaska, USA, 9–12 October 2011; pp. 1886–1890.
- Mei, Z.G. The Concept and Computation Method of Grey Absolute Correlation Degree. Syst. Eng. 1992, 10, 43–44, (In Chinese with English Abstract). [Google Scholar]
- Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef]
- Aas, E.; Høkedal, J.; Sørensen, K. Secchi depth in the Oslofjord-Skagerrak area: Theory, experiments and relationships to other quantities. Ocean Sci. 2014, 10, 177–199. [Google Scholar] [CrossRef]
- Lee, Z.P.; Shang, S.L.; Hu, C.M.; Du, K.P.; Weidemann, A.; Hou, W.L.; Lin, J.F.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef]
- Lee, Z.P.; Shang, S.L.; Qi, L.; Yang, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Raymont, J.E.G. Plankton and Productivity in the Oceans; Pergamon Press: Oxford, UK, 1967. [Google Scholar]
- Aertebjerg, G.; Bresta, A.M. Guidelines for the Measurement of Phytoplankton Primary Production, 2nd ed.; Baltic Marine Biologists Publication: Charlottenlund, Denmark, 1984. [Google Scholar]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
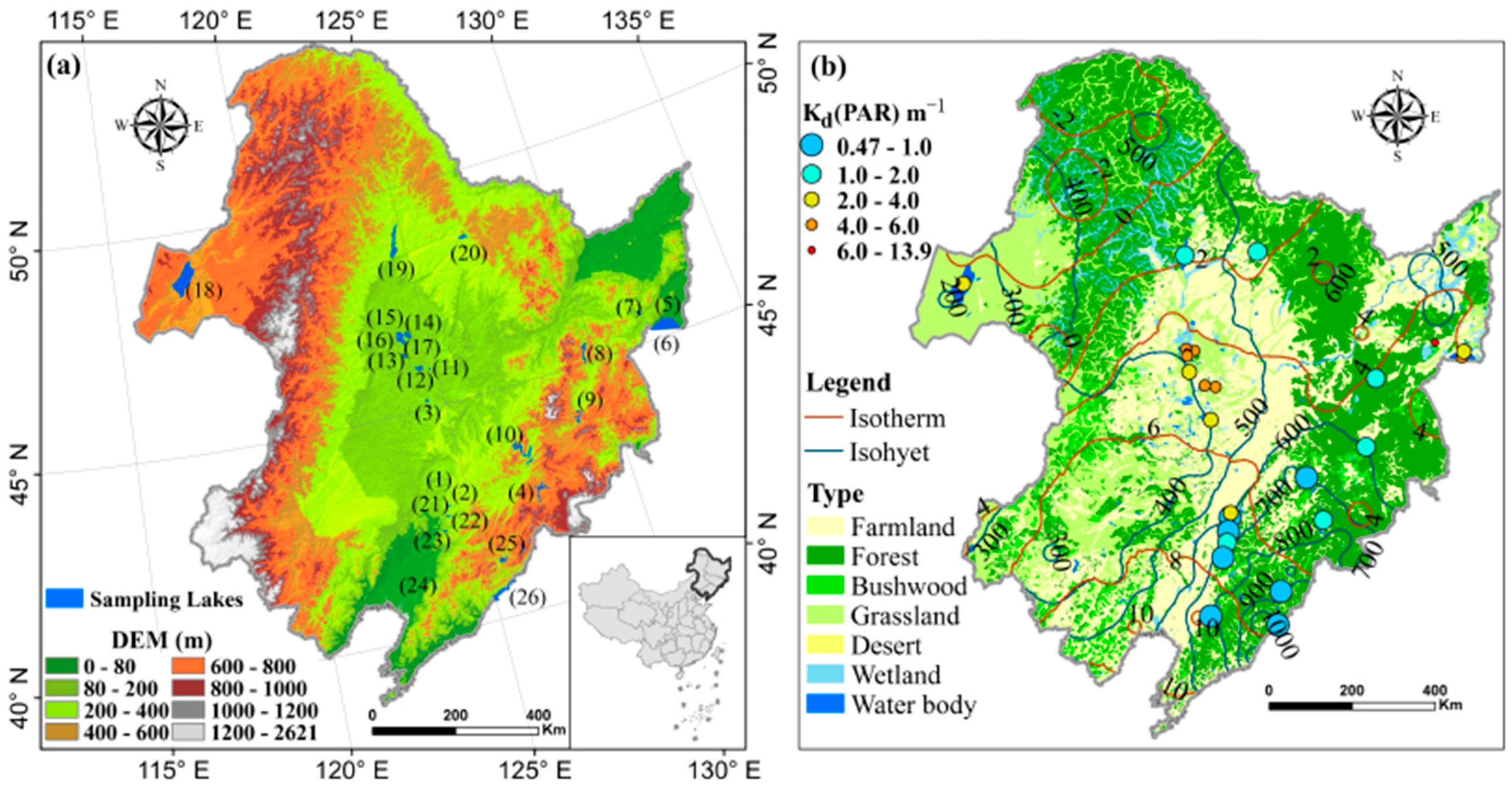


| Water Name a | Abbreviation (Number) | Area (km2) | Date | N | Kd(PAR) m−1 | SDD (m) | TSM (mg/L) | aCDOM(355) m−1 | Chl-a (μg/L) |
|---|---|---|---|---|---|---|---|---|---|
| Shanmen R. | SMR(1) | 1.5 | 21 April 2015 | 4 | 0.77 | 1.543 | 3.17 | 7.86 | 5.88 |
| Xiasantai R. | XSTR(2) | 1.3 | 21 April 2015 | 4 | 2.73 | 0.703 | 18.75 | 10.56 | 32.84 |
| Xinmiaopao | XMP(3) | 26.6 | 24 April 2015 | 8 | 2.53 | 0.506 | 26.01 | 3.51 | 7.66 |
| Baishan R. | BSR(4) | 90.0 | 4 May 2015 | 24 | 1.11 | 1.283 | 6.29 | 5.08 | 28.02 |
| Xiaoxingkai L. | XXKL(5) | 162.1 | 15 August 2015 | 13 | 3.65 | 0.362 | 34.77 | 4.43 | 6.21 |
| Daxingkai L. | DXKL(6) | 1062.4 | 17 August 2015 | 8 | 5.43 | 0.226 | 55.17 | 1.85 | 6.58 |
| Qingnian R. | QNR(7) | 41.1 | 18 August 2015 | 4 | 13.93 | 0.113 | 174.50 | 5.14 | 4.31 |
| Lianhua L. | LHL(8) | 111.7 | 19 August 2015 | 14 | 1.80 | 1.284 | 8.12 | 4.30 | 16.89 |
| Jingbo L. | JBL(9) | 88.8 | 20 August 2015 | 11 | 1.22 | 1.520 | 4.61 | 4.84 | 23.00 |
| Songhua L. | SHL(10) | 216.2 | 21 August 2015 | 7 | 0.68 | 2.599 | 1.48 | 2.41 | 5.41 |
| Kulipao | KLP(11) | 11.6 | 6 September 2015 | 4 | 4.32 | 0.328 | 22.10 | 10.56 | 3.74 |
| Nanyin R. | NYR(12) | 96.4 | 7 September 2015 | 3 | 5.35 | 0.253 | 34.17 | 3.22 | 40.04 |
| Lamasipao | LMSP(13) | 47.9 | 8 September 2015 | 7 | 2.81 | 0.440 | 16.10 | 6.03 | 59.80 |
| Longhupao | LHP(14) | 126.9 | 9 September 2015 | 10 | 4.11 | 0.280 | 36.33 | 4.69 | 12.27 |
| Talahongpao | TLHP(15) | 67.5 | 10 September 2015 | 2 | 5.63 | 0.240 | 56.00 | 6.49 | 20.62 |
| Xihulupao | XHLP(16) | 57.9 | 10 September 2015 | 7 | 6.23 | 0.254 | 50.00 | 4.71 | 21.25 |
| Huoshaolipao | HSLP(17) | 64.3 | 10 September 2015 | 8 | 4.00 | 0.371 | 27.18 | 4.53 | 9.02 |
| Hulun L. | HLL(18) | 2050.2 | 14 September 2015 | 28 | 3.54 | 0.402 | 28.38 | 5.23 | 7.37 |
| Nierji R. | NEJR(19) | 429.6 | 16 September 2015 | 16 | 1.56 | 1.678 | 4.24 | 6.53 | 4.46 |
| Shankou R. | SKR(20) | 64.9 | 17 September 2015 | 3 | 1.27 | 1.847 | 1.99 | 7.59 | 6.88 |
| Nanchengzi R. | NCZR(21) | 10.7 | 14 April 2016 | 4 | 0.85 | 1.80 | 1.98 | 2.45 | 2.97 |
| Qinghe R. | QHR(22) | 17.3 | 15 April 2016 | 3 | 1.49 | 1.24 | 8.61 | 1.98 | 5.03 |
| Chaihe R. | CHR(23) | 12.1 | 15 April 2016 | 3 | 1.00 | 1.17 | 4.00 | 1.83 | 8.12 |
| Tanghe R. | THR(24) | 18.1 | 18 April 2016 | 4 | 0.92 | 1.85 | 4.47 | 1.07 | 3.25 |
| Huanren R. | HRR(25) | 69.6 | 19 April 2016 | 2 | 0.47 | 2.74 | 2.63 | 1.92 | 3.58 |
| Shuifeng R. | SFR(26) | 165.7 | 20 April 2016 | 5 | 0.97 | 1.45 | 8.85 | 1.98 | 3.94 |
| Name | OACs | GI 1 | GI 2 | GI 3 | Name | OACs | GI 1 | GI 2 | GI 3 |
|---|---|---|---|---|---|---|---|---|---|
| All points | TSM | 0.82 | 0.81 | 0.97 | Jingbo L. | TSM | 0.73 | 0.73 | 0.94 |
| aCDOM(355) | 0.51 | 0.69 | 0.86 | aCDOM(355) | 0.63 | 0.87 | 0.92 | ||
| Chl-a | 0.63 | 0.66 | 0.85 | Chl-a | 0.58 | 0.81 | 0.83 | ||
| Baishan R. | TSM | 0.77 | 0.91 | 0.92 | Longhupao | TSM | 0.73 | 0.65 | 0.86 |
| aCDOM(355) | 0.47 | 0.78 | 0.82 | aCDOM(355) | 0.66 | 0.45 | 0.63 | ||
| Chl-a | 0.73 | 0.87 | 0.91 | Chl-a | 0.71 | 0.53 | 0.82 | ||
| Xiaoxingkai L. | TSM | 0.83 | 0.77 | 0.88 | Hulun L. | TSM | 0.73 | 0.54 | 0.78 |
| aCDOM(355) | 0.57 | 0.47 | 0.76 | aCDOM(355) | 0.68 | 0.45 | 0.76 | ||
| Chl-a | 0.73 | 0.74 | 0.74 | Chl-a | 0.65 | 0.30 | 0.75 | ||
| Lianhua L. | TSM | 0.86 | 0.93 | 0.92 | Nierji R. | TSM | 0.72 | 0.71 | 0.89 |
| aCDOM(355) | 0.55 | 0.71 | 0.89 | aCDOM(355) | 0.62 | 0.56 | 0.81 | ||
| Chl-a | 0.66 | 0.72 | 0.77 | Chl-a | 0.57 | 0.46 | 0.87 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Song, K.; Wen, Z.; Zhao, Y.; Shang, Y.; Fang, C.; Du, J. Spatial Distribution of Diffuse Attenuation of Photosynthetic Active Radiation and Its Main Regulating Factors in Inland Waters of Northeast China. Remote Sens. 2016, 8, 964. https://doi.org/10.3390/rs8110964
Ma J, Song K, Wen Z, Zhao Y, Shang Y, Fang C, Du J. Spatial Distribution of Diffuse Attenuation of Photosynthetic Active Radiation and Its Main Regulating Factors in Inland Waters of Northeast China. Remote Sensing. 2016; 8(11):964. https://doi.org/10.3390/rs8110964
Chicago/Turabian StyleMa, Jianhang, Kaishan Song, Zhidan Wen, Ying Zhao, Yingxin Shang, Chong Fang, and Jia Du. 2016. "Spatial Distribution of Diffuse Attenuation of Photosynthetic Active Radiation and Its Main Regulating Factors in Inland Waters of Northeast China" Remote Sensing 8, no. 11: 964. https://doi.org/10.3390/rs8110964
APA StyleMa, J., Song, K., Wen, Z., Zhao, Y., Shang, Y., Fang, C., & Du, J. (2016). Spatial Distribution of Diffuse Attenuation of Photosynthetic Active Radiation and Its Main Regulating Factors in Inland Waters of Northeast China. Remote Sensing, 8(11), 964. https://doi.org/10.3390/rs8110964