Next Article in Journal
High-Precision Satellite Clock Offset Estimated by SRIF Based on Epoch-Wise Updated Orbit
Previous Article in Journal
Remote Sensing Image Segmentation Using Vision Mamba and Multi-Scale Multi-Frequency Feature Fusion
Previous Article in Special Issue
Geodetic Observations and Seismogenic Structures of the 2025 Mw 7.0 Dingri Earthquake: The Largest Normal Faulting Event in the Southern Tibet Rift
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 8
10.3390/rs17081389
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

Coseismic Rupture and Postseismic Afterslip of the 2020 Nima Mw 6.4 Earthquake

by
Shaojun Wang
1,2,
Ling Bai
1,2,* and
Chaoya Liu
1,2
1
State Key Laboratory of Tibetan Plateau Earth System, Environment and Resources, Institute of Tibetan Plateau Research, Chinese Academy of Sciences, Beijing 100101, China
2
University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(8), 1389; https://doi.org/10.3390/rs17081389
Submission received: 6 March 2025 / Revised: 5 April 2025 / Accepted: 5 April 2025 / Published: 14 April 2025
(This article belongs to the Special Issue Advanced SAR/InSAR Techniques in Understanding and Monitoring Geohazards)
Browse Figures
Versions Notes

Abstract

:
On 22 July 2020, an Mw 6.4 earthquake occurred in Nima County in the Qiangtang Terrane of the central Tibetan Plateau. This event, caused by normal faulting, remains controversial in terms of its rupture process and causative fault due to the complex tectonics of the region. In this study, we analyzed the coseismic and postseismic deformation using differential interferometric synthetic aperture radar (D-InSAR). The coseismic slip distribution was independently estimated through InSAR inversion and teleseismic waveform analysis, while the afterslip distribution was inferred from postseismic deformation. Coulomb stress failure analysis was conducted to assess the potential seismic hazard. Our results showed a maximum line-of-sight (LOS) coseismic deformation of about 29 cm away from the satellite, with quasi-vertical subsidence peaking at 35 cm. Four distinct deformation zones were observed in the quasi-east–west direction. Coseismic deformation and slip models based on InSAR and teleseismic data indicate that the Nima earthquake ruptured the West Yibu Chaka fault. The seismogenic fault had a strike of 26°, an eastward dip of 43°, and a rake of −87.28°, with rupture patches at depths of 3–13 km and a maximum slip of 1.1 m. Postseismic deformation showed cumulative LOS displacement of up to 0.05 m. Afterslip was concentrated in the up-dip and down-dip areas of the coseismic rupture zone, reaching a maximum of 0.11 m. Afterslip was also observed along the East Yibu Caka fault. Coulomb stress modeling indicates an increased seismic risk between the Yibu Caka fault and the Jiangai Zangbu fault, highlighting the vulnerability of the region to future seismic activity.

1. Introduction

The continuous collision between the Indian and Eurasian plates is the main driving force behind the tectonic deformation of the Tibetan Plateau (TP) [1,2,3,4]. During its tectonic evolution, the nearly east–west suture zones have divided the TP and the Himalayas into several tectonic units [3,4,5] (Figure 1). The north–south trending rifts and conjugate strike-slip faults traverse the east–west trending tectonic units, extending south to the Himalayas and north through the Lhasa and Qiangtang terranes [3,4,5,6,7,8] (Figure 1a). The conjugate strike-slip faults and normal fault systems that developed on both sides of the Bangong–Nujiang suture (BNS) are responsible for the deformation of the TP [3,4,7,8]. These typical rifts are high-angle normal faults, with dip angles typically in the range of 40° to 60°, although some are low-angle faults [5,6]. In recent years, teleseismic waveforms and differential interferometric synthetic aperture radar (D-InSAR) have been used in coseismic and postseismic observations to understand the tectonic deformation of the normal faulting earthquakes and rift systems [9,10,11,12,13,14,15]. The dynamic mechanism and temporal evolution of the north–south trending rift in the TP are still controversial, especially in the central region of the TP. The normal fault earthquakes provide constraints on the tectonic deformation of the TP.
On 22 July 2020, an Mw 6.4 earthquake occurred in Nima County (86.864°E, 33.144°N; Figure 1b) in the central TP. Fault plane solutions provided by several institutions (Table 1) indicate that this earthquake is associated with a normal faulting. The epicenter was located in the Qiangtang terrane, north of the BNS, near the eastern segment of the left-lateral Rigan Pei Co Fault (RCF) and the western segment of the Jiangai Zangbu Fault (JZF) (Figure 1b) [4,7,8]. The RCF extends northeast near the Yibu Chaka graben and branched into the east-dipping West Yibu Chaka fault (WYCF) and the west-dipping East Yibu Chaka Fault (EYCF) [4,7,8]. The WYCF and EYCF serve as the eastern and western structural boundaries of the Yibu Chaka graben [8,17,18]. The left-lateral strike-slip JZF is approximately parallel to the RCF [8]. In addition, the Jiaomu Fault (JF) and unnamed active normal faults are located to the east of the EYCF [18,19]. These faults together control the tectonic setting of the source area of the 2020 Nima earthquake.
The 2020 Nima earthquake has been studied using interferometric synthetic aperture radar (InSAR) coseismic interferograms, teleseismic waveforms, and geological data to model the coseismic slip distribution and postseismic deformation [17,18,19,20,21,22,23]. Some studies have suggested the east-dipping WYCF model as the causative fault [17,19,21,22,23,24,25], while others propose the EYCF as the responsible fault [17,18,20]. It is usually difficult to determine which of the two fault plans is the causative fault using a single type of dataset. The afterslip occurred either on the coseismic causative fault [23], the inferred secondary fault approximately 2 km away to coseismic causative fault [17], or on a steeper postseismic fault [22]. The mechanisms of the postseismic deformation of the 2020 Nima earthquake remain unclear.
To further investigate the fault plane solution of the 2020 Nima earthquake, we estimate the coseismic slip distribution and the postseismic deformation integrating the InSAR deformation and teleseismic waveform data. We compared the two fault planes with different dip directions and discussed the causative fault. We also processed the early postseismic deformation from over 6 months of InSAR observations to obtain a kinematics afterslip model. Then, we explore the relationships between the coseismic slip distribution and the postseismic afterslip. Finally, based on the coseismic model, we discuss the regional seismic hazard by evaluating the changes in Coulomb stress failure stress.

2. InSAR Data and Processing

Sentinel-1A/B TOPS SAR images from ascending track 12 and descending track 121 and 19 (Table 2) were utilized to generate the coseismic deformation of the 2020 Nima earthquake. All interferograms were processed in the InSAR Scientific Computing Environment (ISCE, version 2.6.0) [26] using precise orbit files provided by the European Space Agency, with orbit errors corrected. Multi-looking (10 in azimuth and 2 in range) was applied to the interferogram. The 1-arc second (90 m) Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM) was employed to reduce topographic phases [27]. The Goldstein filter method [28] was used to filter the wrapped interferograms, and the statistical network flow algorithm (SNAPHU) [29] was used to unwrap the phase. The Generic Atmospheric Correction Online Service (GACOS) for InSAR was used to reduce atmospheric effects [30]. Finally, the unwrapped interferogram was geocoded to the LOS coseismic deformation field.
The LOS deformation field obtained from D-InSAR is shown in Figure 2, with an elliptical subsidence. The displacements from tracks 12, 121, and 19 show a movement away from the satellite of about 0.29 m, 0.26 m, and 0.24 m, and a movement towards the satellite of about 0.09 m, 0.04 m, and 0.04 m, respectively. The clear subsidence consistent with a normal fault earthquake and the continuous interferograms (Figure 2a–c) suggest that the fault has not ruptured to the surface. The main extent of deformation almost reaches the WYCF and EYCF (Figure 2d–f), suggesting that the seismogenic fault may be related to fault activity at the boundary of the Yibu Chaka graben.
Three-dimensional coseismic surface deformation fields are crucial for assessing the geometric and kinematic characteristics of earthquake rupture faults. The three-dimensional surface deformation can be derived from the relationship between the LOS deformation and the satellite imaging geometric model [31]. Due to lack of other satellite coverage for the source region, we ignored the north–south deformation in solving the three-dimensional deformation field. Instead, we derived the two-dimensional surface deformation by utilizing ascending track 12 and descending track 121, which encompass the entire coseismic deformation area [32]. The least-squares method was applied to derive the quasi-east–west and quasi-vertical deformation fields (Figure 2g,h). The result shows that there are four significant deformation zones in quasi-east–west deformation field (Figure 2g): extension between R1 and R2, and R3, and R4, along the WYCF and EYCF, respectively, and compression between R2 and R3. The quasi-vertical deformation field (Figure 2h) shows a maximum subsidence of up to 35 cm. This subsidence, resulting from the significant vertical displacement of the hanging wall caused by fault rupture, is consistent with the characteristics of a normal fault earthquake. While this complex deformation pattern reflects the stress state in the source region due to the neglect of north–south deformation, it may also be due to the mixing of postseismic deformation signals. We note that the InSAR images for track 12 and track 121 were acquired on the seventh day and the third day after the earthquake due to the orbital design, respectively. We cannot completely separate the coseismic and postseismic deformation signals from the coseismic interferogram.
We processed ascending track 12 data from 30 July 2020 to 7 February 2021 and descending track 121 data from 26 July 2020 to 15 February 2021 Sentinel-1A SAR for postseismic deformation. The stack module of the InSAR Scientific Computing Environment, ISCE version 6.1, was used to generate multi-looking registration images, resulting in 16 and 17 pairs of interferograms from the ascending and descending tracks, respectively. The MialPy (version 0.2.1) software was used to produce time series of surface deformation [33], with phase time series correction by MintPy [34] to obtain the cumulative postseismic deformation field. The atmospheric error phases were corrected by the GACOS products [30]. Figure 3 shows the cumulative postseismic deformation field. The maximum subsidence over 6 months after the earthquake is up to 5 cm in the ascending track (Figure 3a), which is broadly consistent with the coseismic deformation field, but the deformation gradient appears to have shifted towards the WYCF compared to the coseismic deformation field. There is minor uplift on the western side of the WYCF and minor subsidence on the eastern side of the EYCF. However, the cumulative deformation of the descending track shows subsidence on the western side of the WYCF and slight uplift on the eastern side of the EYCF, which is very different from the coseismic descending observations. The opposite movement trend on the eastern side of the EYCF suggests a possible strike-slip component or afterslip in the EYCF. This different deformation pattern from the coseismic field suggests different subsurface processes occurring during the postseismic period. The distribution of aftershocks within 6 months following the earthquake is relatively dispersed, possibly indicating a complex tectonic adjustment mechanism in the region.

3. Coseismic Slip Distribution Inversion

3.1. InSAR Coseismic Slip Distribution Inversion

The coseismic source mechanisms are critical to understanding regional tectonics. Geological investigations indicate that the Nima earthquake did not rupture to the surface [18], leaving the causative fault models without reliable surface constraints. Various studies had reported that the seismogenic fault could be either the EYCF or the WYCF [17,18,19,20,21,22,23]. We incorporated focal mechanism solutions from the USGS and other institutions (Table 1), with regional geological data [18] and coseismic deformation. As a result, we identified two candidate finite fault models: an east-dipping fault model with the fault strike along the WYCF and a west-dipping fault model with the fault strike along the EYCF. The detailed fault parameters are listed in Table 3.
The fault model was designed as a single segment model in an elastic half-space, with a Poisson’s ratio of 0.25 and a shear modulus of 30 GPa. We divided each candidate fault into a finite fault model with 2 km by 2 km patches. The Steepest Decent Method (SDM) software package (version 2011), published by Wang et al. [35], was utilized for slip distributed inversion. This method is primarily based on the least squares principle and the steepest descent algorithm, applied under constrained conditions. The deformation fields were downsampled using a gradient-based quadtree algorithm [36] to reduce the data size (Figures S1 and S2), with an equal weighting ratio of 1:1:1 for the three tracks. The smoothing factors for the east-dipping and west-dipping models, determined through trial and error by minimizing the misfit [37], were 0.1 and 0.13, respectively. The optimal dip angle is 43° for the east-dipping and 40° for the west-dipping fault models.
The slip distributions on the fault planes are shown in Figure 4. For the east-dipping model (Figure 4a), the slip area is concentrated at depths of 3–13 km, with a maximum slip of about 1.1 m and a rake angle of −87.28°, indicating a normal fault with a slight sinistral component. The estimated moment was 3.67 × 10 18 Nm, corresponding to a Mw 6.31 event. Meanwhile, for the west-dipping fault model (Figure 4b), most of the slip patchesare was in a depth range of 3–13 km, with a maximum slip of approximately 0.93 m and a rake angle of −95.54°, indicating a normal fault with a slight dextral component. The estimated moment is 3.09 × 10 18 Nm, corresponding to a Mw 6.26 event. The specific parameters for the fault models we obtained are shown in Table 3. The root mean square error is less than 0.1 m (Figures S1 and S2).

3.2. Teleseismic Waveform Data Inversion

The broadband waveforms from the Global Seismographic Network (GSN) of the Incorporated Research Institutions for Seismology (IRIS) seismic data center were used for the teleseismic waveform inversion. Data with epicentral distances between 30° and 90° were selected. Stations were chosen at approximately 5° intervals in azimuth from 33 stations (Figure S3). We used the AK135 global continental velocity structure model [38] and the method developed by Wang et al. [39] to compute Green’s functions. The geometric parameters of the fault models were taken from the InSAR inversion in Section 3.1. We then used the method developed by Zhang et al. [40] to divide the fault plan into finite faults, each with a length and width of 2 km × 2 km, for slip distribution inversion. We applied bandpass filtering with a frequency range of 0.01 to 0.2 Hz to remove background noise and ensure a high signal-to-noise ratio (Figures S4 and S5).
The slip distributions obtained from the teleseismic waveforms are shown in Figure 5. Figure 5a shows the east-dipping fault model with a strike of 26°. The slip distribution on the fault plane has an elliptical shape, concentrated between distance along dip of 5 and 18 km with a maximum slip of about 1.1 m. Figure 5b shows the west-dipping fault rupture model with a strike of 203° with a maximum slip of approximately 0.8 m and the rupture extends to the surface along the fault plane.

4. Afterslip Model

There are three mechanisms of postseismic deformation: afterslip, poroelastic rebound, and viscoelastic relaxation [19,22,23,41]. Especially for moderate earthquakes, early postseismic deformation is primarily influenced by afterslip [41]. The afterslip distribution reflects the postseismic adjustment of the earthquake faults. For the Nima event, we suggest that the postseismic deformation was dominated by afterslip due to the short period of postseismic observation. The cumulative deformation observed over the 6 months following the mainshock was about 0.05 m, which is close to the background noise level. Therefore, we used a uniform sampling method [12] to downsample the cumulative postseismic deformation (Figure 6, first line) for the afterslip inversion to reduce computational complexity. This method can effectively and uniformly distribute the weight of far-field and near-field deformation during the inversion. Based on the postseismic deformation characteristics, we used the two fault models for afterslip inversion, one was named F1, and the other one was named F2. For F1, the fault source parameters are inherited from the coseismic east-dipping fault. The dip angle of the F2 fault was set to 45° to account for the deformation zone on the eastern side of the EYCF, where active faults with dip angles of 40–50° are exposed at the surface, as identified in geological surveys [18]. Detailed fault parameters of the afterslip model are given in Table 4. The kinematic afterslip was then calculated using the SDM software package (version 2011) [35].
In the forward modeling shown in Figure 6 (the central column), the simulated deformation shows an 82% agreement with the observed data, suggesting that our rupture model effectively simulates the cumulative postseismic deformation. However, discrepancies on the eastern side of the F2 fault may suggest a more complex mechanism behind the postseismic deformation. The afterslip in Figure 7 shows irregular afterslip mainly in the up-dip and down-dip regions of the coseismic rupture area. The maximum afterslip on the F1 fault reaches 0.11 m, with shallow afterslip extending into the coseismic rupture zone. The afterslip distribution on the F2 fault is concentrated at shallow depths, with a maximum slip of 0.05 m. Assuming a shear modulus of 30 GPa, the total accumulative moment released over 6 months was 3.09 × 10 18 Nm, equivalent to a Mw 5.9 earthquake.

5. Discussion

5.1. The 2020 Nima Earthquake Fault Geometry

We measured the surface deformation caused by the 2020 Nima earthquake using D-InSAR. The coseismic interferograms (Figure 2a–c) show continuity without decoherence from the surface rupture, indicating that the Nima earthquake occurred with a blind fault. The observed subsidence in the coseismic LOS deformation field (Figure 2d–f) and the quasi-vertical deformation field (Figure 2h) are consistent with the characteristics typical of a normal fault earthquake. In the quasi-east–west deformation field (Figure 2g), four opposing deformation signals are distributed along the EYCF and WYCF, suggesting a complex pattern of extensional and compressional deformation in the Yibu Chaka basin. In addition, it is possible that the coseismic and two-dimensional deformation fields contain early postseismic information due to the observation period [9,42,43]. Based on the coseismic deformation field, we inferred either of the east-dipping and west-dipping normal fault models near the graben boundaries (EYCF and WYCF) for the 2020 Nima earthquake, which reasonably reproduce the surface deformation (Figures S1 and S2). However, the slip distribution derived from the teleseismic waveforms (Figure 5) indicates that the west-dipping model suggests the rupture zone extends to the surface, which was not observed in the coseismic deformation (Figure 2a–c), and the east-dipping model shows that rupture occurs exclusively at subsurface depths, which is consistent with the east-dipping slip distribution model based on InSAR (Figure 4a). Furthermore, the east-dipping model has smaller residuals (Figures S1), which is consistent with previous results [21,24]. In addition, the early postseismic cumulative deformation field (Figure 3a,b) near the WYCF shows a larger gradient, as previous studies have suggested that normal faulting postseismic deformation shows a strong spatial association with the coseismic causative fault [9,43].
We infer that the coseismic causative fault model for the 2020 Nima earthquake is an east-dipping fault model with a strike of 26°, a dip of 45°, and a rake of −85.67°, which ruptured the WYCF on the western side of the Yibu Chaka basin. Previous studies have suggested that the coseismic fault is the WYCF, based solely on surface fissures, InSAR deformation, or magnetic mineral alteration [17,18,19,20,21,22,23]. In contrast, we provide new evidence for the east-dipping model, supported by teleseismic waveforms and InSAR deformation. Consistent with most normal fault earthquakes on the TP, the 2020 Nima earthquake occurred on a high-angle normal fault, indicating the mature state of the rift [5,6,10]. The continuous sinistral slip along the RCF and the JZF is expected to induce extensional deformation in the Yibu Chaka basin, accommodating the accumulation of extensional strain. This strain will eventually be released through by normal faulting earthquakes probably underlying beneath the surface. Given the complexity of such tectonic settings, we recommend the integration of both geological and geophysical observations when inferring the source parameters of moderate earthquakes.

5.2. Coseismic Slip Distribution and Afterslip

Based on over 6 months of postseismic cumulative deformation data and kinematic afterslip inversion, we developed a postseismic afterslip model (Figure 7) for the 2020 Nima earthquake. The afterslip model shows that on the F1 fault (Figure 7a), afterslip is distributed in the up-dip and down-dip regions of the coseismic rupture zone and is unevenly distributed along strike. On the F2 fault (Figure 7b), afterslip occurs mainly along the fault plane at shallow depths above 9 km. Compared to the fault model by Yang et al. [22], our model shows that afterslip occurs at greater depths below the coseismic rupture zone and also on the opposite EYCF. Yang’s model used about 6 months of postseismic data from the ascending track 12. Previous studies suggested that the afterslip of dip-slip earthquakes in the northern and central TP mainly occurs above the coseismic rupture area [12]. Instead, our afterslip model is consistent with the afterslip model of the 2020 Nima earthquake as analyzed by Hong et al. [19]. And it resembles the along-strike heterogeneous afterslip distribution observed in the 2008 Damxung Mw 6.3 earthquake in southern TP by Bie et al. [9]. An irregular afterslip distribution is also observed in the 2009 L’Aquila Mw 6.3 normal fault earthquake in Italy [44]. The heterogeneity in the afterslip distribution may be related to the geometric and frictional properties of the fault plane. The observed scarcity of aftershocks in afterslip zones indicates these fault patches are frictionally unstable, satisfying the velocity-weakening criterion under steady-state conditions as described by rate-and-state friction theory [44].
To evaluate the effect of coseismic slip, we modeled the F1 fault as source fault, with a friction coefficient of 0.4 [23] and the F2 fault as a receiver fault, and we calculated the Coulomb stress perturbation on the fault plane (Figure 8a). We observed clear stress loading (with stress loading exceeding the stress triggering threshold) in the up-dip and down-dip regions of the coseismic rupture zone on the F1 fault, where afterslip was mainly distributed along the stress-loaded areas. The afterslip was mainly distributed along the stress-loaded area. In the up-dip region of the F2 fault, the afterslip corresponds to areas of Coulomb stress loading, although the afterslip zone does not fully correspond to the coseismic Coulomb stress loading area, which may be due to model errors. Previous studies have suggested that the WYCF and EYCF faults may integrate at depth to form a negative flower structure (Figure 8b) [17,18,19]. A feature of this structure is a dip-slip movement along the fault plane caused by extensional components [45]. We propose that stress loading from the coseismic rupture may account for the observed afterslip on the F1 fault, as well as the postseismic slip on the F2 fault, leading to the observed deformation on the eastern side of the EYCF. The Coulomb stress changes were identified as the primary triggering factor for three moderate-sized Zhongba earthquake sequences within the Lunggar rift system, southern TP from (2004–2008) [11]. Similarly, the 1989 normal faulting sequences in the Dobi graben (central Afar) was attributed to coseismic Coulomb stress changes that reactivated secondary faults [46]. During the 1997 Umbria-Marche earthquake sequence (Italy), Coulomb stress changes induced by repeated normal fault earthquakes activated slip on adjacent faults [47]. These cases highlight the important role of static Coulomb stress in influencing fault rupture behavior, particularly for normal fault earthquakes in rift environments. Normal fault earthquakes in grabens may cause large damage and warrant further investigations [46].

5.3. Potential Hazards in the 2020 Nima Earthquake Source Area

The evaluation of Coulomb stress changes is an essential method for earthquake hazard analysis. Coulomb stress changes greater than 0.01 MPa can trigger subsequent earthquakes [48,49]. We calculated the coseismic Coulomb stress perturbations (Figure 9) in the region using the east-dipping fault as both the source fault and the receiver fault. At depths of 3, 5, 7.5, and 10 km, the Coulomb stress changes predominantly exhibit negative values, indicating the release of regional stress. At depths of 3 km and 15 km, significant Coulomb stress increase is observed in the EYCF area. We cannot rule out the possibility of earthquakes occurring at depths within 3 km. One reason is that the shallow parts of mature continental faults are filled with fault gouge, which inhibits the nucleation of earthquakes [50]. Meanwhile, a depth of 15 km is considered a typical depth for earthquake nucleation in and around TP. The 3–20 km depth range shows concentrated Coulomb stress accumulation between the EYCF’s northeastern segment and JZF’s southwestern segment. This coupled with reduced aftershock activity indicates significant seismic potential requiring focused assessment.

6. Conclusions

The InSAR coseismic deformation field of the 2020 Nima earthquake showed an elliptical pattern, with maximum subsidence measurements of 0.29 m, 0.26 m, and 0.24 m recorded on three tracks. The quasi-vertical deformation field was dominated by subsidence with a maximum of 35 cm, while the quasi-east–west field showed four deformation zones with both extensional and compressional features. By integrating InSAR deformation and teleseismic waveform analysis, the geometric parameters of the causative fault were determined as a strike of 26°, a dip of 43°, and a rake of −87.28°, with rupture occurring along the WYCF. Continuous sinistral slip along the RCF and the JZF has induced extensional strain in the Yibu Chaka basin, which was eventually released by the normal faulting of the 2020 Nima earthquake. Early postseismic cumulative LOS deformation reached 5 cm, with a maximum afterslip of 0.11 m, concentrated in the up-dip and down-dip regions of the coseismic rupture zone. In addition, the adjacent EYCF experienced shallow afterslip of about 0.05 m, probably triggered by Coulomb stress perturbation from the 2020 Nima earthquake. The stress perturbation effects on nearby fault zones highlight the increased seismic risk in the northeastern EYCF and southwestern JZF seismic gap regions.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs17081389/s1, Figure S1: The observation, model, and residuals of the east-dipping fault model. Figure S2: The observation, model, and residuals of the west-dipping fault model. Figure S3: Spatial distribution map of teleseismic stations. Figure S4: Waveform fitting for the east-dipping fault model. Figure S5: Waveform fitting for the west-dipping fault model.

Author Contributions

All authors participated in editing and reviewing the manuscript. Conceptualization, S.W. and L.B.; methodology, S.W. and C.L.; validation, S.W., L.B. and C.L.; formal analysis, S.W. and L.B.; data curation, S.W.; writing—original draft preparation, S.W.; writing—review and editing, S.W., L.B. and C.L.; visualization, S.W.; supervision, L.B.; project administration, L.B.; funding acquisition, L.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by the grants of the National Nature Science Foundation of China (No. 42130312), and the Second Tibetan Plateau Scientific Expedition and Research Program (No. 2019QZKK07).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Acknowledgments

The Sentinal data were downloaded from the Alaska website (https://search.asf.alaska.edu/, accessed on 20 January 2021) by the European Space Agency (ESA). The SDM program provided by Professor Rongjiang Wang from the Potsdam Center for Geosciences (GFZ) in the Germany, and the aftershock data were from the China Earthquake Network Center, and most of the drawings were drawn by GMT (version 6.4) [51]. The ISCE software (version 2.6.0) is available on https://github.com/isce-framework/isce2. We are very grateful to Zhiwen Chen and Hongru Li for their insightful discussions. We thank the reviewers and editors for their help in improving this manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Armijo, R.; Tapponnier, P.; Mercier, J.; Han, T.L. Quaternary extension in southern Tibet: Field observations and tectonic implications. J. Geophys. Res. Solid Earth 1986, 91, 13803–13872. [Google Scholar] [CrossRef]
  2. Tapponnier, P.; Zhiqin, X.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Jingsui, Y. Oblique stepwise rise and growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
  3. Yin, A. Mode of Cenozoic east-west extension in Tibet suggesting a common origin of rifts in Asia during the Indo-Asian collision. J. Geophys. Res. Solid Earth 2000, 105, 21745–21759. [Google Scholar] [CrossRef]
  4. Yin, A.; Taylor, M.H. Mechanics of V-shaped conjugate strike-slip faults and the corresponding continuum mode of continental deformation. Bulletin 2011, 123, 1798–1821. [Google Scholar] [CrossRef]
  5. Kapp, P.; Yin, A.; Manning, C.E.; Harrison, T.M.; Taylor, M.H.; Ding, L. Tectonic evolution of the early Mesozoic blueschist-bearing Qiangtang metamorphic belt, central Tibet. Tectonics 2003, 22, 17A. [Google Scholar] [CrossRef]
  6. Kapp, P.; Taylor, M.; Stockli, D.; Ding, L. Development of active low-angle normal fault systems during orogenic collapse: Insight from Tibet. Geology 2008, 36, 7–10. [Google Scholar] [CrossRef]
  7. Taylor, M.; Peltzer, G. Current slip rates on conjugate strike-slip faults in central Tibet using synthetic aperture radar interferometry. J. Geophys. Res. Solid Earth 2006, 111, B12402. [Google Scholar] [CrossRef]
  8. Taylor, M.; Yin, A.; Ryerson, F.J.; Kapp, P.; Ding, L. Conjugate strike-slip faulting along the Bangong-Nujiang suture zone accommodates coeval east-west extension and north-south shortening in the interior of the Tibetan Plateau. Tectonics 2003, 22, 18A. [Google Scholar] [CrossRef]
  9. Bie, L.; Ryder, I.; Nippress, S.E.; Bürgmann, R. Coseismic and post-seismic activity associated with the 2008 M w 6.3 Damxung earthquake, Tibet, constrained by InSAR. Geophys. J. Int. 2014, 196, 788–803. [Google Scholar] [CrossRef]
  10. Elliott, J.; Walters, R.; England, P.; Jackson, J.; Li, Z.; Parsons, B. Extension on the Tibetan plateau: Recent normal faulting measured by InSAR and body wave seismology. Geophys. J. Int. 2010, 183, 503–535. [Google Scholar] [CrossRef]
  11. Ryder, I.; Bürgmann, R.; Fielding, E. Static stress interactions in extensional earthquake sequences: An example from the South Lunggar Rift, Tibet. J. Geophys. Res. Solid Earth 2012, 117, B09405. [Google Scholar] [CrossRef]
  12. Ryder, I.; Bürgmann, R.; Sun, J. Tandem afterslip on connected fault planes following the 2008 Nima-Gaize (Tibet) earthquake. J. Geophys. Res. Solid Earth 2010, 115, B03404. [Google Scholar] [CrossRef]
  13. Sun, J.; Shen, Z.; Xu, X.; Bürgmann, R. Synthetic normal faulting of the 9 January 2008 Nima (Tibet) earthquake from conventional and along-track SAR interferometry. Geophys. Res. Lett. 2008, 35, L22308. [Google Scholar] [CrossRef]
  14. Wang, H.; Wright, T.J.; Liu-Zeng, J.; Peng, L. Strain rate distribution in south-central Tibet from two decades of InSAR and GPS. Geophys. Res. Lett. 2019, 46, 5170–5179. [Google Scholar] [CrossRef]
  15. Bai, L.; Chen, Z.; Wang, S. The 2025 Dingri MS6.8 earthquake in Xizang: Analysis of tectonic background and discussion of source characteristics. Rev. Geophys. Planet. Phys. 2025, 56, 258–263. [Google Scholar] [CrossRef]
  16. Wang, M.; Shen, Z.K. Present-day crustal deformation of continental China derived from GPS and its tectonic implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef]
  17. Gao, H.; Liao, M.; Liang, X.; Feng, G.; Wang, G. Coseismic and postseismic fault kinematics of the July 22, 2020, Nima (Tibet) Ms6. 6 earthquake: Implications of the forming mechanism of the active N-S-trending grabens in Qiangtang, Tibet. Tectonics 2022, 41, e2021TC006949. [Google Scholar] [CrossRef]
  18. Liu, F.; Pan, J.; Li, H.; Sun, Z.; Liu, D.; Lu, H.; Zheng, Y.; Wang, S.; Bai, M.; Chevalier, M. Characteristics of quaternary activities along the Riganpei co fault and seismogenic structure of the July 23, 2020 Mw6. 4 Nima Earthquake, Central Tibet. Acta Geosci. Sin. 2021, 43, 173–188. [Google Scholar] [CrossRef]
  19. Hong, S.; Liu, M.; Zhou, X.; Meng, G.; Dong, Y. Afterslip on Conjugate Faults of the 2020 M w 6.3 Nima Earthquake in the Central Tibetan Plateau: Evidence from InSAR Measurements. Bull. Seismol. Soc. Am. 2023, 113, 2026–2040. [Google Scholar] [CrossRef]
  20. Liu, D.; Ferré, E.C.; Li, H.; Chou, Y.-M.; Wang, H.; Horng, C.-S.; Sun, Z.; Pan, J.; Chevalier, M.-L.; Zheng, Y. Magnetic evidence of seismic fluid processes along the East Yibug Chaka Fault, Tibet. Tectonophysics 2022, 838, 229500. [Google Scholar] [CrossRef]
  21. Li, K.; Li, Y.; Tapponnier, P.; Xu, X.; Li, D.; He, Z. Joint InSAR and field constraints on faulting during the Mw 6.4, July 23, 2020, Nima/Rongma earthquake in central Tibet. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022212. [Google Scholar] [CrossRef]
  22. Yang, J.; Xu, C.; Wen, Y.; Xu, G. The July 2020 M w 6.3 Nima Earthquake, Central Tibet: A Shallow Normal-Faulting Event Rupturing in a Stepover Zone. Seismol. Soc. Am. 2022, 93, 45–55. [Google Scholar] [CrossRef]
  23. Zhang, M.; Li, Z.; Yu, C.; Liu, Z.; Zhang, X.; Wang, J.; Yang, J.; Han, B.; Peng, J. Co-and Postseismic Deformation of the 2020 Mw 6.3 Nima (Tibet, China) Earthquake Revealed by InSAR Observations. Remote Sens. 2022, 14, 5390. [Google Scholar] [CrossRef]
  24. ChengTao, L.; Qi, L.; Kai, T.; XiaoFei, L. Coseismic deformation characteristics of the 2020 Nima, Xizang M W 6.3 earthquake from Sentinel-1A/B InSAR data and rupture slip distribution. Chin. J. Geophys. 2021, 64, 2297–2310. [Google Scholar] [CrossRef]
  25. Gong, W.; Zhang, Y.; Li, T.; Wen, S.; Zhao, D.; Hou, L.; Shan, X. Multi-sensor geodetic observations and modeling of the 2017 Mw 6.3 Jinghe earthquake. Remote Sens. 2019, 11, 2157. [Google Scholar] [CrossRef]
  26. Rosen, P.A.; Gurrola, E.; Sacco, G.F.; Zebker, H. The InSAR scientific computing environment. In Proceedings of the EUSAR 2012, 9th European Conference on Synthetic Aperture Radar, Nuremberg, Germany, 23–26 April 2012; pp. 730–733. [Google Scholar]
  27. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
  28. Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
  29. Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
  30. Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
  31. Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 Mw7. 1 Hector Mine earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
  32. Fujiwara, S.; Nishimura, T.; Murakami, M.; Nakagawa, H.; Tobita, M.; Rosen, P.A. 2.5-D surface deformation of M6. 1 earthquake near Mt Iwate detected by SAR interferometry. Geophys. Res. Lett. 2000, 27, 2049–2052. [Google Scholar] [CrossRef]
  33. Mirzaee, S.; Amelung, F.; Fattahi, H. Non-linear phase linking using joined distributed and persistent scatterers. Comput. Geosci. 2023, 171, 105291. [Google Scholar] [CrossRef]
  34. Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
  35. Wang, R.; Diao, F.; Hoechner, A. SDM-A geodetic inversion code incorporating with layered crust structure and curved fault geometry. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 7–12 April 2013; p. EGU2013-2411. [Google Scholar]
  36. Jónsson, S.; Zebker, H.; Segall, P.; Amelung, F. Fault slip distribution of the 1999 M w 7.1 Hector Mine, California, earthquake, estimated from satellite radar and GPS measurements. Bull. Seismol. Soc. Am. 2002, 92, 1377–1389. [Google Scholar] [CrossRef]
  37. Feng, W.; Li, Z.; Elliott, J.R.; Fukushima, Y.; Hoey, T.; Singleton, A.; Cook, R.; Xu, Z. The 2011 MW 6.8 Burma earthquake: Fault constraints provided by multiple SAR techniques. Geophys. J. Int. 2013, 195, 650–660. [Google Scholar] [CrossRef]
  38. Kennett, B.L.; Engdahl, E.; Buland, R. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 1995, 122, 108–124. [Google Scholar] [CrossRef]
  39. Wang, R. A simple orthonormalization method for stable and efficient computation of Green’s functions. Bull. Seismol. Soc. Am. 1999, 89, 733–741. [Google Scholar] [CrossRef]
  40. Zhang, Y.; Feng, W.; Chen, Y.; Xu, L.; Li, Z.; Forrest, D. The 2009 L’Aquila MW 6.3 earthquake: A new technique to locate the hypocentre in the joint inversion of earthquake rupture process. Geophys. J. Int. 2012, 191, 1417–1426. [Google Scholar] [CrossRef]
  41. Avouac, J.-P. From geodetic imaging of seismic and aseismic fault slip to dynamic modeling of the seismic cycle. Annu. Rev. Earth Planet. Sci. 2015, 43, 233–271. [Google Scholar] [CrossRef]
  42. Floyd, M.A.; Walters, R.J.; Elliott, J.R.; Funning, G.J.; Svarc, J.L.; Murray, J.R.; Hooper, A.J.; Larsen, Y.; Marinkovic, P.; Bürgmann, R. Spatial variations in fault friction related to lithology from rupture and afterslip of the 2014 South Napa, California, earthquake. Geophys. Res. Lett. 2016, 43, 6808–6816. [Google Scholar] [CrossRef]
  43. Ragon, T.; Sladen, A.; Bletery, Q.; Vergnolle, M.; Cavalié, O.; Avallone, A.; Balestra, J.; Delouis, B. Joint inversion of coseismic and early postseismic slip to optimize the information content in geodetic data: Application to the 2009 M w 6.3 L’Aquila earthquake, Central Italy. J. Geophys. Res. Solid Earth 2019, 124, 10522–10543. [Google Scholar] [CrossRef]
  44. D’agostino, N.; Cheloni, D.; Fornaro, G.; Giuliani, R.; Reale, D. Space-time distribution of afterslip following the 2009 L’Aquila earthquake. J. Geophys. Res. Solid Earth 2012, 117, B02402. [Google Scholar] [CrossRef]
  45. Fossen, H. Structural Geology; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
  46. Jacques, E.; Kidane, T.; Tapponnier, P.; Manighetti, I.; Gaudemer, Y.; Meyer, B.; Ruegg, J.; Audin, L.; Armijo, R. Normal faulting during the August 1989 earthquakes in central Afar: Sequential triggering and propagation of rupture along the Dobi Graben. Bull. Seismol. Soc. Am. 2011, 101, 994–1023. [Google Scholar] [CrossRef]
  47. Nostro, C.; Chiaraluce, L.; Cocco, M.; Baumont, D.; Scotti, O. Coulomb stress changes caused by repeated normal faulting earthquakes during the 1997 Umbria-Marche (central Italy) seismic sequence. J. Geophys. Res. Solid Earth 2005, 110, B05S20. [Google Scholar] [CrossRef]
  48. Deng, J.; Sykes, L.R. Evolution of the stress field in southern California and triggering of moderate-size earthquakes: A 200-year perspective. J. Geophys. Res. Solid Earth 1997, 102, 9859–9886. [Google Scholar] [CrossRef]
  49. Harris, R.A. Introduction to Special Section: Stress Triggers, Stress Shadows, and Implications for Seismic Hazard; Wiley Online Library: Hoboken, NJ, USA, 1998; Volume 103, pp. 24347–24358. [Google Scholar]
  50. Luo, Y.; Ni, S.; Zeng, X.; Zheng, Y.; Chen, Q.; Chen, Y. A shallow aftershock sequence in the north-eastern end of the Wenchuan earthquake aftershock zone. Sci. China Earth Sci. 2010, 53, 1655–1664. [Google Scholar] [CrossRef]
  51. Wessel, P.; Smith, W.H.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. Eos Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
Remotesensing 17 01389 g001
Figure 1. Tectonic map of the 2020 Nima earthquake. (a) Tectonic setting of the TP, the red box shows the region of (b). (b) The red star marks the epicenter of the 2020 Nima earthquake as determined by the China Earthquake Networks Center (CENC). Red beach ball are focal mechanisms of the 2020 Nima earthquake determined by different institutions. Black focal mechanisms represent earthquake of Mw ≥ 5.0 occurred between 1964 and 2020. Colored circles denote aftershocks that occurred within 6 months after the mainshock, with variable focal depths (https://data.earthquake.cn, accessed on 20 January 2021). The blue box represents the coverage area of the Sentinel 1A/B. The purple arrow represents the GPS horizontal velocity field, relative to stable Eurasia [16]. (c) The region of the black box in (b). BNS: Bangong–Nujiang Suture, RCF: Riganpei Co Fault, WYCF: West Yibu Chaka Fault, EYCF: East Yibu Chaka Fault, JZF: Jiangai Zangbu Fault, JF: Jiaomu Fault.
Figure 1. Tectonic map of the 2020 Nima earthquake. (a) Tectonic setting of the TP, the red box shows the region of (b). (b) The red star marks the epicenter of the 2020 Nima earthquake as determined by the China Earthquake Networks Center (CENC). Red beach ball are focal mechanisms of the 2020 Nima earthquake determined by different institutions. Black focal mechanisms represent earthquake of Mw ≥ 5.0 occurred between 1964 and 2020. Colored circles denote aftershocks that occurred within 6 months after the mainshock, with variable focal depths (https://data.earthquake.cn, accessed on 20 January 2021). The blue box represents the coverage area of the Sentinel 1A/B. The purple arrow represents the GPS horizontal velocity field, relative to stable Eurasia [16]. (c) The region of the black box in (b). BNS: Bangong–Nujiang Suture, RCF: Riganpei Co Fault, WYCF: West Yibu Chaka Fault, EYCF: East Yibu Chaka Fault, JZF: Jiangai Zangbu Fault, JF: Jiaomu Fault.
Remotesensing 17 01389 g001
Remotesensing 17 01389 g002
Figure 2. (a–c) are the coseismic interferograms from the ascending track 12, descending track 121 and track 19, respectively. (d–f) are the coseismic LOS deformations from the ascending track 12, descending track121 and track 19, respectively. The red star marks the epicenter of the 2020 Nima earthquake as determined by the China Earthquake Networks Center (CENC). The red beach ball represents the focal mechanism solution of the 2020 Nima earthquake from the USGS catalog. The positive values represent the motion towards the satellite and negative values represent the motion away from the satellite. (g,h) are the acquired coseismic quasi-east–west and quasi-vertical deformations, respectively. (i) shows profiles of coseismic LOS displacements and topography along the A–B profile.
Figure 2. (a–c) are the coseismic interferograms from the ascending track 12, descending track 121 and track 19, respectively. (d–f) are the coseismic LOS deformations from the ascending track 12, descending track121 and track 19, respectively. The red star marks the epicenter of the 2020 Nima earthquake as determined by the China Earthquake Networks Center (CENC). The red beach ball represents the focal mechanism solution of the 2020 Nima earthquake from the USGS catalog. The positive values represent the motion towards the satellite and negative values represent the motion away from the satellite. (g,h) are the acquired coseismic quasi-east–west and quasi-vertical deformations, respectively. (i) shows profiles of coseismic LOS displacements and topography along the A–B profile.
Remotesensing 17 01389 g002
Remotesensing 17 01389 g003
Figure 3. Postseismic deformation observation. (a,b) are postseismic deformation from ascending track 12 and descending track 121, respectively. (c,d) are profiles of postseismic LOS displacements along A–B from track 121 and 12, respectively. The colored circle shows the aftershocks within 6 months.
Figure 3. Postseismic deformation observation. (a,b) are postseismic deformation from ascending track 12 and descending track 121, respectively. (c,d) are profiles of postseismic LOS displacements along A–B from track 121 and 12, respectively. The colored circle shows the aftershocks within 6 months.
Remotesensing 17 01389 g003
Remotesensing 17 01389 g004
Figure 4. Estimated slip distribution of (a) the east-dipping model and (b) the west-dipping model derived from InSAR data. Blue stars denote the location of the mainshock from the USGS. Black dashed contours indicate slip distribution. Green circles depict aftershock distribution within 6 months postseismic period, with circle diameter proportional to earthquake magnitude. Black arrows represent the slip direction.
Figure 4. Estimated slip distribution of (a) the east-dipping model and (b) the west-dipping model derived from InSAR data. Blue stars denote the location of the mainshock from the USGS. Black dashed contours indicate slip distribution. Green circles depict aftershock distribution within 6 months postseismic period, with circle diameter proportional to earthquake magnitude. Black arrows represent the slip direction.
Remotesensing 17 01389 g004
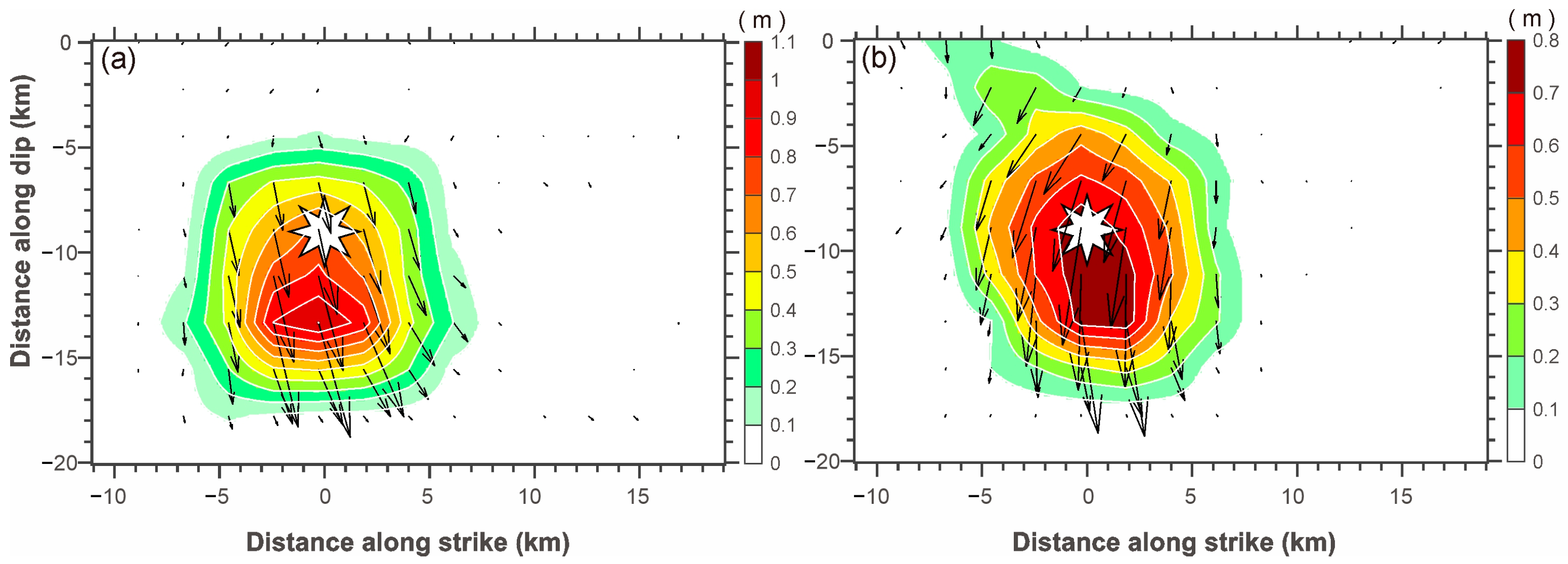
Remotesensing 17 01389 g005
Figure 5. Estimated slip distribution of (a) the east-dipping fault model and (b) the west-dipping fault model derived from teleseismic waveforms. White stars indicate the centroid location of the Nima earthquake as determined from the InSAR data. Black arrows represent the slip direction.
Figure 5. Estimated slip distribution of (a) the east-dipping fault model and (b) the west-dipping fault model derived from teleseismic waveforms. White stars indicate the centroid location of the Nima earthquake as determined from the InSAR data. Black arrows represent the slip direction.
Remotesensing 17 01389 g005
Remotesensing 17 01389 g006
Figure 6. Down-sampled observations (Obs, the left column), and forward modeling results (Sim, the central column), and residual (Res, the right column) of the afterslip model. The red and blue lines represent the inferred fault traces, respectively. The rectangular box represents the surface projection of the fault plane.
Figure 6. Down-sampled observations (Obs, the left column), and forward modeling results (Sim, the central column), and residual (Res, the right column) of the afterslip model. The red and blue lines represent the inferred fault traces, respectively. The rectangular box represents the surface projection of the fault plane.
Remotesensing 17 01389 g006
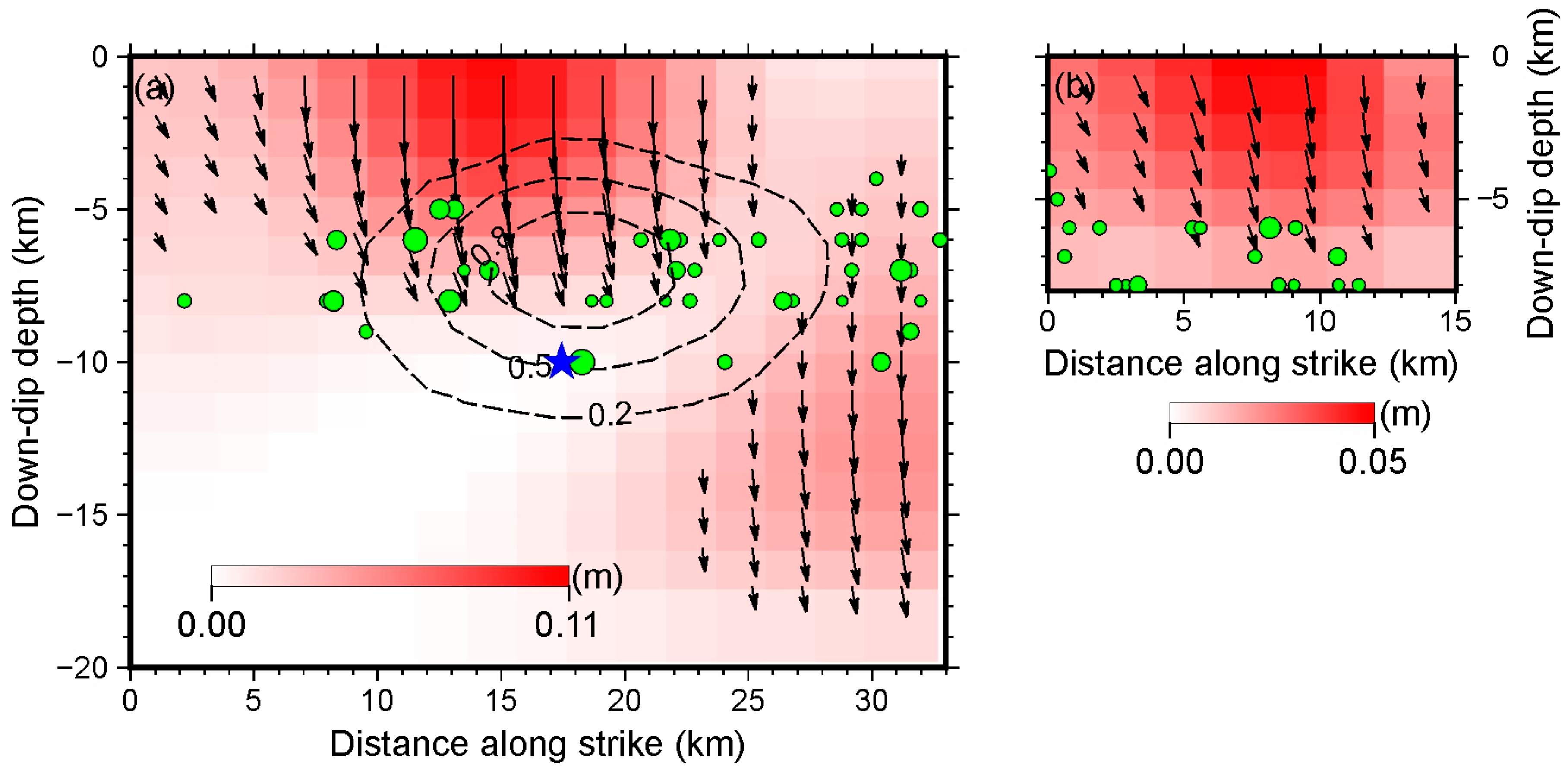
Remotesensing 17 01389 g007
Figure 7. Afterslip distribution of the 2020 Nima earthquake (the blue star). (a) Afterslip distribution on the F1 fault plane. (b) Afterslip distribution on the F2 fault plane. Blue stars denote the location of the mainshock from the USGS. Black arrows represent the slip direction. Black contours delineate coseismic slip distribution. The green circles represent aftershocks occurring within 6 months after the mainshock.
Figure 7. Afterslip distribution of the 2020 Nima earthquake (the blue star). (a) Afterslip distribution on the F1 fault plane. (b) Afterslip distribution on the F2 fault plane. Blue stars denote the location of the mainshock from the USGS. Black arrows represent the slip direction. Black contours delineate coseismic slip distribution. The green circles represent aftershocks occurring within 6 months after the mainshock.
Remotesensing 17 01389 g007
Remotesensing 17 01389 g008
Figure 8. (a) The change of Coulomb stress resolved on the earthquake fault plane (friction coefficient = 0.4). The contouring indicates the cumulative afterslip distributions (in m). Blue stars denote the location of the mainshock from the USGS. Green circles represent aftershocks occurring within 6 months. (b) Model of genetic mechanism of the 2020 Nima earthquake.
Figure 8. (a) The change of Coulomb stress resolved on the earthquake fault plane (friction coefficient = 0.4). The contouring indicates the cumulative afterslip distributions (in m). Blue stars denote the location of the mainshock from the USGS. Green circles represent aftershocks occurring within 6 months. (b) Model of genetic mechanism of the 2020 Nima earthquake.
Remotesensing 17 01389 g008
Remotesensing 17 01389 g009
Figure 9. Static Coulomb failure stress changes of the 2020 Nima earthquake. The rectangle is the surface projection of the seismic fault. The red lines are the surface projection of seismic fault traces. The green circles show the aftershocks within 6 months.
Figure 9. Static Coulomb failure stress changes of the 2020 Nima earthquake. The rectangle is the surface projection of the seismic fault. The red lines are the surface projection of seismic fault traces. The green circles show the aftershocks within 6 months.
Remotesensing 17 01389 g009
Table 1. Focal mechanism solution of the 2020 Nima earthquake from different studies.
Table 1. Focal mechanism solution of the 2020 Nima earthquake from different studies.
ModelsLongitude (°)Latitude (°)Depth (km)Strike (°)Dip (°)Rake (°)Magnitude
USGS86.86433.14410203/2029/61−88/−94Mw 6.27
GCMT86.8633.0917.3187/1214/46−94/−86Mw 6.40
GFZ86.7833.1310204/35341/52−65/109Mw 6.40
NEIC86.8433.13110203/2029/61−88/−91Mw 6.30
CENC86.8133.191010/17750/41−81/−100Ms 6.60
This study86.9033.177.52643−87.28Mw 6.31
USGS: U. S. Geological Survey; GCMT: Global Centroid-Moment-Tensor; GFZ: German Research Centre for Geoscience; NEIC: National Earthquake Information Center; CENC: China Earthquake Networks Center; Mw: Moment magnitude; Ms: surface-wave magnitude.
Table 2. Detailed SAR information applied for coseismic deformation of the 2020 Nima earthquake.
Table 2. Detailed SAR information applied for coseismic deformation of the 2020 Nima earthquake.
SatellitesReference DaySecondary DayIncidence (°)Azimuth (°)TracksOrbits
Sentinal 1A2020.7.182020.7.3041.99−10.0412Ascend
Sentinal 1A2020.7.142020.7.2642.91−170.21121Descend
Sentinal 1B2020.7.132020.7.2534.63−169.3419Descend
Table 3. Determined source parameters for different fault models.
Table 3. Determined source parameters for different fault models.
ModelsLongitude (°)Latitude (°)Depth (km)Strike (°)Dip (°)Rake (°)Range (km)Slip (m)Mw
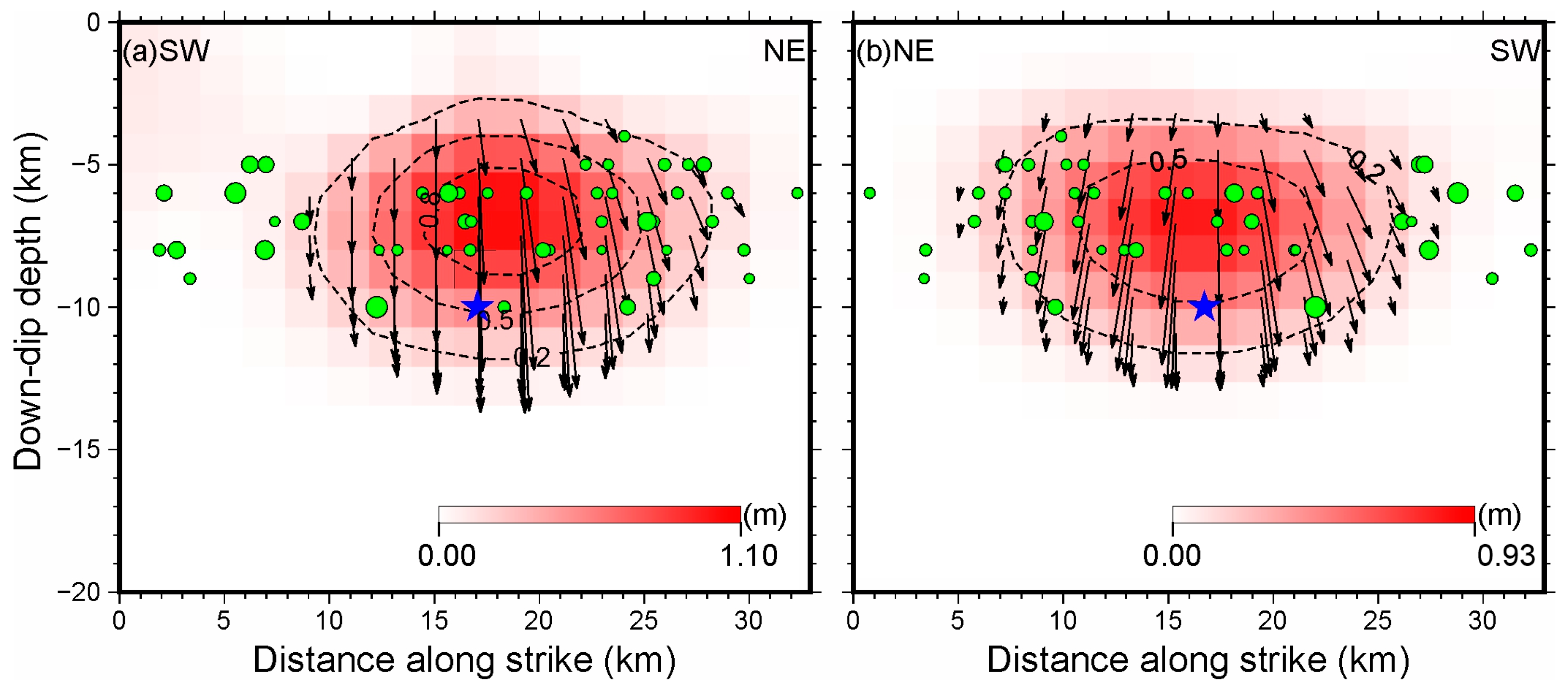
F186.9033.177.502643−87.283~131.106.31
F286.8733.187.0520340−95.543~130.936.26
Table 4. Determined source parameters for afterslip fault models.
Table 4. Determined source parameters for afterslip fault models.
ModelsStrike (°)Dip (°)Rake (°)Slip (m)
F12643−87.280.11
F220340−95.540.05
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, S.; Bai, L.; Liu, C. Coseismic Rupture and Postseismic Afterslip of the 2020 Nima Mw 6.4 Earthquake. Remote Sens. 2025, 17, 1389. https://doi.org/10.3390/rs17081389

AMA Style

Wang S, Bai L, Liu C. Coseismic Rupture and Postseismic Afterslip of the 2020 Nima Mw 6.4 Earthquake. Remote Sensing. 2025; 17(8):1389. https://doi.org/10.3390/rs17081389

Chicago/Turabian Style

Wang, Shaojun, Ling Bai, and Chaoya Liu. 2025. "Coseismic Rupture and Postseismic Afterslip of the 2020 Nima Mw 6.4 Earthquake" Remote Sensing 17, no. 8: 1389. https://doi.org/10.3390/rs17081389

APA Style

Wang, S., Bai, L., & Liu, C. (2025). Coseismic Rupture and Postseismic Afterslip of the 2020 Nima Mw 6.4 Earthquake. Remote Sensing, 17(8), 1389. https://doi.org/10.3390/rs17081389

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop