Seismo-Traveling Ionospheric Disturbances from the 2024 Hualien Earthquake: Altitude-Dependent Propagation Insights
Abstract
1. Introduction
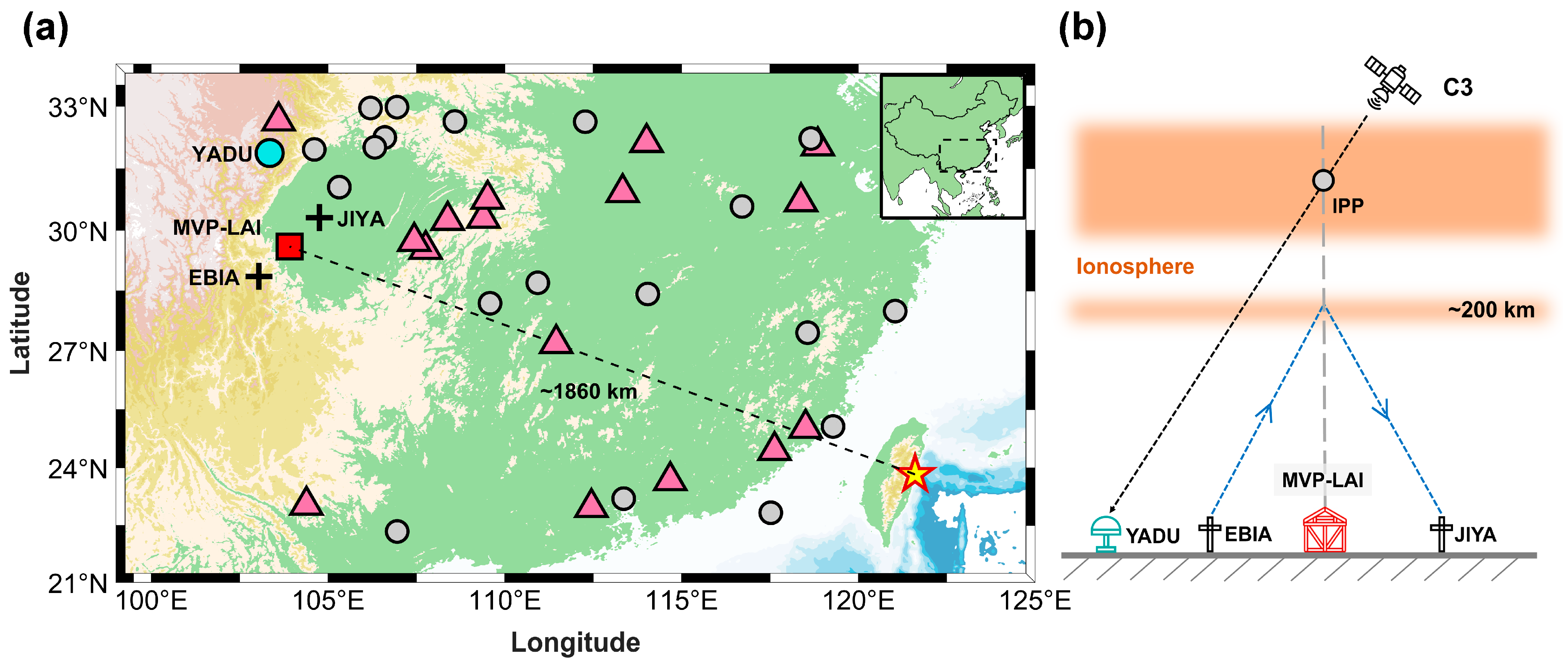
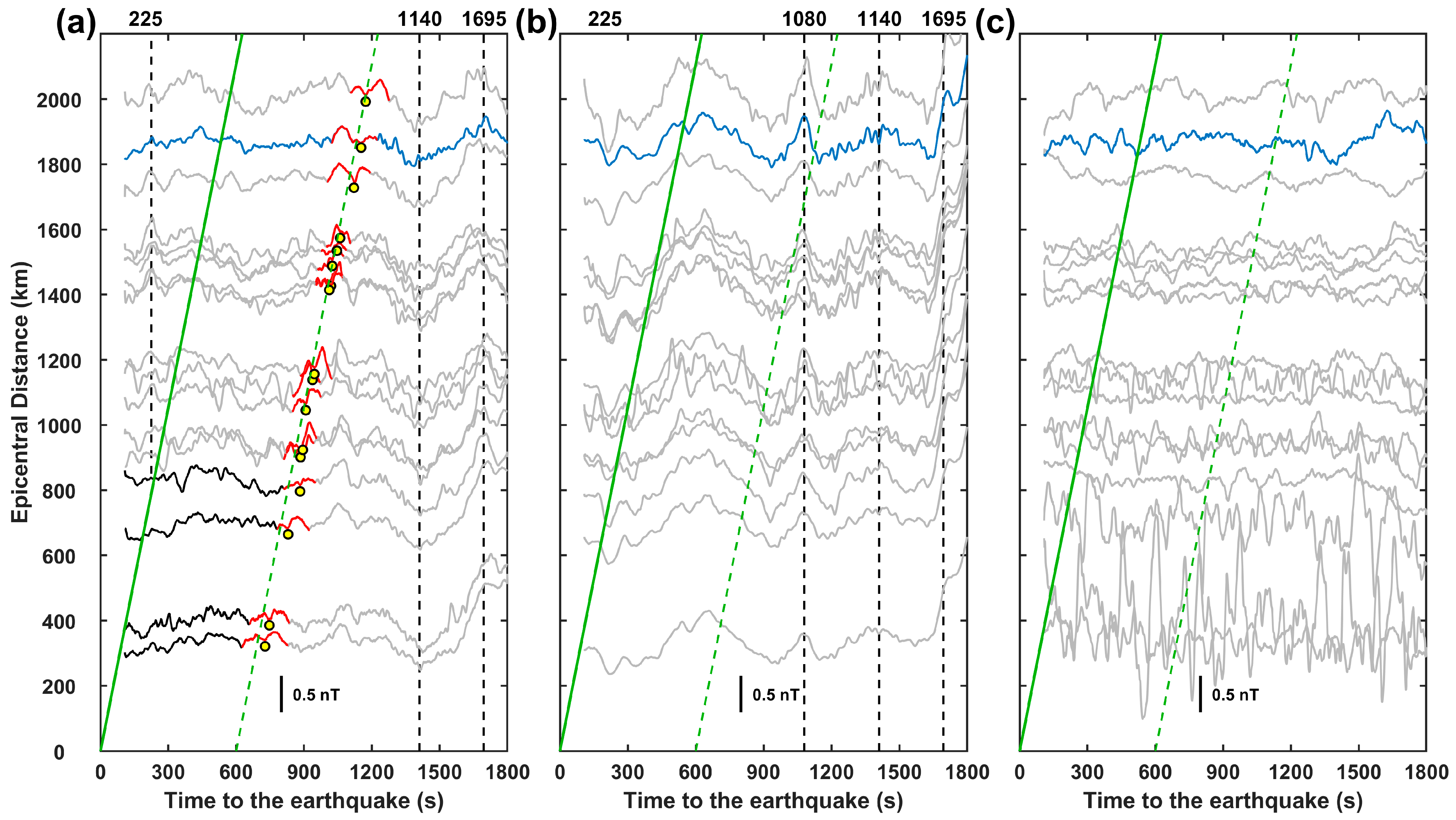
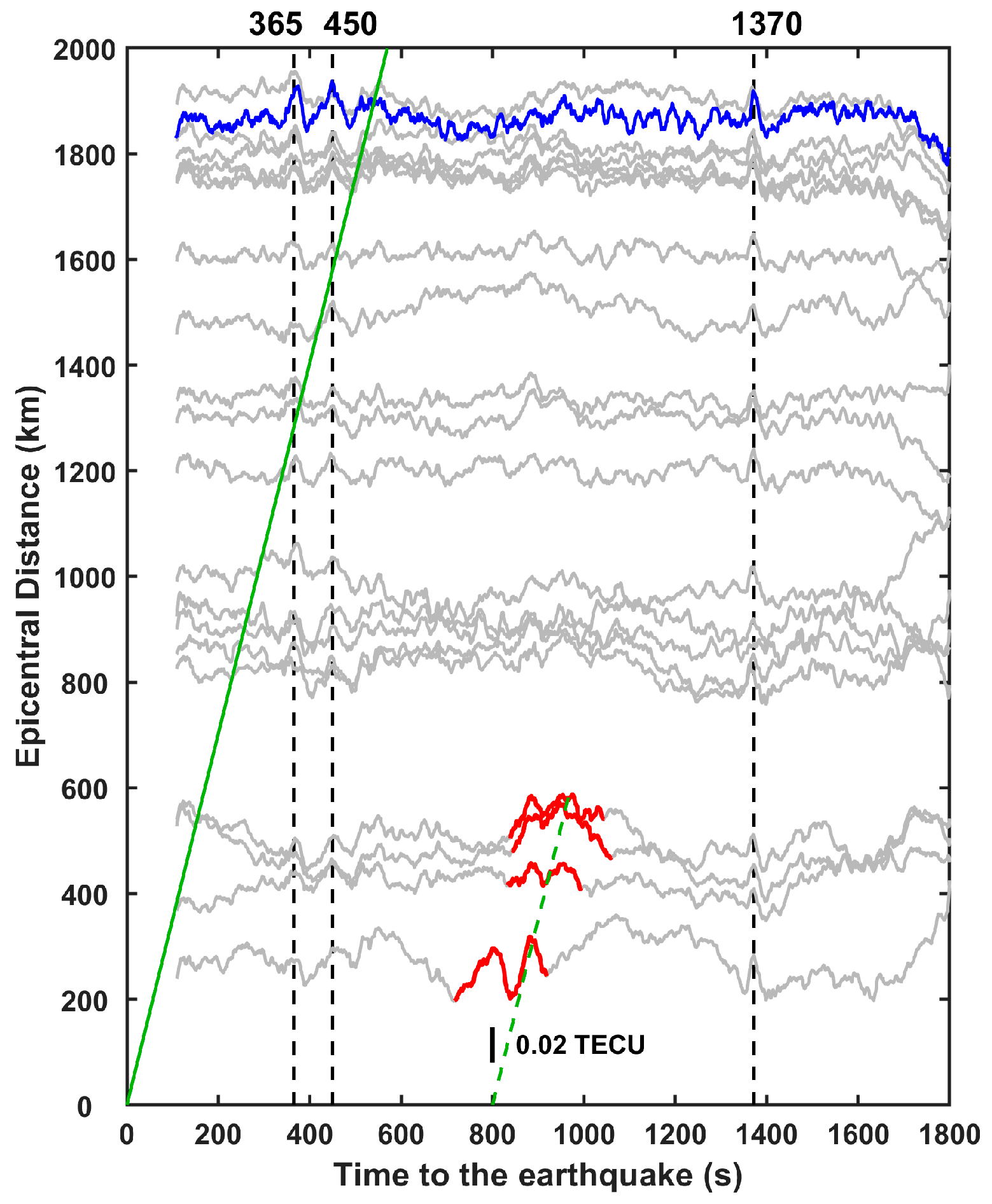
2. Observation and Interpretation
3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davies, K.; Baker, D.M. Ionospheric Effects Observed around the Time of the Alaskan Earthquake of March 28, 1964. J. Geophys. Res. 1965, 70, 2251–2253. [Google Scholar] [CrossRef]
- Calais, E.; Minster, J.B. GPS Detection of Ionospheric Perturbations Following the January 17, 1994, Northridge Earthquake. Geophys. Res. Lett. 1995, 22, 1045–1048. [Google Scholar] [CrossRef]
- Iyemori, T.; Nose, M.; Han, D.; Gao, Y.; Hashizume, M.; Choosakul, N.; Shinagawa, H.; Tanaka, Y.; Utsugi, M.; Saito, A.; et al. Geomagnetic Pulsations Caused by the Sumatra Earthquake on December 26, 2004. Geophys. Res. Lett. 2005, 32, 2005GL024083. [Google Scholar] [CrossRef]
- Yeh, K.C.; Liu, C.H. Acoustic-gravity Waves in the Upper Atmosphere. Rev. Geophys. 1974, 12, 193–216. [Google Scholar] [CrossRef]
- Blanc, E. Observations in the Upper Atmosphere of Infrasonic Waves from Natural or Artificial Sources—A Summary. Ann. Geophys. 1985, 3, 673–687. [Google Scholar]
- Meng, X.; Vergados, P.; Komjathy, A.; Verkhoglyadova, O. Upper Atmospheric Responses to Surface Disturbances: An Observational Perspective. Radio Sci. 2019, 54, 1076–1098. [Google Scholar] [CrossRef]
- Davies, K. Ionospheric Radio; IEE Electromagnetic Waves Series; P. Peregrinus on Behalf of the Institution of Electrical Engineers: London, UK, 1989; ISBN 978-0-86341-186-1. [Google Scholar]
- Heki, K.; Ping, J. Directivity and Apparent Velocity of the Coseismic Ionospheric Disturbances Observed with a Dense GPS Array. Earth Planet. Sci. Lett. 2005, 236, 845–855. [Google Scholar] [CrossRef]
- Jin, S.; Occhipinti, G.; Jin, R. GNSS Ionospheric Seismology: Recent Observation Evidences and Characteristics. Earth-Sci. Rev. 2015, 147, 54–64. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Chen, C.-Y.; Sun, Y.-Y.; Lee, I.-T.; Chum, J. Fluctuations on Vertical Profiles of the Ionospheric Electron Density Perturbed by the March 11, 2011 M9.0 Tohoku Earthquake and Tsunami. GPS Solut. 2019, 23, 76. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; López-Urías, C.; Trejo-Soto, M.E.; Vidal-Vega, A.I. Evaluating Ionospheric Total Electron Content (TEC) Variations as Precursors to Seismic Activity: Insights from the 2024 Noto Peninsula and Nichinan Earthquakes of Japan. Atmosphere 2024, 15, 1492. [Google Scholar] [CrossRef]
- Rolland, L.M.; Lognonné, P.; Munekane, H. Detection and Modeling of Rayleigh Wave Induced Patterns in the Ionosphere. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Chum, J.; Liu, J.-Y.; Podolská, K.; Šindelářová, T. Infrasound in the Ionosphere from Earthquakes and Typhoons. J. Atmos. Sol.-Terr. Phys. 2018, 171, 72–82. [Google Scholar] [CrossRef]
- Thomas, D.; Bagiya, M.S.; Hazarika, N.K.; Ramesh, D.S. On the Rayleigh Wave Induced Ionospheric Perturbations During the Mw 9.0 11 March 2011 Tohoku-Oki Earthquake. J. Geophys. Res. Space Phys. 2022, 127, e2021JA029250. [Google Scholar] [CrossRef]
- Astafyeva, E. Ionospheric Detection of Natural Hazards. Rev. Geophys. 2019, 57, 1265–1288. [Google Scholar] [CrossRef]
- Hines, C.O. Internal Atmospheric Gravity Waves at Ionospheric Heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Blanc, E.; Le Pichon, A.; Ceranna, L.; Farges, T.; Marty, J.; Herry, P. Global Scale Monitoring of Acoustic and Gravity Waves for the Study of the Atmospheric Dynamics. In Infrasound Monitoring for Atmospheric Studies; Le Pichon, A., Blanc, E., Hauchecorne, A., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 647–664. ISBN 978-1-4020-9507-8. [Google Scholar]
- Bagiya, M.S.; Heki, K.; Gahalaut, V.K. Anisotropy of the Near-Field Coseismic Ionospheric Perturbation Amplitudes Reflecting the Source Process: The 2023 February Turkey Earthquakes. Geophys. Res. Lett. 2023, 50, e2023GL103931. [Google Scholar] [CrossRef]
- Iyemori, T.; Kamei, T.; Tanaka, Y.; Takeda, M.; Hashimoto, T.; Araki, T.; Okamoto, T.; Watanabe, K.; Sumitomo, N.; Oshiman, N. Co-Seismic Geomagnetic Variations Observed at the 1995 Hyogoken-Nanbu Earthquake. J. Geomagn. Geoelectr. 1996, 48, 1059–1070. [Google Scholar] [CrossRef]
- Artru, J.; Farges, T.; Lognonné, P. Acoustic Waves Generated from Seismic Surface Waves: Propagation Properties Determined from Doppler Sounding Observations and Normal-Mode Modelling: Propagation of Seismic Acoustic Waves. Geophys. J. Int. 2004, 158, 1067–1077. [Google Scholar] [CrossRef]
- Bondár, I.; Šindelářová, T.; Ghica, D.; Mitterbauer, U.; Liashchuk, A.; Baše, J.; Chum, J.; Czanik, C.; Ionescu, C.; Neagoe, C.; et al. Central and Eastern European Infrasound Network: Contribution to Infrasound Monitoring. Geophys. J. Int. 2022, 230, 565–579. [Google Scholar] [CrossRef]
- Shearer, P.M. Introduction to Seismology, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019; ISBN 978-1-316-87711-1. [Google Scholar]
- Kelley, M.C. The Earth’s Ionosphere: Plasma Physics and Electrodynamics, 2nd ed.; International Geophysics Series; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2009; ISBN 978-0-12-088425-4. [Google Scholar]
- Utada, H.; Shimizu, H.; Ogawa, T.; Maeda, T.; Furumura, T.; Yamamoto, T.; Yamazaki, N.; Yoshitake, Y.; Nagamachi, S. Geomagnetic Field Changes in Response to the 2011 off the Pacific Coast of Tohoku Earthquake and Tsunami. Earth Planet. Sci. Lett. 2011, 311, 11–27. [Google Scholar] [CrossRef]
- Hasbi, A.M.; Momani, M.A.; Mohd Ali, M.A.; Misran, N.; Shiokawa, K.; Otsuka, Y.; Yumoto, K. Ionospheric and Geomagnetic Disturbances during the 2005 Sumatran Earthquakes. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1992–2005. [Google Scholar] [CrossRef]
- Iyemori, T.; Tanaka, Y.; Odagi, Y.; Sano, Y.; Takeda, M.; Nose, M.; Utsugi, M.; Rosales, D.; Choque, E.; Ishitsuka, J.; et al. Barometric and Magnetic Observations of Vertical Acoustic Resonance and Resultant Generation of Field-Aligned Current Associated with Earthquakes. Earth Planet Space 2013, 65, 901–909. [Google Scholar] [CrossRef]
- Hao, Y.Q.; Xiao, Z.; Zhang, D.H. Teleseismic Magnetic Effects (TMDs) of 2011 Tohoku Earthquake. J. Geophys. Res. Space Phys. 2013, 118, 3914–3923. [Google Scholar] [CrossRef]
- Zhao, B.; Hao, Y. Ionospheric and Geomagnetic Disturbances Caused by the 2008 Wenchuan Earthquake: A Revisit. J. Geophys. Res. Space Phys. 2015, 120, 5758–5777. [Google Scholar] [CrossRef]
- Yen, H.-Y.; Chen, C.-R.; Lo, Y.-T.; Shin, T.-C.; Li, Q. Seismo-Geomagnetic Pulsations Triggered by Rayleigh Waves of the 11 March 2011 M 9.0 Tohoku-Oki Earthquake. Terr. Atmos. Ocean. Sci. 2015, 26, 95–101. [Google Scholar] [CrossRef]
- Laštovička, J.; Chum, J. A Review of Results of the International Ionospheric Doppler Sounder Network. Adv. Space Res. 2017, 60, 1629–1643. [Google Scholar] [CrossRef]
- Chum, J.; Hruska, F.; Zednik, J.; Lastovicka, J. Ionospheric Disturbances (Infrasound Waves) over the Czech Republic Excited by the 2011 Tohoku Earthquake. J. Geophys. Res. Space Phys. 2012, 117, A08319. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tsai, H.F.; Jung, T.K. Total Electron Content Obtained by Using the Global Positioning System. Terr. Atmos. Ocean. Sci. 1996, 7, 107. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Chen, C.-H.; Lin, C.-H.; Tsai, H.-F.; Chen, C.-H.; Kamogawa, M. Ionospheric Disturbances Triggered by the 11 March 2011 M 9.0 Tohoku Earthquake. J. Geophys. Res. Space Phys. 2011, 116, A06319. [Google Scholar] [CrossRef]
- Chen, C.; Sun, Y.; Xu, R.; Lin, K.; Wang, F.; Zhang, D.; Zhou, Y.; Gao, Y.; Zhang, X.; Yu, H.; et al. Resident Waves in the Ionosphere Before the M6.1 Dali and M7.3 Qinghai Earthquakes of 21–22 May 2021. Earth Space Sci. 2022, 9, e2021EA002159. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Zhang, X.; Wang, F.; Lin, K.; Gao, Y.; Tang, C.-C.; Lyu, J.; Huang, R.; Huang, Q. Far-Field Coupling and Interactions in Multiple Geospheres After the Tonga Volcano Eruptions. Surv. Geophys. 2023, 44, 587–601. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Liu, J.-Y.; Lin, C.-Y.; Tsai, H.-F.; Chang, L.C.; Chen, C.-Y.; Chen, C.-H. Ionospheric F2 Region Perturbed by the 25 April 2015 Nepal Earthquake. J. Geophys. Res. Space Phys. 2016, 121, 5778–5784. [Google Scholar] [CrossRef]
- Haralambous, H.; Guerra, M.; Chum, J.; Verhulst, T.G.W.; Barta, V.; Altadill, D.; Cesaroni, C.; Galkin, I.; Márta, K.; Mielich, J.; et al. Multi-Instrument Observations of Various Ionospheric Disturbances Caused by the 6 February 2023 Turkey Earthquake. J. Geophys. Res. Space Phys. 2023, 128, e2023JA031691. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Lin, K.; Zhou, C.; Xu, R.; Qing, H.; Gao, Y.; Chen, T.; Wang, F.; Yu, H.; et al. A New Instrumental Array in Sichuan, China, to Monitor Vibrations and Perturbations of the Lithosphere, Atmosphere, and Ionosphere. Surv. Geophys. 2021, 42, 1425–1442. [Google Scholar] [CrossRef]
- Jin, S.; Wang, Q.; Dardanelli, G. A Review on Multi-GNSS for Earth Observation and Emerging Applications. Remote Sens. 2022, 14, 3930. [Google Scholar] [CrossRef]
- Jia, X.; Liu, J.; Zhang, X. The Analysis of Ionospheric TEC Anomalies Prior to the Jiuzhaigou Ms7.0 Earthquake Based on BeiDou GEO Satellite Data. Remote Sens. 2024, 16, 660. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X.; Dong, L.; Liu, J.; Mao, Z.; Lin, K.; Chen, C.-H. Monitoring Seismo-TEC Perturbations Utilizing the Beidou Geostationary Satellites. Remote Sens. 2023, 15, 2608. [Google Scholar] [CrossRef]
- Tsugawa, T.; Otsuka, Y.; Coster, A.J.; Saito, A. Medium-Scale Traveling Ionospheric Disturbances Detected with Dense and Wide TEC Maps over North America. Geophys. Res. Lett. 2007, 34, L22101. [Google Scholar] [CrossRef]
- Rao, H.; Chen, C.; Meng, G.; Liu, J.; Sun, Y.; Lin, K.; Gao, Y.; Rapoport, Y.; Wang, F.; Yisimayili, A.; et al. Relationship Between TEC Perturbations and Rayleigh Waves Associated With 2023 Turkey Earthquake Doublet. J. Geophys. Res. Space Phys. 2025, 130, e2024JA033267. [Google Scholar] [CrossRef]
- Liu, J.Y.; Chen, C.H.; Sun, Y.Y.; Chen, C.H.; Tsai, H.F.; Yen, H.Y.; Chum, J.; Lastovicka, J.; Yang, Q.S.; Chen, W.S.; et al. The Vertical Propagation of Disturbances Triggered by Seismic Waves of the 11 March 2011 M 9.0 Tohoku Earthquake over Taiwan. Geophys. Res. Lett. 2016, 43, 1759–1765. [Google Scholar] [CrossRef]
- Chum, J.; Cabrera, M.A.; Mošna, Z.; Fagre, M.; Baše, J.; Fišer, J. Nonlinear Acoustic Waves in the Viscous Thermosphere and Ionosphere above Earthquake. J. Geophys. Res. Space Phys. 2016, 121. [Google Scholar] [CrossRef]
- Nakata, H.; Takaboshi, K.; Takano, T.; Tomizawa, I. Vertical Propagation of Coseismic Ionospheric Disturbances Associated with the Foreshock of the Tohoku Earthquake Observed Using HF Doppler Sounding. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028600. [Google Scholar] [CrossRef]
- Hao, Y.Q.; Xiao, Z.; Zhang, D.H. Multi-Instrument Observation on Co-Seismic Ionospheric Effects after Great Tohoku Earthquake. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Chen, C.-H.; Zhang, X.; Sun, Y.-Y.; Wang, F.; Liu, T.-C.; Lin, C.-Y.; Gao, Y.; Lyu, J.; Jin, X.; Zhao, X.; et al. Individual Wave Propagations in Ionosphere and Troposphere Triggered by the Hunga Tonga-Hunga Ha’apai Underwater Volcano Eruption on 15 January 2022. Remote Sens. 2022, 14, 2179. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, C.; Zhang, P.; Li, S.; Xu, H.; Yu, T.; Lin, K.; Mao, Z.; Zhang, D.; Lin, C.; et al. Explosive Eruption of the Tonga Underwater Volcano Modulates the Ionospheric E -Region Current on 15 January 2022. Geophys. Res. Lett. 2022, 49, e2022GL099621. [Google Scholar] [CrossRef]
- Smith, Z.; Murtagh, W.; Smithtro, C. Relationship between Solar Wind Low-energy Energetic Ion Enhancements and Large Geomagnetic Storms. J. Geophys. Res. Space Phys. 2004, 109, 2003JA010044. [Google Scholar] [CrossRef]
- Vassiliadis, D.V.; Sharma, A.S.; Eastman, T.E.; Papadopoulos, K. Low-dimensional Chaos in Magnetospheric Activity from AE Time Series. Geophys. Res. Lett. 1990, 17, 1841–1844. [Google Scholar] [CrossRef]
- Chen, C.; Lin, J.; Gao, Y.; Lin, C.; Han, P.; Chen, C.; Lin, L.; Huang, R.; Liu, J. Magnetic Pulsations Triggered by Microseismic Ground Motion. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021416. [Google Scholar] [CrossRef]
- Krasnov, V.; Drobzheva, Y.; Lastovicka, J. Acoustic Energy Transfer to the Upper Atmosphere from Sinusoidal Sources and a Role of Nonlinear Processes. J. Atmos. Sol.-Terr. Phys. 2007, 69, 1357–1365. [Google Scholar] [CrossRef]
- Laštovička, J.; Baše, J.; Hruška, F.; Chum, J.; Šindelářová, T.; Horálek, J.; Zedník, J.; Krasnov, V. Simultaneous Infrasonic, Seismic, Magnetic and Ionospheric Observations in an Earthquake Epicentre. J. Atmos. Sol.-Terr. Phys. 2010, 72, 1231–1240. [Google Scholar] [CrossRef]
- Occhipinti, G.; Dorey, P.; Farges, T.; Lognonné, P. Nostradamus: The Radar That Wanted to Be a Seismometer. Geophys. Res. Lett. 2010, 37, 2010GL044009. [Google Scholar] [CrossRef]
- Zettergren, M.D.; Snively, J.B. Latitude and Longitude Dependence of Ionospheric TEC and Magnetic Perturbations From Infrasonic-Acoustic Waves Generated by Strong Seismic Events. Geophys. Res. Lett. 2019, 46, 1132–1140. [Google Scholar] [CrossRef]
- Liu, T.; Yu, Z.; Ding, Z.; Nie, W.; Xu, G. Observation of Ionospheric Gravity Waves Introduced by Thunderstorms in Low Latitudes China by GNSS. Remote Sens. 2021, 13, 4131. [Google Scholar] [CrossRef]
- Nayak, K.; Romero-Andrade, R.; Sharma, G.; Zavala, J.L.C.; Urias, C.L.; Trejo Soto, M.E.; Aggarwal, S.P. A Combined Approach Using B-Value and Ionospheric GPS-TEC for Large Earthquake Precursor Detection: A Case Study for the Colima Earthquake of 7.7 Mw, Mexico. Acta Geod. Geophys. 2023, 58, 515–538. [Google Scholar] [CrossRef]
- Sharma, G.; Nayak, K.; Romero-Andrade, R.; Aslam, M.A.M.; Sarma, K.K.; Aggarwal, S.P. Low Ionosphere Density Above the Earthquake Epicentre Region of Mw 7.2, El Mayor–Cucapah Earthquake Evident from Dense CORS Data. J. Indian Soc. Remote Sens. 2024, 52, 543–555. [Google Scholar] [CrossRef]
- Pozrikidis, C. Fluid Dynamics: Theory, Computation, and Numerical Simulation, 2nd ed.; Springer: New York, NY, USA; London, UK, 2009; ISBN 978-0-387-95869-9. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, Z.; Chen, C.-H.; Yisimayili, A.; Liu, J.; Zhang, X.; Sun, Y.-Y.; Gao, Y.; Zhang, S.; Teng, C.; Zhao, J. Seismo-Traveling Ionospheric Disturbances from the 2024 Hualien Earthquake: Altitude-Dependent Propagation Insights. Remote Sens. 2025, 17, 1241. https://doi.org/10.3390/rs17071241
Mao Z, Chen C-H, Yisimayili A, Liu J, Zhang X, Sun Y-Y, Gao Y, Zhang S, Teng C, Zhao J. Seismo-Traveling Ionospheric Disturbances from the 2024 Hualien Earthquake: Altitude-Dependent Propagation Insights. Remote Sensing. 2025; 17(7):1241. https://doi.org/10.3390/rs17071241
Chicago/Turabian StyleMao, Zhiqiang, Chieh-Hung Chen, Aisa Yisimayili, Jing Liu, Xuemin Zhang, Yang-Yi Sun, Yongxin Gao, Shengjia Zhang, Chuanqi Teng, and Jianjun Zhao. 2025. "Seismo-Traveling Ionospheric Disturbances from the 2024 Hualien Earthquake: Altitude-Dependent Propagation Insights" Remote Sensing 17, no. 7: 1241. https://doi.org/10.3390/rs17071241
APA StyleMao, Z., Chen, C.-H., Yisimayili, A., Liu, J., Zhang, X., Sun, Y.-Y., Gao, Y., Zhang, S., Teng, C., & Zhao, J. (2025). Seismo-Traveling Ionospheric Disturbances from the 2024 Hualien Earthquake: Altitude-Dependent Propagation Insights. Remote Sensing, 17(7), 1241. https://doi.org/10.3390/rs17071241







