Improving Satellite-Derived Bathymetry in Complex Coastal Environments: A Generalised Linear Model and Multi-Temporal Sentinel-2 Approach
Highlights
- Demonstrates that combining a multi-image with Generalised Linear Model (GLM) workflow improves Satellite-Derived Bathymetry (SDB) accuracy in optically complex shallow waters (MAE = 0.34 m).
- Evaluates the suitable number and timing of satellite images required for an effective multi-image SDB approach.
- Provides practical guidance for selecting suitable satellite imagery to ensure reliable and accurate SDB retrievals.
- Shows the robustness and applicability of SDB in nearshore environments, enabling broader application in coastal mapping and monitoring.
Abstract
1. Introduction
2. Methodology
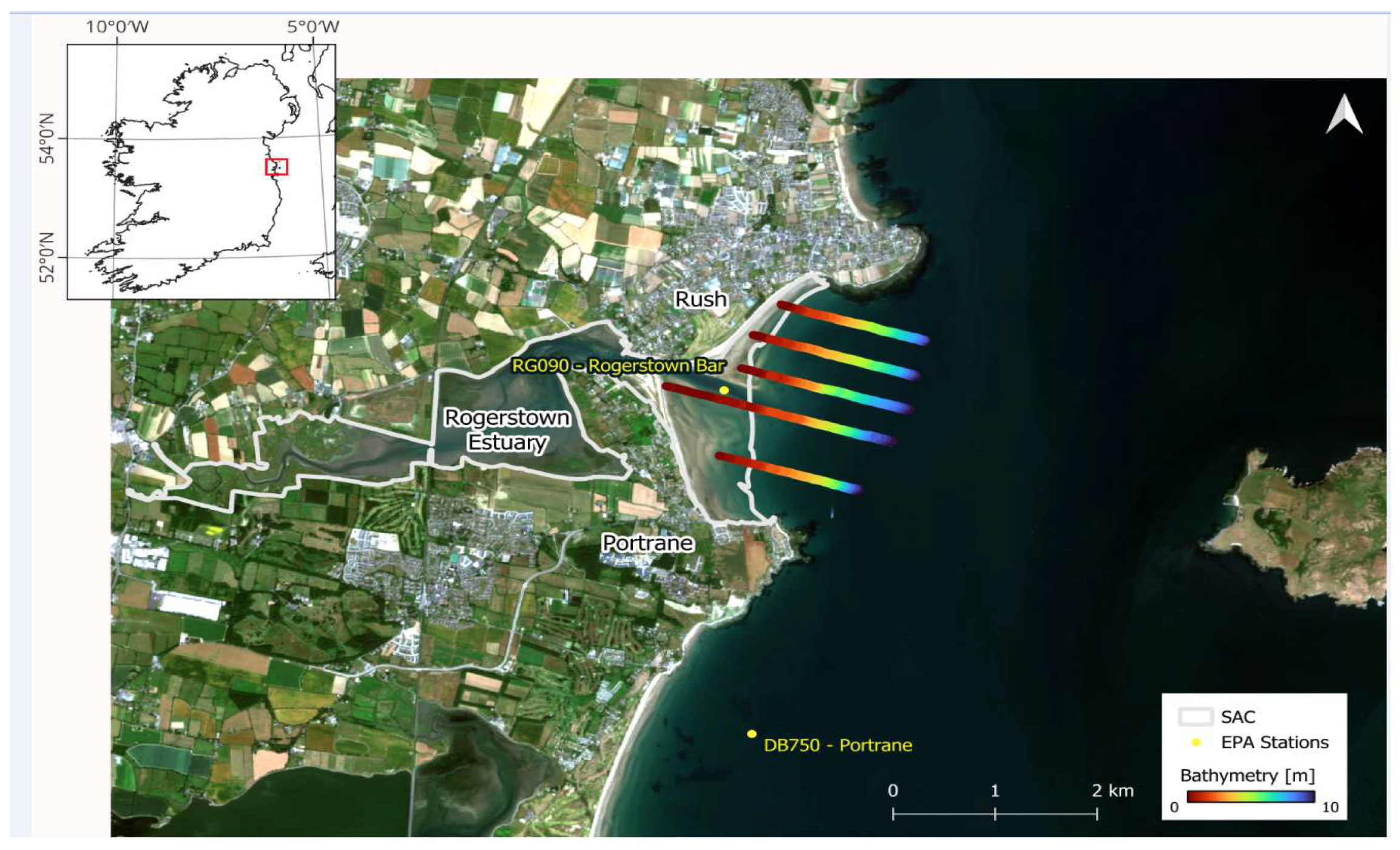
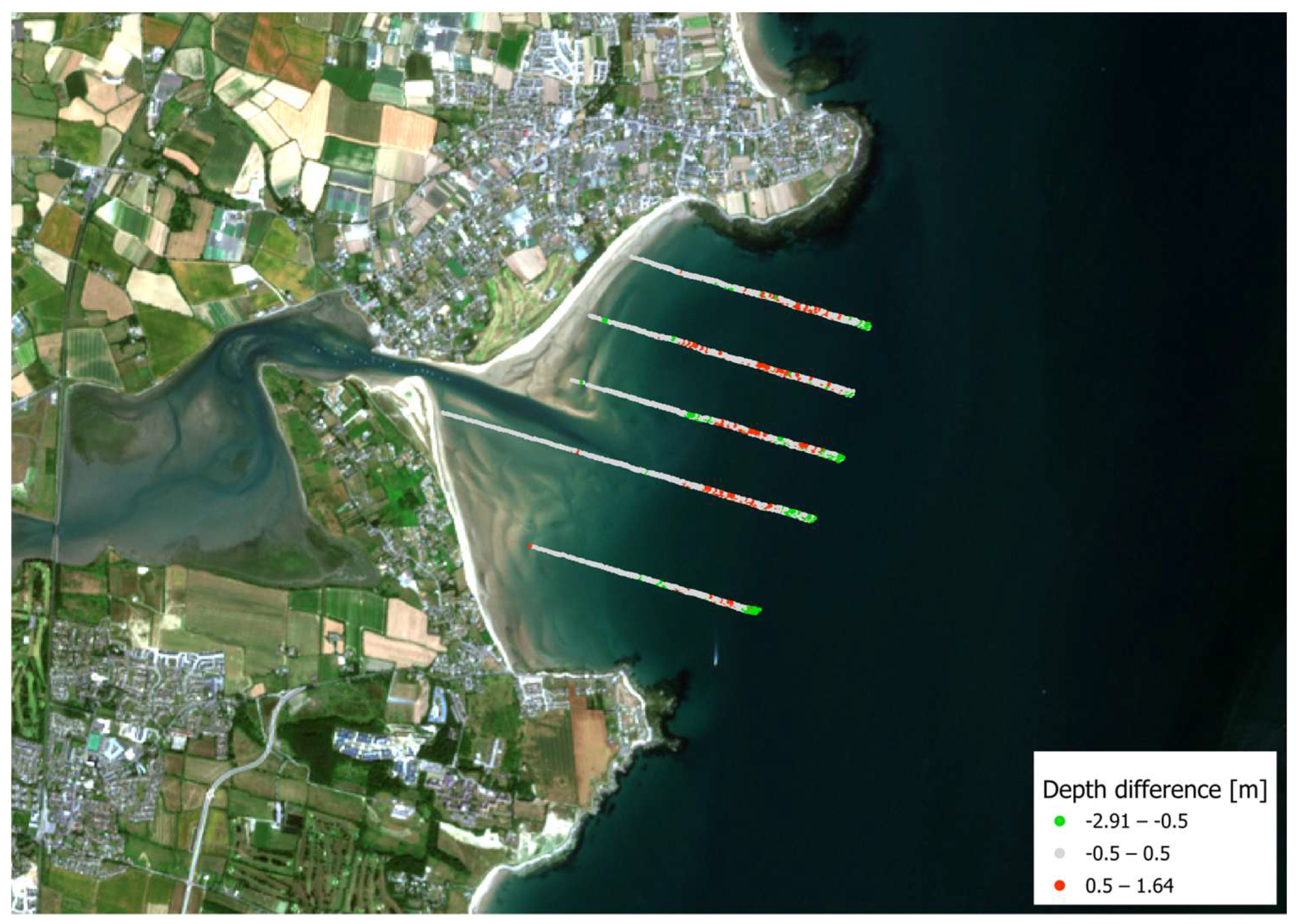
2.1. Study Area
2.2. Satellite and In Situ Bathymetric Data
2.2.1. Satellite Images
2.2.2. In Situ Bathymetric Data
2.3. SDB Empirical Models
2.3.1. Lyzenga Model
2.3.2. Stumpf Model
2.3.3. Generalised Linear Model (GLM)
2.4. Multi-Temporal Image Analysis
2.5. Model Performance Evaluation
3. Results
3.1. Comparison of SDB Models
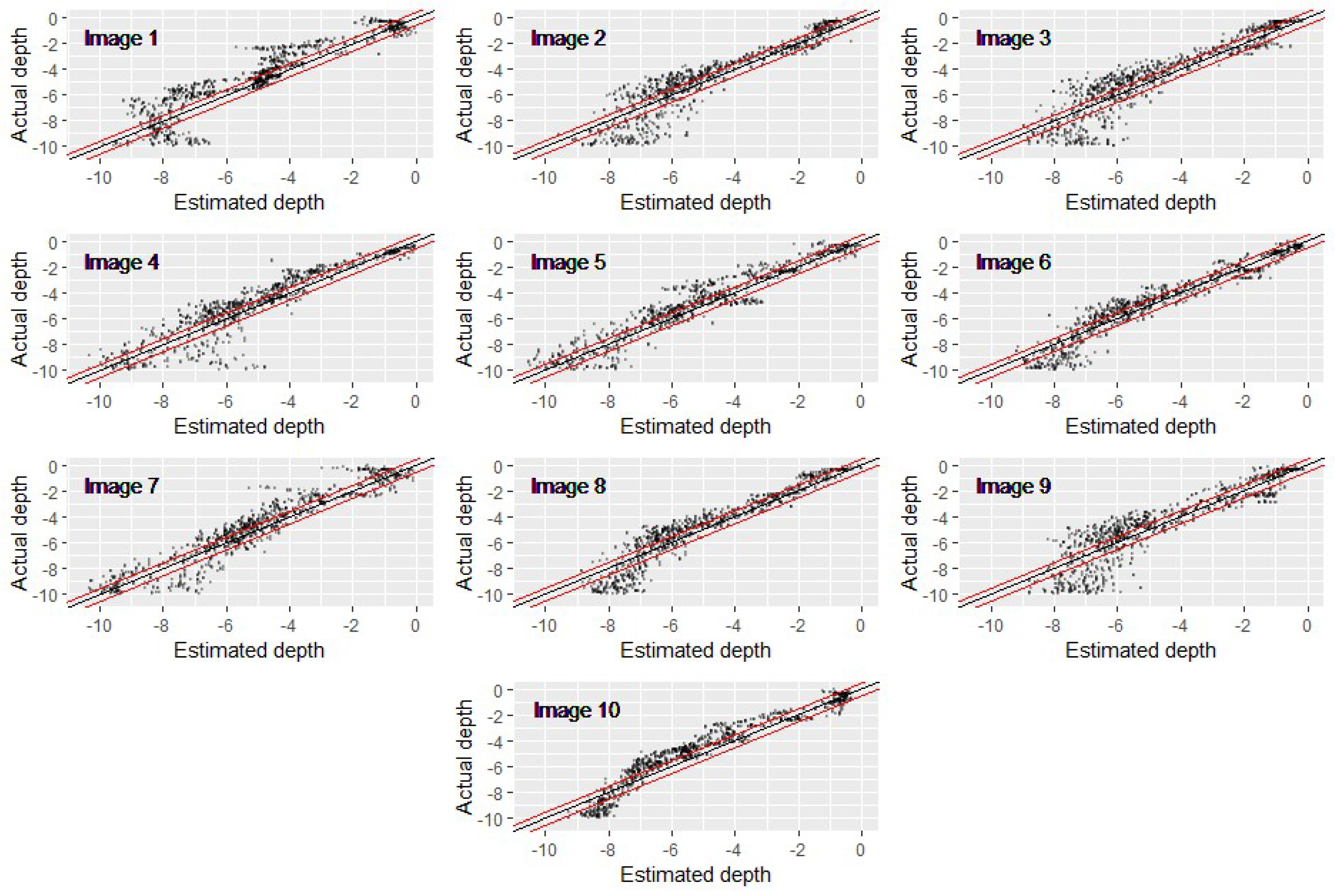
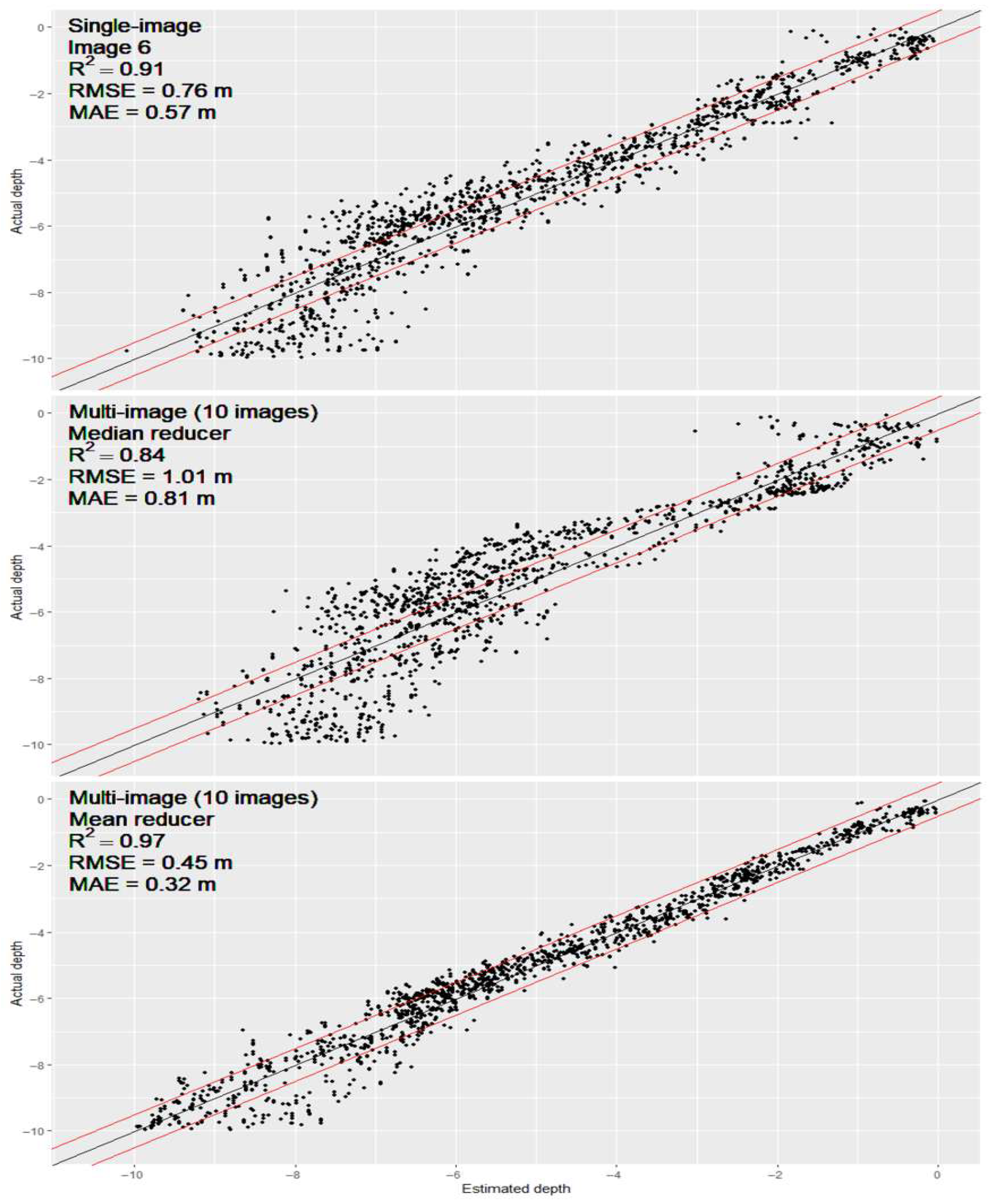
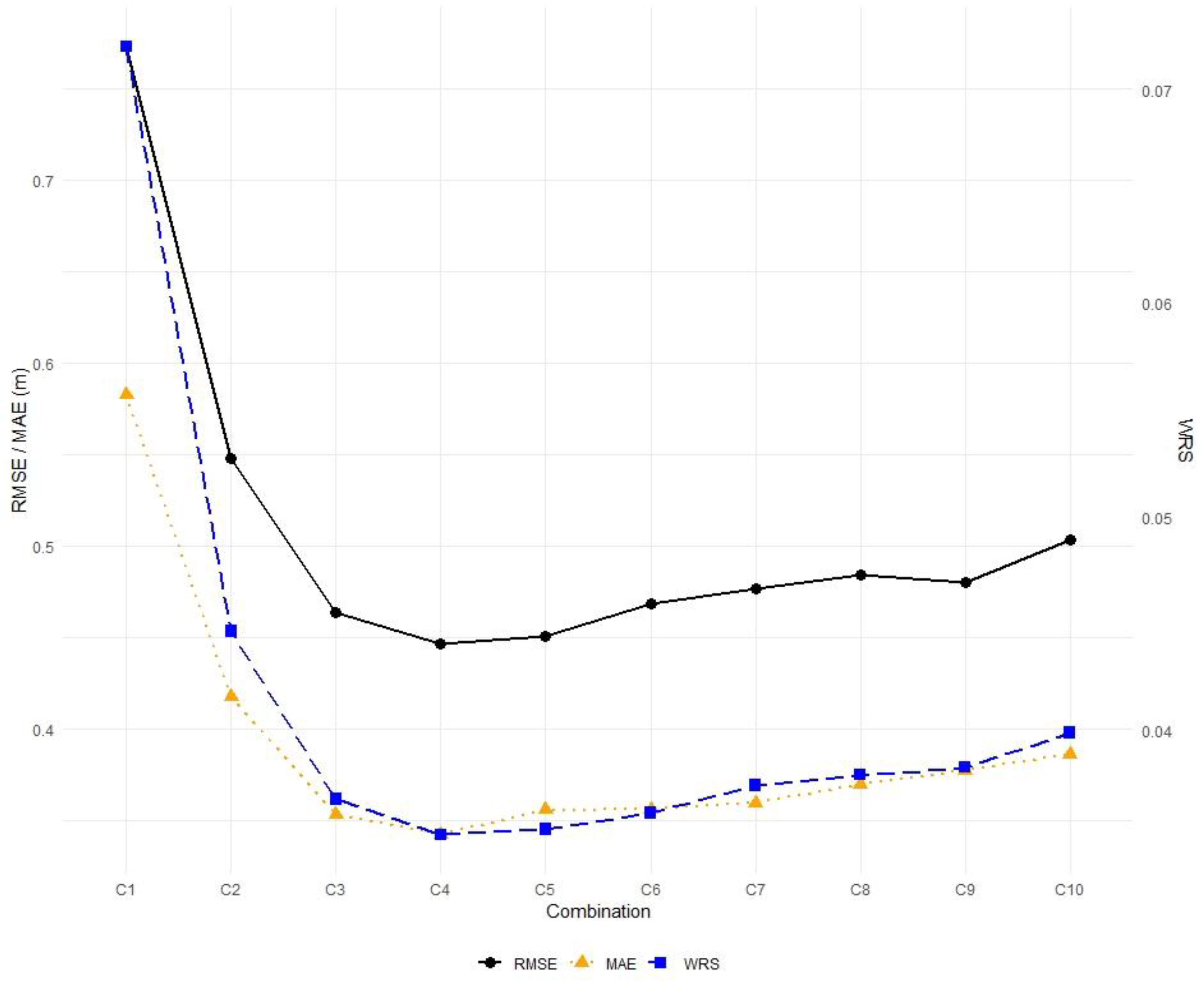
3.2. Evaluation of Multi-Temporal Image Analysis
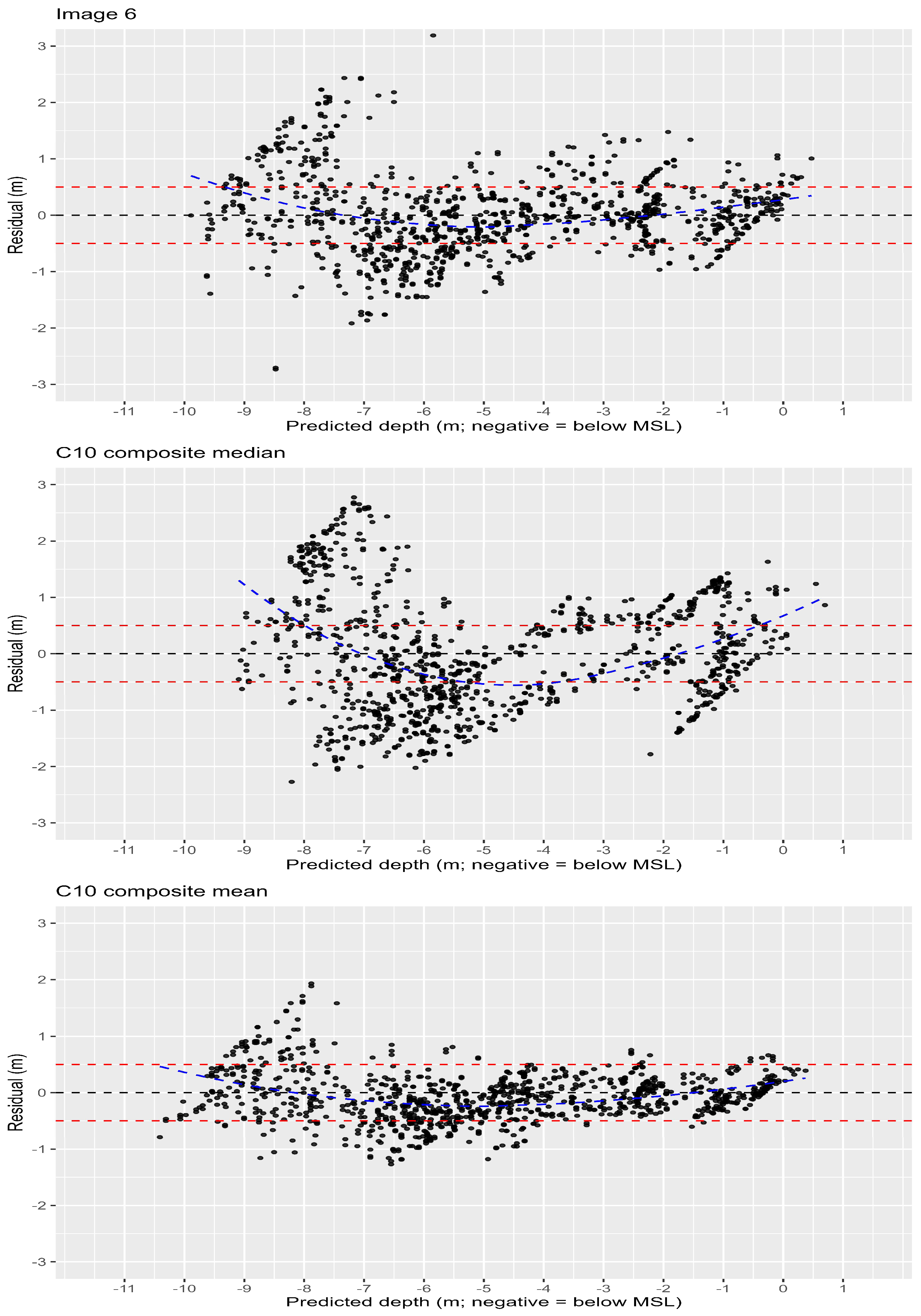
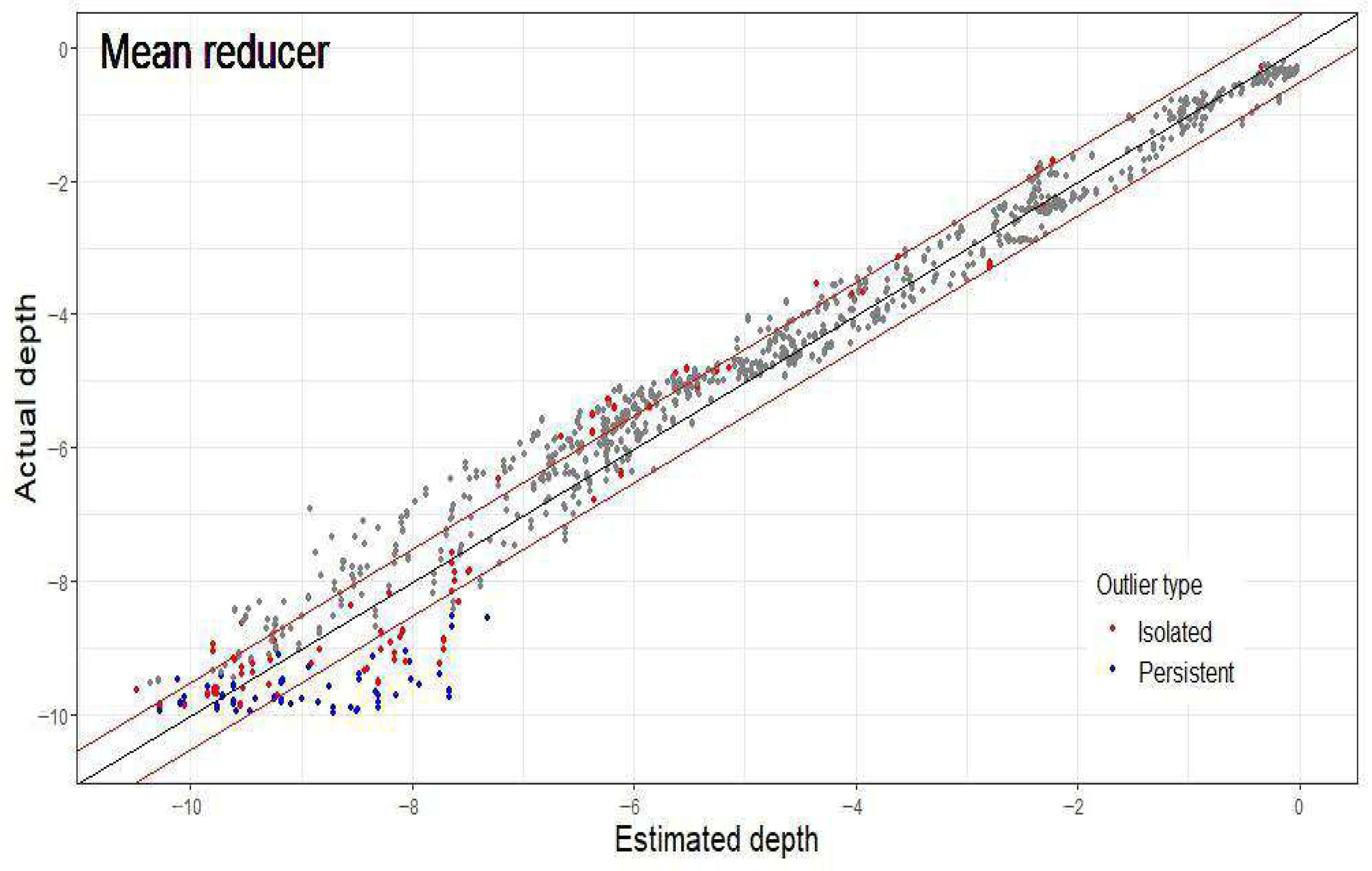
3.3. Outlier Analysis
4. Discussion
4.1. Water Clarity and Optical Conditions
4.2. Image Selection and Compositing Strategy
4.3. Depth-Dependent Error Patterns
4.4. Generalised Linear Model Interpretation
4.5. Limitations and Practical Implications
4.6. Comparison with Other Studies
5. Conclusions
- The generalised linear model (GLM) demonstrated superior performance compared with other empirical models in minimising error margins, particularly when emphasis was placed on predictive accuracy rather than isolating the effects of individual parameters.
- The use of multiple image composites demonstrated superior performance compared to single-image analysis, contingent on the application of the mean reducer function. Moreover, the integration of multiple images effectively reduces the occurrence of outliers in single images. Composites of 3 to 8 images delivered near optimal accuracy; adding more images beyond this did not yield further improvements.
- The application of the generalised linear model (GLM) to a composite dataset of four images resulted in overall error margins of 0.45 m for the RMSE and 0.34 m for the MAE. These error metrics were further reduced to an RMSE of 0.31 m and an MAE of 0.24 m when the analysis was restricted to the optimal water depth range of 0 to 7 m. While these error levels are broadly comparable to shallow water tolerances referenced in IHO S-44, they are most relevant to selected applications and contexts. The obtained accuracy levels are particularly significant for monitoring coastal nearshore areas, with numerous interdisciplinary applications, including the assessment of marine habitats and the prediction of coastal changes over time. Future studies should explore the integration of seabed classification techniques and artificial intelligence models to further improve predictive accuracy and account for spatial heterogeneity in optically complex environments.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Halpern, B.S.; Walbridge, S.; Selkoe, K.A.; Kappel, C.V.; Micheli, F.; D’Agrosa, C.; Bruno, J.F.; Casey, K.S.; Ebert, C.; Fox, H.E.; et al. A global map of human impact on marine ecosystems. Science 2008, 319, 948–952. [Google Scholar] [CrossRef]
- Lipiec, E.; Ruggiero, P.; Mills, A.; Serafin, K.A.; Bolte, J.; Corcoran, P.; Walczak, J.; Tillmann, P.; O’Neill, S.M.; Goupee, J. A multi-objective evaluation of coastal protection alternatives under extreme sea level scenarios. J. Coast. Res. 2018, 34, 1196–1208. [Google Scholar] [CrossRef]
- Wölfl, A.-C.; Snaith, H.; Amirebrahimi, S.; Devey, C.W.; Dorschel, B.; Ferrini, V.; Huvenne, V.A.I.; Jakobsson, M.; Jencks, J.; Johnston, G.; et al. Seafloor mapping—The challenge of a truly global ocean bathymetry. Front. Mar. Sci. 2019, 6, 283. [Google Scholar] [CrossRef]
- Ridente, D.; Martorelli, E.; Bosman, A.; Chiocci, F.L. High-resolution morpho-bathymetry of the Messina Strait (South-ern Italy): New insights on the 1908 earthquake and tsunami. Geomorphology 2014, 208, 149–159. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.J.; Barrilero, O.; Laporte, J.; Koetz, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Mielck, F.; Hass, H.C.; Michaelis, R. Morphological changes due to marine aggregate extraction for beach replenishment in the German Bight (SE North Sea). Geo-Mar. Lett. 2019, 39, 47–58. [Google Scholar] [CrossRef]
- Barnard, P.L.; Erikson, L.H.; Foxgrover, A.C. Dynamic flood modeling essential to assess the coastal impacts of climate change. Sci. Rep. 2019, 9, 4309. [Google Scholar] [CrossRef]
- Convention on Biological Diversity. Kunming-Montreal Global Biodiversity Framework: Target 3. United Nations Environment Programme. 2022. Available online: https://www.cbd.int/gbf/targets/3/ (accessed on 9 November 2025).
- Guinan, J.; McKeon, C.; O’Keeffe, E.; Monteys, X.; Sacchetti, F.; Coughlan, M.; Nic Aonghusa, C. INFOMAR data supports offshore energy development and marine spatial planning in the Irish offshore via the EMODnet Geology Portal. Q. J. Eng. Geol. Hydrogeol. 2021, 54, qjegh2020-033. [Google Scholar] [CrossRef]
- Daniell, J.J. The Combination of Soundings and Remotely Sensed Bathymetry in the GEBCO Grid; GEBCO Science Day Proceedings: Lima, Peru, 2010; 15p, Available online: https://www.gebco.net (accessed on 9 November 2025).
- Lebrec, U.; Paumard, V.; O’Leary, M.J.; Lang, S.C. Towards a high-resolution global seabed sediment and rock type map: The Sand, Silt, and Rock (SSR) database. Earth Syst. Sci. Data 2021, 13, 5191–5212. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Copernicus. 2023. Available online: https://sentiwiki.copernicus.eu/web/s2-mission (accessed on 9 November 2025).
- Duplančić Leder, T.; Baui, M.; Leder, N.; Gili, F. Optical satellite derived bathymetry: An overview and WoS and Scopus bibliometric analysis. Remote Sens. 2023, 15, 1294. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsema, C.; Phinn, S.R. Efficient radiative transfer model inversion for remote sensing applications. Remote Sens. Environ. 2009, 113, 2527–2532. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Shallow-water bathymetry using combined LiDAR and passive multispectral scanner data. Int. J. Remote Sens. 1985, 6, 115–125. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Casal, G.; Monteys, X.; Hedley, J.; Harris, P.; Cahalane, C.; McCarthy, T. Assessment of empirical algorithms for bathymetry extraction using Sentinel-2 data. Int. J. Remote Sens. 2019, 40, 2855–2879. [Google Scholar] [CrossRef]
- Vojinovic, Z.; Abebe, Y.A.; Ranasinghe, R.; Vacher, A.; Martens, P.; Mandl, D.J.; Frye, S.W.; van Ettinger, E.; de Zeeuw, R. A machine learning approach for estimation of shallow water depths from optical satellite images and sonar measurements. J. Hydroinform. 2013, 15, 1408–1424. [Google Scholar] [CrossRef]
- Sánchez-Carnero, N.; Ojeda-Zújar, J.; Rodríguez-Pérez, D.; Márquez-Pérez, J. Assessment of different models for bathymetry calculation using SPOT multispectral images in a high-turbidity area. Int. J. Remote Sens. 2014, 35, 493–514. [Google Scholar] [CrossRef]
- Chybicki, A. Three-dimensional geographically weighted inverse regression (3GWR) model for satellite-derived bathymetry using Sentinel-2 observations. Mar. Geod. 2017, 41, 1–23. [Google Scholar] [CrossRef]
- Casal, G.; Harris, P.; Monteys, X.; Hedley, J.; Cahalane, C.; McCarthy, T. Understanding satellite-derived bathymetry using Sentinel-2 imagery and spatial prediction models. GIScience Remote Sens. 2020, 57, 271–286. [Google Scholar] [CrossRef]
- Xu, N.; Wang, L.; Zhang, H.S.; Tang, S.; Mo, F.; Ma, X. Machine learning based estimation of coastal bathymetry from ICESat-2 and Sentinel-2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 14, 1748–1754. [Google Scholar] [CrossRef]
- Mudiyanselage, S.S.J.D.; Abd-Elrahman, A.; Wilkinson, B.; Lecours, V. Multi-temporal satellite derived bathymetry using Sentinel-2 and machine learning. GIScience Remote Sens. 2022, 59, 1143–1158. [Google Scholar] [CrossRef]
- Al Najar, M.; Thoumyre, G.; Bergsma, E.W.J.; Almar, R.; Benshila, R.; Wilson, D.G. Satellite derived bathymetry using deep learning. Mach. Learn. 2023, 112, 1107–1130. [Google Scholar] [CrossRef]
- Susa, T. Satellite derived bathymetry with Sentinel-2 imagery: Comparing traditional techniques with advanced methods and machine learning ensemble models. Mar. Geod. 2022, 45, 435–461. [Google Scholar] [CrossRef]
- Evagorou, E.; Argyriou, A.; Papadopoulos, N.; Mettas, C.; Alexandrakis, G.; Hadjimitsis, D. Evaluation of satellite-derived bathymetry from high and medium-resolution sensors using empirical methods. Remote Sens. 2022, 14, 772. [Google Scholar] [CrossRef]
- Ilori, C.O.; Knudby, A. An approach to minimize atmospheric correction error and improve physics-based satellite-derived bathymetry in a coastal environment. Remote Sens. 2020, 12, 2752. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Deriving highly accurate shallow water bathymetry from Sentinel-2 and ICESat-2 datasets by a multitemporal stacking method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6677–6685. [Google Scholar] [CrossRef]
- Viaña-Borja, S.P.; Fernández-Mora, A.; Stumpf, R.P.; Navarro, G.; Caballero, I. Semi-automated bathymetry using Sentinel-2 for coastal monitoring in the Western Mediterranean. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103328. [Google Scholar] [CrossRef]
- Lowell, K.; Hermann, J. Accuracy of Bathymetric Depth Change and Change Rate Estimations in Shallow Waters Based on Landsat 7 and Landsat 8 Data. J. Mar. Sci. Eng. 2024, 12, 1401. [Google Scholar] [CrossRef]
- Traganos, D.; Poursanidis, D.; Aggarwal, B.; Chrysoulakis, N.; Reinartz, P. Estimating satellite-derived bathymetry (SDB) with the google earth engine and sentinel-2. Remote Sens. 2018, 10, 859. [Google Scholar] [CrossRef]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite derived bathymetry using machine learning and multi-temporal satellite images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef]
- Saeidi, V.; Seydi, S.T.; Kalantar, B.; Ueda, N.; Tajfirooz, B.; Shabani, F. Water depth estimation from Sentinel-2 imagery using advanced machine learning methods and explainable artificial intelligence. Geomat. Nat. Hazards Risk 2023, 14, 2225691. [Google Scholar] [CrossRef]
- IHO S-44; IHO Standards for Hydrographic Surveys, Edition 6.0.0. International Hydrographic Organization (IHO): Monte Carlo, Monaco, 2020. [CrossRef]
- Caballero, I.; Stumpf, R.P. Atmospheric correction for satellite-derived bathymetry in the Caribbean waters: From a single image to multi-temporal approaches using Sentinel-2A/B. Opt. Express 2020, 28, 11742–11766. [Google Scholar] [CrossRef] [PubMed]
- Cahalane, C.; Magee, A.; Monteys, X.; Casal, G.; Hanafin, J.; Harris, P. A comparison of Landsat 8, RapidEye and Pleiades products for improving empirical predictions of satellite-derived bathymetry. Remote Sens. Environ. 2019, 233, 111414. [Google Scholar] [CrossRef] [PubMed]
- European Commission, DG-ENV. Interpretation Manual of European Union Habitats, Version EUR 28. 2013. Available online: https://circabc.europa.eu/ui/group/3f466d71-92a7-49eb-9c63-6cb0fadf29dc/library/37d9e6d9-b7de-42ce-b789-622e9741b68f/details (accessed on 9 November 2025).
- Calder, K. Rogerstown Coastal Flood Erosion Risk Management Study Stage 1: Coastal Flood and Erosion Risk Assessment; RPS Ireland Ltd.: Belfast, UK, 2020. [Google Scholar]
- Pegau, W.; Gray, D.; Zaneveld, J. Absorption and attenuation of visible and near-infrared light in water: Dependence on temperature and salinity. Appl. Opt. 1997, 36, 6035–6046. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, J.M.; Twardowski, M.S.; Zaneveld, J.R.V.; Moore, C.M.; Barnard, A.H.; Donaghay, P.L.; Rhoades, B. Hyperspectral temperature and salinity dependencies of absorption by water and heavy water in the 400–750 nm spectral range. Appl. Opt. 2006, 45, 5294–5309. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Image and Signal Processing for Remote Sensing XXIII; SPIE: Bellingham, WA, USA, 2017; Volume 10427, p. 1042704. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef]
- O’Toole, R.; Judge, M.; Sacchetti, F.; Furey, T.; Mac Craith, M.; Monteys, X. Seabed and habitat mapping in Irish waters: INFOMAR and beyond. Geol. Soc. London Spec. Publ. 2022, 505, 71–96. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Casal, G.; Hedley, J.D.; Monteys, X.; Harris, P.; Cahalane, C.; McCarthy, T. Satellite-derived bathymetry in optically complex waters using a model inversion approach and Sentinel-2 data. Estuar. Coast. Shelf Sci. 2020, 241, 106814. [Google Scholar] [CrossRef]
- Bramante, J.F.; Raju, D.K.; Sin, T.M. Multispectral derivation of bathymetry in Singapore’s shallow, turbid waters. Int. J. Remote Sens. 2013, 34, 2070–2088. [Google Scholar] [CrossRef]
- Kim, J.H. Multicollinearity and misleading statistical results. Korean J. Anesthesiol. 2019, 72, 558–569. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 367–402. [Google Scholar]
- Graham, M.H. Confronting multicollinearity in ecological multiple regression. Ecology 2003, 84, 2809–2815. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? —Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Leys, C.; Ley, C.; Klein, O.; Bernard, P.; Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. J. Exp. Soc. Psychol. 2013, 49, 764–766. [Google Scholar] [CrossRef]
- Miller, R.G. Simultaneous Statistical Inference, 2nd ed.; Springer: New York, NY, USA, 1991. [Google Scholar]
- McKee, D.; Cunningham, A.; Slater, J.; Maberly, S. Identification of phytoplankton communities using multi- and hyperspectral remote sensing techniques. Limnol. Oceanogr. 2007, 52, 117–126. [Google Scholar]
- Duplančić Leder, T.; Leder, N.; Peroš, J. Satellite derived bathymetry survey method—Example of Hramina Bay. Trans. Marit. Sci. 2019, 8, 99–108. [Google Scholar] [CrossRef]
- Monteys, X.; Cahalane, C.; Harris, P.; McCarthy, T.; Hanafin, J.; Casal, G. Spatial prediction of coastal bathymetry based on multispectral satellite imagery and multibeam data. Irish J. Earth Sci. 2015, 33, 1–20. [Google Scholar] [CrossRef]
- Mobley, C.D.; Gentili, B.; Gordon, H.R.; Jin, Z.; Kattawar, G.W.; Morel, A.; Reinersman, P.; Stamnes, K.; Stavn, R.H. Comparison of numerical models for computing underwater light fields. Appl. Opt. 1993, 32, 7484–7504. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman & Hall: London, UK, 1989. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; García Marquéz, J.R.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Lee, M.E.; Lewis, M.R. A new method for the measurement of the optical properties of natural waters: Absorption and fluorescence excitation spectra. J. Atmos. Ocean. Technol. 2003, 20, 563–571. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zuur, A.F. Mixed Effects Models and Extensions in Ecology with R; Springer: New York, NY, USA; London, UK, 2009. [Google Scholar]
- Hengl, T. A Practical Guide to Geostatistical Mapping of Environmental Variables; EUR 22904 EN; Office for Official Publications of the European Communities: Luxembourg, 2008. [Google Scholar]
- Kumar, L.; Sinha, P.; Taylor, S.; Alqurashi, A.F. Review of the use of remote sensing for characterising tidal flats. Remote Sens. 2020, 12, 3858. [Google Scholar] [CrossRef]
| Station No | Survey Date | Water Depth (m) | Secchi Disk (m) | Chlorophyll a (µg/L) | Salinity (‰) | Temperature (°C) | pH |
|---|---|---|---|---|---|---|---|
| RG090 | 26 May 2021 | 2.8 | 1 | 4.11 | 32.78 | 12.3 | 8.2 |
| RG090 | 7 July 2021 | 2.5 | 2 | 1.34 | 31.31 | 15.8 | 8.1 |
| DB750 | 2 July 2020 | 6.3 | 4 | N/A | 33.36 | 14.3 | 8.1 |
| DB750 | 18 August 2020 | 7.1 | 3 | N/A | 33.20 | 16.6 | 8.1 |
| Image ID | Sentinel-2 Tile | Date | Tide (LAT) (m) |
|---|---|---|---|
| 1 | S2B_MSIL2A_20210405T114349 | 5 April 2021 | 1.14 |
| 2 | S2B_MSIL2A_20210415T114349 | 15 April 2021 | 3.57 |
| 3 | S2A_MSIL2A_20210417T113311 | 17 April 2021 | 2.64 |
| 4 | S2B_MSIL2A_20210422T113309 | 22 April 2021 | 1.78 |
| 5 | S2B_MSIL2A_20210604T114349 | 4 June 2021 | 1.50 |
| 6 | S2A_MSIL2A_20210716T113321 | 16 July 2021 | 1.63 |
| 7 | S2A_MSIL2A_20210719T114351 | 19 July 2021 | 1.03 |
| 8 | S2B_MSIL2A_20210721T113319 | 21 July 2021 | 2.53 |
| 9 | S2A_MSIL2A_20210828T114351 | 28 August 2021 | 2.31 |
| 10 | S2A_MSIL2A_20210914T113321 | 14 September 2021 | 1.56 |
| Image ID | Sentinel-2 Tile | Date | Model | R2 | RMSE (m) | MAE (m) | MBE (m) | WRS |
|---|---|---|---|---|---|---|---|---|
| 1 | S2B_MSIL2A_20210405 | 5 April 2021 | Stumpf | 0.347 | 2.341 | 1.884 | 0.262 | 0.358 |
| Lyzenga | 0.831 | 1.136 | 0.899 | 0.238 | 0.124 | |||
| GLM | 0.851 | 1.096 | 0.855 | 0.332 | 0.115 | |||
| 2 | S2B_MSIL2A_20210415 | 15 April 2021 | Stumpf | 0.769 | 1.304 | 1.012 | 0.079 | 0.154 |
| Lyzenga | 0.828 | 1.124 | 0.884 | −0.067 | 0.124 | |||
| GLM | 0.863 | 1.017 | 0.761 | −0.022 | 0.105 | |||
| 3 | S2A_MSIL2A_20210417 | 17 April 2021 | Stumpf | 0.745 | 1.403 | 1.118 | 0.090 | 0.169 |
| Lyzenga | 0.833 | 1.115 | 0.869 | 0.017 | 0.122 | |||
| GLM | 0.839 | 1.090 | 0.824 | 0.010 | 0.117 | |||
| 4 | S2B_MSIL2A_20210422 | 22 April 2021 | Stumpf | 0.820 | 1.166 | 0.894 | 0.181 | 0.129 |
| Lyzenga | 0.854 | 1.036 | 0.775 | 0.101 | 0.109 | |||
| GLM | 0.864 | 1.005 | 0.735 | 0.117 | 0.103 | |||
| 5 | S2B_MSIL2A_20210604 | 4 June 2021 | Stumpf | 0.610 | 1.704 | 1.364 | 0.235 | 0.232 |
| Lyzenga | 0.879 | 0.981 | 0.787 | 0.119 | 0.099 | |||
| GLM | 0.916 | 0.824 | 0.637 | 0.238 | 0.077 | |||
| 6 | S2A_MSIL2A_20210716 | 16 July 2021 | Stumpf | 0.471 | 1.987 | 1.548 | 0.275 | 0.294 |
| Lyzenga | 0.888 | 0.919 | 0.728 | 0.030 | 0.092 | |||
| GLM | 0.920 | 0.773 | 0.583 | −0.072 | 0.072 | |||
| 7 | S2A_MSIL2A_20210719 | 19 July 2021 | Stumpf | 0.656 | 1.693 | 1.386 | 0.472 | 0.217 |
| Lyzenga | 0.884 | 0.927 | 0.716 | 0.104 | 0.095 | |||
| GLM | 0.902 | 0.867 | 0.665 | 0.159 | 0.085 | |||
| 8 | S2B_MSIL2A_20210721 | 21 July 2021 | Stumpf | 0.749 | 1.424 | 1.130 | 0.047 | 0.169 |
| Lyzenga | 0.885 | 0.969 | 0.780 | 0.124 | 0.097 | |||
| GLM | 0.904 | 0.881 | 0.679 | 0.077 | 0.084 | |||
| 9 | S2A_MSIL2A_20210828 | 28 August 2021 | Stumpf | 0.586 | 1.777 | 1.467 | −0.065 | 0.246 |
| Lyzenga | 0.792 | 1.240 | 1.003 | 0.0095 | 0.144 | |||
| GLM | 0.819 | 1.156 | 0.892 | −0.0606 | 0.129 | |||
| 10 | S2A_MSIL2A_20210914 | 14 September 2021 | Stumpf | 0.709 | 1.475 | 1.195 | 0.1624 | 0.186 |
| Lyzenga | 0.822 | 1.149 | 0.966 | 0.0601 | 0.130 | |||
| GLM | 0.922 | 0.802 | 0.669 | 0.2661 | 0.075 |
| Image ID | Images | Single/ Multi-Image | Reducer | R2 | RMSE (m) | MAE (m) | MBE (m) | WRS |
|---|---|---|---|---|---|---|---|---|
| 6 | 16 July 2021 | Single | - | 0.92 | 0.77 | 0.58 | −0.07 | 0.072 |
| C10 | All 10 images combined | Multi-image | Mean | 0.97 | 0.50 | 0.39 | −0.13 | 0.040 |
| Median | 0.86 | 1.00 | 0.83 | −0.05 | 0.108 |
| Ranking | Combination Number | Number of Images | Image IDs | R2 | RMSE (m) | MAE (m) | WRS |
|---|---|---|---|---|---|---|---|
| 1 | 297 | 4 | 2, 5, 6, 8 | 0.974 | 0.446 | 0.342 | 0.035 |
| 2 | 157 | 3 | 5, 6, 8 | 0.971 | 0.463 | 0.353 | 0.037 |
| 3 | 571 | 5 | 2, 5, 6, 8, 10 | 0.974 | 0.450 | 0.356 | 0.035 |
| 4 | 803 | 6 | 2, 4, 5, 6, 8, 10 | 0.974 | 0.468 | 0.356 | 0.036 |
| 5 | 814 | 6 | 2, 5, 6, 7, 8, 9 | 0.970 | 0.469 | 0.356 | 0.037 |
| 6 | 105 | 5 | 2, 5, 6, 8, 9 | 0.971 | 0.474 | 0.357 | 0.037 |
| 7 | 548 | 6 | 2, 4, 5, 6, 7, 8 | 0.972 | 0.478 | 0.358 | 0.037 |
| 8 | 567 | 5 | 2, 5, 6, 7, 8 | 0.971 | 0.471 | 0.359 | 0.037 |
| 9 | 948 | 6 | 2, 3, 5, 6, 8, 10 | 0.971 | 0.477 | 0.359 | 0.037 |
| 10 | 815 | 6 | 2, 5, 6, 7, 8, 10 | 0.972 | 0.472 | 0.361 | 0.037 |
| Image ID | Image Date | Total Outliers | Isolated Outliers | Persistent Outliers | Validation Points | % Isolated Outliers | % Persistent Outliers |
|---|---|---|---|---|---|---|---|
| 1 | 5 April 2021 | 29 | 11 | 18 | 1085 | 1.0% | 1.7% |
| 2 | 15 April 2021 | 22 | 6 | 16 | 1085 | 0.6% | 1.5% |
| 3 | 17 April 2021 | 55 | 26 | 29 | 1085 | 2.4% | 2.7% |
| 4 | 22 April 2021 | 46 | 18 | 28 | 1085 | 1.7% | 2.6% |
| 5 | 4 June 2021 | 27 | 10 | 17 | 1085 | 0.9% | 1.6% |
| 6 | 16 July 2021 | 29 | 11 | 18 | 1085 | 1.0% | 1.7% |
| 7 | 19 July 2021 | 18 | 5 | 13 | 1085 | 0.5% | 1.2% |
| 8 | 21 July 2021 | 17 | 4 | 13 | 1085 | 0.4% | 1.2% |
| 9 | 28 August 2021 | 13 | 0 | 13 | 1085 | 0.0% | 1.2% |
| 10 | 14 September 2021 | 1 | 0 | 1 | 1085 | 0.0% | 0.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monteys, X.; Isler, T.; Casal, G.; Gallagher, C. Improving Satellite-Derived Bathymetry in Complex Coastal Environments: A Generalised Linear Model and Multi-Temporal Sentinel-2 Approach. Remote Sens. 2025, 17, 3834. https://doi.org/10.3390/rs17233834
Monteys X, Isler T, Casal G, Gallagher C. Improving Satellite-Derived Bathymetry in Complex Coastal Environments: A Generalised Linear Model and Multi-Temporal Sentinel-2 Approach. Remote Sensing. 2025; 17(23):3834. https://doi.org/10.3390/rs17233834
Chicago/Turabian StyleMonteys, Xavier, Tea Isler, Gema Casal, and Colman Gallagher. 2025. "Improving Satellite-Derived Bathymetry in Complex Coastal Environments: A Generalised Linear Model and Multi-Temporal Sentinel-2 Approach" Remote Sensing 17, no. 23: 3834. https://doi.org/10.3390/rs17233834
APA StyleMonteys, X., Isler, T., Casal, G., & Gallagher, C. (2025). Improving Satellite-Derived Bathymetry in Complex Coastal Environments: A Generalised Linear Model and Multi-Temporal Sentinel-2 Approach. Remote Sensing, 17(23), 3834. https://doi.org/10.3390/rs17233834






