Bidirectional Reflectance Sensitivity to Hemispherical Samplings: Implications for Snow Surface BRDF and Albedo Retrieval
Highlights
- Different illuminating–observing sampling distribution schemes can influence BRDF and albedo more for longer wavelengths.
- An angular information index (AII) was proposed based on a kernel-driven model, in cooperation with a weighting mechanism and information effectiveness to evaluate the information content of various sampling distribution schemes.
- The angular sampling configuration is demonstrated to be a key factor influencing the accuracy of BRDF and albedo derived from the kernel-driven model.
- The AII provides a practical metric for guiding future sensor parameterization and for evaluating the quality of multi-angular data before operational application.
Abstract
1. Introduction
2. Data
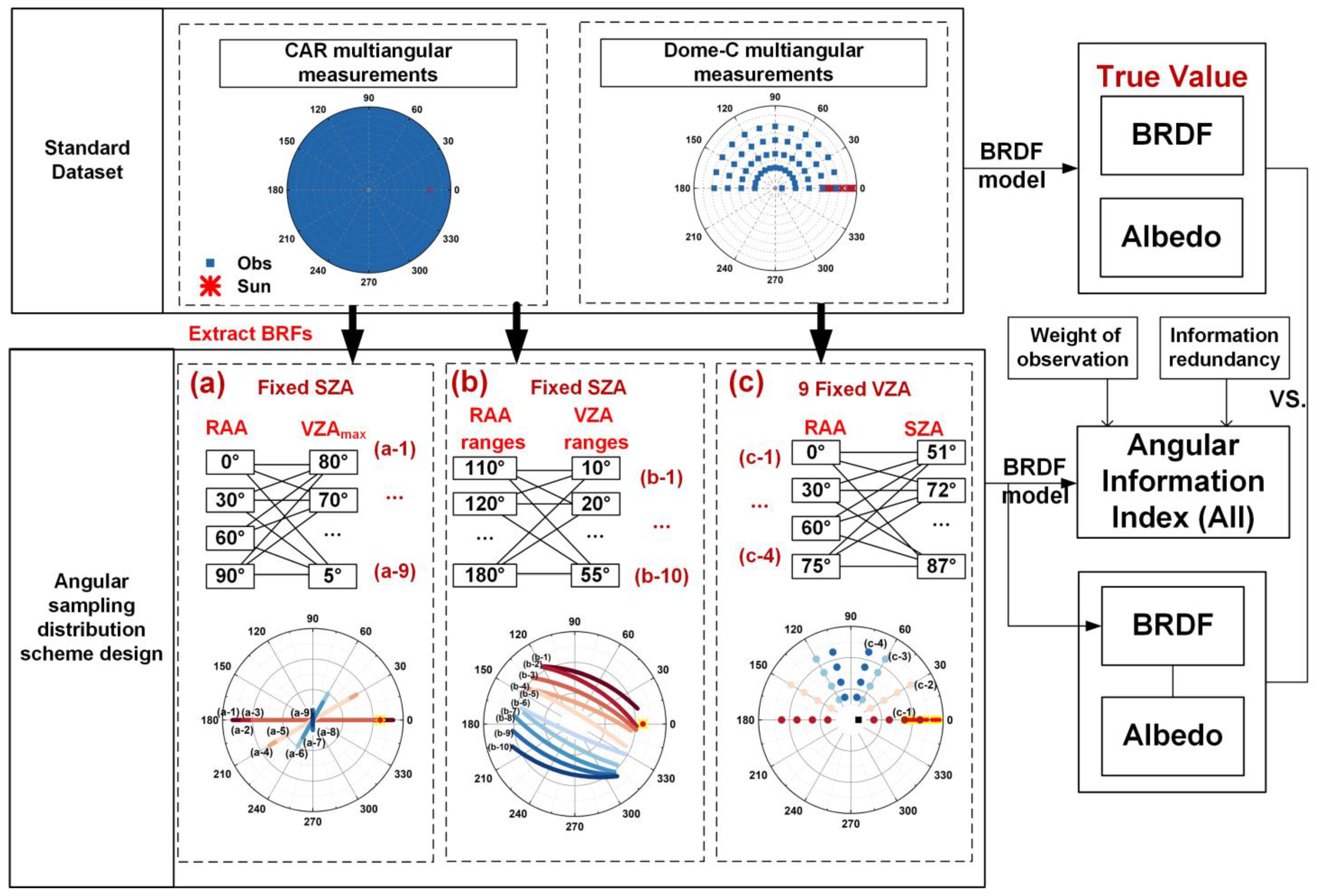
2.1. CAR Multi-Angular Data
2.2. Dome-C Multi-Angular Data
3. Methods
3.1. Angular Sampling Scheme Design
- Observations sampled along a single RAA under a fixed SZA:
- 2.
- Observations sampled along multiple RAA and VZA ranges under a fixed SZA:
- 3.
- Sampling along a single RAA under varied SZAs:
3.2. Kernel-Driven Model
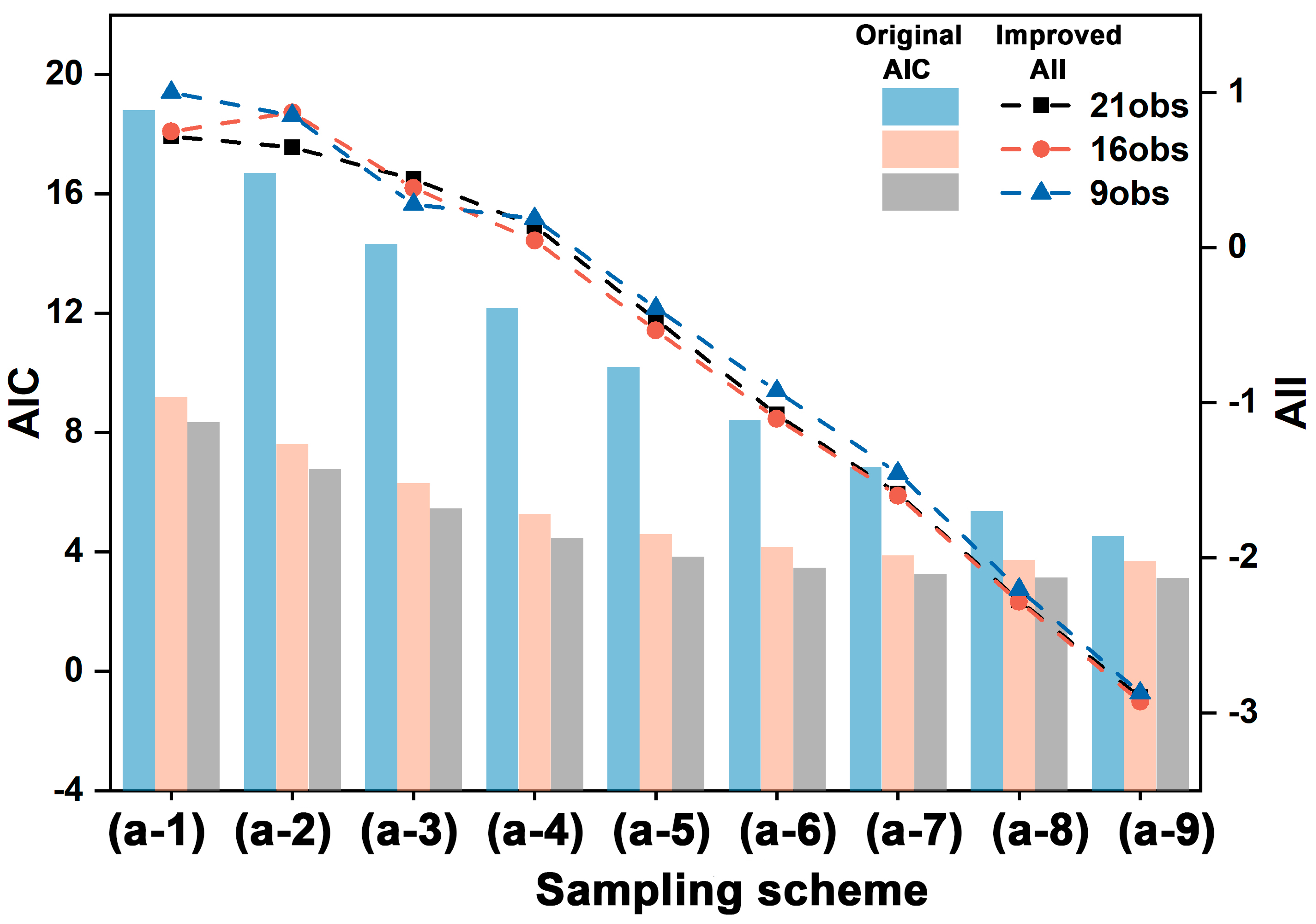
3.3. Angular Information Index (AII)
- (1)
- Based on the principle that the PP carries the most informative BRDF signals [16,40,43,44], a weighting mechanism was introduced for each observation. Specifically, different weights were assigned according to the varying levels of information effectiveness. The new eigenvalues are denoted as λ1W–4W, then IW can be calculated:
- (2)
- Cosine similarity was employed to quantify the redundancy between the observations [45].
4. Results and Analysis
4.1. The AII of Different Sampling Schemes
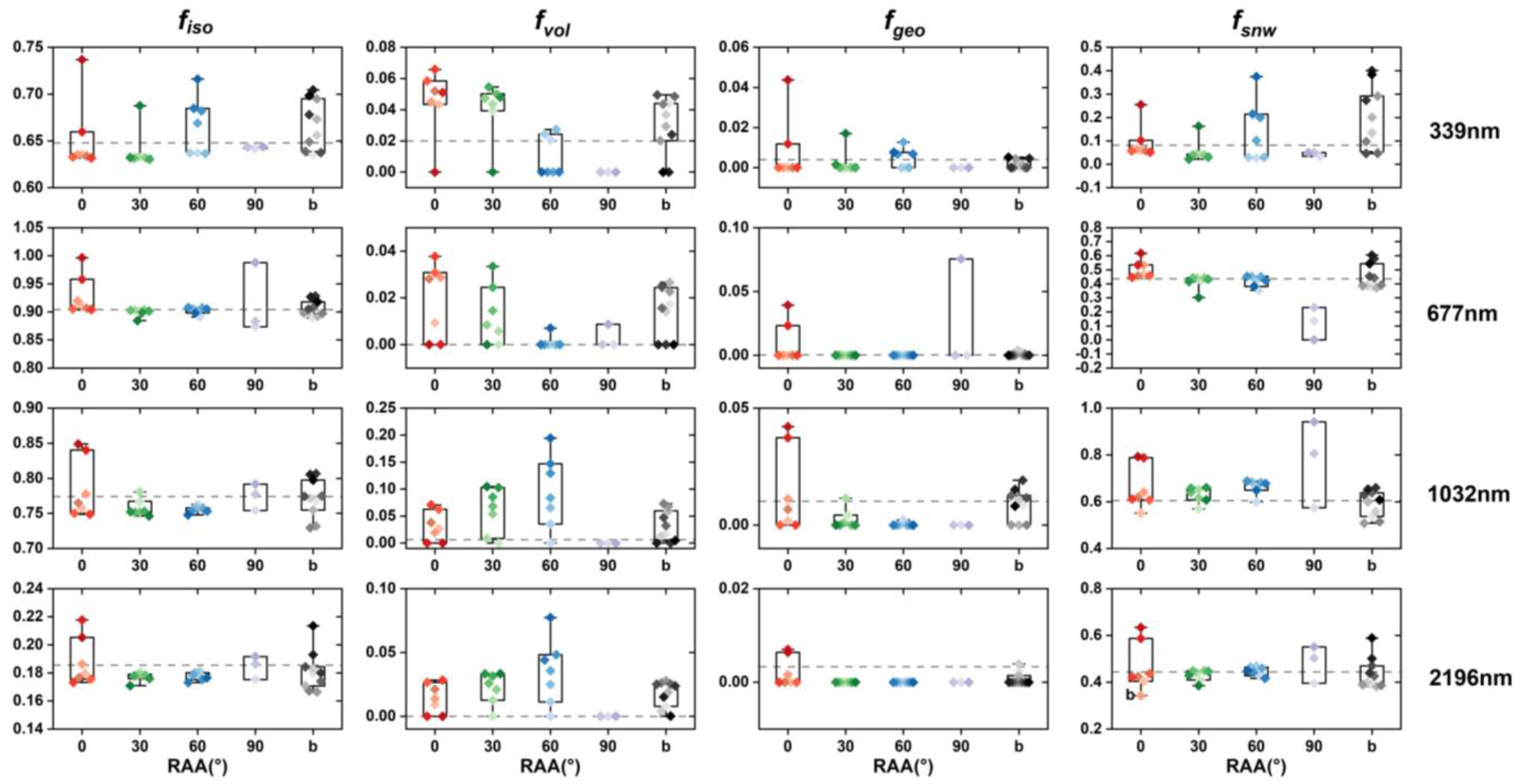
4.2. The BRDF and Albedo Difference Analysis for Scheme (a) and Scheme (b)
4.2.1. The BRDF Difference
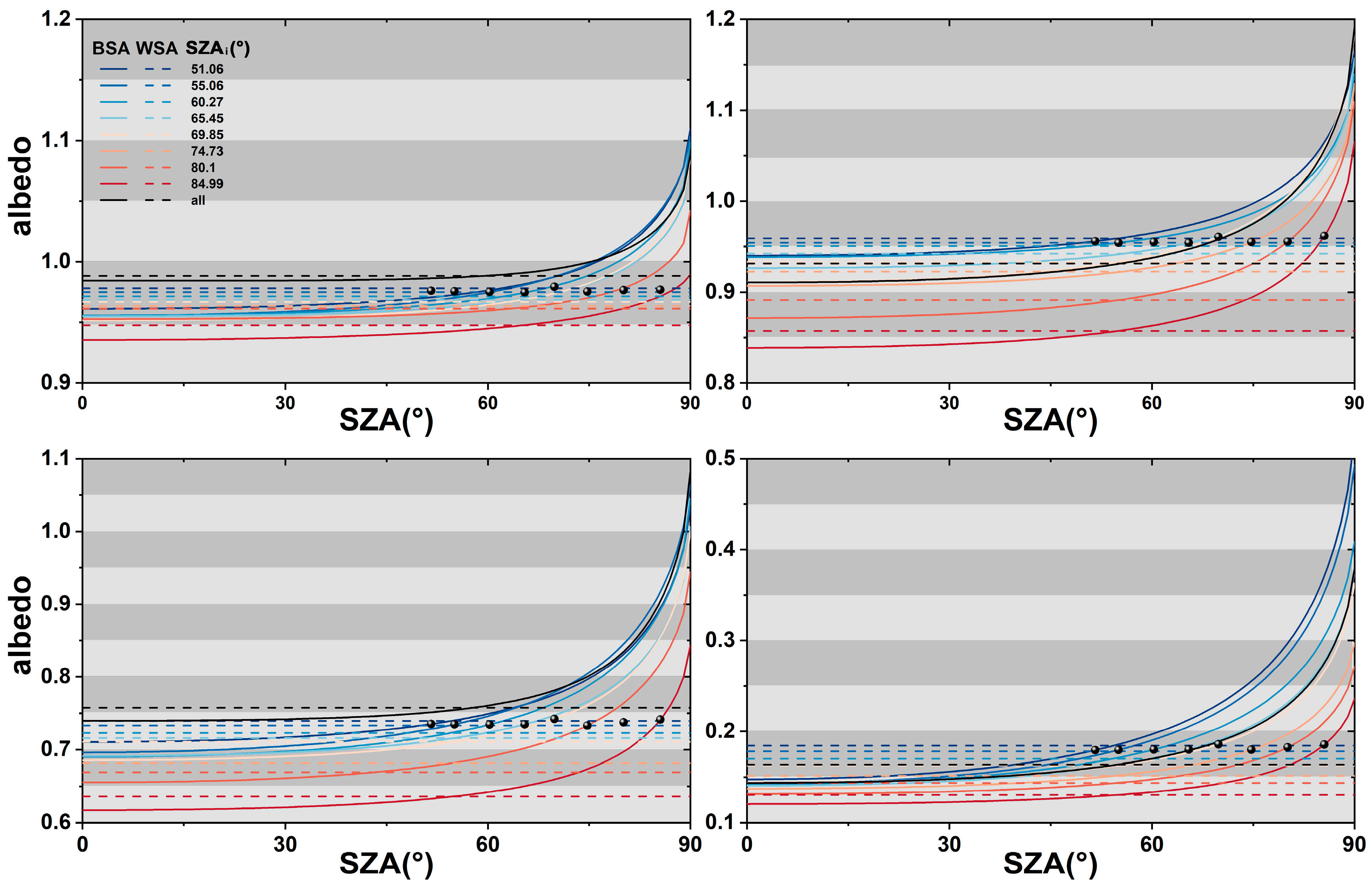
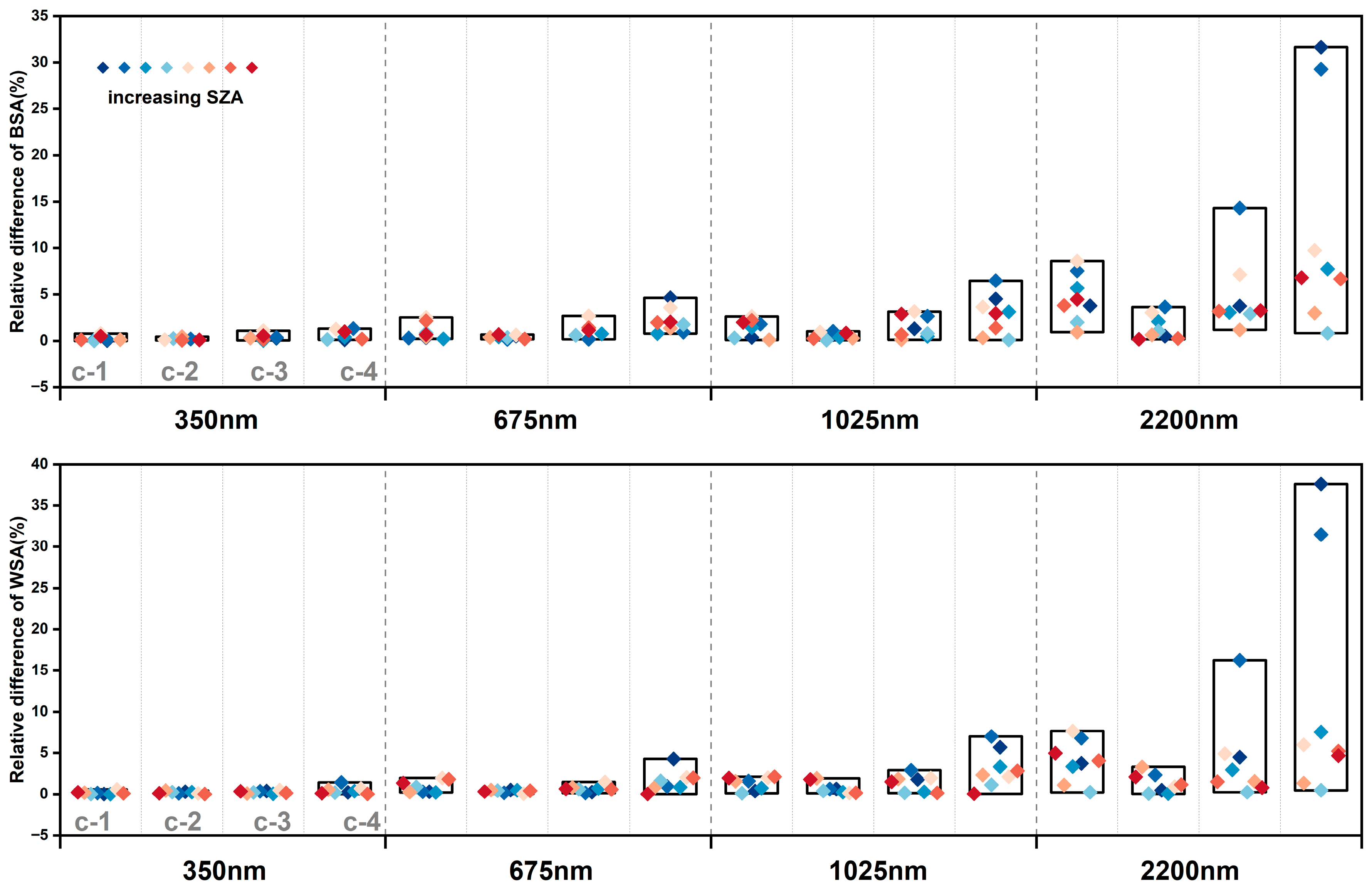
4.2.2. The Albedo Difference
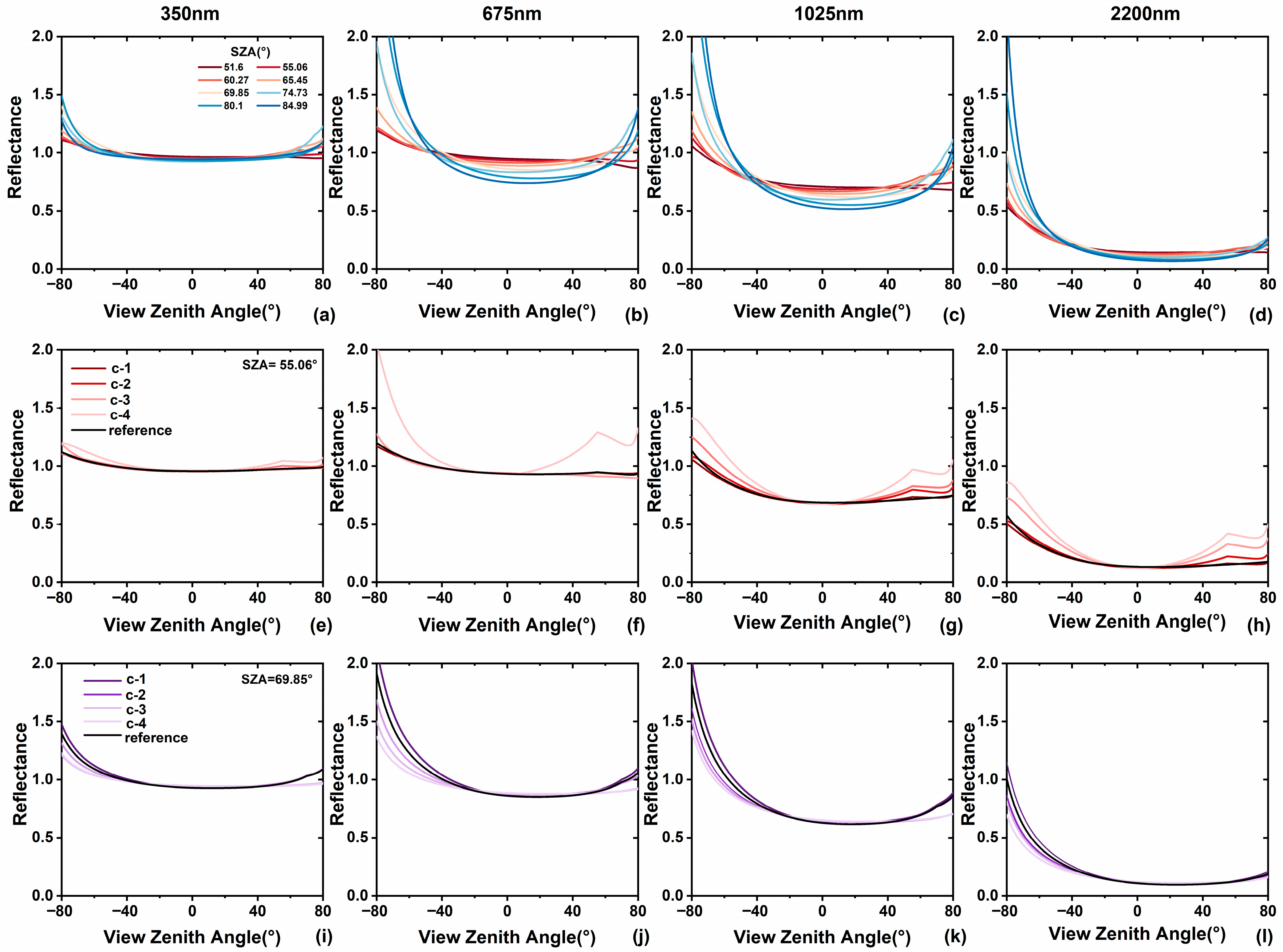
4.3. The BRDF and Albedo Difference Analysis for Scheme (c)
5. Conclusions
6. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical Considerations and Nomenclature for Reflectance (National Bureau of Standards (U.S.). 1977. Available online: http://www.researchgate.net/publication/313489884_Geometrical_considerations_and_nomenclature_for_reflectance_National_bureau_of_standards_U_S (accessed on 26 November 2023).
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Cui, L.; Zhang, H.; Zhang, X.; Yin, S.; Ding, A.; Chang, Y.; Xie, R.; Guo, J. Assessment of the Hotspot Effect for the PROSAIL Model with POLDER Hotspot Observations Based on the Hotspot-Enhanced Kernel-Driven BRDF Model. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8048–8064. [Google Scholar] [CrossRef]
- Chang, Y.; Jiao, Z.; Zhang, X.; Mei, L.; Dong, Y.; Yin, S.; Cui, L.; Ding, A.; Guo, J.; Xie, R.; et al. Assessment of Improved Ross–Li BRDF Models Emphasizing Albedo Estimates at Large Solar Angles Using POLDER Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9968–9986. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.-Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Aoki, T.; Aoki, T.; Fukabori, M.; Hachikubo, A.; Tachibana, Y.; Nishio, F. Effects of snow physical parameters on spectral albedo and bidirectional reflectance of snow surface. J. Geophys. Res. Atmos. 2000, 105, 10219–10236. [Google Scholar] [CrossRef]
- Zege, E.P.; Katsev, I.L.; Malinka, A.V.; Prikhach, A.S.; Heygster, G.; Wiebe, H. Algorithm for retrieval of the effective snow grain size and pollution amount from satellite measurements. Remote Sens. Environ. 2011, 115, 2674–2685. [Google Scholar] [CrossRef]
- Nolin, A.; Fetterer, F.; Scambos, T. Surface roughness characterizations of sea ice and ice sheets: Case studies with MISR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1605–1615. [Google Scholar] [CrossRef]
- Colgan, M.S.; Baldeck, C.A.; Féret, J.-B.; Asner, G.P. Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data. Remote Sens. 2012, 4, 3462–3480. [Google Scholar] [CrossRef]
- Buchhorn, M.; Raynolds, M.K.; Walker, D.A. Influence of BRDF on NDVI and biomass estimations of Alaska Arctic tundra. Environ. Res. Lett. 2016, 11, 125002. [Google Scholar] [CrossRef]
- Jensen, D.J.; Simard, M.; Cavanaugh, K.C.; Thompson, D.R. Imaging Spectroscopy BRDF Correction for Mapping Louisiana’s Coastal Ecosystems. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1739–1748. [Google Scholar] [CrossRef]
- Viterbo, P.; Betts, A.K. Impact on ECMWF forecasts of changes to the albedo of the boreal forests in the presence of snow. J. Geophys. Res. Atmos. 1999, 104, 27803–27810. [Google Scholar] [CrossRef]
- Wang, K.; Liu, J.; Zhou, X.; Sparrow, M.; Ma, M.; Sun, Z.; Jiang, W. Validation of the MODIS global land surface albedo product using ground measurements in a semidesert region on the Tibetan Plateau. J. Geophys. Res. Atmos. 2004, 109, D05107. [Google Scholar] [CrossRef]
- Gao, F.; He, T.; Wang, Z.; Ghimire, B.; Shuai, Y.; Masek, J.G.; Schaaf, C.; Williams, C. Multiscale climatological albedo look-up maps derived from moderate resolution imaging spectroradiometer BRDF/albedo products. JARS 2014, 8, 083532. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.H. Retrieval of surface BRDF from multiangle remotely sensed data. Remote Sens. Environ. 1994, 50, 18–30. [Google Scholar] [CrossRef]
- Jiao, Z.; Ding, A.; Kokhanovsky, A.; Schaaf, C.; Bréon, F.-M.; Dong, Y.; Wang, Z.; Liu, Y.; Zhang, X.; Yin, S.; et al. Development of a snow kernel to better model the anisotropic reflectance of pure snow in a kernel-driven BRDF model framework. Remote Sens. Environ. 2019, 221, 198–209. [Google Scholar] [CrossRef]
- Loeb, N.G.; Smith, N.M.; Kato, S.; Miller, W.F.; Gupta, S.K.; Minnis, P.; Wielicki, B.A. Angular distribution models for top-of-atmosphere radiative flux estimation from the Clouds and the Earth’s Radiant Energy System instrument on the Tropical Rainfall Measuring Mission Satellite. Part I: Methodology. J. Appl. Meteorol. 2003, 42, 240–265. [Google Scholar] [CrossRef]
- Barnsley, M.J.; Settle, J.J.; Cutter, M.A.; Lobb, D.R.; Teston, F. The PROBA/CHRIS mission: A low-cost smallsat for hyperspectral multiangle observations of the Earth surface and atmosphere. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1512–1520. [Google Scholar] [CrossRef]
- Diner, D.J.; Beckert, J.; Reilly, T.; Bruegge, C.; Conel, J.; Kahn, R.; Martonchik, J.; Ackerman, T.; Davies, R.; Gerstl, S.; et al. Multi-angle Imaging SpectroRadiometer (MISR) instrument description and experiment overview. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1072–1087. [Google Scholar] [CrossRef]
- Leroy, M.; Deuzé, J.L.; Bréon, F.M.; Hautecoeur, O.; Herman, M.; Buriez, J.C.; Tanré, D.; Bouffiès, S.; Chazette, P.; Roujean, J.L. Retrieval of atmospheric properties and surface bidirectional reflectances over land from POLDER/ADEOS. J. Geophys. Res. Atmos. 1997, 102, 17023–17037. [Google Scholar] [CrossRef]
- Chen, L.; Shang, H.; Fan, M.; Tao, J.; Husi, L.; Zhang, Y.; Wang, H.; Cheng, L.; Zhang, X.; Wei, L.; et al. Mission overview of the GF-5 satellite for atmospheric parameter monitoring. J. Remote Sens. 2021, 25, 1917–1931. [Google Scholar] [CrossRef]
- Nishihama, M.; Wolfe, R.; Solomon, D.; Patt, F.; Blanchette, J.; Fleig, A.; Masuoka, E. MODIS Level 1A Earth Location: Algorithm Theoretical Basis Document Version 3.0. NASA GSFC. 26 August 1997. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod28_v3.pdf (accessed on 10 September 2023).
- Baker, N.; Kilcoyne, H. Joint Polar Satellite System (JPSS) VIIRS Geolocation Algorithm Theoretical Basis Document (ATBD). NASA GSFC. 5 December 2011. Available online: https://www.star.nesdis.noaa.gov/jpss/documents/ATBD/D0001-M01-S01-004_JPSS_ATBD_VIIRS-Geolocation_B.pdf (accessed on 10 September 2023).
- Hu, B.; Lucht, W.; Strahler, A.H.; Schaaf, C.B.; Smith, M. Surface Albedos and Angle-Corrected NDVI from AVHRR Observations of South America. Remote Sens. Environ. 2000, 71, 119–132. [Google Scholar] [CrossRef]
- Yan, G.; Jiang, H.; Yan, K.; Cheng, S.; Song, W.; Tong, Y.; Liu, Y.; Qi, J.; Mu, X.; Zhang, W.; et al. Review of optical multi-angle quantitative remote sensing. J. Remote Sens. 2021, 25, 83–108. [Google Scholar] [CrossRef]
- Durpaire, J.-P.; Gentet, T.; Phulpin, T.; Arnaud, M. Spot-4 vegetation instrument: Vegetation monitoring on a global scale. Acta Astronaut. 1995, 35, 453–459. [Google Scholar] [CrossRef]
- Roy, D.P.; Li, J.; Zhang, H.K.; Yan, L.; Huang, H.; Li, Z. Examination of Sentinel-2A multi-spectral instrument (MSI) reflectance anisotropy and the suitability of a general method to normalize MSI reflectance to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2017, 199, 25–38. [Google Scholar] [CrossRef]
- Matsuoka, M.; Takagi, M.; Akatsuka, S.; Honda, R.; Nonomura, A.; Moriya, H.; Yoshioka, H. Bidirectional Reflectance Modeling of the Geostationary Sensor Himawari-8/Ahi Using a Kernel-Driven Brdf Model. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-7, 3–8. [Google Scholar] [CrossRef][Green Version]
- Sun, Y.; Wang, Z.; Qin, Q.; Han, G.; Ren, H.; Huang, J. Retrieval of surface albedo based on GF-4 geostationary satellite image data. J. Remote Sens. 2018, 22, 220–233. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Lucht, W.; Lewis, P. Theoretical noise sensitivity of BRDF and albedo retrieval from the EOS-MODIS and MISR sensors with respect to angular sampling. Int. J. Remote Sens. 2000, 21, 81–98. [Google Scholar] [CrossRef]
- Zhang, X.; Jiao, Z.; Zhao, C.; Guo, J.; Zhu, Z.; Liu, Z.; Dong, Y.; Yin, S.; Zhang, H.; Cui, L.; et al. Evaluation of BRDF Information Retrieved from Time-Series Multiangle Data of the Himawari-8 AHI. Remote Sens. 2022, 14, 139. [Google Scholar] [CrossRef]
- Jin, Y.; Gao, F.; Schaaf, C.; Li, X.; Strahler, A.; Bruegge, C.; Martonchik, J. Improving MODIS surface BRDF/Albedo retrieval with MISR multiangle observations. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1593–1604. [Google Scholar] [CrossRef]
- Zhang, T.; You, D.; Wen, J.; Tang, Y. The Optimal Angular Sampling for Bi-directional Reflectance Distribution Function Retrieval. Remote Sens. Technol. Appl. 2023, 38, 66–77. [Google Scholar] [CrossRef]
- Gatebe, C.K.; King, M.D. Airborne spectral BRDF of various surface types (ocean, vegetation, snow, desert, wetlands, cloud decks, smoke layers) for remote sensing applications. Remote Sens. Environ. 2016, 179, 131–148. [Google Scholar] [CrossRef]
- Dong, Y.; Jiao, Z.; Ding, A.; Zhang, H.; Zhang, X.; Li, Y.; He, D.; Yin, S.; Cui, L. A modified version of the kernel-driven model for correcting the diffuse light of ground multi-angular measurements. Remote Sens. Environ. 2018, 210, 325–344. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Jiao, Z.; Burrows, J.P. A new snow bidirectional reflectance distribution function model in spectral regions from UV to SWIR: Model development and application to ground-based, aircraft and satellite observations. ISPRS J. Photogramm. Remote Sens. 2022, 188, 269–285. [Google Scholar] [CrossRef]
- Hudson, S.R.; Warren, S.G.; Brandt, R.E.; Grenfell, T.C.; Six, D. Spectral bidirectional reflectance of Antarctic snow: Measurements and parameterization. J. Geophys. Res. Atmos. 2006, 111, D18106. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Zege, E.P. Scattering optics of snow. Appl. Opt. 2004, 43, 1589–1602. [Google Scholar] [CrossRef] [PubMed]
- Kokhanovsky, A.; Breon, F.-M. Validation of an Analytical Snow BRDF Model Using PARASOL Multi-Angular and Multispectral Observations. IEEE Geosci. Remote Sens. Lett. 2012, 9, 928–932. [Google Scholar] [CrossRef]
- Jin, Y.; Schaaf, C.B.; Gao, F.; Li, X.; Strahler, A.H.; Lucht, W.; Liang, S. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 1. Algorithm performance. J. Geophys. Res. Atmos. 2003, 108, D5. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Dong, Y.; Zhang, X.; Peltoniemi, J.I.; Mei, L.; Guo, J.; Yin, S.; Cui, L.; Chang, Y.; et al. Evaluation of the Snow Albedo Retrieved from the Snow Kernel Improved the Ross-Roujean BRDF Model. Remote Sens. 2019, 11, 1611. [Google Scholar] [CrossRef]
- Breon, F.-M.; Maignan, F. A BRDF–BPDF database for the analysis of Earth target reflectances. Earth Syst. Sci. Data 2017, 9, 31–45. [Google Scholar] [CrossRef]
- Ding, A.; Jiao, Z.; Dong, Y.; Qu, Y.; Zhang, X.; Xiong, C.; He, D.; Yin, S.; Cui, L.; Chang, Y. An assessment of the performance of two snow kernels in characterizing snow scattering properties. Int. J. Remote Sens. 2019, 40, 6315–6335. [Google Scholar] [CrossRef]
- Lee, H.; Lee, K.; Kim, J.H.; Na, Y.; Park, J.; Choi, J.P.; Hwang, J.Y. Local Similarity Siamese Network for Urban Land Change Detection on Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4139–4149. [Google Scholar] [CrossRef]
- Li, X.; Gao, F.; Wang, J.; Strahler, A. A priori knowledge accumulation and its application to linear BRDF model inversion. J. Geophys. Res. Atmos. 2001, 106, 11925–11935. [Google Scholar] [CrossRef]
- Wang, X.; Zender, C.S. MODIS snow albedo bias at high solar zenith angles relative to theory and to in situ observations in Greenland. Remote Sens. Environ. 2010, 114, 563–575. [Google Scholar] [CrossRef]
- Xiong, C.; Shi, J. Simulating polarized light scattering in terrestrial snow based on bicontinuous random medium and Monte Carlo ray tracing. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 177–189. [Google Scholar] [CrossRef]
- Qi, J.; Xie, D.; Yin, T.; Yan, G.; Gastellu-Etchegorry, J.-P.; Li, L.; Zhang, W.; Mu, X.; Norford, L.K. LESS: LargE-Scale remote sensing data and image simulation framework over heterogeneous 3D scenes. Remote Sens. Environ. 2019, 221, 695–706. [Google Scholar] [CrossRef]
- Warren, S.G. Optical properties of snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
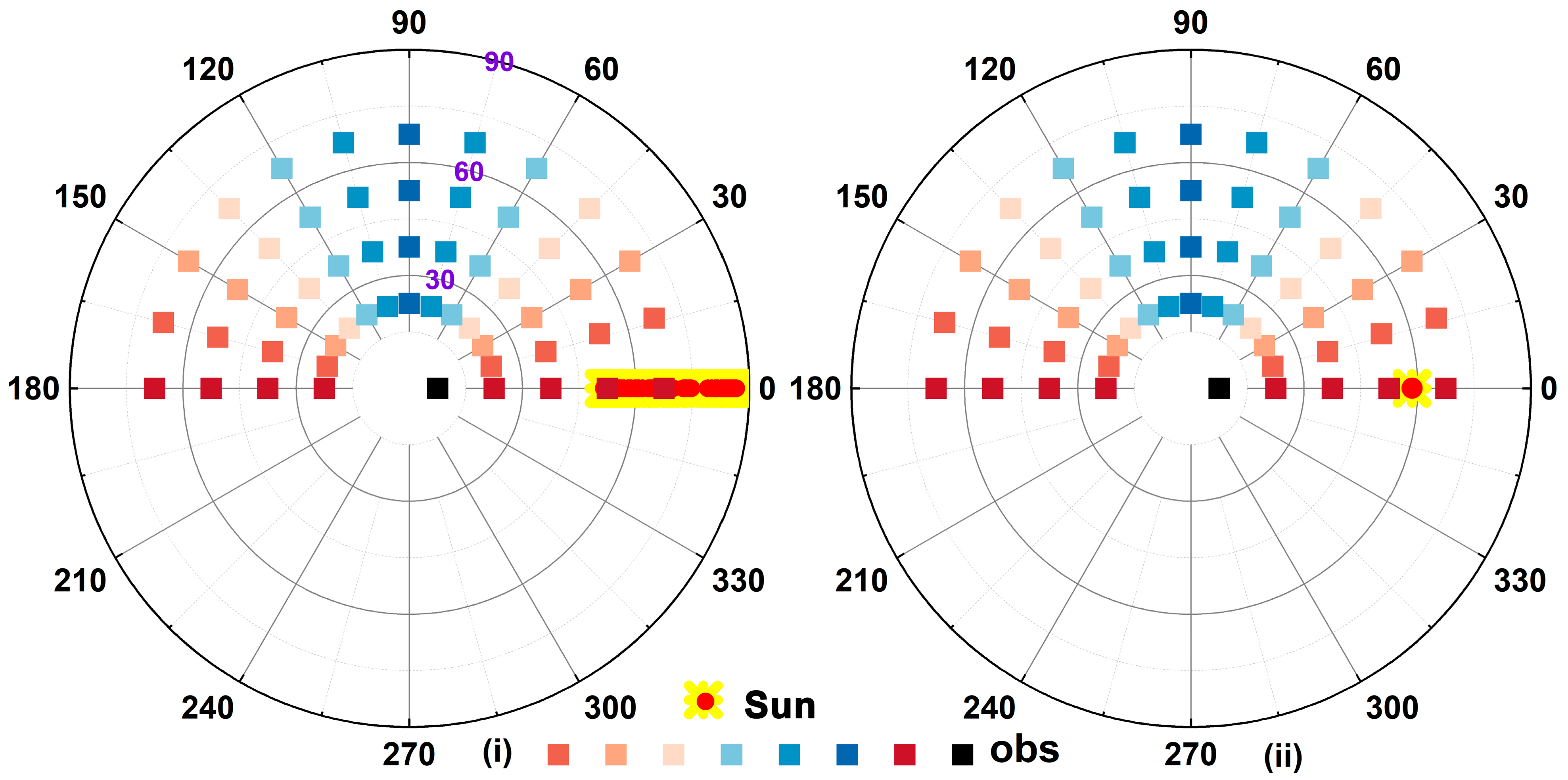
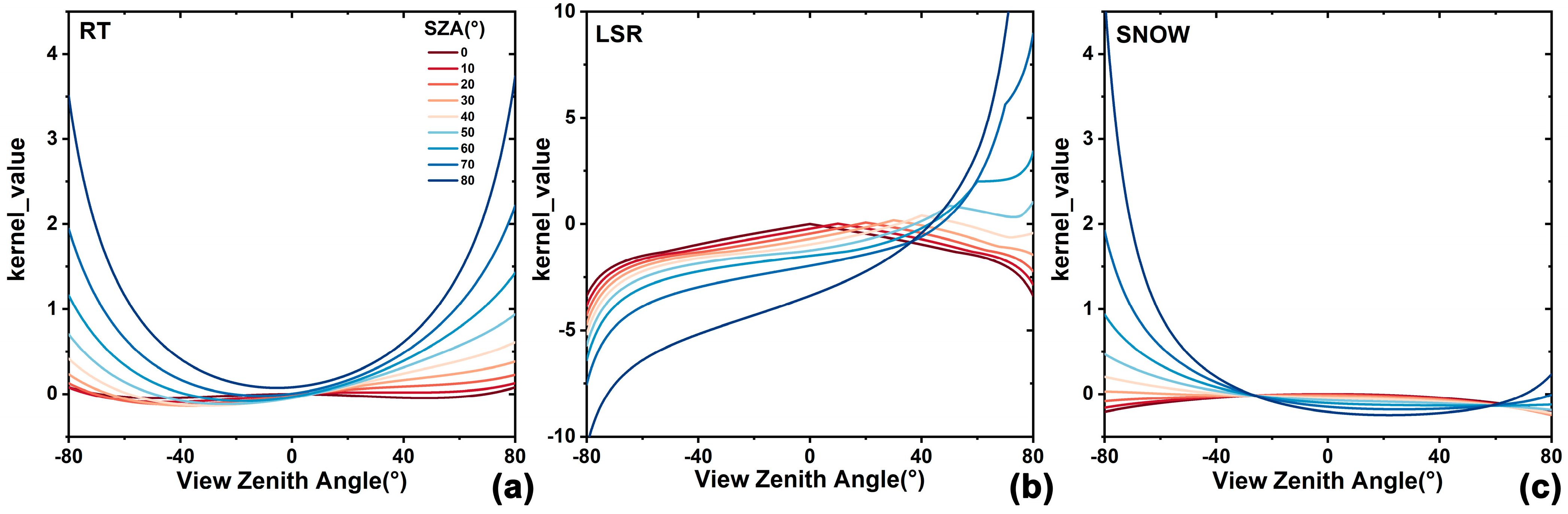
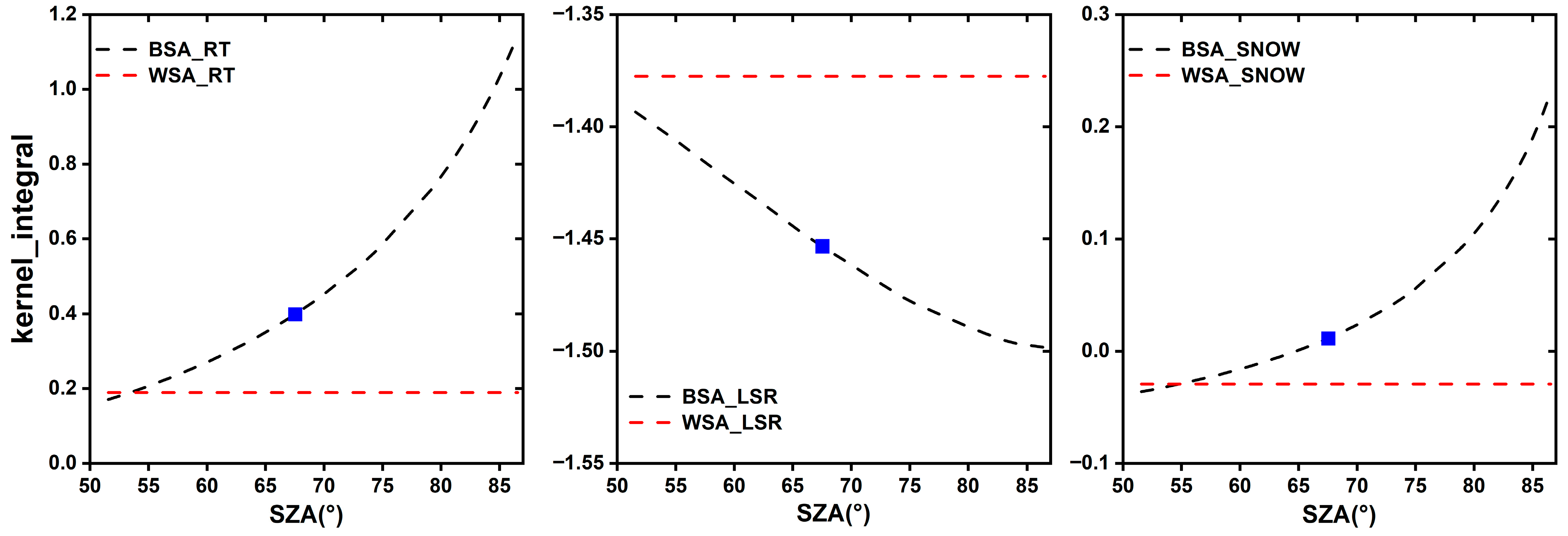

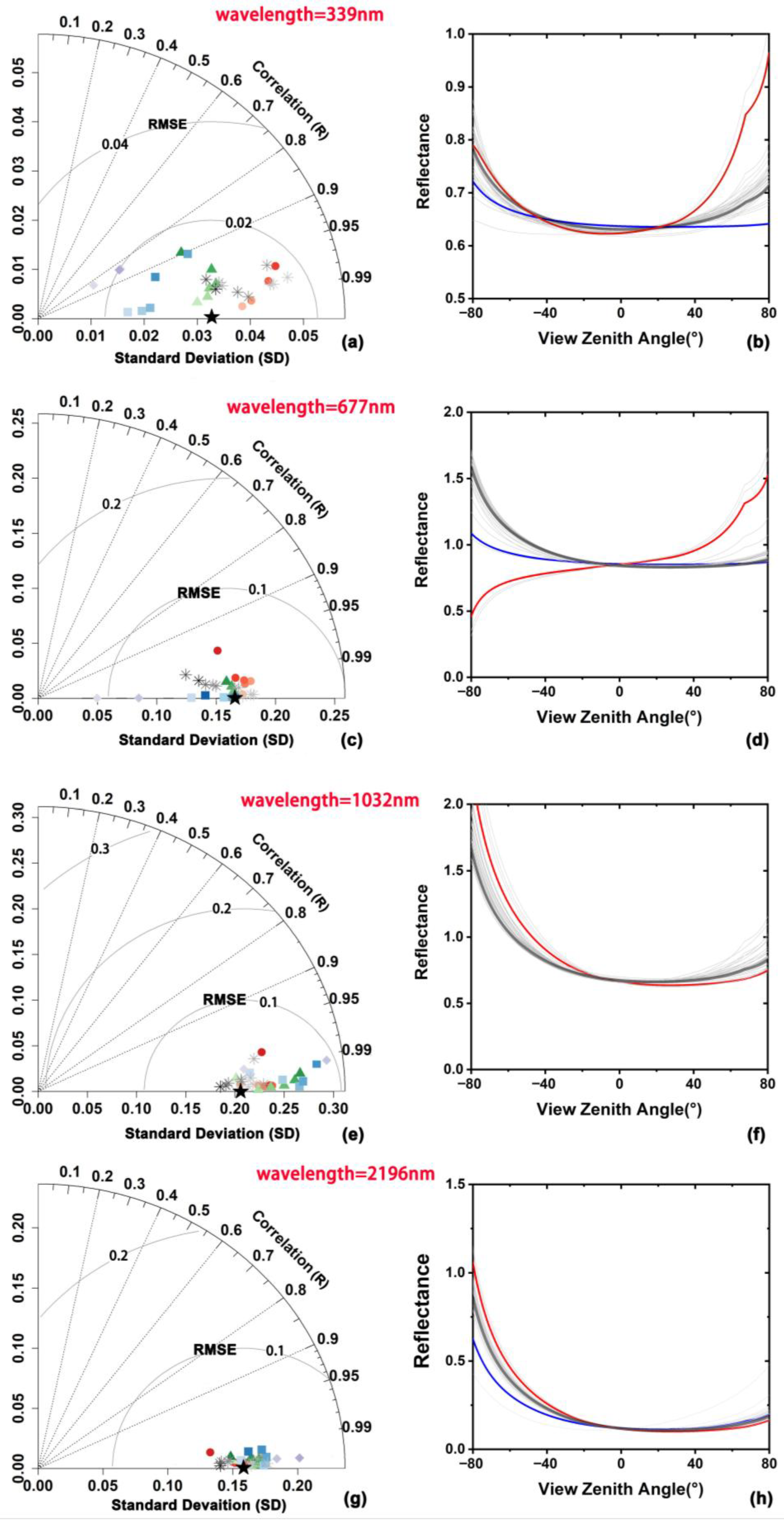

| Wavelength (nm) | SZA | R2 | RMSE |
|---|---|---|---|
| 339 | 67.5° | 0.9014 | 0.0076 |
| 677 | 0.9685 | 0.0187 | |
| 1032 | 0.9805 | 0.0193 | |
| 2196 | 0.9888 | 0.0109 |
| Wavelength (nm) | R2 (i) | RMSE (i) | R2 (ii) | RMSE (ii) |
|---|---|---|---|---|
| 350 | 0.72 | 0.019 | [0.87, 0.99] | [0.0077, 0.038] |
| 675 | 0.62 | 0.070 | [0.82, 0.99] | [0.006, 0.045] |
| 1025 | 0.72 | 0.069 | [0.58, 0.99] | [0.004, 0.032] |
| 2200 | 0.88 | 0.030 | [0.94, 0.99] | [0.004, 0.025] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Jiao, Z.; Ding, A.; Li, Z.; Wang, C.; Yang, F.; Gao, G.; Tan, Z.; Chen, S.; Dong, X. Bidirectional Reflectance Sensitivity to Hemispherical Samplings: Implications for Snow Surface BRDF and Albedo Retrieval. Remote Sens. 2025, 17, 3614. https://doi.org/10.3390/rs17213614
Guo J, Jiao Z, Ding A, Li Z, Wang C, Yang F, Gao G, Tan Z, Chen S, Dong X. Bidirectional Reflectance Sensitivity to Hemispherical Samplings: Implications for Snow Surface BRDF and Albedo Retrieval. Remote Sensing. 2025; 17(21):3614. https://doi.org/10.3390/rs17213614
Chicago/Turabian StyleGuo, Jing, Ziti Jiao, Anxin Ding, Zhilong Li, Chenxia Wang, Fangwen Yang, Ge Gao, Zheyou Tan, Sizhe Chen, and Xin Dong. 2025. "Bidirectional Reflectance Sensitivity to Hemispherical Samplings: Implications for Snow Surface BRDF and Albedo Retrieval" Remote Sensing 17, no. 21: 3614. https://doi.org/10.3390/rs17213614
APA StyleGuo, J., Jiao, Z., Ding, A., Li, Z., Wang, C., Yang, F., Gao, G., Tan, Z., Chen, S., & Dong, X. (2025). Bidirectional Reflectance Sensitivity to Hemispherical Samplings: Implications for Snow Surface BRDF and Albedo Retrieval. Remote Sensing, 17(21), 3614. https://doi.org/10.3390/rs17213614






