Low-Cost Real-Time Remote Sensing and Geolocation of Moving Targets via Monocular Bearing-Only Micro UAVs
Highlights
- A bearing-only localization framework is proposed for micro UAVs operating over uneven terrain, combining a pseudo-linear Kalman filter (PLKF) with a sliding-window nonlinear least squares optimization to achieve real-time 3D positioning and motion prediction.
- An observability-enhanced flight trajectory planning method is designed based on the Fisher Information Matrix (FIM), which improves localization accuracy in flight experiments, with an average gain of up to 4.34 m.
- The method addresses the limitations of monocular cameras with scale ambiguity and lack of depth measurement, providing a practical solution for low-cost UAVs in remote sensing and moving target localization.
- The results suggest potential applications in emergency response, target monitoring, and traffic security, demonstrating the feasibility of high-accuracy localization on resource-constrained UAV platforms.
Abstract
1. Introduction
1.1. Background and Significance
1.2. Related Works
1.3. Contributions
1.4. Organization
2. Problem Formulation
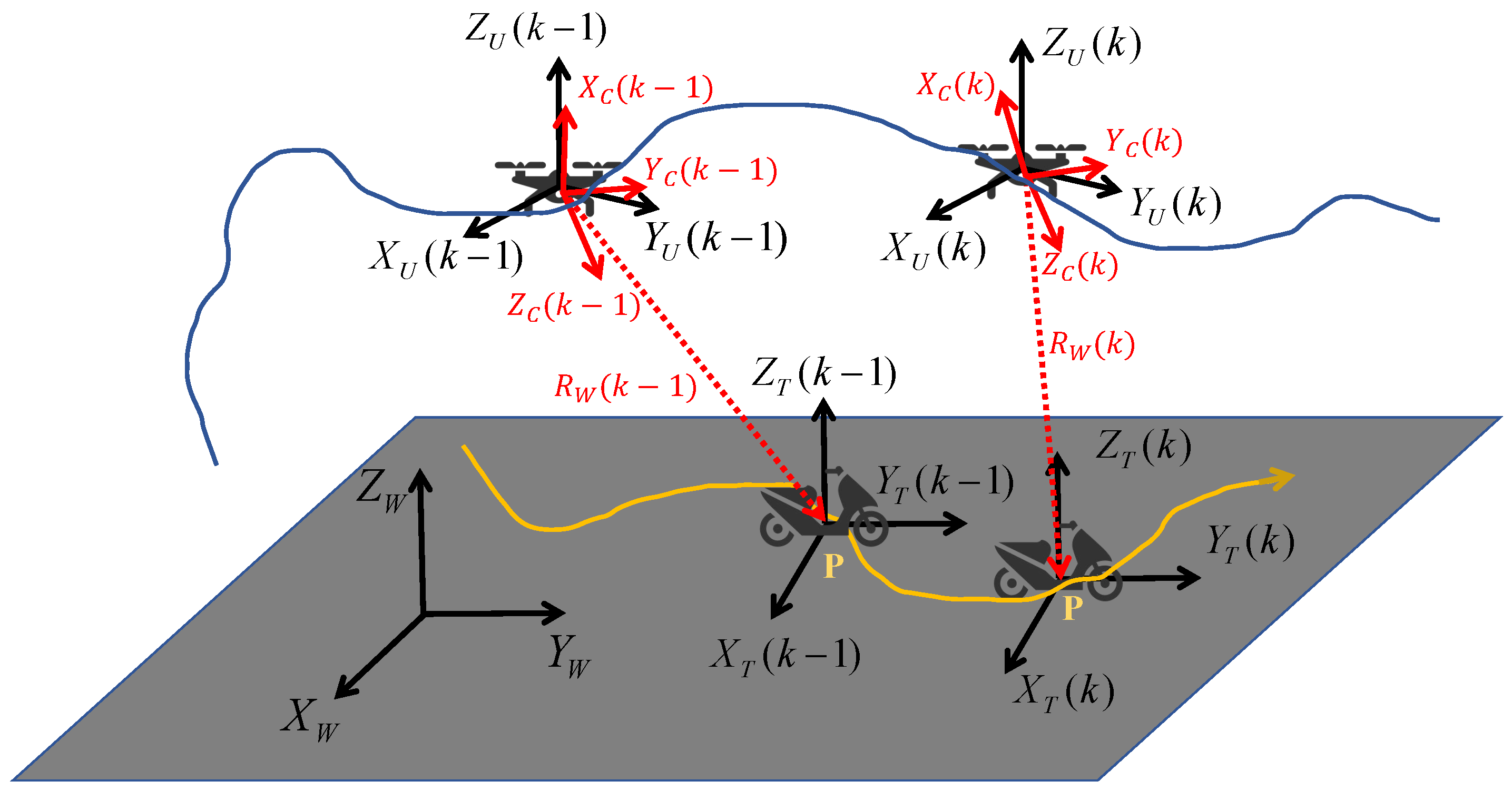
2.1. System Overview
2.2. Measurement Model
3. Methodology
3.1. Inter-Frame Target Motion Estimation Based on Bearing-Only Measurements
3.2. Target Position Optimization Based on Nonlinear Least Squares
3.3. Observability-Enhanced Trajectory Planning
4. Results
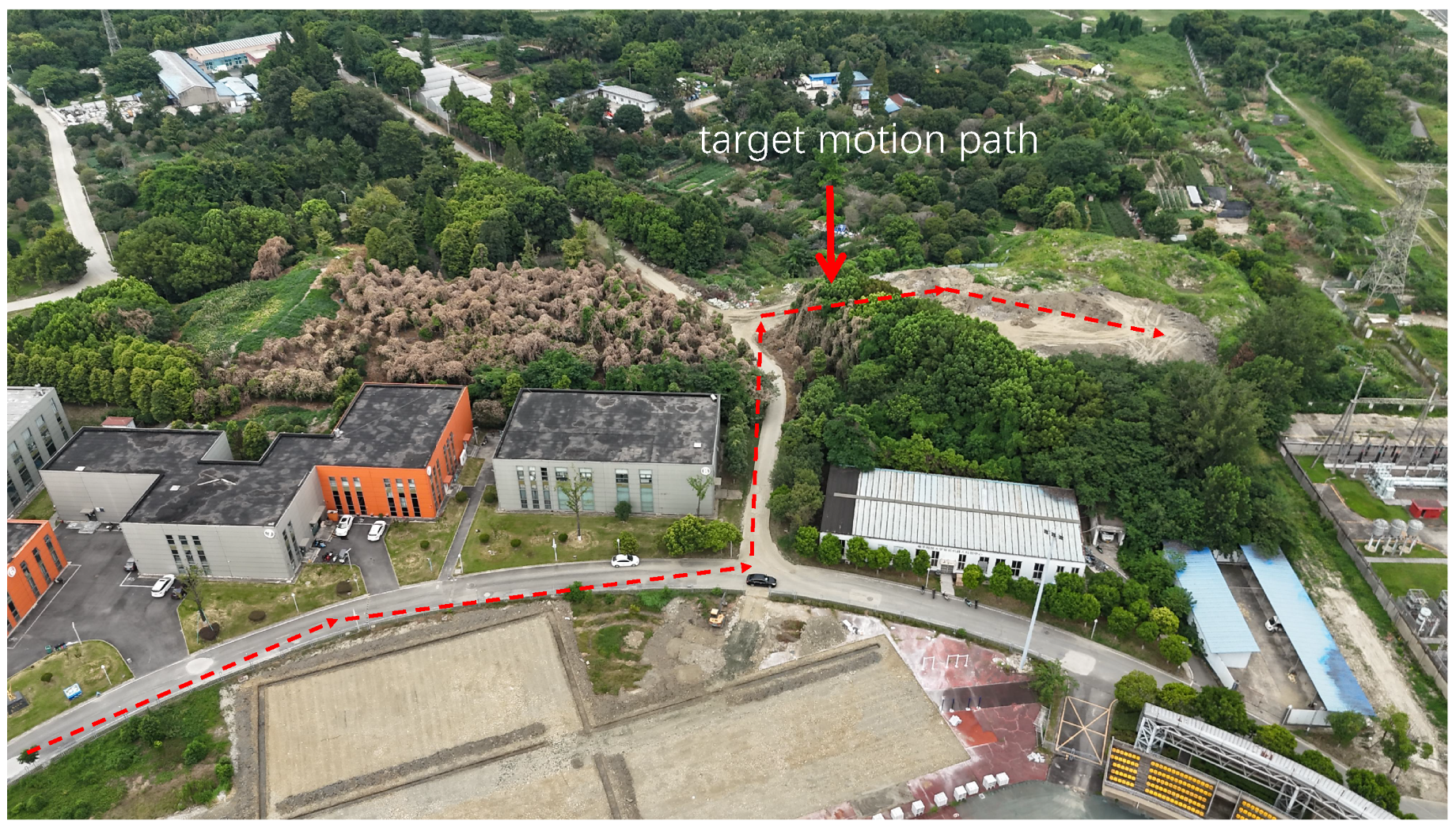
4.1. Flight Experiment Details
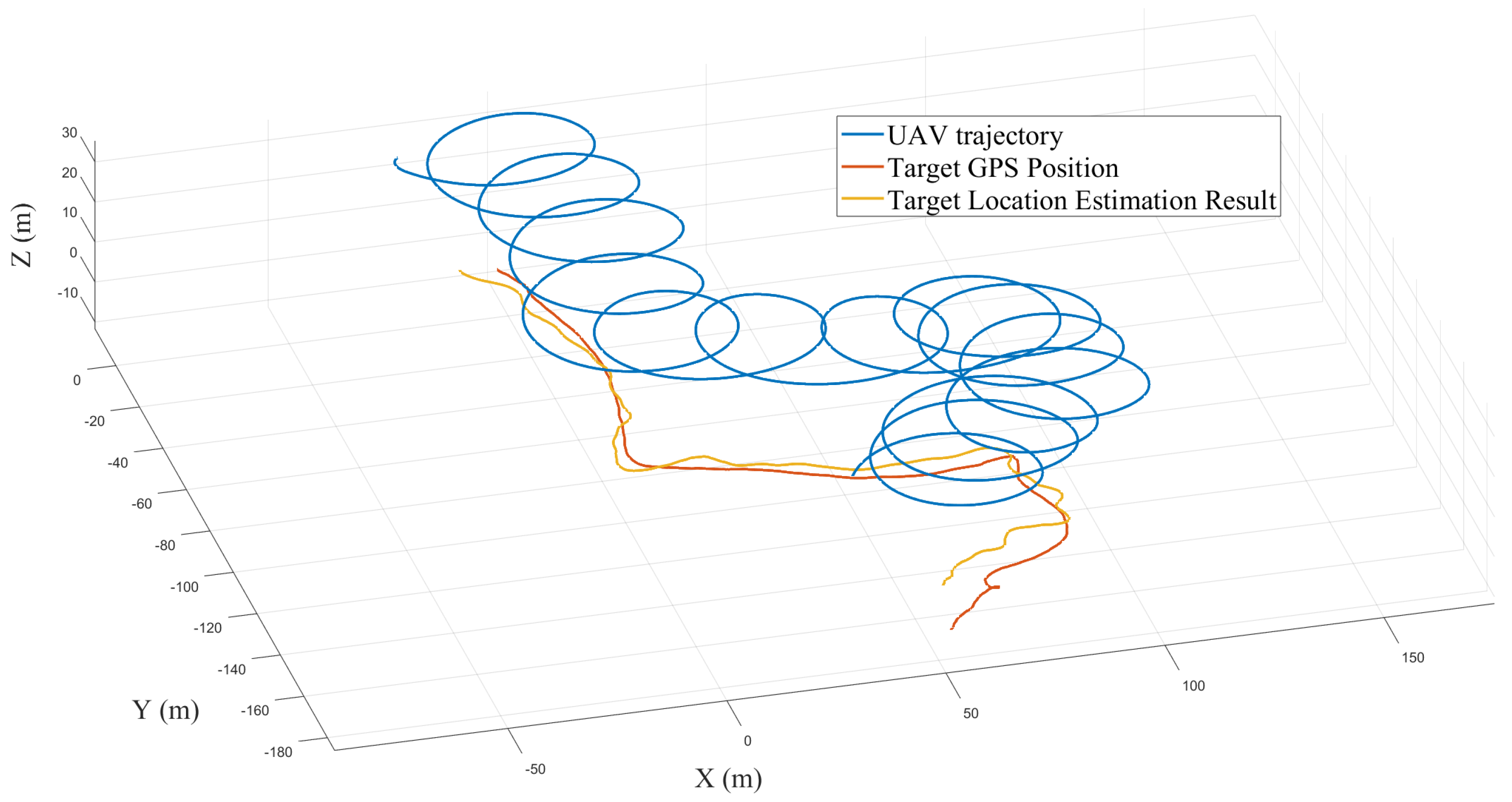
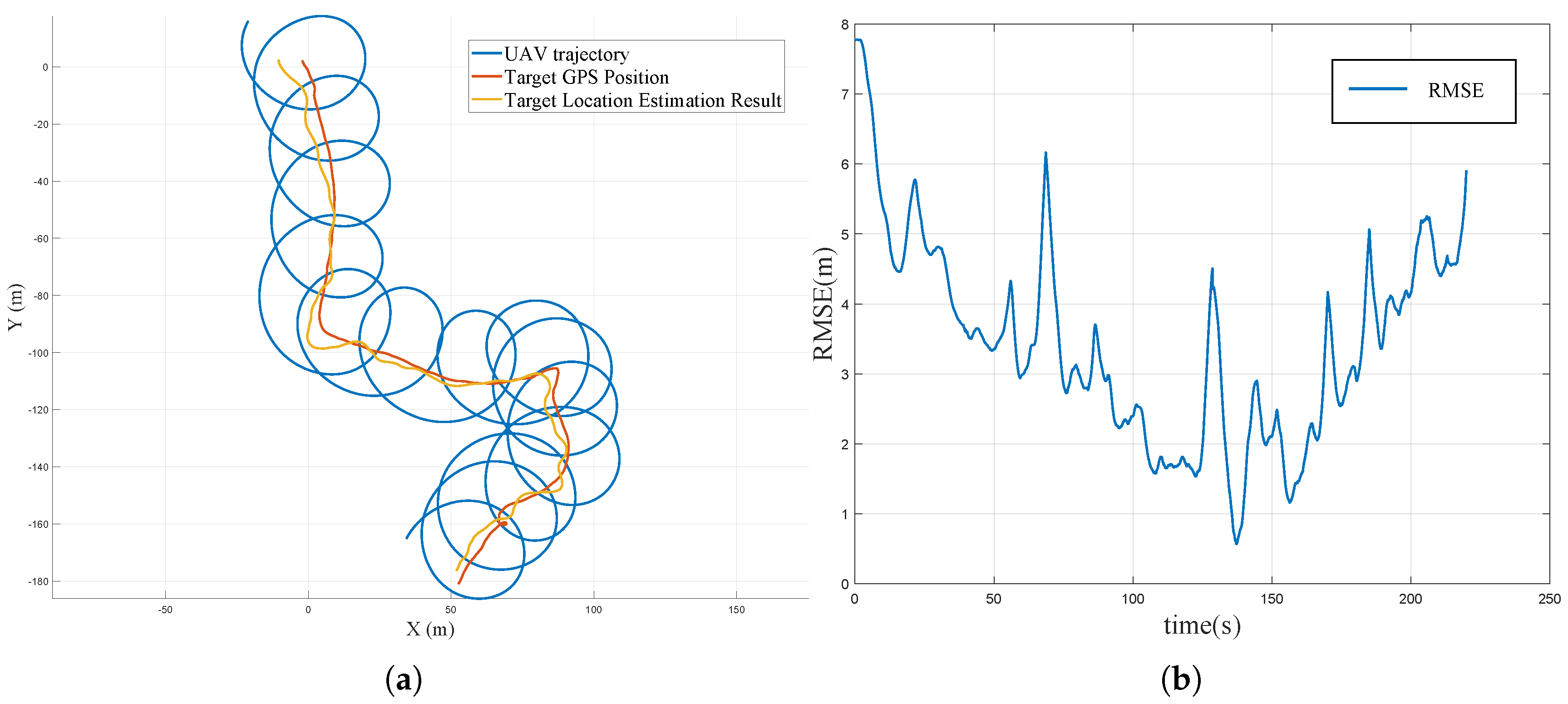
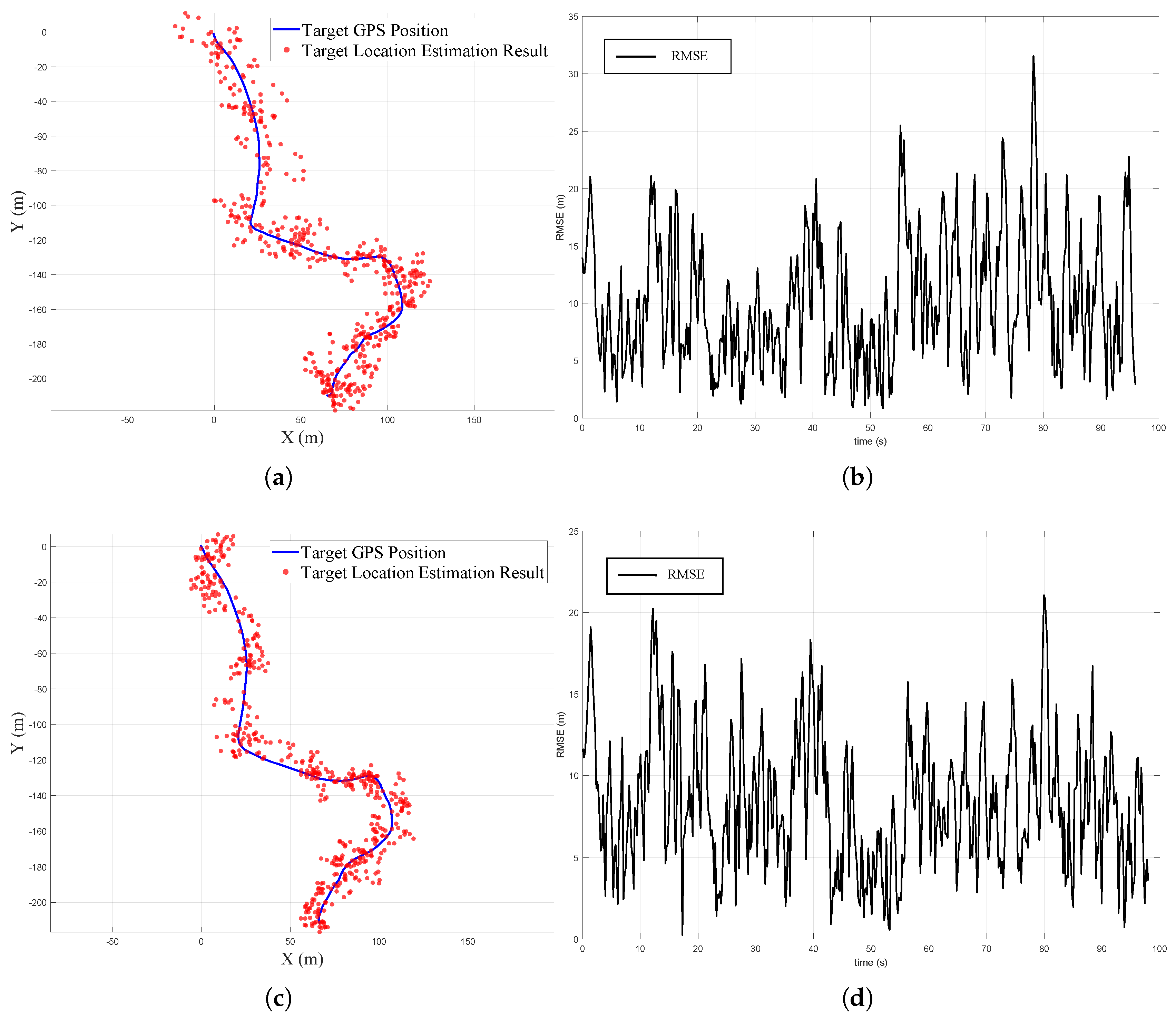
4.2. UAV Target Localization Performance Analysis
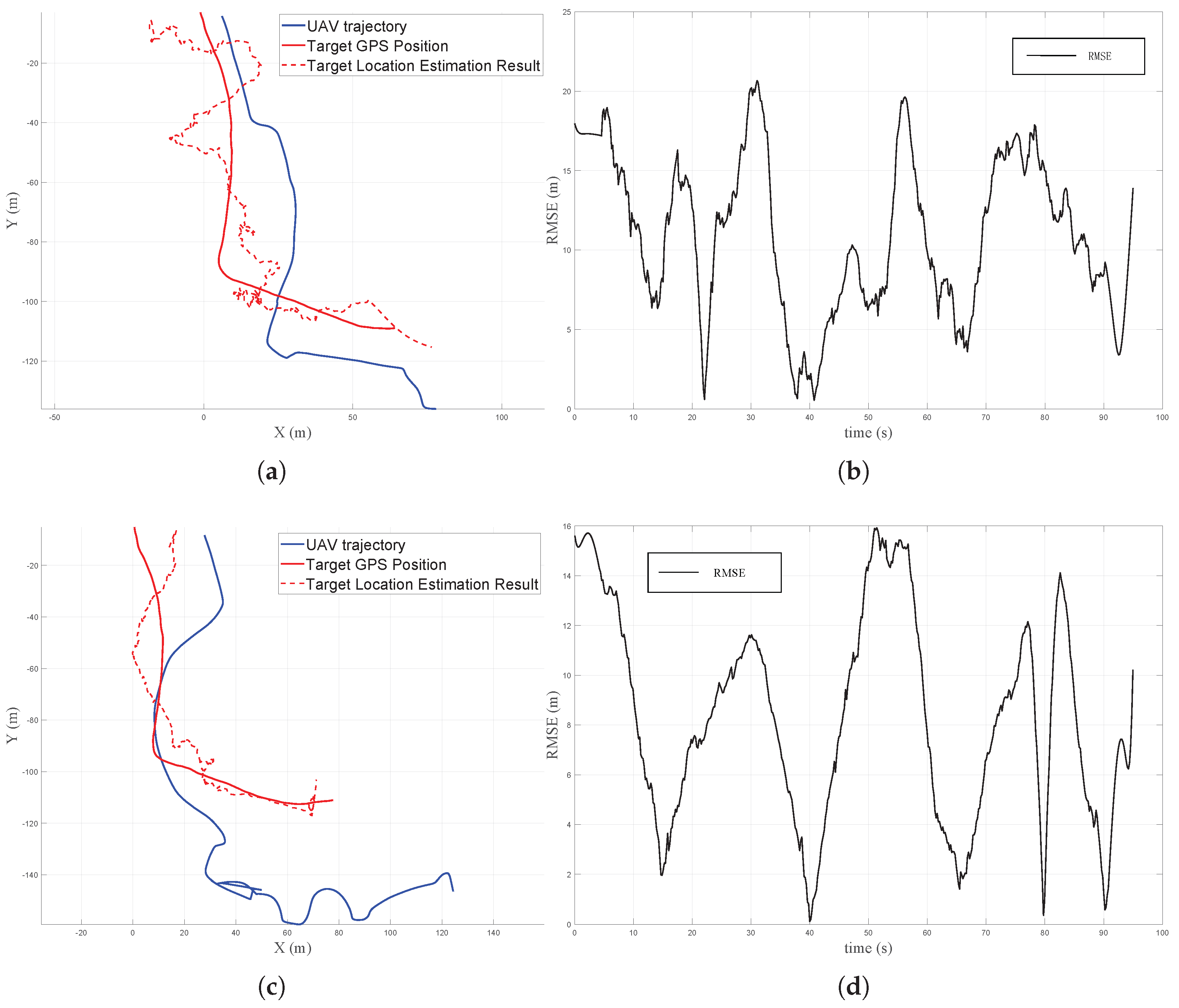
4.3. Comparative Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, Z.; Gong, W.; Jaboyedoff, M.; Chen, J.; Derron, M.-H.; Zhao, F. Landslide Identification in UAV Images Through Recognition of Landslide Boundaries and Ground Surface Cracks. Remote Sens. 2025, 17, 1900. [Google Scholar] [CrossRef]
- de Moraes, R.S.; de Freitas, E.P. Multi-UAV Based Crowd Monitoring System. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1332–1345. [Google Scholar] [CrossRef]
- Li, W.; Yan, S.; Shi, L.; Yue, J.; Shi, M.; Lin, B.; Qin, K. Multiagent Consensus Tracking Control over Asynchronous Cooperation–Competition Networks. IEEE Trans. Cybern. 2025, 55, 4347–4360. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Huang, X. A Coarse-to-Fine Weakly Supervised Learning Method for Green Plastic Cover Segmentation Using High-Resolution Remote Sensing Images. ISPRS J. Photogramm. Remote Sens. 2022, 188, 157–176. [Google Scholar] [CrossRef]
- Li, W.; Yue, J.; Shi, M.; Lin, B.; Qin, K. Neural Network-Based Dynamic Target Enclosing Control for Uncertain Nonlinear Multi-Agent Systems over Signed Networks. Neural Netw. 2025, 184, 107057. [Google Scholar] [CrossRef] [PubMed]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned Aerial Vehicles for Search and Rescue: A Survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Liu, C.; Peng, S.; Li, S.; Qiu, H.; Xia, Y.; Li, Z.; Zhao, L. A Novel EAGLe Framework for Robust UAV-View Geo-Localization. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5629917. [Google Scholar] [CrossRef]
- Zhou, S.; Fan, X.; Wang, Z.; Wang, W.; Zhang, Y. High-Order Temporal Context-Aware Aerial Tracking with Heterogeneous Visual Experts. Remote Sens. 2025, 17, 2237. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.; Cho, K.; Kim, J.; Han, D. Two-Stage Trajectory Planning for Stable Image Acquisition of a Fixed Wing UAV. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2405–2415. [Google Scholar] [CrossRef]
- Sun, N.; Zhao, J.; Shi, Q.; Liu, C.; Liu, P. Moving Target Tracking by Unmanned Aerial Vehicle: A Survey and Taxonomy. IEEE Trans. Ind. Inform. 2024, 20, 7056–7068. [Google Scholar] [CrossRef]
- Zhang, T.; Li, C.; Zhao, K.; Shen, H.; Pang, T. ROAR: A Robust Autonomous Aerial Tracking System for Challenging Scenarios. IEEE Robot. Autom. Lett. 2025, 10, 7571–7578. [Google Scholar] [CrossRef]
- Tian, R.; Ji, R.; Bai, C.; Guo, J. A Vision-Based Ground Moving Target Tracking System for Quadrotor UAVs. In Proceedings of the 2023 IEEE International Conference on Unmanned Systems (ICUS), Hefei, China, 20–22 October 2023; pp. 1750–1754. [Google Scholar] [CrossRef]
- Li, R.; Zhao, X. LSwinSR: UAV Imagery Super-Resolution Based on Linear Swin Transformer. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5641013. [Google Scholar] [CrossRef]
- Meng, C.; Yang, H.; Jiang, C.; Hu, Q.; Li, D. Improving UAV Remote Sensing Photogrammetry Accuracy Under Navigation Interference Using Anomaly Detection and Data Fusion. Remote Sens. 2025, 17, 2176. [Google Scholar] [CrossRef]
- Yang, H.; Dong, H.; Zhao, X. Safety-Critical Control Allocation for Obstacle Avoidance of Quadrotor Aerial Photography. IEEE Control Syst. Lett. 2024, 8, 1973–1978. [Google Scholar] [CrossRef]
- Savkin, A.V.; Huang, H. Navigation of a UAV Network for Optimal Surveillance of a Group of Ground Targets Moving Along a Road. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9281–9285. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, F.; Sun, Y.; Chen, X.; Wu, R. Research on Target Localization in Airborne Electro-Optical Stabilized Platforms Based on Adaptive Extended Kalman Filtering. Measurement 2024, 234, 114794. [Google Scholar] [CrossRef]
- Zhou, X.; Jia, W.; He, R.; Sun, W. High-Precision Localization Tracking and Motion State Estimation of Ground-Based Moving Target Utilizing Unmanned Aerial Vehicle High-Altitude Reconnaissance. Remote Sens. 2025, 17, 735. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, D.; Zhou, H.; Xiang, X. Moving Target Geolocation and Trajectory Prediction Using a Fixed-Wing UAV in Cluttered Environments. Remote Sens. 2025, 17, 969. [Google Scholar] [CrossRef]
- Pizani Domiciano, M.A.; Shiguemori, E.H.; Vieira Dias, L.A.; de Cunha, A.M. Particle Collision Algorithm Applied to Automatic Estimation of Digital Elevation Model From Images Captured by UAV. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1630–1634. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Li, X.; Wang, Z.; Zhang, B. UAV Image Target Localization Method Based on Outlier Filter and Frame Buffer. Chin. J. Aeronaut. 2024, 37, 375–390. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, F.; Zhou, J.; Yao, Y.; Hu, C.; Zhou, B. AIGDet: Altitude-Information-Guided Vehicle Target Detection in UAV-Based Images. IEEE Sens. J. 2024, 24, 22672–22684. [Google Scholar] [CrossRef]
- Zhang, L.; Deng, F.; Chen, J.; Bi, Y.; Phang, S.K.; Chen, X.; Chen, B.M. Vision-Based Target Three-Dimensional Geolocation Using Unmanned Aerial Vehicles. IEEE Trans. Ind. Electron. 2018, 65, 8052–8061. [Google Scholar] [CrossRef]
- Farina, A. Target Tracking with Bearings–Only Measurements. Signal Process. 1999, 78, 61–78. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Qi, B.; Hao, Y.; Li, S. Optimal Maneuver Strategy for an Autonomous Underwater Vehicle with Bearing-Only Measurements. Ocean Eng. 2023, 278, 114350. [Google Scholar] [CrossRef]
- Chu, X.; Liang, Z.; Li, Y. Trajectory Optimization for Rendezvous with Bearing-Only Tracking. Acta Astronaut. 2020, 171, 311–322. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Z.; Piao, H.; He, S. Three-Dimensional Bearing-Only Helical Homing Guidance. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4794–4807. [Google Scholar] [CrossRef]
- Li, J.; Ning, Z.; He, S.; Lee, C.-H.; Zhao, S. Three-Dimensional Bearing-Only Target Following via Observability-Enhanced Helical Guidance. IEEE Trans. Robot. 2023, 39, 1509–1526. [Google Scholar] [CrossRef]
- Ferdowsi, M.H. Observability Conditions for Target States with Bearing-Only Measurements in Three-Dimensional Case. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, International Conference on Control Applications, and International Symposium on Intelligent Control (CACSD-CCA-ISIC), Munich, Germany, 4–6 October 2006; pp. 1444–1449. [Google Scholar] [CrossRef]
- Song, T.; Speyer, J. A Stochastic Analysis of a Modified Gain Extended Kalman Filter with Applications to Estimation with Bearings-Only Measurements. IEEE Trans. Autom. Control 1985, 30, 940–949. [Google Scholar] [CrossRef]
- Zhao, S.; Zelazo, D. Bearing Rigidity Theory and Its Applications for Control and Estimation of Network Systems: Life Beyond Distance Rigidity. IEEE Control Syst. Mag. 2019, 39, 66–83. [Google Scholar] [CrossRef]
- Jiang, H.; Cai, Y.; Yu, Z. Observability Metrics for Single-Target Tracking with Bearings-Only Measurements. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1065–1077. [Google Scholar] [CrossRef]
- Woffinden, D.C.; Geller, D.K. Observability Criteria for Angles-Only Navigation. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1194–1208. [Google Scholar] [CrossRef]
- Zheng, C.; Guo, H.; Zhao, S. A Cooperative Bearing-Rate Approach for Observability-Enhanced Target Motion Estimation. In Proceedings of the 2025 IEEE International Conference on Robotics and Automation (ICRA), Atlanta, GA, USA, 19–23 May 2025; pp. 12579–12585. [Google Scholar] [CrossRef]
- Lu, J.; Ze, K.; Yue, S.; Liu, K.; Wang, W.; Sun, G. Concurrent-Learning Based Relative Localization in Shape Formation of Robot Swarms. IEEE Trans. Autom. Sci. Eng. 2025, 22, 11188–11204. [Google Scholar] [CrossRef]
- Liu, Y.; Xi, L.; Sun, Z.; Zhang, L.; Dong, W.; Lu, M.; Chen, C.; Deng, F. Air-to-Air Detection and Tracking of Non-Cooperative UAVs for 3D Reconstruction. In Proceedings of the 2024 IEEE 18th International Conference on Control & Automation (ICCA), Reykjavík, Iceland, 18–21 June 2024; pp. 936–941. [Google Scholar] [CrossRef]
- He, S.; Wang, J.; Lin, D. Three-Dimensional Bias-Compensation Pseudomeasurement Kalman Filter for Bearing-Only Measurement. J. Guid. Control Dyn. 2018, 41, 2675–2683. [Google Scholar] [CrossRef]
- Torrente, G.; Kaufmann, E.; Föhn, P.; Scaramuzza, D. Data-Driven MPC for Quadrotors. IEEE Robot. Autom. Lett. 2021, 6, 3769–3776. [Google Scholar] [CrossRef]
- Kim, J.; Suh, T.; Ryu, J. Bearings-Only Target Motion Analysis of a Highly Manoeuvring Target. IET Radar Sonar Navig. 2017, 11, 1011–1019. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Tong, S.; Qin, K.; Luo, Z.; Lin, B.; Shi, M. Low-Cost Real-Time Remote Sensing and Geolocation of Moving Targets via Monocular Bearing-Only Micro UAVs. Remote Sens. 2025, 17, 3836. https://doi.org/10.3390/rs17233836
Sun P, Tong S, Qin K, Luo Z, Lin B, Shi M. Low-Cost Real-Time Remote Sensing and Geolocation of Moving Targets via Monocular Bearing-Only Micro UAVs. Remote Sensing. 2025; 17(23):3836. https://doi.org/10.3390/rs17233836
Chicago/Turabian StyleSun, Peng, Shiji Tong, Kaiyu Qin, Zhenbing Luo, Boxian Lin, and Mengji Shi. 2025. "Low-Cost Real-Time Remote Sensing and Geolocation of Moving Targets via Monocular Bearing-Only Micro UAVs" Remote Sensing 17, no. 23: 3836. https://doi.org/10.3390/rs17233836
APA StyleSun, P., Tong, S., Qin, K., Luo, Z., Lin, B., & Shi, M. (2025). Low-Cost Real-Time Remote Sensing and Geolocation of Moving Targets via Monocular Bearing-Only Micro UAVs. Remote Sensing, 17(23), 3836. https://doi.org/10.3390/rs17233836






