Global Self-Attention-Driven Graph Clustering Ensemble
Highlights
- The proposed global self-attention-driven graph clustering ensemble (GSAGCE) effectively fuses attribute and structural information through a novel global self-attention graph autoencoder that captures long-range vertex dependencies.
- Our double-weighted graph partitioning consensus function simultaneously considers both global and local diversity within base clusterings, enhancing the overall consensus clustering performance.
- GSAGCE addresses critical limitations in existing clustering ensemble methods for graph-structured data.
- The self-supervised strategy we designed provides more reliable guidance for producing high-quality base clusterings, which can be extended to other domains requiring effective processing of complex graph-structured data.
Abstract
1. Introduction
- We propose a novel global self-attention-driven graph clustering ensemble method. In the process of capturing structural information, a novel global self-attention graph autoencoder is constructed to introduce extra expressive power to the graph convolutional network. It addresses the limitations of graph convolutional network in capturing global structural information. Moreover, the self-supervised strategy we designed can guide the learning of clustering distribution to achieve clearer boundaries and higher accuracy, significantly enhancing the clustering performance after training.
- In the ensemble strategy, a novel double-weighted graph-partitioning consensus function is devised to incorporate a global weighting uncertainty measure into a local weighting framework. Through this approach, it not only reflects the underlying relationships between clusters but also considers the differences between base clusterings, thereby enhancing the consensus clustering performance.
- The comprehensive experiments on seven benchmark datasets have demonstrated that our method significantly outperforms comparative state-of-the-art algorithms.
2. Related Work
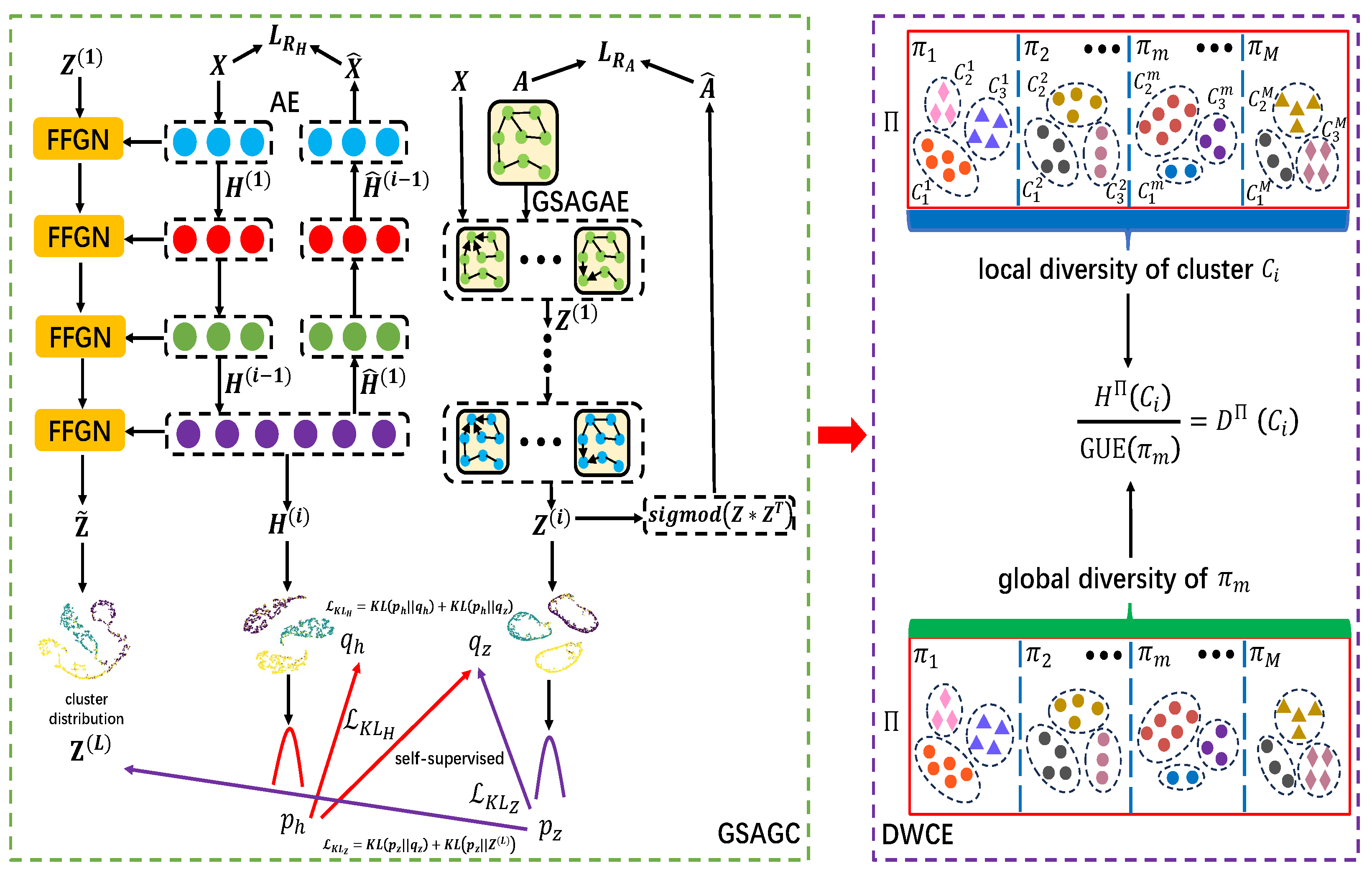
3. Global Self-Attention-Driven Graph Clustering Ensemble
3.1. Global Self-Attention-Driven Graph Clustering (GSAGC)
3.1.1. Attributed Feature Representation via Autoencoder
3.1.2. Structural Information via Global Self-Attention Graph Autoencoder
3.1.3. Feature Fusion Graph Network
3.1.4. Self-Supervised Strategy
| Algorithm 1 Training process of GSAGC |
|
3.2. Double-Weighted Clustering Ensemble (DWCE)
3.2.1. Global Uncertainty Estimation
3.2.2. Local Uncertainty Measurement
3.2.3. Hybrid Ensemble-Driven Cluster Estimation
3.3. Method Discussions
4. Experiments and Results
4.1. Datasets
4.2. Experimental Settings
4.3. Analysis of Comparison Experiment
- Clustering ensemble methods: Base clusterings employ a shallow clustering model, which can only utilize node attribute information and cannot utilize structural information.
- -
- RSEC [35] addresses the noise issue in the co-association matrix by learning a robust representation through low-rank constraint.
- -
- SECWK [36] aims to alleviate the high time and space complexities of clustering ensemble through a more efficient utilization of the co-association matrix.
- -
- LWEA and LWGP [38] consider ensemble-driven cluster uncertainty estimation and local weighting strategy in clustering ensemble.
- -
- DREC [37] uses a dense representation-based ensemble clustering algorithm by weakening the influence of outliers.
- -
- LRTCE [57] refines the co-association matrix from a global perspective through a novel constrained low-rank tensor approximation model.
- -
- ECCMS [58] utilizes a co-association matrix self-enhancement method to strengthen its quality.
- -
- ACMK [39] exploits an adaptive consensus multiple k-means method by improving the quality of base clustering.
- -
- SCCABG [40] gradually incorporates data from more reliable to less reliable sources in consensus learning using adaptive bipartite graph learning.
- -
- CEAM [41] learns an updated representation using a manifold ranking model through adaptive multiplex.
- Deep clustering methods:
- -
- AE-kmeans [59] learns embedded vectors of raw data using a basic autoencoder and then performs the k-means algorithm on the embedding.
- -
- DEC [47] utilizes denoising autoencoders for representation learning and enhances cluster cohesion through a KL divergence loss function.
- -
- IDEC [48] enhances DEC by incorporating a decoder network to preserve local structures.
- -
- SDCN [27] integrates structural information into deep clustering for the first time by transferring representations learned by autoencoders to graph convolutional networks.
- -
- DFCN [28] enhances clustering performance by dynamically combining autoencoders and graph neural networks while leveraging both attribute and structural information.
- -
- DCRN [51] is a self-supervised deep graph clustering method that addresses the issue of representation collapse during graph node encoding.
4.4. Analysis of Ablation Experiment
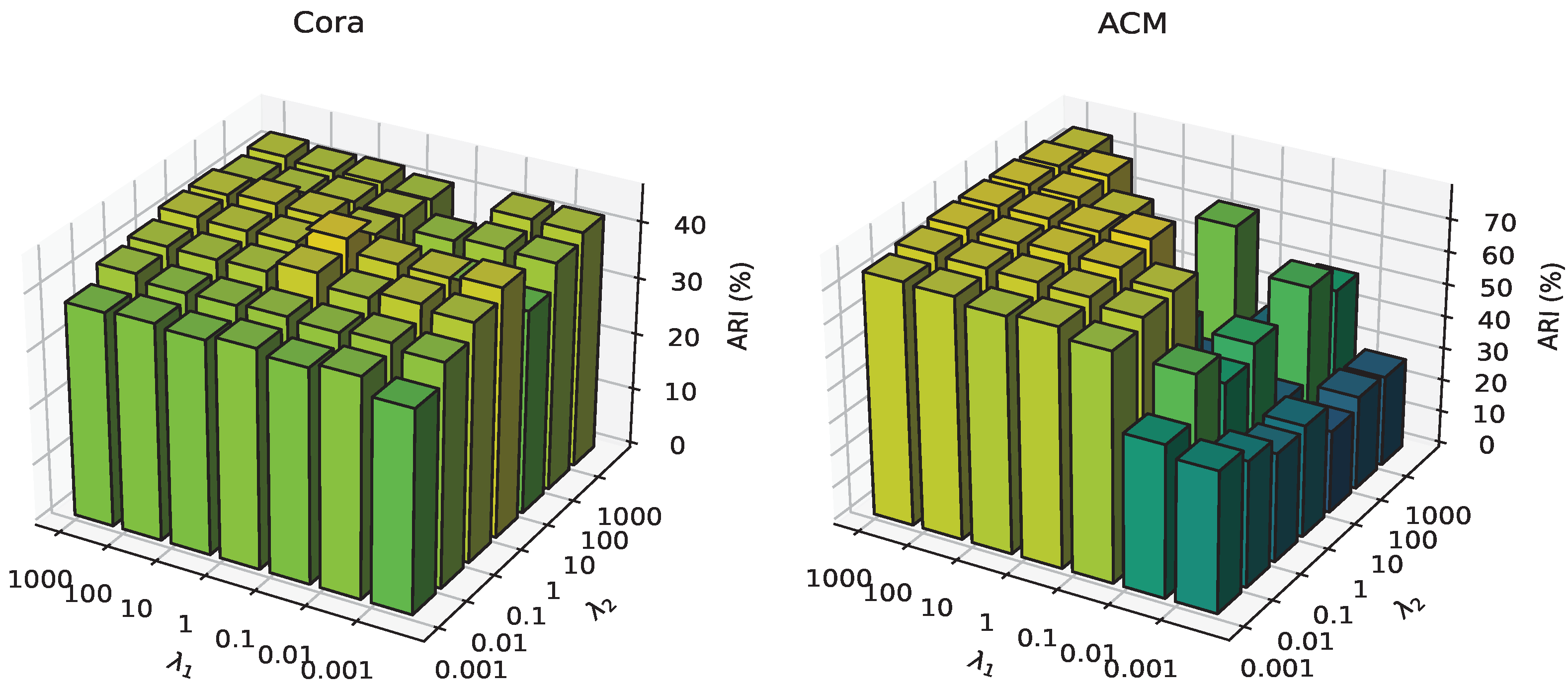
4.5. Analysis of Hyper-Parameters Sensitivity
4.6. Analysis of Visualization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.; Li, T.; Zhou, T.; Peng, Y. Deep Spatial-Spectral Subspace Clustering for Hyperspectral Images Based on Contrastive Learning. Remote Sens. 2021, 13, 4418. [Google Scholar] [CrossRef]
- Wang, W.; Wang, W.; Liu, H. Correlation-Guided Ensemble Clustering for Hyperspectral Band Selection. Remote Sens. 2022, 14, 1156. [Google Scholar] [CrossRef]
- Zhang, M. Weighted clustering ensemble: A review. Pattern Recognit. 2022, 124, 108428. [Google Scholar] [CrossRef]
- Golalipour, K.; Akbari, E.; Hamidi, S.S.; Lee, M.; Enayatifar, R. From clustering to clustering ensemble selection: A review. Eng. Appl. Artif. Intell. 2021, 104, 104388. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, H.; Li, P.; Zhang, L. Hyperspectral image clustering: Current achievements and future lines. IEEE Geosci. Remote Sens. Mag. 2021, 9, 35–67. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X. Deep spectral clustering with regularized linear embedding for hyperspectral image clustering. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509311. [Google Scholar] [CrossRef]
- Guo, D.; Zhang, S.; Zhang, J.; Yang, B.; Lin, Y. Exploring Contextual Knowledge-Enhanced Speech Recognition in Air Traffic Control Communication: A Comparative Study. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 16085–16099. [Google Scholar] [CrossRef]
- Li, J.; Deng, W.; Dang, X.; Zhao, H. Cross-Domain Adaptation Fault Diagnosis with Maximum Classifier Discrepancy and Deep Feature Alignment Under Variable Working Conditions. IEEE Trans. Reliab. 2025, 74, 4106–4115. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, X.; Wang, G. A Clustering Ensemble Method for Cell Type Detection by Multiobjective Particle Optimization. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 1–14. [Google Scholar] [CrossRef]
- Nie, X.; Qin, D.; Zhou, X.; Duo, H.; Hao, Y.; Li, B.; Liang, G. Clustering ensemble in scRNA-seq data analysis: Methods, applications and challenges. Comput. Biol. Med. 2023, 159, 106939. [Google Scholar] [CrossRef]
- Yu, J.; Kang, J. Clustering ensemble-based novelty score for outlier detection. Eng. Appl. Artif. Intell. 2023, 121, 106164. [Google Scholar] [CrossRef]
- Ray, B.; Ghosh, S.; Ahmed, S.; Sarkar, R.; Nasipuri, M. Outlier detection using an ensemble of clustering algorithms. Multimed. Tools Appl. 2022, 81, 2681–2709. [Google Scholar] [CrossRef]
- Yang, Y.; Lv, H.; Chen, N. A survey on ensemble learning under the era of deep learning. Artif. Intell. Rev. 2023, 56, 5545–5589. [Google Scholar] [CrossRef]
- Demirbaga, U.; Aujla, G.S.; Jindal, A.; Kalyon, O. Big Data Analytics: Theory, Techniques, Platforms, and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Chi, M.; Plaza, A.; Benediktsson, J.A.; Sun, Z.; Shen, J.; Zhu, Y. Big data for remote sensing: Challenges and opportunities. Proc. IEEE 2016, 104, 2207–2219. [Google Scholar] [CrossRef]
- Chen, H.; Sun, Y.; Li, X.; Zheng, B.; Chen, T. Dual-Scale Complementary Spatial-Spectral Joint Model for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 6772–6789. [Google Scholar] [CrossRef]
- Deng, W.; Shen, J.; Ding, J.; Zhao, H. Robust Dual-Model Collaborative Broad Learning System for Classification Under Label Noise Environments. IEEE Internet Things J. 2025, 12, 21055–21067. [Google Scholar] [CrossRef]
- Chunaev, P. Community detection in node-attributed social networks: A survey. Comput. Sci. Rev. 2020, 37, 100286. [Google Scholar] [CrossRef]
- Kumar, S.; Mallik, A.; Khetarpal, A.; Panda, B.S. Influence maximization in social networks using graph embedding and graph neural network. Inf. Sci. 2022, 607, 1617–1636. [Google Scholar] [CrossRef]
- Ramos, R.H.; Ferreira, C.O.L.; Simao, A. Human protein-protein interaction networks: A topological comparison review. Heliyon 2024, 10, e27278. [Google Scholar] [CrossRef]
- Jha, K.; Saha, S.; Singh, H. Prediction of protein-protein interaction using graph neural networks. Sci. Rep. 2022, 12, 8360. [Google Scholar] [CrossRef]
- Wu, L.; Cui, P.; Pei, J.; Zhao, L.; Guo, X. Graph neural networks: Foundation, frontiers and applications. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 4840–4841. [Google Scholar]
- Zhao, Q.; Li, L.; Chu, Y.; Yang, Z.; Wang, Z.; Shan, W. Efficient supervised image clustering based on density division and graph neural networks. Remote Sens. 2022, 14, 3768. [Google Scholar] [CrossRef]
- Marfo, W.; Tosh, D.K.; Moore, S.V. Enhancing Network Anomaly Detection Using Graph Neural Networks. In Proceedings of the 22nd Mediterranean Communication and Computer Networking Conference (MedComNet), Nice, France, 11–13 June 2024; pp. 1–10. [Google Scholar]
- Li, M.; Micheli, A.; Wang, Y.G.; Pan, S.; Lió, P.; Gnecco, G.S.; Sanguineti, M. Guest Editorial: Deep Neural Networks for Graphs: Theory, Models, Algorithms, and Applications. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 4367–4372. [Google Scholar] [CrossRef]
- Villaizan-Vallelado, M.; Salvatori, M.; Carro, B.; Sanchez-Esguevillas, A.J. Graph neural network contextual embedding for deep learning on tabular data. Neural Netw. 2024, 173, 106180. [Google Scholar] [CrossRef]
- Bo, D.; Wang, X.; Shi, C.; Zhu, M.; Lu, E.; Cui, P. Structural deep clustering network. In Proceedings of the Web Conference, Taipei, Taiwan, 20–24 April 2020; pp. 1400–1410. [Google Scholar]
- Tu, W.; Zhou, S.; Liu, X.; Guo, X.; Cai, Z.; Zhu, E.; Cheng, J. Deep fusion clustering network. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 9978–9987. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef]
- Yu, P.; Tan, Z.; Lu, G.; Bao, B.K. Multi-view graph convolutional network for multimedia recommendation. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 6576–6585. [Google Scholar]
- Majumdar, A. Graph structured autoencoder. Neural Netw. 2018, 106, 271–280. [Google Scholar] [CrossRef]
- Tu, W.; Liao, Q.; Zhou, S.; Peng, X.; Ma, C.; Liu, Z.; Liu, X.; Cai, Z.; He, K. RARE: Robust Masked Graph Autoencoder. IEEE Trans. Knowl. Data Eng. 2024, 36, 5340–5353. [Google Scholar] [CrossRef]
- Jurek, A.; Bi, Y.; Wu, S.; Nugent, C. A survey of commonly used ensemble-based classification techniques. Knowl. Eng. Rev. 2014, 29, 551–581. [Google Scholar] [CrossRef]
- Vega-Pons, S.; Ruiz-Shulcloper, J. A survey of clustering ensemble algorithms. Int. J. Pattern Recognit. Artif. Intell. 2011, 25, 337–372. [Google Scholar] [CrossRef]
- Tao, Z.; Liu, H.; Li, S.; Fu, Y. Robust spectral ensemble clustering. In Proceedings of the 25th ACM International on Conference on Information and Knowledge Management, Indianapolis, IN, USA, 24–28 October 2016; pp. 367–376. [Google Scholar]
- Liu, H.; Wu, J.; Liu, T.; Tao, D.; Fu, Y. Spectral ensemble clustering via weighted k-means: Theoretical and practical evidence. IEEE Trans. Knowl. Data Eng. 2017, 29, 1129–1143. [Google Scholar] [CrossRef]
- Zhou, J.; Zheng, H.; Pan, L. Ensemble clustering based on dense representation. Neurocomputing 2019, 357, 66–76. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Lai, J.H. Locally weighted ensemble clustering. IEEE Trans. Cybern. 2017, 48, 1460–1473. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Du, L.; Li, X. Adaptive consensus clustering for multiple k-means via base results refining. IEEE Trans. Knowl. Data Eng. 2023, 35, 10251–10264. [Google Scholar] [CrossRef]
- Zhou, P.; Liu, X.; Du, L.; Li, X. Self-paced adaptive bipartite graph learning for consensus clustering. ACM Trans. Knowl. Discov. Data 2023, 17, 62. [Google Scholar] [CrossRef]
- Zhou, P.; Hu, B.; Yan, D.; Du, L. Clustering ensemble via diffusion on adaptive multiplex. IEEE Trans. Knowl. Data Eng. 2024, 36, 1463–1474. [Google Scholar] [CrossRef]
- Ren, Y.; Pu, J.; Yang, Z.; Xu, J.; Li, G.; Pu, X.; Philip, S.Y.; He, L. Deep clustering: A comprehensive survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 5858–5878. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, W.; Ou-Yang, L.; Wang, R.; Kwong, S. GRESS: Grouping Belief-Based Deep Contrastive Subspace Clustering. IEEE Trans. Cybern. 2024, 55, 148–160. [Google Scholar] [CrossRef]
- Ye, X.; Zhao, J.; Zhang, L.; Guo, L. A nonparametric deep generative model for multimanifold clustering. IEEE Trans. Cybern. 2019, 49, 2664–2677. [Google Scholar] [CrossRef]
- Chen, R.; Tang, Y.; Tian, L.; Zhang, C.; Zhang, W. Deep convolutional self-paced clustering. Appl. Intell. 2022, 52, 4858–4872. [Google Scholar]
- Cai, J.; Zhang, Y.; Wang, S.; Fan, J.; Guo, W. Wasserstein Embedding Learning for Deep Clustering: A Generative Approach. IEEE Trans. Multimed. 2024, 26, 7567–7580. [Google Scholar] [CrossRef]
- Xie, J.; Girshick, R.; Farhadi, A. Unsupervised deep embedding for clustering analysis. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 478–487. [Google Scholar]
- Guo, X.; Gao, L.; Liu, X.; Yin, J. Improved deep embedded clustering with local structure preservation. In Proceedings of the International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 1753–1759. [Google Scholar]
- Guo, X.; Liu, X.; Zhu, E.; Yin, J. Deep clustering with convolutional autoencoders. In Proceedings of the 24th International Conference on Neural Information Processing, Guangzhou, China, 14–18 November 2017; pp. 373–382. [Google Scholar]
- Alqahtani, A.; Xie, X.; Deng, J.; Jones, M. A deep convolutional auto-encoder with embedded clustering. In Proceedings of the 25th IEEE International Conference on Image Processing, Athens, Greece, 7–10 October 2018; pp. 4058–4062. [Google Scholar]
- Liu, Y.; Tu, W.; Zhou, S.; Liu, X.; Song, L.; Yang, X.; Zhu, E. Deep graph clustering via dual correlation reduction. In Proceedings of the AAAI Conference on Artificial Intelligence, Tel-Aviv, Israel, 22 February–1 March 2022; Volume 36, No. 7. pp. 7603–7611. [Google Scholar]
- Akkem, Y.; Biswas, S.K.; Varanasi, A. A comprehensive review of synthetic data generation in smart farming by using variational autoencoder and generative adversarial network. Eng. Appl. Artif. Intell. 2024, 131, 107881. [Google Scholar] [CrossRef]
- Shirazi, H.; Muramudalige, S.R.; Ray, I.; Jayasumana, A.P.; Wang, H. Adversarial autoencoder data synthesis for enhancing machine learning-based phishing detection algorithms. IEEE Trans. Serv. Comput. 2023, 16, 2411–2422. [Google Scholar] [CrossRef]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Pan, S.; Hu, R.; Fung, S.F.; Long, G.; Jiang, J.; Zhang, C. Learning graph embedding with adversarial training methods. IEEE Trans. Cybern. 2020, 50, 2475–2487. [Google Scholar] [CrossRef]
- Oyewole, G.J.; Thopil, G.A. Data clustering: Application and trends. Artif. Intell. Rev. 2023, 56, 6439–6475. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Liu, H.; Hou, J.; Zhang, Q. Clustering ensemble meets low-rank tensor approximation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, No. 9. pp. 7970–7978. [Google Scholar]
- Jia, Y.; Tao, S.; Wang, R.; Wang, Y. Ensemble clustering via co-association matrix self-enhancement. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11168–11179. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]

| Notations | Descriptions |
|---|---|
| The attribute feature data matrix | |
| The graph structure | |
| The number of clusters | |
| The node set and the edge set | |
| The original adjacency matrix | |
| The i-th layer encoder part of autoencoder | |
| The dimension of the i-th layer network | |
| The i-th layer decoder part of autoencoder | |
| The global self-attention representation | |
| The representation of GSAGAE | |
| The reconstruction of graph adjacency structure | |
| The attention coefficient matrix of FFGN | |
| The fused representation of AE and GSAGAE | |
| The clustering probability distribution | |
| The similarity between and cluster center | |
| The auxiliary distribution of | |
| The similarity between and cluster center | |
| The auxiliary distribution of | |
| The clustering ensemble set | |
| M | The number of base clusterings |
| The m-th base clustering | |
| The number of clusters for | |
| The similarity between and | |
| The global uncertainty estimation of | |
| The uncertainty of cluster | |
| The hybrid ensemble-driven cluster estimation of |
| Data Name | Sample | Feature | Category | Type | Edges |
|---|---|---|---|---|---|
| Cora | 2708 | 1433 | 7 | graph | 5278 |
| ACM | 3025 | 1870 | 3 | graph | 13,128 |
| Pubmed | 19,717 | 500 | 3 | graph | 44,326 |
| IMDB | 4780 | 1232 | 2 | graph | 49,005 |
| USPS | 9298 | 256 | 10 | image | - |
| HAR | 10,299 | 561 | 6 | record | - |
| REUT | 10,000 | 2000 | 4 | text | - |
| Method | Metrics | Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| Cora | ACM | Pubmed | IMDB | USPS | HAR | REUT | ||
| RSEC | ACC | 33.62 ± 3.23 | 66.89 ± 1.88 | 50.65 ± 7.48 | 62.17 ± 5.88 | 57.17 ± 4.63 | 67.13 ± 4.98 | 60.63 ± 6.40 |
| NMI | 12.63 ± 2.13 | 33.36 ± 1.17 | 15.86 ± 7.16 | 1.20 ± 0.46 | 60.51 ± 3.40 | 67.38 ± 5.01 | 40.44 ± 8.29 | |
| ARI | 8.88 ± 1.98 | 30.93 ± 1.11 | 13.20 ± 8.16 | −3.87 ± 0.81 | 46.39 ± 5.36 | 57.11 ± 5.58 | 34.01 ± 13.09 | |
| F1 | 31.43 ± 3.41 | 67.10 ± 2.03 | 49.16 ± 11.48 | 44.15 ± 0.88 | 52.81 ± 4.69 | 64.69 ± 7.06 | 53.57 ± 7.23 | |
| SECWK | ACC | 34.95 ± 2.28 | 58.91 ± 7.37 | 51.86 ± 6.65 | 74.79 ± 1.78 | 53.52 ± 5.79 | 49.01 ± 5.57 | 67.80 ± 10.58 |
| NMI | 14.95 ± 2.18 | 22.33 ± 8.59 | 21.11 ± 11.09 | 0.34 ± 0.29 | 54.53 ± 4.84 | 51.25 ± 8.77 | 43.14 ± 11.62 | |
| ARI | 9.25 ± 2.00 | 19.83 ± 8.26 | 17.98 ± 11.63 | −0.68 ± 1.75 | 35.47 ± 8.94 | 32.44 ± 10.60 | 40.76 ± 16.86 | |
| F1 | 29.76 ± 2.57 | 55.79 ± 10.01 | 43.28 ± 12.37 | 44.64 ± 1.78 | 51.22 ± 6.32 | 45.66 ± 6.19 | 54.57 ± 13.69 | |
| LWEA | ACC | 35.67 ± 2.94 | 73.36 ± 2.65 | 52.44 ± 4.19 | 74.03 ± 0.18 | 74.05 ± 2.37 | 69.37 ± 6.29 | 67.24 ± 7.85 |
| NMI | 16.34 ± 3.04 | 38.94 ± 2.69 | 15.49 ± 5.32 | 0.45 ± 0.05 | 75.67 ± 1.15 | 74.91 ± 1.88 | 48.54 ± 5.44 | |
| ARI | 8.62 ± 2.60 | 37.52 ± 3.06 | 14.44 ± 7.41 | −2.08 ± 0.14 | 67.68 ± 2.59 | 63.92 ± 3.50 | 45.04 ± 10.72 | |
| F1 | 26.09 ± 5.73 | 73.55 ± 2.59 | 49.17 ± 6.28 | 43.99 ± 0.08 | 71.53 ± 2.78 | 63.23 ± 8.51 | 56.33 ± 8.82 | |
| LWGP | ACC | 32.95 ± 3.06 | 65.57 ± 1.94 | 46.08 ± 4.31 | 74.18 ± 0.41 | 73.44 ± 5.46 | 65.41 ± 3.39 | 55.18 ± 7.11 |
| NMI | 15.13 ± 1.98 | 32.69 ± 0.68 | 6.92 ± 2.92 | 0.36 ± 0.14 | 75.84 ± 1.15 | 69.61 ± 1.81 | 39.73 ± 10.02 | |
| ARI | 7.60 ± 2.52 | 30.07 ± 1.06 | 4.51 ± 4.72 | −1.76 ± 0.38 | 67.48 ± 4.36 | 59.27 ± 2.16 | 27.73 ± 10.58 | |
| F1 | 25.69 ± 4.08 | 65.73 ± 2.02 | 38.03 ± 7.66 | 44.21 ± 0.59 | 70.80 ± 6.45 | 59.76 ± 4.31 | 41.14 ± 9.09 | |
| DREC | ACC | 36.91 ± 2.16 | 69.64 ± 1.85 | 47.29 ± 4.11 | 74.02 ± 0.88 | 68.13 ± 2.85 | 71.93 ± 3.39 | 74.46 ± 3.59 |
| NMI | 16.77 ± 2.42 | 35.43 ± 1.60 | 8.24 ± 3.93 | 0.50 ± 0.17 | 68.75 ± 1.23 | 68.89 ± 2.32 | 47.97 ± 5.56 | |
| ARI | 11.83 ± 2.10 | 33.31 ± 2.08 | 5.30 ± 5.22 | −2.13 ± 0.58 | 57.28 ± 1.98 | 59.45 ± 2.85 | 50.65 ± 9.55 | |
| F1 | 34.79 ± 2.37 | 69.93 ± 1.82 | 37.38 ± 6.81 | 43.88 ± 0.17 | 66.67 ± 3.66 | 70.79 ± 4.85 | 62.31 ± 4.56 | |
| LRTCE | ACC | 29.03 ± 9.68 | 68.40 ± 7.31 | 59.54 ± 8.39 | 57.59 ± 4.28 | 65.56 ± 2.16 | 56.91 ± 4.39 | 68.17 ± 8.12 |
| NMI | 9.72 ± 8.34 | 34.24 ± 6.61 | 31.19 ± 7.21 | 0.22 ± 0.30 | 62.06 ± 0.89 | 60.20 ± 0.71 | 48.49 ± 8.88 | |
| ARI | 7.05 ± 6.17 | 31.96 ± 6.45 | 28.05 ± 8.67 | −1.04 ± 1.17 | 53.58 ± 1.71 | 44.22 ± 2.59 | 42.27 ± 11.66 | |
| F1 | 27.39 ± 9.50 | 68.78 ± 7.33 | 58.21 ± 9.03 | 47.32 ± 1.43 | 63.42 ± 2.26 | 55.00 ± 4.70 | 58.62 ± 4.65 | |
| ECCMS | ACC | 30.29 ± 0.03 | 35.04 ± 0.19 | 40.93 ± 2.10 | 73.85 ± 0.41 | 46.72 ± 11.49 | 39.50 ± 7.88 | 43.27 ± 6.64 |
| NMI | 0.48 ± 0.05 | 0.26 ± 0.23 | 1.38 ± 1.66 | 0.48 ± 0.28 | 60.15 ± 12.24 | 57.47 ± 6.34 | 17.45 ± 7.20 | |
| ARI | 0.03 ± 0.03 | 0.02 ± 0.02 | 0.44 ± 0.80 | −2.07 ± 0.67 | 40.02 ± 14.39 | 36.44 ± 7.62 | 3.04 ± 9.72 | |
| F1 | 6.91 ± 0.08 | 17.61 ± 0.25 | 22.15 ± 3.73 | 44.16 ± 0.72 | 28.51 ± 11.62 | 24.92 ± 9.22 | 25.75 ± 7.87 | |
| ACMK | ACC | 18.47 ± 0.95 | 36.67 ± 2.68 | 39.89 ± 1.62 | 51.14 ± 0.94 | 63.03 ± 3.28 | 47.32 ± 7.31 | 35.76 ± 6.77 |
| NMI | 1.18 ± 0.29 | 0.88 ± 1.44 | 2.51 ± 0.84 | 0.08 ± 0.05 | 59.16 ± 3.32 | 44.44 ± 7.72 | 8.71 ± 11.16 | |
| ARI | 0.45 ± 0.16 | 0.87 ± 1.54 | 1.92 ± 0.84 | 0.02 ± 0.13 | 51.10 ± 3.22 | 30.08 ± 8.52 | 6.50 ± 7.70 | |
| F1 | 17.59 ± 0.81 | 36.61 ± 2.63 | 39.94 ± 1.70 | 47.14 ± 0.98 | 60.49 ± 3.75 | 45.84 ± 7.43 | 32.03 ± 4.98 | |
| SCCABG | ACC | 30.79 ± 0.75 | 35.09 ± 0.05 | 40.24 ± 0.45 | 73.10 ± 0.90 | 37.72 ± 20.66 | - | 39.16 ± 0.01 |
| NMI | 1.61 ± 1.42 | 0.15 ± 0.04 | 0.94 ± 0.80 | 0.15 ± 0.14 | 35.84 ± 34.46 | - | 14.43 ± 1.46 | |
| ARI | 0.15 ± 0.15 | 0.31 ± 0.05 | 0.02 ± 0.10 | −0.44 ± 0.75 | 25.95 ± 25.89 | - | −2.06 ± 0.16 | |
| F1 | 8.20 ± 3.41 | 17.39 ± 0.07 | 20.26 ± 1.07 | 43.53 ± 0.21 | 24.60 ± 20.86 | - | 21.21 ± 0.16 | |
| CEAM | ACC | 28.37 ± 2.15 | 59.45 ± 7.21 | 41.06 ± 2.27 | 69.28 ± 2.02 | 47.65 ± 14.09 | 55.41 ± 5.59 | 48.03 ± 10.52 |
| NMI | 10.56 ± 1.52 | 21.72 ± 7.41 | 0.51 ± 0.55 | 0.68 ± 0.03 | 50.67 ± 13.57 | 59.27 ± 4.31 | 27.68 ± 13.12 | |
| ARI | 5.96 ± 2.19 | 20.96 ± 7.11 | 0.29 ± 0.60 | −3.62 ± 0.23 | 36.24 ± 15.67 | 44.01 ± 6.29 | 15.79 ± 15.21 | |
| F1 | 23.02 ± 1.11 | 59.42 ± 7.63 | 22.48 ± 5.57 | 45.01 ± 0.47 | 38.23 ± 18.60 | 51.28 ± 6.48 | 35.95 ± 11.89 | |
| GSAGCE | ACC | 69.08 ± 2.21 | 91.76 ± 1.03 | 63.57 ± 3.21 | 75.27 ± 2.32 | 74.38 ± 2.23 | 82.47 ± 1.13 | 76.63 ± 1.86 |
| NMI | 51.22 ± 1.47 | 72.00 ± 0.86 | 23.30 ± 2.46 | 4.27 ± 1.02 | 75.89 ± 1.36 | 82.91 ± 1.85 | 50.26 ± 2.18 | |
| ARI | 45.46 ± 1.36 | 78.49 ± 0.70 | 23.28 ± 3.01 | 13.71 ± 1.54 | 67.85 ± 2.40 | 74.89 ± 2.91 | 53.89 ± 2.03 | |
| F1 | 65.44 ± 2.04 | 91.77 ± 0.92 | 63.79 ± 2.89 | 58.56 ± 2.11 | 72.72 ± 1.87 | 81.78 ± 2.58 | 65.38 ± 2.87 | |
| Dataset | Metrics | AE-kmeans | DEC | IDEC | SDCN | DFCN | DCRN | GSAGCE |
|---|---|---|---|---|---|---|---|---|
| Cora | ACC | 35.44 ± 2.12 | 45.53 ± 2.23 | 45.20 ± 1.74 | 46.76 ± 6.00 | 44.67 ± 4.85 | 54.90 ± 8.37 | 69.08 ± 2.21 |
| NMI | 14.52 ± 2.02 | 24.26 ± 1.94 | 25.44 ± 1.81 | 27.17 ± 4.45 | 33.09 ± 7.39 | 45.55 ± 6.41 | 51.22 ± 1.47 | |
| ARI | 10.69 ± 1.72 | 19.21 ± 1.87 | 18.82 ± 2.08 | 21.67 ± 4.69 | 28.70 ± 5.24 | 33.43 ± 7.64 | 45.46 ± 1.36 | |
| F1 | 33.43 ± 2.09 | 44.11 ± 2.32 | 45.00 ± 1.78 | 39.90 ± 5.69 | 27.43 ± 4.92 | 48.01 ± 9.00 | 65.44 ± 2.04 | |
| ACM | ACC | 56.03 ± 6.59 | 59.63 ± 6.76 | 73.57 ± 7.46 | 87.56 ± 1.44 | 90.77 ± 0.25 | 90.93 ± 0.42 | 91.76 ± 1.03 |
| NMI | 19.18 ± 3.12 | 22.84 ± 4.78 | 36.64 ± 8.03 | 62.24 ± 2.77 | 69.32 ± 0.63 | 69.66 ± 0.95 | 72.00 ± 0.86 | |
| ARI | 18.61 ± 3.79 | 21.50 ± 5.36 | 39.94 ± 10.15 | 67.22 ± 3.19 | 74.77 ± 0.62 | 75.13 ± 1.07 | 78.49 ± 0.70 | |
| F1 | 55.97 ± 6.71 | 59.94 ± 6.89 | 73.38 ± 7.72 | 87.46 ± 1.51 | 90.71 ± 0.26 | 90.93 ± 0.39 | 91.77 ± 0.92 | |
| Pubmed | ACC | 53.42 ± 6.32 | 57.48 ± 4.73 | 57.11 ± 3.39 | 57.70 ± 4.77 | 50.67 ± 0.36 | oom | 63.57 ± 3.21 |
| NMI | 17.17 ± 4.50 | 20.46 ± 3.38 | 19.73 ± 2.67 | 17.72 ± 4.59 | 6.80 ± 0.20 | oom | 23.30 ± 2.46 | |
| ARI | 14.26 ± 4.94 | 17.42 ± 4.25 | 16.26 ± 3.13 | 15.15 ± 5.03 | 6.75 ± 0.36 | oom | 23.28 ± 3.01 | |
| F1 | 53.62 ± 6.54 | 57.94 ± 5.17 | 57.38 ± 3.62 | 58.06 ± 5.50 | 41.23 ± 0.35 | oom | 63.79 ± 2.89 | |
| IMDB | ACC | 52.67 ± 1.55 | 52.73 ± 1.37 | 52.28 ± 1.98 | 53.35 ± 2.47 | 67.94 ± 9.65 | 71.34 ± 0.65 | 75.27 ± 2.32 |
| NMI | 0.23 ± 0.27 | 0.88 ± 0.87 | 0.98 ± 1.10 | 1.94 ± 0.99 | 2.19 ± 1.52 | 0.43 ± 0.29 | 4.27 ± 1.02 | |
| ARI | 0.10 ± 0.37 | −0.33 ± 0.33 | 0.03 ± 0.72 | −0.02 ± 1.43 | 1.09 ± 2.29 | −2.58 ± 1.15 | 13.71 ± 1.54 | |
| F1 | 47.76 ± 1.93 | 47.86 ± 2.72 | 48.10 ± 3.34 | 50.27 ± 3.48 | 48.98 ± 5.34 | 45.44 ± 1.01 | 58.56 ± 2.11 | |
| USPS | ACC | 65.90 ± 3.17 | 66.97 ± 2.80 | 71.25 ± 3.30 | 72.74 ± 5.08 | 73.51 ± 0.30 | 23.43 ± 3.72 | 74.38 ± 2.23 |
| NMI | 63.65 ± 1.98 | 65.07 ± 1.26 | 73.61 ± 1.70 | 75.78 ± 2.53 | 75.49 ± 0.18 | 16.32 ± 7.63 | 75.89 ± 1.36 | |
| ARI | 55.39 ± 2.47 | 56.87 ± 1.74 | 64.17 ± 2.57 | 67.54 ± 4.10 | 67.45 ± 0.30 | 3.21 ± 5.62 | 67.85 ± 2.40 | |
| F1 | 63.71 ± 4.22 | 64.99 ± 3.60 | 69.26 ± 4.87 | 70.43 ± 6.68 | 72.42 ± 0.35 | 15.14 ± 0.45 | 72.72 ± 1.87 | |
| HAR | ACC | 62.94 ± 6.19 | 62.63 ± 3.23 | 70.91 ± 4.79 | 62.66 ± 5.52 | 77.26 ± 6.44 | 41.41 ± 2.51 | 82.47 ± 1.13 |
| NMI | 57.41 ± 3.21 | 62.14 ± 2.99 | 77.00 ± 4.72 | 67.62 ± 2.42 | 81.09 ± 4.93 | 51.27 ± 0.64 | 82.91 ± 1.85 | |
| ARI | 49.71 ± 3.37 | 53.25 ± 3.27 | 66.75 ± 4.59 | 53.26 ± 3.81 | 71.29 ± 6.05 | 30.65 ± 1.52 | 74.89 ± 2.91 | |
| F1 | 60.53 ± 7.33 | 60.82 ± 3.99 | 68.12 ± 5.27 | 54.17 ± 7.48 | 76.34 ± 7.91 | 34.17 ± 2.43 | 81.78 ± 2.58 | |
| REUT | ACC | 56.69 ± 3.98 | 56.39 ± 2.23 | 59.72 ± 2.80 | 61.33 ± 6.09 | 63.82 ± 5.23 | 50.34 ± 4.61 | 76.63 ± 1.86 |
| NMI | 27.77 ± 4.12 | 28.24 ± 3.45 | 34.54 ± 2.89 | 37.21 ± 10.39 | 41.23 ± 4.36 | 22.56 ± 8.51 | 50.26 ± 2.18 | |
| ARI | 26.40 ± 5.01 | 26.49 ± 3.39 | 30.63 ± 3.33 | 36.20 ± 11.11 | 42.52 ± 6.72 | 15.99 ± 6.40 | 53.89 ± 2.03 | |
| F1 | 51.79 ± 4.27 | 51.51 ± 2.49 | 54.26 ± 3.73 | 54.07 ± 9.14 | 57.86 ± 6.18 | 33.31 ± 3.81 | 65.38 ± 2.87 |
| Dataset | Metrics | noGSA | noKLh | noKLz | noHECE | GSAGCE |
|---|---|---|---|---|---|---|
| Cora | ACC | 66.84 ± 1.72 | 66.46 ± 1.46 | 47.41 ± 5.73 | 67.14 ± 1.89 | 69.08 ± 2.21 |
| NMI | 47.45 ± 1.63 | 46.15 ± 1.44 | 28.72 ± 4.64 | 50.41 ± 2.01 | 51.22 ± 1.47 | |
| ARI | 42.69 ± 1.24 | 43.15 ± 2.16 | 20.35 ± 5.78 | 43.84 ± 1.56 | 45.46 ± 1.36 | |
| F1 | 62.09 ± 0.53 | 61.20 ± 1.24 | 35.86 ± 5.20 | 64.81 ± 2.47 | 65.44 ± 2.04 | |
| ACM | ACC | 91.21 ± 0.83 | 65.78 ± 1.76 | 75.30 ± 6.32 | 91.23 ± 0.86 | 91.76 ± 1.03 |
| NMI | 69.84 ± 2.04 | 28.94 ± 5.04 | 47.22 ± 10.01 | 70.58 ± 0.63 | 72.00 ± 0.86 | |
| ARI | 75.90 ± 2.03 | 25.66 ± 3.91 | 48.34 ± 11.03 | 76.82 ± 1.05 | 78.49 ± 0.70 | |
| F1 | 91.26 ± 0.86 | 66.61 ± 1.70 | 72.62 ± 7.70 | 91.20 ± 1.14 | 91.77 ± 0.92 | |
| Pubmed | ACC | 61.58 ± 2.86 | 60.17 ± 3.05 | 52.05 ± 2.41 | 60.32 ± 2.68 | 63.57 ± 3.21 |
| NMI | 20.00 ± 2.12 | 12.42 ± 2.24 | 16.42 ± 1.79 | 20.16 ± 2.43 | 23.30 ± 2.46 | |
| ARI | 18.69 ± 2.65 | 14.96 ± 3.14 | 17.75 ± 2.86 | 20.16 ± 2.79 | 23.28 ± 3.01 | |
| F1 | 61.80 ± 2.25 | 55.13 ± 3.39 | 48.11 ± 2.91 | 60.58 ± 2.93 | 63.79 ± 2.89 | |
| IMDB | ACC | 71.69 ± 0.23 | 72.35 ± 2.33 | 66.78 ± 6.87 | 74.30 ± 2.46 | 75.27 ± 2.32 |
| NMI | 3.44 ± 0.23 | 3.72 ± 1.59 | 0.37 ± 2.72 | 3.94 ± 0.67 | 4.27 ± 1.02 | |
| ARI | 9.98 ± 6.44 | 9.55 ± 3.79 | 0.91 ± 4.80 | 11.89 ± 1.94 | 13.71 ± 1.54 | |
| F1 | 55.31 ± 7.25 | 54.28 ± 4.20 | 43.31 ± 7.22 | 57.86 ± 2.33 | 58.56 ± 2.11 | |
| USPS | ACC | 72.45 ± 3.51 | 68.83 ± 6.87 | 53.37 ± 4.33 | 73.83 ± 2.10 | 74.38 ± 2.23 |
| NMI | 72.08 ± 6.02 | 65.78 ± 2.72 | 56.29 ± 4.94 | 75.32 ± 1.17 | 75.89 ± 1.36 | |
| ARI | 63.10 ± 5.57 | 57.10 ± 4.80 | 39.17 ± 6.65 | 67.51 ± 2.32 | 67.85 ± 2.40 | |
| F1 | 65.79 ± 6.68 | 67.27 ± 7.22 | 43.36 ± 6.14 | 72.12 ± 2.06 | 72.72 ± 1.87 | |
| HAR | ACC | 80.32 ± 1.27 | 78.66 ± 1.51 | 63.06 ± 4.85 | 81.36 ± 0.68 | 82.47 ± 1.13 |
| NMI | 80.88 ± 1.53 | 71.06 ± 1.49 | 61.99 ± 3.42 | 81.76 ± 1.20 | 82.91 ± 1.85 | |
| ARI | 72.36 ± 3.06 | 63.38 ± 2.83 | 47.41 ± 4.58 | 72.54 ± 2.87 | 74.89 ± 2.91 | |
| F1 | 80.42 ± 3.22 | 77.88 ± 2.53 | 55.16 ± 5.57 | 80.64 ± 3.05 | 81.78 ± 2.58 | |
| REUT | ACC | 49.85 ± 1.47 | 39.36 ± 1.82 | 47.54 ± 2.25 | 75.31 ± 2.28 | 76.63 ± 1.86 |
| NMI | 14.33 ± 1.29 | 3.10 ± 3.55 | 3.66 ± 2.56 | 48.88 ± 2.53 | 50.26 ± 2.18 | |
| ARI | 7.55 ± 1.57 | 1.23 ± 2.61 | 7.37 ± 3.00 | 52.79 ± 2.76 | 53.89 ± 2.03 | |
| F1 | 32.65 ± 2.51 | 26.79 ± 4.96 | 32.02 ± 6.14 | 64.90 ± 3.05 | 65.38 ± 2.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Yao, S.; Huang, Y.; Xiao, L.; Cheng, Y.; Qian, Y. Global Self-Attention-Driven Graph Clustering Ensemble. Remote Sens. 2025, 17, 3680. https://doi.org/10.3390/rs17223680
Zeng L, Yao S, Huang Y, Xiao L, Cheng Y, Qian Y. Global Self-Attention-Driven Graph Clustering Ensemble. Remote Sensing. 2025; 17(22):3680. https://doi.org/10.3390/rs17223680
Chicago/Turabian StyleZeng, Lingbin, Shixin Yao, You Huang, Liquan Xiao, Yong Cheng, and Yue Qian. 2025. "Global Self-Attention-Driven Graph Clustering Ensemble" Remote Sensing 17, no. 22: 3680. https://doi.org/10.3390/rs17223680
APA StyleZeng, L., Yao, S., Huang, Y., Xiao, L., Cheng, Y., & Qian, Y. (2025). Global Self-Attention-Driven Graph Clustering Ensemble. Remote Sensing, 17(22), 3680. https://doi.org/10.3390/rs17223680







