Geographically Weighted Quantile Machine Learning for Probabilistic Soil Moisture Prediction from Spatially Resolved Remote Sensing
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
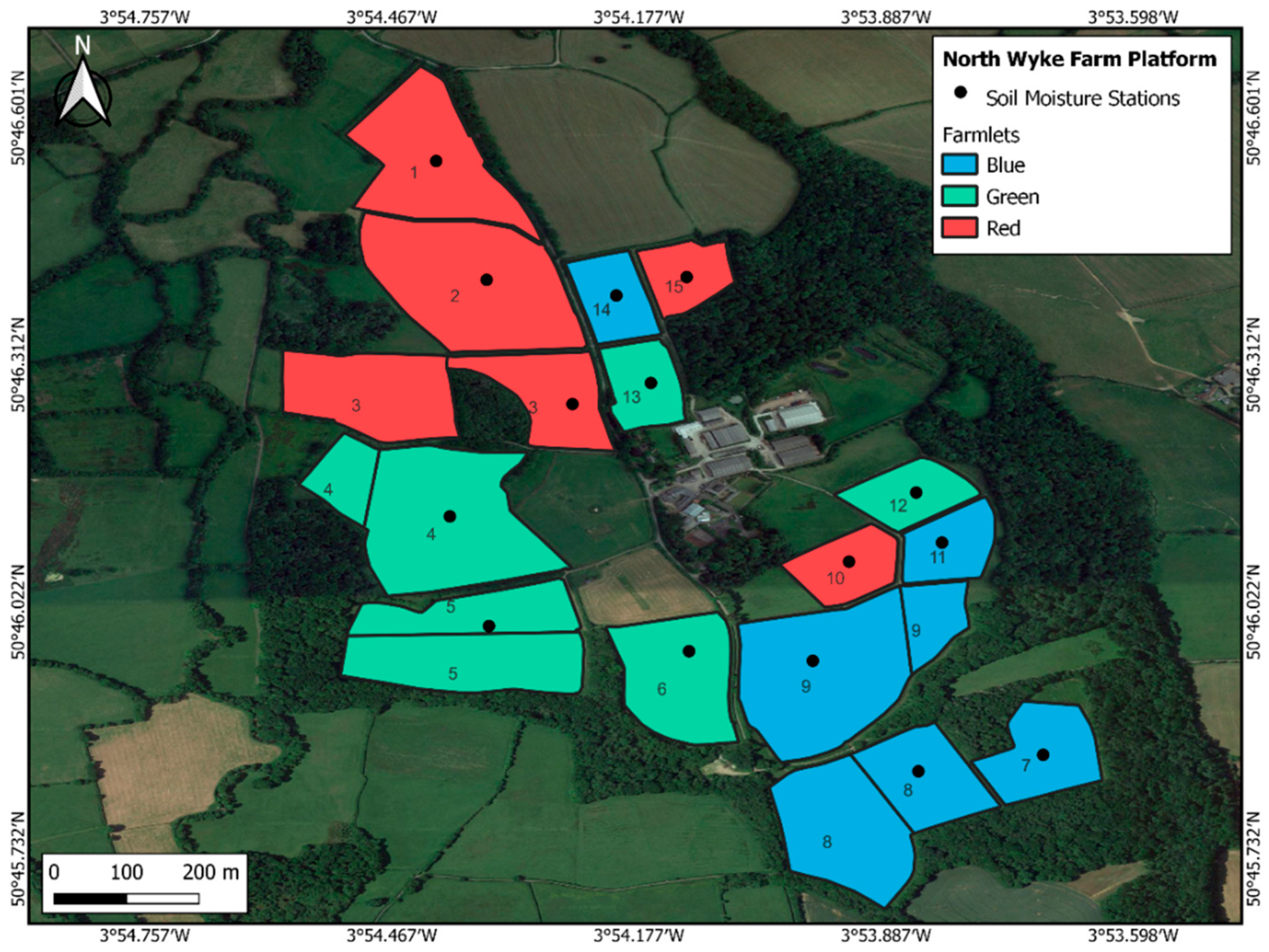
2.2. Soil Moisture Data
2.3. Satellite-Derived and Temporal Predictors
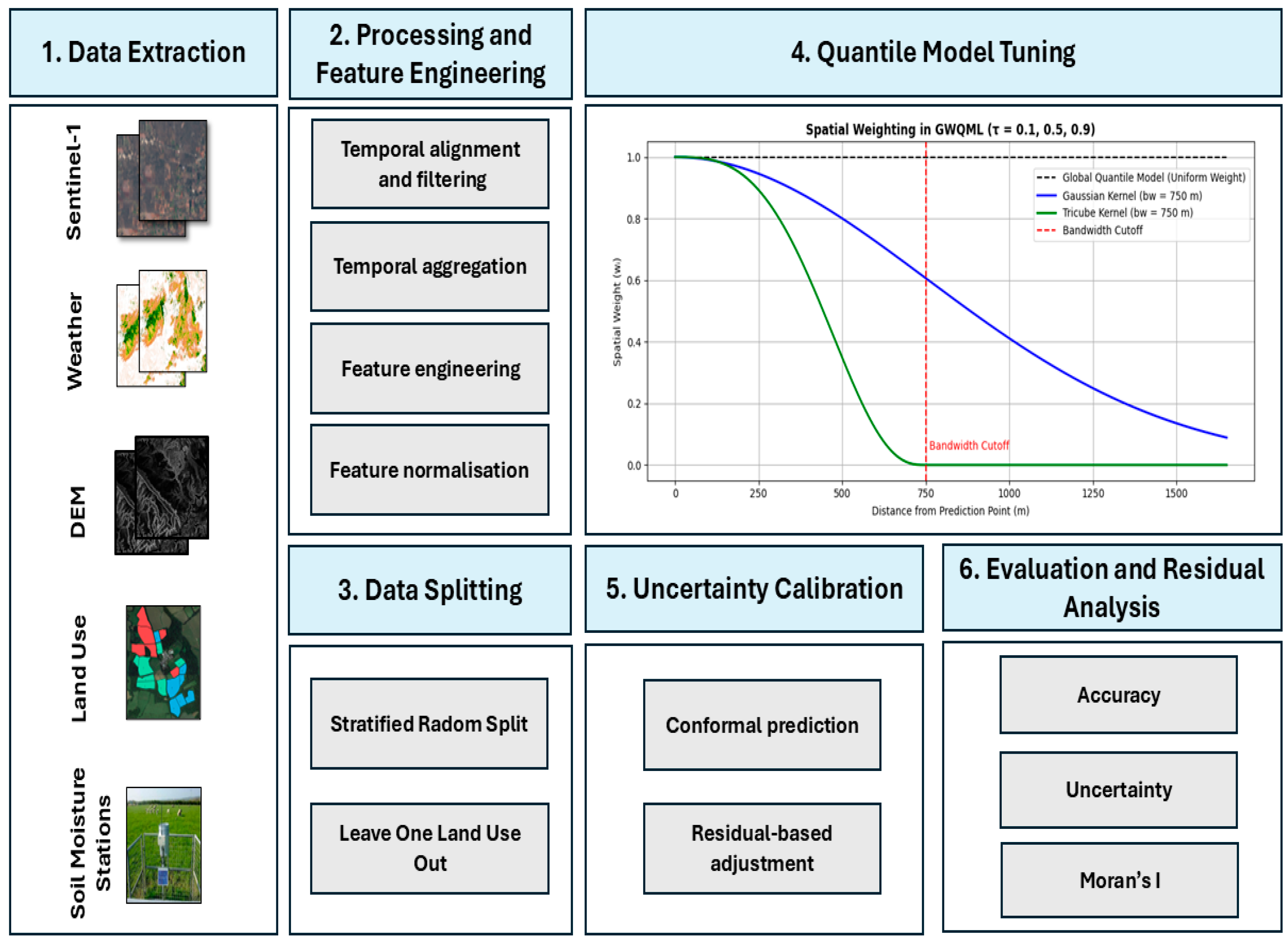
2.4. Methodological Framework
2.5. Model Performance
2.6. Spatial Autocorrelation Analysis
3. Results
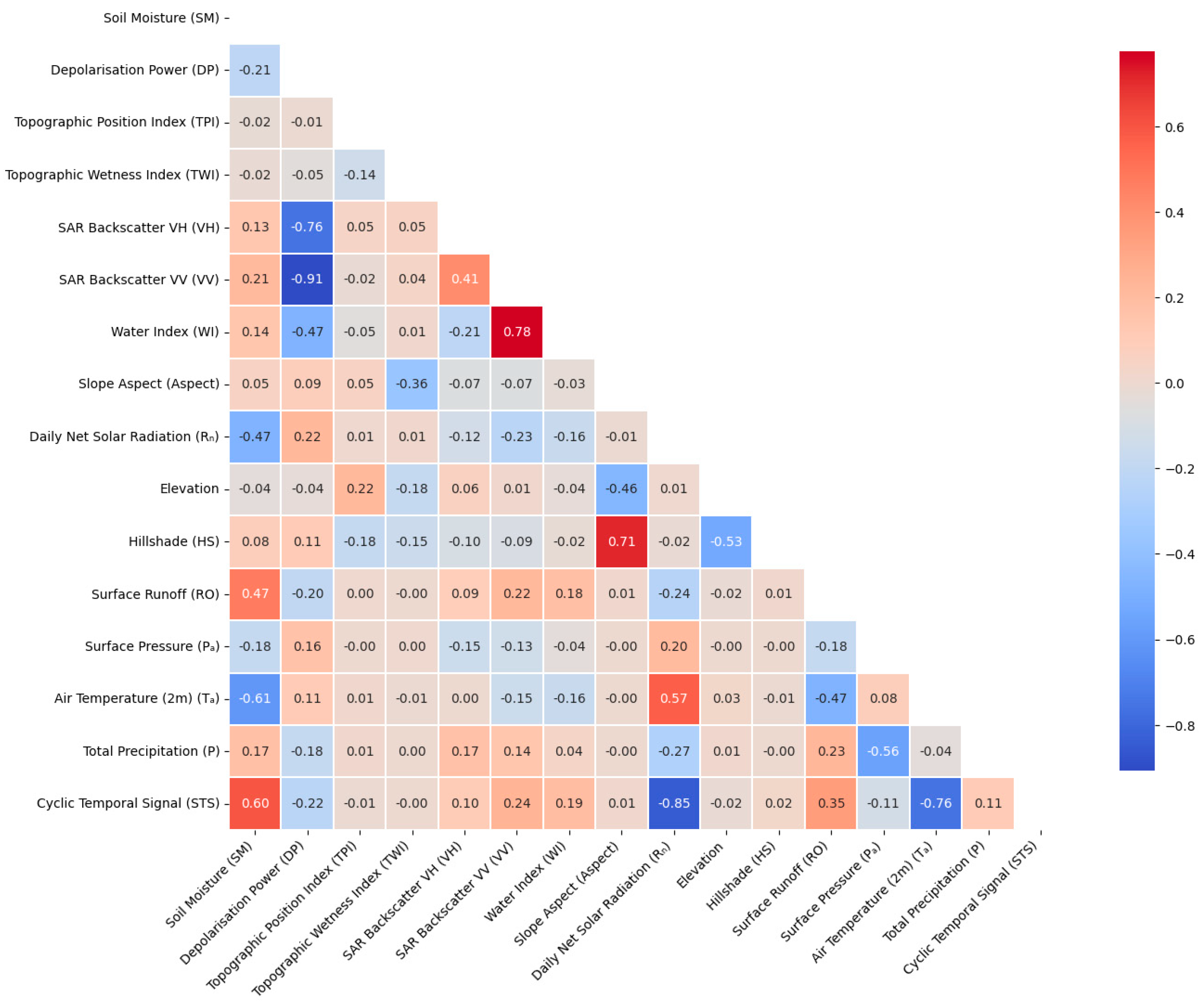
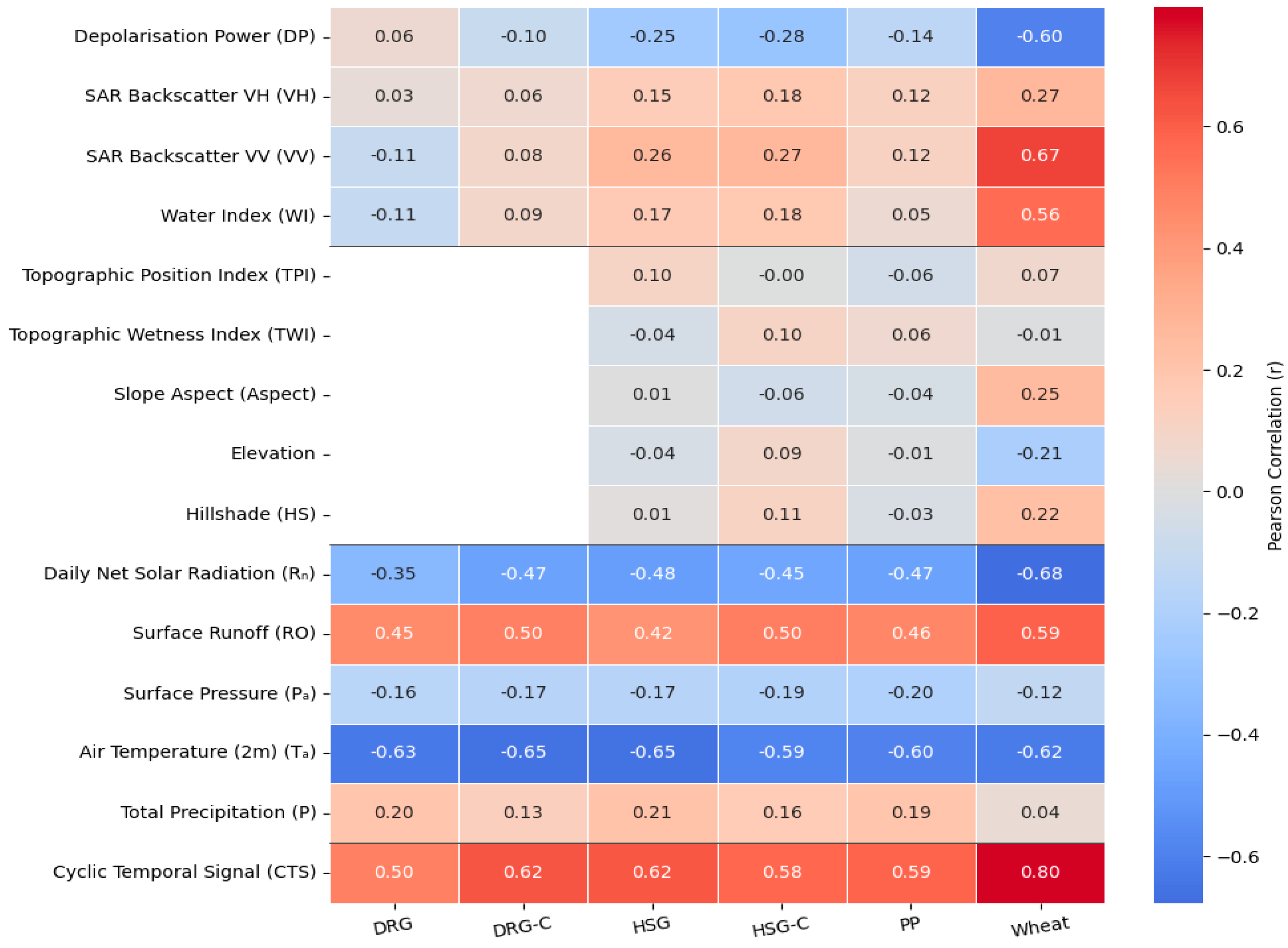
3.1. Feature Correlation Analysis
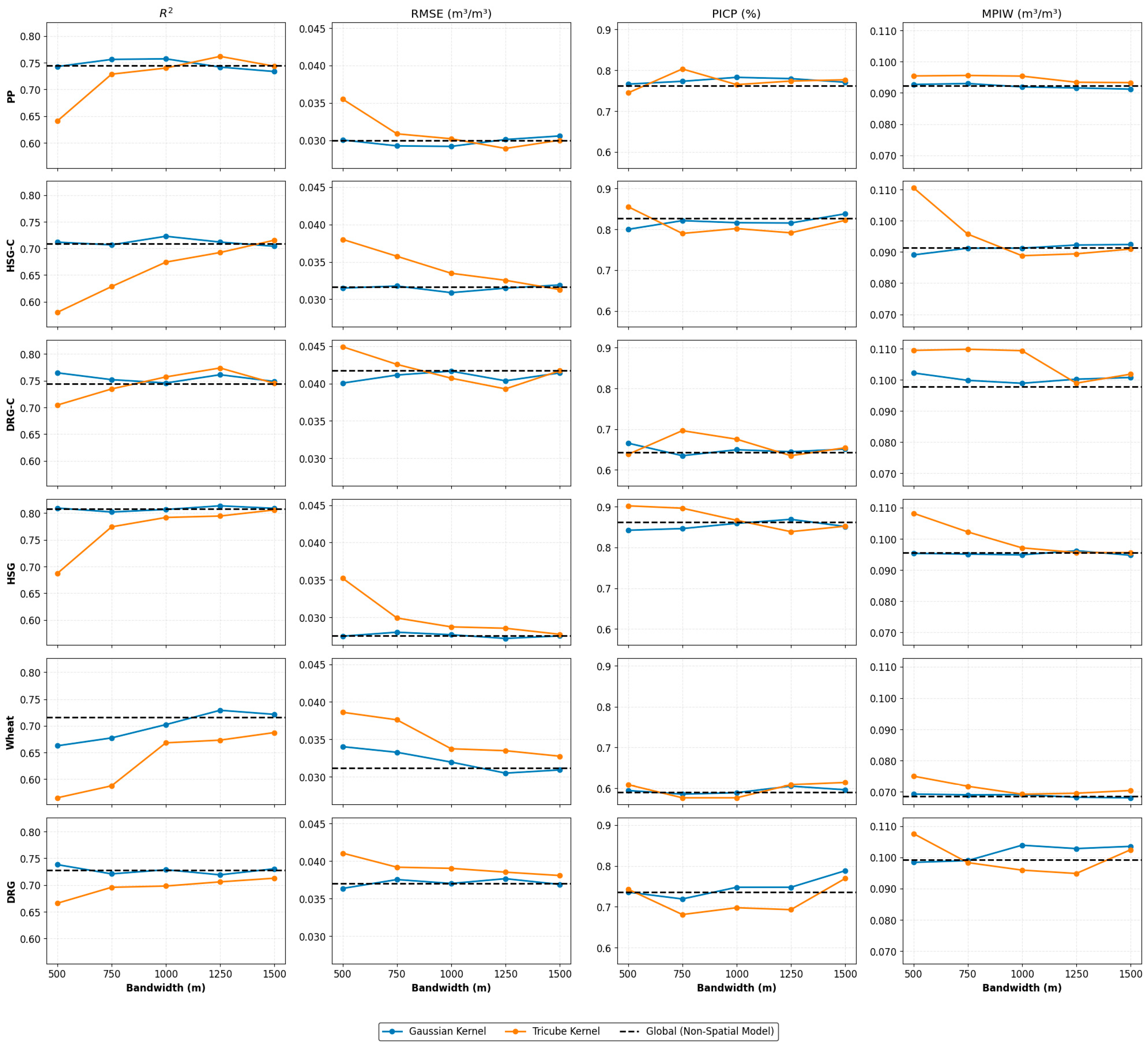
3.2. Model Evaluation and Bandwidth Analysis
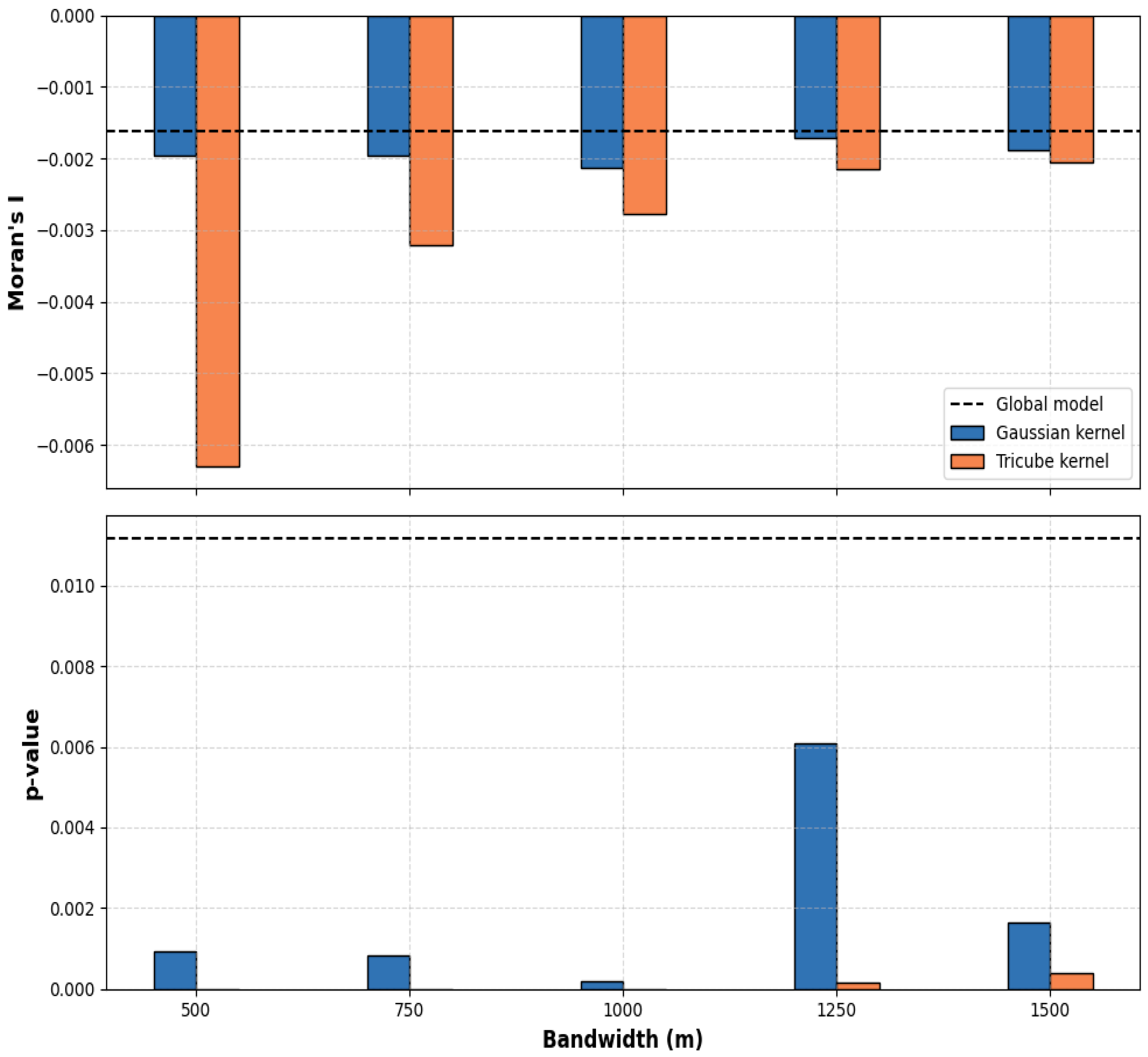
3.3. Spatial Autocorrelation of Residuals
4. Discussion
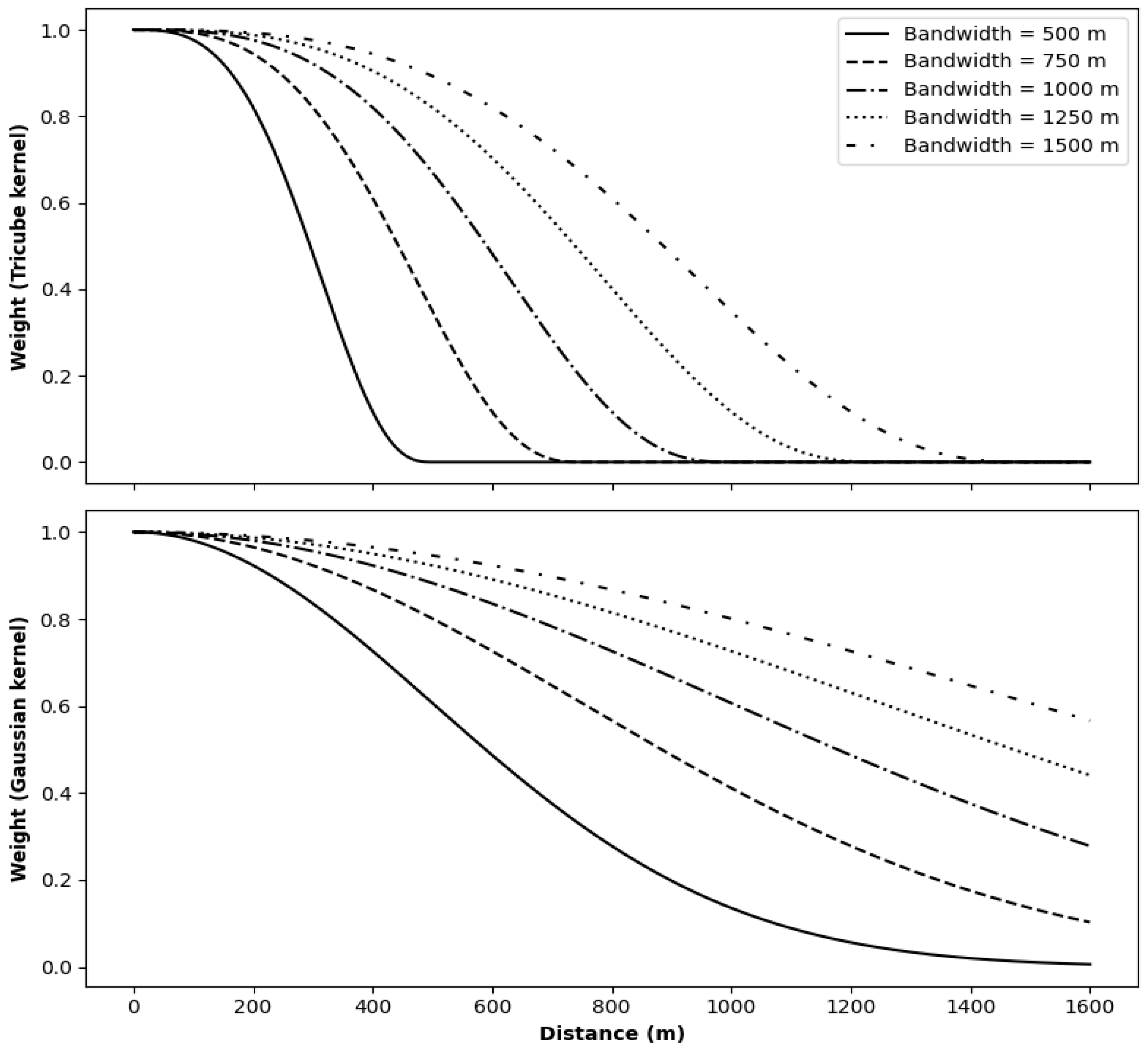
4.1. Bandwidth Sensitivity and Kernel Effect in Geographically Weighted Quantile Models
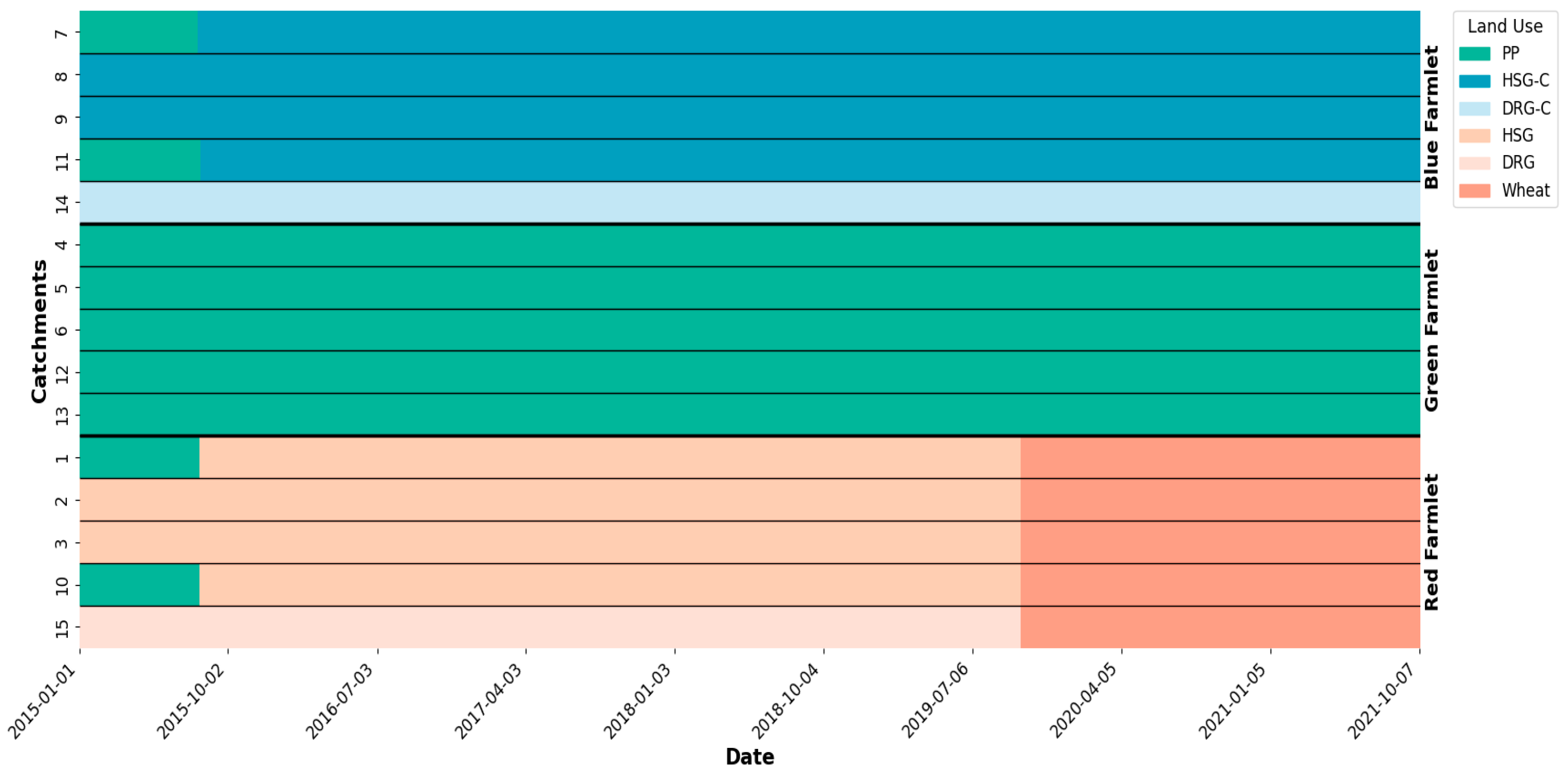
4.2. Generalisation Across Land Use Systems
4.3. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CTS | Cyclic Temporal Signal |
| DEM | Digital Elevation Model |
| DRG | Deep-Rooted Grass |
| DRG-C | Deep-Rooted Grass with Clover |
| ERA5 | ECMWF Re-analysis V5 |
| GEE | Google Earth Engine |
| GWML | Geographically Weighted Machine Learning |
| GWQML | Geographically Weighted Quantile Machine Learning |
| HSG | High-Sugar Grass |
| HSG-C | High-Sugar Grass with Clover |
| LOLUO | Leave-One-Land-Use-Out |
| PP | Permanent Pasture |
Appendix A
| Land Use | Year | N (obs.) | Mean (m3/m3) | SD (m3/m3) | Min (m3/m3) | Q1 (m3/m3) | Median (m3/m3) | Q3 (m3/m3) | Max (m3/m3) |
|---|---|---|---|---|---|---|---|---|---|
| DRG | 2015 | 34 | 0.351 | 0.043 | 0.23 | 0.335 | 0.372 | 0.379 | 0.395 |
| DRG | 2016 | 70 | 0.338 | 0.047 | 0.221 | 0.305 | 0.349 | 0.383 | 0.399 |
| DRG | 2017 | 106 | 0.363 | 0.047 | 0.181 | 0.361 | 0.385 | 0.388 | 0.398 |
| DRG | 2018 | 165 | 0.277 | 0.087 | 0.15 | 0.186 | 0.279 | 0.36 | 0.393 |
| DRG | 2019 | 64 | 0.343 | 0.035 | 0.258 | 0.329 | 0.358 | 0.367 | 0.39 |
| DRG-C | 2015 | 34 | 0.341 | 0.068 | 0.203 | 0.307 | 0.379 | 0.39 | 0.412 |
| DRG-C | 2016 | 70 | 0.355 | 0.038 | 0.267 | 0.337 | 0.369 | 0.39 | 0.393 |
| DRG-C | 2017 | 106 | 0.372 | 0.033 | 0.269 | 0.361 | 0.386 | 0.392 | 0.404 |
| DRG-C | 2018 | 165 | 0.291 | 0.103 | 0.157 | 0.178 | 0.288 | 0.401 | 0.417 |
| DRG-C | 2019 | 88 | 0.345 | 0.073 | 0.176 | 0.287 | 0.386 | 0.404 | 0.452 |
| DRG-C | 2020 | 95 | 0.345 | 0.095 | 0.161 | 0.25 | 0.404 | 0.424 | 0.429 |
| DRG-C | 2021 | 91 | 0.355 | 0.069 | 0.211 | 0.306 | 0.376 | 0.42 | 0.43 |
| HSG | 2015 | 105 | 0.349 | 0.07 | 0.127 | 0.34 | 0.382 | 0.394 | 0.432 |
| HSG | 2016 | 276 | 0.358 | 0.043 | 0.235 | 0.335 | 0.368 | 0.393 | 0.404 |
| HSG | 2017 | 462 | 0.372 | 0.035 | 0.225 | 0.36 | 0.386 | 0.397 | 0.405 |
| HSG | 2018 | 656 | 0.321 | 0.078 | 0.176 | 0.25 | 0.342 | 0.399 | 0.406 |
| HSG | 2019 | 310 | 0.346 | 0.053 | 0.212 | 0.306 | 0.368 | 0.392 | 0.404 |
| HSG-C | 2015 | 106 | 0.355 | 0.044 | 0.217 | 0.33 | 0.367 | 0.391 | 0.403 |
| HSG-C | 2016 | 268 | 0.339 | 0.045 | 0.243 | 0.306 | 0.343 | 0.372 | 0.406 |
| HSG-C | 2017 | 480 | 0.356 | 0.035 | 0.225 | 0.344 | 0.369 | 0.379 | 0.401 |
| HSG-C | 2018 | 660 | 0.302 | 0.078 | 0.162 | 0.231 | 0.311 | 0.381 | 0.417 |
| HSG-C | 2019 | 448 | 0.35 | 0.046 | 0.24 | 0.313 | 0.369 | 0.382 | 0.413 |
| HSG-C | 2020 | 399 | 0.347 | 0.055 | 0.212 | 0.308 | 0.372 | 0.388 | 0.41 |
| HSG-C | 2021 | 346 | 0.349 | 0.042 | 0.25 | 0.318 | 0.358 | 0.383 | 0.409 |
| PP | 2015 | 234 | 0.348 | 0.053 | 0.167 | 0.317 | 0.364 | 0.388 | 0.427 |
| PP | 2016 | 348 | 0.339 | 0.053 | 0.223 | 0.291 | 0.349 | 0.39 | 0.41 |
| PP | 2017 | 589 | 0.37 | 0.036 | 0.21 | 0.357 | 0.379 | 0.395 | 0.409 |
| PP | 2018 | 815 | 0.319 | 0.08 | 0.163 | 0.244 | 0.342 | 0.397 | 0.41 |
| PP | 2019 | 584 | 0.358 | 0.049 | 0.183 | 0.334 | 0.373 | 0.394 | 0.426 |
| PP | 2020 | 486 | 0.366 | 0.045 | 0.232 | 0.341 | 0.383 | 0.403 | 0.411 |
| PP | 2021 | 386 | 0.366 | 0.034 | 0.274 | 0.345 | 0.374 | 0.395 | 0.408 |
| Wheat | 2019 | 95 | 0.391 | 0.022 | 0.325 | 0.37 | 0.402 | 0.404 | 0.414 |
| Wheat | 2020 | 350 | 0.355 | 0.07 | 0.194 | 0.281 | 0.396 | 0.406 | 0.416 |
| Wheat | 2021 | 216 | 0.361 | 0.044 | 0.237 | 0.336 | 0.371 | 0.395 | 0.413 |
Appendix B
References
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil Moisture for Hydrological Applications: Open Questions and New Opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, S.; Yu, B.; Zhang, Y.; Keenan, T.; Fu, B. Soil Moisture-Atmosphere Interactions Drive Terrestrial Carbon-Water Trade-Offs. Commun. Earth Environ. 2025, 6, 169. [Google Scholar] [CrossRef]
- Berg, A.; Sheffield, J. Climate Change and Drought: The Soil Moisture Perspective. Curr. Clim. Change Rep. 2018, 4, 180–191. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, Q.; Xu, Y.; Luo, S.; Zhou, C.; Yu, Z.; Xu, C.-Y. Soil Moisture Dynamics and Associated Rainfall-Runoff Processes under Different Land Uses and Land Covers in a Humid Mountainous Watershed. J. Hydrol. 2024, 636, 131249. [Google Scholar] [CrossRef]
- Soothar, R.K.; Singha, A.; Soomro, S.A.; Chachar, A.; Kalhoro, F.; Rahaman, M.A. Effect of Different Soil Moisture Regimes on Plant Growth and Water Use Efficiency of Sunflower: Experimental Study and Modeling. Bull. Natl. Res. Cent. 2021, 45, 121. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; D’Odorico, P.; Porporato, A.; Ridolfi, L. On the Spatial and Temporal Links between Vegetation, Climate, and Soil Moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.J.; et al. A Roadmap for High-Resolution Satellite Soil Moisture Applications—Confronting Product Characteristics with User Requirements. Remote Sens. Environ. 2021, 252, 112162. [Google Scholar] [CrossRef]
- Ma, H.; Zeng, J.; Chen, N.; Zhang, X.; Cosh, M.H.; Wang, W. Satellite Surface Soil Moisture from SMAP, SMOS, AMSR2 and ESA CCI: A Comprehensive Assessment Using Global Ground-Based Observations. Remote Sens. Environ. 2019, 231, 111215. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS Performance in Terms of Global Soil Moisture Monitoring after Six Years in Operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Farahani, A.; Moradikhaneghahi, M.; Ghayoomi, M.; Jacobs, J.M. Application of Soil Moisture Active Passive (SMAP) Satellite Data in Seismic Response Assessment. Remote Sens. 2022, 14, 4375. [Google Scholar] [CrossRef]
- Meng, X.; Zeng, J.; Yang, Y.; Zhao, W.; Ma, H.; Letu, H.; Zhu, Q.; Liu, Y.; Wang, P.; Peng, J. High-Resolution Soil Moisture Mapping through Passive Microwave Remote Sensing Downscaling. Innov. Geosci. 2024, 2, 100105-1. [Google Scholar] [CrossRef]
- Fan, D.; Zhao, T.; Jiang, X.; García-García, A.; Schmidt, T.; Samaniego, L.; Attinger, S.; Wu, H.; Jiang, Y.; Shi, J.; et al. A Sentinel-1 SAR-Based Global 1-Km Resolution Soil Moisture Data Product: Algorithm and Preliminary Assessment. Remote Sens. Environ. 2025, 318, 114579. [Google Scholar] [CrossRef]
- Atun, R.; Gürsoy, Ö.; Koşaroğlu, S. Field Scale Soil Moisture Estimation with Ground Penetrating Radar and Sentinel 1 Data. Sustainability 2024, 16, 10995. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Zhang, S.; Hao, X.; Dasgupta, S. Soil Moisture Estimation Using MODIS and Ground Measurements in Eastern China. Int. J. Remote Sens. 2007, 28, 1413–1418. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, S.; Zhu, Z.; Ma, H.; He, T. Soil Moisture Content Retrieval from Landsat 8 Data Using Ensemble Learning. ISPRS J. Photogramm. Remote Sens. 2022, 185, 32–47. [Google Scholar] [CrossRef]
- Zou, X.; Wang, G.; Hagan, D.F.T.; Li, S.; Wei, J.; Lu, J.; Qiao, Y.; Zhu, C.; Ullah, W.; Yeboah, E. Precipitation Sensitivity to Soil Moisture Changes in Multiple Global Climate Models. Atmosphere 2023, 14, 1531. [Google Scholar] [CrossRef]
- Koohikeradeh, E.; Jose Gumiere, S.; Bonakdari, H. NDMI-Derived Field-Scale Soil Moisture Prediction Using ERA5 and LSTM for Precision Agriculture. Sustainability 2025, 17, 2399. [Google Scholar] [CrossRef]
- Schönauer, M.; Asabere, S.B.; Sauer, D.; Drollinger, S. Topographic Indices and ERA5-Land Data to Describe Soil Moisture Variability in a Central European Beech Forest. J. Hydrol. Reg. Stud. 2025, 59, 102456. [Google Scholar] [CrossRef]
- Wanders, N.; Karssenberg, D.; Bierkens, M.; Parinussa, R.; de Jeu, R.; van Dam, J.; de Jong, S. Observation Uncertainty of Satellite Soil Moisture Products Determined with Physically-Based Modeling. Remote Sens. Environ. 2012, 127, 341–356. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Pignotti, G.; Crawford, M.; Han, E.; Williams, M.R.; Chaubey, I. SMAP Soil Moisture Data Assimilation Impacts on Water Quality and Crop Yield Predictions in Watershed Modeling. J. Hydrol. 2023, 617, 129122. [Google Scholar] [CrossRef]
- Bwambale, E.; Abagale, F.K.; Anornu, G.K. Data-Driven Modelling of Soil Moisture Dynamics for Smart Irrigation Scheduling. Smart Agric. Technol. 2023, 5, 100251. [Google Scholar] [CrossRef]
- Kolassa, J.; Reichle, R.H.; Liu, Q.; Alemohammad, S.H.; Gentine, P.; Aida, K.; Asanuma, J.; Bircher, S.; Caldwell, T.; Colliander, A.; et al. Estimating Surface Soil Moisture from SMAP Observations Using a Neural Network Technique. Remote Sens. Environ. 2018, 204, 43–59. [Google Scholar] [CrossRef] [PubMed]
- Parada, L.M.; Liang, X. Impacts of Spatial Resolutions and Data Quality on Soil Moisture Data Assimilation. J. Geophys. Res. Atmos. 2008, 113, D10101. [Google Scholar] [CrossRef]
- Behrens, T.; Schmidt, K.; Viscarra Rossel, R.; Gries, P.; Scholten, T.; Macmillan, R.A. Spatial Modelling with Euclidean Distance Fields and Machine Learning. Eur. J. Soil. Sci. 2018, 69, 757–770. [Google Scholar] [CrossRef]
- Price, A.G.; Bauer, B.O. Small-Scale Heterogeneity and Soil-Moisture Variability in the Unsaturated Zone. J. Hydrol. 1984, 70, 277–293. [Google Scholar] [CrossRef]
- Yetbarek, E.; Kumar, S.; Ojha, R. Effects of Soil Heterogeneity on Subsurface Water Movement in Agricultural Fields: A Numerical Study. J. Hydrol. 2020, 590, 125420. [Google Scholar] [CrossRef]
- Western, A.W.; Blöschl, G. On the Spatial Scaling of Soil Moisture. J. Hydrol. 1999, 217, 203–224. [Google Scholar] [CrossRef]
- Song, P.; Huang, J.; Mansaray, L.R. An Improved Surface Soil Moisture Downscaling Approach over Cloudy Areas Based on Geographically Weighted Regression. Agric. Meteorol. 2019, 275, 146–158. [Google Scholar] [CrossRef]
- Jia, Y.; Zou, J.; Jin, S.; Yan, Q.; Chen, Y.; Jin, Y.; Savi, P. Multiresolution Soil Moisture Products Based on a Spatially Adaptive Estimation Model and CYGNSS Data. GIsci. Remote Sens. 2024, 61, 2313812. [Google Scholar] [CrossRef]
- Zhong, Y.; Hong, S.; Wei, Z.; Walker, J.P.; Wang, Y.; Huang, C. Spatial Downscaling of SMAP Soil Moisture Estimation Using Multiscale Geographically Weighted Regression during SMAPVEX16. J. Hydrol. 2024, 637, 131348. [Google Scholar] [CrossRef]
- Tong, C.; Ye, Y.; Zhao, T.; Bao, H.; Wang, H. Soil Moisture Disaggregation via Coupling Geographically Weighted Regression and Radiative Transfer Model. J Hydrol 2024, 634, 131053. [Google Scholar] [CrossRef]
- Jung, C.; Lee, Y.; Lee, J.; Kim, S. Performance Evaluation of the Multiple Quantile Regression Model for Estimating Spatial Soil Moisture after Filtering Soil Moisture Outliers. Remote Sens. 2020, 12, 1678. [Google Scholar] [CrossRef]
- Yu, C.; Wang, D.; Singh, V.P.; Xu, P.; Zhang, A.; Yang, Z.; Wang, Z.; Zeng, X.; Jiang, J.; Wu, J. An Ensemble Vine Copula Quantile Regression Model with Non-Stationary Margins (EVQR-NS) for Soil Moisture Prediction. J. Hydrol. 2025, 659, 133248. [Google Scholar] [CrossRef]
- Zare, S.; Abtahi, A.; Dehghani, M.; Fallah Shamsi, S.R.; Baghernejad, M.; Lagacherie, P. Chapter 21—Quantile Random Forest Technique for Soil Moisture Contents Digital Mapping, Sarvestan Plain, Iran. In Advanced Tools for Studying Soil Erosion Processes; Pourghasemi, H.R., Kariminejad, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 351–368. ISBN 978-0-443-22262-7. [Google Scholar] [CrossRef]
- Dega, S.; Dietrich, P.; Schrön, M.; Paasche, H. Probabilistic Prediction by Means of the Propagation of Response Variable Uncertainty through a Monte Carlo Approach in Regression Random Forest: Application to Soil Moisture Regionalization. Front. Environ. Sci. 2023, 11, 1009191. [Google Scholar] [CrossRef]
- Murray, P.J.; Griffith, B.A.; Research, R.; Shepherd, A. The North Wyke Farm Platform: A New UK National Capability for Research into Sustainability of Agricultural Temperate Grassland Management. In Proceedings of the 22nd International Grassland Congress, Sydney, Australia, 15–19 September 2013. [Google Scholar]
- Takahashi, T.; Harris, P.; Blackwell, M.S.A.; Cardenas, L.M.; Collins, A.L.; Dungait, J.A.J.; Hawkins, J.M.B.; Misselbrook, T.H.; McAuliffe, G.A.; McFadzean, J.N.; et al. Roles of Instrumented Farm-Scale Trials in Trade-off Assessments of Pasture-Based Ruminant Production Systems. Animal 2018, 12, 1766–1776. [Google Scholar] [CrossRef]
- Orr, R.J.; Murray, P.J.; Eyles, C.J.; Blackwell, M.S.A.; Cardenas, L.M.; Collins, A.L.; Dungait, J.A.J.; Goulding, K.W.T.; Griffith, B.A.; Gurr, S.J.; et al. The North Wyke Farm Platform: Effect of Temperate Grassland Farming Systems on Soil Moisture Contents, Runoff and Associated Water Quality Dynamics. Eur. J. Soil. Sci. 2016, 67, 374–385. [Google Scholar] [CrossRef]
- Harrod, T.R.; Hogan, D.V. The Soils of North Wyke and Rowden. Soil Surv. Engl. Wales 2008, 1–54. Available online: https://repository.rothamsted.ac.uk/item/96xqw/the-soils-of-north-wyke-and-rowden (accessed on 15 March 2025).
- Pulley, S.; Collins, A.L. Field-Based Determination of Controls on Runoff and Fine Sediment Generation from Lowland Grazing Livestock Fields. J. Environ. Manag. 2019, 249, 109365. [Google Scholar] [CrossRef]
- Hawkins, J.M.B.; Harris, P. North Wyke Farm Platform User Guide: Fine Resolution (15-Minute) Soil Moisture Station Data; Rothamsted Research: Harpenden, UK, 2023. [Google Scholar] [CrossRef]
- Hawkins, J.M.B.; Griffith, B.A.; Sint, H.M.; Harris, P. The North Wyke Farm Platform: Design, Establishment and Development; Rothamsted Research: Harpenden, UK, 2023. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Vanderhoof, M.K.; Alexander, L.; Christensen, J.; Solvik, K.; Nieuwlandt, P.; Sagehorn, M. High-Frequency Time Series Comparison of Sentinel-1 and Sentinel-2 Satellites for Mapping Open and Vegetated Water across the United States (2017–2021). Remote Sens. Environ. 2023, 288, 113498. [Google Scholar] [CrossRef]
- Skentos, A. TOPOGRAPHIC POSITION INDEX BASED LANDFORM ANALYSIS OF MESSARIA (IKARIA ISLAND, GREECE). Acta Geobalc. 2017, 4, 7–15. [Google Scholar] [CrossRef]
- Winzeler, H.E.; Owens, P.R.; Read, Q.D.; Libohova, Z.; Ashworth, A.; Sauer, T. Topographic Wetness Index as a Proxy for Soil Moisture in a Hillslope Catena: Flow Algorithms and Map Generalization. Land 2022, 11, 2018. [Google Scholar] [CrossRef]
- Kopecký, M.; Macek, M.; Wild, J. Topographic Wetness Index Calculation Guidelines Based on Measured Soil Moisture and Plant Species Composition. Sci. Total Environ. 2021, 757, 143785. [Google Scholar] [CrossRef] [PubMed]
- Eskandari, H.; Saadatmand, H.; Ramzan, M.; Mousapour, M. Innovative Framework for Accurate and Transparent Forecasting of Energy Consumption: A Fusion of Feature Selection and Interpretable Machine Learning. Appl. Energy 2024, 366, 123314. [Google Scholar] [CrossRef]
- Li, M.; Yan, Y. Comparative Analysis of Machine-Learning Models for Soil Moisture Estimation Using High-Resolution Remote-Sensing Data. Land 2024, 13, 1331. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. 3—Data Preprocessing. In Data Mining: Concepts and Techniques, 3rd ed.; Han, J., Kamber, M., Pei, J., Eds.; Morgan Kaufmann: Boston, MA, USA, 2012; pp. 83–124. ISBN 978-0-12-381479-1. [Google Scholar]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Comber, A.; Wulder, M. Considering Spatiotemporal Processes in Big Data Analysis: Insights from Remote Sensing of Land Cover and Land Use. Trans. GIS 2019, 23, 879–891. [Google Scholar] [CrossRef]
- Comber, A.; Brunsdon, C.; Charlton, M.; Dong, G.; Harris, R.; Lu, B.; Lü, Y.; Murakami, D.; Nakaya, T.; Wang, Y.; et al. A Route Map for Successful Applications of Geographically Weighted Regression. Geogr. Anal. 2023, 55, 155–178. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Henderson, M.; Wang, G.; Chen, M.; Fu, Y.; Dou, Z.; Zhou, W.; Huang, W.; Liu, B. Effect of Land Use Type on Soil Moisture Dynamics in the Sloping Lands of the Black Soil (Mollisols) Region of Northeast China. Agriculture 2024, 14, 1261. [Google Scholar] [CrossRef]
- Lu, B.; Charlton, M.; Harris, P.; Fotheringham, A.S. Geographically Weighted Regression with a Non-Euclidean Distance Metric: A Case Study Using Hedonic House Price Data. Int. J. Geogr. Inf. Sci. 2014, 28, 660–681. [Google Scholar] [CrossRef]
- Srisuradetchai, P.; Suksrikran, K. Random Kernel K-Nearest Neighbors Regression. Front. Big Data 2024, 7, 1402384. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Ni, Y.; Ma, Y.; Lu, P. Smoothing Homotopy Methods for Solving Nonlinear Optimal Control Problems. J. Guid. Control Dyn. 2023, 46, 1470–1484. [Google Scholar] [CrossRef]
- Allerbo, O.; Jörnsten, R. Bandwidth Selection for Gaussian Kernel Ridge Regression via Jacobian Control. arXiv 2022, arXiv:2205.11956. [Google Scholar]
- Guo, L.; Ma, Z.; Zhang, L. Comparison of Bandwidth Selection in Application of Geographically Weighted Regression: A Case Study. Can. J. For. Res. 2008, 38, 2526–2534. [Google Scholar] [CrossRef]
- Bitter, C.; Mulligan, G.F.; Dall’erba, S. Incorporating Spatial Variation in Housing Attribute Prices: A Comparison of Geographically Weighted Regression and the Spatial Expansion Method. J. Geogr. Syst. 2007, 9, 7–27. [Google Scholar] [CrossRef]
- Sun, Y.; Phillips, P.C.B. Optimal Bandwidth Choice for Interval Estimation in GMM Regression; Cowles Foundation Discussion Paper No. 1965; Cowles Foundation for Research in Economics, Yale University: New Haven, CT, USA, 2008; Available online: https://elischolar.library.yale.edu/cowles-discussion-paper-series/1965 (accessed on 1 March 2025).
- Sugiyama, M.; Krauledat, M.; Müller, K.-R. Covariate Shift Adaptation by Importance Weighted Cross Validation. J. Mach. Learn. Res. 2007, 8, 985–1005. [Google Scholar]
- Fang, K.; Kifer, D.; Lawson, K.; Feng, D.; Shen, C. The Data Synergy Effects of Time-Series Deep Learning Models in Hydrology. Water Resour. Res. 2022, 58, e2021WR029583. [Google Scholar] [CrossRef]
- Gaudin, A.C.M.; Westra, S.; Loucks, C.E.S.; Janovicek, K.; Martin, R.C.; Deen, W. Improving Resilience of Northern Field Crop Systems Using Inter-Seeded Red Clover: A Review. Agronomy 2013, 3, 148–180. [Google Scholar] [CrossRef]
- Haynes, R.J.; Beare, M.H. Influence of Six Crop Species on Aggregate Stability and Some Labile Organic Matter Fractions. Soil Biol. Biochem. 1997, 29, 1647–1653. [Google Scholar] [CrossRef]
- Black, A.D.; Laidlaw, A.S.; Moot, D.J.; O’Kiely, P. Comparative growth and management of white and red clovers. Ir. J. Agric. Food Res. 2009, 48, 149–166. [Google Scholar]
- Zribi, M.; Ciarletti, V.; Taconet, O.; Paillé, J.; Boissard, P. Characterisation of the Soil Structure and Microwave Backscattering Based on Numerical Three-Dimensional Surface Representation: Analysis with a Fractional Brownian Model. Remote Sens. Environ. 2000, 72, 159–169. [Google Scholar] [CrossRef]
- Khabbazan, S.; Steele-Dunne, S.C.; Vermunt, P.; Judge, J.; Vreugdenhil, M.; Gao, G. The Influence of Surface Canopy Water on the Relationship between L-Band Backscatter and Biophysical Variables in Agricultural Monitoring. Remote Sens. Environ. 2022, 268, 112789. [Google Scholar] [CrossRef]
- Alemohammad, S.H.; Konings, A.G.; Jagdhuber, T.; Moghaddam, M.; Entekhabi, D. Characterization of vegetation and soil scattering mechanisms across different biomes using P-band SAR polarimetry. Remote Sens. Environ. 2018, 209, 107–117. [Google Scholar] [CrossRef]
- Yin, L.; Ghosh, R.; Lin, C.; Hale, D.; Weigl, C.; Obarowski, J.; Zhou, J.; Till, J.; Jia, X.; You, N.; et al. Mapping Smallholder Cashew Plantations to Inform Sustainable Tree Crop Expansion in Benin. Remote Sens. Environ. 2023, 295, 113695. [Google Scholar] [CrossRef]
- Wigneron, J.P.; Jackson, T.J.; O’Neill, P.; De Lannoy, G.; de Rosnay, P.; Walker, J.P.; Ferrazzoli, P.; Mironov, V.; Bircher, S.; Grant, J.P.; et al. Modelling the Passive Microwave Signature from Land Surfaces: A Review of Recent Results and Application to the L-Band SMOS & SMAP Soil Moisture Retrieval Algorithms. Remote Sens. Environ. 2017, 192, 238–262. [Google Scholar]
- Shafian, S.; Maas, S.J. Index of Soil Moisture Using Raw Landsat Image Digital Count Data in Texas High Plains. Remote Sens. 2015, 7, 2352–2372. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. Aquacrop-the FAO Crop Model to Simulate Yield Response to Water: I. Concepts Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- van Diepen, C.A.; Wolf, J.; van Keulen, H.; Rappoldt, C. WOFOST: A Simulation Model of Crop Production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]


| Land Use | N (obs.) | Mean (m3/m3) | SD (m3/m3) | Min (m3/m3) | Q1 (m3/m3) | Median (m3/m3) | Q3 (m3/m3) | Max (m3/m3) |
|---|---|---|---|---|---|---|---|---|
| DRG | 439 | 0.32 | 0.07 | 0.15 | 0.27 | 0.35 | 0.38 | 0.39 |
| DRG-C | 649 | 0.33 | 0.08 | 0.15 | 0.28 | 0.37 | 0.40 | 0.45 |
| HSG | 1809 | 0.34 | 0.06 | 0.12 | 0.30 | 0.37 | 0.39 | 0.43 |
| HSG-C | 2707 | 0.33 | 0.05 | 0.16 | 0.30 | 0.35 | 0.38 | 0.41 |
| PP | 3442 | 0.35 | 0.05 | 0.16 | 0.31 | 0.37 | 0.39 | 0.42 |
| Wheat | 661 | 0.36 | 0.05 | 0.19 | 0.34 | 0.39 | 0.40 | 0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oulaid, B.; Harris, P.; Maas, E.; Fakeye, I.A.; Baker, C. Geographically Weighted Quantile Machine Learning for Probabilistic Soil Moisture Prediction from Spatially Resolved Remote Sensing. Remote Sens. 2025, 17, 2907. https://doi.org/10.3390/rs17162907
Oulaid B, Harris P, Maas E, Fakeye IA, Baker C. Geographically Weighted Quantile Machine Learning for Probabilistic Soil Moisture Prediction from Spatially Resolved Remote Sensing. Remote Sensing. 2025; 17(16):2907. https://doi.org/10.3390/rs17162907
Chicago/Turabian StyleOulaid, Bader, Paul Harris, Ellen Maas, Ireoluwa Akinlolu Fakeye, and Chris Baker. 2025. "Geographically Weighted Quantile Machine Learning for Probabilistic Soil Moisture Prediction from Spatially Resolved Remote Sensing" Remote Sensing 17, no. 16: 2907. https://doi.org/10.3390/rs17162907
APA StyleOulaid, B., Harris, P., Maas, E., Fakeye, I. A., & Baker, C. (2025). Geographically Weighted Quantile Machine Learning for Probabilistic Soil Moisture Prediction from Spatially Resolved Remote Sensing. Remote Sensing, 17(16), 2907. https://doi.org/10.3390/rs17162907







