A Semantic Segmentation-Based GNSS Signal Occlusion Detection and Optimization Method
Abstract
1. Introduction
- To more accurately extract the sky region and types of occlusions from sky images, this study leverages the semantic feature learning capabilities of deep learning models, particularly their adaptability to edges and textures, for image segmentation. The extraction accuracy is compared with that of existing methods.
- Based on satellite attitude information, the satellite projection is mapped onto the images processed by the deep learning model, enabling the classification and detection of GNSS signal types. These signals are categorized into LOS, attenuated LOS, and NLOS.
- The degree of occlusion is quantified by calculating the shortest pixel distance from the satellite projection point to the nearest sky region. Additionally, a weight optimization scheme is developed based on different types of obstacles.
- Different optimization strategies are applied depending on the type of GNSS signal occlusion. Comparative results demonstrate that the proposed method achieves more accurate positioning and navigation performance than existing approaches.
2. Materials and Methods
2.1. Semantic Segmentation of Sky-Directed Images
2.1.1. Image Acquisition
2.1.2. Image Preprocessing and Model Training
2.1.3. Semantic Segmentation of Images
2.2. Satellite Signal Projection
2.3. GNSS Signal Weight Optimization
| Algorithm 1. GNSS Signal Occlusion detection and Correction |
| Input: GNSS information, heading information, and sky environment information. |
| Output: Weights GNSS signal categories, weights, positioning results. |
| Steps: |
| for i = 1, 2, … N |
| Segment the Nth sky environment image following the steps in Section 2-B. |
| for j = 1, 2, … M |
| Obtain the array of sky edge pixel coordinates. |
| Based on (1) and (2), construct a satellite signal projection model to project the Mth satellite from the image’s corresponding epoch onto the segmented image. |
| Based on (3), construct an occlusion-degree representation model to calculate the distance from the projection point to the sky edge |
| Obtain the GNSS signal category. |
| if |
| Satellite discarding. |
| Obtain 0. |
| else if |
| Use the optimization method for tree occluders from (4). |
| Obtain w. |
| else |
| Use the optimization method for buildings or other occluders from (4). |
| Obtain w. |
| end |
| end |
| end |
| Perform positioning calculation, obtain the positioning results. |
3. Vehicle-Mounted Experiment
3.1. Experimental Platform
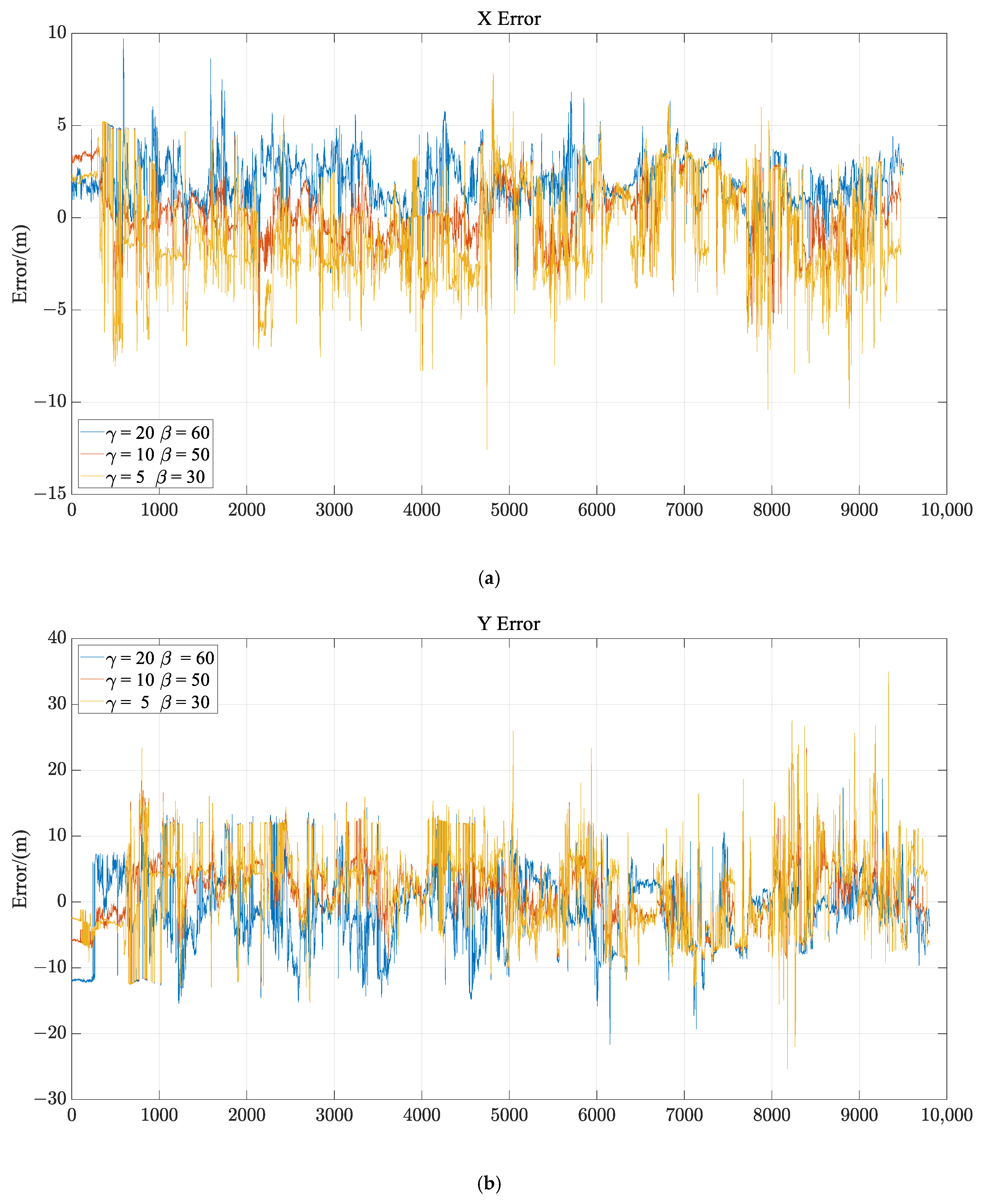
3.2. Selection of and
3.3. Experimental Results and Analysis
- Canny Edge Detection Method: The original sky image is first converted to a grayscale image, followed by dilation and erosion operations. Then, Canny edge detection is applied. In this paper, this method is referred to as Canny.
- Flood Fill Method: The center pixel of the image is first selected as the seed point. The algorithm then propagates to neighboring pixels, identifying all points with the same or similar color and filling them with a new color to form a connected region. In this paper, this method is referred to as Flood Fill.
- The proposed method in this paper involves training and segmenting images using DeepLabV3+, with obstructions classified as buildings and trees. This method is referred to as Deep-Air.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, W.; Yue, Z.; Lian, Z.; Li, K.; Sun, C.; Zhang, M. An Elastic Filtering Algorithm with Visual Perception for Vehicle GNSS Navigation and Positioning. Sensors 2024, 24, 8019. [Google Scholar] [CrossRef] [PubMed]
- Ning, B.; Zhao, F.; Luo, H.; Luo, D.; Shao, W. Robust GNSS/INS Tightly Coupled Positioning Using Factor Graph Optimization with P-Spline and Dynamic Prediction. Remote Sens. 2025, 17, 1792. [Google Scholar] [CrossRef]
- Xiao, G.; Xiao, Z.; Zhou, P.; Liu, C.; Wei, H.; Li, P. Performance evaluation of Galileo high accuracy service for PPP ambiguity resolution. GPS Solut. 2025, 29, 96. [Google Scholar] [CrossRef]
- Li, X.; Xu, Q.; Li, X.; Xin, H.; Yuan, Y.; Shen, Z.; Zhou, Y. Improving PPP-RTK-based vehicle navigation in urban environments via multilayer perceptron-based NLOS signal detection. GPS Solut. 2023, 28, 29. [Google Scholar] [CrossRef]
- Lyu, Z.; Gao, Y. An efficient pixel shader-based ray-tracing method for correcting GNSS non-line-of-sight error with large-scale surfaces. GPS Solut. 2023, 27, 159. [Google Scholar] [CrossRef]
- Suzuki, T.; Matsuo, K.; Amano, Y. Rotating GNSS Antennas: Simultaneous LOS and NLOS Multipath Mitigation. GPS Solut. 2020, 24, 86. [Google Scholar] [CrossRef]
- Jiang, C.H.; Xu, B.; Hsu, L.T. Probabilistic approach to detect and correct GNSS NLOS signals using an augmented state vector in the extended Kalman filter. GPS Solut. 2021, 25, 72. [Google Scholar] [CrossRef]
- Xu, B.; Jia, Q.; Hsu, L.T. Vector Tracking Loop-Based GNSS NLOS Detection and Correction: Algorithm Design and Performance Analysis. IEEE Trans. Instrum. Meas. 2020, 69, 4604–4619. [Google Scholar] [CrossRef]
- Han, J.; Huang, G.; Zhang, Q.; Tu, R.; Du, Y.; Wang, X. A New Azimuth-Dependent Elevation Weight (ADEW) Model for Real-Time Deformation Monitoring in Complex Environment by Multi-GNSS. Sensors 2018, 18, 2473. [Google Scholar] [CrossRef]
- Zidan, J.; Anyaegbu, E.; Kampert, E.; Higgins, M.D.; Ford, C. Doppler and Pseudorange Measurements as Prediction Features for Multi-Constellation GNSS LoS/NLoS Signal Classification. In Proceedings of the 2023 IEEE Smart World Congress (SWC), Portsmouth, UK, 28–31 August 2023; pp. 1–8. [Google Scholar]
- Ng, H.F.; Zhang, G.H.; Yang, K.Y.; Yang, S.X.; Hsu, L.T. Improved weighting scheme using consumer-level GNSS L5/E5a/B2a pseudorange measurements in the urban area. Adv. Space Res. 2020, 66, 1647–1658. [Google Scholar] [CrossRef]
- Liu, C.; LI, F. Comparison and analysis of different GNSS weighting methods. Sci. Surv. Mapp. 2018, 43, 39–44. [Google Scholar] [CrossRef]
- Hsu, L.T. GNSS multipath detection using a machine learning approach. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; pp. 1–6. [Google Scholar]
- Luo, H.; Liu, J.; He, D. GNSS Signal Labeling, Classification, and Positioning in Urban Scenes Based on PSO–LGBM–WLS Algorithm. IEEE Trans. Instrum. Meas. 2023, 72, 2528213. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, Z.; Zhang, Y.; Yang, H.; Gao, Y. Deep-Learning-Enhanced Outlier Detection for Precise GNSS Positioning With Smartphones. IEEE Trans. Instrum. Meas. 2025, 74, 2526013. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, C.; Shang, R.; Peng, Z.; Zhang, R.; Gan, L.; Gao, W. NLOS signal detection and correction for smartphone using convolutional neural network and variational mode decomposition in urban environment. GPS Solut. 2022, 27, 31. [Google Scholar] [CrossRef]
- Li, L.T.; Elhajj, M.; Feng, Y.X.; Ochieng, W.Y. Machine learning based GNSS signal classification and weighting scheme design in the built environment: A comparative experiment. Satell. Navig. 2023, 4, 12. [Google Scholar] [CrossRef]
- Bétaille, D.; Peyret, F.; Ortiz, M.; Miquel, S.; Fontenay, L. A New Modeling Based on Urban Trenches to Improve GNSS Positioning Quality of Service in Cities. IEEE Intel. Transp. Syst. 2013, 5, 59–70. [Google Scholar] [CrossRef]
- Luo, H.; Mi, X.; Yang, Y.; Chen, W.; Weng, D. Multiepoch Grid-Based 3DMA Positioning in Dense Urban Canyons by Optimizing Reflection Modeling. IEEE Trans. Instrum. Meas. 2025, 74, 8503213. [Google Scholar] [CrossRef]
- Wen, W.W.; Zhang, G.; Hsu, L.T. GNSS NLOS Exclusion Based on Dynamic Object Detection Using LiDAR Point Cloud. IEEE Trans. Instrum. Meas. 2021, 22, 853–862. [Google Scholar] [CrossRef]
- Wang, L.; Groves, P.D.; Ziebart, M.K. GNSS Shadow Matching: Improving Urban Positioning Accuracy Using a 3D City Model with Optimized Visibility Scoring Scheme. NAVIGATION 2013, 60, 195–207. [Google Scholar] [CrossRef]
- Marais, J.; Meurie, C.; Attia, D.; Ruichek, Y.; Flancquart, A. Toward accurate localization in guided transport: Combining GNSS data and imaging information. Transp. Res. C-Emer. 2014, 43, 188–197. [Google Scholar] [CrossRef]
- Kato, S.; Kitamura, M.; Suzuki, T.; Amano, Y. NLOS Satellite Detection Using a Fish-Eye Camera for Improving GNSS Positioning Accuracy in Urban Area. J. Robot. Mechatron. 2016, 28, 31–39. [Google Scholar] [CrossRef]
- Sanromà Sánchez, J.; Gerhmann, A.; Thevenon, P.; Brocard, P.; Ben Afia, A.; Julien, O. Use of a FishEye Camera for GNSS NLOS Exclusion and Characterization in Urban Environments. In Proceedings of the ION ITM 2016, International Technical Meeting, Monterey, CA, USA, 25 January 2016. [Google Scholar]
- Wen, W.S.; Bai, X.W.; Kan, Y.C.; Hsu, L.T. Tightly Coupled GNSS/INS Integration via Factor Graph and Aided by Fish-Eye Camera. IEEE T Veh. Technol. 2019, 68, 10651–10662. [Google Scholar] [CrossRef]
- Yue, Z.; Ma, W.Z.; Gao, Y.T.; Sun, C.C.; Zhang, M.S.; Lian, Z.Z.; Li, K.Z. Vehicle-mounted GNSS navigation and positioning algorithm considering signal obstruction and fuzzy logic in urban environment. Measurement 2025, 248, 116919. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, L.; Li, X. Characterization and modeling of GNSS site-specific unmodeled errors under reflection and diffraction using a data-driven approach. Satell. Navig. 2025, 6, 8. [Google Scholar] [CrossRef]
- Kou, R.X.; Tan, R.C.; Wang, S.Y.; Yang, B.S.; Dong, Z.; Yang, S.W.; Liang, F.X. Satellite visibility analysis considering signal attenuation by trees using airborne laser scanning point cloud. GPS Solut. 2023, 27, 64. [Google Scholar] [CrossRef]
- Dan, S.; Santra, A.; Mahato, S.; Dey, S.; Koley, C.; Bose, A. Multi-constellation GNSS Performance Study Under Indian Forest Canopy. In Advances in Communication, Devices and Networking; Springer: Singapore, 2022; pp. 179–186. [Google Scholar]
- Nishida, Y.; Li, Y.; Kamiya, T. Environment Recognition from A Spherical Camera Image Based on DeepLab v3+. In Proceedings of the 2021 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; pp. 2043–2046. [Google Scholar]
- Qu, Z.; Wei, C. A Spatial Non-cooperative Target Image Semantic Segmentation Algorithm with Improved Deeplab V3+. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 1633–1638. [Google Scholar]
- Humphrey, V.; Frankenberg, C. Continuous ground monitoring of vegetation optical depth and water content with GPS signals. Biogeosciences 2023, 20, 1789–1811. [Google Scholar] [CrossRef]
- Hsu, L.-T. Analysis and modeling GPS NLOS effect in highly urbanized area. GPS Solut. 2017, 22, 7. [Google Scholar] [CrossRef]
- Herrera, A.M.; Suhandri, H.F.; Realini, E.; Reguzzoni, M.; de Lacy, M.C. goGPS: Open-source MATLAB software. GPS Solut. 2016, 20, 595–603. [Google Scholar] [CrossRef]
- Wen, W.W.; Hsu, L.T. 3D LiDAR Aided GNSS NLOS Mitigation in Urban Canyons. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18224–18236. [Google Scholar] [CrossRef]
- Zeng, K.; Wang, Q.; Tang, J.; Li, Z.; Xie, K.; Xie, S. Mitigating NLOS Interference in GNSS Single-Point Positioning Based on Dual Self-Attention Networks. IEEE Internet Things J. 2025, 12, 4318–4330. [Google Scholar] [CrossRef]






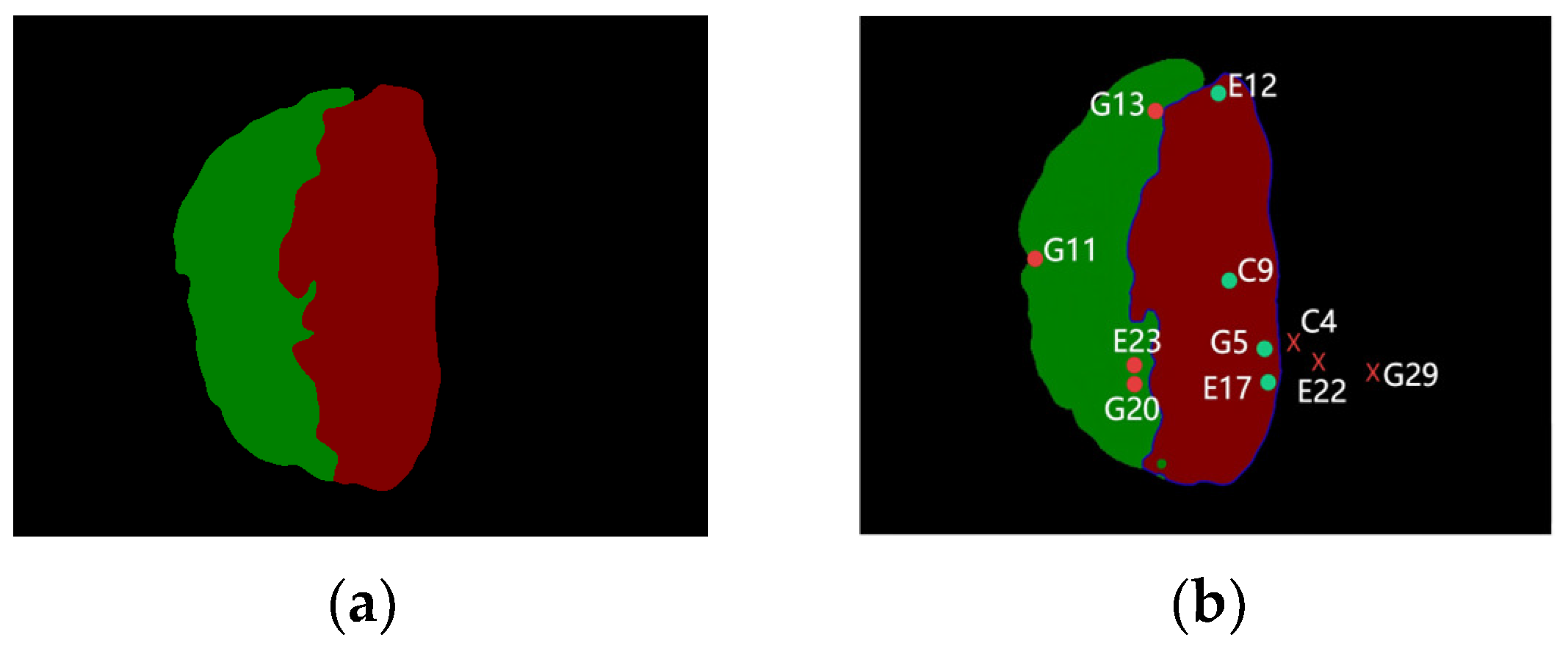
















| LOS | Attenuation | NLOS | |
|---|---|---|---|
| PRN | E12 E17 C9 G5 | G11 G13 E23 G20 | C4 E22 G29 |
| GNSS and Camera | |
|---|---|
| SPAN-SE | dual-frequency L1/L2GPS + GLONASS + B1-2/B2bBDS |
| Combination | CGI-410 |
| Focal length | 2.2 mm |
| VFOV | 90% |
| Image resolution | 640 × 9480 |
| Image frame rate | 20 fps |
| Path 1 RMSE(m) | Path 2 RMSE(m) | |||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| 2.37 | 5.83 | 7.09 | 1.53 | 2.82 | 5.40 | |
| 1.77 | 5.20 | 4.57 | 0.99 | 1.65 | 4.14 | |
| 2.73 | 6.36 | 5.26 | 1.17 | 2.58 | 3.83 | |
| Path 1 RMSE(m) | Path 2 RMSE(m) | |||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| 1.83 | 5.20 | 5.84 | 1.55 | 1.84 | 4.43 | |
| 1.84 | 5.18 | 5.08 | 1.26 | 1.80 | 4.31 | |
| 1.79 | 5.34 | 4.79 | 1.00 | 1.83 | 4.24 | |
| 1.77 | 5.70 | 4.69 | 1.02 | 1.88 | 4.19 | |
| 1.77 | 5.20 | 4.57 | 0.99 | 1.65 | 4.14 | |
| 1.81 | 5.43 | 4.62 | 1.01 | 1.70 | 4.12 | |
| 1.85 | 5.58 | 4.63 | 1.01 | 1.74 | 4.10 | |
| Path 1 RMSE(m) | Path 2 RMSE(m) | |||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| 1.80 | 6.07 | 4.76 | 1.06 | 1.68 | 4.30 | |
| 1.77 | 5.20 | 4.57 | 0.99 | 1.65 | 4.14 | |
| 1.77 | 5.20 | 4.63 | 0.98 | 1.94 | 4.08 | |
| 1.78 | 5.24 | 4.65 | 0.97 | 1.95 | 4.06 | |
| 1.79 | 5.11 | 4.66 | 0.97 | 1.96 | 4.03 | |
| Methods | Sky Area Accuracy | Number of Pixels |
|---|---|---|
| Canny | 79.1% | 44,789 |
| Flood Fill | 89.0% | 62,790 |
| Deep-Air | 98.9% | 57,196 |
| RMSE (m) | ME (m) | |||||
|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | |
| GNSS/INS/Flood Fill | 0.80 | 2.91 | 3.09 | −0.35 | 2.21 | 1.65 |
| GNSS/INS/Canny | 0.88 | 2.99 | 3.25 | 0.37 | 2.40 | 1.79 |
| GNSS/INS/Deep-Air | 0.64 | 2.75 | 2.52 | −0.05 | 2.25 | 1.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Z.; Sun, C.; Zhang, X.; Tang, C.; Gao, Y.; Li, K. A Semantic Segmentation-Based GNSS Signal Occlusion Detection and Optimization Method. Remote Sens. 2025, 17, 2725. https://doi.org/10.3390/rs17152725
Yue Z, Sun C, Zhang X, Tang C, Gao Y, Li K. A Semantic Segmentation-Based GNSS Signal Occlusion Detection and Optimization Method. Remote Sensing. 2025; 17(15):2725. https://doi.org/10.3390/rs17152725
Chicago/Turabian StyleYue, Zhe, Chenchen Sun, Xuerong Zhang, Chengkai Tang, Yuting Gao, and Kezhao Li. 2025. "A Semantic Segmentation-Based GNSS Signal Occlusion Detection and Optimization Method" Remote Sensing 17, no. 15: 2725. https://doi.org/10.3390/rs17152725
APA StyleYue, Z., Sun, C., Zhang, X., Tang, C., Gao, Y., & Li, K. (2025). A Semantic Segmentation-Based GNSS Signal Occlusion Detection and Optimization Method. Remote Sensing, 17(15), 2725. https://doi.org/10.3390/rs17152725







