Channel Amplitude and Phase Error Estimation of Fully Polarimetric Airborne SAR with 0.1 m Resolution
Abstract
1. Introduction
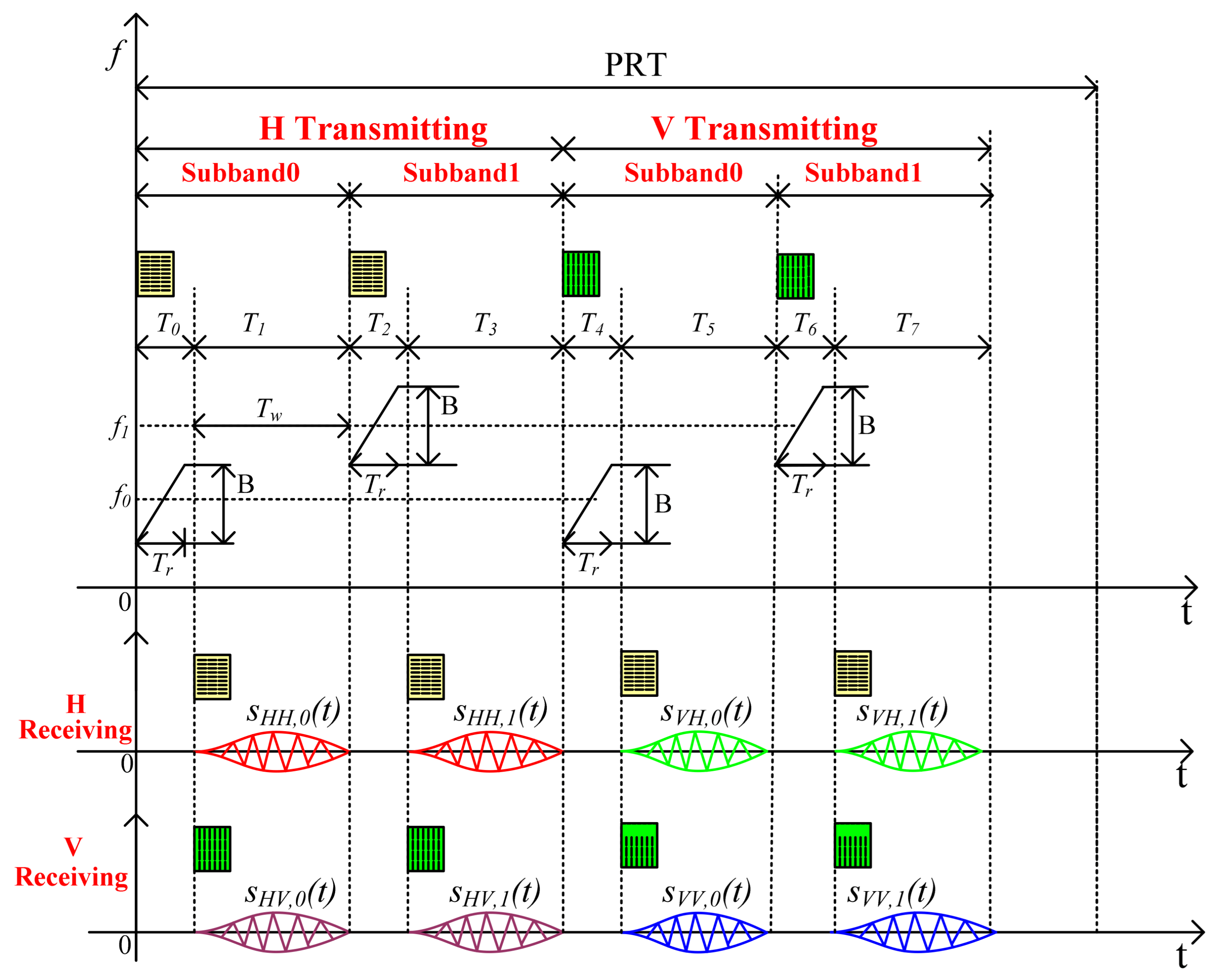
2. The Channel Amplitude and Phase Error Model
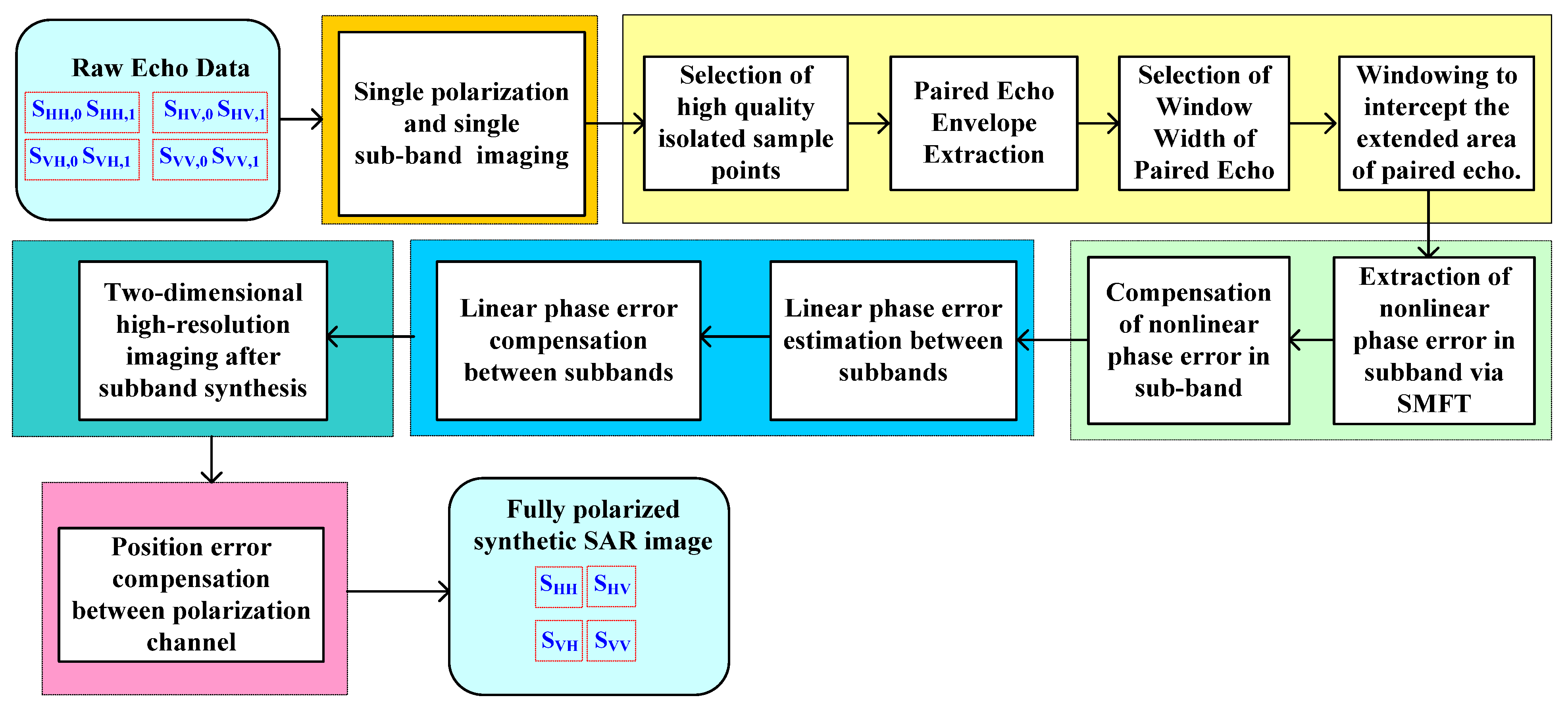
3. Channel Amplitude and Phase Error Estimation
3.1. Estimation of Spectrum Amplitude Distortion Within the Subband
3.2. Estimation of the Paired-Echo Window Width
3.3. In-Band Nonlinear Phase Error Estimation
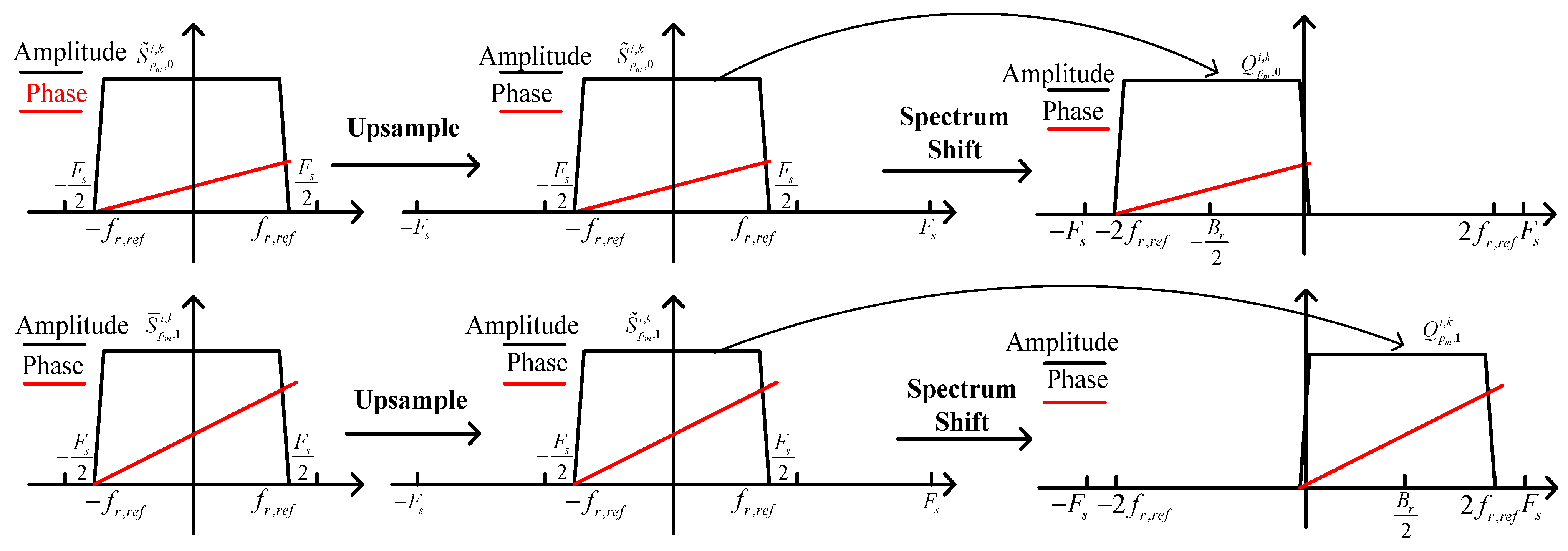
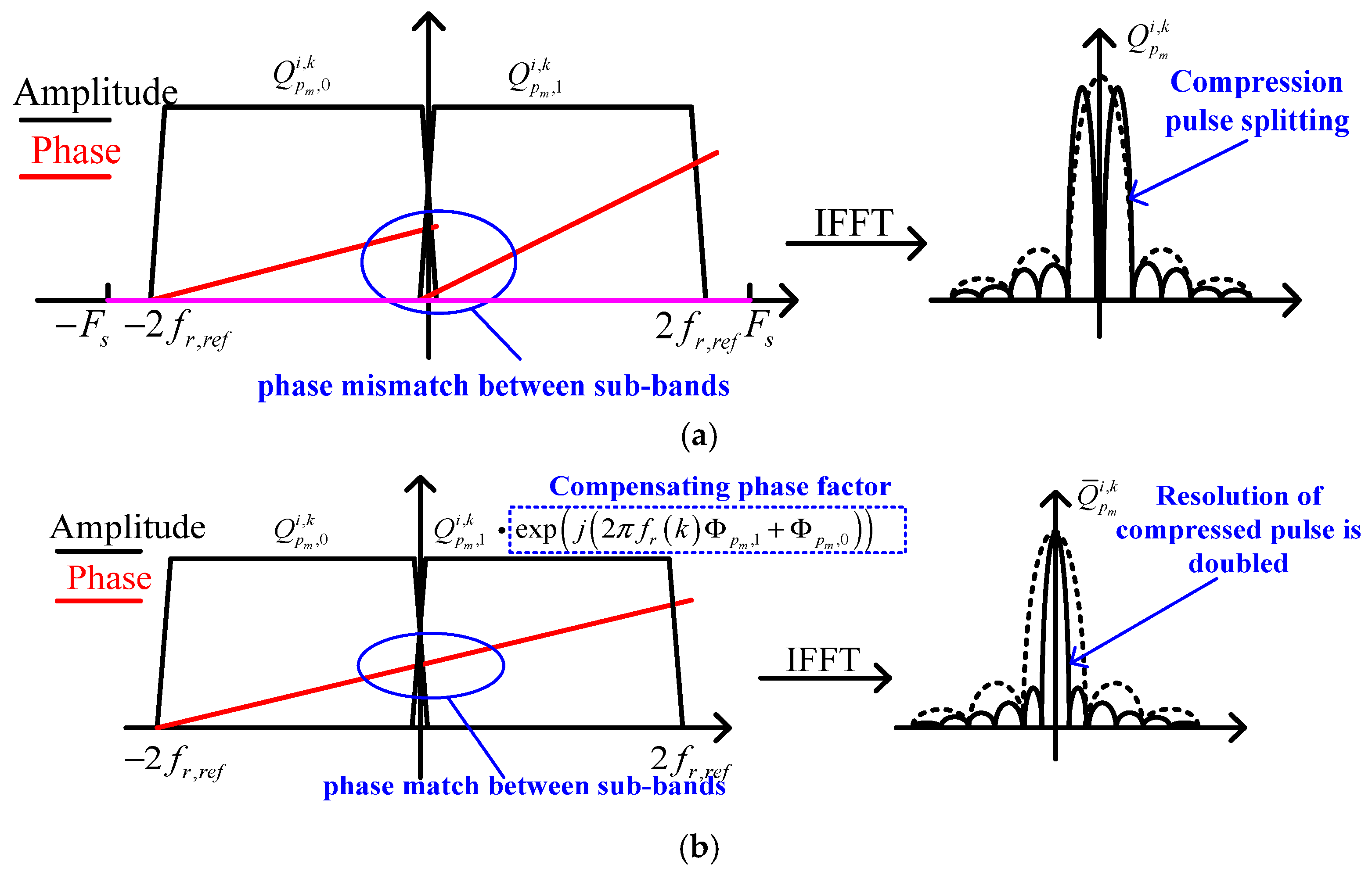
3.4. Linear Phase Error Estimation Between Subbands
3.5. Estimation of Position Deviation Between Polarized Channels
3.6. Computational Complexity Analysis of the Algorithm
4. Experimental Results
4.1. Fully Polarimetric Airborne SAR with 0.1 m Resolution
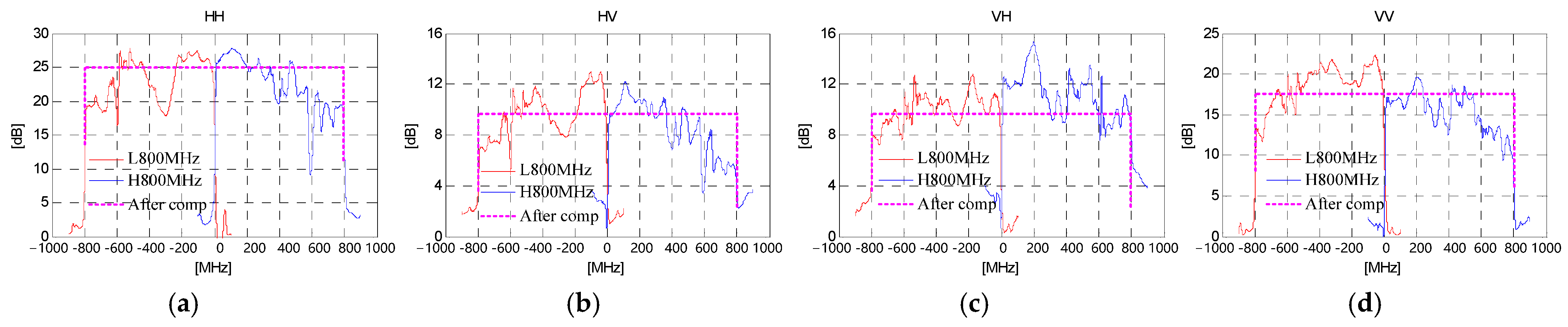
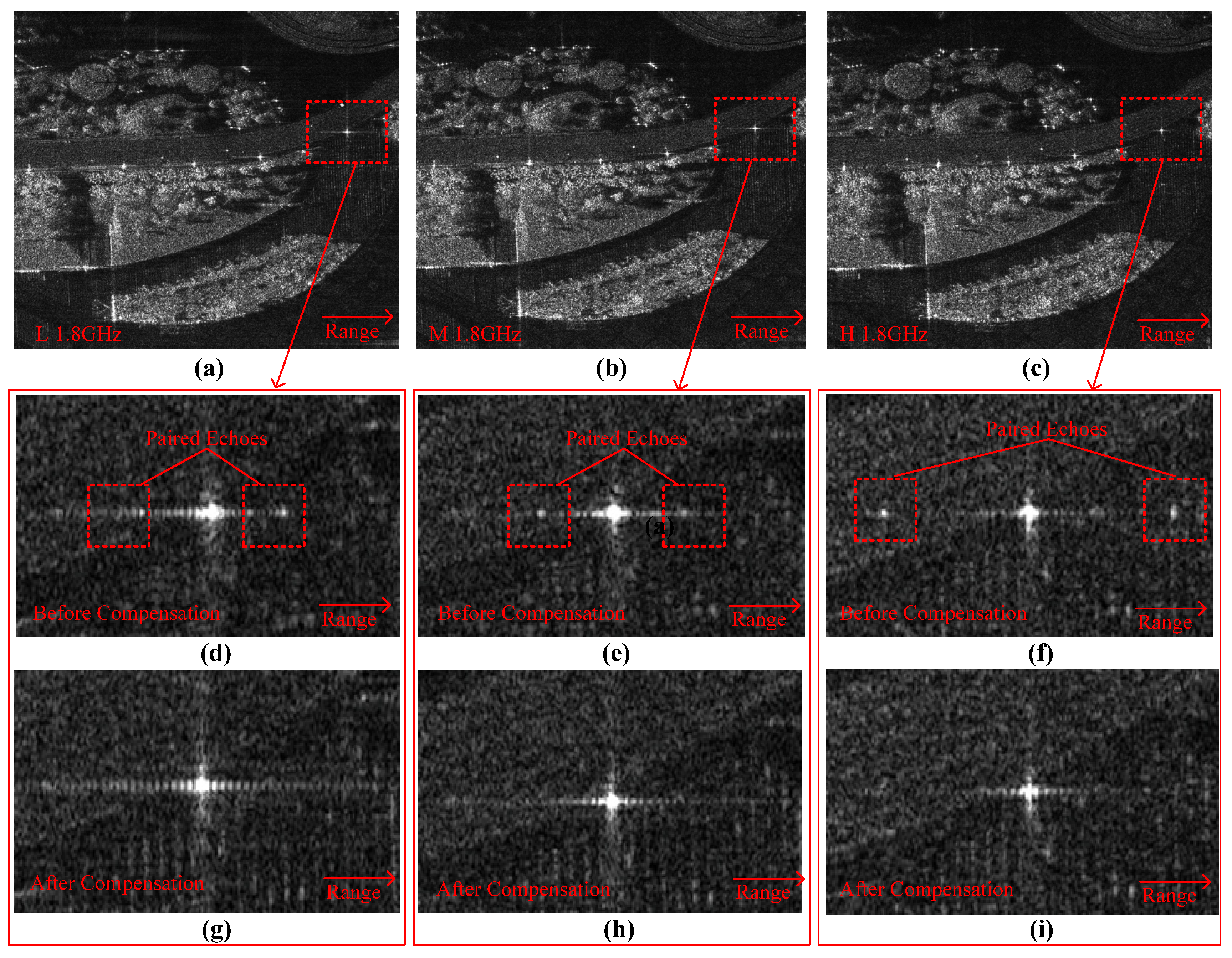
4.1.1. Subband Spectrum Amplitude Correction for Fully Polarimetric Airborne SAR
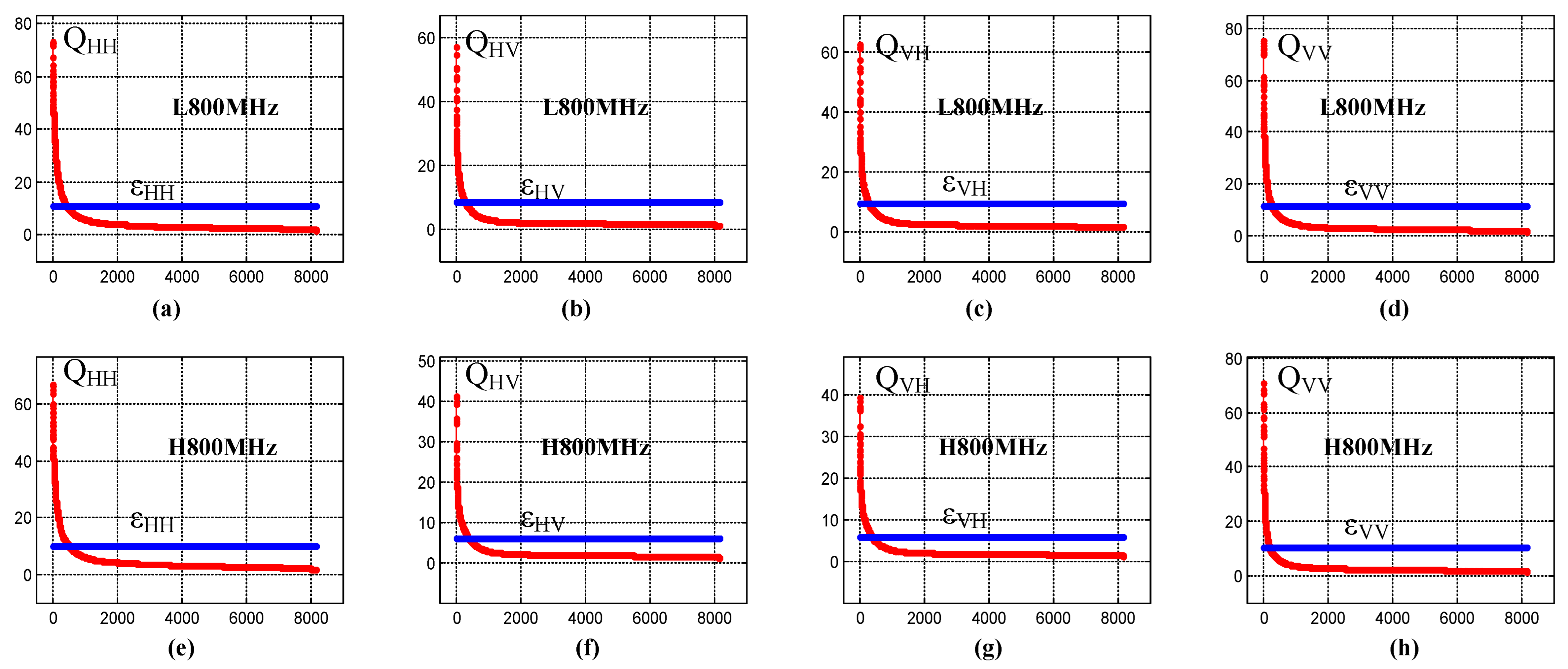
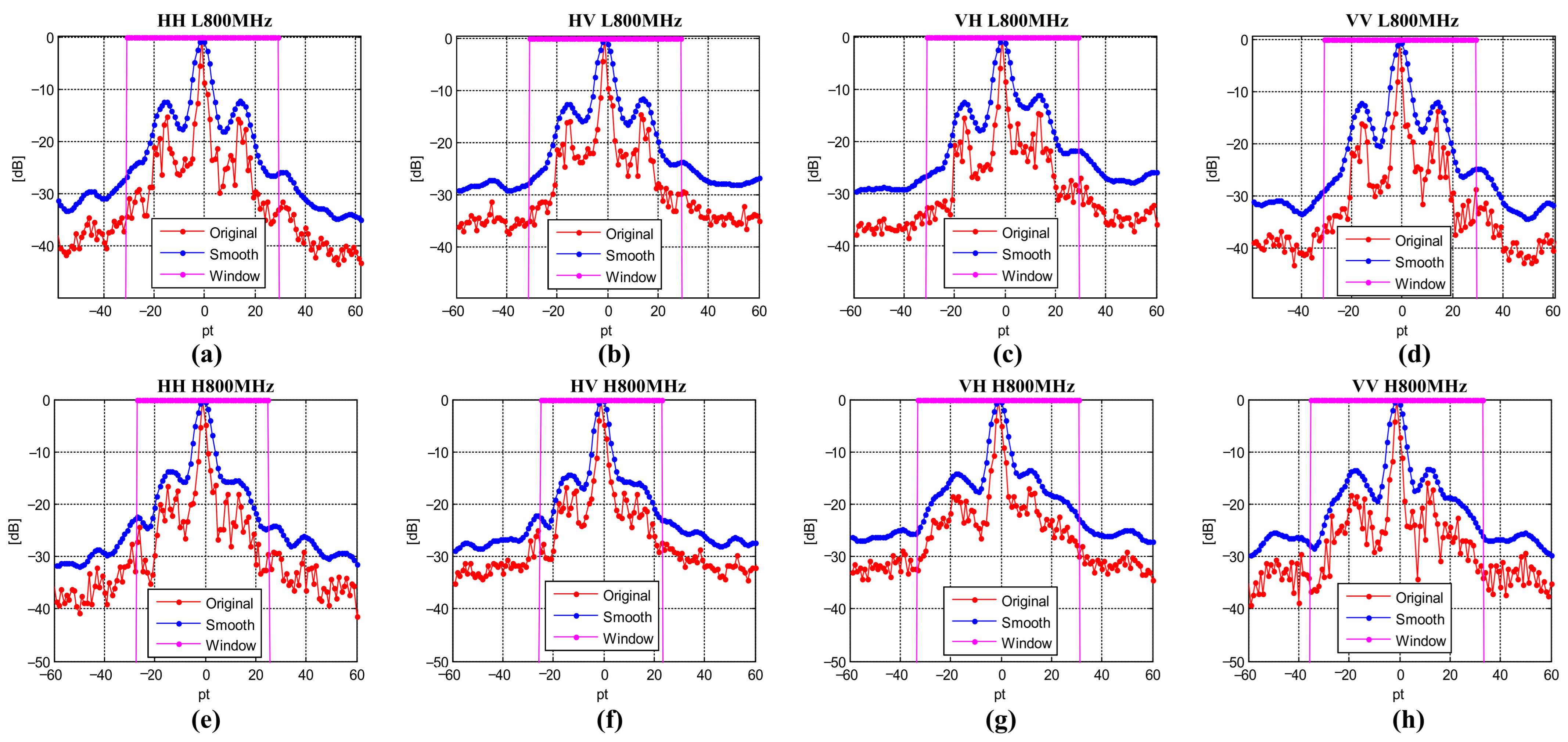
4.1.2. Selection of High-Quality Dominant Points and Determination of the Window Width of the Expansion Curve
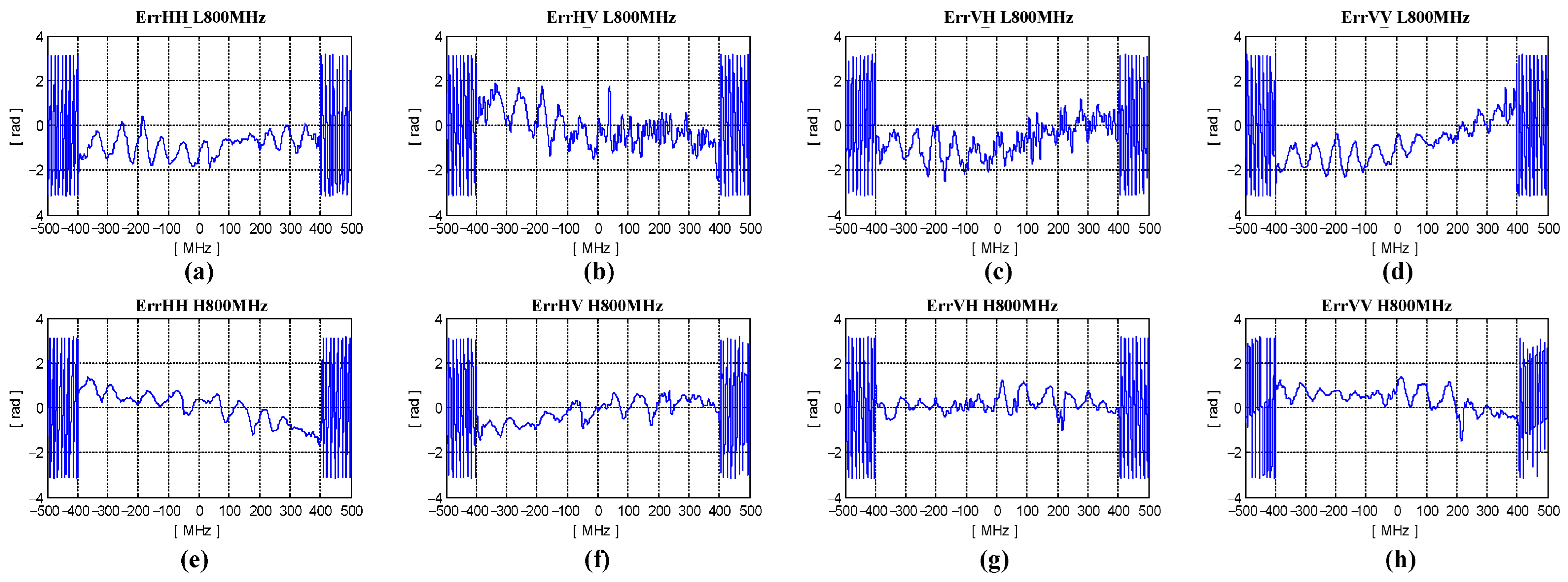
4.1.3. Nonlinear Phase Error Estimation for Fully Polarimetric Airborne SAR
4.1.4. Linear Phase Error Estimation Between Subbands
4.1.5. Estimation of Position Error Between Polarization Channels
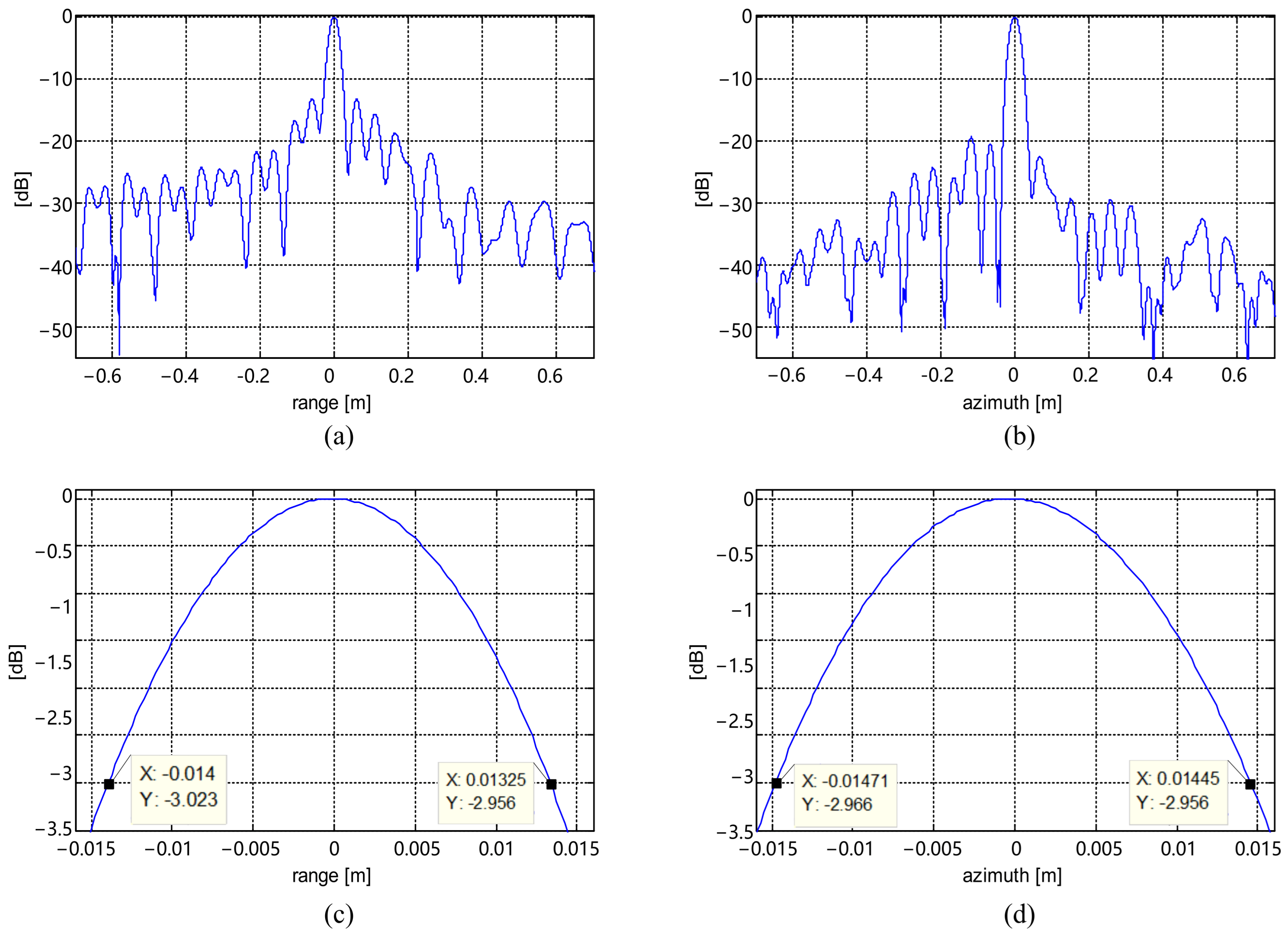
4.1.6. Fully Polarimetric Imaging After Amplitude and Phase Error Compensation
4.2. Ultrahigh-Resolution Single Polarimetric Airborne SAR with a 0.03 m Resolution
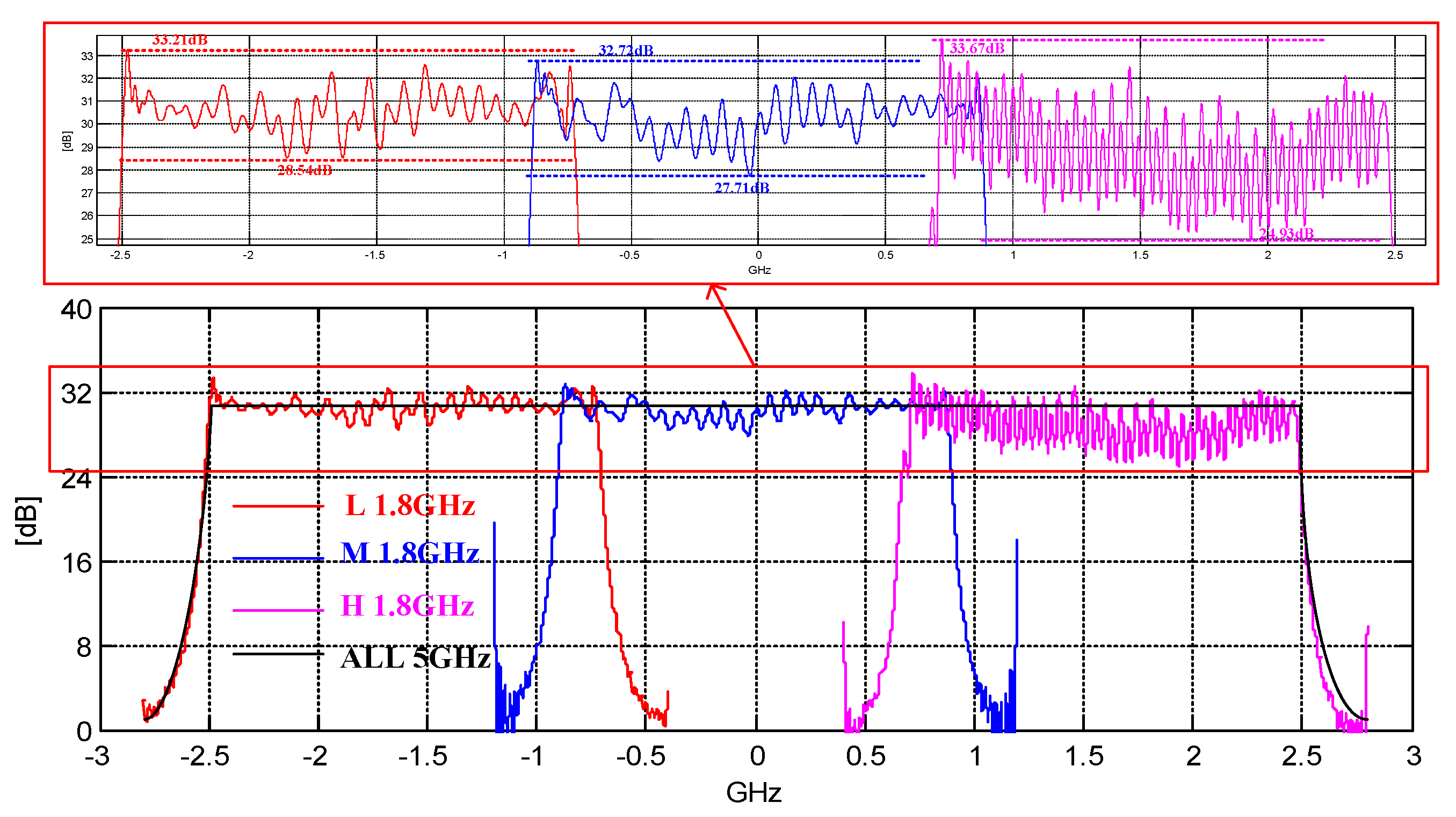
4.2.1. Subband Spectrum Amplitude Correction for Ultrahigh-Resolution Airborne SAR
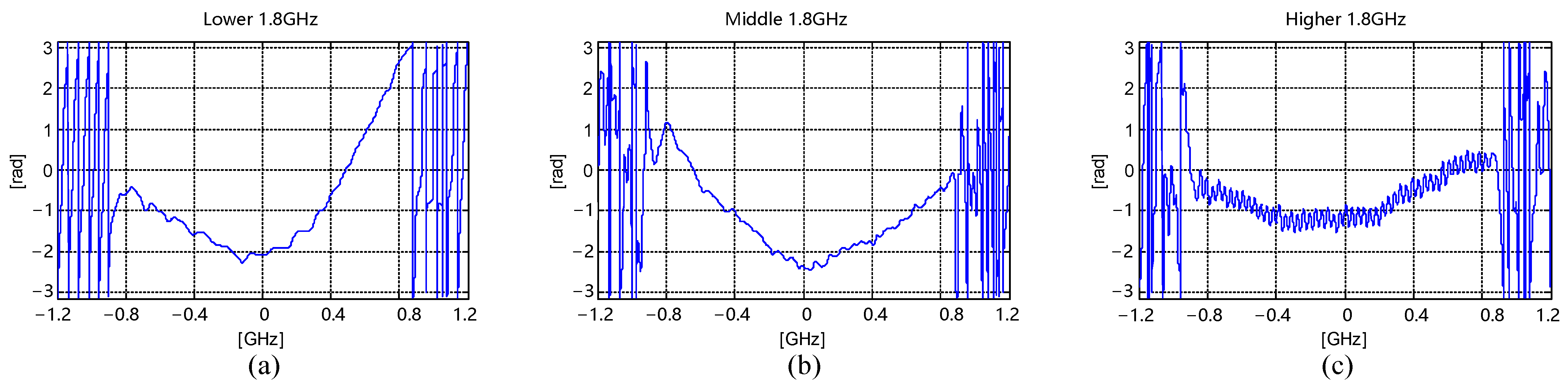
4.2.2. Nonlinear Phase Error Estimation in the Subband for Ultrahigh-Resolution Airborne SAR
4.2.3. Linear Phase Error Estimation Between Subbands for Ultrahigh-Resolution Airborne SAR
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Li, H.; Han, S. The Theory and Method of Pulse Coding for Radar and its Applications. J. Radars 2019, 8, 1–16. [Google Scholar]
- Deng, Y.; Yu, W.; Wang, P.; Xiao, D.; Wang, W.; Liu, K.; Zhang, H. The High-Resolution Synthetic Aperture Radar System and Signal Processing Techniques: Current progress and future prospects. IEEE Geosci. Remote Sens. Mag. 2024, 12, 169–189. [Google Scholar] [CrossRef]
- Yi, X.; Wang, C.; Lu, M.; Wang, J.; Grajal, J.; Han, R. 4.8 A Terahertz FMCW Comb Radar in 65 nm CMOS with 100GHz Bandwidth. IEEE Int. Solid-State Circuits Conf. 2020, 21, 90–92. [Google Scholar]
- Yi, X.; Wang, C.; Lu, M.; Wang, J.; Grajal, J.; Han, R. A 220-to-320-GHz FMCW Radar in 65-nm CMOS Using a Frequency-Comb Architecture. IEEE J. Solid-State Circuits 2021, 56, 327–339. [Google Scholar] [CrossRef]
- Hong, A.; Xiang, Y.; Wang, Y.; Hu, J.; He, Z.; He, G.; Yang, Y.; Lai, J.; He, H.; Deng, Z.; et al. A Terahertz FMCW Radar with 169-GHz Synthetic Bandwidth and Reconfigurable Polarization in 40-nm CMOS. IEEE Radio Freq. Integr. Circuits Symp. 2025, 3, 1–4. [Google Scholar]
- Deng, Y.; Wang, Y.; Liu, K.; Ou, N.; Liu, D.; Zhang, H.; Wang, J. Key Technologies for Spaceborne SAR Payload of LuTan-1 Satellite System. Acta Geod. Cartogr. Sinca 2021, 53, 1881–1895. [Google Scholar]
- Shi, L.; Li, P.; Zhang, L.; Ding, X.; Zhao, L. Polarimetric SAR Calibration and Residual Error Estimation When Corner Reflectors Are Unavailable. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4454–4471. [Google Scholar] [CrossRef]
- Sabry, R. Hybrid Products for Enhanced and Unified Full and Compact Polarimetric SAR Data Exploitations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 12059–12073. [Google Scholar] [CrossRef]
- Dong, F.; Yin, Q.; Hong, W. An Improved Man-Made Structure Detection Method for Multi-aspect Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 5717–5732. [Google Scholar] [CrossRef]
- McNairn, H.; Jiao, X. Monitoring Crop Condition Using Polarimetric SAR. IEEE Int. Geosci. Remote Sens. Symp. 2024, 1, 1700–1702. [Google Scholar]
- Long, T.; Zhang, T.; Ding, Z.; Yin, W. Effect Analysis of Antenna Vibration on GEO SAR Image. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1708–1721. [Google Scholar] [CrossRef]
- Liang, Y.; Li, G.; Zhang, G.; Xiang, C.; Wu, J. A Nonparametric Paired Echo Suppression Method for Helicopter-Borne SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2020, 17, 2080–2083. [Google Scholar] [CrossRef]
- Liang, W.; Jia, Z.; Hong, J.; Zhang, Q.; Wang, A.; Dong, Z. Polarimetric Calibration Scheme Combining Internal and External Calibrations, and Experiment for Gaofen-3. IEEE Access 2024, 8, 7659–7671. [Google Scholar] [CrossRef]
- Jung, C.; Bae, K.; Kim, D.; Park, S. Internal Calibration System Using Learning Algorithm With Gradient Descent. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1503–1507. [Google Scholar] [CrossRef]
- Wang, Q.; Pepin, M.; Beach, R.; Dunkel, R.; Atwood, T.; Santhanam, B.; Gerstle, W.; Doerry, A.; Hayat, M. SAR-based vibration estimation using the discrete fractional Fourier transform. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4145–4156. [Google Scholar] [CrossRef]
- Wang, Q.; Pepin, M.; Wright, A.; Dunkel, R.; Atwood, T.; Santhanam, B.; Gerstle, W.; Doerry, A.; Hayat, M. Reduction of vibration-induced artifacts in synthetic aperture radar imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3063–3073. [Google Scholar] [CrossRef]
- Li, Y.; Ding, L.; Zheng, Q.; Zhu, Y.; Sheng, J. A novel high frequency vibration error estimation and compensation algorithm for THz-SAR imaging based on local FrFT. Sensors 2020, 20, 2669. [Google Scholar] [CrossRef]
- Shi, S.; Li, C.; Hu, J.; Zhang, X.; Fang, G. A High Frequency Vibration Compensation Approach For Terahertz SAR Based on Sinusoidal Frequency Modulation Fourier Transform. IEEE Sens. J. 2021, 21, 10796–10803. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zhao, B.; Xu, L. Enhancement of azimuth focus performance in high-resolution SAR imaging based on the compensation for sensors platform vibration. IEEE Sens. J. 2016, 16, 6333–6345. [Google Scholar] [CrossRef]
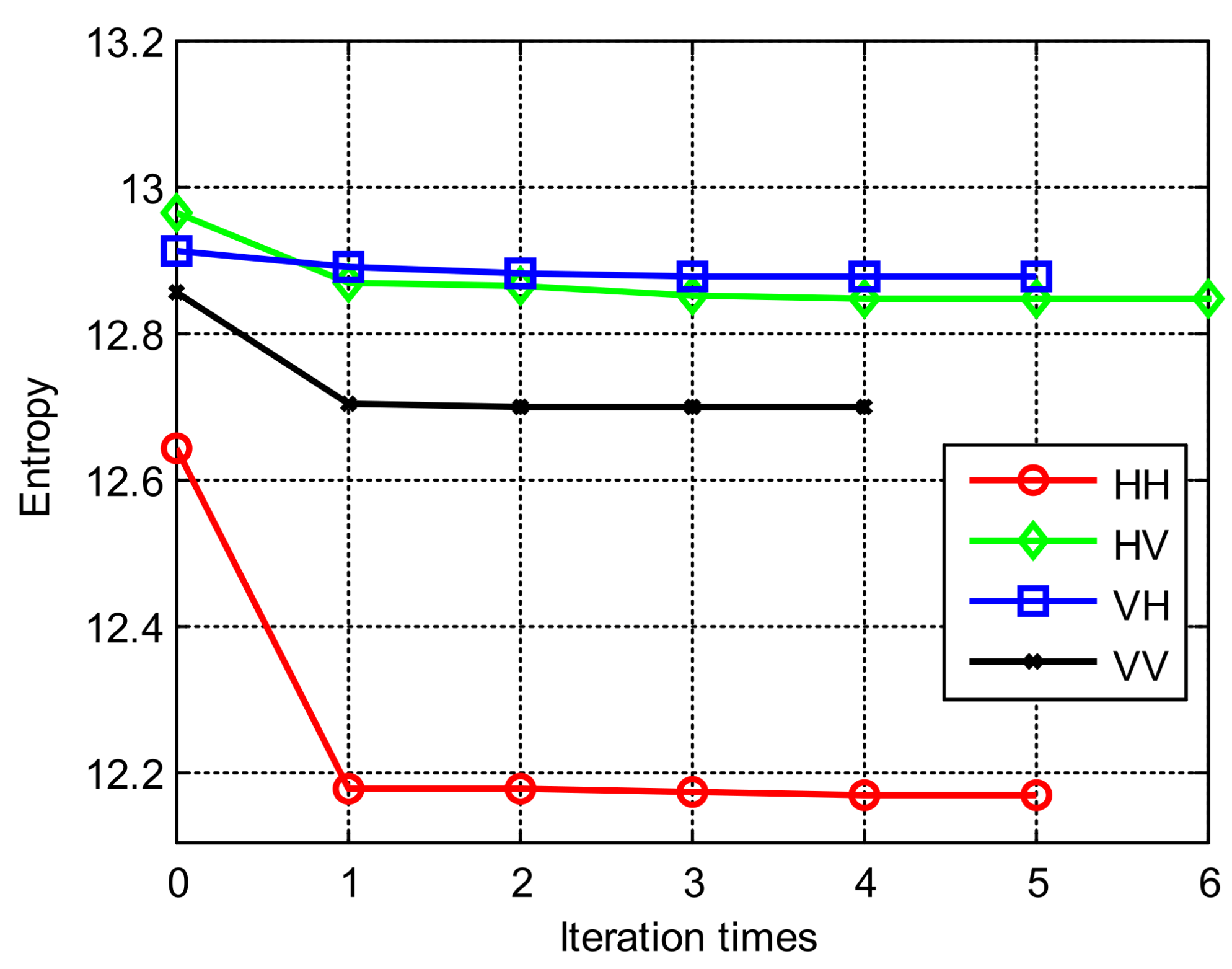
- Shi, S.; Li, C.; Hu, J.; Zhang, X.; Fang, G. Motion Compensation for Terahertz Synthetic Aperture Radar Based on Subaperture Decomposition and Minimum Entropy Theorem. IEEE Sens. J. 2020, 20, 14940–14949. [Google Scholar] [CrossRef]
- Meng, Z.; Zhang, L.; Ma, Y.; Wang, G.; Jiang, H. Accelerating Minimum Entropy Autofocus With Stochastic Gradient for UAV SAR Imagery. IEEE Trans. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4017805–4017809. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, K. Earth-Based Radar Imaging Technology of the Moon Based on Minimum Entropy Autofocus Algorithm. In Proceedings of the IEEE 7th International Conference on Information Communication and Signal Processing, Zhoushan, China, 21–23 September 2024; pp. 626–630. [Google Scholar]
- Shao, W.; Hu, J.; Ji, Y.; Pan, J.; Fang, G. Phase Error Correction in Sparse Linear MIMO Radar Based on the Equivalent Phase Center Principle. Remote Sens. 2024, 16, 3685. [Google Scholar] [CrossRef]
- Evers, A.; Jacsin, J. Generalized Phase Gradient Autofocus Using Semidefinite Relaxation Phase Estimation. IEEE Trans. Geosci. Remote Sens. 2020, 6, 291–303. [Google Scholar] [CrossRef]
- Li, Y.; Young, S. Kalman Filter Disciplined Phase Gradient Autofocus for Stripmap SAR. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6298–6308. [Google Scholar] [CrossRef]
- Hu, L.; Wei, J.; Su, S.; Huang, S.; Zhao, Z.; Tong, X. A New SAR Autofocus Method Based on Error Coefficient Optimization. In Proceedings of the IEEE 10th International Conference on Computer and Communications, Chengdu, China, 13–16 December 2024; pp. 746–750. [Google Scholar]
- Wang, C.; Zhang, Q.; Hu, J.; Fang, G. An Efficient Algorithm Based on Frequency Scaling for THz Stepped-Frequency SAR Imaging. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
















| Operation of Algorithm | Step of Algorithm | Quantity | Computational Complexity |
|---|---|---|---|
| Correction of subband spectrum amplitude | Range FFT of subband signal * | 8 channels | * |
| Average amplitude spectrum | |||
| Subband spectrum amplitude correction * | * | ||
| Estimation of paired-echo window width | Calculate contrast of range line | 8 channels | |
| Normalize amplitude of high-quality line | |||
| Correction of in-band nonlinear phase error | Nonlinear phase error estimation in subband | 8 channels | |
| Nonlinear phase error compensation in subband * | * | ||
| Correction of linear phase error between subbands | Phase error compensation | 4 channels L iterations | |
| IFFT of synthesized spectrum | |||
| Calculate image entropy | |||
| Calculate intermediate variables | |||
| Calculate gradient | |||
| Linear phase error compensation * | 4 channels | * | |
| Correction of position deviation between polarized channels | 2D FFT of image sample | 4 channels | |
| Conjugate multiplication | |||
| 2D IFFT of the result of conjugate multiplication | |||
| Computational complexity for estimation | |||
| Other computational complexity * | |||
| Technical Parameter | Technical Parameter Value |
|---|---|
| Center frequency | 15 GHz |
| Polarization channel number | 4 |
| Subband pulse width | 20 µs |
| Flight altitude | 3000 m |
| Subband bandwidth | 800 MHz |
| Total bandwidth | 1600 MHz |
| Number of subbands | 2 |
| detection range | >10 km |
| Polarization Mode | Computational Time for Linear Phase Error Estimation Between Subbands (s) |
|---|---|
| HH | 0.1104 |
| HV | 0.1275 |
| VH | 0.1178 |
| VV | 0.1065 |
| Total computational time | 0.4622 |
| Polarization Mode | Subband Range Resolution (m) | Synthesized Range Resolution Without Compensation (m) | Synthesized Range Resolution with Compensation (m) |
|---|---|---|---|
| HH | 0.1827 | 0.2833 | 0.0979 |
| HV | 0.1800 | 0.1332 | 0.0985 |
| VH | 0.1800 | 0.1530 | 0.0981 |
| VV | 0.1875 | 0.1450 | 0.0982 |
| Technical Parameter | Technical Parameter Value |
|---|---|
| Center frequency | 15 GHz |
| Polarization mode | VV |
| Work pattern | Strip-map/Spotlight |
| Subband pulse width | 10 µs |
| Flight altitude | 2500 m |
| Subband bandwidth | 1.8 GHz |
| Total bandwidth | 5.0 GHz |
| Number of subbands | 3 |
| Resolution | 0.03 × 0.03 m |
| detection range | >10 km |
| Point Target | Range Resolution (m) | Azimuth Resolution (m) |
|---|---|---|
| A | 0.0273 | 0.0292 |
| B | 0.0286 | 0.0282 |
| C | 0.0280 | 0.0285 |
| D | 0.0271 | 0.0291 |
| E | 0.0288 | 0.0289 |
| Average value | 0.0280 | 0.0288 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Wang, Y.; Xie, J.; Fang, G.; Chen, H.; Shen, Y.; Yang, Z.; Zhang, X. Channel Amplitude and Phase Error Estimation of Fully Polarimetric Airborne SAR with 0.1 m Resolution. Remote Sens. 2025, 17, 2699. https://doi.org/10.3390/rs17152699
Hu J, Wang Y, Xie J, Fang G, Chen H, Shen Y, Yang Z, Zhang X. Channel Amplitude and Phase Error Estimation of Fully Polarimetric Airborne SAR with 0.1 m Resolution. Remote Sensing. 2025; 17(15):2699. https://doi.org/10.3390/rs17152699
Chicago/Turabian StyleHu, Jianmin, Yanfei Wang, Jinting Xie, Guangyou Fang, Huanjun Chen, Yan Shen, Zhenyu Yang, and Xinwen Zhang. 2025. "Channel Amplitude and Phase Error Estimation of Fully Polarimetric Airborne SAR with 0.1 m Resolution" Remote Sensing 17, no. 15: 2699. https://doi.org/10.3390/rs17152699
APA StyleHu, J., Wang, Y., Xie, J., Fang, G., Chen, H., Shen, Y., Yang, Z., & Zhang, X. (2025). Channel Amplitude and Phase Error Estimation of Fully Polarimetric Airborne SAR with 0.1 m Resolution. Remote Sensing, 17(15), 2699. https://doi.org/10.3390/rs17152699








