Abstract
For tropical forests characterized by tall and densely packed trees, even long-wavelength SAR signals may fail to achieve full penetration, posing a significant challenge for retrieving sub-canopy terrain using polarimetric interferometric SAR (InSAR)(PolInSAR) techniques. This paper proposes a single-baseline PolInSAR-based correction method for sub-canopy terrain estimation based on a one-dimensional lookup table (LUT) that links forest height to unpenetrated depth. The approach begins by applying an optimal normal matrix approximation to constrain the complex coherence measurements. Subsequently, the difference between the PolInSAR Digital Terrain Model (DTM) derived from the Random Volume over Ground (RVoG) model and the LiDAR DTM is defined as the unpenetrated depth. A nonlinear iterative optimization algorithm is then employed to estimate forest height, from which a fundamental mapping between forest height and unpenetrated depth is established. This mapping can be used to correct the bias in sub-canopy terrain estimation based on the PolInSAR RVoG model, even with only a small amount of sparse LiDAR DTM data. To validate the effectiveness of the method, experiments were conducted using fully polarimetric P-band airborne SAR data acquired by the European Space Agency (ESA) during the AfriSAR campaign over the Mabounie region in Gabon, Africa, in 2016. The experimental results demonstrate that the proposed method effectively mitigates terrain estimation errors caused by insufficient signal penetration or the limitation of single-interferometric geometry. Further analysis reveals that the availability of sufficient and precise forest height data significantly improves sub-canopy terrain accuracy. Compared with LiDAR-derived DTM, the proposed method achieves an average root mean square error (RMSE) of 5.90 m, representing an accuracy improvement of approximately 38.3% over traditional RVoG-derived InSAR DTM retrieval. These findings further confirm that there exist unpenetrated phenomena in single-baseline low-frequency PolInSAR-derived DTMs of tropical forested areas. Nevertheless, when sparse LiDAR topographic data is available, the integration of fully PolInSAR data with LUT-based compensation enables improved sub-canopy terrain retrieval. This provides a promising technical pathway with single-baseline configuration for spaceborne missions, such as ESA’s BIOMASS mission, to estimate sub-canopy terrain in tropical-rainforest regions.
1. Introduction
Sub-canopy terrain information constitutes a fundamental dataset for the monitoring of forest ecosystems. Accurate characterization of the bare-earth terrain enables more precise estimation of forest vertical structure and geomorphological features. This is critically important for monitoring geological hazards in forested areas, supporting climate change adaptation, informing carbon emission reduction strategies, and enhancing our understanding of forest ecosystems’ functioning and stability [1,2,3,4,5,6,7].
Interferometric Synthetic Aperture Radar (InSAR) technology provides unique advantages for large-scale Earth observation, due to its all-weather, day-and-night imaging capabilities and partial penetration through vegetation, including terrain mapping [8,9,10], disaster monitoring [11,12,13], and forest investigation [14,15,16], etc. Currently, global Digital Elevation Models (DEMs) derived from InSAR are primarily based on short-wavelength radar data. For example, the Shuttle Radar Topography Mission (SRTM), jointly carried out by National Aeronautics and Space Administration (NASA) and the National Geospatial-Intelligence Agency (NGA), employed single-platform interferometry with dual antennas to acquire elevation data for approximately 80% of the Earth’s land surface, primarily using C-band radar [3]. Similarly, the TanDEM-X mission, operated by the German Aerospace Center (DLR) and the European Space Agency (ESA), generated a global DEM with spatial resolutions of 12 m (high-resolution) and 30 m (standard version) using X-band SAR data [2]. However, the accuracy of sub-canopy terrain estimation using InSAR is inherently constrained by factors such as radar wavelength, forest structure, and vegetation density, etc. [17,18,19]. In forested regions, short-wavelength SAR signals (e.g., X- and C-band) often suffer from insufficient signal penetration, leading to interferometric phase centers that are located within or above the canopy layer. Consequently, the resulting Digital Elevation Models (DEMs) tend to represent Digital Surface Models (DSMs) that incorporate canopy height, rather than the actual bare-earth topography beneath the forest cover.
Therefore, accurately retrieving sub-canopy terrain fundamentally relies on the effective separation of canopy and ground-scattering components in interferometric measurements. A straightforward approach involves subtracting existing global forest-height products from available DEMs to estimate the sub-canopy terrain [1,20]. However, the applicability of this method is limited by the spatial coverage and accuracy of forest-height datasets, making the availability of high-accuracy, wide-coverage forest-height products a critical constraint. SAR tomography (TomoSAR) exploits multiple image acquisitions to synthesize an aperture in the cross-range direction, enabling direct 3D imaging of forest structure as well as the estimation of high-resolution forest-height and sub-canopy terrain products [15,21,22,23,24]. Nevertheless, due to the stringent baseline configuration requirements, only airborne SAR systems currently meet the technical conditions for TomoSAR imaging, limiting its scalability for large-area topographic mapping.
The integration of polarimetric observations with InSAR measurements offers new opportunities for large-scale sub-canopy terrain estimation. Different polarizations (e.g., HH, HV, VH, VV) exhibit distinct scattering responses to the forest medium and varying penetration depths [25,26]. By leveraging low-frequency SAR and parametric models, such as the coherence optimization-based phase separation method and the Random Volume over Ground (RVoG) model, it becomes possible to more effectively separate canopy and ground scattering, thereby improving the retrieval accuracy of both sub-canopy terrain and forest-height products [27,28,29,30,31,32]. Phase separation fundamentally relies on exploiting the scattering mechanism diversity across polarizations to identify complex coherence components most sensitive to either canopy or ground. These components can then be directly transformed into ground phase estimates through the phase-to-height operator. However, such methods typically do not incorporate the physical relationships between forest biophysical parameters and polarimetric InSAR (PolInSAR) observables, and their reliability is limited by the radar’s actual penetration capability. In contrast, the RVoG model establishes a theoretical relationship between multi-polarimetric InSAR measurements and forest structural parameters, including forest height, ground elevation, extinction coefficient, and ground-to-volume amplitude ratio. Under ideal observation conditions, the complex coherences align along a straight line, and one point of intersection with the coherence region circle indicates the ground phase [27,28,29]. This enables ground-phase retrieval through the linear fitting of multi-polarimetric complex coherences. Nevertheless, even SAR systems operating at long wavelengths (e.g., P-band) may fail to fully penetrate dense, tall forests such as tropical forests. In such cases, the ground phase obtained through the linear fitting of the RVoG model may deviate from the true bare-earth surface, leading to inaccuracies in the DTM derived from the model. In addition, it has been demonstrated that the PolInSAR inversion performance depends on different optimal interferometric geometry in the case of different forest heights; the single-interferometric geometry-based method is unable to handle complex forest scenes with diverse tree heights, which can lead to deviations in the estimated DTM products in areas with inappropriate tree heights [33,34]. Thus, while the RVoG model provides a compensatory improvement over direct inversion methods, its performance remains limited in severely penetration-constrained environments or with poor geometric configuration. To address these limitations, it is essential to develop a correction strategy that incorporates the prior forest structural information to correct RVoG-derived terrain estimates, thereby improving accuracy in tropical forest areas with the configuration of single-baseline low-frequency SAR.
LiDAR can provide highly accurate DTM products but is often limited in spatial coverage due to acquisition costs and platform constraints. In contrast, PolInSAR enables large-scale mapping with sensitivity to forest structure. Therefore, the motivation of this paper lies in developing an effective method for accurately retrieving sub-canopy terrain by leveraging the complementary strengths of sparse LiDAR data and spatially continuous PolInSAR observations. This paper proposes a method for correcting sub-canopy terrain using a one-dimensional lookup table (LUT). The core idea of the method is to compute the difference between a LiDAR-derived DTM and the DTM estimated from PolInSAR data using the RVoG model—referred to here as the “unpenetrated depth”. By establishing a LUT that relates this unpenetrated depth to RVoG-derived forest height, the method can be extended to larger areas where only PolInSAR data is available, and LiDAR coverage is lacking. To validate the effectiveness of the proposed method, we employed airborne PolInSAR data acquired during the AfriSAR campaign, conducted by ESA in 2016 over the Mabounie region in Gabon, Africa.
The primary contributions of this study are (1) discovering the existence of unpenetrated phenomena in single-baseline low-frequency PolInSAR-derived DTMs of tropical forested areas, and (2) developing a new method for correcting PolInSAR-derived sub-canopy terrain using a one-dimensional lookup table.
2. Materials and Methods
2.1. The Overview of RVoG Model
The RVoG model provides a simplified physical representation of radar-wave penetration through vegetated areas by modeling the forest as a penetrable random volume of vegetation overlying the ground surface. This representation enables the separation of volume and ground-scattering components in PolInSAR data. The model further establishes a mathematical relationship between the polarized interferometric complex coherence and forest structural parameters, such as forest height, ground phase, the ground-to-volume amplitude ratio, and the extinction coefficient. The analytical expression of this relationship is given in Equation (1) [28,29].
where represents the interferometric phase associated with the ground surface; the ground-to-volume amplitude ratio determines the relative contribution of ground and volume scattering components for a given polarization , and is dependent on system geometry and forest structure; and denotes the pure volume coherence, which is solely attributed to the vegetation layer, excluding any contribution from ground scattering. Under this model, the pure volume coherence is given by
where represents the forest height; is the extinction coefficient, which characterizes the attenuation of radar signals as they propagate through the vegetation layer; denotes the radar incidence angle; and is the interferometric vertical wavenumber, describing the spatial frequency of the interferometric phase variation in the vertical direction. The interferometric vertical wavenumber is computed as
where represents the radar wavelength, represents the interferometric perpendicular baseline, and denotes the distance between the ground objects and sensors. is a sensor-specific coefficient: for monostatic configurations, ; for bistatic configurations, .
The interferometric vertical wavenumber not only directly impacts the accuracy of terrain-elevation retrieval but also plays a critical role in vegetation height inversion and terrain correction. Typically, based on prior knowledge of the tree height range in the test area, the range of can be used to select appropriate interferometric baseline pairs for forest height and sub-canopy terrain inversion. In principle, to avoid phase-wrapping issues, the height of ambiguity should generally be greater than twice the tree height. The formula for calculating the height of ambiguity is as follows.
Equation (2) provides the closed-form solution for the RVoG model. The model parameters can be solved using polarimetric interferometric complex coherence, with well-known methods such as the nonlinear iterative optimization algorithm [28] and the three-stage algorithm [29]. However, the RVoG model is inherently linear, and the polarimetric complex coherence from single-baseline interferometry exhibits linear dependencies, leading to rank deficiency in the solution, as shown in Figure 1. Therefore, this paper employs the best normal matrix approximation solution to constrain the complex coherence matrix to obtain the endpoints of the visible coherence line for maximum coherence separation [35]. The two complex coherences resulting from the maximum coherence separation directly determine the intersection point of the coherence line and the complex unit circle. By evaluating the sign of , the ground phase is determined according to the criteria as follows [34]:
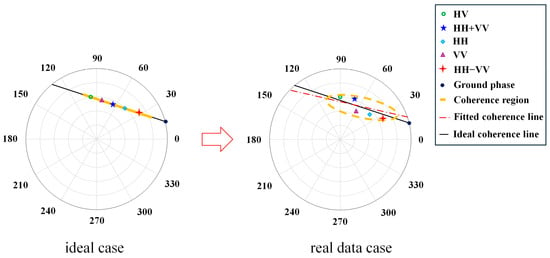
Figure 1.
Schematic diagram of the position of the complex coherence coefficient in the unit polarization circle based on the RVoG model.
Once the ground phase is obtained, the ground elevation can be calculated using the height-to-phase conversion operator, as follows:
where represents the terrain obtained by the RVoG model, represents the elevation obtained through the phase-to-height conversion, and represents the removed reference topography during PolInSAR data processing, for example, TanDEM-X DEM used in the paper.
To obtain the forest height and address the rank deficiency issue in the RVoG parameter inversion, two complex coherences resulting from maximum phase separation, constrained by the best normal matrix approximation, are used to construct equations [36]. A 4-D nonlinear iterative optimization algorithm is employed to estimate the unknown parameters. During the iteration process, the ground phase is treated as the truth without error, as follows:
where and represent two endpoint complex coherences along the visible coherence line after applying the best normal matrix approximation, corresponding to the maximum phase separation, and are the ground-to-volume amplitude ratios corresponding to and , represents the RVoG model, and represents the Euclidean vector norm.
2.2. Penetration Depth Model
Differences in radar wavelength led to variations in the interferometric phase-height positions obtained with the same polarization mode when penetrating through forested areas. Additionally, factors such as regional differences, forest type, tree species, and density can cause discrepancies in the elevation derived from the interferometric phase. As shown in Figure 2, the relationship between the penetration depth of the radar wave, forest height, and sub-canopy terrain is illustrated. Empirically, it is widely observed that as forest height and density increase, the penetration depth of the radar wave decreases, and the unpenetrated depth increases. Previous studies have established a linear relationship between forest height and penetration depth to correct DTM estimation biases caused by insufficient penetration [17]. This paper proposes a novel approach that establishes a relationship between the model-estimated forest height and unpenetrated depth and uses a one-dimensional LUT to correct DTM biases resulting from unpenetrated depth or poor interferometric geometry. The unpenetrated depth represents the difference between the DTM obtained by the RVoG model and the LiDAR DTM, which is expressed as follows.
where represents an external LiDAR DTM, which is considered as the ground truth, and represents the DTM obtained by the RVoG model. Therefore, this study corrects the sub-canopy terrain estimation bias caused by insufficient penetration or poor geometric configuration by establishing mapping between the forest height and the unpenetrated depth, expressed as
where denotes the mapping function between and .
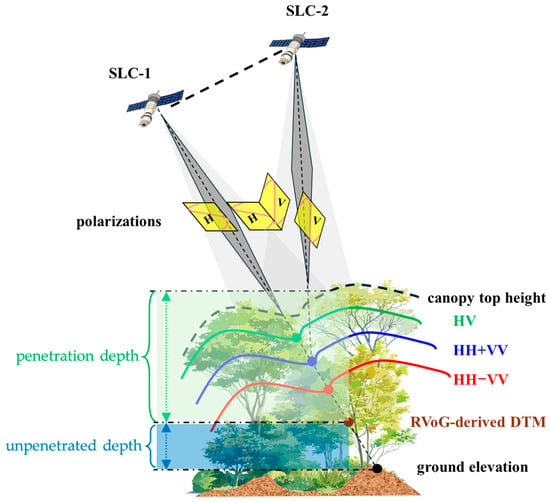
Figure 2.
Schematic diagram of the penetration of fully polarized radar waves in a forest area.
In practice, we constructed this mapping by discretizing the forest height into 5 m intervals (including 0–5 m, 5–10 m, 10–15 m, 15–20 m, 20–25 m, 25–30 m, 30–35 m, 35–40 m, 40–45 m, 45–50 m, 50–55 m, 55–60 m, etc.), sampling the corresponding values, and computing the mean within each height bin. A continuous relationship was then obtained through the one-dimensional interpolation method. Notably, the forest height used to construct the mapping can be obtained either from RVoG-based inversion or from sparse LiDAR-derived height products. For example, Global Ecosystem Dynamics Investigation (GEDI) measurements can be utilized to define the mapping function, which can subsequently be applied to correct DTM estimation biases across fully SAR-covered areas using the RVoG-derived forest height. Considering the observational strategy of the GEDI mission, although the data nominally covers latitudes between 51.6°N and 51.6°S globally, the along-track spacing between the adjacent laser footprints is approximately 600 m, and the across-track swath is sparse due to the instrument’s configuration of three parallel laser tracks with limited beam divergence. As a result, GEDI cannot provide continuous spatial coverage. Therefore, the proposed method provides a promising technical solution for large-scale sub-canopy terrain retrieval.
The overall workflow proposed in this study is illustrated in Figure 3 and consists of the following five steps:
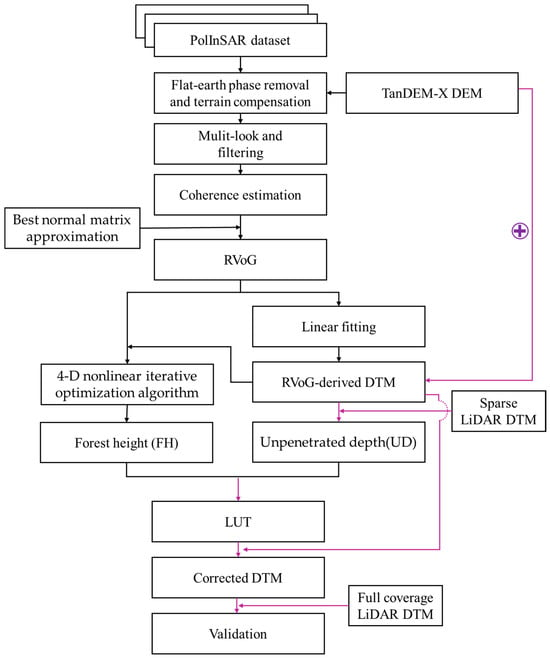
Figure 3.
The data-processing flowchart for correcting sub-canopy terrain using a one-dimensional LUT method.
- (1)
- Data preprocessing: the PolInSAR data was preprocessed using the PolSARpro v6.0 software [37], including flattening and terrain compensation, the multi-looking operator, speckle noise filtering, and complex coherence estimation;
- (2)
- Best normal matrix approximation [36]: a regularization constraint was applied to the complex coherence matrix to extract the two endpoints of the visible coherence line corresponding to the maximum phase separation;
- (3)
- Ground-phase estimation: based on the sign of the interferometric vertical wavenumber, the ground phase was selected from two intersection points of the coherence line and the complex unit circle. A coherence threshold and height-of-ambiguity range mask were then applied to suppress phase-unwrapping errors and speckle noise;
- (4)
- Unpenetrated depth and forest height estimation: the ground elevation was calculated using Equation (6) and was subtracted from the TanDEM-X DEM to obtain the penetration depth. A one-dimensional lookup table mapping between the RVoG-derived forest height and unpenetrated depth was then constructed using Equations (8) and (9);
- (5)
- Sub-canopy terrain correction: the derived LUT was used to correct the DTM bias caused by the unpenetrated depth of the radar wave, resulting in a more accurate estimation of the sub-canopy terrain.
2.3. The Test Site and SAR Dataset
The AfriSAR campaign is a key Earth observation initiative led by the European Space Agency (ESA), in collaboration with partner institutions such as the German Aerospace Center (DLR) and the French Aerospace Laboratory (ONERA). The primary objective of AfriSAR is to support the development of the upcoming BIOMASS mission by providing reference datasets for the algorithm development, calibration, and validation of geophysical products related to biomass and forest structure.
The study area selected in this paper is located in the Mabounie region of western Gabon, along the central west coast of Africa. As shown in Figure 4, the SAR imagery covers a region characterized by gently undulating hilly terrain, with elevations ranging from 10 m to 200 m. This area is representative of dense tropical rainforest environments, with an average forest height of approximately 30 m.
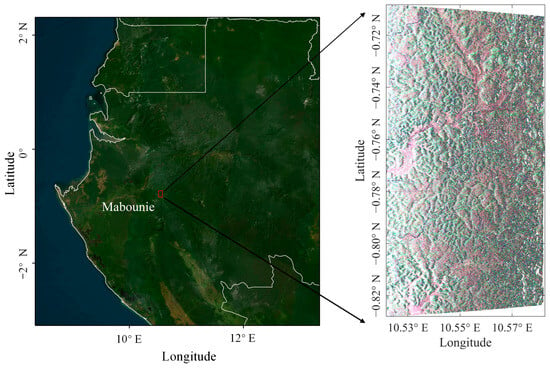
Figure 4.
Geographic location of the Mabounie region in western Gabon and the coverage extent of the color composite image derived from PolInSAR data acquired during the AfriSAR campaign.
The P-band PolInSAR data used in this study was acquired by DLR’s F-SAR system on February 11, 2016. The acquired dataset offers a slant-range resolution of approximately 1.2 m and an azimuth resolution of 0.9 m. Table 1 summarizes the key acquisition parameters of the PolInSAR dataset. All SAR preprocessing, including imaging and co-registration, was conducted by DLR. Using scene 0708 as the reference image, the corresponding vertical wavenumber and incidence angle parameters were derived for each interferometric pair. In this study, an interferometric pair with a baseline of approximately 30 m was selected, which is optimal for forest-parameter retrieval using the RVoG model.

Table 1.
The parameters of PolInSAR image data.
In parallel with the radar campaign, airborne LiDAR measurements were conducted in February and March 2016 by a consortium of international agencies, including ESA, DLR, ONERA, and NASA. The data was acquired using the Land, Vegetation, and Ice Sensor (LVIS), a full-waveform LiDAR instrument onboard NASA’s Langley B200 aircraft. The resulting LiDAR products, with a spatial resolution of 20 m, include both DTM and forest height, as shown in Figure 5a,b, respectively. Due to cloud cover and other weather-related limitations, LiDAR data was available only for a portion of the SAR-covered area.
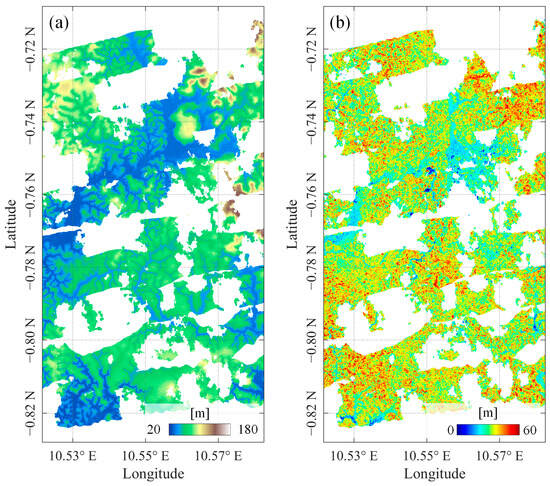
Figure 5.
The LiDAR-derived (a) DTM and (b) forest height.
In this study, the available LiDAR forest height and DTM were used as reference datasets to validate the performance of the proposed sub-canopy terrain retrieval algorithm.
2.4. Accuracy Assessment Metrics
To quantitatively evaluate the accuracy of the sub-canopy terrain retrieval, two standard error metrics were used: root mean square error (RMSE) and bias (mean error). These indicators were computed by comparing the estimated DTM against the LiDAR-derived DTM, and are defined as
where and denote the RVoG-estimated and LiDAR-derived DTM at pixel index , respectively.
In addition, to assess the accuracy of the forest height estimation, the relative error () was adopted and defined as
where and denote the RVoG-estimated and LiDAR-derived forest height at pixel index , respectively. This metric provided a normalized evaluation of the forest-height inversion accuracy.
3. Results
Figure 6 and Figure 7 presents a comparative visualization of four DTMs and their elevation differences with respect to the LiDAR DTM across the study area, including the TanDEM-X DEM, the DTM retrieved using a straightforward subtraction method (i.e., the difference between TanDEM-X DEM and forest height), the DTM retrieved using a linear-fitting-based RVoG model, and the corrected DTM produced by the proposed method. In Figure 6a, the TanDEM-X DEM consistently shows higher elevations compared to the LiDAR DTM. This overestimation is attributed to the limited penetration capability of the X-band SAR signal, where the interferometric phase center typically resides within the upper canopy, thereby failing to represent the true ground topography. The extensive red regions in Figure 7a, indicating elevation errors of 10 to 30 m, further corroborate this, underscoring the inadequacy of X-band InSAR for sub-canopy terrain mapping in densely forested tropical environments. Figure 6b and Figure 7b show the sub-canopy terrain derived by directly subtracting the forest height estimated via a nonlinear iterative optimization algorithm from the TanDEM-X DEM. The resulting terrain exhibits a clear underestimation, suggesting that, despite the limited penetration capability of the X-band, its interferometric phase center does not accurately correspond to the true canopy top height. Moreover, the forest height estimated from the RVoG model is subject to inversion uncertainties, which further limits the accuracy of sub-canopy terrain retrieval when relying solely on the difference between these two height products.
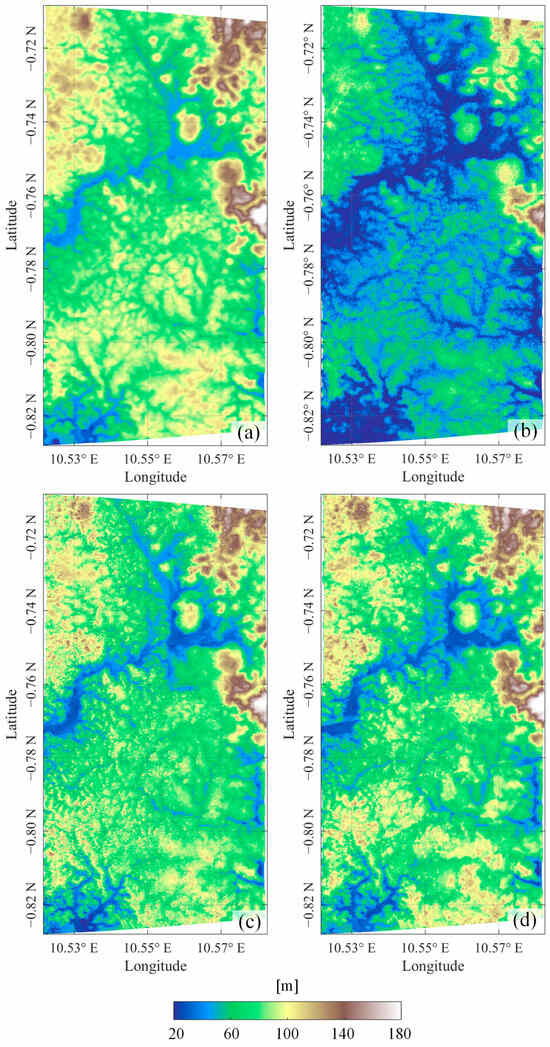
Figure 6.
Comparison of DTMs derived from different methods. (a) TanDEM-X DEM; (b) DTM obtained by straightforward subtraction method; (c) RVoG-derived DTM; (d) corrected DTM using the proposed method.
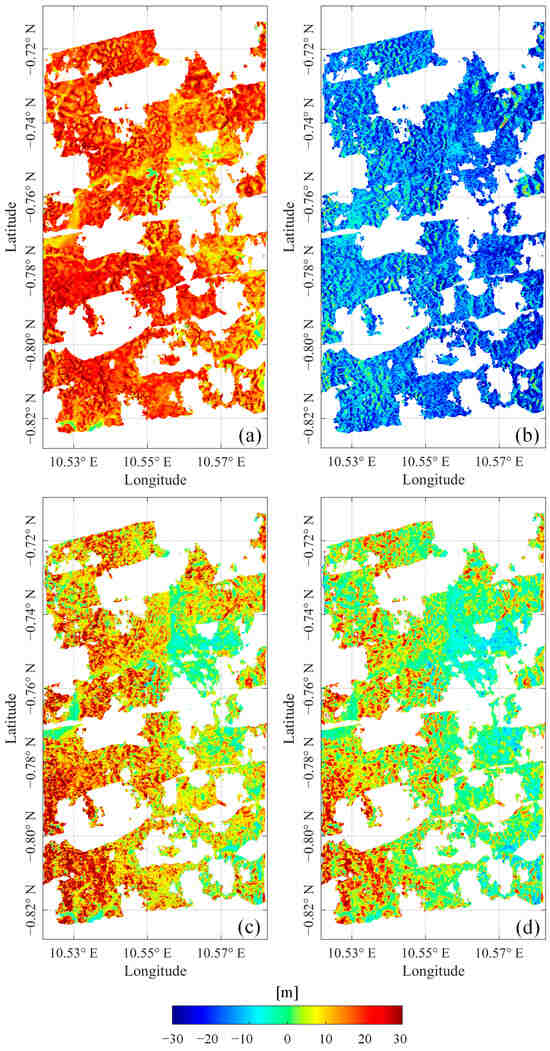
Figure 7.
Differences between DTMs obtained by different methods and LiDAR DTM. (a) TanDEM-X DEM; (b) DTM obtained by straightforward subtraction method; (c) RVoG-derived DTM; (d) corrected DTM using the proposed method.
Figure 6c and Figure 7c show the DTM obtained using the RVoG-based linear fitting method and the corresponding elevation difference with respect to the LiDAR DTM. This method mitigates part of the canopy-induced phase bias by fitting two complex coherence values with maximum phase separation. The resulting terrain estimates are closer to the actual ground surface; however, Figure 7c still reveals systematic overestimation in the range of 5–15 m, particularly in areas with tall or dense vegetation. In this study, the test area is located in a tropical-rainforest region characterized by tall and dense vegetation. Therefore, the systematic overestimation observed in the DTM derived from model fitting is attributed to the insufficient penetration of radar signals or the limitation of single-baseline RVoG inversion. Moreover, whether the geometric configuration of the RVoG model is suitable for sub-canopy terrain retrieval is also a critical factor affecting the accuracy of the results. One of the key assumptions underlying the RVoG model is that the forest can be represented as a two-layer structure composed of homogeneous ground and canopy. However, this assumption may not always hold true in complex, multilayered tropical-rainforest environments. As investigating the detailed structure of real-world forests is beyond the scope of this study, we focused only on general scenarios where the RVoG model assumptions are reasonably satisfied. In contrast, Figure 6d shows the DTM corrected using the proposed method, which employs a compensation strategy based on a one-dimensional mapping between forest height and unpenetrated depth. The corresponding error map in Figure 7d shows a substantial reduction in elevation deviation, with most errors confined within ±5 m. The marked decrease in high-bias regions demonstrates the effectiveness of the proposed method in correcting overestimation caused by incomplete ground return, particularly in areas of dense canopy cover or tall-tree regions. Overall, the results highlight the practical utility of the proposed method in retrieving accurate sub-canopy terrain in challenging tropical-forest environments.
Figure 8 presents scatter plots comparing the elevations derived from four different DTM products against the LiDAR-derived DTM. In Figure 8a, the TanDEM-X DEM exhibits a clear systematic overestimation, with a high RMSE of 17.14 m and a bias of 15.95 m. These results highlight the severe elevation bias associated with X-band SAR data, primarily due to its limited penetration capability. The interferometric phase center is typically located within the upper canopy, rather than on the actual ground surface, leading to substantial overestimation in densely forested areas. In Figure 8b, the DTM obtained by directly subtracting the two height products exhibits a significant underestimation, with an RMSE of 16.46 m and a bias of −14.91 m compared to the LiDAR DTM. This result is consistent with the findings in Figure 7b and further highlights that the accuracy of sub-canopy terrain derived from direct subtraction is fundamentally constrained by the inherent uncertainties in the input height products and the reference-terrain product. Figure 8c demonstrates improved performance using the RVoG-based linear fitting method. The RMSE is reduced to 9.57 m and the bias drops to 6.46 m. While the overall alignment with the LiDAR DTM is improved, the elevation estimates still show a tendency toward overestimation caused by incomplete signal penetration or RVoG-derived estimation bias, particularly in regions with tall and dense canopy cover. In contrast, Figure 8d shows the results of the proposed correction method, which achieved the highest accuracy among the three approaches. The RMSE is further reduced to 5.90 m and the bias to −1.12 m. Notably, the densest cluster of scatter points indicated in red is closely aligned with the 1:1 reference line, reflecting strong agreement between the corrected DTM and the LiDAR-derived ground truth. These results validate the effectiveness of the proposed method in mitigating elevation overestimation and demonstrate its potential to significantly improve sub-canopy terrain retrieval in densely vegetated regions.
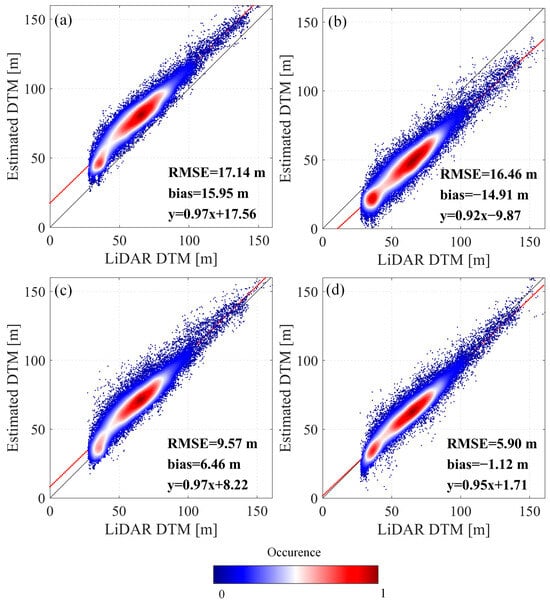
Figure 8.
Scatterplots comparing estimated DTMs with LiDAR DTM: (a) TanDEM-X DEM; (b) DTM obtained by straightforward subtraction method; (c) RVoG-derived DTM; (d) corrected DTM using the proposed method.
These findings underscore that although P-band SAR provides better forest penetration than shorter wavelengths, there exist the unpenetrated phenomena in single-baseline PolInSAR-derived DTMs in the case of tall tropical forests. Therefore, penetration-depth correction based on forest structure is crucial. The proposed method can significantly improve the accuracy of sub-canopy terrain estimation, offering a promising solution for retrieving accurate terrain models beneath dense forest canopies. Furthermore, the approach provides a valuable reference for P-band missions, such as BIOMASS, for addressing sub-canopy terrain-mapping challenges.
4. Discussion
4.1. Analysis of the Law Between Forest Height and Penetration Depth
In forested environments, which act as partially penetrable media, the penetration depth of radar signals varies significantly with wavelength, presenting a major challenge for accurate bare-earth terrain retrieval. Even long-wavelength SAR systems, such as those operating at P-band, experience limitations when attempting to penetrate dense and tall forests, particularly in tropical-rainforest regions.
In this study, we employed fully polarimetric airborne P-band SAR data acquired over the Mabounie region in Gabon, an area characterized by dense tropical vegetation. The experimental results reveal that, despite the use of a parameterized RVoG model, notable elevation estimation biases persisted due to limited signal penetration. This effect was especially pronounced in areas with high canopy closure and elevated forest biomass.
To better quantify the penetration capability of P-band SAR under different vegetation conditions, we investigated the empirical relationship between model-estimated forest height and unpenetrated depth, defined as the vertical difference between the RVoG-derived ground phase center elevation and the LiDAR-derived DTM. The forest heights were grouped into 5 m intervals, and boxplots were generated to visualize the statistical distribution of unpenetrated depth within each height bin, as shown in Figure 9. Furthermore, Figure 10 illustrates the continuous one-dimensional LUT between forest height and unpenetrated depth, constructed using interpolation methods based on the sampled statistics.
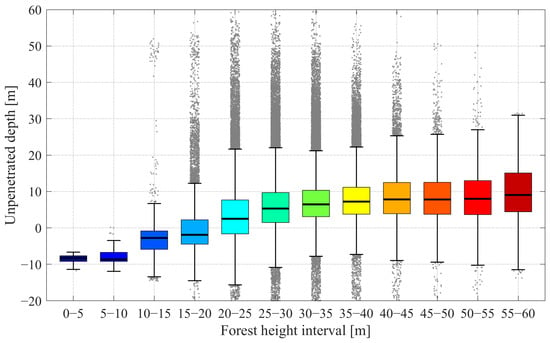
Figure 9.
Boxplot of unpenetrated depth versus RVoG-derived forest height. Note that Different colors in the bars represent different height intervals.
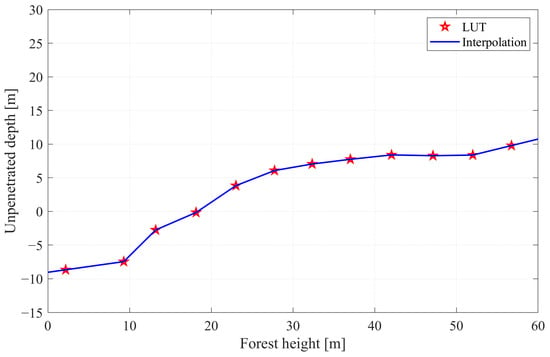
Figure 10.
One-dimensional LUT between unpenetrated depth and RVoG-derived forest height obtained by interpolation.
The results show a clear and consistent trend:
- For forest heights below 25 m, the median unpenetrated depth is near zero or slightly negative, with interquartile ranges mostly within ±5 m. This indicates that the P-band signal is capable of penetrating the vegetation layer and reaching the ground surface in sparse or moderately tall forest areas. The presence of negative values suggests that in the case of forests with low height, the phase center may fall below the actual ground elevation, possibly due to strong penetration causing the signal to penetrate below the ground;
- In contrast, for forest heights above 25 m, the unpenetrated depth becomes increasingly positive, and the spread of the distribution also widens. The median unpenetrated depth increases almost monotonically with forest height. This clearly indicates a height-dependent limitation of penetration: as forest height and associated biomass increase, signal attenuation due to volume scattering intensifies, leading to incomplete ground return and an upward shift in the phase center;
- The increased variance observed in higher bins reflects the heterogeneity of forest structure at large heights. Canopy layering, vertical density gradients, and variations in undergrowth can all affect the backscattering signal, introducing spatial inconsistencies in the phase-center location.
This analysis confirms that even at P-band, which is considered optimal for forest applications, penetration is incomplete in dense tropical forests, particularly in areas with heights exceeding 30–40 m. The observed empirical relationship provides a foundation for model-data mixed correction strategies, such as the height-dependent bias compensation proposed in this study. By exploiting this monotonic relationship, it becomes feasible to mitigate systematic overestimation in terrain elevation and enhance the accuracy of the ground-elevation mapping in forested areas.
From an application perspective, the findings underscore the necessity of incorporating vegetation structure information when utilizing SAR data for DTM retrieval in forested regions. For upcoming spaceborne missions such as BIOMASS, which operates at P-band with full polarimetry and tomography capabilities, such empirical relationships could inform error modeling and fusion strategies with ancillary data (e.g., LiDAR, optical forest height maps) to achieve more accurate ground-elevation estimates.
4.2. Impact of Forest-Height Accuracy
This paper proposes a one-dimensional LUT approach to correct sub-canopy terrain bias, based on the relationship between forest height and unpenetrated depth, as defined in Equation (9). Consequently, the accuracy of the forest-height input plays a crucial role in the effectiveness of the correction.
Figure 11 illustrates the estimated forest height by using the nonlinear iterative optimization algorithm. The accuracy of this estimated forest height was evaluated against the LiDAR-derived forest height, as shown in Figure 11b. The quantitative comparison indicates an average RMSE of 5.15 m, with a bias of −2.20 m and a relative error () of approximately 16.63%. The results indicate substantial systematic deviations, especially at lower canopy heights. Specifically, the forest height derived from nonlinear optimization tends to overestimate lower canopy heights and underestimate taller forests, implying that the forest-height-dependent LUT method may propagate into subsequent terrain corrections. This outcome is consistent with the principles of error propagation: when the forest-height input contains inaccuracies, the derived lookup table will also be biased, thereby introducing additional errors into the corrected sub-canopy terrain. These findings underscore that higher accuracy in forest-height estimation leads to a more reliable mapping between forest height and unpenetrated depth, and consequently, to more accurate sub-canopy terrain correction using the proposed lookup table approach.
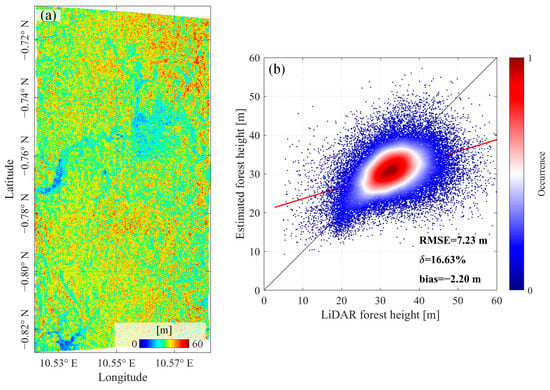
Figure 11.
The estimated forest height by using the nonlinear iterative nonlinear iterative optimization algorithm: (a) estimated forest height; (b) scatterplot comparison of the estimated forest height and LiDAR forest height.
Figure 12 and Figure 13 illustrate the relationship between unpenetrated depth and forest height when the LiDAR-derived forest height is used as the reference input. As shown in the figures, the linear relationship between forest height and unpenetrated depth becomes notably stronger, particularly for forest heights exceeding approximately 25 m. For forests below this threshold, both the LiDAR-based and model-based boxplots indicate unpenetrated depths that are either negative or near zero, suggesting that radar signals fully penetrate the lower-vegetation canopy, occasionally reaching or even penetrating slightly beneath the actual ground surface. However, for forests exceeding 25 m, the LiDAR-based results demonstrate a more distinct and consistent linear increase in unpenetrated depth with increasing canopy height compared to those derived using the RVoG model. This clear divergence highlights how inaccuracies in the model-derived forest height can weaken the empirical correlation between canopy height and unpenetrated depth, emphasizing the critical importance of accurate canopy-height inputs for robust sub-canopy terrain correction.
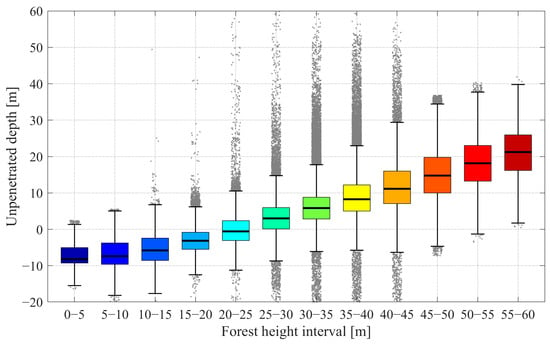
Figure 12.
Boxplot of unpenetrated depth versus LiDAR-derived forest height.
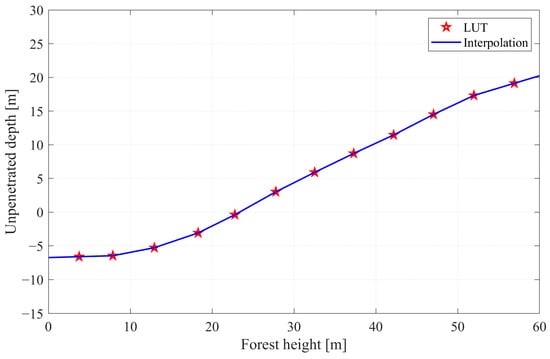
Figure 13.
One-dimensional LUT between unpenetrated depth and LiDAR-derived forest height obtained by interpolation.
Subsequently, the LiDAR-derived forest height was utilized to construct a refined one-dimensional LUT for sub-canopy terrain correction. Specifically, Figure 14a illustrates the corrected DTM obtained using the LiDAR-based LUT, and Figure 14b shows the corresponding elevation differences with respect to the LiDAR DTM. The scatterplot in Figure 14c quantitatively evaluates the corrected DTM accuracy, yielding a RMSE of 4.35 m and a bias of −0.7 m, indicating good agreement with the LiDAR DTM. Compared to the previous correction based on the RVoG-based forest height estimates, which exhibited an RMSE of 5.90 m, the LiDAR-based LUT method achieved an accuracy improvement of approximately 26.3%. This substantial enhancement underscores the direct influence of forest-height accuracy on sub-canopy terrain retrieval accuracy, as errors in canopy-height estimation propagate through the unpenetrated depth calculation, amplifying terrain correction biases.
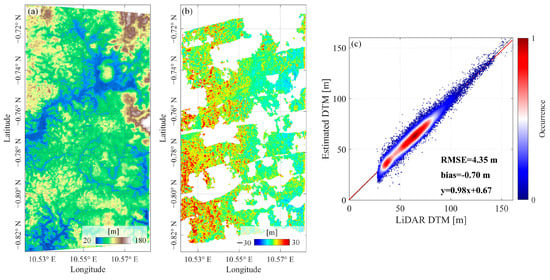
Figure 14.
DTM corrected by the LUT derived from LiDAR forest height and unpenetrated depth: (a) corrected DTM; (b) elevation differences relative to LiDAR DTM; (c) scatterplot comparison of the corrected DTM and LiDAR DTM.
Therefore, acquiring accurate forest height significantly strengthens the relationship between canopy height and radar unpenetrated depth, thereby improving terrain correction reliability. Such precision is particularly essential for mitigating elevation biases in densely vegetated tropical forests, and it holds great promise for spaceborne SAR missions, such as BIOMASS, where integration with accurate ancillary datasets like airborne LiDAR or spaceborne missions such as GEDI can significantly enhance global-scale sub-canopy terrain retrieval performance.
4.3. Impact Analysis of LiDAR Sampling Proportion on Forest Height–Unpenetrated Depth LUT
Accurate forest height information is essential for improving the effectiveness of LUT-based sub-canopy terrain correction. However, the reliability of this correction method depends on the availability and quality of the LiDAR canopy-height measurements. To assess the impact of sparse sampling, we performed a statistical analysis using LiDAR sampling proportions of 1%, 3%, 5%, and 10%. For each sampling case, we evaluated the relationship between the binned mean forest height and the corresponding mean unpenetrated depth, as summarized in Table 2.

Table 2.
Impact of LiDAR forest-height sampling proportion on LUT construction [unit: m].
The analysis reveals the following key findings:
- Across all sampling rates, the LUT curves consistently show negative or near-zero unpenetrated depth values for forest heights below approximately 25 m. This indicates that P-band radar signals effectively penetrate low-vegetation canopies and, in some cases, reach slightly beneath the actual ground surface;
- For forest heights over 25 m, a clear positive linear relationship between forest height and unpenetrated depth emerges in all sampling cases. This trend highlights the limited penetration capability of radar signals in taller and denser forest environments;
- The unpenetrated depth estimates across different sampling proportions show strong consistency and stability, with only minimal fluctuations observed between 1% and 10% samples. This stability across all forest-height bins indicates the robustness of the proposed method, even under relatively sparse LiDAR data scenarios. Notably, the overlap of unpenetrated depth values in all sampling settings suggests that the one-dimensional LUT construction method is not highly sensitive to the LiDAR forest-height sampling rate. This reinforces its applicability to large-scale terrain correction tasks, especially in regions where dense LiDAR coverage is unavailable.
This finding suggests that even limited but well-distributed LiDAR samples can substantially enhance the reliability of sub-canopy terrain correction, especially when integrated into large-scale SAR-based mapping frameworks.
4.4. The Impact of Different Forest Height on Coherence Set Distribution
The RVoG model is one of the most widely used parametric approaches for retrieving forest height and sub-canopy terrain using PolInSAR techniques. Accurate parameter inversion based on the RVoG model depends on two key conditions: first, the observed coherence ellipse, visualized from the full-polarimetric complex coherence coefficients, should be as elongated and narrow as possible, which can be described by the coherence set eccentricity [38] called ecc in Figure 15; second, the overall coherence level must be sufficiently high and the endpoints of the visible coherence line must have a distinct phase-separation degree, which can be evaluated by the coherence separation product [39] called prod in Figure 15. However, in dense tropical forests, the natural volume-scattering medium introduces severe volume decorrelation, which limits the model’s effectiveness. Consequently, forest-height inversion using the RVoG model is constrained by both the linear geometric assumptions and the coherence distribution characteristics of the observed data.
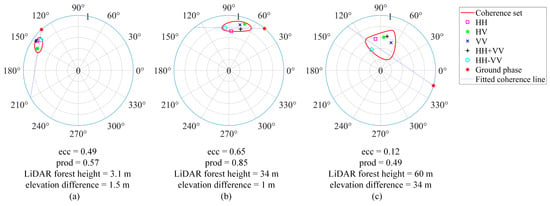
Figure 15.
Coherence set distribution under three types of trees heights. (a) forest height 3.1 m; (b) forest height 34 m; (c) forest height 60 m. The abbreviations ecc and prod represent the coherence set eccentricity and the coherence separation product, respectively. The elevation difference represents the difference between RVoG-derived DTM and LiDAR DTM. HH coherence represents the normalized magnitude of complex coherence coefficient in HH polarization.
Figure 15 illustrates coherence ellipses corresponding to forest heights of approximately 3 m (low vegetation or bare ground), 34 m (medium-height forest), and 60 m (very tall trees). The results show that in areas with low vegetation or bare ground, the coherence set appears as a relatively small ellipse, and the phase and magnitude of complex coherence change relatively little with different polarizations, which indicates near-complete penetration. In such cases, the phase of any single-polarization complex coherence can be considered representative of the true ground surface. For medium-height forests, although the coherence level decreases, the coherence ellipse becomes more elongated and narrower, and the complex coherence coefficients exhibit a more linear distribution. These characteristics closely align with the ideal assumptions of the RVoG model, enabling more accurate terrain estimates with smaller deviations from the LiDAR DTM. In contrast, for very tall trees, due to strong volume decorrelation, the coherence set displays a large and nearly circular ellipse. The complex coherence coefficients show no clear linear trend, with eccentricity of 0.12, which is inconsistent with the prerequisite assumptions of the RVoG linear model. Consequently, the estimated ground phase is affected not only by the limited penetration depth but also by the unfavorable geometric distribution of the coherence set.
Moreover, uncertainties in the inversion results caused by suboptimal coherence-set distribution and volume decorrelation are unavoidable due to the inherent limitations of single-baseline acquisitions. Additional errors arise from the lack of sufficient observation diversity in single-baseline airborne SAR data, especially in regions with complex terrain and diverse forest heights. Multi-baseline observations have been proven to be an effective strategy for improving inversion accuracy, as they can significantly reduce the biases in forest-parameter estimation caused by the poor geometric distribution of the coherence set in single-baseline SAR configuration. This advantage has been validated in multiple experiments [22,39,40,41]. The correction strategy proposed in this study is intended to mitigate the inversion bias caused by insufficient penetration under the single-baseline SAR data condition, offering a practical alternative for large-scale sub-canopy terrain mapping in spaceborne SAR missions.
5. Conclusions
Accurate sub-canopy terrain estimation in densely vegetated environments remains a significant challenge for Earth observation SAR missions. Even utilizing long-wavelength P-band SAR sensors, which are well-known for their enhanced canopy-penetration capabilities, limitations persist due to incomplete signal penetration or single interferometric geometry, especially in dense tropical forests with diverse tree heights. This results in systematic elevation biases and inaccuracies in terrain retrievals when conventional PolInSAR methods, such as the RVoG model, are employed.
This paper introduces a novel correction strategy using a one-dimensional LUT that leverages the empirical relationship between forest height and unpenetrated depth to effectively mitigate terrain elevation biases. By constructing LUTs from accurate forest-height measurements (e.g., airborne LiDAR forest height data), we demonstrate significantly improved accuracy in the retrieval of sub-canopy terrain. Specifically,
- (1)
- Comparative analyses reveal that conventional single-polarization InSAR-derived DTMs, such as TanDEM-X products, exhibit substantial elevation biases with an RMSE as high as 17.14 m relative to LiDAR DTM. In contrast, employing the RVoG model significantly reduces these biases, achieving an RMSE of approximately 9.57 m. However, residual biases persist due to incomplete penetration;
- (2)
- The proposed LUT-based correction method further reduces terrain-estimation biases, achieving an RMSE of approximately 5.90 m when utilizing RVoG-derived forest height. Remarkably, the accuracy further improves to an RMSE of approximately 4.35 m when employing precise LiDAR-derived forest height inputs, underscoring the critical role of accurate forest height data in sub-canopy terrain correction;
- (3)
- An in-depth analysis using boxplots highlights that for forest heights below 25 m, unpenetrated depths are generally negligible or negative, suggesting effective signal penetration. However, forests taller than 25 m exhibit strongly positive and linearly increasing unpenetrated depths, emphasizing that dense and tall forests significantly limit radar penetration. This relationship becomes more evident when accurate LiDAR canopy heights are used, indicating the necessity of high-quality ancillary forest height data for improving terrain estimation.
Overall, this study demonstrates that the accuracy of forest-height input is crucial for effectively addressing the incomplete penetration problem in single-baseline PolInSAR-based terrain retrievals. The proposed one-dimensional LUT correction method, particularly when supported by accurate forest height measurements from sensors like LiDAR or spaceborne systems such as GEDI, offers a robust and practical solution. These findings hold considerable promise for future Earth-observation SAR missions, such as BIOMASS, where integration with precise canopy-height products could substantially enhance the accuracy and reliability of sub-canopy terrain mapping.
Author Contributions
Conceptualization, C.W. and P.S.; methodology, C.W., P.S. and J.H.; software, P.S. and S.W.; validation, C.W., P.S. and J.H.; formal analysis, C.W., P.S. and J.H.; investigation, P.S., G.C. and L.Z.; resources, S.W. and G.C.; data curation, G.C. and L.Z.; writing—original draft preparation, C.W. and P.S.; writing—review and editing, C.W., S.W. and P.S.; visualization, P.S., C.W. and S.W.; supervision, G.C. and S.W.; project administration, S.W. and G.C.; funding acquisition, P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No. 42404029), the China National Postdoctoral Program for Innovative Talents (No. BX20240270), the China Postdoctoral Science Foundation (No. 2024M752479), and the Postdoctoral Project of Hubei Province (No. 2024HBBHCXA062), and it was funded by the National Key Laboratory of Intelligent Spatial Information, China (No. KF2023ZD02-02).
Data Availability Statement
All SAR datasets used in this study were provided by the European Space Agency (ESA) as part of the AfriSAR campaign and are publicly available through the ESA Earth Observation Portal at https://earth.esa.int. The airborne LiDAR data, including the LVIS canopy height and terrain products, were obtained from the National Snow and Ice Data Center (NSIDC) and are freely accessible at https://nsidc.org. No proprietary or restricted-access datasets were used in this research.
Acknowledgments
The authors would like to thank the European Space Agency (ESA) for supporting this work through access to airborne P-band PolInSAR data acquired during the AfriSAR campaign under the framework of Sino-EU Dragon Project (id 95436).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping Forest Canopy Height Globally with Spaceborne Lidar. J. Geophys. Res. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Zink, M.; Bachmann, M.; Brautigam, B.; Fritz, T.; Hajnsek, I.; Moreira, A.; Wessel, B.; Krieger, G. TanDEM-X: The New Global DEM Takes Shape. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–23. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Secretariat, G. Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Update). In Proceedings of the Conference of the Parties (COP), Copenhagen, Denmark, 7–19 December 2009; pp. 7–18. [Google Scholar]
- Bohn, F.J.; Huth, A. The Importance of Forest Structure to Biodiversity–Productivity Relationships. R. Soc. Open Sci. 2017, 4, 160521. [Google Scholar] [CrossRef]
- Mitchard, E.T.A. The Tropical Forest Carbon Cycle and Climate Change. Nature 2018, 559, 527–534. [Google Scholar] [CrossRef]
- GCOS The Global Observing System for Climate: Implementation Needs. World Meteorol. Organ. 2016, 200, 316.
- Fu, H.; Zhu, J.; Wang, C.; Li, Z. Underlying Topography Extraction over Forest Areas from Multi-Baseline PolInSAR Data. J. Geod. 2018, 92, 727–741. [Google Scholar] [CrossRef]
- Fu, H.; Zhu, J.; Wang, C.; Wang, H.; Zhao, R. Underlying Topography Estimation over Forest Areas Using High-Resolution P-Band Single-Baseline PolInSAR Data. Remote Sens. 2017, 9, 363. [Google Scholar] [CrossRef]
- Fu, H.; Wang, C.; Zhu, J.; Xie, Q.; Zhang, B. Estimation of Pine Forest Height and Underlying DEM Using Multi-Baseline P-Band PolInSAR Data. Remote Sens. 2016, 8, 820. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; Liao, M.; Zhang, L.; Dong, J.; Dai, K. Research Progress of Phase Linking Method in Time-Series InSAR. Geomat. Inf. Sci. Wuhan Univ. 2025, 1–15. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; An, B. AdpPL: An Adaptive Phase Linking-Based Distributed Scatterer Interferometry with Emphasis on Interferometric Pair Selection Optimization and Adaptive Regularization. Remote Sens. Environ. 2023, 295, 113687. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Pardini, M.; Armston, J.; Qi, W.; Lee, S.K.; Tello, M.; Cazcarra Bes, V.; Choi, C.; Papathanassiou, K.P.; Dubayah, R.O.; Fatoyinbo, L.E. Early Lessons on Combining Lidar and Multi-Baseline SAR Measurements for Forest Structure Characterization. Surv. Geophys. 2019, 40, 803–837. [Google Scholar] [CrossRef]
- Tebaldini, S.; Ho Tong Minh, D.; Mariotti d’Alessandro, M.; Villard, L.; Le Toan, T.; Chave, J. The Status of Technologies to Measure Forest Biomass and Structural Properties: State of the Art in SAR Tomography of Tropical Forests. Surv. Geophys. 2019, 40, 779–801. [Google Scholar] [CrossRef]
- Wu, C.; Shen, P.; Tebaldini, S.; Liao, M.; Zhang, L. InSAR-Based Estimation of Forest above-Ground Biomass Using Phase Histogram Technique. Int. J. Appl. Earth Obs. Geoinf. 2025, 136, 104350. [Google Scholar] [CrossRef]
- Wang, H.; Fu, H.; Zhu, J.; Liu, Z.; Zhang, B.; Wang, C.; Li, Z.; Hu, J.; Yu, Y. Estimation of Subcanopy Topography Based on Single-Baseline TanDEM-X InSAR Data. J. Geod. 2021, 95, 84. [Google Scholar] [CrossRef]
- Schlund, M.; Baron, D.; Magdon, P.; Erasmi, S. Canopy Penetration Depth Estimation with TanDEM-X and Its Compensation in Temperate Forests. ISPRS J. Photogramm. Remote Sens. 2019, 147, 232–241. [Google Scholar] [CrossRef]
- Dall, J. InSAR Elevation Bias Caused by Penetration into Uniform Volumes. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2319–2324. [Google Scholar] [CrossRef]
- Baugh, C.A.; Bates, P.D.; Schumann, G.; Trigg, M.A. SRTM Vegetation Removal and Hydrodynamic Modeling Accuracy: SRTM VEGETATION ERROR REMOVAL. Water Resour. Res. 2013, 49, 5276–5289. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multibaseline Polarimetric SAR Tomography of a Boreal Forest at P- and L-Bands. IEEE Trans. Geosci. Remote Sens. 2012, 50, 232–246. [Google Scholar] [CrossRef]
- D’Alessandro, M.M.; Tebaldini, S. Digital Terrain Model Retrieval in Tropical Forests through P-Band SAR Tomography. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6774–6781. [Google Scholar] [CrossRef]
- Aghababaee, H.; Ferraioli, G.; Ferro-Famil, L.; Huang, Y.; Mariotti D’Alessandro, M.; Pascazio, V.; Schirinzi, G.; Tebaldini, S. Forest SAR Tomography: Principles and Applications. IEEE Geosci. Remote Sens. Mag. 2020, 8, 30–45. [Google Scholar] [CrossRef]
- Wu, C.; Yang, X.; Yu, Y.; Tebaldini, S.; Zhang, L.; Liao, M. Assessment of Underlying Topography and Forest Height Inversion Based on TomoSAR Methods. Geo-Spat. Inf. Sci. 2022, 27, 311–326. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Treuhaft, R.N.; Siqueira, P.R. Vertical Structure of Vegetated Land Surfaces from Interferometric and Polarimetric Radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-Baseline Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Three-Stage Inversion Process for Polarimetric SAR Interferometry. IEE P-Radar. Son. Nav. 2003, 150, 125. [Google Scholar] [CrossRef]
- Colin, E.; Titin-Schnaider, C.; Tabbara, W. An Interferometric Coherence Optimization Method in Radar Polarimetry for High-Resolution Imagery. IEEE Trans. Geosci. Remote Sens. 2005, 44, 167–175. [Google Scholar] [CrossRef]
- Anthony, F. Fitting a Two-Component Scattering Model to Polarimetric SAR Data From Forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Multibaseline Polarimetric SAR Interferometry Coherence Optimization. IEEE Geosci. Remote Sens. Lett. 2008, 5, 93–97. [Google Scholar] [CrossRef]
- Lee, S.-K.; Fatoyinbo, T.E.; Lagomasino, D.; Feliciano, E.; Trettin, C. Multibaseline Tandem-x Mangrove Height Estimation: The Selection of the Vertical Wavenumber. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3434–3442. [Google Scholar] [CrossRef]
- Kugler, F.; Lee, S.K.; Hajnsek, I.; Papathanassiou, K.P. Forest Height Estimation by Means of Pol-InSAR Data Inversion: The Role of the Vertical Wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Wu, C.; Wang, C.; Shen, P.; Zhu, J.; Fu, H.; Gao, H. Forest Height Estimation Using PolInSAR Optimal Normal Matrix Constraint and Cross-Iteration Method. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1245–1249. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yamada, H.; Park, S.E. PolInSAR Coherence Region Modeling and Inversion: The Best Normal Matrix Approximation Solution. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1048–1060. [Google Scholar] [CrossRef]
- Pottier, E.; Ferro-Famil, L.; Fitrzyk, M.; Desnos, Y.-L. PolSARpro-BIO: The New Scientific Toolbox for ESA & Third Party Fully Polarimetric SAR Missions. In Proceedings of the EUSAR 2018: 12th European Conference on Synthetic Aperture Radar, Aachen, Germany, 5–7 June 2018; VDE: Frankfurt am Main, Germany, 2018; pp. 1–4. [Google Scholar]
- Lee, S.-K.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Multibaseline Polarimetric SAR Interferometry Forest Height Inversion Approaches. In Proceedings of the ESA POLinSAR Workshop, Frascati, Italy, 24–28 January 2011. [Google Scholar]
- Denbina, M.; Simard, M.; Hawkins, B. Forest Height Estimation Using Multibaseline PolInSAR and Sparse Lidar Data Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3415–3433. [Google Scholar] [CrossRef]
- Wan, J.; Wang, C.; Shen, P.; Wei, Y. An Improved Sparse Bayesian Learning SAR Tomography Method and Its Application for Forest Vertical Structure Inversion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 13701–13718. [Google Scholar] [CrossRef]
- Wang, C.; Song, T.; Shen, P. A Novel Iterative Reweighted Method for Forest Height Inversion Using Multibaseline PolInSAR Data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2508105. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).