A Robust Framework for Bamboo Forest AGB Estimation by Integrating Geostatistical Prediction and Ensemble Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.2.1. Field Data Collection and Biomass Estimation
2.2.2. ICESat-2 Data
2.2.3. GEDI Data
2.2.4. Optical and Topographic Predictor Variables
2.3. Research Methods
2.3.1. Spatial Extrapolation of LiDAR Metrics
2.3.2. AGB Estimation Using Stacked Ensemble Modeling
Base Learner Algorithms
Stacking Ensemble Method
2.3.3. Model Performance Assessment
2.3.4. SHAP-Based Model Interpretability
3. Results
3.1. Accuracy of Spatially Extrapolated LiDAR Metrics
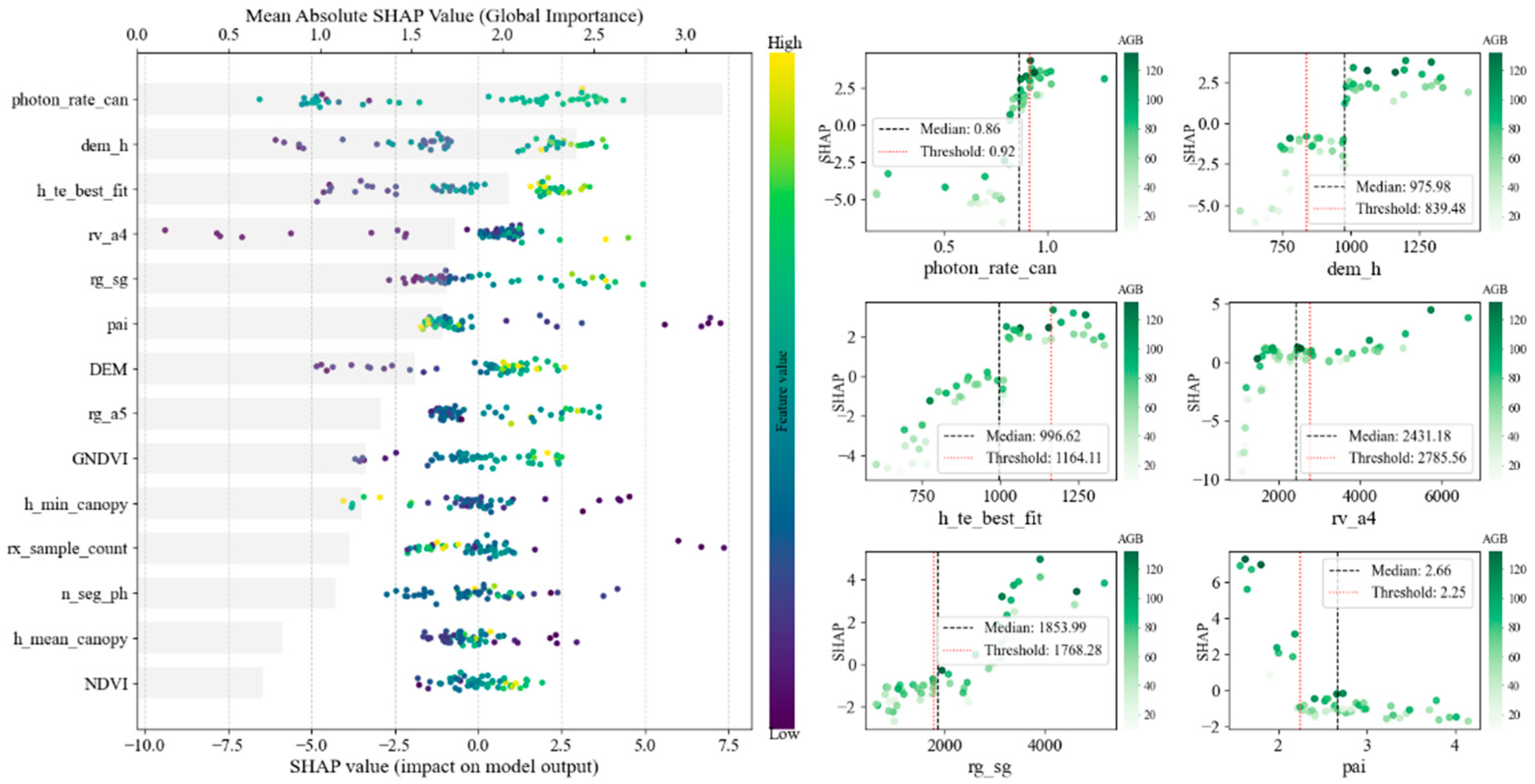
3.2. Feature Importance and Selection for AGB Modeling
3.3. AGB Model Performance
3.4. Mapping and Analysis of D. giganteus AGB
4. Discussion
4.1. Analysis of Spatial Heterogeneity in EBKRP Results
4.2. Influence of Algorithm Selection on Bamboo AGB Estimation
4.3. Ecological Interpretation and Management Implications
4.3.1. Ecological Drivers and Non-Linear Mechanisms
4.3.2. Anthropogenic Influences and Implications for Precision Management
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Above-Ground Biomass |
| AGBD | Above-Ground Biomass Density |
| ATLAS | Advanced Topographic Laser Altimeter System |
| CDF | Cumulative Distribution Function |
| CRPS | Continuous Ranked Probability Score |
| DBH | Diameter at Breast Height |
| DEM | Digital Elevation Model |
| DRAGANN | Differential, Regressive, and Gaussian Adaptive Nearest Neighbor |
| DVI | Difference Vegetation Index |
| EBKRP | Empirical Bayesian Kriging Regression Prediction |
| ESA | European Space Agency |
| EVI | Enhanced Vegetation Index |
| GBDT | Gradient Boosting Decision Tree |
| GDVI | Green Difference Vegetation Index |
| GEDI | Global Ecosystem Dynamics Investigation |
| GNDVI | Green Normalized Difference Vegetation Index |
| GRVI | Green Ratio Vegetation Index |
| ICC | Intraclass Correlation Coefficient |
| ICESat-2 | Ice, Cloud, and land Elevation Satellite-2 |
| InSAR | Interferometric SAR |
| ISS | International Space Station |
| kNN | k-Nearest Neighbor |
| LAI | Leaf Area Index |
| LiDAR | Light Detection and Ranging |
| LOOCV | Leave-One-Out Cross-Validation |
| MAE | Mean Absolute Error |
| NASA | National Aeronautics and Space Administration |
| NDVI | Normalized Difference Vegetation Index |
| NPGI | Normalized Pigment Chlorophyll Index |
| OOF | Out of Fold |
| PCL | Photon Counting LiDAR |
| RBF | Radial Basis Function |
| RF | Random Forest |
| RFE | Recursive Feature Elimination |
| RH | Relative Height |
| RMSE | Root Mean Square Error |
| RR | Ridge Regression |
| RVI | Ratio Vegetation Index |
| SAR | Synthetic Aperture Radar |
| SAVI | Soil-Adjusted Vegetation Index |
| SHAP | SHapley Additive exPlanations |
| SVM | Support Vector Machine |
| XGBoost | eXtreme Gradient Boosting |
References
- Food and Agriculture Organization of the United Nations (FAO). The State of the World’s Forests 2018: Forest Pathways to Sustainable Development; FAO: Rome, Italy, 2018; ISBN 978-92-5-130561-4. [Google Scholar]
- Chen, Q.; McRoberts, R.E.; Wang, C.; Radtke, P.J. Forest Aboveground Biomass Mapping and Estimation across Multiple Spatial Scales Using Model-Based Inference. Remote Sens. Environ. 2016, 184, 350–360. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, C.; Ji, L.; Zuo, Z.; Beckline, M.; Hu, Y.; Li, X.; Xiao, X. Development of Forest Aboveground Biomass Estimation, Its Problems and Future Solutions: A Review. Ecol. Indic. 2024, 159, 111653. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of Multi-Resource Remotely Sensed Data and Allometric Models for Forest Aboveground Biomass Estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Hummel, S.; Hudak, A.T.; Uebler, E.H.; Falkowski, M.J.; Megown, K.A. A Comparison of Accuracy and Cost of LiDAR versus Stand Exam Data for Landscape Management on the Malheur National Forest. J. For. 2011, 109, 267–273. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Quegan, S.; Carreiras, J.; Persson, H.J.; Fransson, J.E.S.; Hoscilo, A.; Ziółkowski, D.; Stereńczak, K.; Lohberger, S.; Stängel, M.; et al. Forest Biomass Retrieval Approaches from Earth Observation in Different Biomes. Int. J. Appl. Earth Obs. Geoinf. 2019, 77, 53–68. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar Sampling for Large-Area Forest Characterization: A Review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground Biomass Density Models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) Lidar Mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 Land and Vegetation Product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Fu, L.; Shu, Q.; Yang, Z.; Xia, C.; Zhang, X.; Zhang, Y.; Li, Z.; Li, S. Accuracy Assessment of Topography and Forest Canopy Height in Complex Terrain Conditions of Southern China Using ICESat-2 and GEDI Data. Front. Plant Sci. 2025, 16, 1547688. [Google Scholar] [CrossRef]
- Li, D.; Wu, B.; Chen, B.; Qin, C.; Wang, Y.; Zhang, Y.; Xue, Y. Open-Surface River Extraction Based on Sentinel-2 MSI Imagery and DEM Data: Case Study of the Upper Yellow River. Remote Sens. 2020, 12, 2737. [Google Scholar] [CrossRef]
- Hajj, M.; Baghdadi, N.; Fayad, I.; Vieilledent, G.; Bailly, J.-S.; Minh, D. Interest of Integrating Spaceborne LiDAR Data to Improve the Estimation of Biomass in High Biomass Forested Areas. Remote Sens. 2017, 9, 213. [Google Scholar] [CrossRef]
- Xia, C.; Zhou, W.; Shu, Q.; Wu, Z.; Wang, M.; Xu, L.; Yang, Z.; Yu, J.; Song, H.; Duan, D. Unlocking Vegetation Health: Optimizing GEDI Data for Accurate Chlorophyll Content Estimation. Front. Plant Sci. 2024, 15, 1492560. [Google Scholar] [CrossRef] [PubMed]
- Chi, H.; Sun, G.; Huang, J.; Li, R.; Ren, X.; Ni, W.; Fu, A. Estimation of Forest Aboveground Biomass in Changbai Mountain Region Using ICESat/GLAS and Landsat/TM Data. Remote Sens. 2017, 9, 707. [Google Scholar] [CrossRef]
- Zhao, X.; Hu, W.; Han, J.; Wei, W.; Xu, J. Urban Above-Ground Biomass Estimation Using GEDI Laser Data and Optical Remote Sensing Images. Remote Sens. 2024, 16, 1229. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J.; et al. Fusing Simulated GEDI, ICESat-2 and NISAR Data for Regional Aboveground Biomass Mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Qi, W.; Saarela, S.; Armston, J.; Ståhl, G.; Dubayah, R. Forest Biomass Estimation over Three Distinct Forest Types Using TanDEM-X InSAR Data and Simulated GEDI Lidar Data. Remote Sens. Environ. 2019, 232, 111283. [Google Scholar] [CrossRef]
- Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping Global Forest Aboveground Biomass with Spaceborne LiDAR, Optical Imagery, and Forest Inventory Data. Remote Sens. 2016, 8, 565. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Bao, G.; Zhang, B.; Wang, Z.; Liu, M.; Man, W.; Liu, J. Improved Object-Based Estimation of Forest Aboveground Biomass by Integrating LiDAR Data from GEDI and ICESat-2 with Multi-Sensor Images in a Heterogeneous Mountainous Region. Remote Sens. 2022, 14, 2743. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass Estimation from Simulated GEDI, ICESat-2 and NISAR across Environmental Gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Sun, Y.; Ruan, H.; Wang, G.; Dai, J.; She, G. Estimating Canopy Structure and Biomass in Bamboo Forests Using Airborne LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2019, 148, 114–129. [Google Scholar] [CrossRef]
- Chaparro, D.; Duveiller, G.; Piles, M.; Cescatti, A.; Vall-llossera, M.; Camps, A.; Entekhabi, D. Sensitivity of L-Band Vegetation Optical Depth to Carbon Stocks in Tropical Forests: A Comparison to Higher Frequencies and Optical Indices. Remote Sens. Environ. 2019, 232, 111303. [Google Scholar] [CrossRef]
- Li, R.; Xia, H.; Zhao, X.; Guo, Y. Mapping Evergreen Forests Using New Phenology Index, Time Series Sentinel-1/2 and Google Earth Engine. Ecol. Indic. 2023, 149, 110157. [Google Scholar] [CrossRef]
- Alavipanah, S.K.; Karimi Firozjaei, M.; Sedighi, A.; Fathololoumi, S.; Zare Naghadehi, S.; Saleh, S.; Naghdizadegan, M.; Gomeh, Z.; Arsanjani, J.J.; Makki, M.; et al. The Shadow Effect on Surface Biophysical Variables Derived from Remote Sensing: A Review. Land 2022, 11, 2025. [Google Scholar] [CrossRef]
- Liu, A.; Cheng, X.; Chen, Z. Performance Evaluation of GEDI and ICESat-2 Laser Altimeter Data for Terrain and Canopy Height Retrievals. Remote Sens. Environ. 2021, 264, 112571. [Google Scholar] [CrossRef]
- Zhao, R.; Ni, W.; Zhang, Z.; Dai, H.; Yang, C.; Li, Z.; Liang, Y.; Liu, Q.; Pang, Y.; Li, Z.; et al. Optimizing Ground Photons for Canopy Height Extraction from ICESat-2 Data in Mountainous Dense Forests. Remote Sens. Environ. 2023, 299, 113851. [Google Scholar] [CrossRef]
- Fu, X.; Sun, M.; Yang, Y.; Qian, Q.; Yu, H.; Hu, X. Application of Remote Sensing in Monitoring Large Sympodial Bamboo Resources in Dehong Prefecture. West. For. Sci. 2012, 41, 88–92. [Google Scholar] [CrossRef]
- Fu, L.; Shu, Q.; Xia, C.; Li, Z.; Zhang, X.; Zhang, Y. ICESat-2 Performance for Terrain and Canopy Height Retrieval in Complex Mountainous Environments. Remote Sens. 2025, 17, 1897. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2): Science Requirements, Concept, and Implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite–2 Mission: A Global Geolocated Photon Product Derived from the Advanced Topographic Laser Altimeter System. Remote Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Pronk, M.; Eleveld, M.; Ledoux, H. Assessing Vertical Accuracy and Spatial Coverage of ICESat-2 and GEDI Spaceborne Lidar for Creating Global Terrain Models. Remote Sens. 2024, 16, 2259. [Google Scholar] [CrossRef]
- Magruder, L.; Brunt, K.; Neumann, T.; Klotz, B.; Alonzo, M. Passive Ground-Based Optical Techniques for Monitoring the On-Orbit ICESat-2 Altimeter Geolocation and Footprint Diameter. Earth Space Sci. 2021, 8, e2020EA001414. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the Forest Canopy Height in Northern China by Synergizing Icesat-2 with Sentinel-2 Using a Stacking Algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-Resolution Laser Ranging of the Earth’s Forests and Topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Zhu, X.; Ren, Z.; Nie, S.; Bao, G.; Ha, G.; Bai, M.; Liang, P. DEM Generation from GF-7 Satellite Stereo Imagery Assisted by Space-Borne LiDAR and Its Application to Active Tectonics. Remote Sens. 2023, 15, 1480. [Google Scholar] [CrossRef]
- Zhou, Y.; Taylor, D.M.; Tang, H. Improved Country-Wide Estimation of above-Ground Tropical Forest Biomass Using Locally Calibrated GEDI Spaceborne LiDAR Data. Environ. Res. Lett. 2025, 20, 014017. [Google Scholar] [CrossRef]
- Liang, M.; González-Roglich, M.; Roehrdanz, P.; Tabor, K.; Zvoleff, A.; Leitold, V.; Silva, J.; Fatoyinbo, T.; Hansen, M.; Duncanson, L. Assessing Protected Area’s Carbon Stocks and Ecological Structure at Regional-Scale Using GEDI Lidar. Glob. Environ. Change 2023, 78, 102621. [Google Scholar] [CrossRef]
- Xia, C.; Zhou, W.; Shu, Q.; Wu, Z.; Xu, L.; Yang, H.; Qin, Z.; Wang, M.; Duan, D. Regional Scale Inversion of Chlorophyll Content of Dendrocalamus Giganteus by Multi-Source Remote Sensing. Forests 2024, 15, 1211. [Google Scholar] [CrossRef]
- Xu, L.; Shu, Q.; Fu, H.; Zhou, W.; Luo, S.; Gao, Y.; Yu, J.; Guo, C.; Yang, Z.; Xiao, J.; et al. Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data. Forests 2023, 14, 876. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Sripada, R.P.; Heiniger, R.W.; White, J.G.; Meijer, A.D. Aerial Color Infrared Photography for Determining Early In-Season Nitrogen Requirements in Corn. Agron. J. 2006, 98, 968–977. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a Green Channel in Remote Sensing of Global Vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Verrelst, J.; Schaepman, M.E.; Koetz, B.; Kneubühler, M. Angular Sensitivity Analysis of Vegetation Indices Derived from CHRIS/PROBA Data. Remote Sens. Environ. 2008, 112, 2341–2353. [Google Scholar] [CrossRef]
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A Commentary Review on the Use of Normalized Difference Vegetation Index (NDVI) in the Era of Popular Remote Sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Carter, G.A. Ratios of Leaf Reflectances in Narrow Wavebands as Indicators of Plant Stress. Int. J. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of Leaf-Area Index from Quality of Light on the Forest Floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Zaresefat, M.; Derakhshani, R.; Griffioen, J. Empirical Bayesian Kriging, a Robust Method for Spatial Data Interpolation of a Large Groundwater Quality Dataset from the Western Netherlands. Water 2024, 16, 2581. [Google Scholar] [CrossRef]
- Albers, A.; Collet, P.; Benoist, A.; Hélias, A. Data and Non-Linear Models for the Estimation of Biomass Growth and Carbon Fixation in Managed Forests. Data Brief 2019, 23, 103841. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Sun, Q.; Hu, J. Generation of Complete SAR Geometric Distortion Maps Based on DEM and Neighbor Gradient Algorithm. Appl. Sci. 2018, 8, 2206. [Google Scholar] [CrossRef]
- Wu, C.; Tao, H.; Zhai, M.; Lin, Y.; Wang, K.; Deng, J.; Shen, A.; Gan, M.; Li, J.; Yang, H. Using Nonparametric Modeling Approaches and Remote Sensing Imagery to Estimate Ecological Welfare Forest Biomass. J. For. Res. 2018, 29, 151–161. [Google Scholar] [CrossRef]
- Meng, Q.; Cieszewski, C.J.; Madden, M.; Borders, B.E. K Nearest Neighbor Method for Forest Inventory Using Remote Sensing Data. GIScience Remote Sens. 2007, 44, 149–165. [Google Scholar] [CrossRef]
- Franco-Lopez, H.; Ek, A.R.; Bauer, M.E. Estimation and Mapping of Forest Stand Density, Volume, and Cover Type Using the k-Nearest Neighbors Method. Remote Sens. Environ. 2001, 77, 251–274. [Google Scholar] [CrossRef]
- Heumann, B.W. An Object-Based Classification of Mangroves Using a Hybrid Decision Tree—Support Vector Machine Approach. Remote Sens. 2011, 3, 2440–2460. [Google Scholar] [CrossRef]
- Wu, C.-H.; Tzeng, G.-H.; Lin, R.-H. A Novel Hybrid Genetic Algorithm for Kernel Function and Parameter Optimization in Support Vector Regression. Expert Syst. Appl. 2009, 36, 4725–4735. [Google Scholar] [CrossRef]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random Forests and Decision Trees. Int. J. Comput. Sci. Issues 2012, 9, 272–278. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Zhang, Y.; Ma, J.; Liang, S.; Li, X.; Liu, J. A Stacking Ensemble Algorithm for Improving the Biases of Forest Aboveground Biomass Estimations from Multiple Remotely Sensed Datasets. GIScience Remote Sens. 2022, 59, 234–249. [Google Scholar] [CrossRef]
- Lamane, H.; Mouhir, L.; Moussadek, R.; Baghdad, B.; Kisi, O.; El Bilali, A. Interpreting Machine Learning Models Based on SHAP Values in Predicting Suspended Sediment Concentration. Int. J. Sediment Res. 2025, 40, 91–107. [Google Scholar] [CrossRef]
- Borselli, L.; Cassi, P.; Torri, D. Prolegomena to Sediment and Flow Connectivity in the Landscape: A GIS and Field Numerical Assessment. CATENA 2008, 75, 268–277. [Google Scholar] [CrossRef]
- Tian, S.; Zheng, G.; Eitel, J.U.; Zhang, Q. A Lidar-Based 3-D Photosynthetically Active Radiation Model Reveals the Spatiotemporal Variations of Forest Sunlit and Shaded Leaves. Remote Sens. 2021, 13, 1002. [Google Scholar] [CrossRef]
- Hardiman, B.S.; Bohrer, G.; Gough, C.M.; Vogel, C.S.; Curtis, P.S. The Role of Canopy Structural Complexity in Wood Net Primary Production of a Maturing Northern Deciduous Forest. Ecology 2011, 92, 1818–1827. [Google Scholar] [CrossRef]
- Zhao, Y.; Staudenmayer, J.; Coull, B.A.; Wand, M.P. General Design Bayesian Generalized Linear Mixed Models. Stat. Sci. 2006, 21, 35–51. [Google Scholar] [CrossRef]
- Li, N.; Hu, M.; Xie, J.; Wei, L.; Wu, T.; Zhang, W.; Gu, S.; Li, L. Enhancing Aboveground Biomass Estimation in Moso Bamboo Forests: The Role of on-Year and off-Year Phenomena in Remote Sensing. Front. For. Glob. Change 2025, 8, 1515767. [Google Scholar] [CrossRef]
- Wang, J.; Du, H.; Li, X.; Mao, F.; Zhang, M.; Liu, E.; Ji, J.; Kang, F. Remote Sensing Estimation of Bamboo Forest Aboveground Biomass Based on Geographically Weighted Regression. Remote Sens. 2021, 13, 2962. [Google Scholar] [CrossRef]
- Chen, Y.; Li, L.; Lu, D.; Li, D. Exploring Bamboo Forest Aboveground Biomass Estimation Using Sentinel-2 Data. Remote Sens. 2019, 11, 7. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative Analysis of Modeling Algorithms for Forest Aboveground Biomass Estimation in a Subtropical Region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Y.; Chen, C.; Li, X.; Mao, F.; Lv, L.; Yu, J.; Song, M.; Huang, L.; Chen, J.; et al. UAV-LiDAR Integration with Sentinel-2 Enhances Precision in AGB Estimation for Bamboo Forests. Remote Sens. 2024, 16, 705. [Google Scholar] [CrossRef]
- Shu, Q.; Xi, L.; Wang, K.; Xie, F.; Pang, Y.; Song, H. Optimization of Samples for Remote Sensing Estimation of Forest Aboveground Biomass at the Regional Scale. Remote Sens. 2022, 14, 4187. [Google Scholar] [CrossRef]
- Fang, Y.; Leung, L.R.; Koven, C.D.; Bisht, G.; Detto, M.; Cheng, Y.; McDowell, N.; Muller-Landau, H.; Wright, S.J.; Chambers, J.Q. Modeling the Topographic Influence on Aboveground Biomass Using a Coupled Model of Hillslope Hydrology and Ecosystem Dynamics. Geosci. Model Dev. 2022, 15, 7879–7901. [Google Scholar] [CrossRef]
- McNichol, B.H.; Wang, R.; Hefner, A.; Helzer, C.; McMahon, S.M.; Russo, S.E. Topography-driven Microclimate Gradients Shape Forest Structure, Diversity, and Composition in a Temperate Refugial Forest. Plant-Environ. Interact. 2024, 5, e10153. [Google Scholar] [CrossRef]
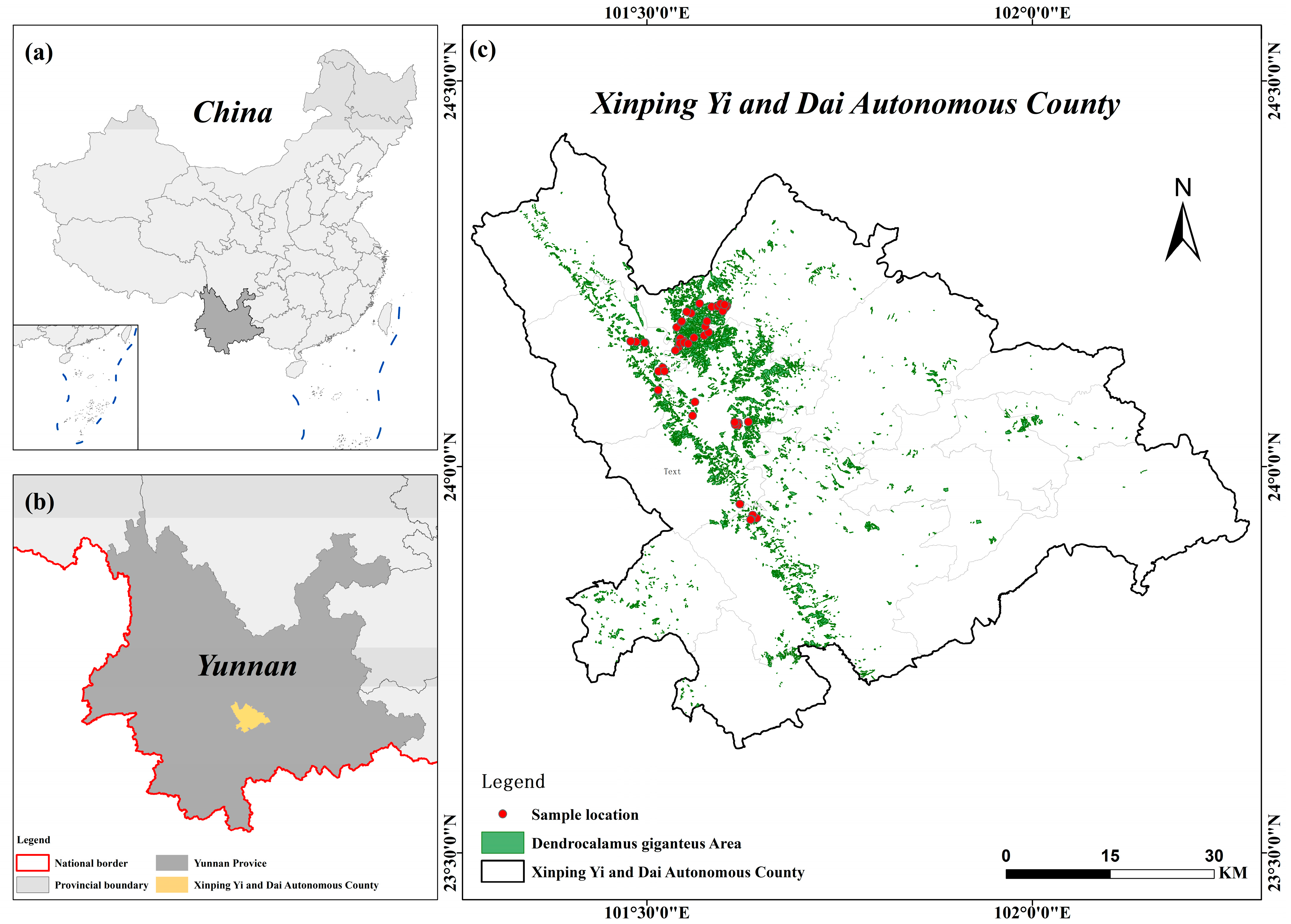





| Variable | N | Minimum | Maximum | Mean | Standard Deviation (SD) |
|---|---|---|---|---|---|
| AGB (Mg ha−1) | 52 | 9.96 | 132.09 | 66.89 | 27.59 |
| Misson | ICESat-2 | GEDI |
|---|---|---|
| Full name | Ice, Cloud, and land Elevation Satellite-2 | Global Ecosystem Dynamics Investigation |
| Launch date | September 15, 2018 | December 5, 2018 |
| Detector type | Photon counting | Full waveform |
| Wavelength | 532 nm (green) | 1064 nm (near IR) |
| across-track spacing | 90 m within pairs 3.3 km between pairs | 600 m |
| Diameter along-track spacing | ~0.7 m | ~60 m |
| Footprint | ~12 m | ~25 m |
| Track number | 6 tracks from 1 laser | 8 tracks from 3 lasers |
| Orbit inclination and coverage | 92°; coverage up to 88°N–88°S latitude | 51.6°; coverage up to 51.6°N–51.6°S latitude |
| Laser power | 120 μJ/30 μJ | 15 mJ/4.5 mJ |
| Temporal resolution (Revisit time) | ~91 days (exact repeat orbit) | ~45 days (non-repeating) |
| Vertical accuracy | ~3–5 cm for flat surfaces | ~1 m (depending on waveform processing and vegetation density) |
| Paramete | Retention Value | Retention Basis |
|---|---|---|
| lon_lowestmode | 101–103°E | Defines the longitudinal extent of the Xinping County study area. |
| lat_lowestmode | 23–25°N | Defines the latitudinal extent of the Xinping County study area. |
| algorithmrun_flag | 1 | Confirms the successful execution of the L2B algorithm and adequate waveform fidelity. |
| quality_flag | 1 | Indicates good-quality footprint data that meets multiple quality criteria and is located over a vegetated land area. |
| Sensitivity | ≥0.90 | Selects valid returns with high sensitivity (values approaching 1 signify high-quality signals). |
| degrade_flag | 0 | Excludes data flagged due to the degraded performance of the instrument or its pointing/positioning systems. |
| Vegetation Indices/Topographic Features | Formula/Description | Citation |
|---|---|---|
| Difference Vegetation Index | [40] | |
| Enhanced Vegetation Index | [41] | |
| Green Difference Vegetation Index | [42] | |
| Green Normalized Difference Vegetation Index | [43] | |
| Green Ratio Vegetation Index | [44] | |
| Normalized Difference Vegetation Index | [45] | |
| Normalized Pigment Chlorophyll Index | [46] | |
| Ratio Vegetation Index | [47] | |
| Soil-Adjusted Vegetation Index | [48] | |
| Elevation | Elevation | |
| Slope | Slope factor extracted by DEM | |
| Aspect | Slope aspect factor extracted by DEM |
| Model | R2 | RMSE (Mg/ha) | MAE (Mg/ha) | Regression Fit |
|---|---|---|---|---|
| Stacking | 0.84 | 11.07 | 8.69 | |
| Random Forest (RF) | 0.72 | 14.53 | 10.53 | |
| Support Vector Machine (SVM) | 0.69 | 15.32 | 9.02 | |
| XGBoost | 0.68 | 15.58 | 11.50 | |
| k-Nearest Neighbor (kNN) | 0.60 | 17.35 | 14.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, L.; Shu, Q.; Xia, C.; Li, Z.; He, H.; Li, Z.; Ma, S.; Qin, C.; Wei, R.; Xiang, Q.; et al. A Robust Framework for Bamboo Forest AGB Estimation by Integrating Geostatistical Prediction and Ensemble Learning. Remote Sens. 2025, 17, 2682. https://doi.org/10.3390/rs17152682
Fu L, Shu Q, Xia C, Li Z, He H, Li Z, Ma S, Qin C, Wei R, Xiang Q, et al. A Robust Framework for Bamboo Forest AGB Estimation by Integrating Geostatistical Prediction and Ensemble Learning. Remote Sensing. 2025; 17(15):2682. https://doi.org/10.3390/rs17152682
Chicago/Turabian StyleFu, Lianjin, Qingtai Shu, Cuifen Xia, Zeyu Li, Hailing He, Zhengying Li, Shaoyang Ma, Chaoguan Qin, Rong Wei, Qin Xiang, and et al. 2025. "A Robust Framework for Bamboo Forest AGB Estimation by Integrating Geostatistical Prediction and Ensemble Learning" Remote Sensing 17, no. 15: 2682. https://doi.org/10.3390/rs17152682
APA StyleFu, L., Shu, Q., Xia, C., Li, Z., He, H., Li, Z., Ma, S., Qin, C., Wei, R., Xiang, Q., Zhang, X., Zhang, Y., & Cai, H. (2025). A Robust Framework for Bamboo Forest AGB Estimation by Integrating Geostatistical Prediction and Ensemble Learning. Remote Sensing, 17(15), 2682. https://doi.org/10.3390/rs17152682






