Abstract
Using interferometric synthetic aperture radar (InSAR) to observe slow ground deformation can be challenging due to many sources of error, with tropospheric phase delay and unwrapping errors being the most significant. While analytical methods, weather models, and data exist to mitigate tropospheric error, most of these techniques are unsuitable for all InSAR applications (e.g., complex tropospheric mixing in the tropics) or are deficient in spatial or temporal resolution. Likewise, there are methods for removing the unwrapping error, but they cannot resolve the true phase when there is a high prevalence (>40%) of unwrapping error in a set of interferograms. Applying tropospheric delay removal techniques is unnecessary for C-band Sentinel-1 InSAR time series studies, and the effect of unwrapping error can be minimized if the full dataset is utilized. We demonstrate that using interferograms with long temporal baselines (800 days to 1600 days) but very short perpendicular baselines (<5 m) (LTSPB) can lower the velocity detection threshold to 2 mm y−1 to 3 mm y−1 for long-term coherent permanent scatterers. The LTSPB interferograms can measure slow deformation rates because the expected differential phases are larger than those of small baselines and potentially exceed the typical noise amplitude while also reducing the sensitivity of the time series estimation to the noise sources. The method takes advantage of the Sentinel-1 mission length (2016 to present), which, for most regions, can yield up to 300 interferograms that meet the LTSPB baseline criteria. We demonstrate that low velocity detection can be achieved by comparing the expected LTSPB differential phase measurements to synthetic tests and tropospheric delay from the Global Navigation Satellite System. We then characterize the slow (~3 mm/y) ground deformation of the Socorro Magma Body, New Mexico, and the Tampa Bay Area using LTSPB InSAR analysis. The method we describe has implications for simplifying the InSAR time series processing chain and enhancing the velocity detection threshold.
1. Introduction
Interferometric synthetic aperture radar (InSAR) is a robust tool for detecting and measuring ground deformation. The method has been extensively used in measuring ground deformation due to geophysical phenomena such as earthquakes [1], volcanic processes [2], landslides [3], and ice sheet motion [4]. InSAR time series analysis extends the utility of InSAR in monitoring slow deformation over a longer period (i.e., more than two repeat passes). Particularly, variants of the small subset baselines algorithm (SBAS) [5] have allowed for the millimetric per year measurement of ground deformation over long periods by exploiting interferometric pairs (interferograms) with the least decorrelation. The minimal decorrelation of interferograms is achieved by constraining the spatial and temporal baselines of the synthetic aperture radar (SAR) acquisitions selected to create interferometric pairs. The SBAS technique reduces sources of error to produce a velocity and displacement time series [5,6]. Unwrapped InSAR observations have four main components of error [7,8] along with the ground deformation:
where is the ground displacement, is the error introduced by differences in orbital geometries, is the error due to topography, which can be removed by using an accurate digital elevation model, is the two-pass propagation delay error due to the ionosphere and the troposphere, and is the noise introduced by sources such as decorrelation [9], phase unwrapping error [8], phase triplet loop non-closure [10], and the intrinsic noise of the sensor.
An error due to orbital geometry can be mitigated using precise orbits. Meanwhile, shorter wavelengths, such as X-band (3 cm) and Sentinel-1 C-band (~5 cm), are less susceptible to ionospheric phase delay error compared to longer wavelengths, like L-band (~24 cm) [11]. Tropospheric phase delay, unwrapping, and phase triplet non-closure are sources of error that require nontrivial methods for their mitigation or removal. Tropospheric phase delay error is caused by the propagation delay due to the changes in refractivity of the atmosphere and is the largest source of error in InSAR measurements [12,13] (see Figure 1a,b). The removal of the tropospheric phase delay error remains a challenging problem to solve. Unwrapping errors produce N2π or integer cycle ambiguity due to unwrapping over the lower coherence areas of an interferogram (see Figure 1b) and the phase triplet residual phase is the result of a change in the backscattering properties that arises from multilooking or spatial averaging [7,14].
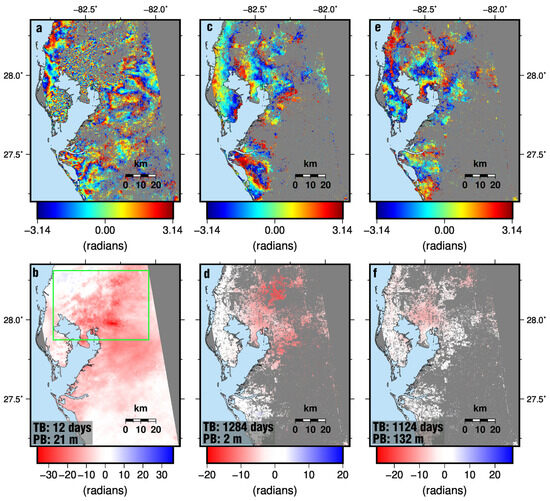
Figure 1.
Sentinel-1A interferograms for Tampa Bay Area, Florida, where pixels with a coherence less than 0.1 are masked out. TB—temporal baselines. PB—perpendicular baselines. Panels (a,b) show a small baseline (12 days) interferogram (6 October 2016 to 14 October 2016) that is wrapped and unwrapped, respectively, with pervasive tropospheric phase delay and unwrapping error highlighted in the green box. Panels (c,d) show wrapped and unwrapped interferogram (14 October 2016 to 20 April 2020) with a long-temporal baseline of 1284 days and with perpendicular baseline of 2 m. Panels (e,f) show a wrapped and unwrapped interferogram (26 October 2016 to 3 March 2020) with a long-temporal baseline of 1124 days and a perpendicular baseline of 132 m and has 82% fewer pixels than the small perpendicular baseline interferogram shown in Panel (c). Interferograms created from Sentinel-1A path 121 and frame 85 data using the method described in Appendix B.
The C-band Sentinel-1 mission started in 2016 and has acquired SAR images globally since early 2014. As of the date of writing, Sentinel-1 acquisitions span over five years in many parts of the globe. The large number of acquisitions can be exploited to increase the signal-to-noise ratio by complementing the small baselines (SBs) with the selection of interferometric pairs with long temporal baselines (800 days to 1400 days) and short (<5 m) perpendicular baselines (LTSPBs), which decreases the likelihood of decorrelation. The Sentinel-1 orbits are in a 200 m tube, ensuring minimal spatial decorrelation, and it is feasible to discount the effects of spatial decorrelation when the perpendicular baseline is less than 5 m, as the coherence is 0.97 [15] (see Figure 1c–f). The temporal baseline coherence for C-Band SAR sensors, such as Sentinel-1, decreases to zero or the long-term coherence after 10 to 90 days, depending on the vegetation cover [15,16]. If scatters have long-term coherence, then an interferogram can measure slow deformation if the displacement between acquisitions exceeds the phase noise due to long-term coherence, i.e., decorrelation, and tropospheric phase delay.
Here, we demonstrate that LTSPB interferograms, compared to SB interferograms, and taking advantage of the Sentinel-1 mission length provide more robust SBAS time series estimation. We first demonstrate that LTSPB provides a better signal-to-noise ratio and can recover 2 to 3 mm y−1 of deformation by assessing the contribution of error due to coherence, tropospheric phase delay, and unwrapping. We then test this strategy to show the extent and magnitude of the slow ground deformation of Socorro, New Mexico. and the Tampa Bay Area (TBA). Socorro, New Mexico, experiences 2.5 mm/y uplift due to the Socorro Magma Body (SMB), a mid-crustal (~19 km) emplacement of magma [17,18,19]. Conversely, previous studies that utilized InSAR [20,21] show that the TBA experiences broadscale (10s of km) subsidence at appreciable rates (6 mm/y). There is also no known process that can explain the pattern of subsidence as the posited driver, groundwater extraction [20], would not cause subsidence because the karst aquifer system does not deform due to fluid withdrawal. Furthermore, GNSS velocities [22] do not indicate that the TBA experiences subsidence. Using the LTSPB method, we show the extent and pattern of inflation produced by the SMB and that there is no broadscale subsidence of the TBA.
2. Coherence Phase Noise
InSAR time series are created by the SBAS method, and our study relies on the SBAS least squares formulation to illustrate how LTSPB C-Band interferograms reduce the sensitivity of SBAS solutions to tropospheric phase delay and unwrapping errors. First, it must be assessed what the detection threshold is for interferograms, discounting both these sources of error. As detailed in the Introduction, there are several sources of noise in phase measurements. Neglecting sources of noise, including inherent noise and thermal noise of the SAR sensor, the coherence (or decorrelation) determines the smallest measurement accuracy that can be achieved by an interferogram.
The coherence of an interferogram, in the most general form, is the product of the temporal or volumetric coherence and the perpendicular baseline coherence [23]. Temporal baseline coherence is inversely related to the noise it introduces [8] and decreases quickly with an increase in temporal baselines, such that, after 90 days, coherence may be reduced to near zero or the long-term coherence. We propose that LTSPB interferograms, for most general cases, be created similarly to the multi-temporal persistent scatter (PS) approach, that is, utilizing amplitude stable single-look pixels with long-term coherence. It is also possible to use LTSPB interferograms with Distributed Scatters if there are sufficient long-term coherence scatters (see Appendix B). If a patch of pixels of a single look interferogram has a long-term coherence of 0.1, then the temporal baseline coherence-induced noise for C-band is ~6 mm (Equation (41) from [24]). That is, the patch of pixels will not be able to resolve a phase difference of 6 mm or lower, even if there are no other sources of error. It follows that the patch of pixels can only measure motion where the cumulative deformation between acquisitions is greater than 6 mm. It should be noted that increasing multilooking significantly decreases the phase noise related to temporal baseline coherence [25]. A multilook of N = 4 and a long-term coherence of 0.1 results in phase noise of ~4 mm [26]. The phase noise attributed to low coherence due to perpendicular baselines can be discounted if the perpendicular baseline is 5 m or less for Sentinel-1 (~0.97 coherence). If the ground deformation rate is 3 mm y−1, an interferogram with a perpendicular baseline < 5 m and a temporal baseline of 800 days (2.2 years) will observe a differential phase of 6.6 mm. Likewise, if the ground deformation rate is 2 mm y−1, an interferogram with a similarly short perpendicular baseline but a 1400-day temporal baseline will observe a differential phase of 7.7 mm. The differential phases measured by both interferograms exceed the phase noise of 6 mm introduced by a temporal baseline coherence of 0.1 (Figure 2). For this reason and due to finite computing resources, we suggest that LTSPB interferograms be created with temporal baselines of 800 days to 1400 days. SB interferograms with a low level of noise due to temporal baseline coherence can measure slow (~3 mm y−1) deformation rates via SBAS. However, this will require a large number of interferograms that may not provide a robust SBAS least squares solution.
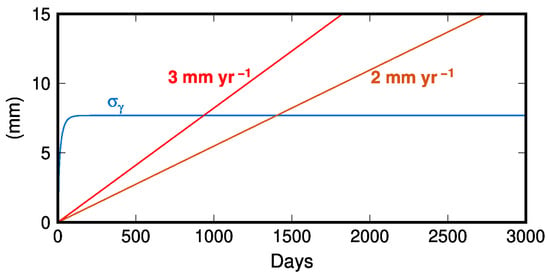
Figure 2.
Phase noise () for single look Sentinel-1 (wavelength 5.6 cm) due to 0.1 long-term temporal baseline coherence (blue line) and cumulative displacements for displacement rates of 3 mm y−1 (red line) and 2 mm y−1 (brown line). The phase noise from coherence as a function of time (temporal decorrelation; Equation (7) in [16]) for single look SAR acquisition is from Equation (4.2.28) in [25].
3. Tropospheric Phase Delay Error
Tropospheric phase delay is governed by changes in tropospheric refractivity, which varies based on density, i.e., temperature and pressure, and water content [25]. Consequently, tropospheric refractivity changes as a function of height. Alone, height-dependent tropospheric refractivity does not impact a two-pass acquisition of an area with relatively uniform elevation but vertically stratified phase delay can arise around high relief (e.g., [27]). Spatially, tropospheric refractivity varies in 3D due to the inherent turbulent mixing of the troposphere. Tropospheric delay estimating techniques have been created to increase the accuracy of the InSAR observations. These methods rely on analytical models such as the linear relationship with topographic relief and the introduced phase error [28] and power law models that estimate the phase error spatially [29], or satellite-derived wet and dry delay estimates such as Global Navigation Satellite System (GNSS) [30], MODIS [31], MERIS [32], or weather models such as, but not limited to, ERA5 [33] and high-resolution ECMWF (commonly employed through the Generic Atmospheric Correction Online Service—GACOS [34]). While these models have improved the accuracy of InSAR observations, they are spatially and temporally coarse, or in the case of GNSS, suffer from low spatial density, or do not incorporate local data and consequently overestimate or underestimate the tropospheric phase delay error, potentially introducing a new source of error [35,36,37,38].
The LTSPB method, compared to small baselines (SBs), provides for more robust SBAS-derived time series estimation by minimizing the effects of tropospheric phase delay. Below, we first determine the minimum detectable phase measurement with regard to only the tropospheric phase delay error. This is accomplished by evaluating the signal-to-noise ratio required for a robust SBAS solution by determining the total error introduced by the tropospheric phase delay in a set of interferograms. We then demonstrate, using real-world total tropospheric phase delay from the GNSS Zenith Total Delay, that LTSPB interferograms are capable of measuring differential phases that exceed this source of noise and achieve velocity detection thresholds of 2 mm y−1 to 3 mm y−1. Then, we show, via a simulation of tropospheric phase delay error, that the LTSPB interferograms do exceed the tropospheric phase delay error and provide robust SBAS-derived time series solutions.
3.1. Tropospheric Phase Delay Error and Time Series Estimation
Tropospheric phase delay is caused by the spatially correlated but temporally uncorrelated changes in the refractivity of the troposphere [9,39] and the phase delay difference in two-pass interferometry is called the atmospheric phase screen (APS). Discounting the APS mitigation strategies previously detailed, it is difficult to discern between the APS and the true LOS difference in phase. Hence, the APS error introduces biases in SBAS-derived InSAR time series [40] (See Appendix D). Here, we show that the LSTPB interferograms decrease the sensitivity of SBAS solutions to APS errors by considering the SBAS least-squares formulation by showing that LTSPB interferograms increase the signal-to-noise ratio.
The phase difference for the set of unwrapped interferograms is described, pixel-wise, as the following system of equations
where and is the phase from the primary and reference acquisition, respectively, for the jth interferogram, and is the measured phase difference. In the most general case, where the interferograms form only one subset network, the phase difference can be solved with the least-squares SBAS formulation [5]
where is the connectivity matrix of the acquisition times for the interferograms, is the modeled incremental displacements between acquisition times and is the vector of the observed differential phases. If the set of interferograms does not constitute one subset, i.e., is rank-deficient, then the SBAS formulation can be solved via singular value decomposition of or by employing a regularization constraint in the least squares estimation. If we consider only the noise due to the APS, the signal-to-noise ratio is
where is the total propagated uncertainty introduced by the APS for the interferograms. The total uncertainty for the APS () can be determined by the linear propagation of measurement error introduced by the tropospheric phase delay for acquisition pairs. For an SBAS analysis, the maximum total uncertainty due to the APS will be for a fully connected network of acquisitions, where
interferograms are created by pairing each acquisition with every other acquisition [5]. Then, , pixel-wise, can be expressed as
where is the uncorrelated tropospheric phase delays for the acquisitions. If we consider the mean and standard deviation () of phase delay for all acquisitions, then Equation (6) can be expressed as
Equation (7) represents the upper limit to error due to tropospheric phase delay for an SBAS analysis. It is unlikely to represent the total APS for most InSAR analyses since a fully connected network is not required. Regardless, for the typical SBAS analysis, the following expression holds
That is, the standard deviation of the tropospheric phase delay for all acquisitions is the total APS error for an SBAS analysis. Considering the signal-to-noise ratio (SNR) described by Equation (4), the SNR is greater than one when the Euclidean norm of observed differential phases is greater than the total propagated error of the APS for all interferograms () resulting in a robust SBAS time series solution. Meanwhile, an SNR less than may produce an SBAS solution that is more sensitive to the APS error. It also follows from Equation (4), in the trivial form, for interferogram , that SNR > 1 when , where is the APS error for interferogram . For robust SBAS-derived timeseries, LTSPB interferograms will better satisfy compared to SB interferograms. An analysis of LTPSB differential phases exceeding the APS is detailed in the next section.
3.2. APS from GNSS Zenith Total Delay
A rigorous analysis of the APS error and its influence on SBAS time series estimation is difficult because of the intractable effort of fully describing the APS error analytically. Instead, we analyze the total APS from line-of-sight projected zenith tropospheric delay (ZTD) from 11 GNSS stations in regions that represent the extreme factors that affect troposphere refractivity, such as humidity, land use, and change in relief (Figure S1).
We retrieved ZTD products from the Nevada Geodetic Laboratory, University of Nevada, Reno (NGL-UNR) [22], for GNSS stations in the Tampa Bay Area (TBA), Florida, Socorro, New Mexico, and western Nicaragua (Table 1). The TBA is a coastal plain with changes in land use from dense urban areas to vegetated areas with herbaceous plants, small trees, and large shrubs, both containing natural and man-made water features such as lakes and retention ponds. The climate of the TBA can be typified as humid and subtropical with thunderstorms during the summer. This contrasts with Socorro, which has an arid climate, fewer water bodies, fewer changes in land cover, and great variation in relief (~1.5 km vertically over 70 km horizontally) compared to the TBA. Western Nicaragua is a tropical coastal shrubland plain that abuts the mountainous highlands (~800 km in relief) with two large lakes and a volcanic arc with volcanoes spaced approximately 5 km apart from each other. These regions represent the extremes in humidity and changes in relief that may induce turbulent or stratified atmospheric conditions (Socorro and western Nicaragua). See Figure S1 for locations of GNSS stations for which ZTD data were retrieved.

Table 1.
The average and standard deviation of LOS-projected ZTD for GNSS station pairs and the probability that the cumulative displacements of 4 mm (2 mm y−1 over 800 days), 8 mm (2 mm y−1 over 1400 days), 7 mm (3 mm y−1 over 800 days), and 12 mm (3 mm y−1 over 1400 days) is greater than an APS, , from a normal distribution.
We determine the total uncertainty due to the APS ( in Equation (6)), i.e., the standard deviation of APS of all acquisitions, for each GNSS station, by first using the ZTD in 12 day increments (representative of the Sentinel-1A repeat pass) at 16:00 local time. Interferograms are relative in space and time and a measured phase difference is always referenced to a stable point in space. For this reason, the ZTD values per station were referenced to another station [25,41]. For this study, there is no information as to which GNSS station is the most stable, so all pair combinations were evaluated. The differential referenced ZTD values were created using the LTSPB strategy with temporal baselines of 800 days to 1400 days and projected into a pseudo-line-of-sight using an incidence angle of 40° (Table 1).
Again, consider a pixel for a set of LTSPB interferograms with temporal baselines of 800 days (2.2 years) that observe 2 mm y−1 of ground deformation, i.e., differential phase measurements of 4.4 mm. For the signal-to-noise ratio to be greater than 1, then, from Equation (4), . This is not the case for the APS error derived from GNSS ZTD (Table 1). However, GNSS ZTD reveals that the probability of a differential phase measurement of 4.4 mm exceeding the APS, , from a normal distribution of the LOS-projected ZTD, is on average 60% (Table 1). Likewise, Table 1 shows the one-tailed probability of the APS noise being lower than the differential phase measurements of 8 mm (2 mm y−1 over 1400 days; average probability of 68%), 7 mm (3 mm y−1 over 800 days; average probability of 64%), and 12 mm (3 mm y−1 over 1400 days; average probability of 75%). Combined with the error due to temporal baseline coherence, it is possible for interferograms, with a temporal baseline of 800 days, to measure 2 mm y−1.
3.3. Tropospheric Phase Delay Simulation
We further explore the effects of tropospheric phase delay on time series estimation by creating simulated SAR acquisitions using the Kolmogorov power law [25] where, assuming isotropy in the three dimensions, the power spectrum of the atmospheric turbulence mixing at different scales can be represented as
where is the power spectrum, is the wavenumber in cycles/km, and , , and are the power spectra for three different regimes of wavelength scales. Using Equation (9), simulated SAR images were created to contain tropospheric phase delay in the order of 3 radians or ~15 cm for C-band Sentinel-1. Tropospheric phase delay in InSAR measurement is seasonal [35,40,42,43] and, hence, the introduced tropospheric phase delay was varied seasonally by varying the spectral index of by , where is the day of the year of the assigned acquisition date (see Section S2 for details on seasonal variation).
Two sets of SAR images were created, which included two deformation sources. We produced two deformation patterns of (1) a circle with a radius of 5.5 km, where the center of the circle has a maximum deformation rate of 5 mm y−1 and linearly decreases to 0 mm y−1 at the circumference and (2) a Gaussian function where the standard deviation is 3 km (Figure 3). The deformation pattern created by the Gaussian function was intended to mimic diffused but broadscale deformation because few ground deformation sources produce a linear velocity gradient. SAR images were also assigned baselines randomly selected from a normal distribution with a mean of 0 m and of 30 m. Simulated interferograms were then created for the SB (daisy-chained acquisition) and LTSPB (800 to 1400 day temporal and <5 m perpendicular baseline) strategies, unwrapped with the SNAPHU code [44], and from which time series were estimated using the MSSBAS code [45] which employs singular value decomposition in the case that isolated subnetworks were created.
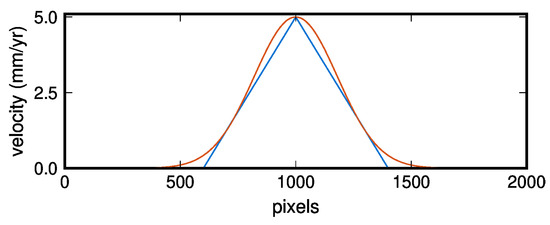
Figure 3.
The cross-section of deformation patterns for linear rate decrease (blue line) and rate decrease by a Gaussian function (red line).
The resulting SBAS-derived timeseries for SB (Figure 4b,e) and LTSPB (Figure 4c,f) demonstrate that the velocity detection threshold of the latter is in the order of 2 mm y−1 to 3 mm y−1. The SBAS method did not reproduce either of the deformation sources, which had a maximum deformation rate of 5 mm y−1. The results do show a limitation of the LTSPB method where broadly diffused deformation, like the Gaussian function-derived deformation pattern, cannot be reproduced due to the high deformation rate gradient and low rates.
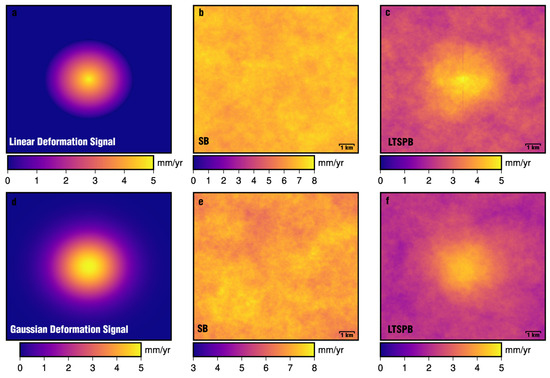
Figure 4.
Simulated deformation for (a) linear decrease of 5 mm/y and to 0 mm/y, (d) a decrease of 5 mm/y and to 0 mm/y governed by a Gaussian function where the standard deviation is 3 km. (b) Velocities using SB interferograms for a linear decreasing deformation pattern. (c) Velocities for using LTSPB interferograms for a linear decreasing deformation pattern. (e) Velocities using SB interferograms for Gaussian function decreasing deformation pattern. (f) Velocities for using LTSPB interferograms for Gaussian function decreasing deformation pattern.
4. Unwrapping Error
Unwrapping errors produce N2π radian steps in SBAS-derived timeseries that approximate a random walk [46] and are a significant source of error because ordinary least squares minimizes the sum of the squared residuals. Unwrapping errors (N2π radians), compared to smaller measured differential phase values, when squared, will have a larger effect on the SBAS solution. The effect of the error on the SBAS solution can be mitigated by increasing the number of interferograms [46], as this error, in the least squares sense, is an outlier bias problem. However, increasing the number of interferograms may not improve the SBAS solution if the prevalence rate of unwrapping errors is the same or greater. The error can be potentially—but not fully—removed by creating bridges between areas of low coherence [47,48] or the error-introduced bias resolved by phase closure loops using a weighted least squares approach [40]. Another more robust approach is solving the phase closure loop using L1 norm minimization, which is less sensitive to outliers [46,48]. Regardless, this error reduction method performs well when less than 40% of the interferogram contains unwrapping errors [46]. Using LTSPB interferograms, along with L1 norm minimization techniques, will decrease the effect of unwrapping errors for SBAS-derived time series. With regard to the SBAS least squares formulation, unwrapping errors pose large N2π radian outliers, and the larger differential phases of LTSBP interferograms, compared to that of SB interferograms, will reduce the influence of unwrapping errors on the SBAS solution.
Unwrapping Error and Time Series Simulation
Unwrapping errors reduce the robustness of SBAS-derived time series estimation. We use simulated phase unwrapping errors in SBAS inversions (see [46]; Figure 5) to show that LTSPB interferograms decrease the sensitivity of the SBAS solution to unwrapping errors. Pixel-wise, three time series were simulated where time series estimation was done using SBAS least squares with a regularization constraint and 5% of the interferograms were randomly selected to add an unwrapping error. The simulated acquisition times were chosen to represent a repeat pass of 12 days (similar to Sentinel-1A). Differential phases for the pixel were estimated by the deformation between acquisitions using a deformation rate of 4 mm y−1. Figure 5a,b show a simulated time series inverted from 150 SB interferograms by daisy-chaining acquisitions, i.e., a temporal baseline of 12 days. The simulated time series shows the steps in the estimated time series due to unwrapping errors. Figure 5c,d show the simulated time series for an SBAS inversion of 444 SB interferograms created with a temporal baseline of three neighboring acquisitions (i.e., 36 days) and show the reduction in the size of steps due to the increased number of interferograms. However, a velocity bias is still present regardless of the reduction in the magnitude of the steps. Figure 5e,f show the simulated time series using a mixture of SB (30%) and LTSPB (70%) interferograms, which totaled 435 interferograms. The baseline constraints of the LTSPB interferograms allow for the possibility of creating more interferograms but, for comparison to the time series inverted from SB interferograms in Figure 5c, we chose to randomly remove LTSPB interferograms until there was an equivalent number of interferograms (~400). The removal of LTSPB interferograms left acquisitions that were not paired and, to remedy this problem, SB interferograms were created. This simulation demonstrates that the SBAS-derived time series for LTSPB interferograms lessens the sensitivity of unwrapping errors as the introduced bias is significantly reduced.
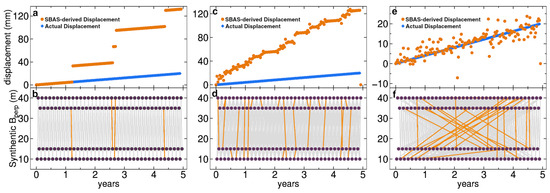
Figure 5.
Simulated SBAS-derived time series estimated from interferograms with an unwrapping error prevalence rate of 5% and their associated baseline network. Acquisitions (purple circles) represent a repeat pass of 12 days. The total number of acquisitions is 150. (a) Time series (orange circles) were created from 150 SB 12 days interferograms with the unwrapping error present. Blue circles are actual displacements for a rate of 4 mm y−1 without unwrapping errors. (b) Temporal baselines (12 days) for interferograms (grey lines) with 5 interferograms containing unwrapping error highlighted (orange line). Y axis is synthetic perpendicular baseline. (c,d) SBAS-derived time series for 444 SB interferograms with 36 day temporal baseline interferograms containing 24 unwrapping errors. (e,f) SBAS-derived time series for 435 interferograms consisting of 70% LTSPB and 30% 12-day SB interferograms with 26 interferograms containing unwrapping errors. Note, y axis for (e) not the same as (a,b), and actual displacements are the same.
5. LTSPB Applied to the TBA and SMB
We test the LTSPB strategy by using Sentinel-1A data and estimating time series and velocities for the regions of Tampa Bay Area (TBA), Florida, and Socorro, New Mexico (Figure 6). Like the choice of GNSS ZTD in Section 3.2, these two regions were selected because they represent end-member cases for water vapor content and seasonal turbulence in the troposphere.
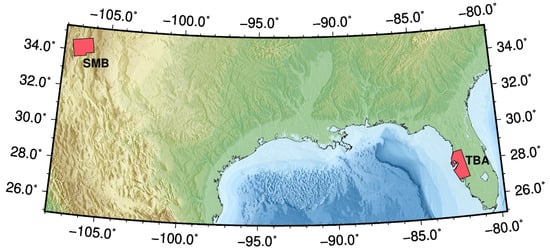
Figure 6.
Sentinel-1 SAR coverage for SMB and TBA used in this study.
For comparison, velocity fields for both the SMB and TBA were estimated using the SB and the LTSPB strategy (Figure 7). Interferograms were created using the GMTSAR V5.5 software [49]. For the SB method, interferometric pairs were created with temporal baselines of 36 days and perpendicular baselines of less than 300 m (Figure 7a,b). Interferometric pairs for the LTSPB method were created using the criteria described in Section 3.1 (Figure 7c,d). To not alias transient deformation, LTSPB interferograms were also complemented with SB interferograms with a temporal baseline of 12 days and perpendicular baselines of 300 m. It should be noted that the LTSPB method does not require SB interferograms when observing slow deformation rates. We processed Sentinel-1A single-look complex images for the SMB (path 96 and frame 107; 13 February 2016 to 13 December 2021) and the TBA (path 121 and frame 85; 17 April 2016 to 2 June 2022). The selection of stable Persistent Scatters (PSs) and LOS time series estimation was done using the StaMPS code [50]. The choice of using PS processing is to identify stable scatters with long-term coherence. Alternatively, the LTSPB method can be successfully employed when using the less computationally intensive distributed scatters method with multilooking if the SAR scene primarily consists of scatters with good long-term coherence, e.g., the arid bare soil of Socorro (see Appendix B). Interferograms were unwrapped with the SNAPHU code. In order to reduce the effects of tropospheric error and unwrapping error, SNAPHU was configured to produce few discontinuities during unwrapping (see Appendix A). InSAR-derived velocities for the SMB and TBA were then compared to those of GNSS stations. GNSS velocity estimation and projection into LOS are detailed in Appendix C.
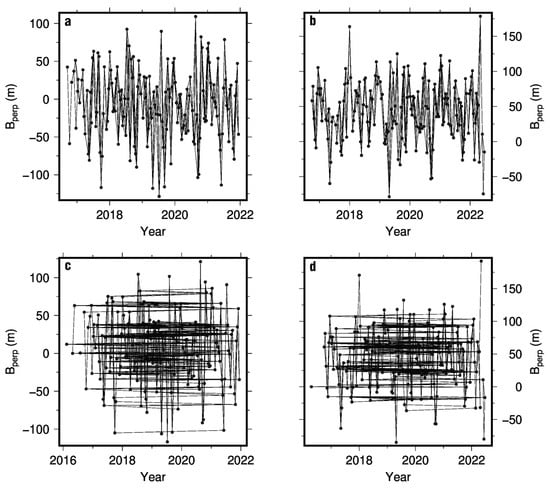
Figure 7.
Baseline networks for SBAS (a) TBA and SMB (b), and LTSPB for TBA (c) and SMB (d).
Separately, we created time series for the TBA by applying the GACOS atmospheric correction models to LTSPB interferograms. GACOS products are the most widely used APS correction method and have been shown to be superior to other correction methods [51]. We apply these corrections to qualify their efficacy and assess the introduced uncertainty.
The resulting velocities (Figure 8 and Figure 9) show that the LTSPB strategy produces better velocity fields with a qualitatively lower RMS and fewer artefacts compared to the SB strategy. From 2017 to 2022, GNSS station CDVV experienced uplift rates of 3 ± 2 mm/y (see Table S1 and Figure 8a,b). The SBAS-derived SB velocity field of the SMB has a mean LOS velocity of −8.1 mm/y with a standard deviation of 5.6 mm/y, and large negative values associated with relief (Figure 8a) and the maximum LOS uplift value being ~6 mm/y. The SBAS-derived LTSPB velocity field has a mean LOS velocity of 0.5 mm/y with a standard deviation of 0.8 mm/y (Figure 8b). The LTSPB method yields an inflation signature that is equivalent in magnitude to the GNSS station CDDV, with a maximum LOS uplift value of 4 mm/y. Meanwhile, [20] reported broadscale (10 s of km in extent) subsidence rates of 6 mm/y in the TBA. Likewise, the SBAS-derived SB velocities show broadscale subsidence at rates of 5 mm/y to 7 mm/y, contradicting the GNSS LOS velocities of the region (Figure 9a). LTSPB InSAR velocities agree with GNSS velocities and show that there is no broadscale subsidence in the TBA (Figure 9b). Our velocity fields for both the TBA and SMB demonstrate that the LTSPB is better suited for slow deformation rates. Furthermore, the LTSPB strategy obviates the need for tropospheric delay models like GACOS. Figure 9c shows the inclusion of the GACOS correction to LTSPB interferograms and the resulting short wavelength (5 km to 10 km) artefacts in the velocity field.
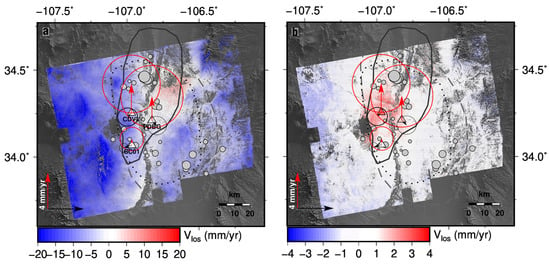
Figure 8.
SBAS-derived LOS velocities for the SMB for 2017 to 2022 using (a) SB and (b) LTSPB methods. Red pixels are LOS velocities towards the sensor. Triangles are GNSS velocities projected into the LOS using the same symbols as LOS velocity. Red arrows are vertical GNSS velocities. Black arrows are horizontal GNSS velocities that are referenced to the GNSS station P120 (see Table S1). Red and black circles are ±σ of vertical and horizontal GNSS velocities, respectively. Grey circles are earthquakes from the NEIC catalog [52]. Outlines of SMB from previous studies: solid line—[53], dashed line—[54], and dotted line—[55]. Note that the extremes of the color scale are different for each panel. Missing patches are due to very high amplitude dispersion for pixels that were not selected for processing.
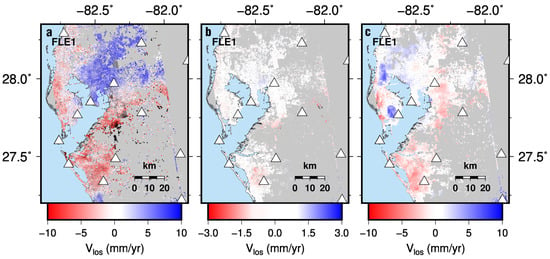
Figure 9.
SBAS-derived LOS velocities for the TBA for 2017 to 2023 using the (a) SB method, (b) LTSPB methods, and (c) GACOS correction and the LTSPB method. Symbols are the same as in Figure 8.
6. Discussion
The LTSPB strategy excels at measuring slow rates of deformation. We demonstrated that, by using interferometric pairs with long temporal baselines (800 days to 1400 days) to enhance the signal-to-noise ratio with very short perpendicular baselines (<5 m) (LTSPB), to avoid decorrelation, it is possible to detect slow ground deformation at rates of 2 mm y−1 to 3 mm y−1. Our simulations and real-world tests of the LTSPB strategy show that it produces velocity fields with better precision and substantially lower RMS compared to the SB strategy. While the LTSPB strategy is well suited for slow rates of deformation, a clear limitation is that transient deformation will be aliased if there are not enough interferograms that temporally span the event. Another limitation is the case of events that produce large discontinuities (e.g., earthquakes) over a short period (less than the repeat pass). Due to the SBAS least squares method and the irregular availability of LTSPB interferograms in time, the measured large differential phases may be attributed to the wrong acquisition time, resulting in a time series solution where the discontinuity appears at many acquisition times. To correct this problem, baseline networks will have to be constructed around the event and connected via a single interferogram. This may affect the number of interferograms that fit the baseline criteria for the LTSPB method.
Our InSAR analysis of ground deformation due to the SMB and in the TBA, using the LTSPB method, revealed deformation patterns that are contradictory to previously published InSAR studies. The inflation due to SMB using InSAR has been described as “sombrero” shaped and due to a large sill emplacement [17,56]. The inflation signature of the SMB does not lend well to a single sill emplacement. Due to the shorter wavelength features (Figure 8b), the observed inflation may be due to overpressured lenses of magma at various depths or uplift due to reactivated faulting, which is mechanically preferable (e.g., [57]). Earthquakes associated with the SMB, from 2002 to 2022, were analyzed with clusters identified and relocated by [58]. The work shows that seismicity occurred over an area of 20 km × 30 km area, at a maximum depth of 10.7 km, in pulses with little temporal correlation. Most of the earthquakes occurred on steep dipping activated rifting faults that are a part of the Rio Grande Rift zone. The stress state of the crust in the Rio Grande Rift zone may be highly heterogeneous due to lenses of overpressure magma, resulting in the InSAR velocities we observe. However, it is more likely that uplift is due to the magma overpressure of a sill-like emplacement and accommodated on the rift faults due to the spatiotemporal distribution of seismicity and lack of a uniform dome signal in the InSAR velocities.
For the TBA, the LTSPB-derived InSAR velocities show that there is no broadscale subsidence (Figure 9b). There are areas of localized subsidence in the velocity field we present. This subsidence is due to the loading of large structures (e.g., large buildings and phosphate mining tailings), soil consolidation due to dewatering driven by anthropogenic factors, and possible sinkhole activity.
The precision of InSAR measurements can be further increased by time series analysis. The unwrapping error will manifest as value jumps in InSAR-derived time series. Likewise, so can tropospheric phase delay, in particular, offsets might arise if there is long-standing atmospheric turbulence shared by many interferograms or the SB and LTSPB interferogram sets may include SAR acquisitions, common to many interferograms, that may have very different tropospheric phase delay characteristics compared to the other acquisitions (see example in Appendix D). The biases introduced by the offsets and seasonal signals can be reduced by fitting the following equation to the LTSPB SBAS-derived time series to estimate the velocity,
where denotes the amplitudes of the step functions , and denote the amplitudes of the annual and semi-annual seasonal component, denotes the phase lag of the annual and semi-annual seasonal components, and denotes the velocity. This has long been the treatment of many geophysical signals, such as tide gauges (e.g., [59]) and GNSS (e.g., [60,61]), that vary seasonally. Due to the computationally expensive nature of detecting offsets in geophysical signals (e.g., [61]) and repeating this process on an InSAR-derived velocity field that may be up to several millions of single-look pixels per Sentinel-1 subswath, we advise the manual identification of pixels representative of regions suspected to be biased by tropospheric delay error and the inspection of the time series to determine where offsets are apparent and unexpected. Complementing Sentinel-1 LTSPB interferograms with the time series treatment previously described would decrease the LOS velocity detection threshold to 2 mm y−1 and reduce the need for unwrapping error removal methods and tropospheric phase delay models that may be unsuitable or introduce error [62].
Tropospheric models have been shown to increase the accuracy of the InSAR measurements and lower the RMS of the velocity field (e.g., [34]). However, tropospheric models suffer from being spatiotemporally coarse and introduce another source of error. For example, the GACOS corrections are produced at resolutions of 0.125° at 6 h intervals and utilize the European Centre for Medium-Range Weather Forecasts. We applied the GACOS correction to the LTSPB strategy interferograms used to produce the velocity field for the TBA to demonstrate the error associated with the correction (Figure 9c). While the RMS of the velocity using the GACOS corrections is relatively low (2.5 mm y−1; Figure 9c), there are areas where the corrections performed poorly, possibly due to the localized climatic conditions that cannot be captured by the correction. Regardless, GACOS corrections introduced artefacts, such as up to 10 mm/y of uplift, that are not representative of the vertical land motion in the TBA. The results of the LTSPB method and removal of the seasonal biases and steps in the time series achieved a much lower RMS (Figure 9b) compared to the strategy being complemented by GACOS corrections.
7. Conclusions
Tropospheric turbulence and unwrapping error are a significant source of error for estimating InSAR time series. We demonstrated that utilizing the data length of the Sentinel-1 dataset by incorporating interferograms with long temporal (800 days to 1600 days) but very short perpendicular (<5 m) baselines (LTSPBs) increases the ability to detect slow deformation against the error introduced by tropospheric turbulence and unwrapping. While tropospheric phase delay models are useful, they often suffer from deficiencies such as coarse spatiotemporal scales that make them unsuitable for removing tropospheric phase delay error. Furthermore, identifying and removing steps in the InSAR time series that result from these errors further lowers the velocity detection threshold of the Sentinel-1 SAR dataset. This technique should be employed to detect low velocity (~3 mm/y) ground deformation in regions that have particularly complex tropospheric mixing and unwrapping errors due to unwrapping across areas of poor coherence.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/rs17142420/s1, Figure S1: GNSS stations used in ZTD analysis. (a) Tampa Bay Area, Florida. (b) Socorro, New Mexico. (c) Western Nicaragua.; Figure S2: Power spectra for two interferograms of the TBA created from Sentinel-1 SAR acquisitions in the dry season (2017-11-14 and 2017-11-26, red line) and wet season (2017-07-17 and 2017-07-29, blue line); Figure S3: Interferograms for the (a) wet season (acquisitions 2017-07-17 and 2017-07-29) and (b) dry season (2017-11-14 and 2017-11-26).; Table S1: GNSS velocities in ITRF-NA reference frame for the 2017 to 2022.
Author Contributions
Conceptualization, M.H. and S.W.; methodology, M.H.; software, M.H.; validation, M.H. and S.W.; formal analysis, M.H.; investigation, M.H.; resources, M.H. and S.W.; data curation, M.H.; writing—original draft preparation, M.H.; writing—review and editing, M.H. and S.W.; visualization, M.H.; supervision, S.W.; project administration, S.W.; funding acquisition, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Aeronautics and Space Administration (NASA) grant #80NSSC22K0462 and the National Science Foundation grant EAR-2321754 awarded to S.W. This is contribution #2017 from the Institute of Environment at Florida International University.
Data Availability Statement
The scripts used in this study to simulate SAR scenes can be accessed at https://doi.org/10.5281/zenodo.13626385. GNSS data used in this study were retrieved from the Nevada Geodetic Laboratory, University of Nevada, Reno (https://geodesy.unr.edu/NGLStationPages/GlobalStationList, Last accessed 4 June, 2024). The sentinel-1 SAR scenes used in this study can be downloaded from the Alaska Satellite Facility (https://search.asf.alaska.edu, Last accessed 29 May 2024).
Acknowledgments
We would like to thank Falk Amelung for the fruitful discussions and the Academic Editors and reviewers who helped strengthened this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| APS | Atmospheric phase screen |
| GACOS | Generic Atmospheric Correction Online Service |
| GNSS | Global Navigation Satellite System |
| InSAR | Interferometric synthetic aperture radar |
| LOS | Line of sight |
| LTSPB | Long-temporal short-perpendicular baselines |
| SAR | Synthetic aperture radar |
| SBAS | Short baselines |
| SMB | Socorro magma body |
| TBA | Tampa bay area |
| ZTD | Zenith total delay |
Appendix A
- SNAPHU configuration parameters used to ensure smooth unwrapping:
- DEFOMAX_CYCLE 0
- DEFOCONST 0.01
Appendix B
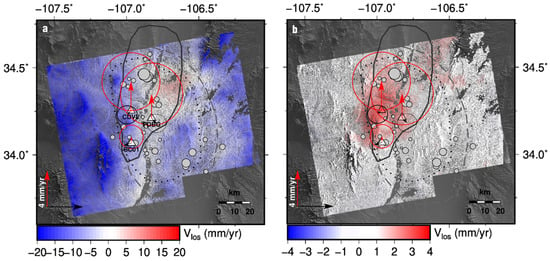
Figure A1.
Distributed scatters LOS velocities for the SMB for 2017 to 2022 using (a) SBAS and (b) LTSPB methods. Distributed scatters were multilooked 20 in range and 8 in azimuth. Interferograms were created using the GMTSAR software [49] and pixels with less than 0.1 coherence were interpolated using the nearest-neighbor approach. Interferograms were then unwrapped with SNAPHU software [44]. Time series and velocity were estimated using the MSBAS V3 software [45]. Symbols are the same as Figure 4.
Appendix C
Daily positions in the North American ITRF2014 reference frame (ITRF2014-NA) [63] for GNSS stations in Socorro, New Mexico, with data exceeding 2.5 years, were retrieved from the Nevada Geodetic Laboratory, University of Nevada, Reno (NGL-UNR) [22]. Velocities for the period covering Sentinel-1 SAR acquisitions were estimated by fitting a linear trend. Velocity uncertainties were estimated by the RMSE of the linear fit. Velocities were then referenced to the GNSS station P120 (https://doi.org/10.7283/T5SQ8XDS). See Table S1. For the TBA, GNSS horizontal velocities and uncertainties retrieved from the NGL-UNR were in the order of ~2 mm/y in the ITRF2014-NA reference frame [64]. Therefore, only vertical GNSS NGL-UNR reported velocities were used in our TBA analysis. GNSS velocities for the SMB and TBA were projected in LOS using the following equation
where is the vertical GNSS velocity projected into LOS, , is the vertical GNSS velocity, and is the incidence angle of the SAR acquisition.
Appendix D
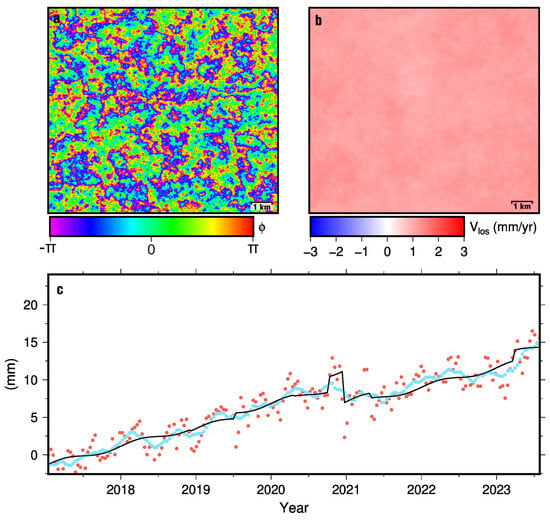
Figure A2.
(a) A simulated wrapped SAR scene with an introduced atmospheric delay of <15 cm with temporal baselines of 1116 days. (b) SBAS-derived velocity field of simulated InSAR using the LTSPB strategy. (c) Simulated InSAR-derived LTSPB time series (red circles) for a pixel (same as Figure 5c) with moving mean with a window of 10 acquisitions (blue circles) and offset an annual seasonal signal fit (black line). Linear fit velocity of the time series is 1.2 mm/y, while the velocity of the fitted function is 1.5 mm/y.
References
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The Displacement Field of the Landers Earthquake Mapped by Radar Interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Pinel, V.; Poland, M.P.; Hooper, A. Volcanology: Lessons Learned from Synthetic Aperture Radar Imagery. J. Volcanol. Geotherm. Res. 2014, 289, 81–113. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Prati, C.; Rocca, F. Monitoring Landslides and Tectonic Motions with the Permanent Scatterers Technique. Eng. Geol. 2003, 68, 3–14. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Engelhardt, H.; Kamb, B.; Frolich, R.M. Satellite Radar Interferometry for Monitoring Ice Sheet Motion: Application to an Antarctic Ice Stream. Science 1993, 262, 1525–1530. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Casu, F.; Manzo, M.; Lanari, R. A Quantitative Assessment of the SBAS Algorithm Performance for Surface Deformation Retrieval from DInSAR Data. Remote Sens. Environ. 2006, 102, 195–210. [Google Scholar] [CrossRef]
- Agram, P.S.; Simons, M. A Noise Model for InSAR Time Series. J. Geophys. Res. Solid Earth 2015, 120, 2752–2771. [Google Scholar] [CrossRef]
- Pepe, A. Multi-Temporal Small Baseline Interferometric Sar Algorithms: Error Budget and Theoretical Performance. Remote Sens. 2021, 13, 557. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in Interferometric Radar Echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Fattahi, H.; Simons, M.; Agram, P. InSAR Time-Series Estimation of the Ionospheric Phase Delay: An Extension of the Split Range-Spectrum Technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5984–5996. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar Interferometry and Its Application to Changes in the Earth’s Surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps. J. Geophys. Res. Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Zheng, Y.; Fattahi, H.; Agram, P.; Simons, M.; Rosen, P. On Closure Phase and Systematic Bias in Multilooked SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Sica, F.; Pulella, A.; Nannini, M.; Pinheiro, M.; Rizzoli, P. Repeat-Pass SAR Interferometry for Land Cover Classification: A Methodology Using Sentinel-1 Short-Time-Series. Remote Sens. Environ. 2019, 232, 111277. [Google Scholar] [CrossRef]
- Morishita, Y.; Hanssen, R.F. Temporal Decorrelation in L-, C-, and X-Band Satellite Radar Interferometry for Pasture on Drained Peat Soils. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1096–1104. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M. Evidence for On-Going Inflation of the Socorro Magma Body, New Mexico, from Interferometric Synthetic Aperture Radar Imaging. Geophys. Res. Lett. 2001, 28, 3549–3552. [Google Scholar] [CrossRef]
- Havazli, E.; Wdowinski, S. Detection Threshold Estimates for Insar Time Series: A Simulation of Tropospheric Delay Approach. Sensors 2021, 21, 1124. [Google Scholar] [CrossRef]
- Finnegan, N.J.; Pritchard, M.E. Magnitude and Duration of Surface Uplift above the Socorro Magma Body. Geology 2009, 37, 231–234. [Google Scholar] [CrossRef]
- Wu, P.; Wei, M.; D’Hondt, S. Subsidence in Coastal Cities Throughout the World Observed by InSAR. Geophys. Res. Lett. 2022, 49, e2022GL098477. [Google Scholar] [CrossRef]
- Ohenhen, L.O.; Shirzaei, M.; Ojha, C.; Sherpa, S.F.; Nicholls, R.J. Disappearing Cities on US Coasts. Nature 2024, 627, 108–115. [Google Scholar] [CrossRef]
- Blewitt, G.; Kreemer, C.; Hammond, W.C.; Gazeaux, J. MIDAS Robust Trend Estimator for Accurate GPS Station Velocities without Step Detection. J. Geophys. Res. Solid Earth 2016, 121, 2054–2068. [Google Scholar] [CrossRef] [PubMed]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic Aperture Radar Interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Dordrecht, The Netherlands, 2001; Volume 2. [Google Scholar]
- Rodriguez, E.; Martin, J.M. Theory and Design of Interferometric Synthetic Aperture Radars. In IEE Proceedings F (Radar and Signal Processing); IEE: London, UK, 1992; Volume 139, pp. 147–159. [Google Scholar]
- Delacourt, C.; Briole, P.; Achache, J. Tropospheric Corrections of SAR Interferograms with Strong Topography. Application to Etna. Geophys. Res. Lett. 1998, 25, 2849–2852. [Google Scholar] [CrossRef]
- Lin, Y.N.N.; Simons, M.; Hetland, E.A.; Muse, P.; Dicaprio, C. A Multiscale Approach to Estimating Topographically Correlated Propagation Delays in Radar Interferograms. Geochem. Geophys. Geosystems 2010, 11, 1–17. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A Spatially Variable Power Law Tropospheric Correction Technique for InSAR Data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Onn, F.; Zebker, H.A. Correction for Interferometric Synthetic Aperture Radar Atmospheric Phase Artifacts Using Time Series of Zenith Wet Delay Observations from a GPS Network. J. Geophys. Res. Solid Earth 2006, 111, 1–16. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.P.; Cross, P.; Fielding, E.J. Interferometric Synthetic Aperture Radar (InSAR) Atmospheric Correction: GPS, Moderate Resolution Imaging Spectroradiometer (MODIS), and InSAR Integration. J. Geophys. Res. Solid Earth 2005, 110, 1–10. [Google Scholar] [CrossRef]
- Li, Z.; Muller, J.P.; Cross, P.; Albert, P.; Fischer, J.; Bennartz, R. Assessment of the Potential of MERIS Near-Infrared Water Vapour Products to Correct ASAR Interferometric Measurements. Int. J. Remote Sens. 2006, 27, 349–365. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR Tropospheric Phase Delay Corrections from Global Meteorological Reanalysis Data. Geophys. Res. Lett. 2011, 38, 1–6. [Google Scholar] [CrossRef]
- Stephens, K.J.; Wauthier, C.; Bussard, R.C.; Higgins, M. Assessment of Mitigation Strategies for Tropospheric Phase Contributions to InSAR Time-Series Datasets over Two Nicaraguan Volcanoes. Remote Sens. 2020, 12, 782. [Google Scholar] [CrossRef]
- Yang, Q.; Zuo, X.; Guo, S.; Zhao, Y. Evaluation of InSAR Tropospheric Delay Correction Methods in the Plateau Monsoon Climate Region Considering Spatial–Temporal Variability. Sensors 2023, 23, 9574. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical Comparison of InSAR Tropospheric Correction Techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Burgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. InSAR Bias and Uncertainty Due to the Systematic and Stochastic Tropospheric Delay. J. Geophys. Res. Solid Earth 2015, 120, 8758–8773. [Google Scholar] [CrossRef]
- Janssen, V.; Ge, L.; Rizos, C. Tropospheric Corrections to SAR Interferometry from GPS Observations. GPS Solut. 2004, 8, 140–151. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of Stratified Tropospheric Delays in SAR Interferometry: Validation with Global Atmospheric Models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Trishchenko, A.P.; Tiampo, K.; González, P.J.; Zhang, Y.; Fernández, J. Removal of Systematic Seasonal Atmospheric Signal from Interferometric Synthetic Aperture Radar Ground Deformation Time Series. Geophys. Res. Lett. 2014, 41, 6123–6130. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase Unwrapping for Large SAR Interferograms: Statistical Segmentation and Generalized Network Models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef]
- Samsonov, S.V. User Manual, Source Code, and Test Set for MSBASv3 (Multidimensional Small Baseline Subset Version 3) for One-and Two-Dimensional Deformation Analysis. Geomat. Can. Open File 2019, 45, 13. [Google Scholar]
- Xu, X.; Sandwell, D.T. InSAR: Correcting for Earth Tides and Phase. IEEE Trans. Geosci. Remote Sens. 2020, 58, 726–733. [Google Scholar] [CrossRef]
- Oliver-Cabrera, T.; Jones, C.E.; Yunjun, Z.; Simard, M. InSAR Phase Unwrapping Error Correction for Rapid Repeat Measurements of Water Level Change in Wetlands. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small Baseline InSAR Time Series Analysis: Unwrapping Error Correction and Noise Reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Xu, X.; Mellors, R.; Wei, M.; Tong, X.; Wessel, P. GMTSAR: An InSAR Processing System Based on Generic Mapping Tools, 2nd ed.; Scripps Institution of Oceanography: San Diego, CA, USA, 2016. [Google Scholar]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Murray, K.D.; Ebinger, C.J. Active Deformation in the Central Section of the East African Rift from Tectonic, Volcanic, and Hydrologic Processes: Observations from Satellite Geodesy. J. African Earth Sci. 2024, 219, 105390. [Google Scholar] [CrossRef]
- Massé, R.P.; Needham, R.E. NEIC-The National Earthquake Information Center. Earthq. Volcanoes (USGS) 1989, 21, 4–44. [Google Scholar]
- Rinehart, E.J.; Sanford, A.R. Upper Crustal Structure of the Rio Grande Rift near Socorro, New Mexico, from Inversion of Microearthquake S-Wave Reflections. Bull. Seismol. Soc. Am. 1981, 71, 437–450. [Google Scholar]
- Balch, R.S.; Hartse, H.E.; Sanford, A.R.; Lin, K. A New Map of the Geographic Extent of the Socorro Mid-Crustal Magma Body. Bull. Seismol. Soc. Am. 1997, 87, 174–182. [Google Scholar] [CrossRef]
- Sanford, A.R.; Alptekin, Ö.; Toppozada, T.R. Use of Reflection Phases on Microearthquake Seismograms to Map an Unusual Discontinuity beneath the Rio Grande Rift. Bull. Seismol. Soc. Am. 1973, 63, 2021–2034. [Google Scholar] [CrossRef]
- Block, G.A.; Roy, M.; Graves, E.; Grapenthin, R. Pressurizing Magma Within Heterogeneous Crust: A Case Study at the Socorro Magma Body, New Mexico, USA. Geophys. Res. Lett. 2023, 50, e2023GL105689. [Google Scholar] [CrossRef]
- MacQueen, P.; Delgado, F.; Reath, K.; Pritchard, M.E.; Bagnardi, M.; Milillo, P.; Lundgren, P.; Macedo, O.; Aguilar, V.; Ortega, M.; et al. Volcano-Tectonic Interactions at Sabancaya Volcano, Peru: Eruptions, Magmatic Inflation, Moderate Earthquakes, and Fault Creep. J. Geophys. Res. Solid Earth 2020, 125, 1–25. [Google Scholar] [CrossRef]
- Aerts, J. Earthquake Relocation and Characterization Methods and Their Application to the Area Above the Socorro Magma Body in Central New Mexico and to Icequake Swarms in the Beaufort Sea; New Mexico Institute of Mining and Technology: Socorro, NM, USA, 2024. [Google Scholar]
- Tsimplis, M.N.; Woodworth, P.L. The Global Distribution of the Seasonal Sea Level Cycle Calculated from Coastal Tide Gauge Data. J. Geophys. Res. Ocean. 1994, 99, 16031–16039. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of Annual Signals on Geodetic Velocity. J. Geophys. Res. 2002, 107, ETG 9-1–ETG 9-11. [Google Scholar] [CrossRef]
- Bos, M.S.; Fernandes, R.M.S.; Williams, S.D.P.; Bastos, L. Fast Error Analysis of Continuous GNSS Observations with Missing Data. J. Geod. 2013, 87, 351–360. [Google Scholar] [CrossRef]
- Kirui, P.K.; Reinosch, E.; Isya, N.; Riedel, B.; Gerke, M. Mitigation of Atmospheric Artefacts in Multi Temporal InSAR: A Review. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 89, 251–272. [Google Scholar] [CrossRef]
- Altamimi, Z.; Métivier, L.; Rebischung, P.; Rouby, H.; Collilieux, X. ITRF2014 Plate Motion Model. Geophys. J. Int. 2017, 209, 1906–1912. [Google Scholar] [CrossRef]
- Kreemer, C.; Klein, E.; Shen, Z.K.; Wang, M.; Estey, L.; Wier, S.; Boler, F. A Geodetic Plate Motion and Global Strain Rate Model. Geochem. Geophys. Geosyst. 2014, 15, 3849–3889. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).