A Deep Reinforcement Learning Method with a Low Intercept Probability in a Netted Synthetic Aperture Radar
Abstract
1. Introduction
2. Problem Formulation
2.1. Performance Characterization of SAR Detection
2.1.1. Single-Pulse SNR
2.1.2. SNR in SAR Imaging
2.1.3. Range and Azimuth Resolution
2.2. Performance Characterization of LPI Radar
2.3. Optimization Model of NCEVR in Netted Radar SAR Imaging
| Algorithm 1 Calculate the azimuth resolution of LPI netted radar for SAR |
| Input: The positions of the M radars in time T. The positions of the N targets. The single-pulse signal-to-noise ratio from M radars to N targets in time T. Output: Azimuth resolution of each target for the whole task time.
|
3. Data-Driven Resource Allocation Policy Method
3.1. Algorithm
| Algorithm 2 LPI netted radar for SAR imaging in PPO |
|
3.2. Applicability to the Optimization Model
4. Simulation
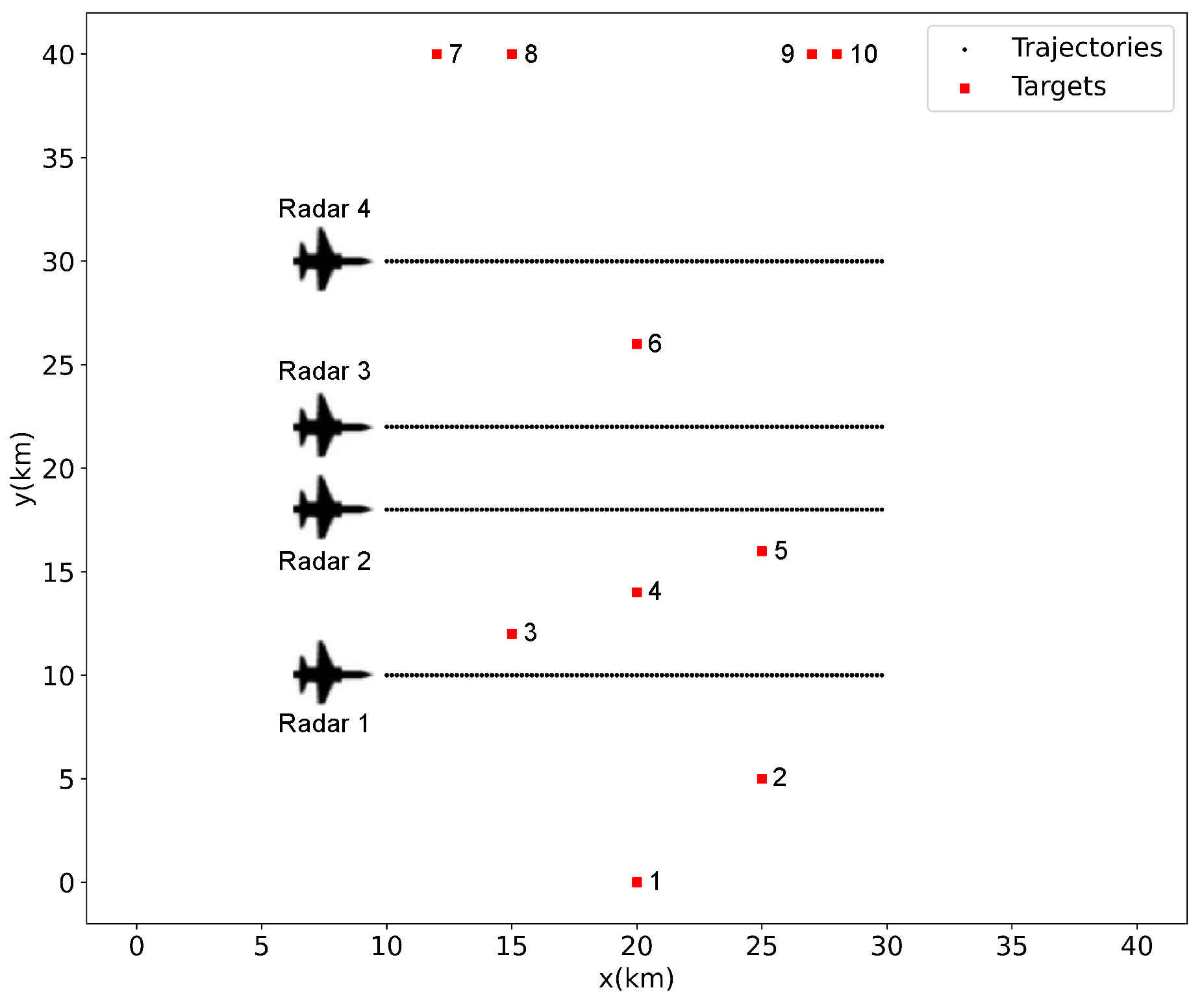
4.1. Simulation Setting
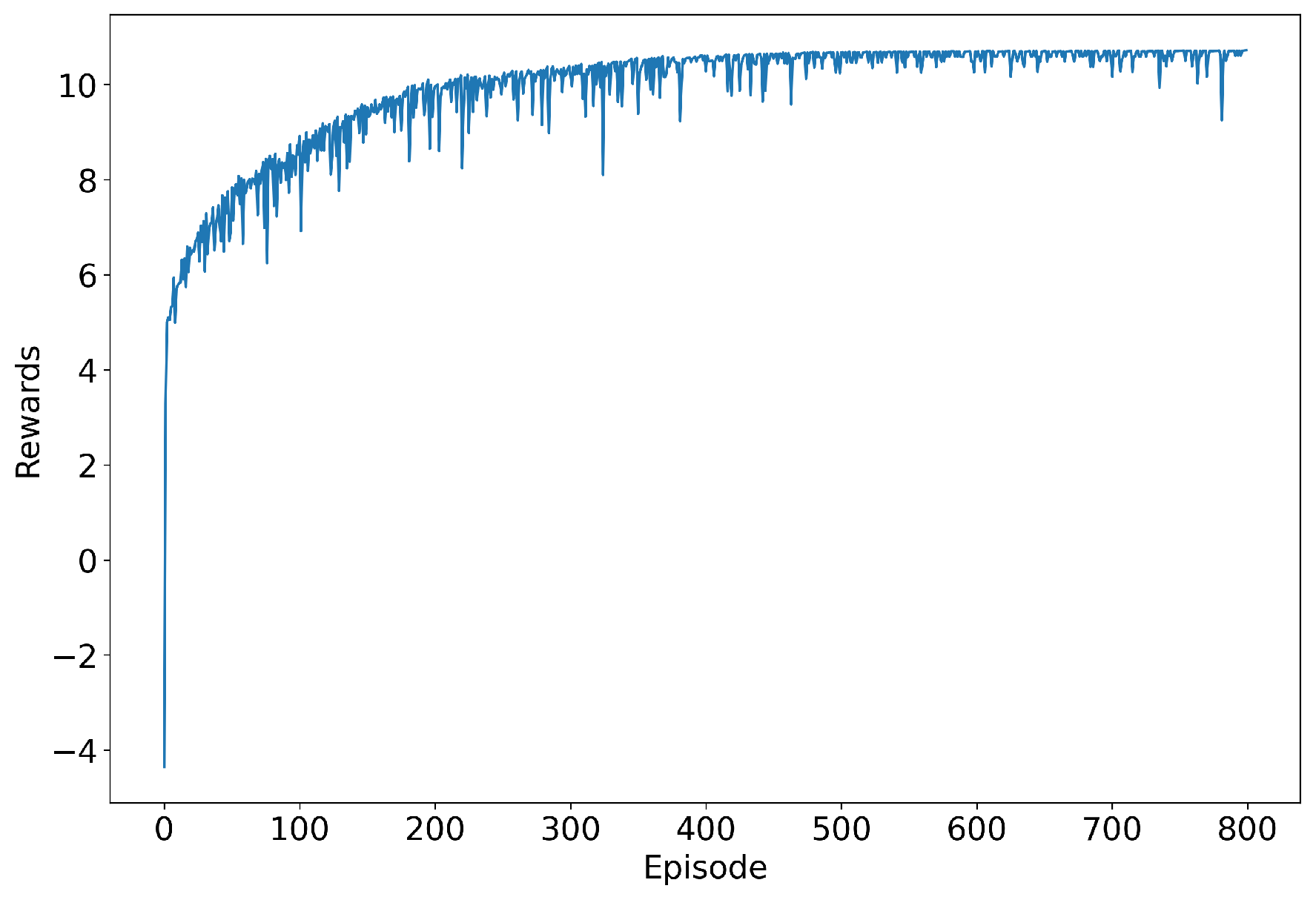
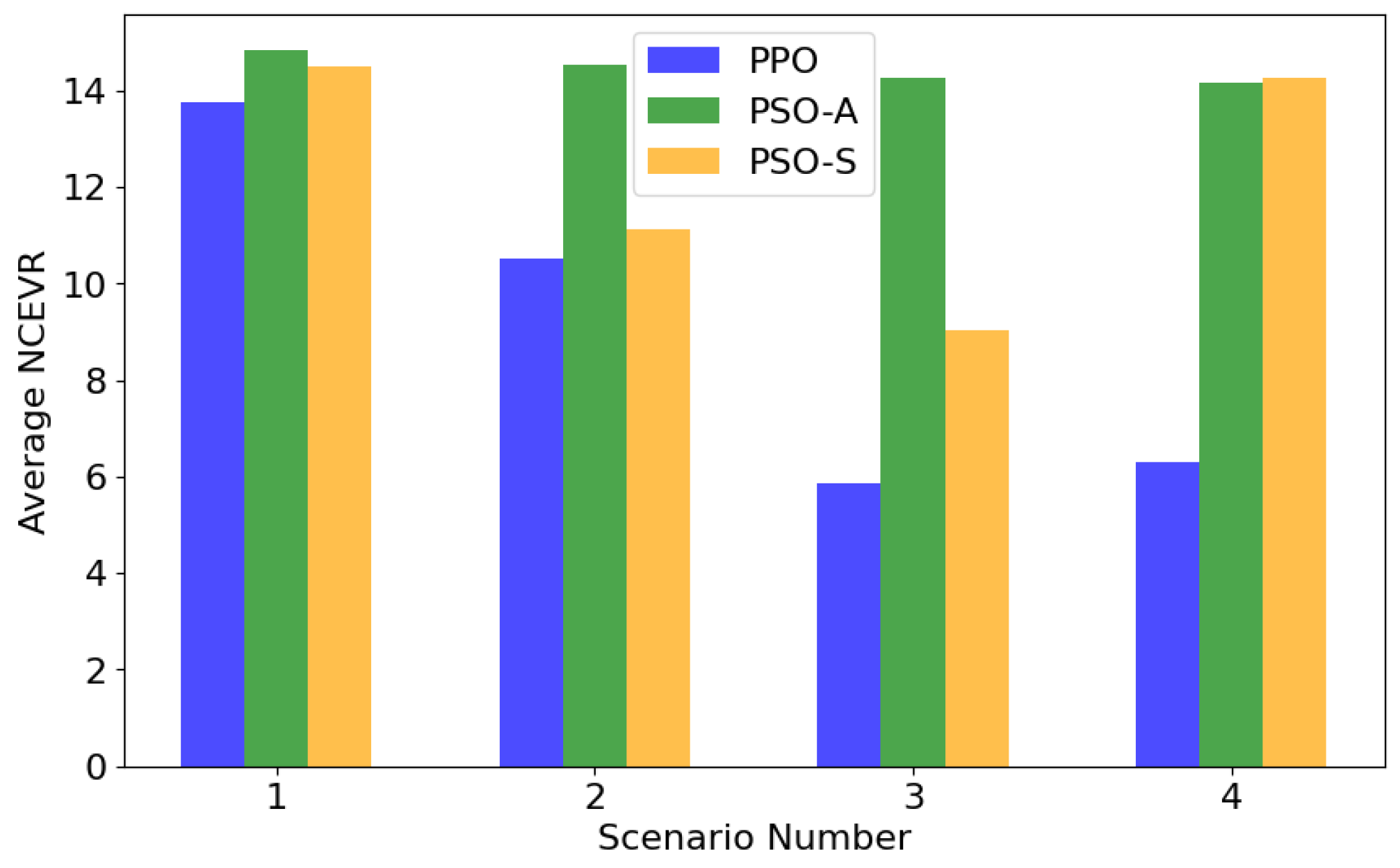
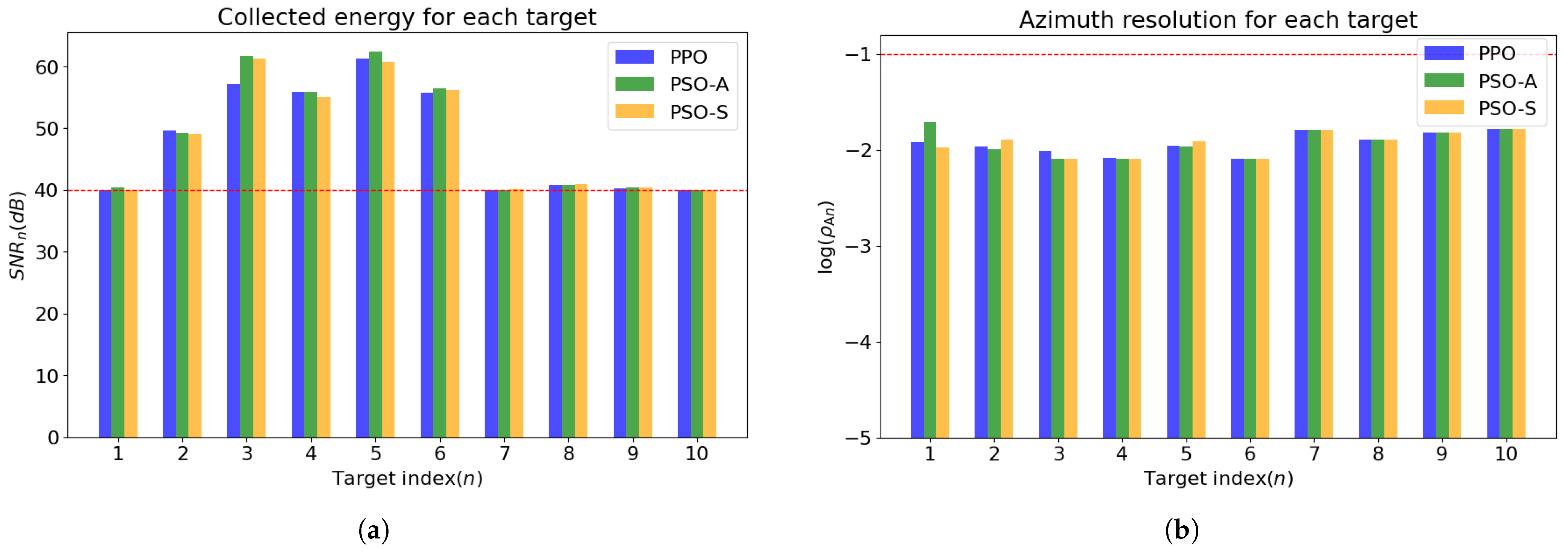
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brenner, A.R.; Ender, J.H. Demonstration of advanced reconnaissance techniques with the airborne SAR/GMTI sensor PAMIR. IEE Proc.-Radar Sonar Navig. 2006, 153, 152–162. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, R.; Zou, L.; Tang, H. Hierarchical Distribution-Based Exemplar Replay for Incremental SAR Automatic Target Recognition. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 6576–6588. [Google Scholar] [CrossRef]
- Butt, F.A.; Jalil, M. An overview of electronic warfare in radar systems. In Proceedings of the 2013 The International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Konya, Turkey, 9–11 May 2013; pp. 213–217. [Google Scholar]
- Schleher, D.C. Low probability of intercept radar. In Proceedings of the International Radar Conference, Arlington, VA, USA, 6–9 May 1985; pp. 346–349. [Google Scholar]
- Li, J.; Stoica, P. MIMO radar with colocated antennas. IEEE Signal Process. Mag. 2007, 24, 106–114. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, J.; Wang, F. LPI based resource management for target tracking in distributed radar network. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–5. [Google Scholar]
- Yi, W.; Yuan, Y.; Hoseinnezhad, R.; Kong, L. Resource scheduling for distributed multi-target tracking in netted colocated MIMO radar systems. IEEE Trans. Signal Process. 2020, 68, 1602–1617. [Google Scholar] [CrossRef]
- Zhang, H.; Xie, J.; Zong, B. Bi-objective particle swarm optimization algorithm for the search and track tasks in the distributed multiple-input and multiple-output radar. Appl. Soft Comput. 2021, 101, 107000. [Google Scholar] [CrossRef]
- Sun, H.; Li, M.; Zuo, L.; Zhang, P. Joint radar scheduling and beampattern design for multitarget tracking in netted colocated MIMO radar systems. IEEE Signal Process. Lett. 2021, 28, 1863–1867. [Google Scholar] [CrossRef]
- Zheng, W.; Shi, J.; Li, Y.; Huang, Z.; Zhang, Z.; Li, Z. D 2 AF-Net: A Dual-Domain Adaptive Fusion Method for Radar Deception Jamming Recognition. IEEE Trans. Aerosp. Electron. Syst. 2025, 1–15. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, W.; Zhang, Q.; Zhang, L.; Liu, B.; Xu, H.X. Joint Power, Bandwidth, and Subchannel Allocation in a UAV-Assisted DFRC Network. IEEE Internet Things J. 2025, 12, 11633–11651. [Google Scholar] [CrossRef]
- Zhang, H.; Weijian, L.; Zhang, Q.; Taiyong, F. A robust joint frequency spectrum and power allocation strategy in a coexisting radar and communication system. Chin. J. Aeronaut. 2024, 37, 393–409. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, J.; Wang, F. Low probability of intercept optimization for radar network based on mutual information. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; pp. 683–687. [Google Scholar]
- She, J.; Zhou, J.; Wang, F.; Li, H. LPI optimization framework for radar network based on minimum mean-square error estimation. Entropy 2017, 19, 397. [Google Scholar] [CrossRef]
- Lu, X.; Yi, W.; Lai, Y.; Su, Y. LPI-based joint node selection and power allocation strategy for target tracking in distributed MIMO radar. In Proceedings of the 2022 25th International Conference on Information Fusion (FUSION), Linköping, Sweden, 4–7 July 2022; pp. 1–7. [Google Scholar]
- Shi, C.; Zhou, J.; Wang, F. Adaptive resource management algorithm for target tracking in radar network based on low probability of intercept. Multidimens. Syst. Signal Process. 2018, 29, 1203–1226. [Google Scholar] [CrossRef]
- Liu, D.; Wang, F.; Shi, C.; Zhang, J. LPI based optimal power and dwell time allocation for radar network system. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar]
- Shi, C.; Ding, L.; Wang, F.; Salous, S.; Zhou, J. Low probability of intercept-based collaborative power and bandwidth allocation strategy for multi-target tracking in distributed radar network system. IEEE Sens. J. 2020, 20, 6367–6377. [Google Scholar] [CrossRef]
- Zhang, W.; Shi, C.; Zhou, J. LPI-based joint node selection and power allocation for target localization in non-coherent distributed MIMO radar with low complexity. In Proceedings of the IET International Radar Conference (IET IRC 2020), Online, 4–6 November 2020; Volume 2020, pp. 138–143. [Google Scholar]
- Hu, J.; Zuo, L.; Varshney, P.K.; Gao, Y. Resource Allocation for Distributed Multi-Target Tracking in Radar Networks with Missing Data. IEEE Trans. Signal Process. 2024, 72, 718–734. [Google Scholar] [CrossRef]
- Xie, M.; Yi, W.; Kirubarajan, T.; Kong, L. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks. IEEE Trans. Signal Process. 2017, 66, 729–743. [Google Scholar] [CrossRef]
- Su, Y.; He, Z.; Cheng, T.; Wang, J. Joint Node and Resource Scheduling Strategy for the Distributed MIMO Radar Network Target Tracking via Convex Programming. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4098–4101. [Google Scholar]
- Wu, P.H. On sensitivity analysis of low probability of intercept (LPI) capability. In Proceedings of the MILCOM 2005-2005 IEEE Military Communications Conference, Atlantic City, NJ, USA, 17–20 October 2005; pp. 2889–2895. [Google Scholar]
- Shyalika, C.; Silva, T.; Karunananda, A. Reinforcement learning in dynamic task scheduling: A review. SN Comput. Sci. 2020, 1, 306. [Google Scholar] [CrossRef]
- Li, Y. Deep Reinforcement Learning: An Overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Shi, Y.; Jiu, B.; Yan, J.; Liu, H. Data-driven radar selection and power allocation method for target tracking in multiple radar system. IEEE Sens. J. 2021, 21, 19296–19306. [Google Scholar] [CrossRef]
- Shi, Y.; Jiu, B.; Yan, J.; Liu, H.; Li, K. Data-driven simultaneous multibeam power allocation: When multiple targets tracking meets deep reinforcement learning. IEEE Syst. J. 2020, 15, 1264–1274. [Google Scholar] [CrossRef]
- Shi, Y.; Zheng, H.; Li, K. Data-Driven Joint Beam Selection and Power Allocation for Multiple Target Tracking. Remote Sens. 2022, 14, 1674. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.; Liang, Y.; Hu, J.; Yan, S. Learning-based airborne sensor task assignment in unknown dynamic environments. Eng. Appl. Artif. Intell. 2022, 111, 104747. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Y.; Zhang, H.; Gu, Y. Domain knowledge-assisted deep reinforcement learning power allocation for MIMO radar detection. IEEE Sens. J. 2022, 22, 23117–23128. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, X.; Cao, X.; Greco, M.S.; Gini, F. Reinforcement learning based dual-functional massive MIMO systems for multi-target detection and communications. IEEE Trans. Signal Process. 2023, 71, 741–755. [Google Scholar] [CrossRef]
- Yuan, Y.; Liu, X.; Zhang, T.; Cui, G.; Kong, L. Reinforcement Learning-Enhanced Adaption of Signal Power and Modulation for LPI Radar System. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 8555–8568. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing; Mcgraw-Hill: New York, NY, USA, 2005; Volume 1. [Google Scholar]
- Doerry, A.W. Performance Limits for Synthetic Aperture Radar; Technical Report; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2006. [Google Scholar]
- Van Zyl, J.J. Synthetic Aperture Radar Polarimetry; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Wei, J.; Li, Y.; Yang, R.; Li, L.; Guo, L. Method of high signal-to-noise ratio and wide swath SAR imaging based on continuous pulse coding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2185–2196. [Google Scholar] [CrossRef]
- Makas, E.; Aslan, A.R. Spaceborne SAR System Design Considerations: Minimizing Satellite Size and Mass, System Parameter Trade-Offs, and Optimization. Appl. Sci. 2024, 14, 9661. [Google Scholar] [CrossRef]
- Jiang, M.; Guarnieri, A.M. Distributed scatterer interferometry with the refinement of spatiotemporal coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3987. [Google Scholar] [CrossRef]
- Jiang, M.; Hooper, A.; Tian, X.; Xu, J.; Chen, S.N.; Ma, Z.F.; Cheng, X. Delineation of built-up land change from SAR stack by analysing the coefficient of variation. ISPRS J. Photogramm. Remote Sens. 2020, 169, 93–108. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, M. Integration of optical and SAR imagery for dual PolSAR features optimization and land cover mapping. IEEE J. Miniaturization Air Space Syst. 2022, 3, 67–76. [Google Scholar] [CrossRef]
- Liu, H.-Y.; Song, H.-J.; Cheng, Z.-J. Comparative study on stripmap mode, spotlight mode, and sliding spotlight mode. J. Univ. Chin. Acad. Sci. 2011, 28, 410. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Fisher, M.L. The Lagrangian relaxation method for solving integer programming problems. Manag. Sci. 1981, 27, 1–18. [Google Scholar] [CrossRef]
- Bilgin, E. Mastering Reinforcement Learning with Python: Build Next-Generation, Self-Learning Models Using Reinforcement Learning Techniques and Best Practices; Packt Publishing Ltd.: Birmingham, UK, 2020. [Google Scholar]
- Ng, A.Y.; Harada, D.; Russell, S. Policy invariance under reward transformations: Theory and application to reward shaping. In Proceedings of the ICML, Bled, Slovenia, 27–30 June 1999; Volume 99, pp. 278–287. [Google Scholar]
- Kim, M.; Kim, J.S.; Choi, M.S.; Park, J.H. Adaptive discount factor for deep reinforcement learning in continuing tasks with uncertainty. Sensors 2022, 22, 7266. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Desai, M.D.; Jenkins, W.K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar. IEEE Trans. Image Process. 1992, 1, 505–517. [Google Scholar] [CrossRef] [PubMed]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Cheng, Z.; Li, M.; Li, H. A Deep Reinforcement Learning Method with a Low Intercept Probability in a Netted Synthetic Aperture Radar. Remote Sens. 2025, 17, 2341. https://doi.org/10.3390/rs17142341
Xie L, Cheng Z, Li M, Li H. A Deep Reinforcement Learning Method with a Low Intercept Probability in a Netted Synthetic Aperture Radar. Remote Sensing. 2025; 17(14):2341. https://doi.org/10.3390/rs17142341
Chicago/Turabian StyleXie, Longhao, Ziyang Cheng, Ming Li, and Huiyong Li. 2025. "A Deep Reinforcement Learning Method with a Low Intercept Probability in a Netted Synthetic Aperture Radar" Remote Sensing 17, no. 14: 2341. https://doi.org/10.3390/rs17142341
APA StyleXie, L., Cheng, Z., Li, M., & Li, H. (2025). A Deep Reinforcement Learning Method with a Low Intercept Probability in a Netted Synthetic Aperture Radar. Remote Sensing, 17(14), 2341. https://doi.org/10.3390/rs17142341






