Atmospheric Boundary Layer and Tropopause Retrievals from FY-3/GNOS-II Radio Occultation Profiles
Abstract
1. Introduction
2. FY-3/GNOS-II RO Observations, Radiosonde, and Other Ancillary Data
3. Methods to Retrieve ABLH, TPH, and TPT
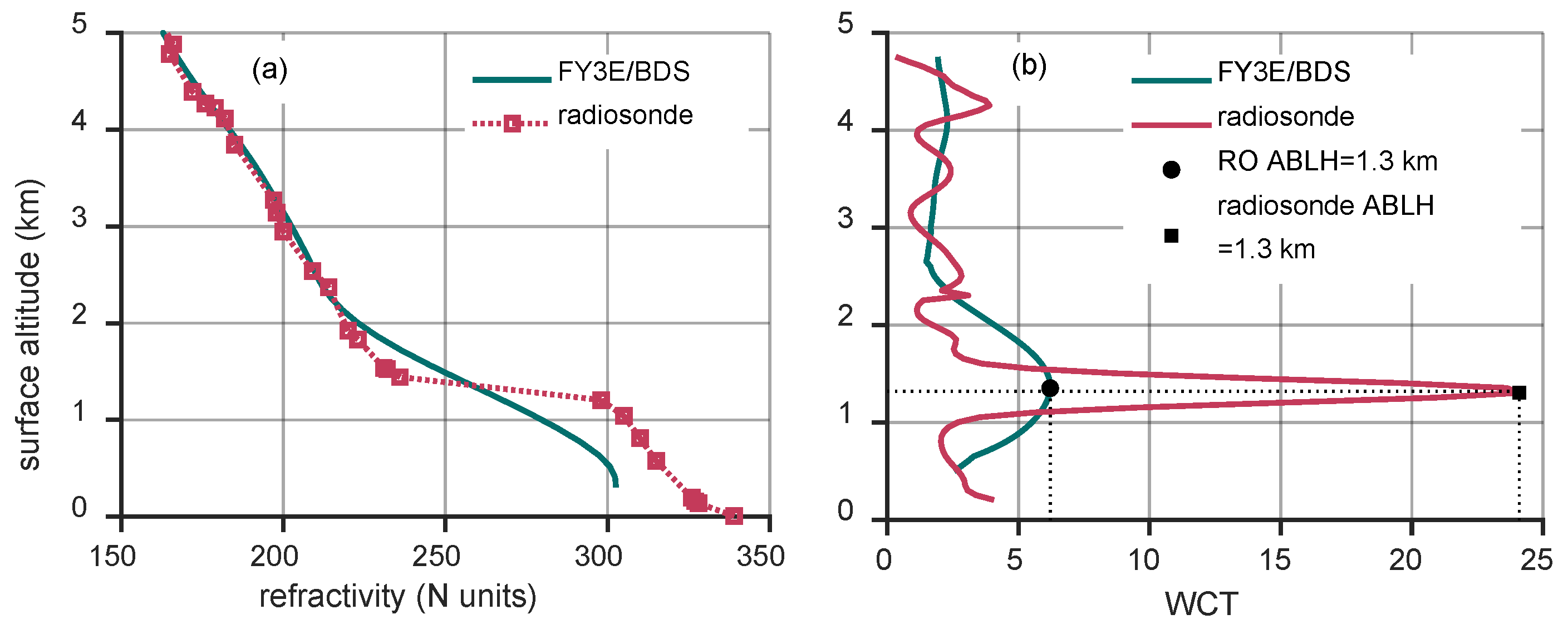
3.1. ABLH Estimation with WCT Method
3.2. Determining the Tropopause Through Temperature Lapse Rate
4. Comparison with Independent Radiosonde Data
4.1. The ABLH Validation
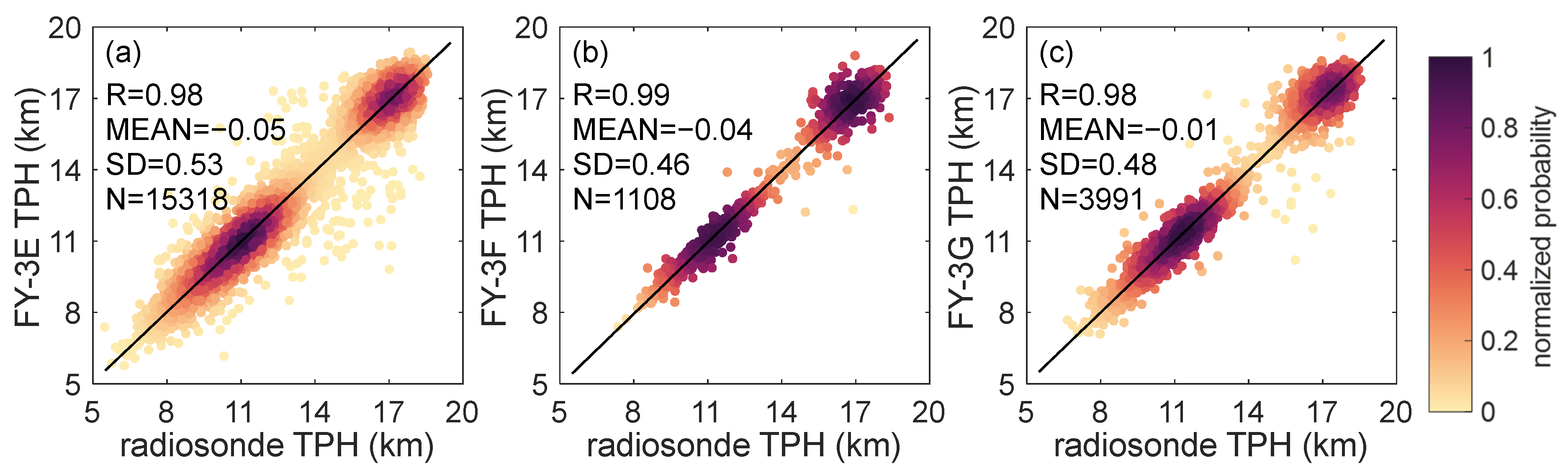
4.2. The TPH Validation
5. Statistical Analyses of the ABL and Thermal Tropopause from FY-3/GNOS-II RO Profiles
5.1. ABLH Results
5.1.1. The Detection Rate
5.1.2. Seasonal Cycle
5.2. TPH and TPT Results
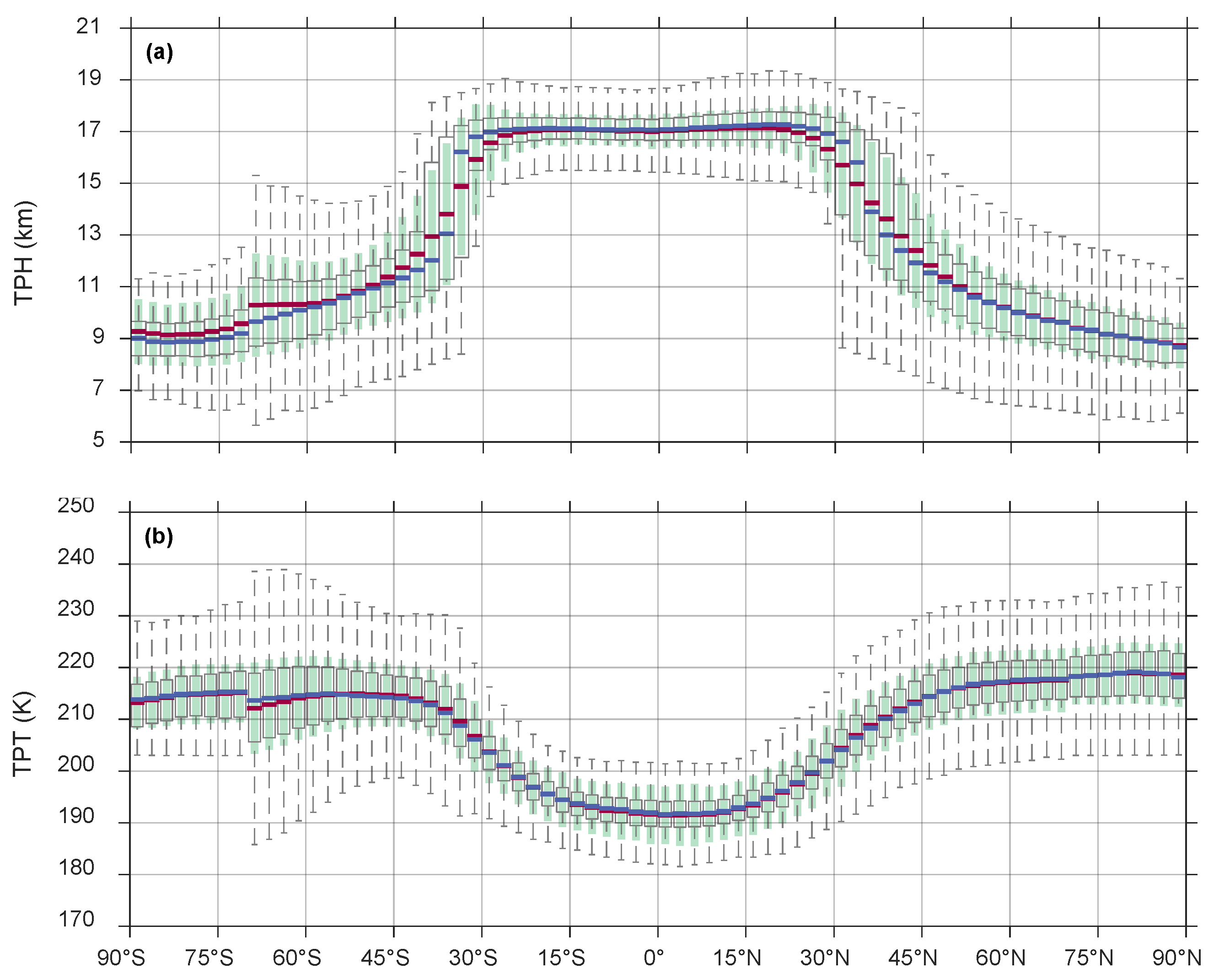
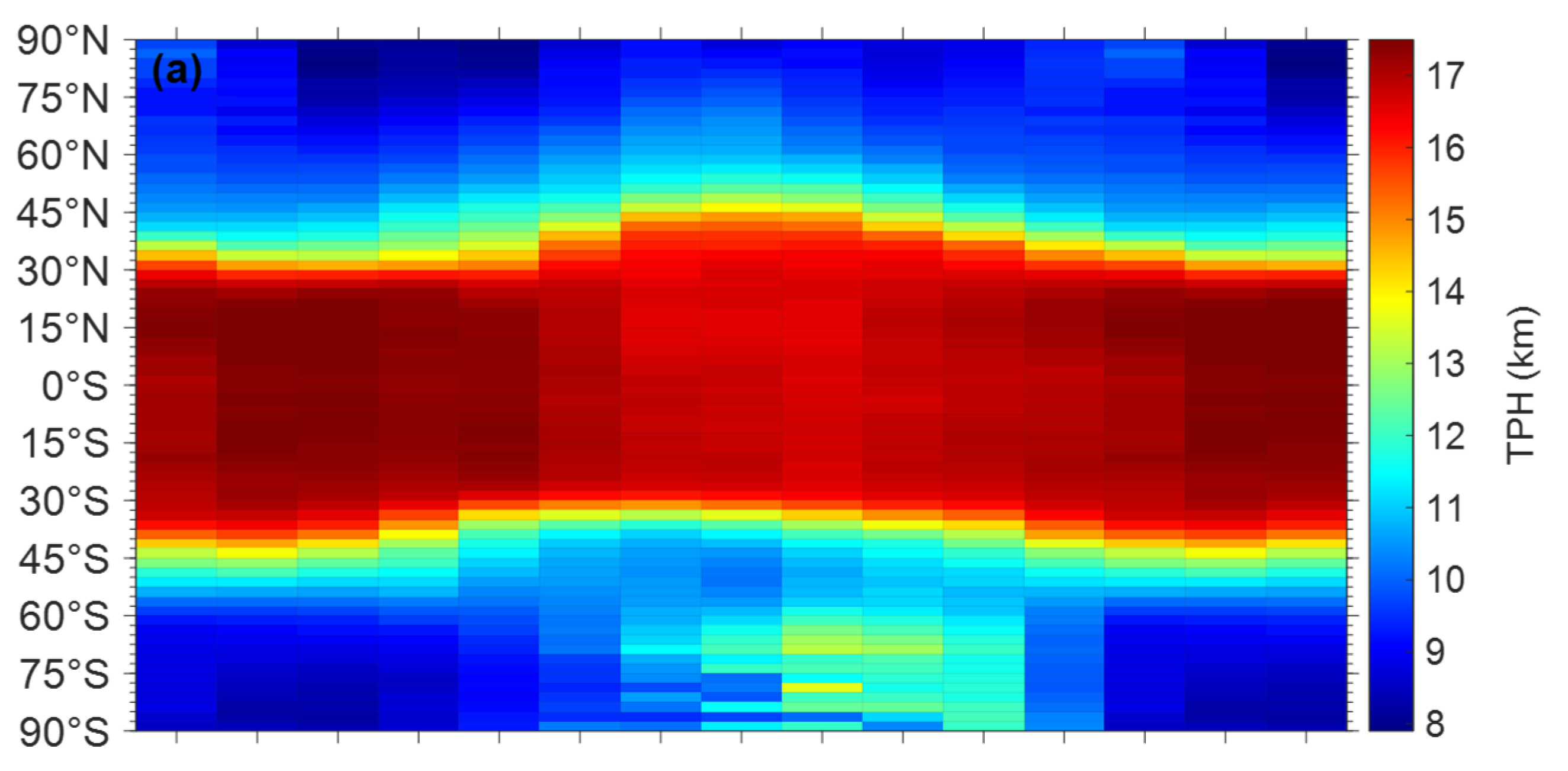
5.2.1. Spatial Structures
5.2.2. Annual Cycle
6. Discussion
7. Conclusions
- FY-3/GNOS-II RO profiles show a high detection rate of the ABL top in low and middle latitudes. The highest detection rates are found in the subtropical eastern Pacific, SH Atlantic, and eastern Indian Ocean, up to 76%. The detection rates over low and mid-latitude oceans are higher in winter than in summer, and the same pattern is observed over some low-latitude land regions. Due to weak ABL inversion, the detection rates in subtropical deserts are lower in spring and summer.
- Seasonality of the ABLH derived from FY-3/GNOS-II RO is clear and distinct. It could be observed that ABLH is lower in summer in a narrow range on both sides of the equator in Africa, influenced by the precipitation of the ITCZ. Other common seasonal characteristics of the ABL are also identified.
- The TPH and TPT retrieved from FY-3/GNOS-II RO feature apparent longitudinal and latitudinal characteristics. For example, TPH shows significant zonal asymmetry in northeastern Canada and easternmost Russia due to the Rossby wave. The presence of a double tropopause separates the mean and median values of TPH and TPT at middle latitudes.
- In latitudes northward of 65°N, the annual cycle of TPH exhibits a double wave pattern. While in latitudes greater than 45°N for TPT, a single wave pattern is presented. Furthermore, the annual cycle of the TPH is reversed near 25°N and 55°S. The reversal of the annual cycle for TPT occurs at 25°N, 45°N, and 45°S. These characteristics of the tropopause are clearly captured by FY-3/GNOS-II RO.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic: Dordrecht, The Netherlands, 1988; pp. 9–16. [Google Scholar] [CrossRef]
- Medeiros, B.; Hall, A.; Stevens, B. What Controls the Mean Depth of the PBL? J. Clim. 2005, 18, 3157–3172. [Google Scholar] [CrossRef]
- von Engeln, A.; Teixeira, J. A Planetary Boundary Layer Height Climatology Derived from ECMWF Reanalysis Data. J. Clim. 2013, 26, 6575–6590. [Google Scholar] [CrossRef]
- Garratt, J.R. Sensitivity of Climate Simulations to Land-Surface and Atmospheric Boundary-Layer Treatments—A Review. J. Clim. 1993, 6, 419–448. [Google Scholar] [CrossRef]
- Ho, S.P.; Anthes, R.A.; Ao, C.O.; Healy, S.; Horanyi, A.; Hunt, D.; Mannucci, A.J.; Pedatella, N.; Randel, W.J.; Simmons, A.; et al. The COSMIC/FORMOSAT-3 Radio Occultation Mission after 12 Years: Accomplishments, Remaining Challenges, and Potential Impacts of COSMIC-2. Bull. Amer. Meteor. Soc. 2020, 101, E1107–E1136. [Google Scholar] [CrossRef]
- Holton, J.R.; Haynes, P.H.; McIntyre, M.E.; Douglass, A.R.; Rood, R.B.; Pfister, L. Stratosphere-troposphere exchange. Rev. Geophys. 1995, 33, 403–439. [Google Scholar] [CrossRef]
- Schmidt, T.; Heise, S.; Wickert, J.; Beyerle, G.; Reigber, C. GPS radio occultation with CHAMP and SAC-C: Global monitoring of thermal tropopause parameters. Atmos. Chem. Phys. 2005, 5, 1473–1488. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. 2010, 115, D16113. [Google Scholar] [CrossRef]
- Pietroni, I.; Argentini, S.; Petenko, I.; Sozzi, R. Measurements and Parametrizations of the Atmospheric Boundary-Layer Height at Dome C. Bound.-Layer Meteor. 2012, 143, 189–206. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Hu, X.M.; Huang, Z.; Wang, G.; Zhang, B.; Zhang, T. Evaluation of retrieval methods of daytime convective boundary layer height based on lidar data. J. Geophys. Res. Atmos. 2017, 122, 4578–4593. [Google Scholar] [CrossRef]
- McGrath-Spangler, E.L.; Denning, A.S. Global seasonal variations of midday planetary boundary layer depth from CALIPSO space-borne LIDAR. J. Geophys. Res. Atmos. 2013, 118, 1226–1233. [Google Scholar] [CrossRef]
- Fetzer, E.J.; Teixeira, J.; Olsen, E.T.; Fishbein, E.F. Satellite remote sounding of atmospheric boundary layer temperature inversions over the subtropical eastern Pacific. Geophys. Res. Lett. 2004, 31, L17102. [Google Scholar] [CrossRef]
- Wood, R.; Bretherton, C.S. Boundary Layer Depth, Entrainment, and Decoupling in the Cloud-Capped Subtropical and Tropical Marine Boundary Layer. J. Clim. 2004, 17, 3576–3588. [Google Scholar] [CrossRef]
- Santer, B.D.; Wehner, M.F.; Wigley, T.M.L.; Sausen, R.; Meehl, G.A.; Taylor, K.E.; Ammann, C.; Arblaster, J.; Washington, W.M.; Boyle, J.S.; et al. Contributions of Anthropogenic and Natural Forcing to Recent Tropopause Height Changes. Science 2003, 301, 479–483. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Fu, Y.; Xiao, Q. Trends in the global tropopause thickness revealed by radiosondes. Geophys. Res. Lett. 2012, 39, L20706. [Google Scholar] [CrossRef]
- Thuburn, J.; Craig, G.C. GCM Tests of Theories for the Height of the Tropopause. J. Atmos. Sci. 1997, 54, 869–882. [Google Scholar] [CrossRef]
- Thuburn, J.; Craig, G.C. Stratospheric Influence on Tropopause Height: The Radiative Constraint. J. Atmos. Sci. 2000, 57, 17–28. [Google Scholar] [CrossRef]
- Vernier, J.P.; Thomason, L.W.; Kar, J. CALIPSO detection of an Asian tropopause aerosol layer. Geophys. Res. Lett. 2011, 38, L07804. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Bertiger, W.I.; Leroy, S.S.; Meehan, T.K.; Romans, L.J.; Schofield, J.T.; McCleese, D.J.; Melbourne, W.G.; Thornton, C.L.; et al. Initial results of radio occultation of Earth’s atmosphere using the global positioning system. Science 1996, 271, 1107–1110. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Ao, C.O.; Waliser, D.E.; Chan, S.K.; Li, J.L.; Tian, B.; Xie, F.; Mannucci, A.J. Planetary boundary layer heights from GPS radio occultation refractivity and humidity profiles. J. Geophys. Res. 2012, 117, D16117. [Google Scholar] [CrossRef]
- Ratnam, M.V.; Tetzlaff, G.; Jacobi, C. Structure and Variability of the Tropopause Obtained from CHAMP Radio Occultation Temperature Profiles. In Earth Observation with CHAMP; Reigber, C., Lühr, H., Schwintzer, P., Wickert, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 579–584. [Google Scholar] [CrossRef]
- von Engeln, A.; Teixeira, J.; Wickert, J.; Buehler, S.A. Using CHAMP radio occultation data to determine the top altitude of the Planetary Boundary Layer. Geophys. Res. Lett. 2005, 32, L06815. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V.; Rocken, C.; Hunt, D.; Schreiner, W.; Johnson, J.; Masters, D.; Esterhuizen, S. GPS profiling of the lower troposphere from space: Inversion and demodulation of the open-loop radio occultation signals. Geophys. Res. Lett. 2006, 33, L14816. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, S.; He, Y.; Wang, S.; Sheng, Z.; Meng, X.; Yu, T. Optimizing GPS L2P radio occultation processing for COSMIC-2 atmospheric bending angle retrieval. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4102410. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V.; Kuo, Y.H.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Monitoring the atmospheric boundary layer by GPS radio occultation signals recorded in the open-loop mode. Geophys. Res. Lett. 2006, 33, L12813. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V.; Rocken, C.; Lenschow, D.H.; Kuo, Y.H.; Anthes, R.A.; Schreiner, W.; Hunt, D. Observing the moist troposphere with radio occultation signals from COSMIC. Geophys. Res. Lett. 2007, 34, L18802. [Google Scholar] [CrossRef]
- Guo, P.; Kuo, Y.H.; Sokolovskiy, S.V.; Lenschow, D.H. Estimating Atmospheric Boundary Layer Depth Using COSMIC Radio Occultation Data. J. Atmos. Sci. 2011, 68, 1703–1713. [Google Scholar] [CrossRef]
- Ho, S.P.; Liang, P.; Anthes, R.A.; Kuo, Y.H.; Lin, H.C. Marine Boundary Layer Heights and Their Longitudinal, Diurnal, and Interseasonal Variability in the Southeastern Pacific Using COSMIC, CALIOP, and Radiosonde Data. J. Clim. 2015, 28, 2856–2872. [Google Scholar] [CrossRef]
- Basha, G.; Kishore, P.; Ratnam, M.V.; Babu, S.R.; Velicogna, I.; Jiang, J.H.; Ao, C.O. Global climatology of planetary boundary layer top obtained from multi-satellite GPS RO observations. Clim. Dyn. 2019, 52, 2385–2398. [Google Scholar] [CrossRef]
- Zhu, Z.; Xu, X.; Luo, J. Inversion and Analysis of Atmospheric Boundary Layer Height Using FY-3C Radio Occultation Refractive Index Data. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 395–401. [Google Scholar] [CrossRef]
- Santosh, M. Estimation of daytime planetary boundary layer height (PBLH) over the tropics and subtropics using COSMIC-2/FORMOSAT-7 GNSS–RO measurements. Atmos. Res. 2022, 279, 106361. [Google Scholar] [CrossRef]
- Ho, S.P.; Gu, G.; Zhou, X. The Planetary Boundary Layer Height Climatology Over Oceans Using COSMIC-2 and Spire GNSS RO Bending Angles From 2019 to 2023: Comparisons to CALIOP, ERA-5, MERRA2, and CFS Reanalysis. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5803314. [Google Scholar] [CrossRef]
- He, Y.; Zhang, S.; Guo, S.; Wu, Y. Quality Assessment of the Atmospheric Radio Occultation Profiles from FY-3E/GNOS-II BDS and GPS Measurements. Remote Sens. 2023, 15, 5313. [Google Scholar] [CrossRef]
- Randel, W.J.; Wu, F.; Rivera Ríos, W. Thermal variability of the tropical tropopause region derived from GPS/MET observations. J. Geophys. Res. 2003, 108, 4024. [Google Scholar] [CrossRef]
- Schmidt, T.; Wickert, J.; Beyerle, G.; Reigber, C. Tropical tropopause parameters derived from GPS radio occultation measurements with CHAMP. J. Geophys. Res. 2004, 109, D13105. [Google Scholar] [CrossRef]
- Son, S.W.; Tandon, N.F.; Polvani, L.M. The fine-scale structure of the global tropopause derived from COSMIC GPS radio occultation measurements. J. Geophys. Res. 2011, 116, D20113. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Bai, W.; Xia, J.; Tan, G.; Cheng, C.; Du, Q.; Wang, X.; Zhao, D.; Tian, Y.; et al. Validation of Preliminary Results of Thermal Tropopause Derived from FY-3C GNOS Data. Remote Sens. 2019, 11, 1139. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, Y.; Bai, W.; Xia, J.; Tan, G.; Cheng, C.; Du, Q.; Wang, X.; Zhao, D.; Tian, Y.; et al. Comparison of RO tropopause height based on different tropopause determination methods. Adv. Space Res. 2021, 67, 845–857. [Google Scholar] [CrossRef]
- Li, W.; Sun, Y.; Bai, W.; Yin, C.; Du, Q.; Liu, C.; Wang, X.; Hu, X.; Yang, G.; Xiao, X. Machine Learning methods of FY-3C tropopause product correction. In Proceedings of the 2021 IEEE Specialist Meeting on Reflectometry Using GNSS and Other Signals of Opportunity (GNSS+R), Beijing, China, 14–17 September 2021; pp. 50–52. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, C.; Du, Q.; Wang, X.; Bai, W.; Kirchengast, G.; Xia, J.; Meng, X.; Wang, D.; Cai, Y.; et al. Global Navigation Satellite System Occultation Sounder II (GNOS II). In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Fort Worth, TX, USA, 23–28 July 2017. pp. 1189–1192. [CrossRef]
- Liao, M.; Zhang, P.; Yang, G.; Bi, Y.; Liu, Y.; Bai, W.; Meng, X.; Du, Q.; Sun, Y. Preliminary validation of the refractivity from the new radio occultation sounder GNOS/FY-3C. Atmos. Meas. Tech. 2016, 9, 781–792. [Google Scholar] [CrossRef]
- Liu, C.; Liao, M.; Sun, Y.; Wang, X.; Liang, J.; Hu, X.; Zhang, P.; Yang, G.; Liu, Y.; Wang, J.; et al. Preliminary Assessment of BDS Radio Occultation Retrieval Quality and Coverage Using FY-3E GNOS II Measurements. Remote Sens. 2023, 15, 5011. [Google Scholar] [CrossRef]
- He, B.; Bao, Q.; Wang, X.; Zhou, L.; Wu, X.; Liu, Y.; Wu, G.; Chen, K.; He, S.; Hu, W.; et al. CAS FGOALS-f3-L model datasets for CMIP6 historical Atmospheric Model Intercomparison Project simulation. Adv. Atmos. Sci. 2019, 36, 771–778. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 Monthly Averaged Data on Single Levels from 1940 to Present. Land-Sea Mask Data. 2023. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels-monthly-means?tab=overview (accessed on 5 August 2024).
- Ratnam, M.V.; Basha, S.G. A robust method to determine global distribution of atmospheric boundary layer top from COSMIC GPS RO measurements. Atmosph. Sci. Lett. 2010, 11, 216–222. [Google Scholar] [CrossRef]
- Brooks, I.M. Finding Boundary Layer Top: Application of a Wavelet Covariance Transform to Lidar Backscatter Profiles. J. Atmos. Ocean. Technol. 2023, 20, 1092–1105. [Google Scholar] [CrossRef]
- Xu, X.; Liu, S.; Luo, J. Analysis on the Variation of Global ABL Top Structure Using COSMIC Radio Occultation Refractivity. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 94–100. [Google Scholar] [CrossRef]
- Reichler, T.; Dameris, M.; Sausen, R. Determining the tropopause height from gridded data. Geophys. Res. Lett. 2003, 30, 2042. [Google Scholar] [CrossRef]
- Chan, K.M.; Wood, R. The seasonal cycle of planetary boundary layer depth determined using COSMIC radio occultation data. J. Geophys. Res. Atmos. 2013, 118, 12422–12434. [Google Scholar] [CrossRef]
- Kalmus, P.M.; Ao, C.O.; Wang, K.N.; Manzi, M.P.; Teixeira, J. A high-resolution planetary boundary layer height seasonal climatology from GNSS radio occultations. Remote Sens. Environ. 2022, 276, 113037. [Google Scholar] [CrossRef]
- Rieckh, T.; Scherllin-Pirscher, B.; Ladstädter, F.; Foelsche, U. Characteristics of tropopause parameters as observed with GPS radio occultation. Atmos. Meas. Tech. 2014, 7, 3947–3958. [Google Scholar] [CrossRef]
- Zängl, G.; Hoinka, K.P. The Tropopause in the Polar Regions. J. Clim. 2001, 14, 3117–3139. [Google Scholar] [CrossRef]
- Highwood, E.J.; Hoskins, B.J. The tropical tropopause. Q. J. R. Meteorol. Soc. 1998, 124, 1579–1604. [Google Scholar] [CrossRef]
- Reid, G.C.; Gage, K.S. The tropical tropopause over the western Pacific: Wave driving, convection, and the annual cycle. J. Geophys. Res. 1996, 101, 21233–21241. [Google Scholar] [CrossRef]
- Li, W.; Yuan, Y.; Chai, Y.; Liou, Y.; Ou, J.; Zhong, S. Characteristics of the global thermal tropopause derived from multiple radio occultation measurements. Atmos. Res. 2017, 185, 142–157. [Google Scholar] [CrossRef]
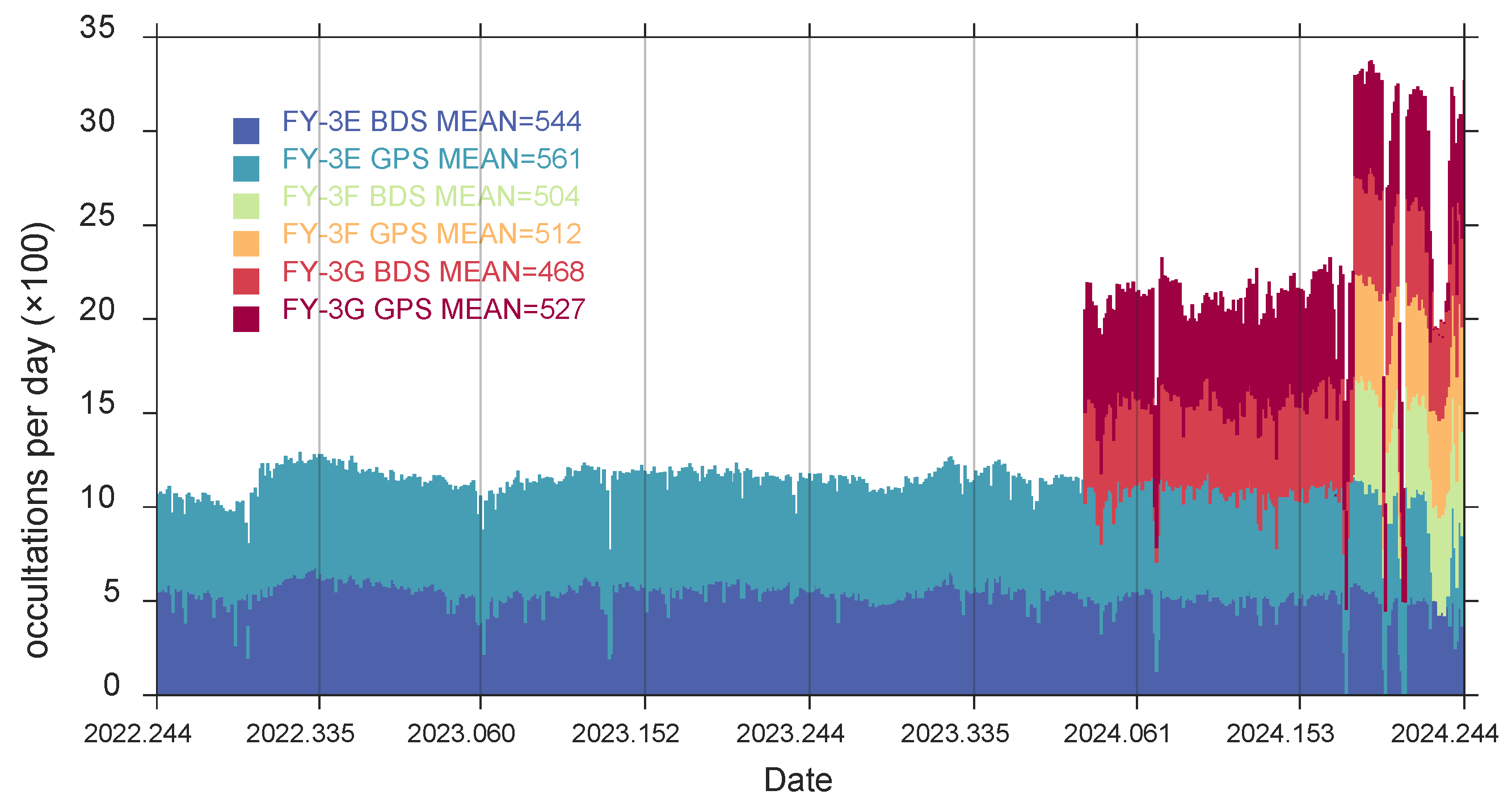








| Mission | Launch Time | Orbital Inclination | Period (yyyy.doy) |
|---|---|---|---|
| FY-3E | 5 July 2021 | 98.75° | 2022.244–2024.244 |
| FY-3F | 3 August 2023 | 98.75° | 2024.032–2024.244 |
| FY-3G | 16 April 2023 | 50° ± 1° | 2024.183–2024.244 |
| Missions | BDS RO | GPS RO | Total |
|---|---|---|---|
| FY-3E | 40% | 55% | 48% |
| FY-3F | 45% | 57% | 51% |
| FY-3G | 47% | 55% | 51% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; He, Y.; Guo, S.; Yu, T. Atmospheric Boundary Layer and Tropopause Retrievals from FY-3/GNOS-II Radio Occultation Profiles. Remote Sens. 2025, 17, 2126. https://doi.org/10.3390/rs17132126
Zhang S, He Y, Guo S, Yu T. Atmospheric Boundary Layer and Tropopause Retrievals from FY-3/GNOS-II Radio Occultation Profiles. Remote Sensing. 2025; 17(13):2126. https://doi.org/10.3390/rs17132126
Chicago/Turabian StyleZhang, Shaocheng, Youlin He, Sheng Guo, and Tao Yu. 2025. "Atmospheric Boundary Layer and Tropopause Retrievals from FY-3/GNOS-II Radio Occultation Profiles" Remote Sensing 17, no. 13: 2126. https://doi.org/10.3390/rs17132126
APA StyleZhang, S., He, Y., Guo, S., & Yu, T. (2025). Atmospheric Boundary Layer and Tropopause Retrievals from FY-3/GNOS-II Radio Occultation Profiles. Remote Sensing, 17(13), 2126. https://doi.org/10.3390/rs17132126






