HyperSMamba: A Lightweight Mamba for Efficient Hyperspectral Image Classification
Abstract
1. Introduction
- 1.
- The proposed Vision Mamba-based HSIC framework, HyperSMamba, significantly improves the extraction of long-range spatial–spectral features while maintaining high computational efficiency.
- 2.
- FusionSSM improves the SSM computation process by incorporating the innovative Multi-Scale Feature Fusion Module (MSFM) after the state transition equation, which facilitates the flow of spatial context information and alleviates the limitations imposed by causal relationships.
- 3.
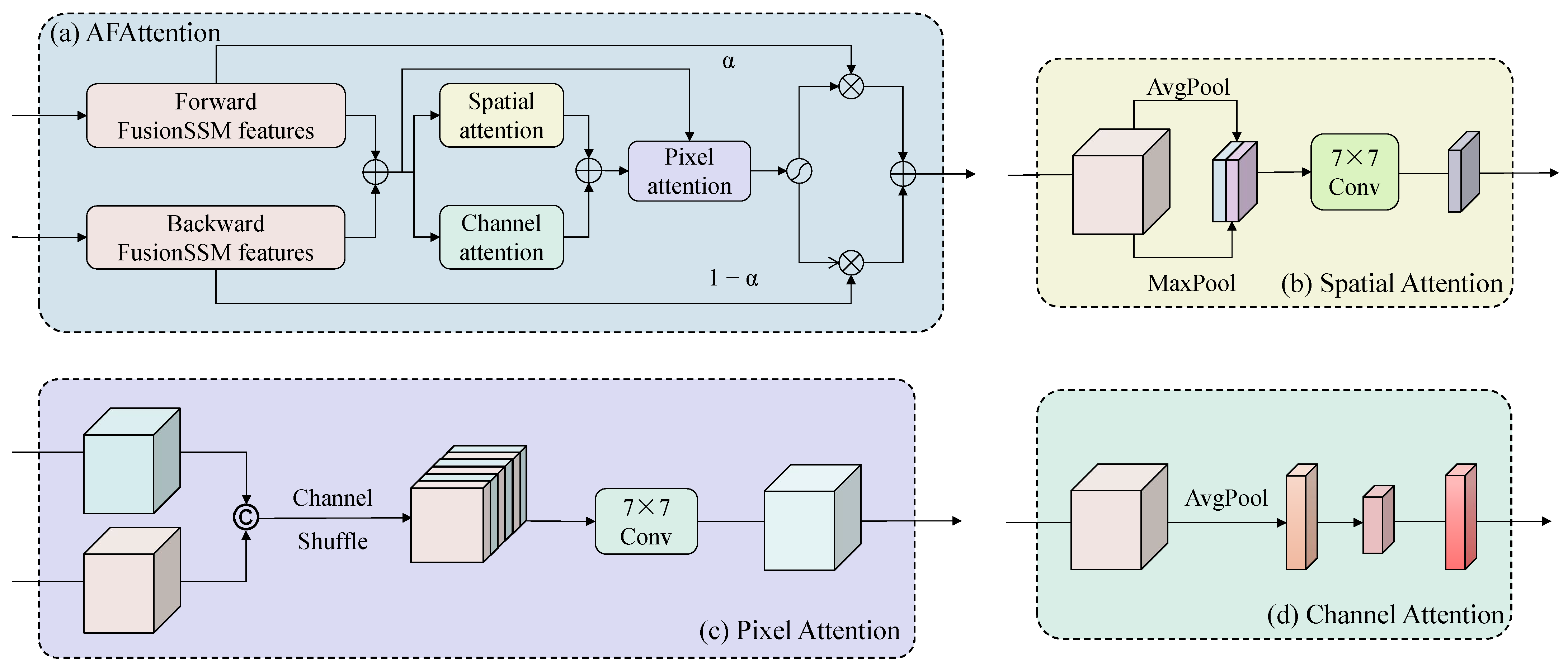
- The Adaptive Fusion Attention Module (AFAttention) is proposed to interact and fuse multi-source spatial–spectral features, allowing the model to autonomously focus on key feature regions.
2. Methods
2.1. Overview
2.2. State-Space Models
2.3. Multi-Scale Spatial Mamba
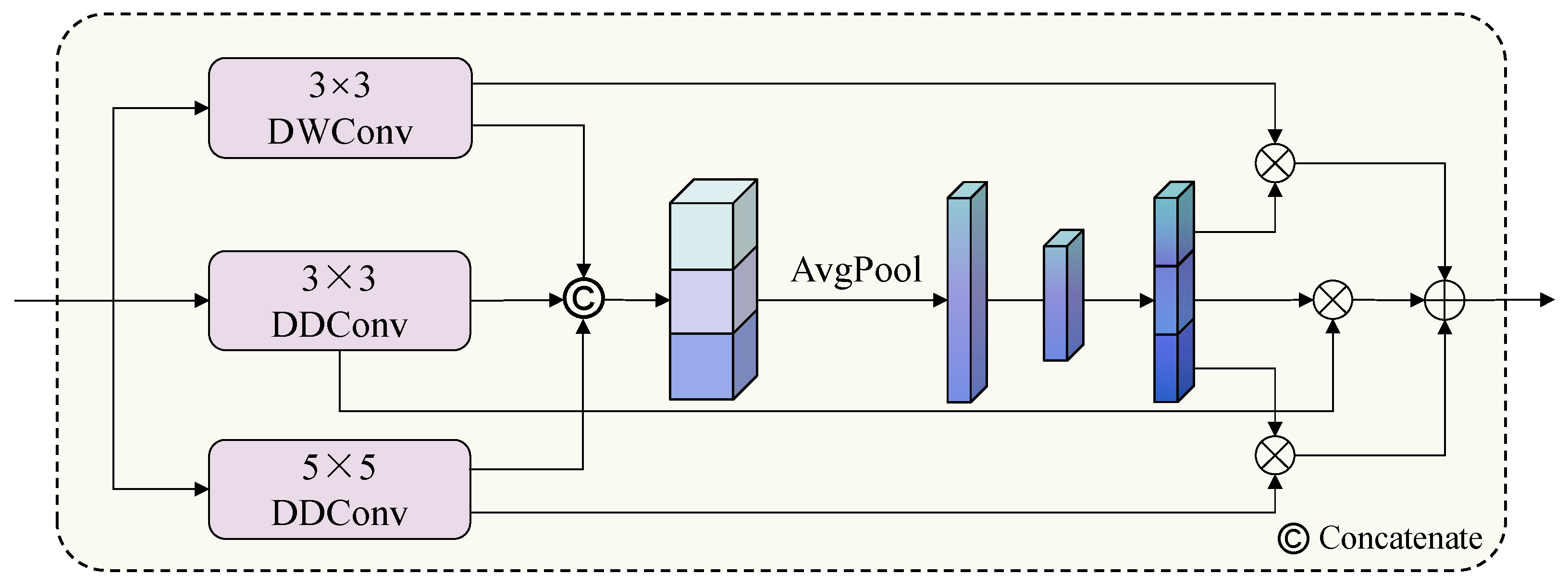
2.4. Multi-Scale State Fusion Module
2.5. Adaptive Fusion Attention Module
3. Results
3.1. Datasets Description
- 1.
- Indian Pines (IP): The IP dataset was collected from the agricultural region of Indiana, USA, and contains pixels. 200 valid bands were retained, covering wavelengths from 400 nm to 2500 nm. The dataset covers 16 different land cover types.
- 2.
- Pavia University (UP): The UP dataset was collected from the University of Pavia, Italy. It consists of pixels and a total of 103 spectral bands. The dataset covers nine different land cover types.
- 3.
- Salinas (SA): This dataset was collected from the Salinas region of California, USA. The HSI size is pixels, covering 16 land cover types. After preprocessing, 204 valid bands were retained.
3.2. Experimental Setup
- 1.
- Implementation Details: All models are implemented using PyTorch 2.5 and trained on an NVIDIA Tesla T4 GPU (16 GB VRAM). The batch size for all models is set to 128, and the number of epochs is set to 400. We use the cross-entropy loss function to update parameters. The AdamW optimizer is used with an initial learning rate of . In the proposed HyperSMamba model, all feature dimensions are normalized to 50. The initial patch sizes are set to for the Indian Pines (IP) dataset and for both the Pavia University (UP) and Salinas (SA) datasets. To ensure reproducibility of the results, the random seed was fixed, and each experiment was repeated 10 times.
- 2.
- Evaluation Metrics: We adopt three standard evaluation metrics, including average accuracy (AA), overall accuracy (OA), and Kappa coefficient .
3.3. Comparative Experimentation
3.3.1. Contrast Experiment Results
3.3.2. Visual Analysis of Classification Results
3.4. Ablation Study
3.4.1. Ablation for the HyperSMamba Architecture
3.4.2. Ablation for Multi-Scale State Fusion Module Design
4. Discussion
4.1. Discussion of the Computational Costs
4.2. Learned Feature Visualizations by T-SNE
4.3. Parameters Analyzed
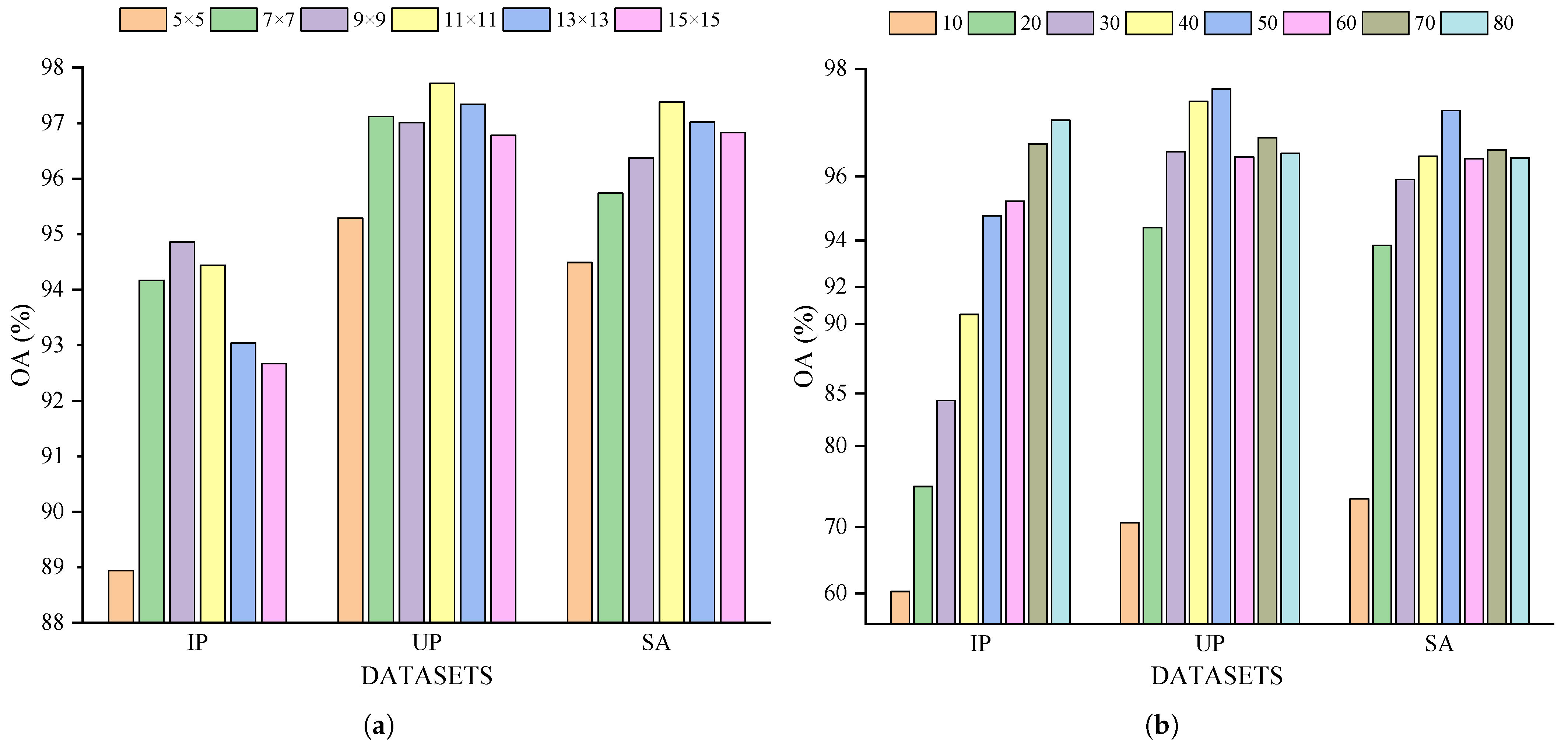
4.3.1. Impact of the Patch Size
4.3.2. Impact of the Number of Bands After PCA
4.4. Discussion of the Strengths and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
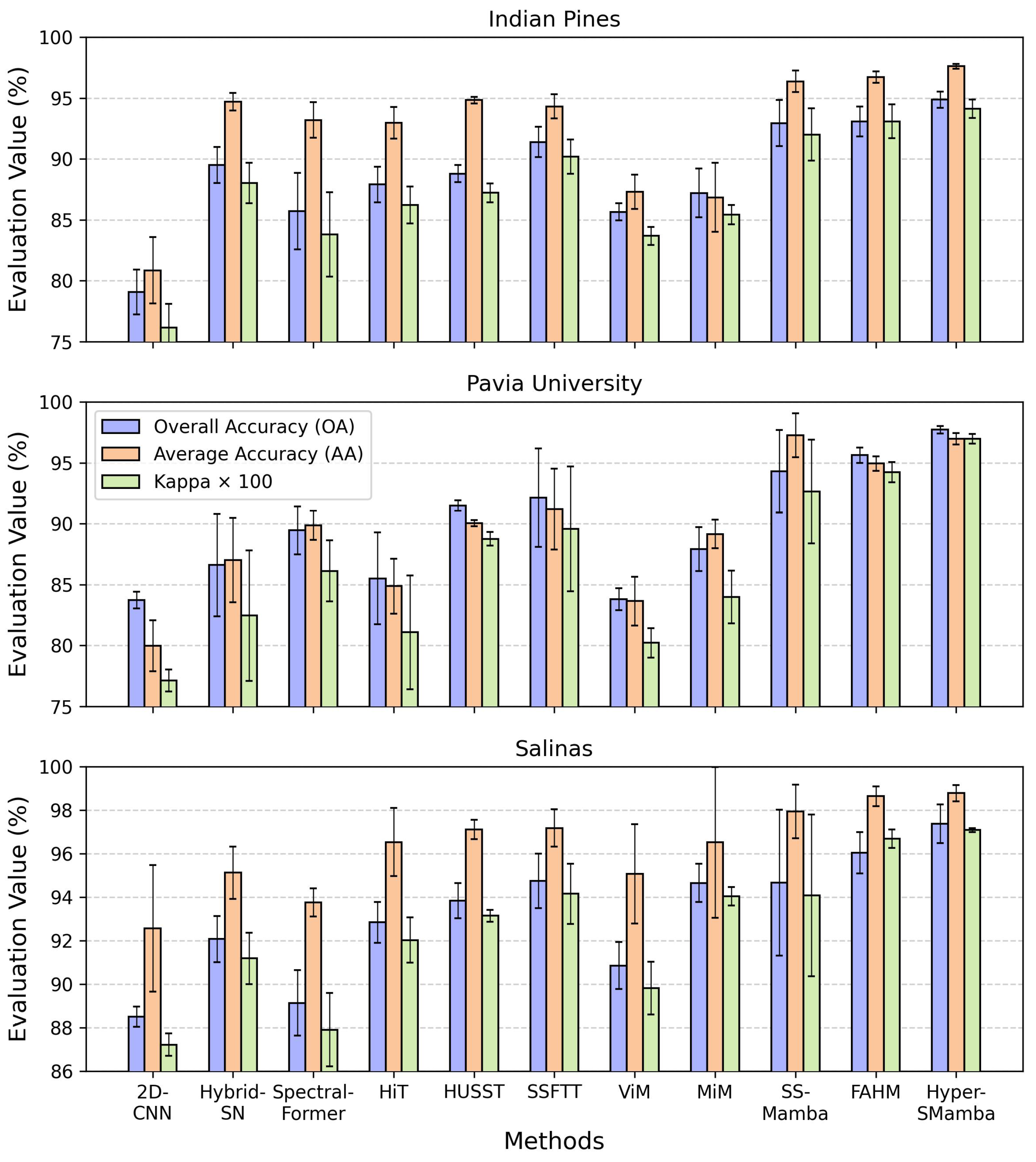
Appendix A.1. Visualization of Comparative Experimental Results
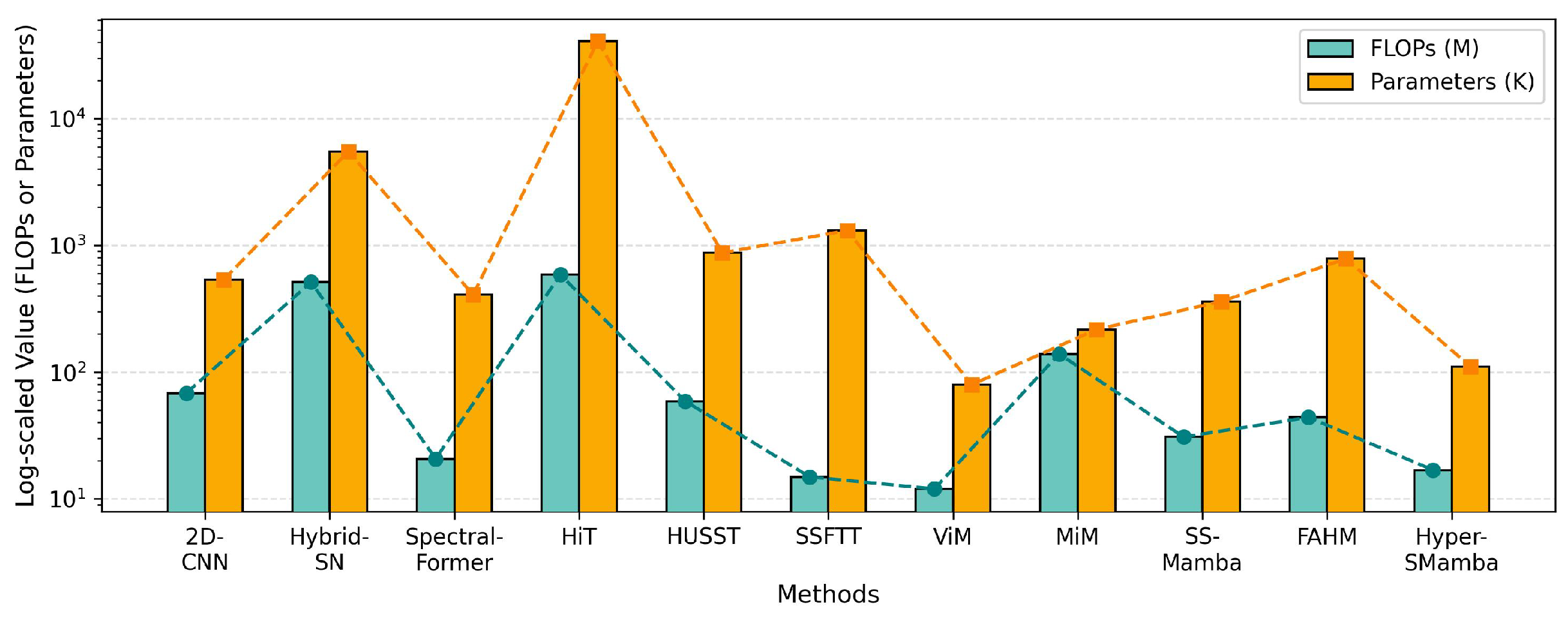
Appendix A.2. Visualization of Model Complexity
References
- Li, D.; Wu, J.; Zhao, J.; Xu, H.; Bian, L. SpectraTrack: Megapixel, Hundred-fps, and Thousand-channel Hyperspectral Imaging. Nat. Commun. 2024, 15, 9459. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.W.; Wang, Y.H.; Chen, J.Y.; Guo, R.L.; Shu, R.M.; Wang, J.Q. Status and Application of Advanced Airborne Hyperspectral Imaging Technology: A Review. Infrared Phys. Technol. 2020, 104, 103115. [Google Scholar] [CrossRef]
- Bhargava, A.; Sachdeva, A.; Sharma, K.; Alsharif, M.H.; Uthansakul, P.; Uthansakul, M. Hyperspectral imaging and its applications: A review. Heliyon 2024, 10, 33208. [Google Scholar] [CrossRef]
- Ahmad, M.; Shabbir, S.; Roy, S.K.; Hong, D.; Wu, X.; Yao, J. Hyperspectral Image Classification—Traditional to Deep Models: A Survey for Future Prospects. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 968–999. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, L. The Track, Hotspot and Frontier of International Hyperspectral Remote Sensing Research 2009–2019—A Bibliometric Analysis Based on SCI Database. Measurement 2022, 187, 110229. [Google Scholar] [CrossRef]
- Ma, X.; Wang, H.; Geng, J. Spectral–spatial Classification of Hyperspectral Image Based on Deep Auto-encoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4073–4085. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yu, C.; Yang, N.; Cai, W. Multi-feature Fusion: Graph Neural Network and CNN Combining for Hyperspectral Image Classification. Neurocomputing 2022, 501, 246–257. [Google Scholar] [CrossRef]
- Song, T.; Wang, Y.; Gao, C.; Chen, H.; Li, J. MSLAN: A Two-branch Multi-directional Spectral–Spatial LSTM Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5528814. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Mei, S.; Song, C.; Ma, M.; Xu, F. Hyperspectral Image Classification Using Group-Aware Hierarchical Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhou, J.; Zeng, S.; Xiao, Z.; Zhou, J.; Li, H.; Kang, Z. An Enhanced Spectral Fusion 3D CNN Model for Hyperspectral Image Classification. Remote Sens. 2022, 14, 5334. [Google Scholar] [CrossRef]
- Xu, Z.; Su, C.; Wang, S.; Zhang, X. Local and Global Spectral Features for Hyperspectral Image Classification. Remote Sens. 2023, 15, 1803. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3D-2D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.J.; Guo, Z.C.; Zhang, X.Y.; Sun, J. Dynamic Region-aware Convolution. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, D.; Wang, H.; Yu, X. Convolutional Transformer Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Lin, Z. Spatial-spectral Transformer for Hyperspectral Image Classification. Remote Sens. 2021, 13, 498. [Google Scholar] [CrossRef]
- Ma, C.; Jiang, J.; Li, H.; Mei, X.; Bai, C. Hyperspectral Image Classification Via Spectral Pooling and Hybrid Transformer. Remote Sens. 2022, 14, 4732. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–Spatial Feature Tokenization Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral Image Transformer Classification Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhou, W.; Kamata, S.I.; Luo, Z.; Chen, X. Hierarchical Unified Spectral-Spatial Aggregated Transformer for Hyperspectral Image Classification. In Proceedings of the 2022 26th International Conference on Pattern Recognition (ICPR), Montreal, QC, Canada, 21–25 August 2022. [Google Scholar] [CrossRef]
- Gu, A.; Goel, K.; Ré, C. Efficiently Modeling Long Sequences with Structured State Spaces. arXiv 2021, arXiv:2111.00396. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time Sequence Modeling with Selective State Spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model. arXiv 2024, arXiv:2401.09417. [Google Scholar] [CrossRef]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Jiao, J.; Liu, Y. Vmamba: Visual State Space Model. arXiv 2024, arXiv:2401.10166. [Google Scholar] [CrossRef]
- Pei, X.; Huang, T.; Xu, C. Efficientvmamba: Atrous Selective Scan for Lightweight Visual Mamba. arXiv 2024, arXiv:2403.09977. [Google Scholar] [CrossRef]
- Huang, T.; Pei, X.; You, S.; Wang, F.; Qian, C.; Xu, C. Localmamba: Visual State Space Model with Windowed Selective Scan. arXiv 2024, arXiv:2403.09338. [Google Scholar] [CrossRef]
- Yao, J.; Hong, D.; Li, C.; Chanussot, J. Spectralmamba: Efficient Mamba for Hyperspectral Image Classification. arXiv 2024, arXiv:2404.08489. [Google Scholar] [CrossRef]
- Yang, J.X.; Zhou, J.; Wang, J.; Tian, H.; Liew, A.W.C. Hsimamba: Hyperspectral Imaging Efficient Feature Learning with Bidirectional State Space for Classification. arXiv 2024, arXiv:2404.00272. [Google Scholar] [CrossRef]
- Chen, K.; Chen, B.; Liu, C.; Li, W.; Zou, Z.; Shi, Z. Rsmamba: Remote Sensing Image Classification with State Space Model. arXiv 2024, arXiv:2403.19654. [Google Scholar] [CrossRef]
- Zhuang, P.; Zhang, X.; Wang, H.; Zhang, T.; Liu, L.; Li, J. FAHM: Frequency-Aware Hierarchical Mamba for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 6299. [Google Scholar] [CrossRef]
- Zhou, W.; Kamata, S.I.; Wang, H.; Wong, M.S.; Hou, H.C. Mamba-in-Mamba: Centralized Mamba-Cross-Scan in Tokenized Mamba Model for Hyperspectral Image Classification. Neurocomputing 2025, 613, 128751. [Google Scholar] [CrossRef]
- Huang, L.; Chen, Y.; He, X. Spectral-Spatial Mamba for Hyperspectral Image Classification. Remote Sens. 2024, 16, 2449. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Zhang, L. Vision Mamba: A Comprehensive Survey and Taxonomy. arXiv 2024, arXiv:2405.04404. [Google Scholar] [CrossRef]
- Xu, R.; Yang, S.; Wang, Y.; Cai, Y.; Du, B.; Chen, H. Visual Mamba: A Survey and New Outlooks. arXiv 2024, arXiv:2404.18861. [Google Scholar] [CrossRef]
- Ma, P.; Ren, J.; Zhao, H.; Sun, G.; Murray, P.; Zheng, J. Multiscale 2-D Singular Spectrum Analysis and Principal Component Analysis for Spatial-Spectral Noise-robust Feature Extraction and Classification of Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1233–1245. [Google Scholar] [CrossRef]
- Yang, A.; Li, M.; Ding, Y.; Hong, D.; Lv, Y.; He, Y. GTFN: GCN and Transformer Fusion Network with Spatial-Spectral Features for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Dao, T.; Gu, A. Transformers Are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality. arXiv 2024, arXiv:2405.21060. [Google Scholar] [CrossRef]
- Gu, A.; Johnson, I.; Goel, K.; Saab, K.; Dao, T.; Rudra, A. Combining Recurrent, Convolutional, and Continuous-Time Models with Linear State Space Layers. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), San Diego, CA, USA, 6–14 December 2021. [Google Scholar]
- Piqueras, S.; Burger, J.; Tauler, R.; de Juan, A. Relevant Aspects of Quantification and Sample Heterogeneity in Hyperspectral Image Resolution. Chemom. Intell. Lab. Syst. 2012, 117, 169–182. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, D.; Zhang, Z.; Lin, S.; Dai, J. An Empirical Study of Spatial Attention Mechanisms in Deep Networks. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar] [CrossRef]

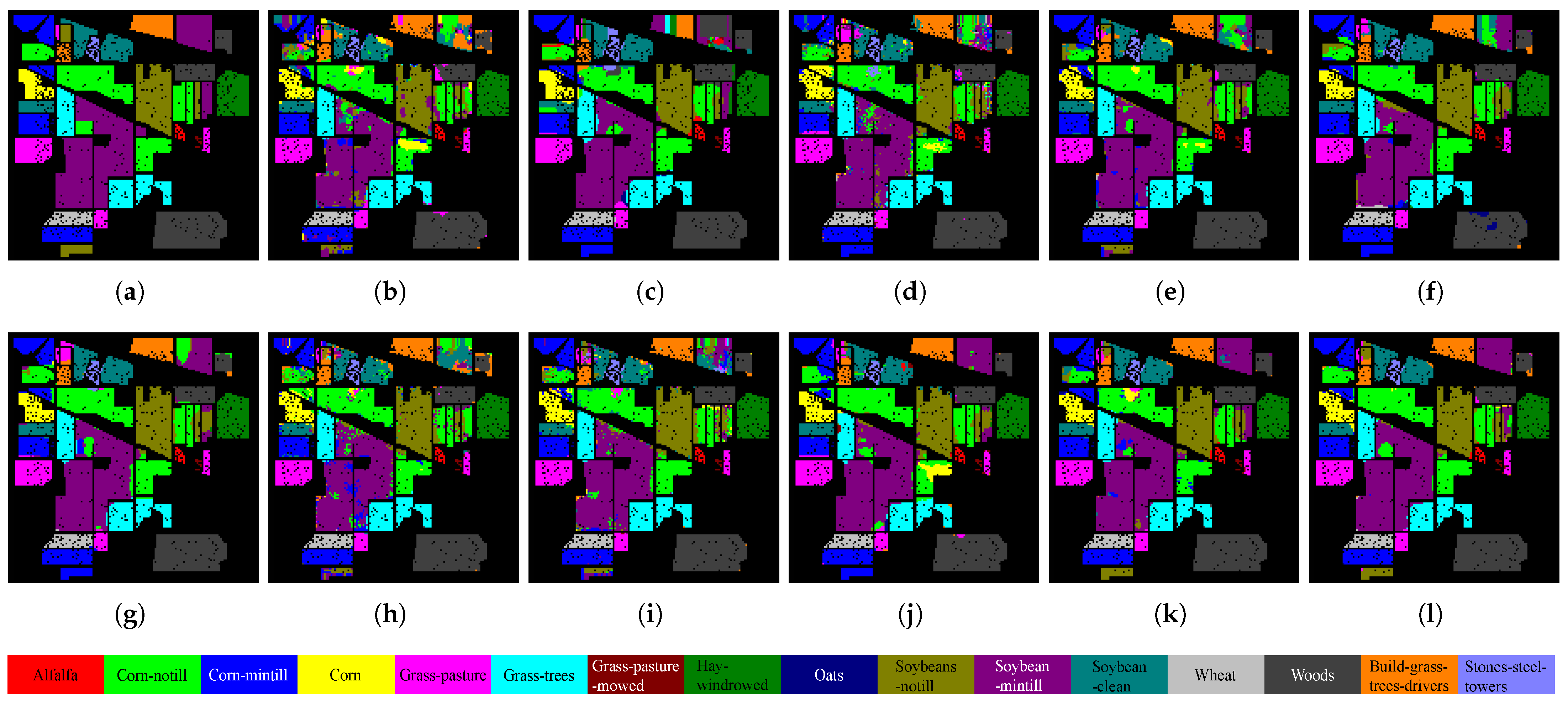

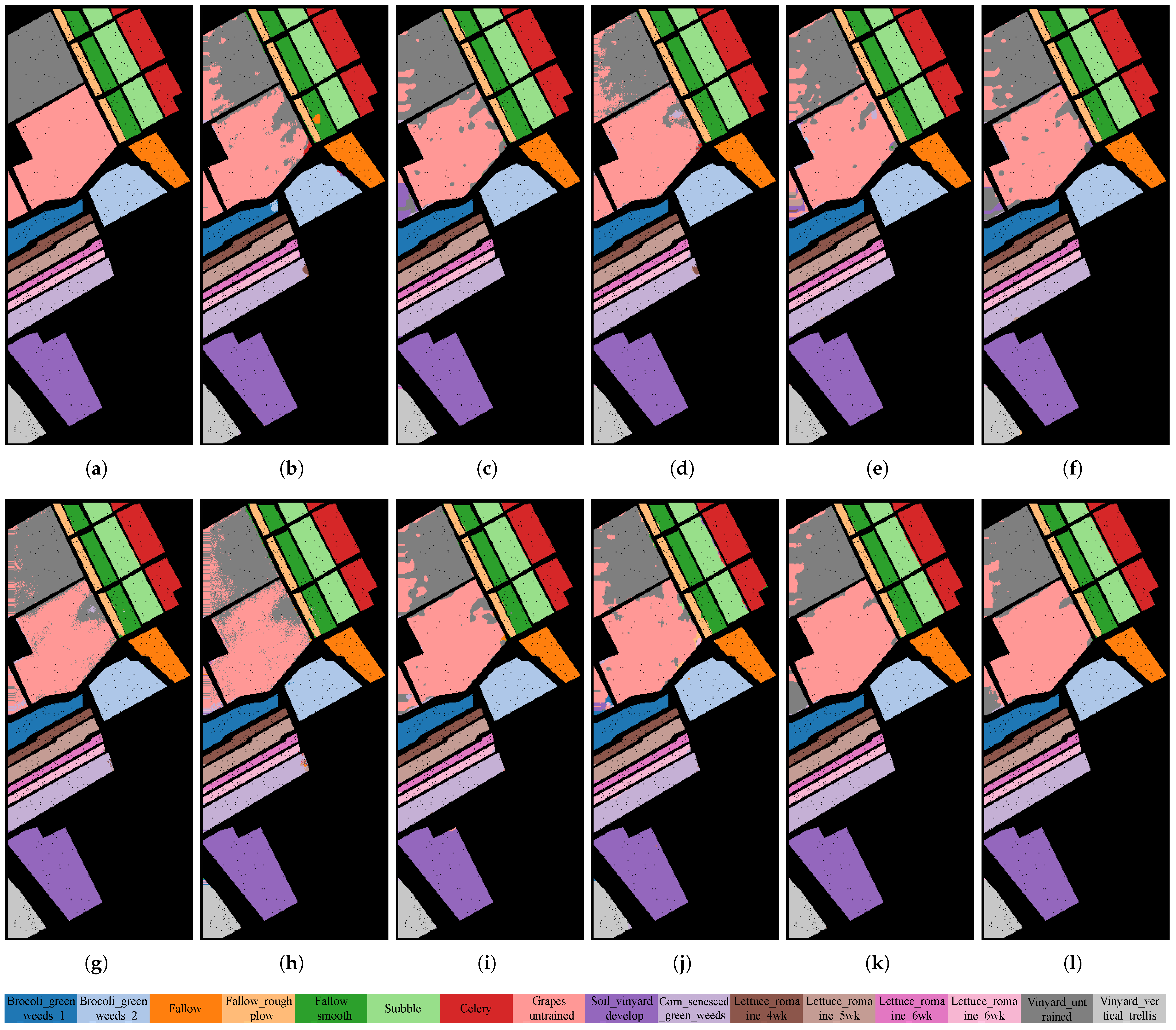
| Class ID | Category | Training | Testing | Total |
|---|---|---|---|---|
| 1 | Alfalfa | 15 | 31 | 46 |
| 2 | Corn-notill | 40 | 1388 | 1428 |
| 3 | Corn-mintill | 40 | 790 | 830 |
| 4 | Corn | 40 | 197 | 237 |
| 5 | Grass-pasture | 40 | 443 | 483 |
| 6 | Grass-trees | 40 | 690 | 730 |
| 7 | Grass-pasture-mowed | 15 | 13 | 28 |
| 8 | Hay-windrowed | 40 | 438 | 478 |
| 9 | Oats | 15 | 5 | 20 |
| 10 | Soybeans-notill | 40 | 932 | 972 |
| 11 | Soybean-mintill | 40 | 2415 | 2455 |
| 12 | Soybean-clean | 40 | 553 | 593 |
| 13 | Wheat | 40 | 165 | 205 |
| 14 | Woods | 40 | 1225 | 1265 |
| 15 | Build-grass-trees-drivers | 40 | 346 | 386 |
| 16 | Stones-steel-towers | 40 | 53 | 93 |
| Total | 565 | 9684 | 10,249 |
| Class ID | Category | Training | Testing | Total |
|---|---|---|---|---|
| 1 | Asphalt | 30 | 6601 | 6631 |
| 2 | Meadows | 30 | 18,619 | 18,649 |
| 3 | Gravel | 30 | 2069 | 2099 |
| 4 | Trees | 30 | 3034 | 3064 |
| 5 | Metal Sheets | 30 | 1315 | 1345 |
| 6 | Bare-soil | 30 | 4999 | 5029 |
| 7 | Bitumen | 30 | 1300 | 1300 |
| 8 | Bricks | 30 | 3652 | 3682 |
| 9 | Shadows | 30 | 917 | 947 |
| Total | 270 | 42,506 | 42,776 |
| Class ID | Category | Training | Testing | Total |
|---|---|---|---|---|
| 1 | Brocoli_green_weeds_1 | 30 | 1979 | 2009 |
| 2 | Brocoli_green_weeds_2 | 30 | 3696 | 3726 |
| 3 | Fallow | 30 | 1946 | 1976 |
| 4 | Fallow_rough_plow | 30 | 1364 | 1394 |
| 5 | Fallow_smooth | 30 | 2648 | 2678 |
| 6 | Stubble | 30 | 3929 | 3959 |
| 7 | Celery | 30 | 3549 | 3579 |
| 8 | Grapes_untrained | 30 | 11,241 | 11,271 |
| 9 | Soil_vinyard_develop | 30 | 6173 | 6203 |
| 10 | SCorn_senesced_green_weeds | 30 | 3248 | 3278 |
| 11 | Lettuce_romaine_4wk | 30 | 1038 | 1068 |
| 12 | Lettuce_romaine_5wk | 30 | 1897 | 1927 |
| 13 | Lettuce_romaine_6wk | 30 | 886 | 916 |
| 14 | Lettuce_romaine_7wk | 30 | 1040 | 1070 |
| 15 | Vinyard_untrained | 30 | 7238 | 7268 |
| 16 | Vinyard_vertical_trellis | 30 | 1777 | 1807 |
| Total | 480 | 53,649 | 54,129 |
| Class No. | 2D CNN | Hybrid SN | Spectral Former | HiT | HUSST | SSFTT | ViM | MiM | SS- Mamba | FAHM | Hyper- SMamba |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 86.21 ± 3.34 | 92.83 ± 6.30 | 97.29 ± 3.27 | 85.05 ± 2.35 | 80.88 ± 1.87 | 89.13 ± 9.82 | 89.79 ± 5.05 | 95.65 ± 7.49 | 99.38 ± 1.88 | 95.90 ± 4.08 | 99.10 ± 1.24 |
| 2 | 71.86 ± 2.13 | 86.76 ± 1.88 | 79.15 ± 2.74 | 81.89 ± 1.42 | 82.16 ± 0.94 | 88.94 ± 2.17 | 77.44 ± 1.30 | 83.40 ± 8.83 | 83.65 ± 5.73 | 88.78 ± 2.00 | 89.99 ± 2.04 |
| 3 | 69.52 ± 2.53 | 90.27 ± 2.93 | 85.73 ± 4.01 | 85.59 ± 0.92 | 87.55 ± 1.65 | 88.36 ± 2.92 | 82.19 ± 2.49 | 78.80 ± 6.94 | 92.10 ± 3.60 | 95.49 ± 1.22 | 92.88 ± 1.31 |
| 4 | 64.92 ± 6.21 | 88.17 ± 5.16 | 80.41 ± 4.94 | 86.42 ± 1.73 | 92.52 ± 0.92 | 92.72 ± 5.44 | 84.04 ± 2.99 | 77.64 ± 10.26 | 99.23 ± 2.16 | 93.10 ± 4.16 | 94.54 ± 2.29 |
| 5 | 80.43 ± 3.75 | 91.10 ± 2.52 | 93.02 ± 3.38 | 89.74 ± 1.12 | 95.37 ± 0.97 | 92.28 ± 1.93 | 88.53 ± 3.62 | 86.13 ± 3.26 | 94.06 ± 1.91 | 97.00 ± 1.89 | 97.81 ± 1.12 |
| 6 | 93.23 ± 0.98 | 95.20 ± 3.67 | 98.63 ± 0.62 | 95.02 ± 0.73 | 97.75 ± 0.36 | 95.30 ± 3.03 | 95.54 ± 1.05 | 96.30 ± 0.78 | 98.89 ± 0.49 | 98.88 ± 0.71 | 99.42 ± 0.26 |
| 7 | 81.67 ± 5.77 | 90.80 ± 9.63 | 88.22 ± 9.25 | 89.12 ± 5.10 | 95.44 ± 4.27 | 75.86 ± 2.64 | 93.43 ± 4.63 | 82.14 ± 7.14 | 100.00 ± 0.00 | 91.48 ± 8.36 | 95.32 ± 2.68 |
| 8 | 95.63 ± 0.38 | 99.24 ± 0.86 | 99.31 ± 0.77 | 96.87 ± 0.49 | 99.39 ± 0.59 | 98.45 ± 1.14 | 96.59 ± 0.61 | 98.95 ± 0.63 | 100.00 ± 0.00 | 99.75 ± 0.34 | 100.00 ± 0.00 |
| 9 | 70.18 ± 12.24 | 72.90 ± 19.62 | 73.92 ± 14.07 | 60.29 ± 9.04 | 77.14 ± 8.11 | 51.29 ± 32.91 | 74.60 ± 14.11 | 70.00 ± 0.15 | 100.00 ± 0.00 | 93.22 ± 1.99 | 94.87 ± 4.74 |
| 10 | 66.41 ± 3.17 | 80.88 ± 4.28 | 78.85 ± 6.70 | 78.00 ± 1.01 | 79.93 ± 1.37 | 83.51 ± 1.40 | 74.11 ± 2.07 | 82.10 ± 5.25 | 91.15 ± 4.76 | 94.03 ± 3.08 | 90.58 ± 0.78 |
| 11 | 76.38 ± 2.08 | 86.49 ± 2.44 | 80.25 ± 5.62 | 88.99 ± 1.21 | 84.74 ± 1.35 | 91.68 ± 1.76 | 86.07 ± 1.06 | 84.93 ± 5.37 | 89.81 ± 5.09 | 91.33 ± 2.45 | 91.72 ± 2.83 |
| 12 | 68.28 ± 5.07 | 87.42 ± 3.37 | 72.95 ± 4.46 | 79.06 ± 2.24 | 83.53 ± 2.34 | 91.24 ± 4.21 | 79.84 ± 1.96 | 84.49 ± 4.89 | 94.07 ± 4.20 | 93.92 ± 4.26 | 94.34 ± 0.99 |
| 13 | 95.03 ± 1.95 | 97.08 ± 2.35 | 98.40 ± 2.23 | 96.70 ± 0.80 | 98.80 ± 0.58 | 96.40 ± 2.58 | 94.81 ± 1.30 | 95.61 ± 3.16 | 100.00 ± 0.00 | 99.64 ± 0.55 | 97.71 ± 1.58 |
| 14 | 96.14 ± 1.05 | 97.37 ± 1.03 | 97.81 ± 0.64 | 97.22 ± 0.35 | 98.82 ± 0.28 | 97.30 ± 0.94 | 96.40 ± 0.54 | 96.60 ± 1.42 | 98.86 ± 0.64 | 98.74 ± 0.97 | 99.35 ± 0.35 |
| 15 | 85.14 ± 7.14 | 89.30 ± 2.70 | 88.70 ± 4.10 | 90.77 ± 1.77 | 95.60 ± 1.19 | 92.26 ± 4.80 | 86.84 ± 3.17 | 91.71 ± 2.60 | 97.33 ± 2.46 | 98.13 ± 1.45 | 97.82 ± 1.57 |
| 16 | 80.49 ± 3.13 | 88.42 ± 10.33 | 86.80 ± 8.83 | 63.85 ± 2.60 | 89.34 ± 2.11 | 81.54 ± 4.58 | 70.19 ± 5.66 | 84.95 ± 7.98 | 99.05 ± 1.05 | 90.92 ± 2.36 | 95.75 ± 3.68 |
| OA (%) | 79.06 ± 1.84 | 89.50 ± 1.48 | 85.69 ± 3.14 | 87.89 ± 1.47 | 88.79 ± 0.69 | 91.38 ± 1.25 | 85.64 ± 0.71 | 87.20 ± 1.99 | 92.94 ± 1.91 | 93.06 ± 1.23 | 94.86 ± 0.67 |
| AA (%) | 80.84 ± 2.73 | 94.70 ± 0.72 | 93.18 ± 1.46 | 92.96 ± 1.30 | 94.83 ± 0.27 | 94.31 ± 1.00 | 87.30 ± 1.41 | 86.83 ± 2.84 | 96.37 ± 0.88 | 96.71 ± 0.46 | 97.60 ± 0.20 |
| 76.13 ± 1.96 | 88.02 ± 1.67 | 83.79 ± 3.45 | 86.21 ± 1.52 | 87.21 ± 0.77 | 90.17 ± 1.41 | 83.67 ± 0.74 | 85.41 ± 0.79 | 92.00 ± 2.16 | 93.07 ± 1.39 | 94.13 ± 0.76 |
| Class No. | 2D CNN | Hybrid SN | Spectral Former | HiT | HUSST | SSFTT | ViM | MiM | SS- Mamba | FAHM | Hyper- SMamba |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 77.86 ± 1.48 | 75.40 ± 6.38 | 88.55 ± 2.57 | 78.53 ± 5.71 | 84.75 ± 1.51 | 89.42 ± 7.15 | 75.39 ± 2.31 | 85.99 ± 2.04 | 94.14 ± 3.47 | 95.64 ± 1.36 | 96.77 ± 0.58 |
| 2 | 88.67 ± 0.89 | 94.62 ± 3.70 | 94.80 ± 1.55 | 94.07 ± 2.78 | 97.64 ± 0.36 | 96.95 ± 2.16 | 94.78 ± 0.64 | 87.17 ± 1.59 | 90.31 ± 7.34 | 98.95 ± 0.39 | 99.66 ± 0.10 |
| 3 | 80.59 ± 6.18 | 76.78 ± 6.06 | 72.20 ± 4.50 | 75.63 ± 7.43 | 87.60 ± 1.12 | 85.69 ± 6.35 | 73.61 ± 2.73 | 83.46 ± 7.35 | 93.67 ± 11.98 | 95.44 ± 2.01 | 93.09 ± 1.67 |
| 4 | 79.70 ± 1.33 | 83.52 ± 4.80 | 93.69 ± 1.80 | 78.94 ± 5.04 | 77.36 ± 0.69 | 89.45 ± 2.11 | 81.08 ± 1.32 | 85.67 ± 5.55 | 99.09 ± 0.38 | 95.19 ± 1.08 | 95.15 ± 0.67 |
| 5 | 88.97 ± 1.89 | 99.33 ± 0.68 | 99.85 ± 0.06 | 97.88 ± 0.45 | 96.12 ± 0.32 | 98.59 ± 1.34 | 98.57 ± 0.22 | 99.33 ± 0.64 | 100.00 ± 0.00 | 98.16 ± 1.05 | 99.34 ± 0.10 |
| 6 | 85.29 ± 1.57 | 91.26 ± 5.46 | 84.87 ± 4.46 | 84.28 ± 5.93 | 95.28 ± 1.17 | 90.60 ± 6.17 | 84.87 ± 1.71 | 93.96 ± 4.37 | 99.43 ± 0.23 | 98.28 ± 1.32 | 99.58 ± 0.16 |
| 7 | 83.54 ± 1.82 | 87.51 ± 9.62 | 89.94 ± 2.71 | 93.23 ± 3.91 | 98.35 ± 0.46 | 94.84 ± 3.61 | 90.32 ± 3.51 | 95.64 ± 3.44 | 99.96 ± 0.12 | 98.40 ± 0.82 | 99.02 ± 0.78 |
| 8 | 61.33 ± 4.12 | 68.54 ± 7.09 | 73.30 ± 3.84 | 86.90 ± 4.35 | 79.49 ± 1.04 | 79.40 ± 7.27 | 66.93 ± 2.51 | 84.68 ± 2.47 | 98.15 ± 3.09 | 95.64 ± 2.24 | 92.23 ± 1.42 |
| 9 | 73.72 ± 1.90 | 68.72 ± 12.10 | 93.76 ± 2.93 | 65.30 ± 12.55 | 80.47 ± 1.81 | 85.17 ± 9.71 | 70.72 ± 3.79 | 86.38 ± 9.76 | 99.99 ± 0.03 | 94.24 ± 1.78 | 96.20 ± 1.06 |
| OA (%) | 83.72 ± 0.69 | 86.59 ± 4.20 | 89.45 ± 1.96 | 85.50 ± 3.77 | 91.49 ± 0.43 | 92.12 ± 4.04 | 83.80 ± 0.91 | 87.91 ± 1.81 | 94.30 ± 3.39 | 95.63 ± 0.63 | 97.72 ± 0.31 |
| AA (%) | 79.96 ± 2.09 | 87.01 ± 3.47 | 89.87 ± 1.19 | 84.86 ± 2.27 | 90.04 ± 0.26 | 91.18 ± 3.32 | 83.63 ± 2.01 | 89.15 ± 1.16 | 97.25 ± 1.80 | 94.94 ± 0.59 | 96.98 ± 0.47 |
| 77.11 ± 0.91 | 82.44 ± 5.37 | 86.11 ± 2.51 | 81.07 ± 4.67 | 88.75 ± 0.55 | 89.56 ± 5.13 | 80.20 ± 1.20 | 83.98 ± 2.16 | 92.62 ± 4.26 | 94.21 ± 0.83 | 96.97 ± 0.41 |
| Class No. | 2D CNN | Hybrid SN | Spectral Former | HiT | HUSST | SSFTT | ViM | MiM | SS- Mamba | FAHM | Hyper- SMamba |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 99.51 ± 0.87 | 99.98 ± 0.02 | 94.19 ± 1.78 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.68 ± 0.56 | 96.84 ± 1.19 | 95.81 ± 0.12 | 100.00 ± 0.00 | 100.00 ± 0.00 | 99.99 ± 0.01 |
| 2 | 99.60 ± 0.53 | 99.93 ± 0.06 | 98.91 ± 0.08 | 99.34 ± 0.49 | 99.56 ± 0.26 | 99.65 ± 0.34 | 98.12 ± 1.01 | 99.95 ± 0.05 | 100.00 ± 0.00 | 99.97 ± 0.04 | 99.99 ± 0.01 |
| 3 | 98.59 ± 0.96 | 99.75 ± 0.24 | 92.02 ± 0.74 | 99.82 ± 0.16 | 99.99 ± 0.01 | 99.29 ± 1.17 | 99.22 ± 0.01 | 99.85 ± 0.02 | 99.86 ± 0.40 | 100.00 ± 0.00 | 100.00 ± 0.00 |
| 4 | 98.67 ± 0.33 | 98.61 ± 1.31 | 97.16 ± 1.25 | 97.49 ± 0.14 | 98.12 ± 0.42 | 95.79 ± 0.95 | 97.46 ± 0.65 | 96.48 ± 1.69 | 99.73 ± 0.31 | 98.92 ± 1.01 | 98.19 ± 0.89 |
| 5 | 97.37 ± 0.82 | 98.78 ± 0.81 | 89.23 ± 1.25 | 98.62 ± 0.22 | 98.48 ± 0.26 | 97.06 ± 2.16 | 97.97 ± 0.57 | 98.24 ± 1.01 | 97.87 ± 2.01 | 99.23 ± 0.33 | 99.42 ± 0.26 |
| 6 | 99.95 ± 0.05 | 99.68 ± 0.24 | 99.67 ± 0.55 | 99.43 ± 0.21 | 99.72 ± 0.13 | 98.13 ± 1.01 | 99.05 ± 0.30 | 98.38 ± 0.09 | 99.97 ± 0.03 | 99.52 ± 0.48 | 99.92 ± 0.06 |
| 7 | 99.59 ± 0.32 | 98.74 ± 0.71 | 97.80 ± 0.20 | 99.41 ± 0.23 | 99.47 ± 0.14 | 98.37 ± 1.04 | 98.98 ± 0.33 | 98.66 ± 0.07 | 99.83 ± 0.11 | 99.44 ± 0.52 | 99.93 ± 0.07 |
| 8 | 86.41 ± 1.54 | 90.29 ± 4.55 | 73.06 ± 2.47 | 83.58 ± 3.61 | 86.43 ± 1.50 | 89.16 ± 2.83 | 80.38 ± 4.70 | 88.66 ± 1.27 | 82.19 ± 17.65 | 93.37 ± 4.91 | 94.42 ± 2.14 |
| 9 | 99.84 ± 0.17 | 99.15 ± 0.60 | 98.76 ± 0.12 | 99.96 ± 0.02 | 99.97 ± 0.02 | 98.99 ± 1.11 | 97.96 ± 1.04 | 99.58 ± 0.06 | 99.99 ± 0.01 | 100.00 ± 0.00 | 99.83 ± 0.07 |
| 10 | 97.63 ± 1.06 | 96.27 ± 1.79 | 94.40 ± 1.65 | 99.49 ± 0.12 | 98.53 ± 0.64 | 96.44 ± 1.60 | 96.85 ± 1.44 | 97.53 ± 0.99 | 99.32 ± 0.64 | 99.73 ± 0.19 | 98.20 ± 1.09 |
| 11 | 98.65 ± 0.76 | 96.36 ± 1.51 | 98.73 ± 0.50 | 98.87 ± 0.02 | 98.72 ± 0.45 | 98.49 ± 1.76 | 98.70 ± 0.15 | 97.00 ± 1.71 | 99.74 ± 0.21 | 99.95 ± 0.05 | 98.60 ± 1.64 |
| 12 | 99.44 ± 0.50 | 98.67 ± 1.38 | 98.86 ± 0.48 | 98.46 ± 0.17 | 98.90 ± 0.35 | 97.37 ± 2.58 | 97.45 ± 0.25 | 97.09 ± 0.53 | 99.89 ± 0.33 | 99.94 ± 0.03 | 99.83 ± 0.15 |
| 13 | 98.81 ± 0.59 | 85.54 ± 5.56 | 97.86 ± 0.63 | 97.13 ± 0.54 | 98.39 ± 0.57 | 94.84 ± 3.31 | 96.10 ± 0.68 | 96.94 ± 1.02 | 99.86 ± 0.18 | 99.81 ± 0.13 | 99.47 ± 0.42 |
| 14 | 98.43 ± 0.56 | 97.40 ± 4.04 | 98.57 ± 0.87 | 97.76 ± 0.47 | 99.14 ± 0.16 | 93.05 ± 5.43 | 96.35 ± 0.62 | 96.54 ± 1.58 | 99.26 ± 0.95 | 99.31 ± 0.32 | 97.78 ± 1.74 |
| 15 | 79.16 ± 2.38 | 63.28 ± 3.25 | 78.46 ± 4.80 | 75.76 ± 4.13 | 78.58 ± 4.91 | 84.85 ± 2.48 | 72.26 ± 3.17 | 86.03 ± 1.93 | 89.56 ± 18.58 | 90.08 ± 5.41 | 91.49 ± 3.31 |
| 16 | 99.43 ± 0.15 | 99.49 ± 0.35 | 96.48 ± 0.34 | 99.11 ± 0.76 | 99.26 ± 0.34 | 98.82 ± 1.22 | 97.19 ± 1.01 | 97.34 ± 0.06 | 99.80 ± 0.28 | 99.87 ± 0.19 | 99.91 ± 0.16 |
| OA (%) | 88.50 ± 0.46 | 92.07 ± 1.06 | 89.13 ± 1.51 | 92.84 ± 0.94 | 93.84 ± 0.94 | 94.74 ± 1.25 | 90.85 ± 1.08 | 94.65 ± 0.88 | 94.66 ± 3.36 | 96.03 ± 0.95 | 97.38 ± 0.89 |
| AA (%) | 92.57 ± 2.91 | 95.12 ± 1.21 | 93.76 ± 0.65 | 96.53 ± 1.57 | 97.11 ± 0.45 | 97.18 ± 0.85 | 95.07 ± 2.29 | 96.52 ± 3.69 | 97.94 ± 1.24 | 98.64 ± 0.45 | 98.78 ± 0.37 |
| 87.21 ± 0.52 | 91.18 ± 1.18 | 87.90 ± 1.69 | 92.02 ± 1.04 | 93.14 ± 0.27 | 94.15 ± 1.38 | 89.81 ± 1.21 | 94.04 ± 0.43 | 94.07 ± 3.72 | 96.69 ± 0.42 | 97.08 ± 0.10 |
| MSFM | AFAttention | Indian Pines | Pavia University | Salinas | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| OA (%) | AA (%) | OA (%) | AA (%) | OA (%) | AA (%) | |||||
| × | × | 86.49 | 88.49 | 85.21 | 85.97 | 86.13 | 82.68 | 94.02 | 97.40 | 94.08 |
| × | ✔ | 90.64 | 94.23 | 89.58 | 93.92 | 92.94 | 92.91 | 96.44 | 98.54 | 96.04 |
| ✔ | × | 92.86 | 96.61 | 91.62 | 96.67 | 95.67 | 95.59 | 96.82 | 98.68 | 96.46 |
| ✔ | ✔ | 94.86 | 97.60 | 94.13 | 97.72 | 96.98 | 96.97 | 97.38 | 98.78 | 97.08 |
| 3 × 3 DWConv | 3 × 3 DDConv | 5 × 5 DDConv | Indian Pines | Pavia University | Salinas |
|---|---|---|---|---|---|
| × | × | × | 90.64 | 93.92 | 96.44 |
| × | ✔ | ✔ | 92.21 | 96.10 | 96.77 |
| ✔ | × | ✔ | 94.01 | 96.27 | 96.71 |
| ✔ | ✔ | × | 92.85 | 96.73 | 97.09 |
| ✔ | ✔ | ✔ | 94.86 | 97.72 | 97.38 |
| Methods | 2D CNN | Hybrid-SN | Spectral-Former | HiT | SSFTT | HUSST | ViM | MiM | SS-Mamba | FAHM | Hyper-Mamba |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FLOPs (M) | 68.53 | 512.94 | 20.77 | 587.92 | 59.25 | 14.96 | 12.02 | 139.4 | 30.89 | 44.12 | 16.93 |
| Parameters (K) | 537.87 | 5490.43 | 407.96 | 40,670.19 | 875.22 | 1310.71 | 79.87 | 217.36 | 360.62 | 784.74 | 110.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Wang, L.; Jiang, S.; Cheng, S.; Tang, L. HyperSMamba: A Lightweight Mamba for Efficient Hyperspectral Image Classification. Remote Sens. 2025, 17, 2008. https://doi.org/10.3390/rs17122008
Sun M, Wang L, Jiang S, Cheng S, Tang L. HyperSMamba: A Lightweight Mamba for Efficient Hyperspectral Image Classification. Remote Sensing. 2025; 17(12):2008. https://doi.org/10.3390/rs17122008
Chicago/Turabian StyleSun, Mengyuan, Liejun Wang, Shaochen Jiang, Shuli Cheng, and Lihan Tang. 2025. "HyperSMamba: A Lightweight Mamba for Efficient Hyperspectral Image Classification" Remote Sensing 17, no. 12: 2008. https://doi.org/10.3390/rs17122008
APA StyleSun, M., Wang, L., Jiang, S., Cheng, S., & Tang, L. (2025). HyperSMamba: A Lightweight Mamba for Efficient Hyperspectral Image Classification. Remote Sensing, 17(12), 2008. https://doi.org/10.3390/rs17122008






