Multi-Scale Validation of Suspended Sediment Retrievals in Dynamic Estuaries: Integrating Geostationary and Low-Earth-Orbiting Optical Imagery for Hangzhou Bay

Abstract

Water color remote sensing is vital for the monitoring and quantification of marine suspended sediment dynamics and their distributions. Yet validations of these observables in coastal regions and deltaic estuaries, including the Hangzhou Bay in the East China Sea, remain challenging, primarily due to the pronounced complex oceanic dynamics that exhibit high spatiotemporal variability in the signals of the suspended sediment concentration (SSC) in the ocean. Here, we integrate satellite images from the sun-synchronous satellites, China’s Huanjing (Chinese for environmental, HJ)-1A/B (charged couple device) CCD (30 m), and from Korea’s Geostationary Ocean Color Imager GOCI (500 m) to the spatiotemporal scale effects to validate SSC remote sensing-retrieved data products. A multi-scale validation framework based on coefficient of variation (CV)-based zoning was developed, where high-resolution HJ CCD SSC data were resampled to the GOCI scale (500 m), and spatial variability was quantified using CV values within corresponding HJ CCD windows. Traditional validation, comparing in situ point measurements directly with GOCI pixel-averaged data, introduces significant uncertainties due to pixel heterogeneity. The results indicate that in regions with high spatial heterogeneity (CV > 0.10), using central pixel values significantly weakens correlations and increases errors, with performance declining further in highly heterogeneous areas (CV > 0.15), underscoring the critical role of spatial averaging in mitigating scale-related biases. This study enhances the quantitative assessment of uncertainties in validating medium-to-low-resolution water color products, providing a robust approach for high-dynamic oceanic environment estuaries and bays.

1. Introduction

Remote sensing technology has revolutionized the monitoring of Earth’s dynamic surface changes through multi-sensor collaborative observations, offering multidimensional data across atmospheric spectral windows to advance Earth system science [1,2]. As satellite geospatial data’s demands evolve toward commensurate observations at the adequate spatiotemporal resolutions for highly dynamic and fine-resolution (scale) features on Earth such as ocean dynamics, sampling resolution remains a central challenge [3]. In remote sensing, “scale” refers to an image’s spatial resolution on the Earth’s surface (e.g., the 500 m pixel size data from the Geostationary Ocean Color Imager (GOCI)), and the temporal sampling frequency is the satellite repeat time (e.g., GOCI’s hourly acquisitions) [4]. These observational scales enable the capture of instantaneous snapshots, like hourly GOCI data, and periodic changes, such as tidal-driven diurnal fluctuations in suspended sediment concentration (SSC).

Notably, the availability of remote sensing satellites in geostationary orbits (35,786 km above mean sea level, and orbital period of 24 h) enhances the temporal sampling requirements to as fine as <hourly sampling. However, geostationary orbit-based remote sensing sensors could only observe a particular part of the Earth and not globally. Sun-synchronous satellites (650–800 km altitude) have an orbital period of 90–120 min and could allow orbital sensors to observe as promptly as 3–30-day temporal sampling.

Despite its advancements, remote sensing technology has been constrained by the inherent limitations of single-sensor resolutions and discrete sampling characteristics, which struggle to fully align with the continuous multi-scale variations in surface phenomena. This mismatch has led to long-standing challenges in product validation due to spatial scale effects, specifically the conflict between sensor resolution and surface heterogeneity, which induces pixel aggregation errors. Such issues are especially evident in dynamic aquatic environments like estuaries and bays [5]. Taking SSC as an example, its spatiotemporal variability is driven by multiple factors, including tidal dynamics and river discharge. Field measurements in regions like Hangzhou Bay reveal intraday SSC fluctuations exceeding 50%, while traditional low-resolution remote sensing products (e.g., GOCI at 500 m) exhibit mean relative validation errors of approximately 15% in high-variability zones [6].

Scale effects, a cornerstone issue in remote sensing science, have seen their theoretical framework continuously refined since Woodcock and Strahler (1987) [7] proposed the “three-scale selection criteria” (information requirements, analytical methods, and scene structure). Their seminal work, employing local variance analysis, revealed the intrinsic relationship between sensor resolution and feature extraction, establishing a paradigmatic foundation for subsequent research. As remote sensing applications expanded across disciplines, Wu et al. (2009) [8] systematically demonstrated the multidimensional impacts of scale effects on measurement errors, inversion models, and product validation. They found that nonlinear responses induced by heterogeneous pixels constitute the core mechanism of cross-scale biases. This bias is particularly detrimental in coastal waters, where tidal dynamics drive hourly fluctuations in SSC exceeding 50% [6]. These findings also resonate with subpixel mixing effects identified in land cover classification (Bartkowiak et al., 2019) [9] and energy flux estimation (Kustas et al., 2003) [10]. Collectively, this body of work forms a methodological consensus: heterogeneous landscapes demand multi-scale validation.

While terrestrial studies have developed scale-correction frameworks using vegetation indices (Wang et al., 2003; Guo et al., 2014; Liu et al., 2019; Tayade et al., 2022) [11,12,13,14], significant progress has been made in this field. For instance, Wang et al. (2003) [11] demonstrated that the Enhanced Vegetation Index (EVI), through its spectral design incorporating blue-band correction and a soil adjustment factor, effectively reduces saturation effects in dense vegetation compared to AVHRR-NDVI, thereby enhancing sensitivity to canopy structural variations in high-biomass ecosystems. Further, Tayade et al. (2022) [14] combined hyperspectral imaging with UAV platforms to evaluate spectral indices for agricultural phenotyping, revealing that modified indices—such as the Modified Soil-Adjusted Vegetation Index (MSAVI)—exhibit reduced sensitivity to subpixel soil–vegetation mixing compared to conventional vegetation indices. In contrast, analogous progress in aquatic remote sensing remains limited due to two unique challenges: (1) the coupling of high-frequency temporal variability with sharp spatial gradients, and (2) the absence of physical constraints in data-driven SSC retrieval models [15,16,17,18].

Global efforts have contributed to diverse retrieval and validation techniques. Studies in regions such as Canada’s Peace-Athabasca Delta and the Mississippi River in the U.S. [19] have advanced our understanding of SSC dynamics. In China, research has focused on typical areas like Hangzhou Bay and the Pearl River Estuary. For example, Liu et al. (2013) [20] developed an HJ CCD-based algorithm tailored for turbid waters (RMSE < 20 mg/L), and Xu et al. (2019) [21] achieved hourly SSC monitoring in Lake Taihu, located at the southern part of the Yangtze River delta and the third largest freshwater lake in China, using GOCI data. While these technological advancements demonstrate progress in regional SSC monitoring, they inadvertently expose two systemic limitations when confronting scale effects in highly dynamic aquatic systems [22]. First, despite machine learning breakthroughs—exemplified by ELM models achieving R² > 0.9 in major rivers [15]—predominant single-sensor approaches neglect cross-resolution synergies: GOCI’s 500 m hourly data lack spatial detail, while HJ CCD’s 30 m imagery suffers temporal sparsity. Second, current scale-correction methods remain reactive (e.g., GAN-based super-resolution [23]) rather than proactively designing scale-aware validation frameworks. These limitations persist despite theoretical consensus from fractal studies [24] and multi-scale validation principles [25], suggesting an implementation gap between terrestrial and aquatic applications.

To bridge this gap, this study proposes a CV-partitioned validation framework grounded in two empirical findings from Hangzhou Bay: (1) HJ CCD-derived SSC heterogeneity maps reveal subpixel CVs up to 0.0944 within GOCI pixels, whereas the corresponding CV of SSC calculated within a 3 × 3-pixel window for the 500 m GOCI image is 0.0528, and (2) spatial averaging (compared to single-point validation) enhances R² by approximately 17% and reduces MRE by approximately 22% in areas with moderate heterogeneity (CV = 0.10–0.15). In regions with high heterogeneity (CV > 0.15, which corresponds to the commonly accepted homogeneity screening threshold [26]), even greater improvements are observed. This study innovatively develops a CV-partitioned framework. By conducting a synergistic scale analysis of HJ CCD and GOCI imagery in Hangzhou Bay—a representative high-dynamic estuarine system—we address two core questions: (1) How can high-resolution HJ CCD data characterize SSC spatial heterogeneity within GOCI pixels? (2) Which scale-transition method (mean vs. central pixel) minimizes validation errors across different CV intervals?

2. Materials and Methods

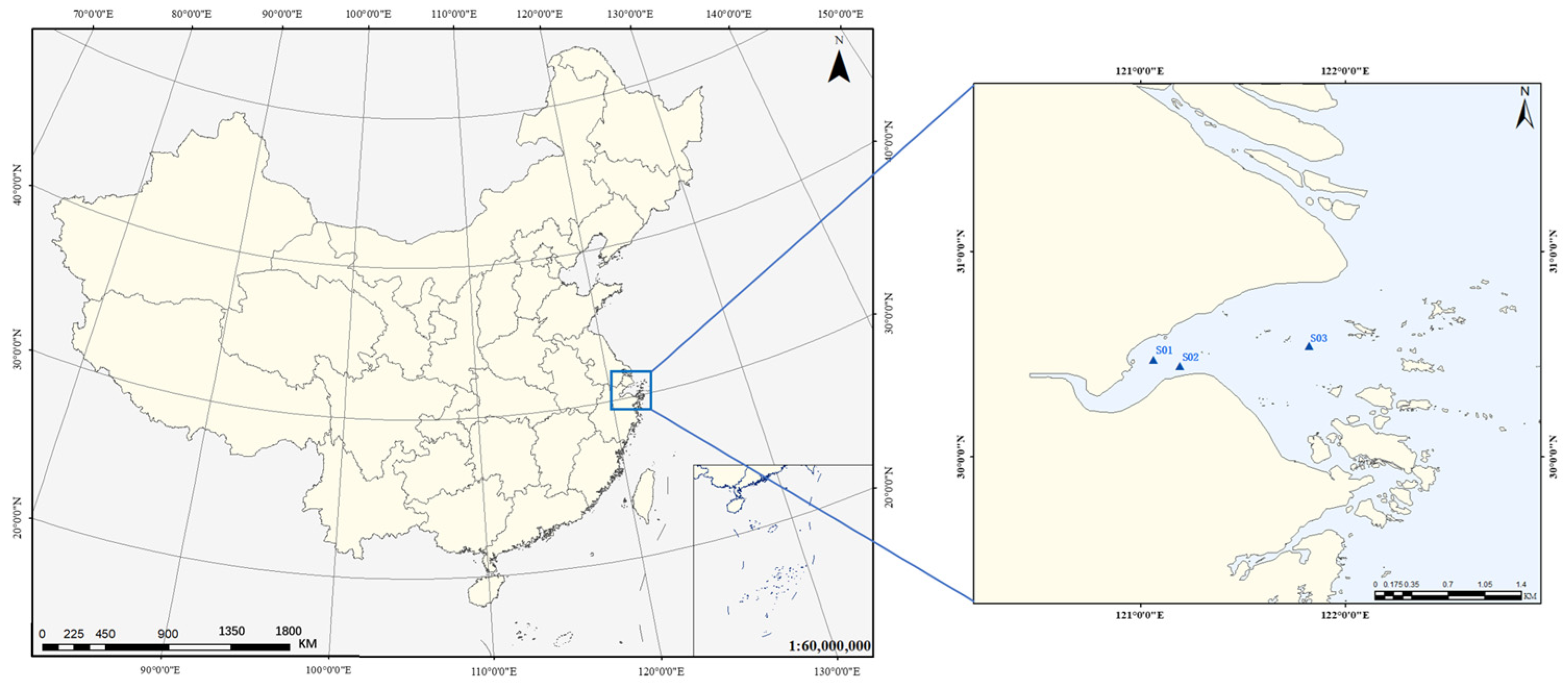
2.1. Study Area and In Situ Data

Hangzhou Bay is located in the northern Zhejiang Province and southern Shanghai (29.92°–30.86°N, 120.95°–122.07°E), China. As the estuary of the Qiantang River and a globally renowned strongly tidal estuarine bay, approximately 435 million tons of sediment (recorded at Datong Station during 1951–2000) is discharged annually from the Yangtze River mouth estuary into the East China Sea, with about 230 million tons transported southward into Hangzhou Bay, thereby constituting the primary sediment source for the bay (Wu et al., 2006) [27]. In this region, the inflow from the upper Qiantang River basin is about one-hundredth of the water coming in with the rising tide from the East China Sea; consequently, the influence of river discharge is minimal, and tidal dynamics predominantly govern the system. Pronounced diurnal variations in tidal current speed and direction, driven by strong tidal currents and circulations, maintain persistently high SSC in Hangzhou Bay.

Between 2 December and 13 December 2011, a 12-day field campaign was conducted in Hangzhou Bay employing a fixed-point observation strategy for synchronous water monitoring. Fixed observations were carried out at three designated stations during high, medium, and low tidal phases. Sampling was performed from 07:30 to 17:30 at hourly intervals at stations Zhapu 1 (S01), Andong 2 (S02), and Jinshan 3 (S03) (see Figure 1). The images used in this study were acquired on 12 December 2011, when the in situ measurements were taken at station Andong 2 under relatively calm conditions, with small wind waves, clear skies, and minimal whitecaps on the water surface.

During the campaign, spectral measurements were obtained using an ASD spectroradiometer via an above-water measurement technique. Spectral data were screened based on solar zenith angle [28], yielding 49 valid spectral curves (see Figure 2). Flow velocity data were recorded using an ADCP instrument, and in situ concentration measurements were performed by on-site filtration. The filters were preserved and later analyzed in the laboratory to extract SSC and other water quality parameters.

2.2. HJ-1A/B and GOCI Data

The HJ-1A/B satellites (hereafter referred to as HJ satellites) of the Environment and Disaster Monitoring and Forecasting Small Satellite Constellation represent a new generation of civil satellites in China following meteorological, oceanographic, and land resource satellites. Launched on 6 September 2008 at 11:25 a.m., both HJ-1A and HJ-1B carry two CCD cameras designed on identical principles. These cameras are mounted symmetrically with respect to the nadir, splitting the field of view and operating concurrently to acquire push broom images over a swath of 700 km with a ground resolution of 30 m, a signal-to-noise ratio of 48 dB, and four spectral bands. When networked, the two CCD cameras achieve a revisit cycle of only 2 days. The wide swath and moderate-to-high resolution of the HJ CCD cameras make them well suited for meso-scale regional monitoring [29]. Their products have been applied to the dynamic monitoring of key coastal zones (e.g., the Yangtze River Estuary, Yellow River Estuary, and Pearl River Estuary) for coastal dynamics, resource and vegetation surveys, and long-term coastal change studies. For this work, prior to atmospheric correction, all HJ-1A/B CCD data had already undergone standard radiometric calibration.

In June 2010, South Korea successfully launched the world’s first geostationary ocean color sensor, the Geostationary Ocean Color Imager (GOCI). The GOCI offers a ground resolution of 500 m, covers an area of 2500 km × 2500 km, and operates at an orbital altitude of 35,786 km. It is equipped with eight spectral bands (six in the visible and two in the near-infrared), each with a signal-to-noise ratio exceeding 1000 [30]. The GOCI acquires images during the daytime from 08:29 to 15:29 (Beijing time) at an hourly frequency (eight acquisitions per day) and has a design life of 7 years, covering most of the Chinese maritime domain.

3. Comparative Retrieval of Suspended Sediment

3.1. Atmospheric Correction and Inversion Model Establishment

Because neither the HJ CCD nor the GOCI sensors include a shortwave infrared (SWIR) band, they cannot effectively retrieve aerosol optical depth (AOD) over turbid waters. In contrast, MODIS, with its two SWIR bands and high sensitivity, can simultaneously derive aerosol type and AOD. In this study, the imaging times for the HJ CCD, GOCI, and MODIS were 10:29 a.m., 10:39 a.m., and 10:05 a.m., respectively, with time differences within approximately 30 min. Consequently, aerosol data retrieved from MODIS imagery were used to perform atmospheric correction for both the HJ CCD and GOCI images. This approach partially overcomes the reliance of radiative transfer model-based atmospheric correction on synchronous ground aerosol measurements [31,32]. Moreover, as the two images differ by only 10 min, the SSC in Hangzhou Bay was assumed to remain relatively stable during the observation period. In fact, the analysis of continuous in situ observation data at station S02 showed that the suspended particle concentration increased from 1029.4 mg/L at 10:25 on 12 December 2011 to 1150.4 mg/L at 11:25, with an average 10 min change of only 1.95%, which proves that the fluctuation of suspended particle concentration within the 10 min offset between HJ-CCD and GOCI is negligible for this comparison. Therefore, the aerosol information derived from Terra/MODIS in the morning is considered applicable as an input parameter for the atmospheric correction of the temporally adjacent HJ CCD and GOCI images over the same region.

Based on the in situ remote sensing reflectance data and SSC measurements, inversion models were developed by calculating the equivalent remote sensing reflectance for the corresponding bands of the HJ CCD and GOCI images. Single-band, band-ratio, and multi-band remote sensing factors were constructed. Two-thirds of the valid in situ data (33 points) were used to establish the models, and one-third (16 points) were reserved for validation. Regression analysis was then employed to develop inversion models relating the remote sensing factors to SSC, and the models were evaluated by the coefficient of determination (R²), root mean square error (RMSE), and mean relative error (MRE) between the modeled and measured SSC values. Ultimately, the optimal inversion models for the HJ CCD and GOCI images were obtained.

By comprehensive comparison, the optimal SSC inversion model for Hangzhou Bay based on the HJ CCD data was derived as follows [20]:

$$\mathrm{SSC}=13.895 \ast \exp (4.5176 \ast \mathrm{X})$$

(1)

where SSC denotes the suspended sediment concentration (mg/L), X = Rrs(b4)/Rrs(b3), and Rrs(b4) and Rrs(b3) represent the remote sensing reflectance of the fourth and third bands, respectively. An F-test confirmed that the regression was statistically significant at the 0.01 level, with an R² of 0.90 and an MRE of 13.60%. Furthermore, the atmospheric correction results for the third and fourth bands of the HJ CCD (ranging from 0.63 to 0.69 and 0.76 to 0.90, respectively) meet the inversion requirements, with relative errors of 18.99% and 12.60%. For the Hangzhou Bay GOCI image, the SSC inversion model is given by the following formula:

$$\mathrm{SSC}=30.795 \ast \exp (3.9748 \ast \mathrm{X})$$

(2)

where X = Rrs(b8)/Rrs(b6), and Rrs(b8) and Rrs(b6) denote the remote sensing reflectance of the eighth and sixth bands, respectively. The regression was statistically significant at the 0.01 level (F-test), with an R² of 0.92 and an MRE of 17.17% (see Figure 3). The atmospheric correction results for GOCI’s sixth and eighth bands (ranging from 0.67 to 0.69 and 0.83 to 0.89, respectively) satisfy the inversion requirements, with relative errors of 12.31% and 2.93%. As the GOCI sixth and eighth bands correspond directly to the HJ CCD third and fourth bands, the selection of bands does not significantly affect the accuracy comparison between the two models.

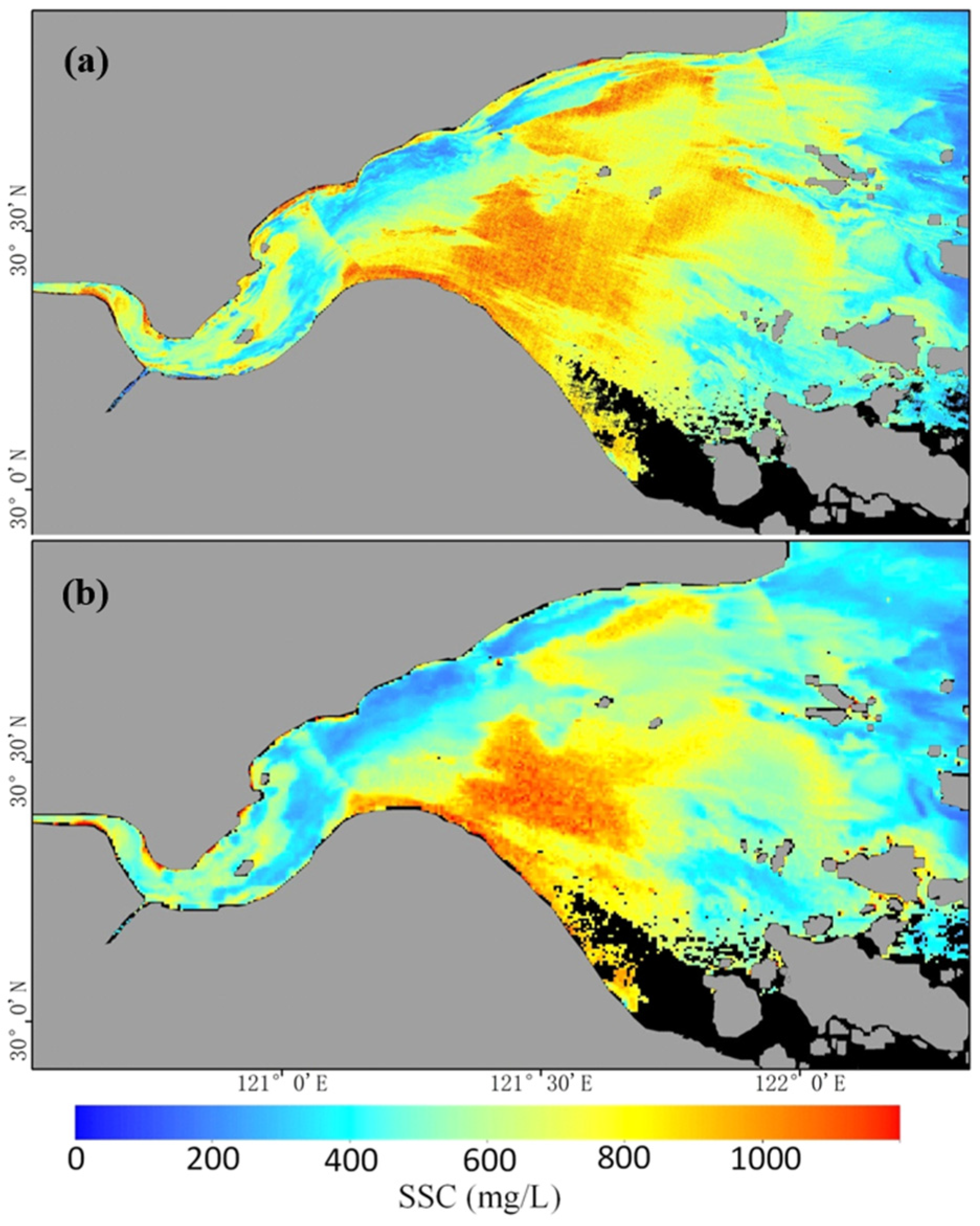
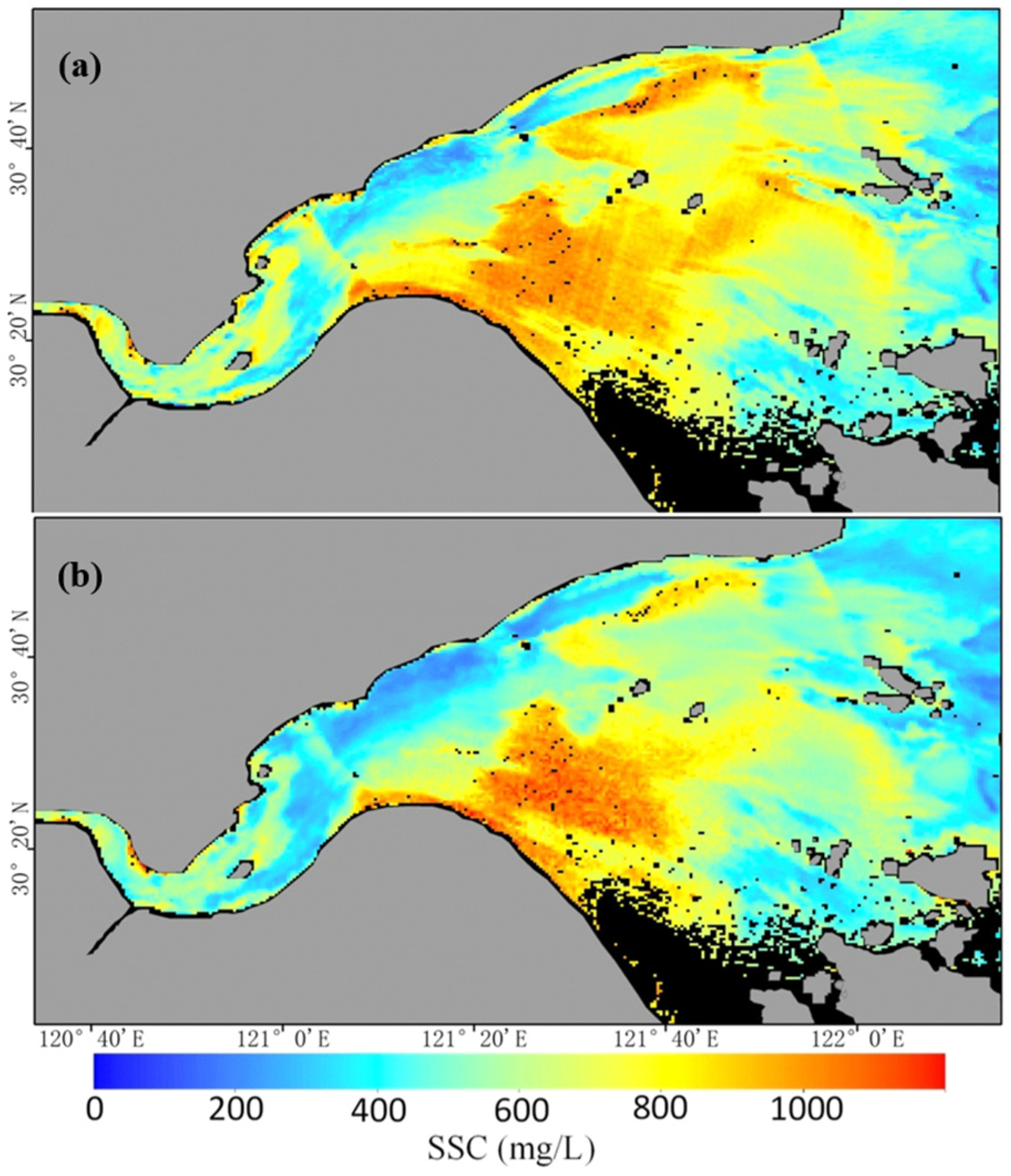
3.2. Comparative Sediment Retrieval Using Synchronous Imagery

Figure 4 presents the SSC retrieval results from the Hangzhou Bay images acquired on 12 December 2011: (a) the HJ CCD image at 10:39 (30 m resolution) and (b) the GOCI image at 10:29 (500 m resolution). The spatial distribution pattern of SSC is consistent between the two images.

Table 1. Statistical values of suspended sediment concentration retrieval results from HJ CCD and GOCI imagery in Hangzhou Bay on 12 December 2011.

Imagery	Spatial Resolution (m)	Hangzhou Bay SSC (mg/L)
		Minimum	Maximum	Mean	Standard Deviation
HJ CCD	30	140.8	1533.4	627.0	215.3
GOCI	500	134.9	1512.9	566.4	206.7

reports the minimum, maximum, mean, and standard deviation of SSC retrieved from the HJ CCD and GOCI images on 12 December 2011. The HJ CCD image yielded a mean SSC of 627.0 mg/L, whereas the GOCI image produced a mean of 566.4 mg/L, indicating that the SSC retrieved from the HJ CCD data is higher than that from the GOCI data.

Given that the selected HJ CCD and GOCI images were acquired nearly simultaneously (with a time difference of roughly 10 min) and the development of both the atmospheric correction and the SSC inversion model has been validated using in situ data, the SSC results from the two sensors are expected to exhibit a certain degree of correlation. To analyze the relationship between the SSC from the HJ CCD and GOCI images, the 30 m resolution HJ CCD SSC data were resampled to 500 m. In the resampling process, the mean SSC was computed from all HJ CCD pixels within each 500 m × 500 m area corresponding to a GOCI pixel. The resampled HJ CCD SSC was then compared with the 500 m GOCI SSC through correlation analysis. Figure 5 shows that the spatial distribution of SSC is consistent between the resampled HJ CCD image and the GOCI image.

By precisely matching geographic locations, 30,145 paired SSC data points were obtained from the GOCI and HJ CCD images over Hangzhou Bay. Regression analysis of these extensive data pairs revealed a strong correlation between the HJ CCD-derived and GOCI-derived SSC, with a coefficient of determination (R²) of 0.8392, and an RMSE of 82.15 mg/L.

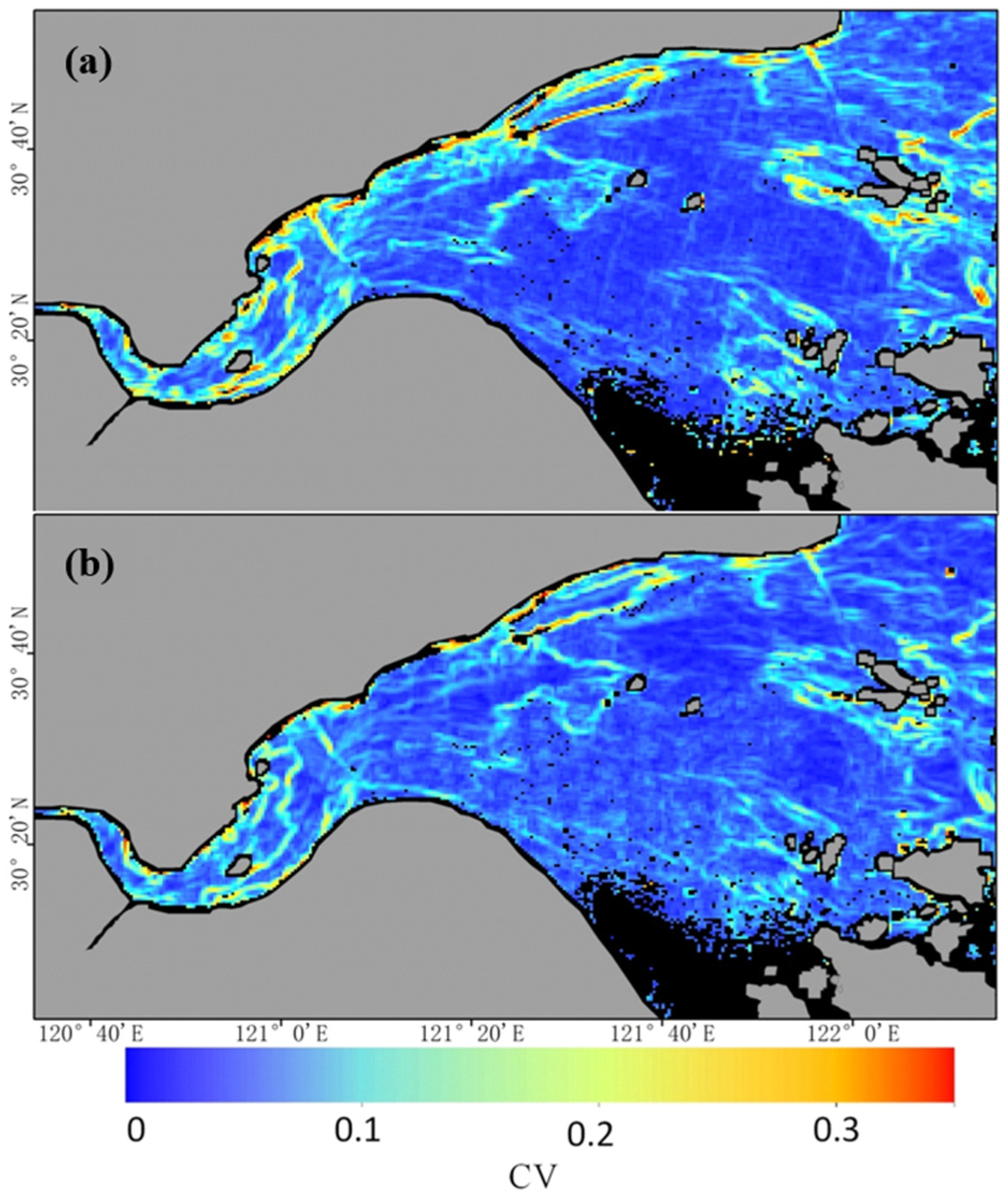
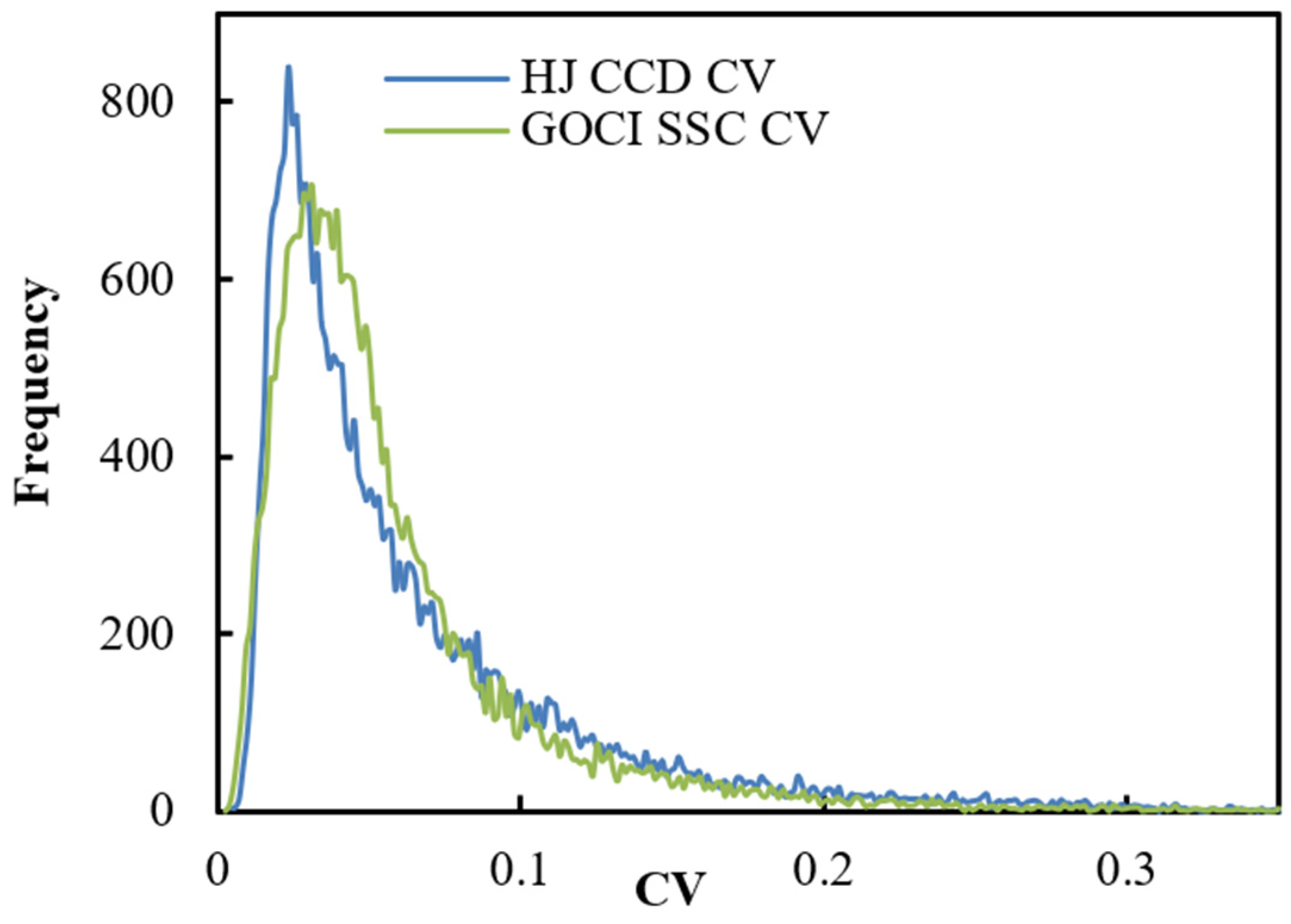
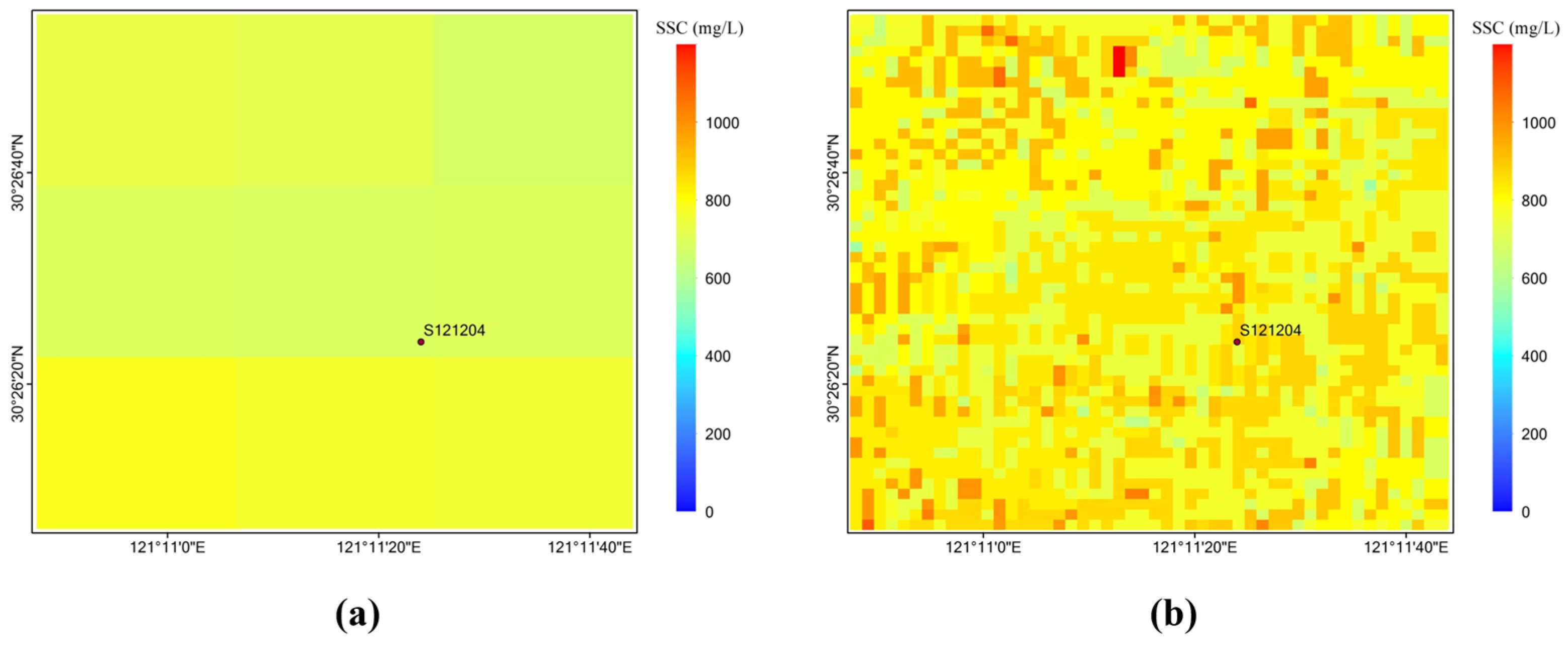
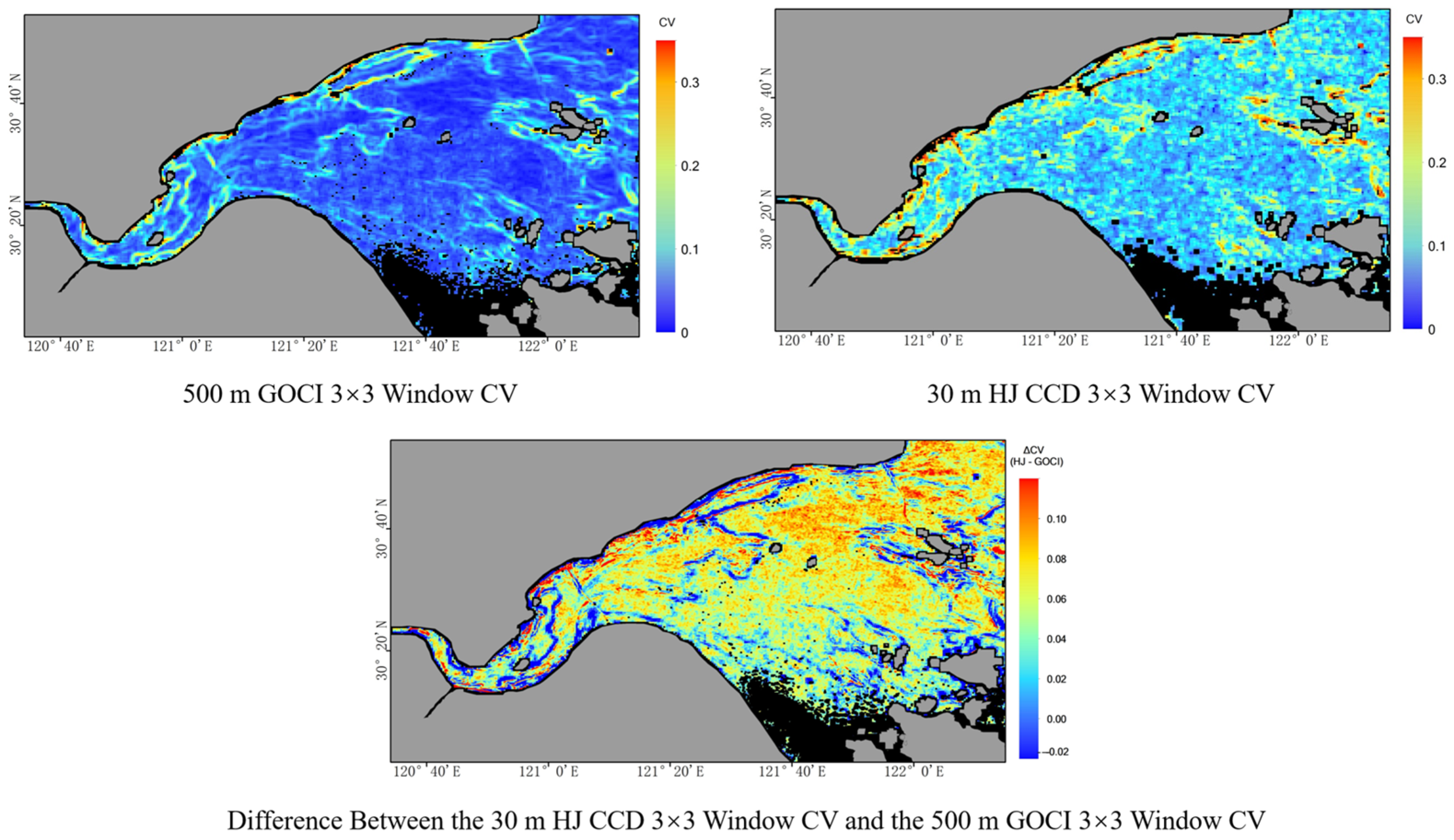
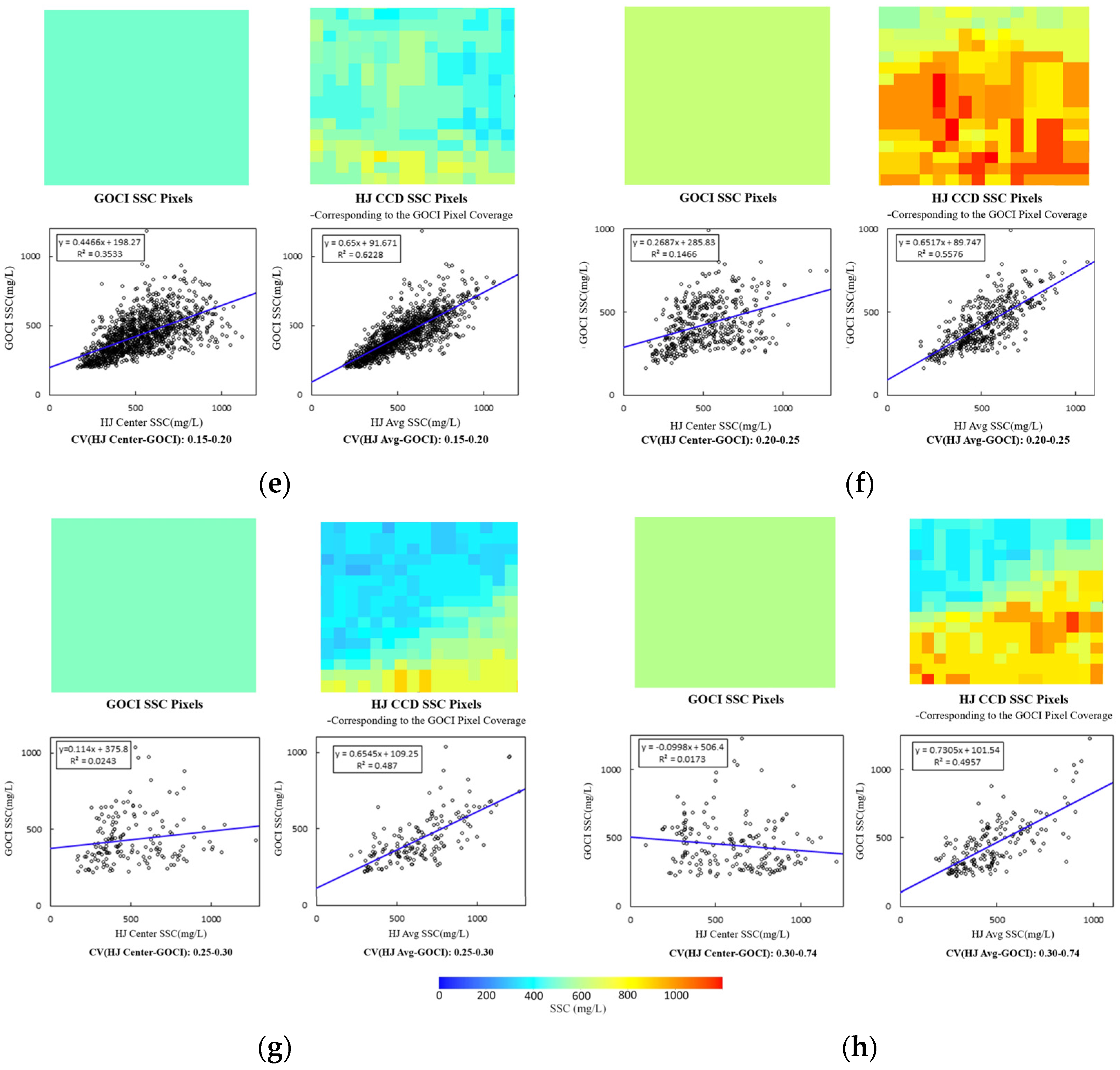
4. SSC Spatial Variability and CV Analysis

Using the SSC inversion results from both GOCI and HJ CCD imagery, the standard deviation and mean within a 3 × 3-pixel window were computed to derive the coefficient of variation (CV) of SSC. The CV is a normalized metric for quantifying data dispersion and is defined as the ratio of the standard deviation (σ) to the arithmetic mean (μ), effectively eliminating the influence of units and reflecting the relative intensity of spatial heterogeneity. High CV values indicate pronounced fluctuations in SSC within a region and serve as a key parameter for evaluating scale effects. Figure 6 presents the spatial distribution of the CV calculated from a 3 × 3 window for the 10:39 HJ CCD (500 m) image and the 10:29 GOCI (500 m) image on 12 December 2011, revealing that the spatial patterns of the CV for the two sensor datasets are consistent. In particular, Figure 6a (HJ-CCD) and 6b (GOCI) show that the highest CV values (>0.20) are concentrated around the Qiantang River mouth and neighboring intertidal shoals—zones well known for intense tidal shear and vigorous bottom-sediment resuspension. By contrast, the central navigation channel (121°10′–121°30′ E) consistently exhibits low CV (<0.08), indicating more uniform SSC dynamics in the deeper main channel. Crucially, both sensors identify the same high- and low-variability hotspots, demonstrating that the CV-based heterogeneity index remains directly comparable across different spatial resolutions. Intermediate CV bands (≈0.12–0.18), depicted as pale-yellow patches along both banks, correspond to rapidly changing optical properties in the tidal flats. This spatial pattern underscores how strongly tidal forcings and bathymetric gradients control SSC variability, and it confirms the utility of CV as a robust metric for cross-sensor scale comparisons.

The CV calculation in this study is based on the following equations:

$$\mu ={\displaystyle \frac{1}{N}}\sum _{i=1}^N{x}_i$$

(3)

$$\sigma =\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(x_i-\mu \right)}^2}$$

(4)

$$CV={\displaystyle \frac{\sigma }{\mu }}$$

(5)

where x_i represents the SSC value (in mg/L) of the i-th pixel within the 3 × 3 window, N is the total number of pixels in the window (N = 9 in this study), and σ and μ denote the standard deviation and the arithmetic mean of SSC, respectively.

Table 2. Spatial variability of SSC retrieval results from HJ CCD and GOCI imagery.

Sensor	Spatial Resolution (m)	CV
		Minimum	Maximum	Mean	Standard Deviation
HJ CCD	500	0.0043	0.3500	0.0638	0.0534
GOCI	500	0.0025	0.3499	0.0564	0.0441

summarizes the minimum, maximum, mean, and standard deviation of the spatial variability of SSC retrieved from the HJ CCD and GOCI imagery. The mean CV for the HJ CCD SSC is 0.0638, whereas that for the GOCI SSC is 0.0564, indicating a greater spatial variability in the HJ CCD data compared to the GOCI data. Furthermore, Figure 7 displays the frequency distribution of the CV calculated from the 3 × 3 window SSC results for both sensors, providing an intuitive visualization of the variability distribution. Specifically, the distributions for HJ-CCD and GOCI share a pronounced primary mode at CV ≈ 0.04–0.06, indicating that most pixels experience only moderate local variability. The HJ-CCD curve also exhibits a longer right-hand tail beyond CV > 0.10, reflecting its finer spatial resolution’s superior ability to capture extreme SSC fluctuations in highly dynamic zones. In contrast, the GOCI shows a slightly elevated frequency in the CV ≈ 0.08–0.12 range, likely because its broader instantaneous field of view averages over more heterogeneous conditions spanning both deeper channels and adjacent shallows. These distributional characteristics—a sharp central peak coupled with an extended high-CV tail—justify our chosen CV bins: the main peak corresponds to relatively quiescent deep-water areas, whereas the tail highlights the highly dynamic estuarine fringes where SSC can vary dramatically.

5. Evaluation of Scale Effects in the Validation of GOCI-Derived SSC

The high temporal resolution of the geostationary ocean color sensor (GOCI) enables a detailed study of the spatiotemporal variability of SSC in Hangzhou Bay, which is critical for understanding sediment transport and deposition processes. Prior to investigating these processes, however, it is necessary to assess the accuracy of the GOCI SSC retrievals. In the validation of GOCI-derived SSC using in situ measurements, scale effects introduce uncertainties that must be quantitatively evaluated. Quantifying the impact of these scale effects on the validation results is a key issue addressed in this study.

Hangzhou Bay exhibits pronounced spatiotemporal variability in SSC, particularly in transition zones between high- and low-sediment waters. Field measurements conducted during high, medium, and low tides indicate that SSC can fluctuate dramatically within an hour [6].

Traditionally, the validation of GOCI SSC retrievals is performed by comparing the in situ measurements with the mean value computed over a 3 × 3 window, where each GOCI pixel represents a 500 m resolution area covering 1500 m × 1500 m. However, in such highly variable environments, a single in situ point may not adequately represent the average conditions within this window, thereby introducing considerable uncertainty in the validation results.

5.1. Limitations of Traditional Validation Methods

For instance, as shown in Figure 8, the coefficient of variation (CV) of SSC within a 3 × 3 window for the 500 m GOCI image is 0.0528, whereas the corresponding CV calculated from a 50 × 50 array of 30 m HJ CCD SSC pixels (covering the same area) is 0.0944. This indicates that the higher spatial resolution of the HJ CCD more accurately captures the true spatial variability.

Figure 9 further illustrates the spatial distribution and differences in CV between the 500 m GOCI and 30 m HJ CCD images, after resampling the GOCI CV image to 30 m resolution for direct comparison. As detailed in

Table 3. Statistical values of the coefficient of variation in a 3 × 3 window for GOCI and HJ CCD.

CV	3 $\mathbf{\times }$ 3 Window Mean	Standard Deviation
30 m HJ	0.1078	0.0355
500 m GOCI	0.0564	0.0441
HJ-GOCI	0.0514	−0.0086

, the average CV in the 3 × 3 window for the 30 m HJ CCD data is nearly twice that of the GOCI data, highlighting significant differences in spatial variability.

Table 4. Comparison of SSC validation results between HJ CCD and GOCI at the measured station.

Sensor	Spatial Resolution (m)	Imaging Time	SSC (mg/L)
			Field Measurement	Image Inversion	R.E. (%)
HJ CCD	30	10:39	993.20	827.9	16.65
GOCI	500	10:29		721.3	27.37

presents the validation results of SSC at an in situ station for both HJ CCD and GOCI images. Despite the superior atmospheric correction and higher R² of the GOCI SSC inversion model, the validation accuracy of the GOCI SSC is lower than that of the HJ CCD data, likely due in part to scale effects. The 30 m resolution HJ CCD data are less affected by scale effects than the 500 m GOCI data.

Table 5. Comparison of SSC from different HJ CCD windows with SSC measured at the station.

Sensor	Spatial Resolution (m)	Imaging Time	SSC (mg/L)
			Field Measurement	Central Pixel	3 $\mathbf{\times }$ 3 Window	17 $\mathbf{\times }$ 17 Window
HJ CCD	30	10:39	993.2	875.7	827.9	702.1

compares SSC from different window sizes of the HJ CCD image with in situ measurements at station S02, showing that the average SSC derived from a 17 × 17 window is closer to the measured value than that from a 3 × 3 window. However, due to the limited number of validation points, further analysis with a larger dataset is required.

5.2. Proposed Method for Scale Effect Evaluation

To address these issues, a scale effect evaluation method for validating GOCI SSC results in highly dynamic waters—based on the CV of HJ CCD SSC within the corresponding GOCI pixel—is proposed. The procedure is as follows:

• Apply appropriate atmospheric correction and SSC inversion models to retrieve the spatial distribution of SSC from both the GOCI image and the nearly simultaneous HJ CCD image and perform preliminary validation with a limited number of in situ data points.
• Resample the 30 m HJ CCD SSC data to a 500 m resolution using two approaches: (a) compute the mean SSC over a 17 × 17 window corresponding to each 500 m GOCI pixel (denoted as HJ-Avg SSC); (b) use the central pixel’s SSC value from the corresponding 17 × 17 HJ CCD window (denoted as HJ-Center SSC).
• Calculate the CV of SSC for each 17 × 17 HJ CCD window corresponding to a GOCI pixel and stratify the CV values into different intervals.
• Within each CV interval, perform regression analyses between GOCI SSC and both HJ-Avg SSC and HJ-Center SSC, determining the RMSE, R², and MRE for each relationship.
• Compare the regression results for the two resampling approaches to evaluate the influence of scale effects within different CV intervals.

The distribution of the CV of the HJ CCD SSC in the corresponding windows ranges from 0 to 0.74. Regression analysis conducted across all CV values (for both resampling approaches) yielded the results shown in Figure 10: the regression between HJ-Center SSC and GOCI SSC produced an RMSE of 107.06 mg/L (approximately 18.9% of the mean GOCI SSC) and an R² of 0.7268, while the regression between HJ-Avg SSC and GOCI SSC resulted in an RMSE of 82.15 mg/L (about 14.7% of the mean GOCI SSC) and an R² of 0.8392. The differences between these regressions suggest that scale effects play a role, although when all data points are considered together, the scale effect is not pronounced.

To further investigate the scale effects under varying degrees of spatial heterogeneity, the CV values were divided into eight intervals: 0–0.07, 0.07–0.08, 0.08–0.10, 0.10–0.15, 0.15–0.20, 0.20–0.25, 0.25–0.30, and 0.30–0.74. Figure 11 displays sample SSC pixels and the regression relationships between the two resampled HJ CCD SSC and GOCI SSC for each interval. It is evident that as the CV increases, the internal variability of HJ CCD SSC becomes more pronounced, and the correlation between the HJ CCD and GOCI SSC decreases progressively.

Table 6. R² and MRE values of regression relationships between different scales of HJ CCD SSC and GOCI SSC for eight variation intervals.

CV Range	Mean CV	HJ Center			HJ Avg
		R2	RMSE (mg/L)	MRE (%)	R2	RMSE (mg/L)	MRE (%)
0.00–0.07	0.064	0.924	67.924	12.03	0.933	63.585	10.27
0.07–0.08	0.076	0.848	85.320	11.41	0.903	68.153	10.21
0.08–0.10	0.091	0.806	95.559	11.84	0.879	75.629	9.49
0.10–0.15	0.114	0.711	98.200	14.89	0.830	75.368	11.63
0.15–0.20	0.169	0.353	112.589	24.63	0.623	85.980	17.61
0.20–0.25	0.222	0.147	122.628	32.14	0.558	88.293	19.60
0.25–0.30	0.270	0.024	156.261	41.26	0.487	113.309	22.37
0.30–0.74	0.377	0.017	179.461	64.10	0.496	128.564	23.62

details the R² and MRE values for the regression relationships corresponding to each CV interval, and Figure 12 illustrates the trend of R² and MRE as the CV increases. Notably, when CV > 0.10, the correlation between the central pixel SSC of the HJ CCD and the GOCI retrieval drops markedly, and the MRE increases significantly; in contrast, the regression using the mean SSC shows a smaller deterioration in terms of both correlation and error. Therefore, in this study, for the HJ CCD SSC and GOCI SSC data, when the CV of SSC within the HJ CCD 17 × 17 window corresponding to a GOCI pixel exceeds 0.1, scale effects become significant. In such regions, directly validating GOCI SSC retrievals with in situ measurements may introduce considerable uncertainty into the evaluation results.

This method, through the construction of a CV-based stratification framework, systematically elucidates the scale effect in validating SSC retrievals from remote sensing data in highly dynamic water bodies. The experimental results demonstrate that the validation method utilizing the HJ CCD window mean enhances the accuracy of correlating GOCI-derived suspended sediment concentration (SSC) products in Hangzhou Bay, particularly under specific heterogeneity conditions. When the coefficient of variation (CV) ranges from 0.10 to 0.15, this method yields a marked improvement in correlation with GOCI products, achieving an R² value of approximately 0.83 compared to approximately 0.71 for traditional single-point validation. Additionally, the mean relative error (MRE) decreases to approximately 11.63% from approximately 14.89% in the same CV range. However, in higher CV intervals (CV > 0.15), although the window-averaged validation continues to outperform single-point validation, both the correlation (R²) and error (MRE) metrics exhibit a gradual decline, with R² dropping below 0.83 and MRE exceeding 11.63%. This approach quantitatively defines the critical threshold for scale effects in highly heterogeneous waters. By integrating multi-scale validation concepts within a CV-based zoning framework, this method offers a solution that is both theoretically robust and practically viable for validating remote sensing products in high-dynamic water environments.

6. Conclusions

This study addresses the long-standing challenge of scale effects in validating suspended sediment concentration (SSC) retrievals for highly dynamic coastal waters by developing a coefficient of variation (CV)-driven multi-scale framework. Using HJ CCD (30 m, sun-synchronous orbit) and GOCI (500 m, geostationary orbit) imagery acquired nearly simultaneously in Hangzhou Bay (within approximately 10 min), three critical findings emerged:

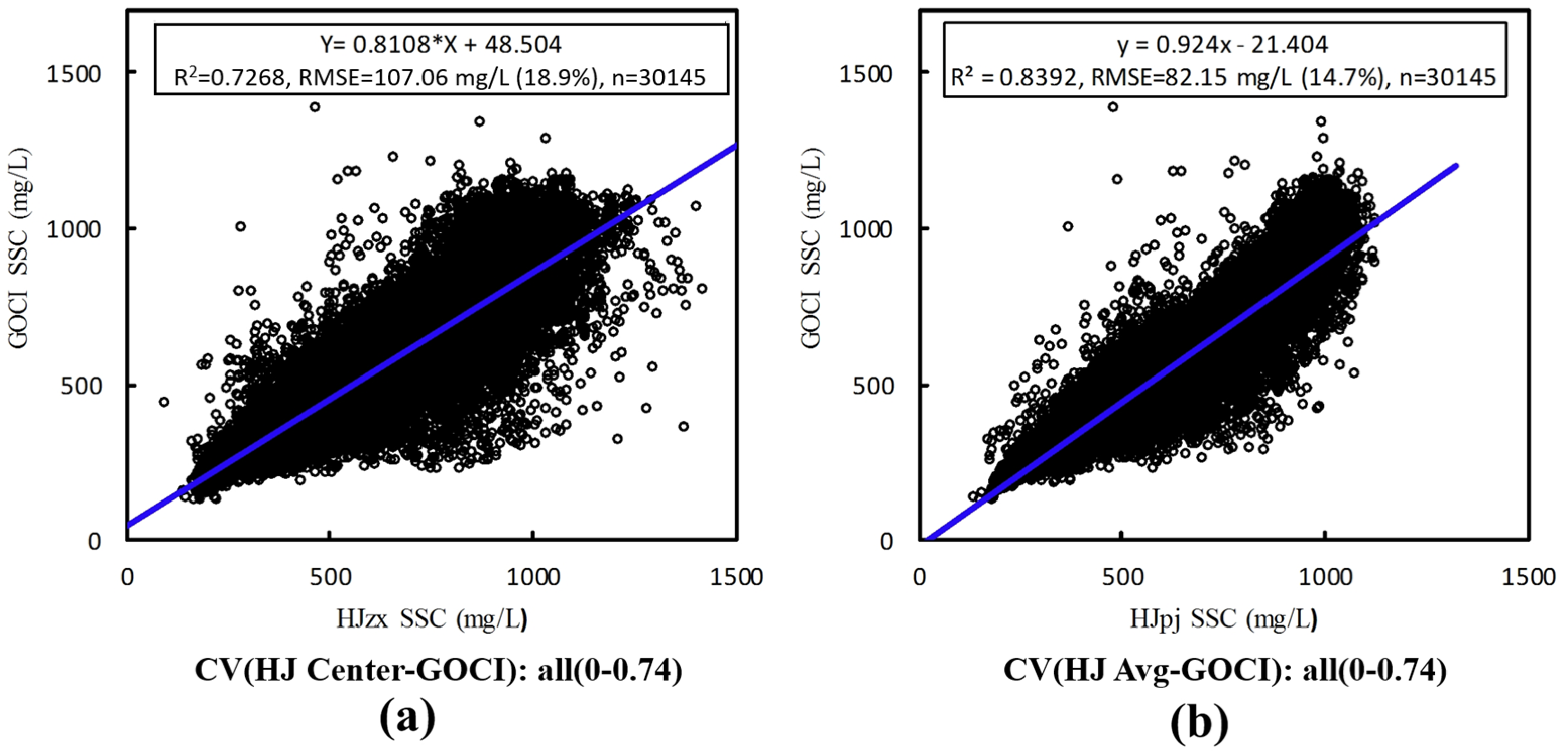
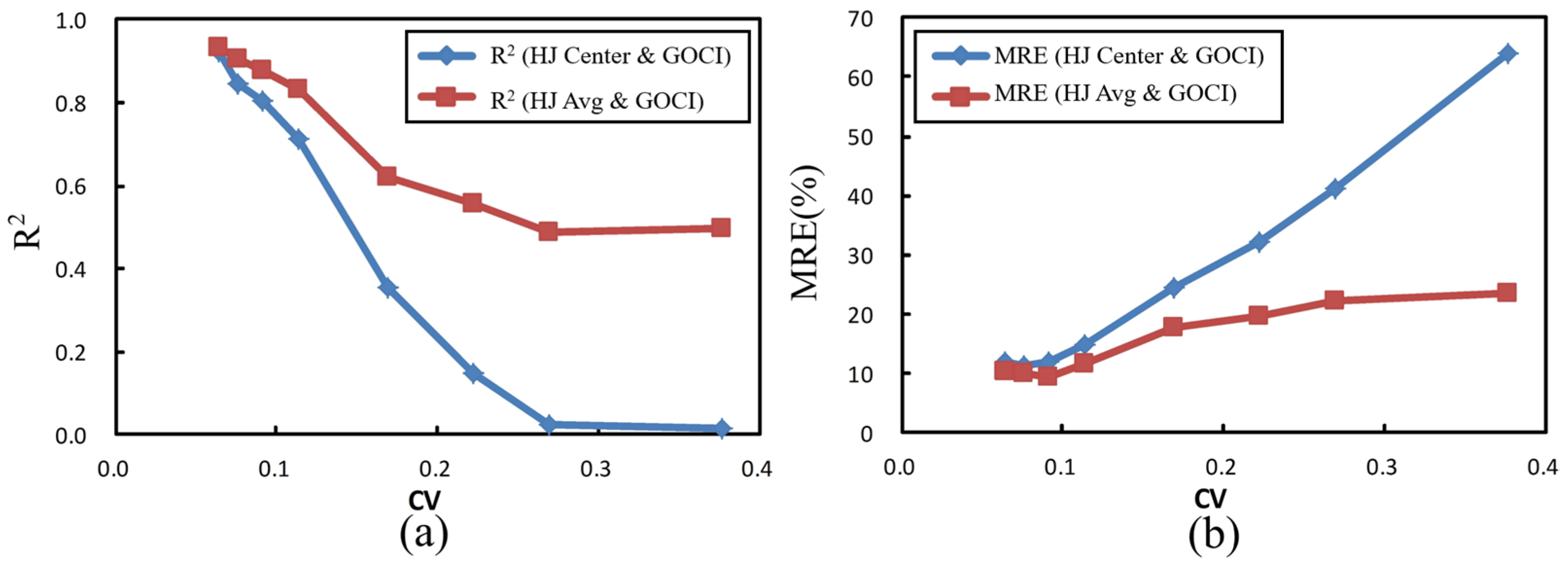
• Spatial averaging outperforms point-based validation: In regions with high spatial heterogeneity (CV > 0.10), the spatial averaging of HJ-CCD data (HJ-Avg) improved the correlation (R²) between HJ-CCD and GOCI retrievals by 17% and reduced the mean relative error (MRE) by 22% compared to central-pixel validation (HJ-Center). In zones where CV exceeds 0.15, HJ-Avg’s R² decreases to approximately 0.80 and its MRE rises to around 13.5% (Table 6 and Figure 12). Nevertheless, this modest decline is much more gradual than the sharp degradation shown by HJ-Center, which falls to an R² of 0.71 and an MRE of 14.89% under the same conditions. Such relative stability confirms the robustness of the spatial-averaging approach in highly dynamic areas.
• The CV threshold defines scale effect dominance: A critical CV threshold of 0.10 was identified, beyond which scale effects dominate validation errors. This threshold aligns with Woodcock and Strahler’s scale theory [7], confirming that sensor resolution must match feature heterogeneity. Subpixel analysis revealed that HJ CCD resolved finer variability (CV up to 0.0944) compared to the GOCI (CV = 0.0528), directly addressing the first question posed in the Introduction on quantifying SSC spatial heterogeneity.
• Uncertainty reduction through multi-scale synergy: The framework reduced SSC validation uncertainty by 22%, lowering the RMSE from 107.06 mg/L (18.9% of the mean SSC) for traditional methods to 82.15 mg/L (14.7% of the mean) (Figure 10). This empirically answers the second question in the Introduction, demonstrating that spatial averaging—not single-point validation—is essential for mitigating scale effects in dynamic waters.

6.1. Innovation and Implications

By integrating CV thresholds with multi-sensor synergies, this work bridges terrestrial scale-correction principles and aquatic dynamics, offering three advancements:

• Operational standardization: The CV-based zoning framework provides the first quantitative criteria for scale-aware validation in coastal waters, adaptable to parameters like chlorophyll and CDOM.
• Methodological replicability: The workflow, leveraging nearly simultaneous data to isolate spatial scale effects, is transferable to other estuaries globally, such as the Mississippi Delta or Pearl River Estuary.
• Theoretical validation: The empirical confirmation of the 0.10 CV threshold reinforces the need for resolution–heterogeneity alignment in sensor design, echoing foundational remote sensing theories.

6.2. Limitations and Future Directions

While this study successfully addresses the scale effect challenges in SSC validation, several limitations highlight avenues for further research. The reliance on temporally proximal datasets, though effective in isolating spatial variability, poses constraints for long-term analysis due to their scarcity. Future investigations should prioritize temporal scale effects driven by tidal dynamics or seasonal sediment fluxes, which remain unaccounted for in the current framework. In particular, different tidal phases can modulate spatial heterogeneity by altering sediment resuspension and transport patterns, thereby shifting CV distributions and potentially modifying the optimal CV threshold for separating low- versus high-variability zones. Additionally, water depth variations within this relatively shallow estuary influence light attenuation and bottom-sediment mixing, impacting the observed CV values and scale effect metrics; integrating bathymetric data into the framework could further refine the identification of heterogeneity hotspots and inform depth-specific threshold adjustments.

The empirical CV threshold of 0.10, while validated in Hangzhou Bay’s high-turbidity environment, requires rigorous testing across diverse estuarine systems—such as low-sediment or microtidal regions—to establish universally applicable criteria. Beyond spatial heterogeneity, the framework’s adaptability to other ocean color parameters (e.g., CDOM or chlorophyll) remains unexplored, necessitating evaluations under varying spectral and hydrodynamic conditions to ensure robustness. Addressing these gaps will enhance the framework’s operational utility and theoretical relevance for global coastal monitoring.

In conclusion, this study directly answers the two questions posed in the Introduction: (1) HJ CCD data effectively resolve SSC spatial heterogeneity within GOCI pixels, revealing subpixel variability (CV up to 0.0944) invisible to coarser sensors; (2) spatial averaging (mean SSC) minimizes validation errors across CV intervals, particularly in high-heterogeneity zones (CV > 0.10), where it reduces MRE by 11.63% compared to central pixel methods. These findings establish a replicable framework for scale-aware validation, bridging the gap between theoretical principles and practical applications in coastal remote sensing. In conclusion, the CV-driven framework not only resolves the “scale mismatch” problem in SSC validation but also establishes a paradigm for cross-resolution data fusion. By addressing the core challenges of spatial heterogeneity and validation biases, it advances the operational monitoring of sediment dynamics in critical coastal ecosystems, offering actionable insights to advance scientific research through sensor design and multi-scale modeling and to enhance coastal management via real-time sediment transport assessment.