Improvement of Lithological Identification Under the Impact of Sparse Vegetation Cover with 1D Discrete Wavelet Transform for Gaofen-5 Hyperspectral Data
Abstract
1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Vegetation Spectral Curves
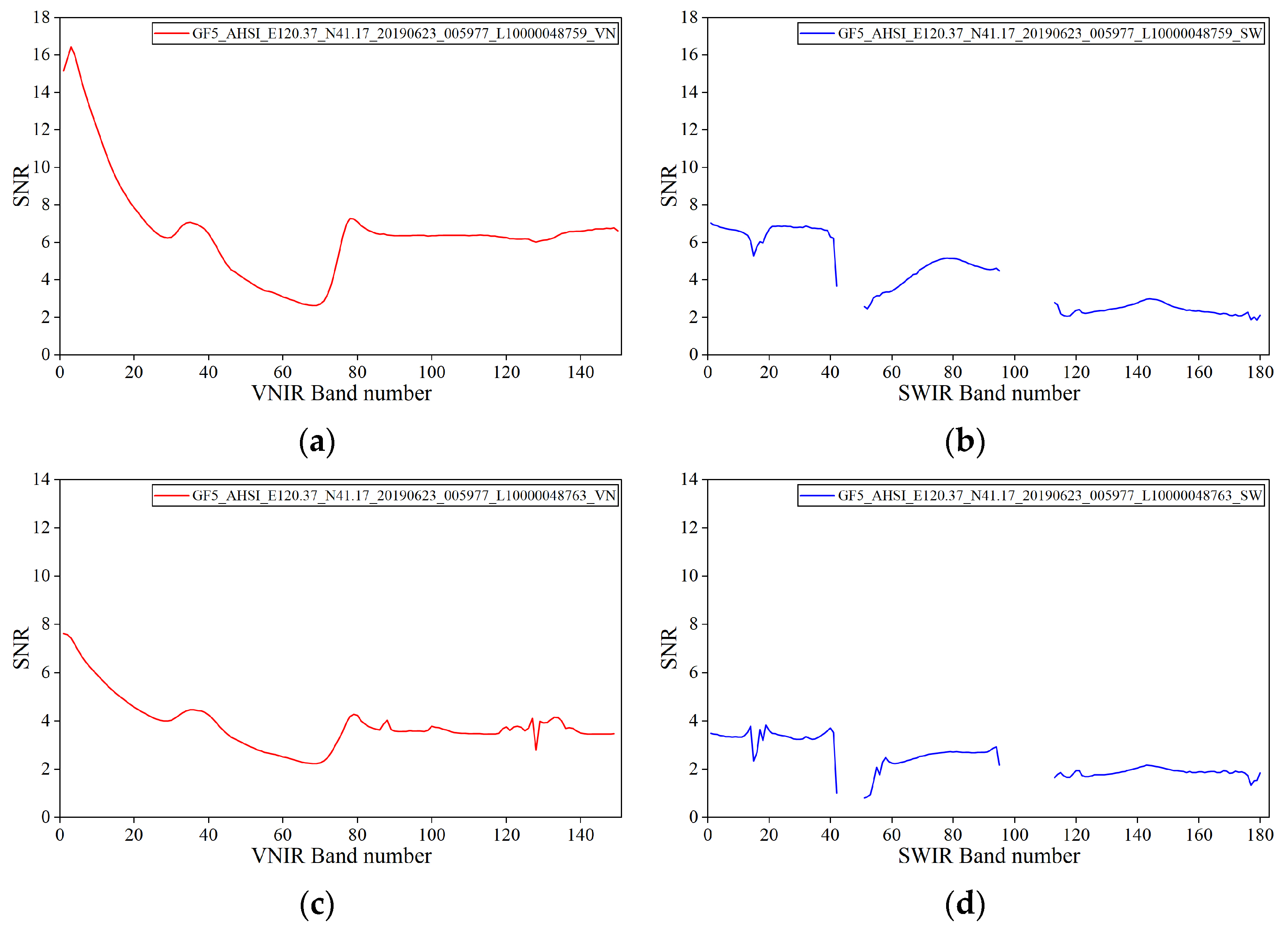
2.3. GF-5 AHSI Data
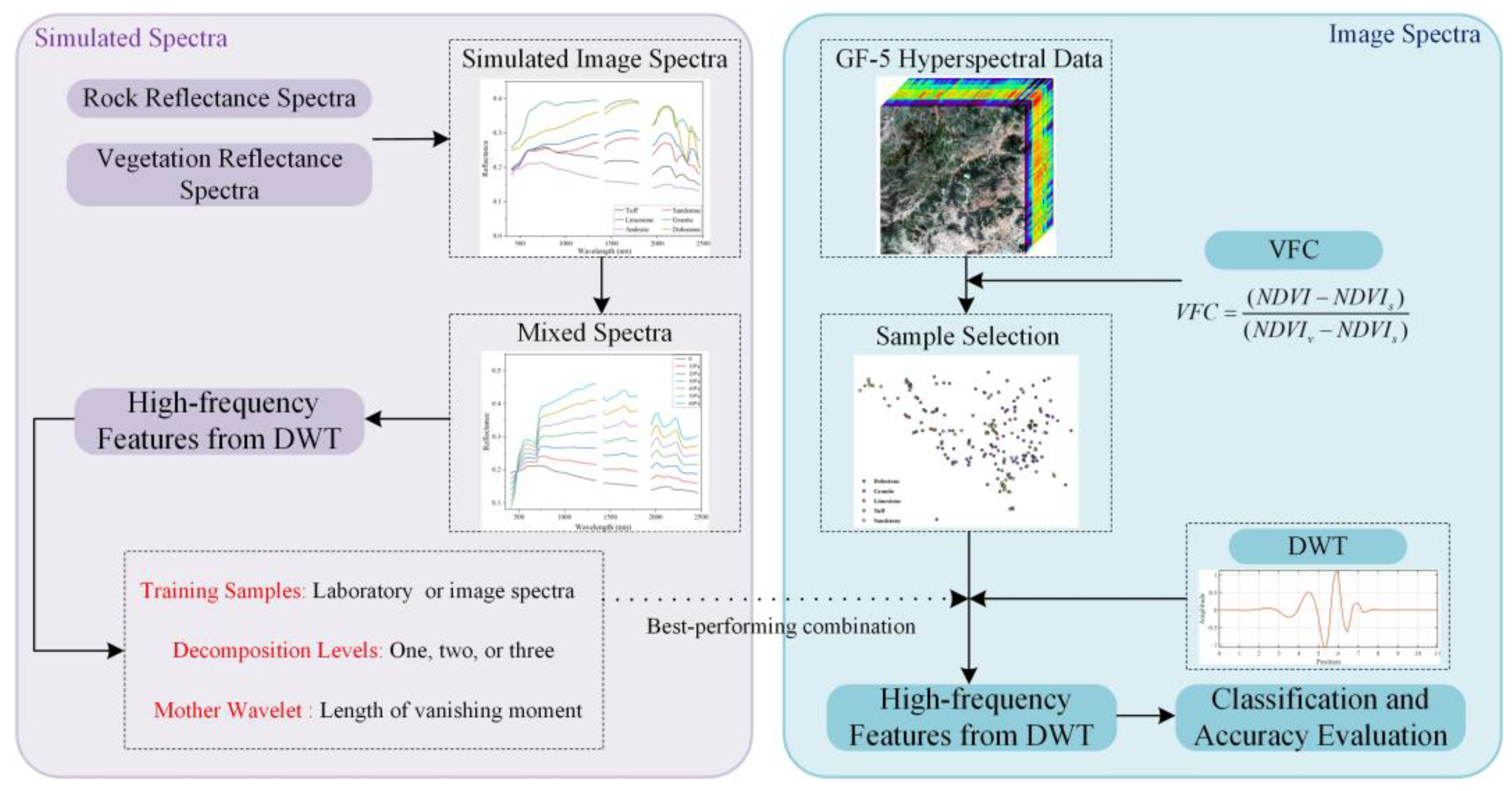
3. Methods
3.1. Pre-Processing of Laboratory Spectra and GF-5 AHSI Data
3.1.1. Rock Reflectance Spectrum Measurement
3.1.2. Pre-Processing of GF-5 AHSI Data
3.1.3. Pre-Processing of Reflectance Spectra
3.2. Mixed Simulation of Vegetation Spectra and Rock Spectra
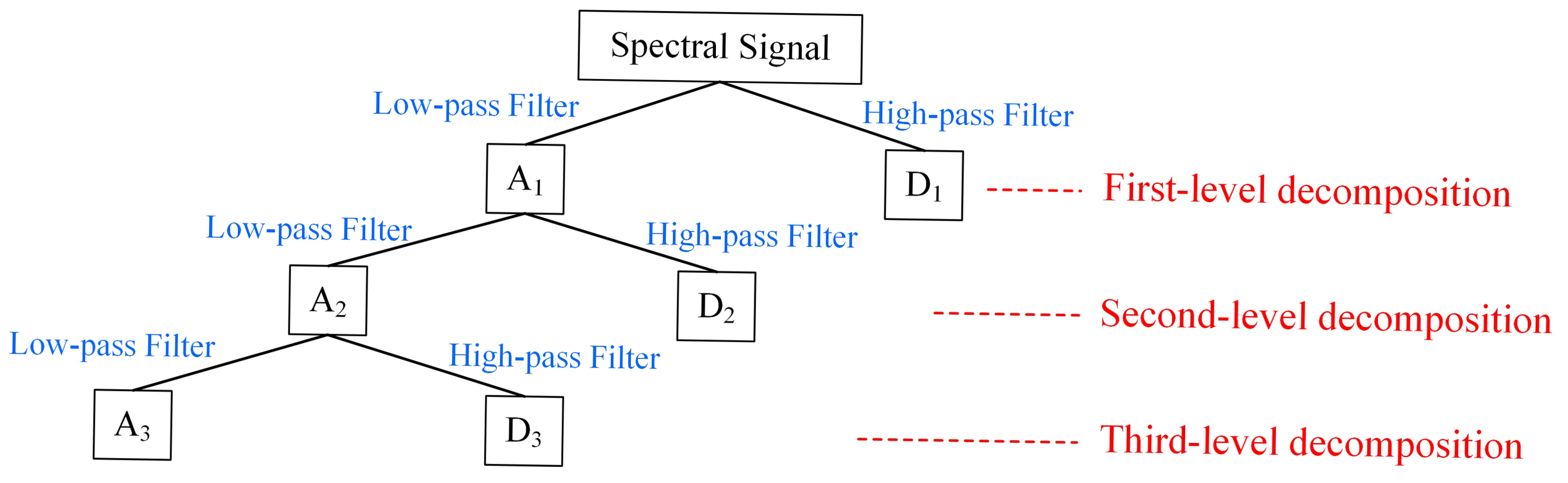
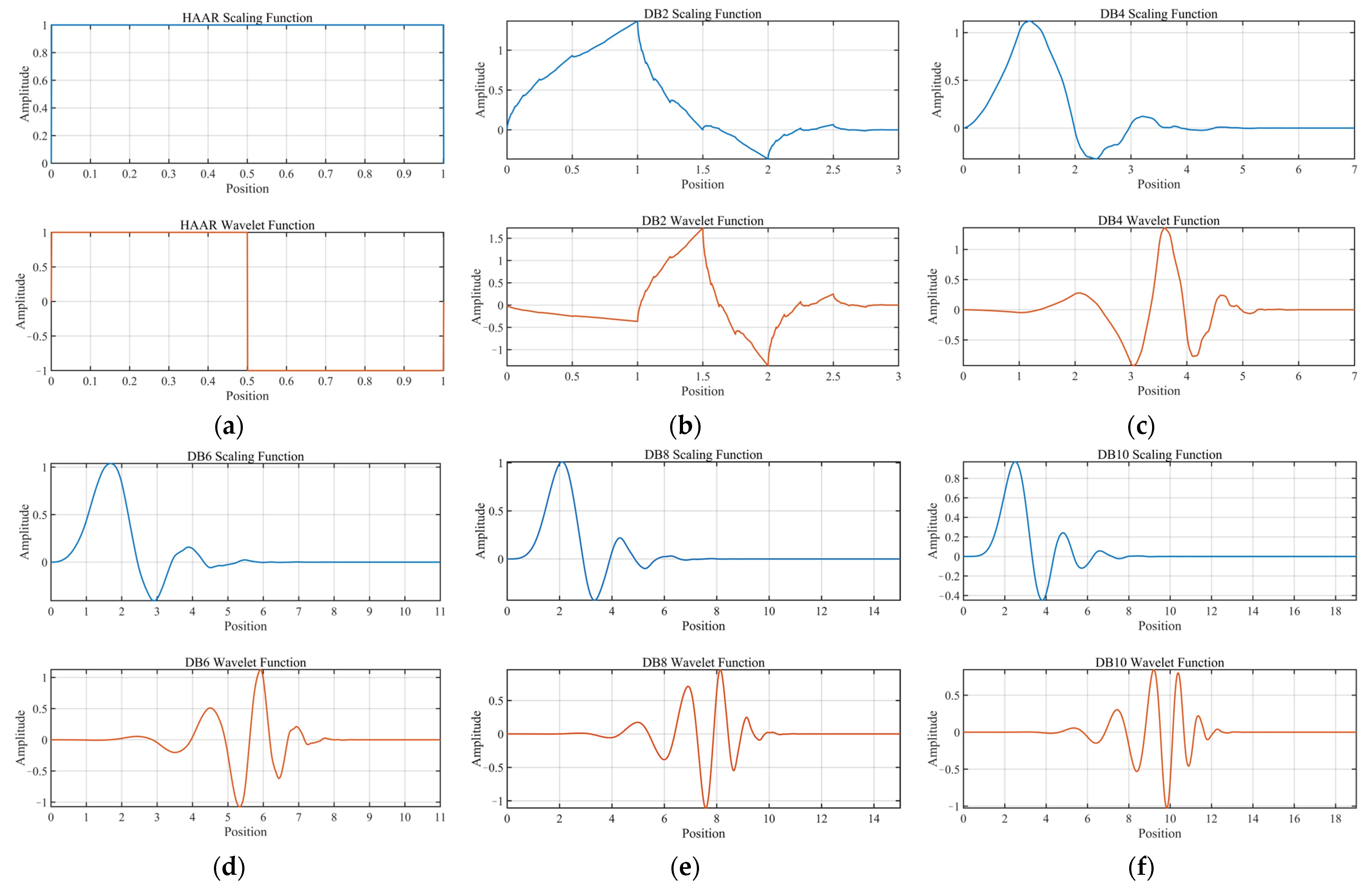
3.3. DWT and High-Frequency Feature Extraction
3.4. Classification of Simulated Mixed Spectra
3.4.1. Types of Training Samples
3.4.2. Bayesian-Optimized Random Forest Classifier
- Data Partitioning: The dataset was split into 70% training and 30% testing subsets while maintaining a balanced class distribution.
- Hyperparameter Optimization: The search space for mtry was defined as integers from 1 to 30, with ntree fixed at 1000. Five-fold cross-validation on the training set was used to evaluate model performance, and the average overall accuracy was set as the optimization objective. After 10 random initializations, 20 iterations of Bayesian optimization were performed using the Expected Improvement (EI) acquisition function.
- Model Training: The optimal mtry value determined by the Bayesian optimization was used to train the final RF model on the entire training set.
- Accuracy Assessment: The model was evaluated on the test set using the overall accuracy (OA), Kappa coefficient (KAPPA), Precision, Recall, and F1-score. These indicators are calculated using the following equation:
3.5. Classification of Image Spectra
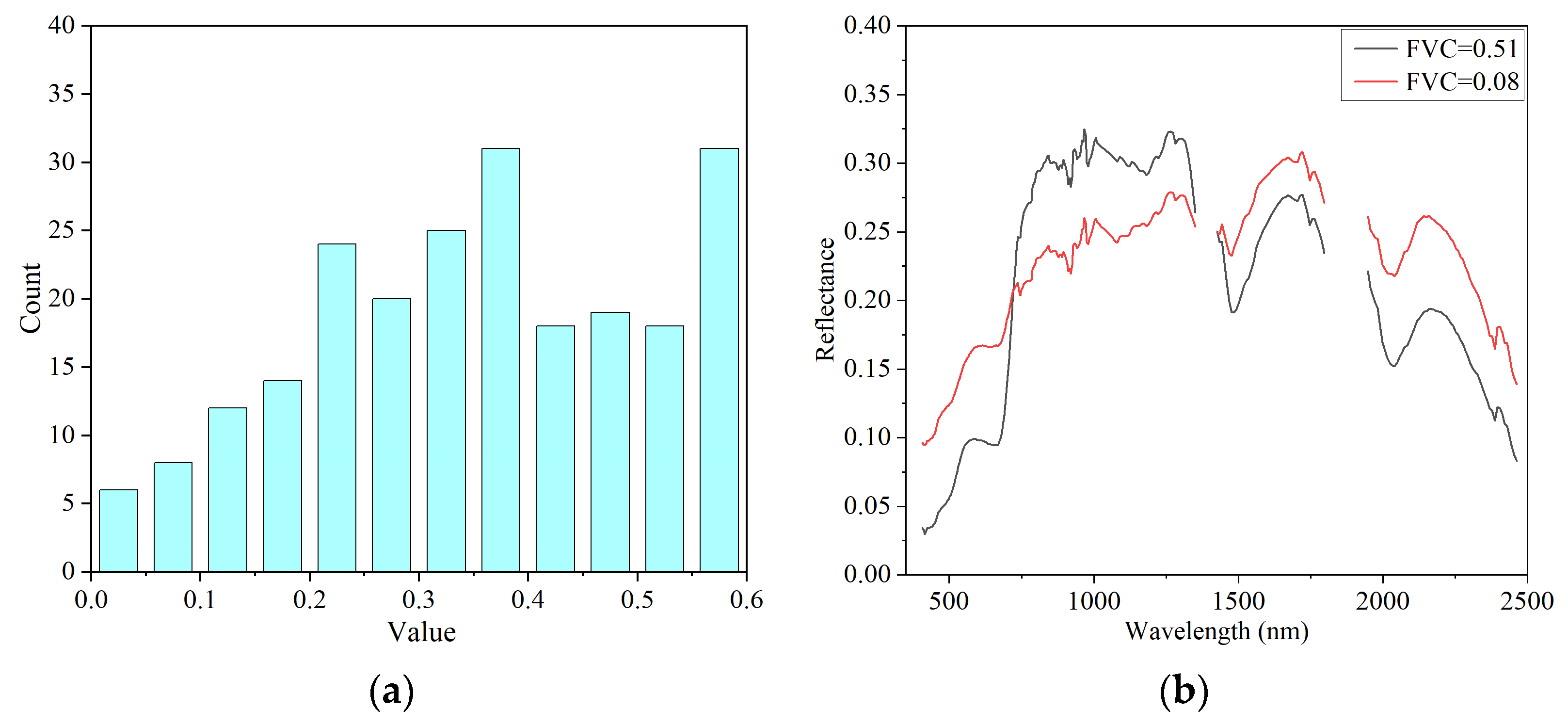
3.5.1. Estimation of Fractional Vegetation Cover
3.5.2. Lithological Classification Based on Image Spectra
4. Results
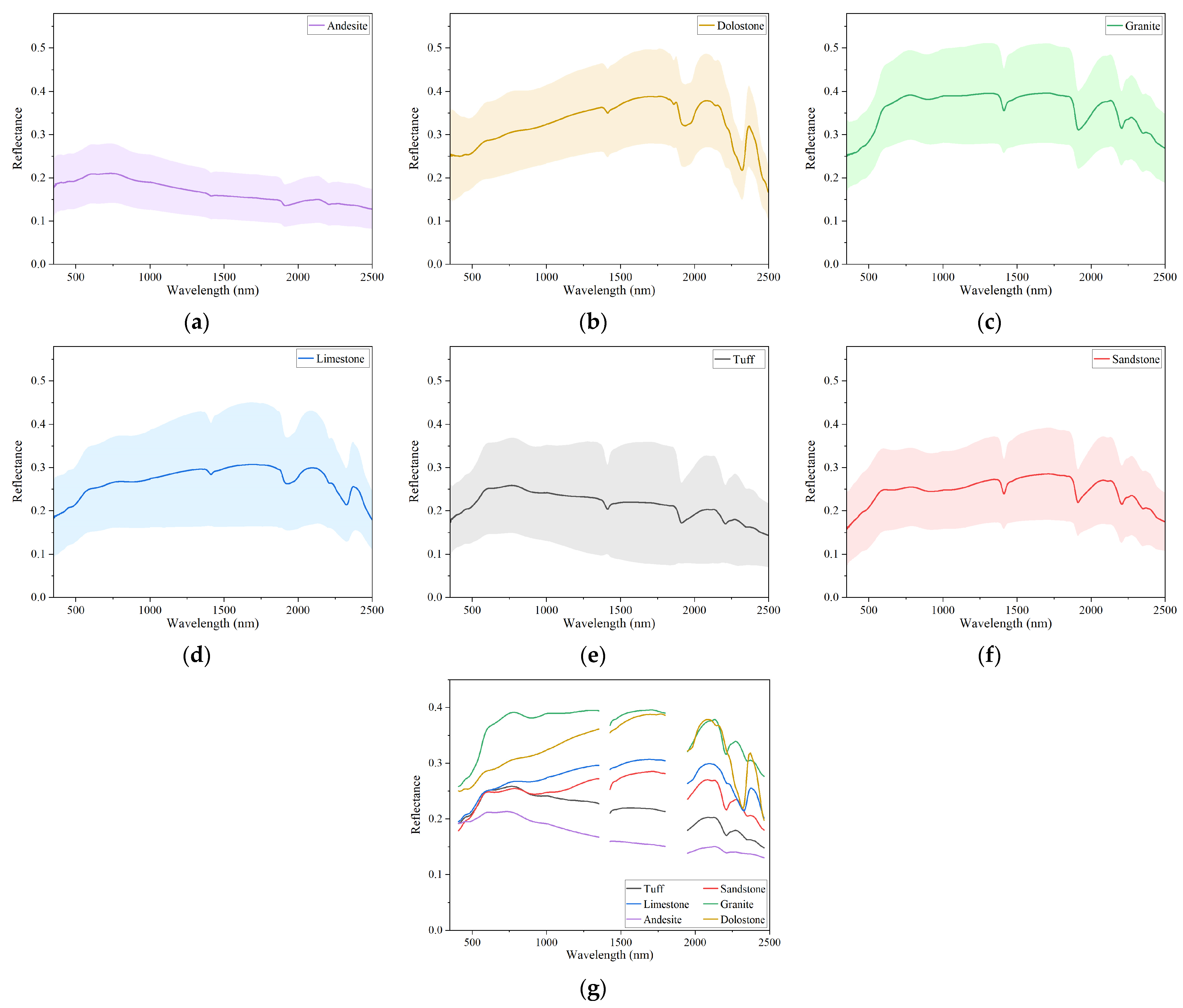
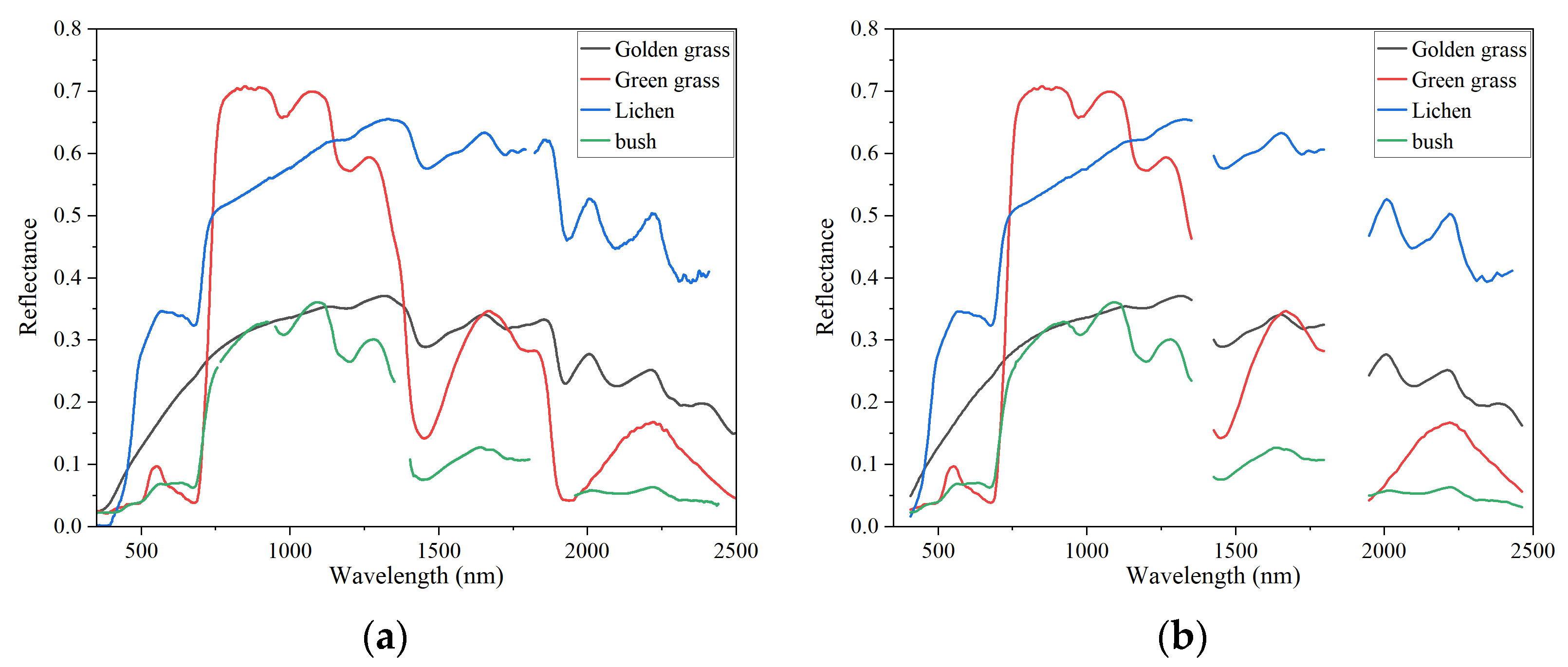
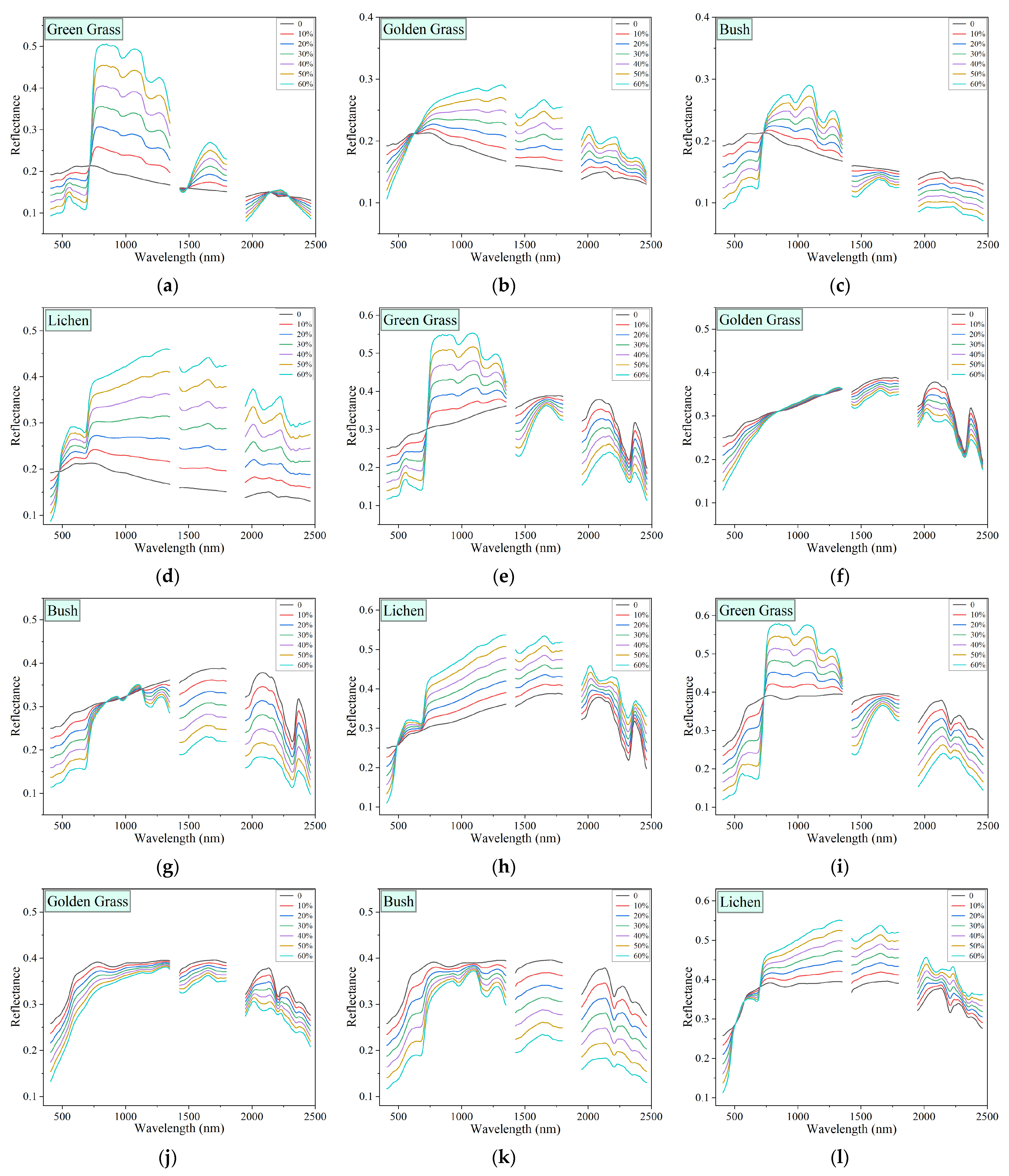
4.1. Rock Spectra, Vegetation Spectra, and Simulated Mixed Spectra
4.1.1. Rock Spectral Features
4.1.2. Vegetation Spectral Features
4.1.3. Simulated Mixed Spectral Features
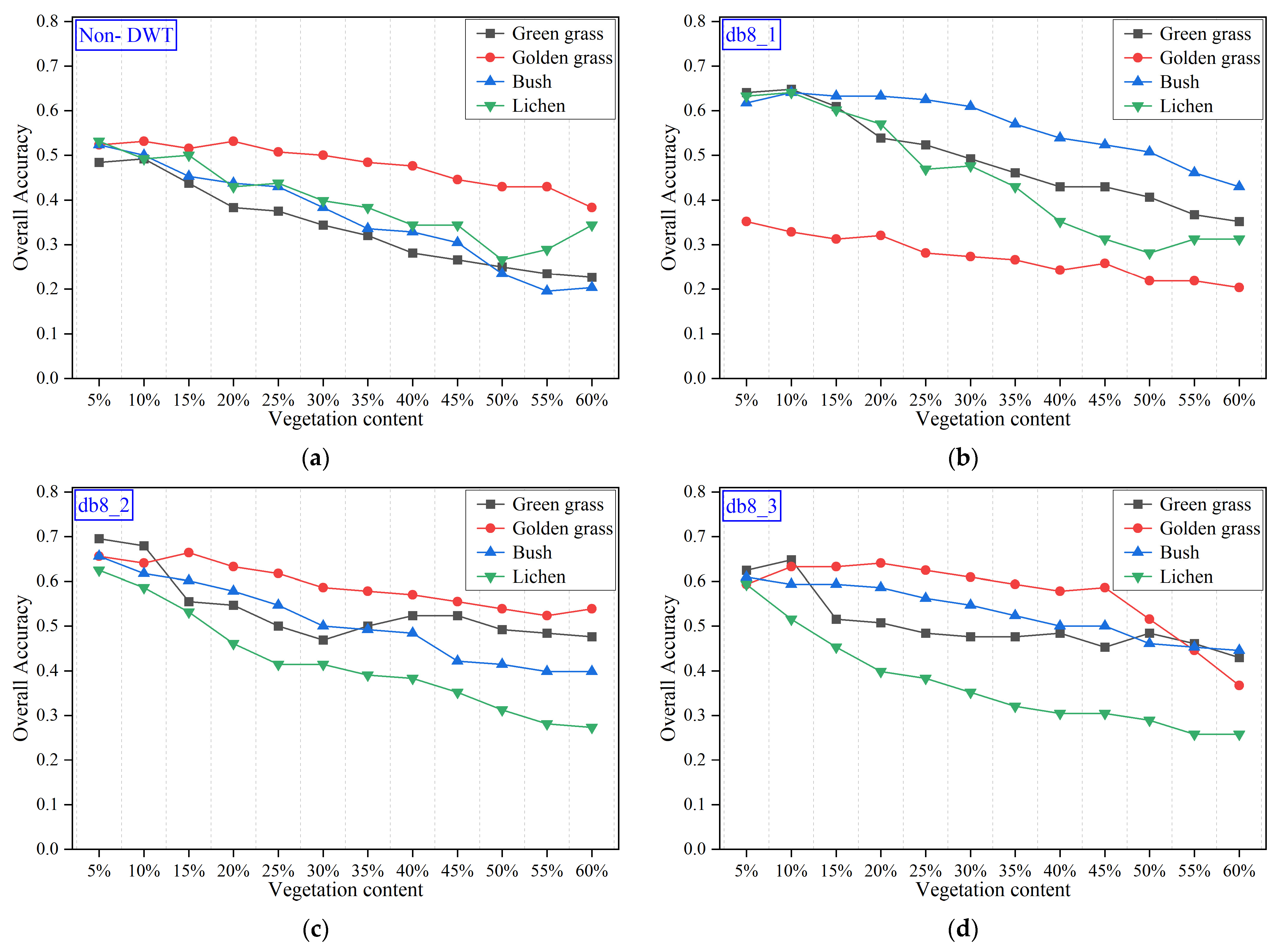
4.2. High-Frequency Feature Extraction Using DWT
4.2.1. High-Frequency Wavelet Features of Rocks
4.2.2. High-Frequency Wavelet Features of Simulated Mixed Spectra
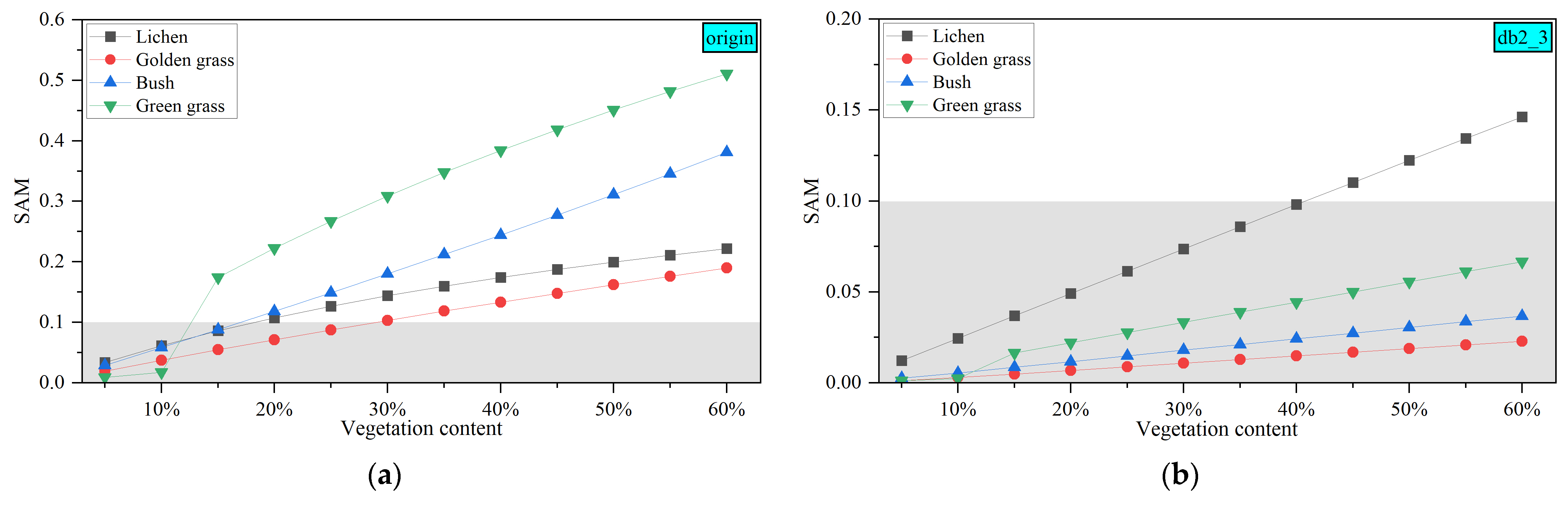
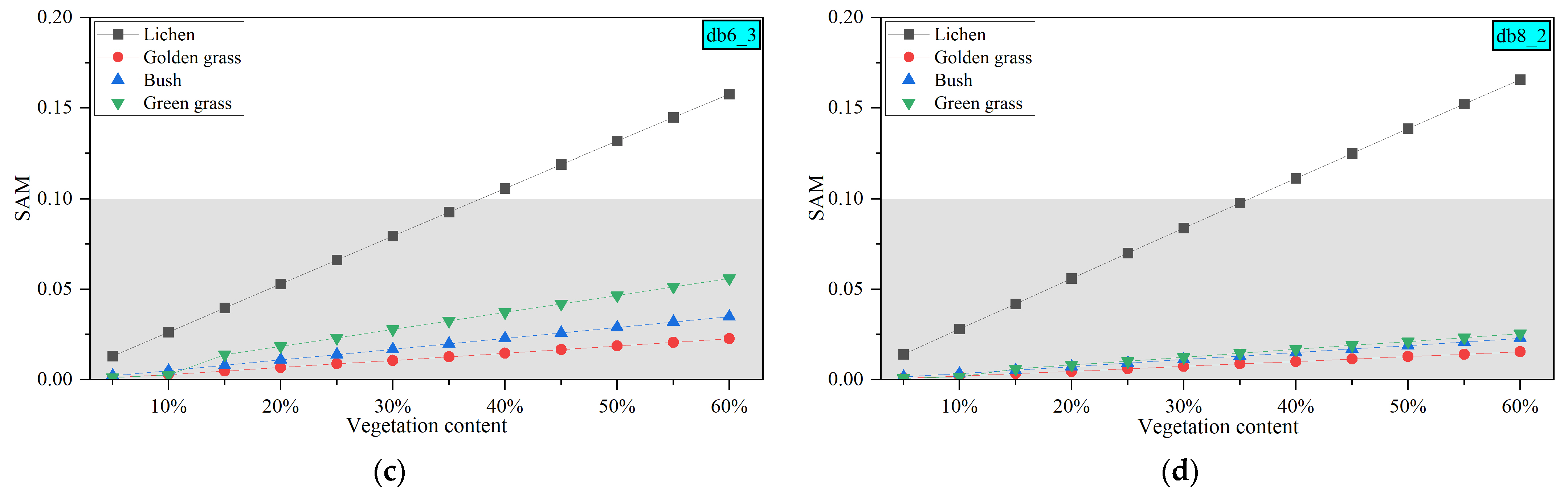
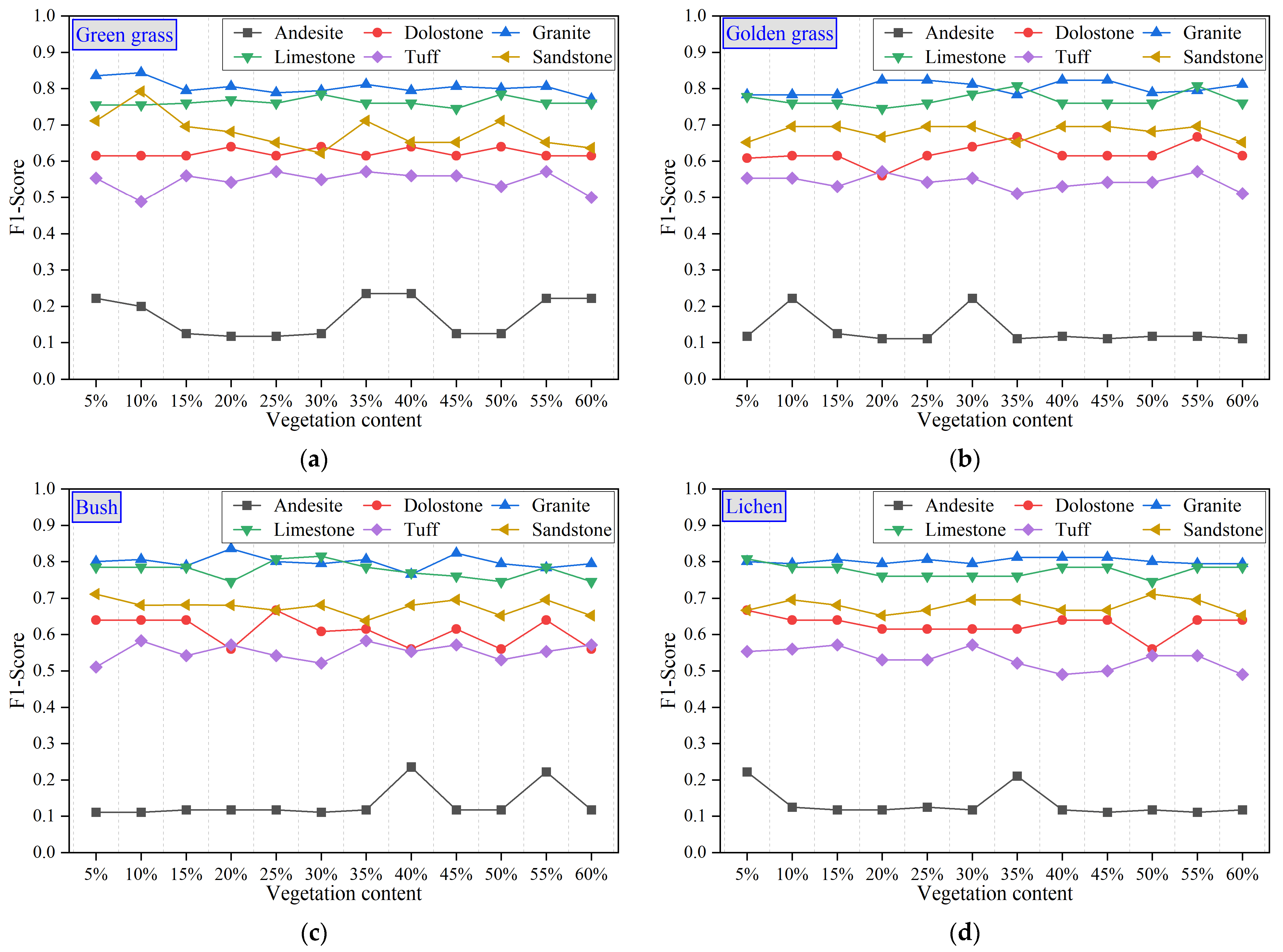
4.3. Impact of Vegetation on Rock Classification
4.4. Classification Accuracy Assessment of Simulated Mixed Spectra
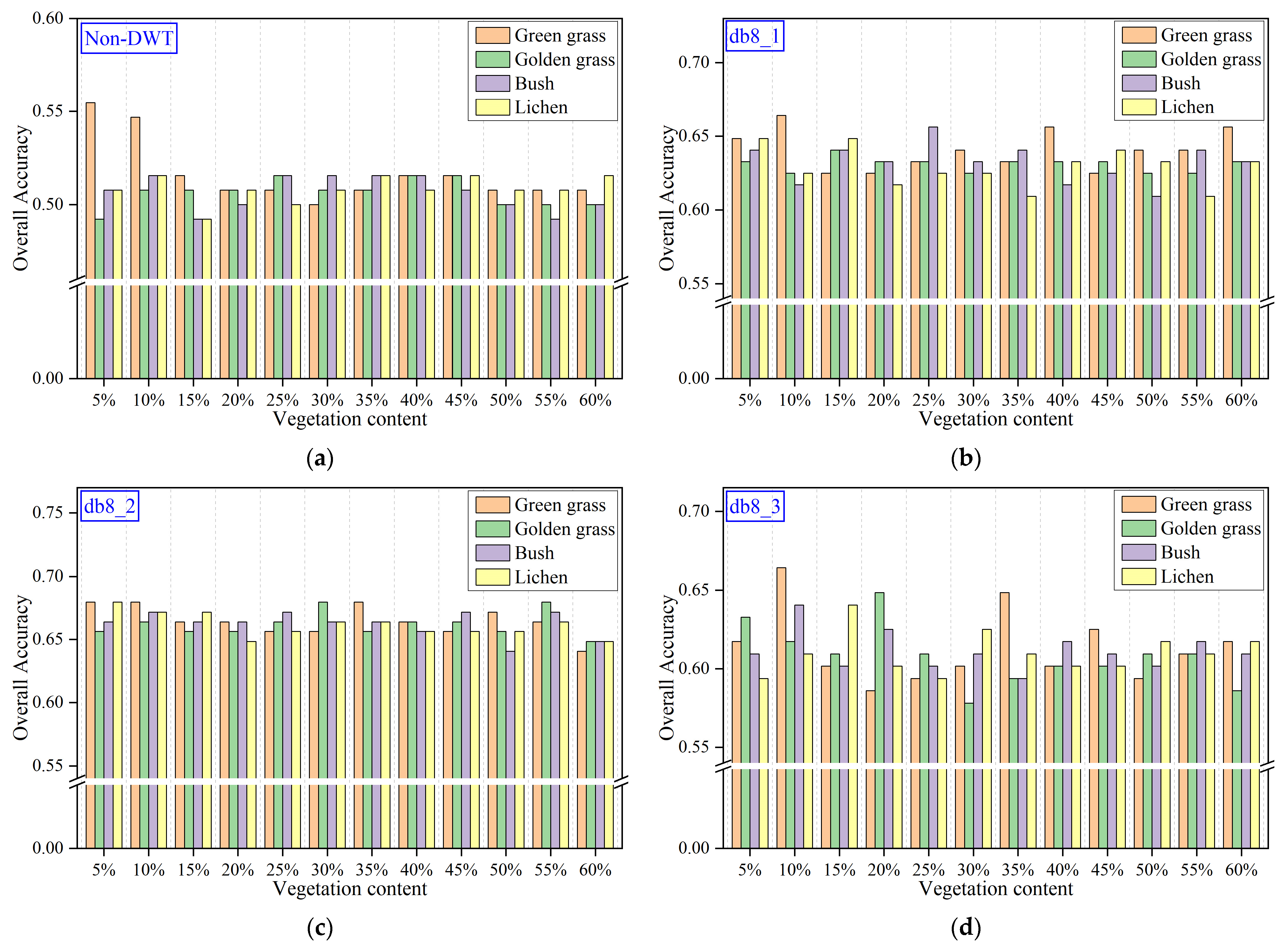
4.4.1. Using Simulated Mixed Spectra as Training Samples
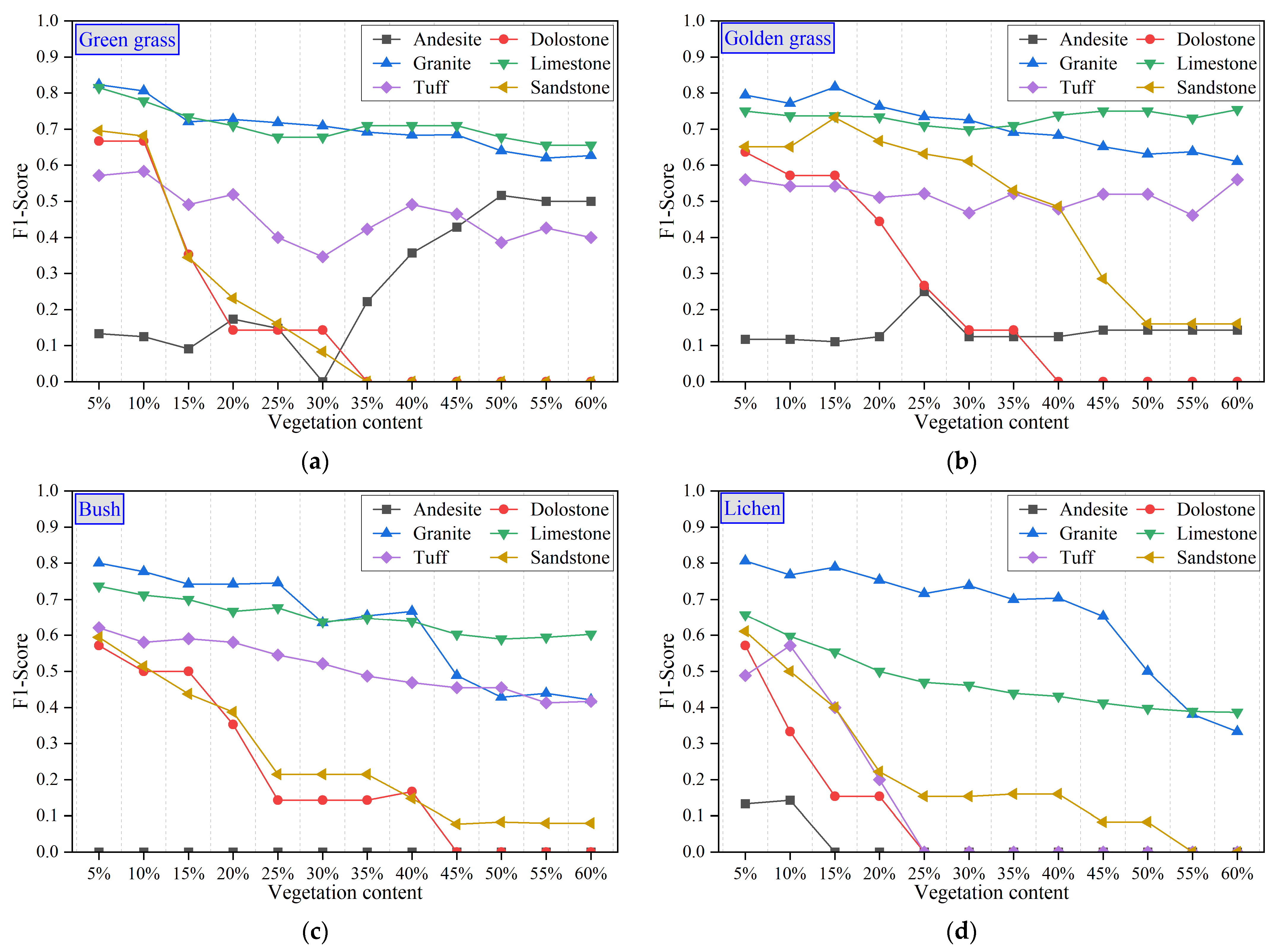
4.4.2. Using Original Rock Spectra as Training Samples
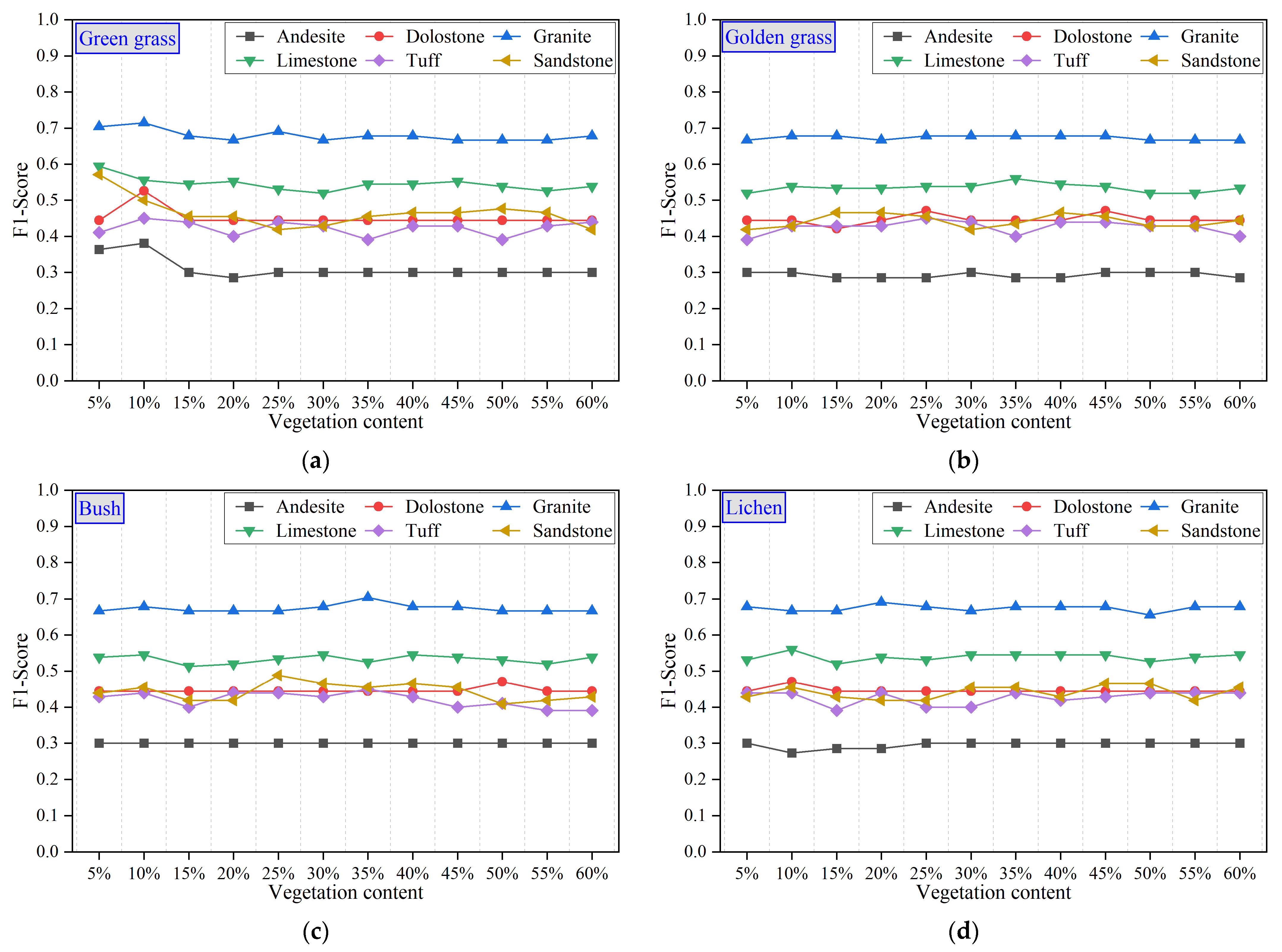
4.5. Evaluation of Classification Accuracy Using AHSI Image Spectra
4.5.1. Selection of Rock Samples
4.5.2. Classification Accuracy Assessment Using Image Spectra
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PRISMA | Prototype Research Instruments and Space Mission Technology Advancement |
| AHSI | Advanced Hyperspectral Imager |
| AVIRIS | Airborne Visible Infrared Imaging Spectrometer |
| VNIR | visible to near-infrared |
| SWIR | shortwave infrared |
| SAM | spectral angle mapper |
| RF | Random Forest |
| SVMs | Support Vector Machines |
| CNNs | Convolutional Neural Networks |
| GF-5 | Gaofen-5 |
| PCA | Principal Component Analysis |
| MNF | Minimum Noise Fraction |
| NDVI | Normalized Difference Vegetation Index |
| DEM | Digital Elevation Model |
| LiDAR | Light Detection and Ranging |
| ATM | Airborne Thematic Mapper |
| SAVI | Soil-Adjusted Vegetation Index |
| DWT | Discrete Wavelet Transform |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| GDEM | Global Digital Elevation Model |
| ASD | Analytical Spectral Devices |
| LMM | Linear Mixing Model |
| DN | Digital Number |
| db | Daubechies |
| IDWT | Inverse Discrete Wavelet Transform |
| EI | Expected Improvement |
| KAPPA | Kappa coefficient |
| OA | overall accuracy |
| FVC | Fractional Vegetation Cover |
| SNR | signal-to-noise ratio |
Appendix A
| Stratigraphic Age | Code | Geological Unit | Code | Geological Unit |
|---|---|---|---|---|
| Quaternary | Q | Sandy–silty clay and gravel layer | ||
| Cretaceous | k1y | Yixian formation: andesite, conglomerate, and tuff | ||
| Jurassic | J2tc | Tuchengzi formation: andesitic sandstone and tuffaceous sandstone | J2t | Tiaojishan formation: basalt, andesite, and tuffaceous sandstone |
| J1y | Yangcaogou formation: conglomerate and feldspathic sandstone | J1b | Beipiao formation: tuffaceous shale interbedded with coal seams | |
| J1x | Xinglonggou formation: basalt and andesite interbedded with volcanic breccia. | |||
| Triassic | T1h | Hongli formation: purple medium-coarse sandstone and tuffaceous sandstone | ||
| Permian | P1–2s | Shanxi formation: feldspathic sandstone interbedded with bauxitic shale | ||
| Carboniferous | C2-P1t | Taiyuan formation: coarse-grained feldspathic sandstone and bauxitic shale | ||
| Ordovician | O2m | Majiagou formation: limestone and dolomitic limestone | O1γ | Yeli formation: dolomitic limestone and bamboo leaf-shaped limestone |
| Cambrian | Ꞓ3c | Chaomidian formation: oolitic limestone interbedded with bamboo leaf-shaped limestone | Ꞓ2z | Zhangxia formation: oolitic crystalline limestone interbedded with calcareous siltstone |
| Ꞓ1c | Changping formation: dolomitic limestone and brecciated limestone | |||
| Sinian | Qnj | Jingeryu formation: purple thin-bedded tabular limestone | Jxw | Wumishan formation: chert-banded dolomite |
| chd | Dahongyu formation: quartz sandstone and feldspathic quartz sandstone | chg | Gaoyuzhuang formation: chert-banded dolomite and fine sandstone | |
| Jurassic (intrusive rock) | Granodiorite | Black mica granite | ||
| Red granite | Fine-grained granite | |||
| Amphibolite | Granite porphyry | |||
| Diorite–porphyrite | ||||
| Archaean | ArSγ | Gneissic granite | ||
| Jurassic (subvolcanic rock) | Andesite | Andesite vein | ||
| Dacite | Rhyolite porphyry |
| Feature | Metrics | Lichen | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% | 55% | 60% | ||
| Non_ DWT | OA | 0.508 | 0.516 | 0.492 | 0.508 | 0.500 | 0.508 | 0.516 | 0.508 | 0.516 | 0.508 | 0.508 | 0.516 |
| KAPPA | 0.386 | 0.397 | 0.367 | 0.387 | 0.376 | 0.386 | 0.396 | 0.386 | 0.396 | 0.386 | 0.386 | 0.396 | |
| haar_1 | OA | 0.648 | 0.625 | 0.648 | 0.648 | 0.617 | 0.609 | 0.641 | 0.648 | 0.617 | 0.625 | 0.633 | 0.641 |
| KAPPA | 0.566 | 0.536 | 0.566 | 0.565 | 0.526 | 0.517 | 0.554 | 0.565 | 0.526 | 0.535 | 0.545 | 0.556 | |
| haar_2 | OA | 0.648 | 0.625 | 0.656 | 0.648 | 0.625 | 0.633 | 0.641 | 0.633 | 0.641 | 0.617 | 0.617 | 0.617 |
| KAPPA | 0.563 | 0.535 | 0.572 | 0.563 | 0.536 | 0.545 | 0.554 | 0.544 | 0.553 | 0.526 | 0.526 | 0.525 | |
| haar_3 | OA | 0.656 | 0.633 | 0.641 | 0.641 | 0.633 | 0.641 | 0.641 | 0.641 | 0.641 | 0.656 | 0.648 | 0.625 |
| KAPPA | 0.573 | 0.545 | 0.555 | 0.555 | 0.545 | 0.554 | 0.555 | 0.554 | 0.553 | 0.573 | 0.564 | 0.536 | |
| db2_1 | OA | 0.641 | 0.625 | 0.633 | 0.641 | 0.633 | 0.633 | 0.656 | 0.633 | 0.617 | 0.633 | 0.641 | 0.641 |
| KAPPA | 0.555 | 0.535 | 0.545 | 0.555 | 0.545 | 0.545 | 0.572 | 0.545 | 0.526 | 0.545 | 0.554 | 0.555 | |
| db2_2 | OA | 0.641 | 0.633 | 0.633 | 0.641 | 0.625 | 0.633 | 0.617 | 0.641 | 0.633 | 0.625 | 0.633 | 0.625 |
| KAPPA | 0.556 | 0.544 | 0.545 | 0.555 | 0.536 | 0.545 | 0.525 | 0.555 | 0.545 | 0.535 | 0.545 | 0.535 | |
| db2_3 | OA | 0.641 | 0.648 | 0.648 | 0.656 | 0.656 | 0.633 | 0.641 | 0.641 | 0.656 | 0.648 | 0.656 | 0.656 |
| KAPPA | 0.554 | 0.564 | 0.564 | 0.572 | 0.573 | 0.544 | 0.553 | 0.554 | 0.573 | 0.563 | 0.572 | 0.574 | |
| db4_1 | OA | 0.625 | 0.609 | 0.594 | 0.602 | 0.602 | 0.602 | 0.609 | 0.602 | 0.625 | 0.617 | 0.602 | 0.625 |
| KAPPA | 0.531 | 0.512 | 0.494 | 0.503 | 0.504 | 0.504 | 0.514 | 0.503 | 0.534 | 0.523 | 0.504 | 0.533 | |
| db4_2 | OA | 0.633 | 0.633 | 0.664 | 0.625 | 0.633 | 0.633 | 0.617 | 0.625 | 0.641 | 0.656 | 0.648 | 0.633 |
| KAPPA | 0.545 | 0.544 | 0.585 | 0.535 | 0.544 | 0.546 | 0.525 | 0.536 | 0.555 | 0.574 | 0.566 | 0.545 | |
| db4_3 | OA | 0.617 | 0.641 | 0.664 | 0.641 | 0.625 | 0.641 | 0.633 | 0.648 | 0.641 | 0.625 | 0.617 | 0.641 |
| KAPPA | 0.528 | 0.556 | 0.583 | 0.555 | 0.536 | 0.556 | 0.546 | 0.564 | 0.556 | 0.536 | 0.527 | 0.556 | |
| db6_1 | OA | 0.648 | 0.648 | 0.648 | 0.641 | 0.633 | 0.648 | 0.633 | 0.648 | 0.656 | 0.633 | 0.648 | 0.641 |
| KAPPA | 0.562 | 0.561 | 0.563 | 0.553 | 0.543 | 0.563 | 0.543 | 0.563 | 0.572 | 0.543 | 0.562 | 0.552 | |
| db6_2 | OA | 0.641 | 0.641 | 0.617 | 0.641 | 0.641 | 0.641 | 0.633 | 0.633 | 0.672 | 0.609 | 0.664 | 0.648 |
| KAPPA | 0.555 | 0.555 | 0.525 | 0.555 | 0.555 | 0.554 | 0.545 | 0.545 | 0.593 | 0.516 | 0.584 | 0.564 | |
| db6_3 | OA | 0.609 | 0.617 | 0.609 | 0.625 | 0.617 | 0.617 | 0.656 | 0.617 | 0.648 | 0.609 | 0.633 | 0.617 |
| KAPPA | 0.518 | 0.528 | 0.519 | 0.537 | 0.529 | 0.528 | 0.574 | 0.529 | 0.565 | 0.519 | 0.547 | 0.529 | |
| db8_1 | OA | 0.648 | 0.625 | 0.648 | 0.617 | 0.625 | 0.625 | 0.609 | 0.633 | 0.641 | 0.633 | 0.609 | 0.633 |
| KAPPA | 0.563 | 0.535 | 0.563 | 0.523 | 0.535 | 0.534 | 0.514 | 0.545 | 0.554 | 0.544 | 0.515 | 0.544 | |
| db8_2 | OA | 0.680 | 0.672 | 0.672 | 0.648 | 0.656 | 0.664 | 0.664 | 0.656 | 0.656 | 0.656 | 0.664 | 0.648 |
| KAPPA | 0.604 | 0.595 | 0.595 | 0.567 | 0.576 | 0.586 | 0.587 | 0.576 | 0.576 | 0.576 | 0.586 | 0.566 | |
| db8_3 | OA | 0.594 | 0.609 | 0.641 | 0.602 | 0.594 | 0.625 | 0.609 | 0.602 | 0.602 | 0.617 | 0.609 | 0.617 |
| KAPPA | 0.501 | 0.520 | 0.556 | 0.510 | 0.500 | 0.539 | 0.519 | 0.509 | 0.511 | 0.528 | 0.519 | 0.528 | |
| db10_1 | OA | 0.578 | 0.578 | 0.570 | 0.563 | 0.570 | 0.570 | 0.555 | 0.555 | 0.563 | 0.563 | 0.555 | 0.578 |
| KAPPA | 0.474 | 0.474 | 0.464 | 0.455 | 0.464 | 0.463 | 0.446 | 0.445 | 0.454 | 0.453 | 0.447 | 0.474 | |
| db10_2 | OA | 0.672 | 0.656 | 0.664 | 0.664 | 0.664 | 0.672 | 0.664 | 0.664 | 0.664 | 0.656 | 0.664 | 0.664 |
| KAPPA | 0.593 | 0.573 | 0.584 | 0.584 | 0.584 | 0.593 | 0.583 | 0.584 | 0.584 | 0.574 | 0.584 | 0.584 | |
| db10_3 | OA | 0.641 | 0.656 | 0.641 | 0.648 | 0.648 | 0.648 | 0.641 | 0.648 | 0.656 | 0.664 | 0.672 | 0.641 |
| KAPPA | 0.557 | 0.575 | 0.556 | 0.567 | 0.566 | 0.567 | 0.557 | 0.567 | 0.577 | 0.586 | 0.596 | 0.557 | |
| Feature | Metrics | Golden Grass | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% | 55% | 60% | ||
| Non_ DWT | OA | 0.492 | 0.508 | 0.508 | 0.508 | 0.516 | 0.508 | 0.508 | 0.516 | 0.516 | 0.500 | 0.500 | 0.500 |
| KAPPA | 0.367 | 0.386 | 0.388 | 0.387 | 0.396 | 0.386 | 0.388 | 0.397 | 0.395 | 0.376 | 0.376 | 0.378 | |
| haar_1 | OA | 0.672 | 0.664 | 0.625 | 0.641 | 0.625 | 0.625 | 0.641 | 0.641 | 0.625 | 0.641 | 0.617 | 0.656 |
| KAPPA | 0.594 | 0.584 | 0.535 | 0.556 | 0.535 | 0.536 | 0.554 | 0.556 | 0.536 | 0.555 | 0.526 | 0.574 | |
| haar_2 | OA | 0.641 | 0.633 | 0.625 | 0.648 | 0.633 | 0.633 | 0.633 | 0.625 | 0.625 | 0.625 | 0.648 | 0.625 |
| KAPPA | 0.553 | 0.545 | 0.535 | 0.563 | 0.544 | 0.543 | 0.545 | 0.535 | 0.535 | 0.535 | 0.563 | 0.534 | |
| haar_3 | OA | 0.633 | 0.617 | 0.656 | 0.625 | 0.633 | 0.633 | 0.641 | 0.641 | 0.633 | 0.633 | 0.609 | 0.633 |
| KAPPA | 0.545 | 0.526 | 0.572 | 0.535 | 0.546 | 0.545 | 0.554 | 0.556 | 0.545 | 0.545 | 0.516 | 0.545 | |
| db2_1 | OA | 0.617 | 0.625 | 0.641 | 0.633 | 0.641 | 0.625 | 0.625 | 0.641 | 0.648 | 0.617 | 0.641 | 0.625 |
| KAPPA | 0.526 | 0.536 | 0.555 | 0.545 | 0.555 | 0.535 | 0.536 | 0.555 | 0.564 | 0.526 | 0.555 | 0.535 | |
| db2_2 | OA | 0.617 | 0.641 | 0.633 | 0.617 | 0.625 | 0.625 | 0.633 | 0.641 | 0.625 | 0.641 | 0.633 | 0.633 |
| KAPPA | 0.527 | 0.555 | 0.545 | 0.527 | 0.536 | 0.536 | 0.546 | 0.554 | 0.536 | 0.553 | 0.546 | 0.546 | |
| db2_3 | OA | 0.641 | 0.664 | 0.656 | 0.664 | 0.656 | 0.672 | 0.664 | 0.648 | 0.656 | 0.648 | 0.656 | 0.656 |
| KAPPA | 0.554 | 0.581 | 0.573 | 0.583 | 0.573 | 0.592 | 0.583 | 0.563 | 0.574 | 0.564 | 0.573 | 0.573 | |
| db4_1 | OA | 0.602 | 0.633 | 0.609 | 0.594 | 0.609 | 0.602 | 0.609 | 0.633 | 0.625 | 0.625 | 0.617 | 0.578 |
| KAPPA | 0.504 | 0.542 | 0.514 | 0.493 | 0.515 | 0.502 | 0.514 | 0.543 | 0.534 | 0.532 | 0.524 | 0.474 | |
| db4_2 | OA | 0.633 | 0.641 | 0.641 | 0.633 | 0.641 | 0.617 | 0.617 | 0.633 | 0.609 | 0.648 | 0.656 | 0.625 |
| KAPPA | 0.545 | 0.555 | 0.556 | 0.545 | 0.555 | 0.526 | 0.526 | 0.545 | 0.516 | 0.564 | 0.573 | 0.535 | |
| db4_3 | OA | 0.633 | 0.633 | 0.656 | 0.641 | 0.641 | 0.617 | 0.648 | 0.625 | 0.656 | 0.633 | 0.633 | 0.641 |
| KAPPA | 0.547 | 0.543 | 0.575 | 0.556 | 0.557 | 0.527 | 0.566 | 0.536 | 0.574 | 0.546 | 0.546 | 0.556 | |
| db6_1 | OA | 0.648 | 0.648 | 0.641 | 0.641 | 0.656 | 0.633 | 0.625 | 0.656 | 0.656 | 0.641 | 0.633 | 0.648 |
| KAPPA | 0.562 | 0.561 | 0.553 | 0.553 | 0.571 | 0.545 | 0.532 | 0.572 | 0.572 | 0.552 | 0.542 | 0.563 | |
| db6_2 | OA | 0.664 | 0.617 | 0.625 | 0.641 | 0.648 | 0.641 | 0.641 | 0.625 | 0.656 | 0.633 | 0.625 | 0.641 |
| KAPPA | 0.583 | 0.523 | 0.535 | 0.555 | 0.564 | 0.555 | 0.554 | 0.535 | 0.574 | 0.544 | 0.535 | 0.556 | |
| db6_3 | OA | 0.617 | 0.617 | 0.625 | 0.609 | 0.617 | 0.625 | 0.609 | 0.617 | 0.633 | 0.625 | 0.633 | 0.609 |
| KAPPA | 0.529 | 0.528 | 0.538 | 0.519 | 0.528 | 0.538 | 0.519 | 0.528 | 0.547 | 0.538 | 0.547 | 0.519 | |
| db8_1 | OA | 0.633 | 0.625 | 0.641 | 0.633 | 0.633 | 0.625 | 0.633 | 0.633 | 0.633 | 0.625 | 0.625 | 0.633 |
| KAPPA | 0.543 | 0.533 | 0.554 | 0.545 | 0.544 | 0.533 | 0.543 | 0.544 | 0.546 | 0.533 | 0.533 | 0.543 | |
| db8_2 | OA | 0.656 | 0.664 | 0.656 | 0.656 | 0.664 | 0.680 | 0.656 | 0.664 | 0.664 | 0.656 | 0.680 | 0.648 |
| KAPPA | 0.574 | 0.586 | 0.576 | 0.576 | 0.586 | 0.605 | 0.576 | 0.586 | 0.586 | 0.576 | 0.604 | 0.567 | |
| db8_3 | OA | 0.633 | 0.617 | 0.609 | 0.648 | 0.609 | 0.578 | 0.594 | 0.602 | 0.602 | 0.609 | 0.609 | 0.586 |
| KAPPA | 0.546 | 0.528 | 0.520 | 0.565 | 0.519 | 0.480 | 0.500 | 0.508 | 0.509 | 0.518 | 0.519 | 0.491 | |
| db10_1 | OA | 0.570 | 0.563 | 0.563 | 0.578 | 0.578 | 0.586 | 0.594 | 0.555 | 0.570 | 0.555 | 0.578 | 0.563 |
| KAPPA | 0.465 | 0.455 | 0.455 | 0.474 | 0.473 | 0.483 | 0.495 | 0.446 | 0.466 | 0.445 | 0.475 | 0.453 | |
| db10_2 | OA | 0.648 | 0.664 | 0.664 | 0.672 | 0.664 | 0.664 | 0.664 | 0.648 | 0.664 | 0.672 | 0.672 | 0.672 |
| KAPPA | 0.565 | 0.584 | 0.584 | 0.594 | 0.583 | 0.583 | 0.584 | 0.564 | 0.584 | 0.593 | 0.593 | 0.593 | |
| db10_3 | OA | 0.648 | 0.633 | 0.633 | 0.664 | 0.625 | 0.664 | 0.633 | 0.656 | 0.648 | 0.656 | 0.656 | 0.648 |
| KAPPA | 0.567 | 0.545 | 0.547 | 0.586 | 0.537 | 0.587 | 0.546 | 0.576 | 0.567 | 0.574 | 0.577 | 0.567 | |
| Feature | Metrics | Green Grass | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% | 55% | 60% | ||
| Non_ DWT | OA | 0.555 | 0.547 | 0.516 | 0.508 | 0.508 | 0.500 | 0.508 | 0.516 | 0.516 | 0.508 | 0.508 | 0.508 |
| KAPPA | 0.447 | 0.437 | 0.396 | 0.387 | 0.386 | 0.376 | 0.386 | 0.396 | 0.396 | 0.386 | 0.386 | 0.386 | |
| haar_1 | OA | 0.648 | 0.680 | 0.625 | 0.625 | 0.633 | 0.641 | 0.641 | 0.641 | 0.633 | 0.617 | 0.641 | 0.656 |
| KAPPA | 0.565 | 0.604 | 0.535 | 0.535 | 0.545 | 0.556 | 0.556 | 0.554 | 0.546 | 0.526 | 0.554 | 0.575 | |
| haar_2 | OA | 0.680 | 0.688 | 0.648 | 0.625 | 0.641 | 0.633 | 0.641 | 0.641 | 0.641 | 0.648 | 0.648 | 0.633 |
| KAPPA | 0.604 | 0.614 | 0.563 | 0.535 | 0.554 | 0.544 | 0.554 | 0.554 | 0.554 | 0.563 | 0.563 | 0.545 | |
| haar_3 | OA | 0.680 | 0.688 | 0.625 | 0.625 | 0.656 | 0.656 | 0.648 | 0.633 | 0.641 | 0.633 | 0.641 | 0.641 |
| KAPPA | 0.603 | 0.614 | 0.535 | 0.536 | 0.572 | 0.574 | 0.564 | 0.546 | 0.553 | 0.545 | 0.553 | 0.554 | |
| db2_1 | OA | 0.633 | 0.680 | 0.633 | 0.617 | 0.641 | 0.633 | 0.633 | 0.625 | 0.625 | 0.641 | 0.633 | 0.641 |
| KAPPA | 0.545 | 0.605 | 0.545 | 0.526 | 0.555 | 0.545 | 0.545 | 0.535 | 0.536 | 0.555 | 0.545 | 0.555 | |
| db2_2 | OA | 0.648 | 0.695 | 0.633 | 0.633 | 0.609 | 0.641 | 0.641 | 0.617 | 0.633 | 0.641 | 0.648 | 0.641 |
| KAPPA | 0.566 | 0.625 | 0.546 | 0.545 | 0.517 | 0.555 | 0.554 | 0.526 | 0.545 | 0.555 | 0.565 | 0.555 | |
| db2_3 | OA | 0.664 | 0.672 | 0.680 | 0.633 | 0.648 | 0.641 | 0.641 | 0.656 | 0.648 | 0.656 | 0.648 | 0.648 |
| KAPPA | 0.585 | 0.594 | 0.601 | 0.545 | 0.563 | 0.553 | 0.555 | 0.573 | 0.563 | 0.573 | 0.564 | 0.563 | |
| db4_1 | OA | 0.625 | 0.656 | 0.602 | 0.625 | 0.586 | 0.625 | 0.617 | 0.617 | 0.617 | 0.617 | 0.602 | 0.594 |
| KAPPA | 0.534 | 0.573 | 0.504 | 0.533 | 0.482 | 0.533 | 0.522 | 0.522 | 0.522 | 0.524 | 0.505 | 0.492 | |
| db4_2 | OA | 0.672 | 0.688 | 0.648 | 0.625 | 0.648 | 0.664 | 0.633 | 0.617 | 0.648 | 0.609 | 0.633 | 0.641 |
| KAPPA | 0.595 | 0.613 | 0.565 | 0.535 | 0.566 | 0.584 | 0.545 | 0.525 | 0.565 | 0.516 | 0.546 | 0.556 | |
| db4_3 | OA | 0.656 | 0.664 | 0.641 | 0.641 | 0.617 | 0.648 | 0.633 | 0.633 | 0.633 | 0.641 | 0.641 | 0.633 |
| KAPPA | 0.572 | 0.586 | 0.556 | 0.555 | 0.527 | 0.566 | 0.547 | 0.546 | 0.546 | 0.555 | 0.556 | 0.545 | |
| db6_1 | OA | 0.641 | 0.672 | 0.656 | 0.641 | 0.648 | 0.625 | 0.641 | 0.641 | 0.641 | 0.656 | 0.656 | 0.641 |
| KAPPA | 0.554 | 0.593 | 0.572 | 0.552 | 0.562 | 0.533 | 0.553 | 0.552 | 0.552 | 0.571 | 0.572 | 0.552 | |
| db6_2 | OA | 0.672 | 0.688 | 0.664 | 0.648 | 0.648 | 0.633 | 0.617 | 0.664 | 0.633 | 0.641 | 0.648 | 0.625 |
| KAPPA | 0.593 | 0.614 | 0.584 | 0.565 | 0.564 | 0.545 | 0.525 | 0.584 | 0.544 | 0.554 | 0.565 | 0.534 | |
| db6_3 | OA | 0.641 | 0.688 | 0.609 | 0.617 | 0.617 | 0.625 | 0.641 | 0.625 | 0.617 | 0.602 | 0.617 | 0.633 |
| KAPPA | 0.558 | 0.616 | 0.519 | 0.529 | 0.528 | 0.538 | 0.556 | 0.538 | 0.528 | 0.509 | 0.529 | 0.547 | |
| db8_1 | OA | 0.648 | 0.664 | 0.625 | 0.625 | 0.633 | 0.641 | 0.633 | 0.656 | 0.625 | 0.641 | 0.641 | 0.656 |
| KAPPA | 0.564 | 0.583 | 0.533 | 0.535 | 0.544 | 0.553 | 0.544 | 0.572 | 0.533 | 0.553 | 0.553 | 0.573 | |
| db8_2 | OA | 0.680 | 0.680 | 0.664 | 0.664 | 0.656 | 0.656 | 0.680 | 0.664 | 0.656 | 0.672 | 0.664 | 0.641 |
| KAPPA | 0.605 | 0.606 | 0.586 | 0.586 | 0.576 | 0.576 | 0.605 | 0.586 | 0.576 | 0.595 | 0.587 | 0.557 | |
| db8_3 | OA | 0.617 | 0.664 | 0.602 | 0.586 | 0.594 | 0.602 | 0.648 | 0.602 | 0.625 | 0.594 | 0.609 | 0.617 |
| KAPPA | 0.529 | 0.587 | 0.508 | 0.491 | 0.500 | 0.508 | 0.566 | 0.509 | 0.538 | 0.500 | 0.519 | 0.525 | |
| db10_1 | OA | 0.594 | 0.586 | 0.563 | 0.555 | 0.555 | 0.570 | 0.570 | 0.555 | 0.578 | 0.563 | 0.570 | 0.539 |
| KAPPA | 0.494 | 0.483 | 0.453 | 0.446 | 0.445 | 0.465 | 0.465 | 0.447 | 0.474 | 0.456 | 0.465 | 0.426 | |
| db10_2 | OA | 0.672 | 0.688 | 0.656 | 0.656 | 0.672 | 0.664 | 0.680 | 0.672 | 0.648 | 0.664 | 0.641 | 0.648 |
| KAPPA | 0.593 | 0.613 | 0.573 | 0.574 | 0.593 | 0.584 | 0.603 | 0.593 | 0.565 | 0.584 | 0.553 | 0.565 | |
| db10_3 | OA | 0.680 | 0.680 | 0.656 | 0.648 | 0.648 | 0.664 | 0.672 | 0.656 | 0.648 | 0.656 | 0.656 | 0.633 |
| KAPPA | 0.604 | 0.607 | 0.574 | 0.566 | 0.566 | 0.586 | 0.595 | 0.576 | 0.567 | 0.575 | 0.576 | 0.547 | |
| Feature | Metrics | Bush | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | 35% | 40% | 45% | 50% | 55% | 60% | ||
| Non_ DWT | OA | 0.508 | 0.516 | 0.492 | 0.500 | 0.516 | 0.516 | 0.516 | 0.516 | 0.508 | 0.500 | 0.492 | 0.500 |
| KAPPA | 0.386 | 0.396 | 0.366 | 0.376 | 0.397 | 0.396 | 0.396 | 0.396 | 0.386 | 0.375 | 0.367 | 0.376 | |
| haar_1 | OA | 0.633 | 0.625 | 0.625 | 0.672 | 0.625 | 0.617 | 0.641 | 0.633 | 0.625 | 0.633 | 0.633 | 0.656 |
| KAPPA | 0.547 | 0.535 | 0.535 | 0.594 | 0.535 | 0.526 | 0.555 | 0.544 | 0.536 | 0.544 | 0.544 | 0.574 | |
| haar_2 | OA | 0.633 | 0.625 | 0.625 | 0.625 | 0.625 | 0.617 | 0.617 | 0.641 | 0.633 | 0.641 | 0.633 | 0.617 |
| KAPPA | 0.545 | 0.533 | 0.534 | 0.535 | 0.535 | 0.526 | 0.525 | 0.554 | 0.543 | 0.554 | 0.544 | 0.526 | |
| haar_3 | OA | 0.633 | 0.633 | 0.641 | 0.648 | 0.633 | 0.633 | 0.641 | 0.625 | 0.625 | 0.664 | 0.625 | 0.633 |
| KAPPA | 0.546 | 0.545 | 0.555 | 0.564 | 0.545 | 0.545 | 0.555 | 0.536 | 0.535 | 0.583 | 0.536 | 0.546 | |
| db2_1 | OA | 0.625 | 0.625 | 0.641 | 0.641 | 0.609 | 0.633 | 0.625 | 0.625 | 0.633 | 0.633 | 0.648 | 0.633 |
| KAPPA | 0.536 | 0.535 | 0.554 | 0.555 | 0.516 | 0.545 | 0.536 | 0.535 | 0.545 | 0.545 | 0.563 | 0.545 | |
| db2_2 | OA | 0.602 | 0.617 | 0.633 | 0.633 | 0.641 | 0.625 | 0.633 | 0.633 | 0.648 | 0.633 | 0.625 | 0.633 |
| KAPPA | 0.507 | 0.525 | 0.546 | 0.546 | 0.556 | 0.536 | 0.545 | 0.545 | 0.564 | 0.545 | 0.535 | 0.545 | |
| db2_3 | OA | 0.648 | 0.680 | 0.633 | 0.648 | 0.664 | 0.641 | 0.664 | 0.656 | 0.641 | 0.641 | 0.648 | 0.633 |
| KAPPA | 0.564 | 0.601 | 0.546 | 0.564 | 0.582 | 0.554 | 0.581 | 0.574 | 0.554 | 0.554 | 0.563 | 0.544 | |
| db4_1 | OA | 0.625 | 0.586 | 0.594 | 0.586 | 0.594 | 0.625 | 0.594 | 0.602 | 0.625 | 0.617 | 0.594 | 0.609 |
| KAPPA | 0.534 | 0.484 | 0.492 | 0.484 | 0.494 | 0.534 | 0.495 | 0.503 | 0.533 | 0.522 | 0.493 | 0.513 | |
| db4_2 | OA | 0.656 | 0.633 | 0.633 | 0.609 | 0.641 | 0.641 | 0.641 | 0.633 | 0.641 | 0.641 | 0.617 | 0.633 |
| KAPPA | 0.574 | 0.545 | 0.544 | 0.516 | 0.553 | 0.556 | 0.556 | 0.545 | 0.555 | 0.554 | 0.524 | 0.546 | |
| db4_3 | OA | 0.641 | 0.633 | 0.641 | 0.633 | 0.617 | 0.625 | 0.609 | 0.641 | 0.641 | 0.633 | 0.633 | 0.641 |
| KAPPA | 0.555 | 0.547 | 0.556 | 0.547 | 0.528 | 0.536 | 0.517 | 0.556 | 0.555 | 0.547 | 0.546 | 0.555 | |
| db6_1 | OA | 0.633 | 0.641 | 0.648 | 0.625 | 0.641 | 0.633 | 0.641 | 0.633 | 0.641 | 0.641 | 0.641 | 0.641 |
| KAPPA | 0.543 | 0.554 | 0.561 | 0.534 | 0.552 | 0.543 | 0.553 | 0.542 | 0.554 | 0.553 | 0.554 | 0.552 | |
| db6_2 | OA | 0.602 | 0.625 | 0.641 | 0.648 | 0.656 | 0.641 | 0.664 | 0.648 | 0.625 | 0.672 | 0.641 | 0.656 |
| KAPPA | 0.505 | 0.534 | 0.555 | 0.565 | 0.574 | 0.554 | 0.584 | 0.564 | 0.535 | 0.593 | 0.554 | 0.575 | |
| db6_3 | OA | 0.625 | 0.617 | 0.609 | 0.617 | 0.609 | 0.617 | 0.617 | 0.617 | 0.617 | 0.625 | 0.609 | 0.617 |
| KAPPA | 0.538 | 0.529 | 0.519 | 0.528 | 0.519 | 0.529 | 0.529 | 0.528 | 0.528 | 0.538 | 0.519 | 0.528 | |
| db8_1 | OA | 0.641 | 0.617 | 0.641 | 0.633 | 0.656 | 0.633 | 0.641 | 0.617 | 0.625 | 0.609 | 0.641 | 0.633 |
| KAPPA | 0.553 | 0.523 | 0.554 | 0.543 | 0.573 | 0.544 | 0.553 | 0.523 | 0.535 | 0.513 | 0.555 | 0.544 | |
| db8_2 | OA | 0.664 | 0.672 | 0.664 | 0.664 | 0.672 | 0.664 | 0.664 | 0.656 | 0.672 | 0.641 | 0.672 | 0.648 |
| KAPPA | 0.586 | 0.596 | 0.585 | 0.586 | 0.594 | 0.585 | 0.586 | 0.576 | 0.596 | 0.557 | 0.595 | 0.566 | |
| db8_3 | OA | 0.609 | 0.641 | 0.602 | 0.625 | 0.602 | 0.609 | 0.594 | 0.617 | 0.609 | 0.602 | 0.617 | 0.609 |
| KAPPA | 0.520 | 0.554 | 0.510 | 0.539 | 0.510 | 0.519 | 0.499 | 0.529 | 0.516 | 0.509 | 0.528 | 0.520 | |
| db10_1 | OA | 0.563 | 0.563 | 0.555 | 0.563 | 0.563 | 0.547 | 0.578 | 0.570 | 0.578 | 0.578 | 0.570 | 0.586 |
| KAPPA | 0.454 | 0.454 | 0.443 | 0.456 | 0.456 | 0.435 | 0.473 | 0.466 | 0.473 | 0.474 | 0.465 | 0.483 | |
| db10_2 | OA | 0.664 | 0.664 | 0.672 | 0.664 | 0.656 | 0.664 | 0.656 | 0.656 | 0.664 | 0.672 | 0.641 | 0.672 |
| KAPPA | 0.584 | 0.584 | 0.593 | 0.584 | 0.575 | 0.584 | 0.574 | 0.574 | 0.584 | 0.594 | 0.553 | 0.593 | |
| db10_3 | OA | 0.664 | 0.633 | 0.648 | 0.633 | 0.648 | 0.656 | 0.656 | 0.633 | 0.664 | 0.664 | 0.680 | 0.656 |
| KAPPA | 0.586 | 0.547 | 0.565 | 0.545 | 0.566 | 0.576 | 0.577 | 0.545 | 0.586 | 0.586 | 0.605 | 0.575 | |
| Round | Green Grass | Golden Grass | Bush | Lichen | ||||
|---|---|---|---|---|---|---|---|---|
| mtry | OA | mtry | OA | mtry | OA | mtry | OA | |
| 1 | 24 | 0.634 | 24 | 0.667 | 24 | 0.631 | 24 | 0.628 |
| 2 | 20 | 0.608 | 20 | 0.624 | 20 | 0.611 | 20 | 0.608 |
| 3 | 3 | 0.579 | 3 | 0.588 | 3 | 0.605 | 3 | 0.582 |
| 4 | 13 | 0.615 | 13 | 0.646 | 13 | 0.627 | 13 | 0.609 |
| 5 | 13 | 0.601 | 13 | 0.595 | 13 | 0.618 | 13 | 0.608 |
| 6 | 21 | 0.592 | 21 | 0.605 | 21 | 0.618 | 21 | 0.631 |
| 7 | 20 | 0.594 | 20 | 0.618 | 20 | 0.631 | 20 | 0.624 |
| 8 | 13 | 0.588 | 13 | 0.617 | 13 | 0.621 | 13 | 0.598 |
| 9 | 10 | 0.613 | 10 | 0.617 | 10 | 0.618 | 10 | 0.601 |
| 10 | 8 | 0.611 | 8 | 0.621 | 8 | 0.611 | 8 | 0.601 |
| 11 | 16 | 0.638 | 25 | 0.636 | 27 | 0.624 | 21 | 0.611 |
| 12 | 15 | 0.588 | 24 | 0.617 | 24 | 0.611 | 21 | 0.611 |
| 13 | 10 | 0.598 | 24 | 0.611 | 24 | 0.621 | 21 | 0.614 |
| 14 | 9 | 0.618 | 24 | 0.621 | 24 | 0.611 | 24 | 0.588 |
| 15 | 19 | 0.605 | 24 | 0.631 | 24 | 0.608 | 21 | 0.620 |
| 16 | 22 | 0.624 | 24 | 0.621 | 24 | 0.618 | 21 | 0.624 |
| 17 | 11 | 0.619 | 24 | 0.638 | 24 | 0.628 | 21 | 0.607 |
| 18 | 13 | 0.608 | 24 | 0.624 | 24 | 0.641 | 21 | 0.585 |
| 19 | 4 | 0.608 | 24 | 0.604 | 30 | 0.605 | 21 | 0.624 |
| 20 | 14 | 0.634 | 24 | 0.604 | 15 | 0.624 | 21 | 0.615 |
| 21 | 1 | 0.545 | 24 | 0.608 | 1 | 0.558 | 21 | 0.621 |
| 22 | 29 | 0.630 | 24 | 0.628 | 5 | 0.597 | 21 | 0.605 |
| 23 | 4 | 0.558 | 24 | 0.608 | 25 | 0.598 | 21 | 0.624 |
| 24 | 24 | 0.591 | 24 | 0.633 | 24 | 0.611 | 21 | 0.611 |
| 25 | 4 | 0.582 | 24 | 0.627 | 13 | 0.598 | 16 | 0.647 |
| 26 | 21 | 0.607 | 24 | 0.611 | 24 | 0.621 | 16 | 0.647 |
| 27 | 29 | 0.618 | 24 | 0.611 | 13 | 0.591 | 16 | 0.628 |
| 28 | 26 | 0.614 | 24 | 0.640 | 21 | 0.615 | 16 | 0.617 |
| 29 | 14 | 0.596 | 24 | 0.650 | 24 | 0.633 | 16 | 0.647 |
| 30 | 4 | 0.589 | 24 | 0.611 | 10 | 0.611 | 16 | 0.602 |
References
- Rowan, L.C.; Mars, J.C.; Simpson, C.J. Lithologic mapping of the Mordor, NT, Australia ultramafic complex by using the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). Remote Sens. Environ. 2005, 99, 105–126. [Google Scholar] [CrossRef]
- Hunt, G.R. Spectroscopic properties of rocks and minerals. In Handbook of Physical Properties of Rocks (1982); CRC Press: Boca Raton, FL, USA, 2017; pp. 295–386. [Google Scholar]
- Leverington, D.W. Discrimination of sedimentary lithologies using Hyperion and Landsat Thematic Mapper data: A case study at Melville Island, Canadian High Arctic. Int. J. Remote Sens. 2010, 31, 233–260. [Google Scholar] [CrossRef]
- Tripathi, P.; Garg, R.D. Potential of DESIS and PRISMA hyperspectral remote sensing data in rock classification and mineral identification: A case study for Banswara in Rajasthan, India. Environ. Monit. Assess. 2023, 195, 575. [Google Scholar] [CrossRef] [PubMed]
- Yokoya, N.; Chan, J.C.-W.; Segl, K. Potential of resolution-enhanced hyperspectral data for mineral mapping using simulated EnMAP and Sentinel-2 images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef]
- Cai, J.; Wang, L.; Huang, Y.; Chen, D.; Liu, H. Formation Lithology Identification Technology along Railway in Complex and Dangerous Mountainous Area Based on Hyperspectral. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Chennai, India, 16–17 September 2020; p. 042049. [Google Scholar]
- Ishidoshiro, N.; Yamaguchi, Y.; Noda, S.; Asano, Y.; Kondo, T.; Kawakami, Y.; Mitsuishi, M.; Nakamura, H. Geological mapping by combining spectral unmixing and cluster analysis for hyperspectral data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 431–435. [Google Scholar] [CrossRef]
- Chen, X.; Warner, T.; Campagna, D. Integrating visible, near-infrared and short wave infrared hyperspectral and multispectral thermal imagery for geologic mapping: Simulated data. Int. J. Remote Sens. 2007, 28, 2415–2430. [Google Scholar] [CrossRef]
- Hunt, G.R. Spectral signatures of particulate minerals in the visible and near infrared. Geophysics 1977, 42, 501–513. [Google Scholar] [CrossRef]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P. Lithological mapping from hyperspectral data by improved use of spectral angle mapper. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 95–109. [Google Scholar] [CrossRef]
- Shebl, A.; Abriha, D.; Fahil, A.S.; El-Dokouny, H.A.; Elrasheed, A.A.; Csámer, Á. PRISMA hyperspectral data for lithological mapping in the Egyptian Eastern Desert: Evaluating the support vector machine, random forest, and XG boost machine learning algorithms. Ore Geol. Rev. 2023, 161, 105652. [Google Scholar] [CrossRef]
- Guha, A.; Mondal, S.; Chatterjee, S.; Kumar, K.V. Airborne imaging spectroscopy of igneous layered complex and their mapping using different spectral enhancement conjugated support vector machine models. Geocarto Int. 2022, 37, 349–365. [Google Scholar] [CrossRef]
- Lin, N.; Fu, J.; Jiang, R.; Li, G.; Yang, Q. Lithological classification by hyperspectral images based on a two-layer XGBoost model, combined with a greedy algorithm. Remote Sens. 2023, 15, 3764. [Google Scholar] [CrossRef]
- Ye, B.; Tian, S.; Cheng, Q.; Ge, Y. Application of lithological mapping based on advanced hyperspectral imager (AHSI) imagery onboard Gaofen-5 (GF-5) satellite. Remote Sens. 2020, 12, 3990. [Google Scholar] [CrossRef]
- Shetty, A.; AV, N. Performance evaluation of dimensionality reduction techniques on hyperspectral data for mineral exploration. Earth Sci. Inform. 2023, 16, 25–36. [Google Scholar]
- Grebby, S.; Cunningham, D.; Tansey, K.; Naden, J. The Impact of Vegetation on Lithological Mapping Using Airborne Multispectral Data: A Case Study for the North Troodos Region, Cyprus. Remote Sens. 2014, 6, 10860–10887. [Google Scholar] [CrossRef]
- van der Werff, H.; Ettema, J.; Sampatirao, A.; Hewson, R. How weather affects over time the repeatability of spectral indices used for geological remote sensing. Remote Sens. 2022, 14, 6303. [Google Scholar] [CrossRef]
- Bayat, B.; Van der Tol, C.; Verhoef, W. Remote sensing of grass response to drought stress using spectroscopic techniques and canopy reflectance model inversion. Remote Sens. 2016, 8, 557. [Google Scholar] [CrossRef]
- Singh, C.; Prabakaran, C. Reflectance spectra of high-altitude lichens based on in situ measurements. In Recent Advances in Lichenology: Modern Methods and Approaches in Biomonitoring and Bioprospection, Volume 1; Springer: Berlin/Heidelberg, Germany, 2015; pp. 181–188. [Google Scholar]
- Yu, L.; Porwal, A.; Holden, E.-J.; Dentith, M.C. Suppression of vegetation in multispectral remote sensing images. Int. J. Remote Sens. 2011, 32, 7343–7357. [Google Scholar] [CrossRef]
- Crippen, R.E.; Blom, R.G. Unveiling the lithology of vegetated terrains in remotely sensed imagery. Photogramm. Eng. Remote Sens. 2001, 67, 935–946. [Google Scholar]
- Pan, T.; Zuo, R.; Wang, Z. Geological mapping via convolutional neural network based on remote sensing and geochemical survey data in vegetation coverage areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3485–3494. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, Y.; Wang, Y.; Zhang, F.; Liu, G.; Sun, P. Machine learning algorithms for lithological mapping using Sentinel-2 and SRTM DEM in highly vegetated areas. Front. Ecol. Evol. 2023, 11, 1250971. [Google Scholar] [CrossRef]
- Grebby, S.; Naden, J.; Cunningham, D.; Tansey, K. Integrating airborne multispectral imagery and airborne LiDAR data for enhanced lithological mapping in vegetated terrain. Remote Sens. Environ. 2011, 115, 214–226. [Google Scholar] [CrossRef]
- Chen, S.-B.; Liu, Y.-L.; Yang, Q.; Zhou, C.; Zhao, L. Lithologic classification from Hyperspectral data in dense vegetation cover area. J. Jilin Univ. (Earth Sci. Ed.) 2012, 42, 1959–1965. [Google Scholar]
- Murphy, R.J.; Monteiro, S.T. Mapping the distribution of ferric iron minerals on a vertical mine face using derivative analysis of hyperspectral imagery (430–970 nm). ISPRS J. Photogramm. Remote Sens. 2013, 75, 29–39. [Google Scholar] [CrossRef]
- Heil, C.E.; Walnut, D.F. Continuous and discrete wavelet transforms. SIAM Rev. 1989, 31, 628–666. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, W.; Su, X.; Xu, Z. Optical remote sensing image denoising and super-resolution reconstructing using optimized generative network in wavelet transform domain. Remote Sens. 2021, 13, 1858. [Google Scholar] [CrossRef]
- Guo, S.; Jiang, Q. Improving rock classification with 1D discrete wavelet transform based on laboratory reflectance spectra and Gaofen-5 hyperspectral data. Remote Sens. 2023, 15, 5334. [Google Scholar] [CrossRef]
- Hu, P.; Liang, C.; Zheng, C.; Zhou, X.; Yang, Y.; Zhu, E. Tectonic transformation and metallogenesis of the Yanshan movement during the late jurassic period: Evidence from geochemistry and zircon U-Pb geochronology of the adamellites in Xingcheng, Western Liaoning, China. Minerals 2019, 9, 518. [Google Scholar] [CrossRef]
- National Cryosphere Desert Data Center. 1:1 Million Vegetation Data Set in China. 2021. Available online: https://www.ncdc.ac.cn/portal/metadata/20d2728d-8845-4a8b-a546-5f4f50fb036d (accessed on 1 December 2024).
- Shouzhang, P. 1-km monthly precipitation dataset for China (1901–2023); National Tibetan Plateau Data Center: Beijing, China, 2024. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; He, C.; Wu, X.; Kong, Z.; Li, X. Spatial database of 1:200,000 digital geologic map of the country (public version). Geosci. Data Discov. 2017, 46, 1–10. [Google Scholar]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.; Lowers, H.A.; Driscoll, R.L. USGS Spectral Library Version 7; US Geological Survey: Menlo Park, CA, USA, 2017.
- Kokaly, R.F.; Rockwell, B.W.; Haire, S.L.; King, T.V. Characterization of post-fire surface cover, soils, and burn severity at the Cerro Grande Fire, New Mexico, using hyperspectral and multispectral remote sensing. Remote Sens. Environ. 2007, 106, 305–325. [Google Scholar] [CrossRef]
- Swayze, G.A.; Kokaly, R.F.; Higgins, C.T.; Clinkenbeard, J.P.; Clark, R.N.; Lowers, H.A.; Sutley, S.J. Mapping potentially asbestos-bearing rocks using imaging spectroscopy. Geology 2009, 37, 763–766. [Google Scholar] [CrossRef]
- China Centre for Resources Satellite Data and Application. Available online: https://data.cresda.cn/#/2dMap (accessed on 15 December 2024).
- Kudela, R.M.; Hooker, S.B.; Guild, L.S.; Houskeeper, H.F.; Taylor, N. Expanded Signal to Noise Ratio Estimates for Validating Next-Generation Satellite Sensors in Oceanic, Coastal, and Inland Waters. Remote Sens. 2024, 16, 1238. [Google Scholar] [CrossRef]
- ASD. FieldSpec® 3 User Manual; Malvern Panalytical: Westborough, MA, USA, 2005. [Google Scholar]
- PIE-Hyp Hyperspectral Image Data Processing Software. Available online: https://engine.piesat.cn/appstore?todetail=EEEaxKPgCyPe6HjS6EEE (accessed on 10 December 2024).
- Yue, Y.M.; Wang, K.L.; Liu, B.; Li, R.; Zhang, B.; Chen, H.S.; Zhang, M.Y. Development of new remote sensing methods for mapping green vegetation and exposed bedrock fractions within heterogeneous landscapes. Int. J. Remote Sens. 2013, 34, 5136–5153. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R. Mapping chaparral in the Santa Monica Mountains using multiple endmember spectral mixture models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Liang, S.-Y.; Ho, Y.-L.; Lin, Y.-H.; Ma, H.-P. Discrete-wavelet-transform-based noise removal and feature extraction for ECG signals. Irbm 2014, 35, 351–361. [Google Scholar] [CrossRef]
- Mohideen, S.K.; Perumal, S.A.; Sathik, M.M. Image de-noising using discrete wavelet transform. Int. J. Comput. Sci. Netw. Secur. 2008, 8, 213–216. [Google Scholar]
- Hamill, J.; Caldwell, G.E.; Derrick, T.R. Reconstructing digital signals using Shannon’s sampling theorem. J. Appl. Biomech. 1997, 13, 226–238. [Google Scholar] [CrossRef]
- MATLAB. 9.14.0.2239454 (R2023a); The MathWorks Inc.: Apple Hill Drive Natick, MA, USA, 2023. [Google Scholar]
- Misiti, Y.; Misiti, M.; Oppenheim, G.; Poggi, J.-M. Micronde: A Matlab Wavelet Toolbox for Signals and Images. In Wavelets and Statistics; Antoniadis, A., Oppenheim, G., Eds.; Springer: New York, NY, USA, 1995; pp. 239–259. [Google Scholar]
- Fathoni, M.N.; Anintika, G.K.; Firda, D.; Kricella, P.; Widayani, P.; Arjakusuma, S.; Kamal, M. Identification of paddy fields based on temporal phase using Spectral Angle Mapper (SAM) on Landsat-8 OLI. In Proceedings of the Seventh Geoinformation Science Symposium 2021, Yogyakarta, Indonesia, 25–28 October 2021; pp. 91–101. [Google Scholar]
- Hecker, C.; Meijde, M.v.d.; Werff, H.v.d.; Meer, F.D. Assessing the Influence of Reference Spectra on Synthetic SAM Classification Results. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4162–4172. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Denize, J.; Hubert-Moy, L.; Betbeder, J.; Corgne, S.; Baudry, J.; Pottier, E. Evaluation of using sentinel-1 and-2 time-series to identify winter land use in agricultural landscapes. Remote Sens. 2018, 11, 37. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Yan, Y. rBayesianOptimization: Bayesian optimization of hyperparameters. CRAN: Contributed Packages. 2016. Available online: https://cran.r-project.org/web/packages/rBayesianOptimization/index.html (accessed on 2 January 2025).
- Kuhn, M. Building predictive models in R using the caret package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef]
- Wong, T.-T.; Yeh, P.-Y. Reliable accuracy estimates from k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1594. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Chang, Q. Combination of continuous wavelet transform and successive projection algorithm for the estimation of winter wheat plant nitrogen concentration. Remote Sens. 2023, 15, 997. [Google Scholar] [CrossRef]
- Ahmad, A.; Nair, A.M. Spectral mixture analysis of intimate mixtures for lithological mapping. ISPRS J. Photogramm. Remote Sens. 2024, 208, 210–232. [Google Scholar] [CrossRef]

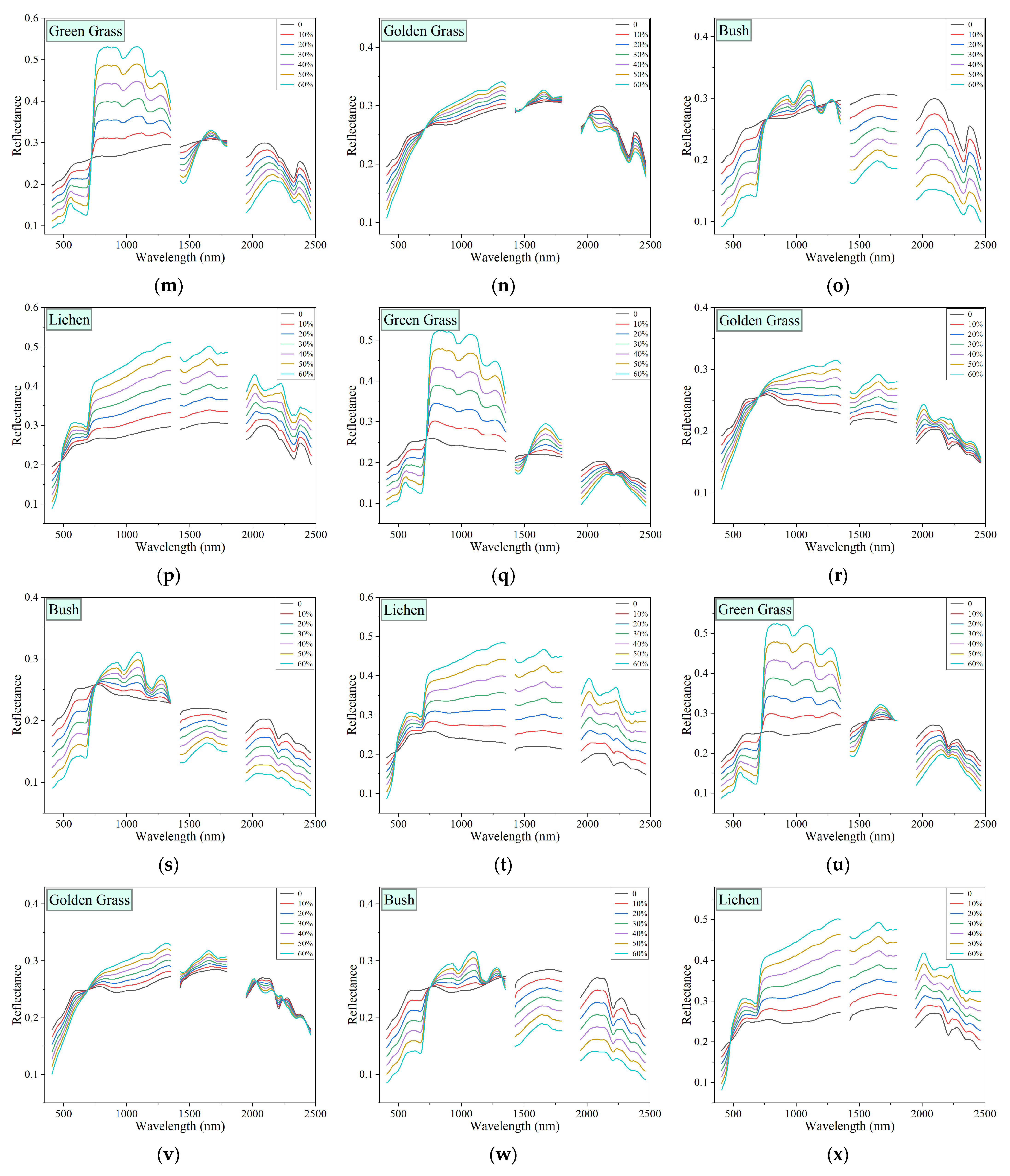

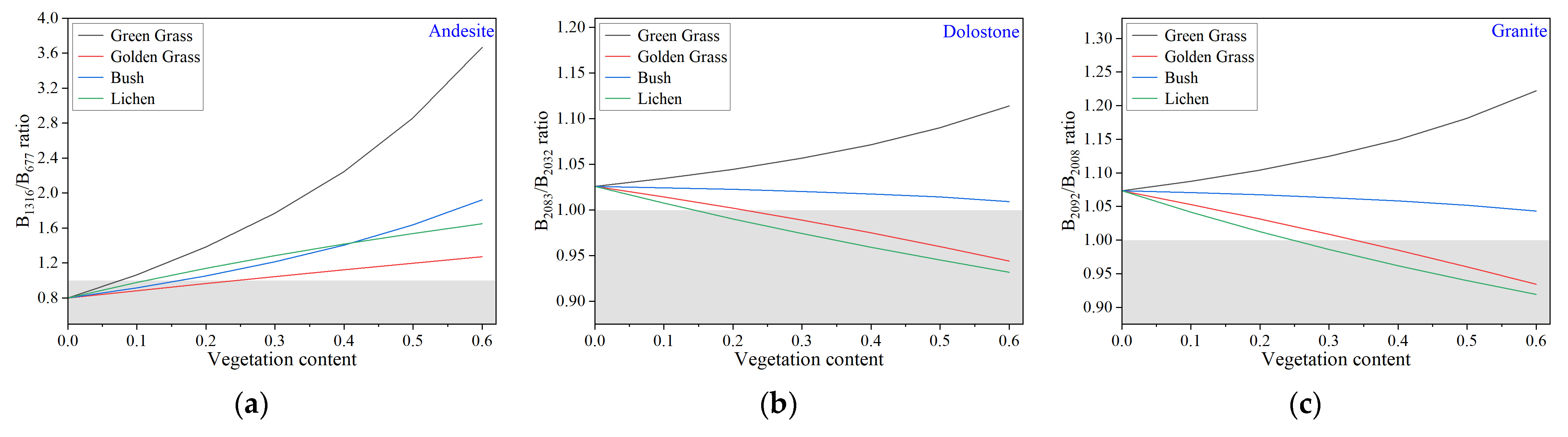



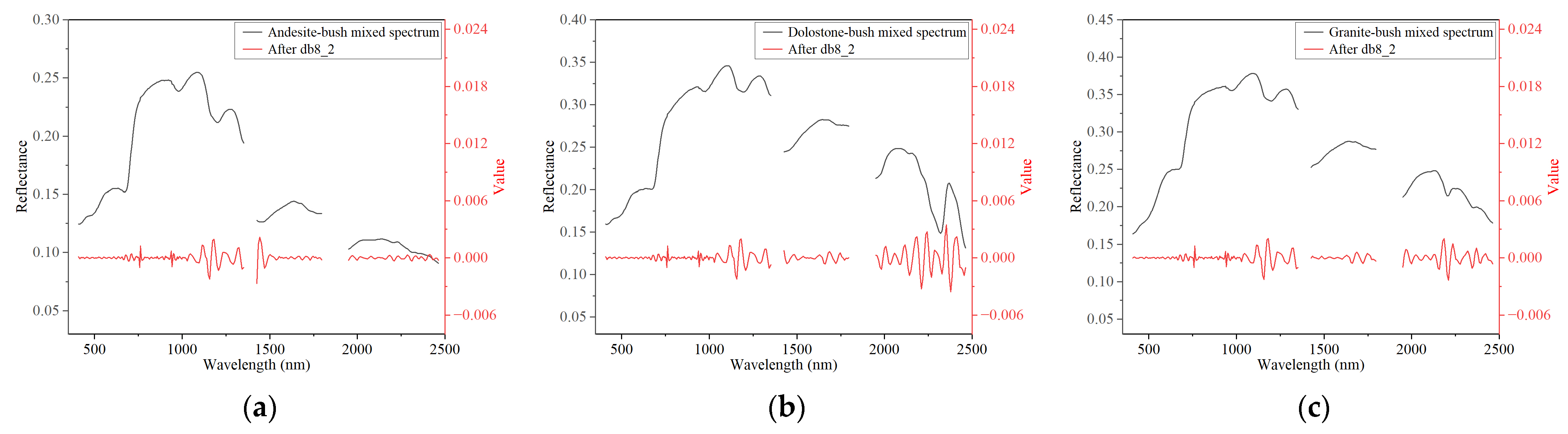
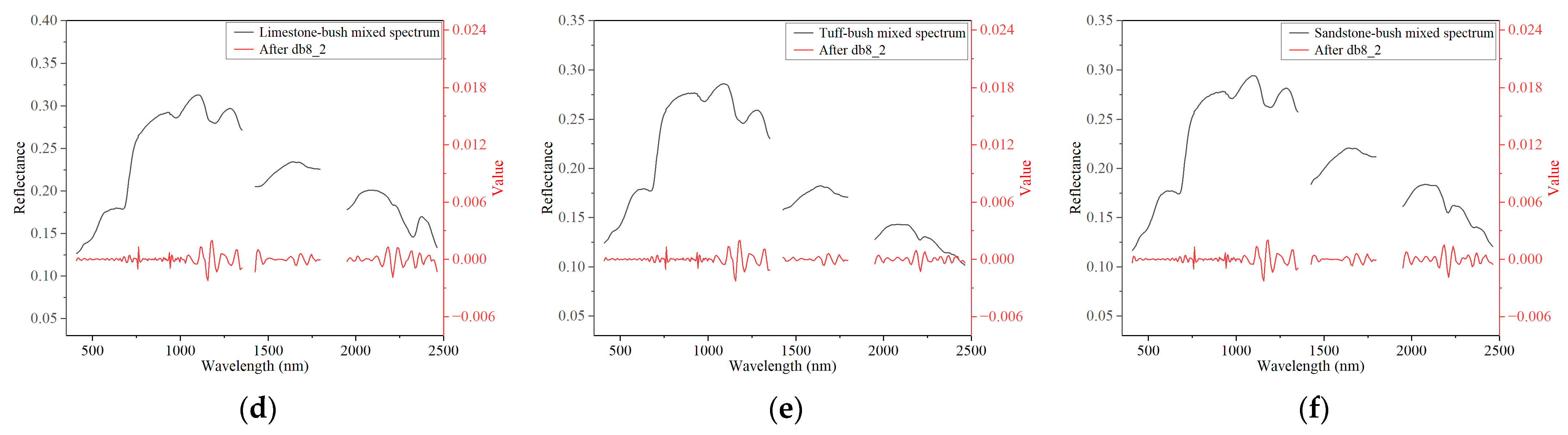


| Vegetation Species | Vegetation Description | Vegetation Type | Corresponding Vegetation Types in the USGS Spectral Library |
|---|---|---|---|
| Asteraceae herbaceous plants Poaceae herbaceous plants Leguminous herbaceous plants | Widely distributed around rocks, most not exceeding 0.5 m in height | Green grass | Lawn_Grass_GDS91_green |
| Golden grass | Grass_Golden_Dry_GDS480 | ||
| Thorn bush Sophora japonica young plant | Clustered around rocks, mostly between 0.5 and 3 m in height | Bush | Manzanita_CA01-ARVI-5_bush |
| Lichen | Attachment to rock surfaces | Lichen | Lichen_Acarospora-1 |
| Vegetation Type | Spectral Name | Reference |
|---|---|---|
| green grass | s07_ASD_Lawn_Grass_GDS91_green_BECKa_AREF | [35] |
| golden grass | s07_ASD_Grass_Golden_Dry_GDS480_ASDFRa_AREF | [36] |
| bush | splib07a_Manzanita_CA01-ARVI-5_bush_5_ASDFRa_AREF | [37] |
| lichen | splib07a_Lichen_Acarospora-1_ASDFRb_AREF | [35] |
| Parameter | GF5_AHSI_E120.37_N41.17_20190623 _005977_L10000048759 | GF5_AHSI_E120.53_N40.68_20190623_005977_L10000048763 |
|---|---|---|
| Satellite Azimuth Angle | 159.520 | 159.727 |
| Satellite Zenith Angle | 0.0754 | 0.0747 |
| Solar Azimuth Angle | 216.884 | 217.940 |
| Production Time | 23 June 2019 | |
| Number of Spectral Bands | 330 | |
| Spatial Resolution | 30 | |
| VNIR Spectral Resolution | 5 nm | |
| SWIR Spectral Resolution | 10 nm | |
| Rock Type | Precision | Recall | F1-Score |
|---|---|---|---|
| Dolostone | 0.58 | 0.29 | 0.37 |
| Granite | 0.42 | 0.53 | 0.46 |
| Limestone | 0.37 | 0.41 | 0.38 |
| Tuff | 0.26 | 0.22 | 0.23 |
| Sandstone | 0.39 | 0.30 | 0.32 |
| OA | 0.37 | KAPPA | 0.18 |
| Rock Type | Precision | Recall | F1-Score |
|---|---|---|---|
| Dolostone | 0.57 | 0.22 | 0.31 |
| Granite | 0.51 | 0.65 | 0.57 |
| Limestone | 0.40 | 0.57 | 0.47 |
| Tuff | 0.91 | 0.59 | 0.71 |
| Sandstone | 0.51 | 0.41 | 0.45 |
| OA | 0.53 | KAPPA | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, S.; Jiang, Q. Improvement of Lithological Identification Under the Impact of Sparse Vegetation Cover with 1D Discrete Wavelet Transform for Gaofen-5 Hyperspectral Data. Remote Sens. 2025, 17, 1974. https://doi.org/10.3390/rs17121974
Guo S, Jiang Q. Improvement of Lithological Identification Under the Impact of Sparse Vegetation Cover with 1D Discrete Wavelet Transform for Gaofen-5 Hyperspectral Data. Remote Sensing. 2025; 17(12):1974. https://doi.org/10.3390/rs17121974
Chicago/Turabian StyleGuo, Senmiao, and Qigang Jiang. 2025. "Improvement of Lithological Identification Under the Impact of Sparse Vegetation Cover with 1D Discrete Wavelet Transform for Gaofen-5 Hyperspectral Data" Remote Sensing 17, no. 12: 1974. https://doi.org/10.3390/rs17121974
APA StyleGuo, S., & Jiang, Q. (2025). Improvement of Lithological Identification Under the Impact of Sparse Vegetation Cover with 1D Discrete Wavelet Transform for Gaofen-5 Hyperspectral Data. Remote Sensing, 17(12), 1974. https://doi.org/10.3390/rs17121974





