Cross-Level Adaptive Feature Aggregation Network for Arbitrary-Oriented SAR Ship Detection
Abstract
1. Introduction
- (1)
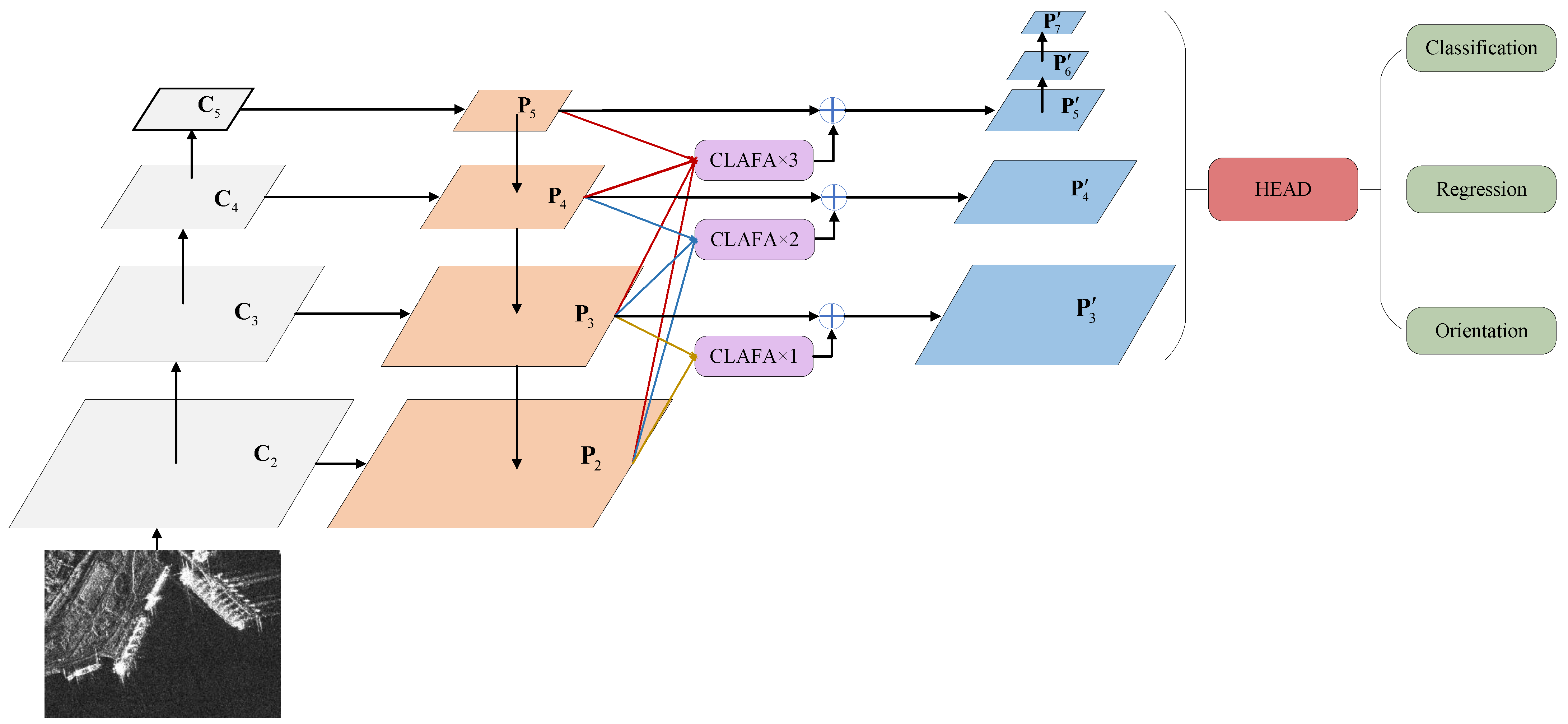
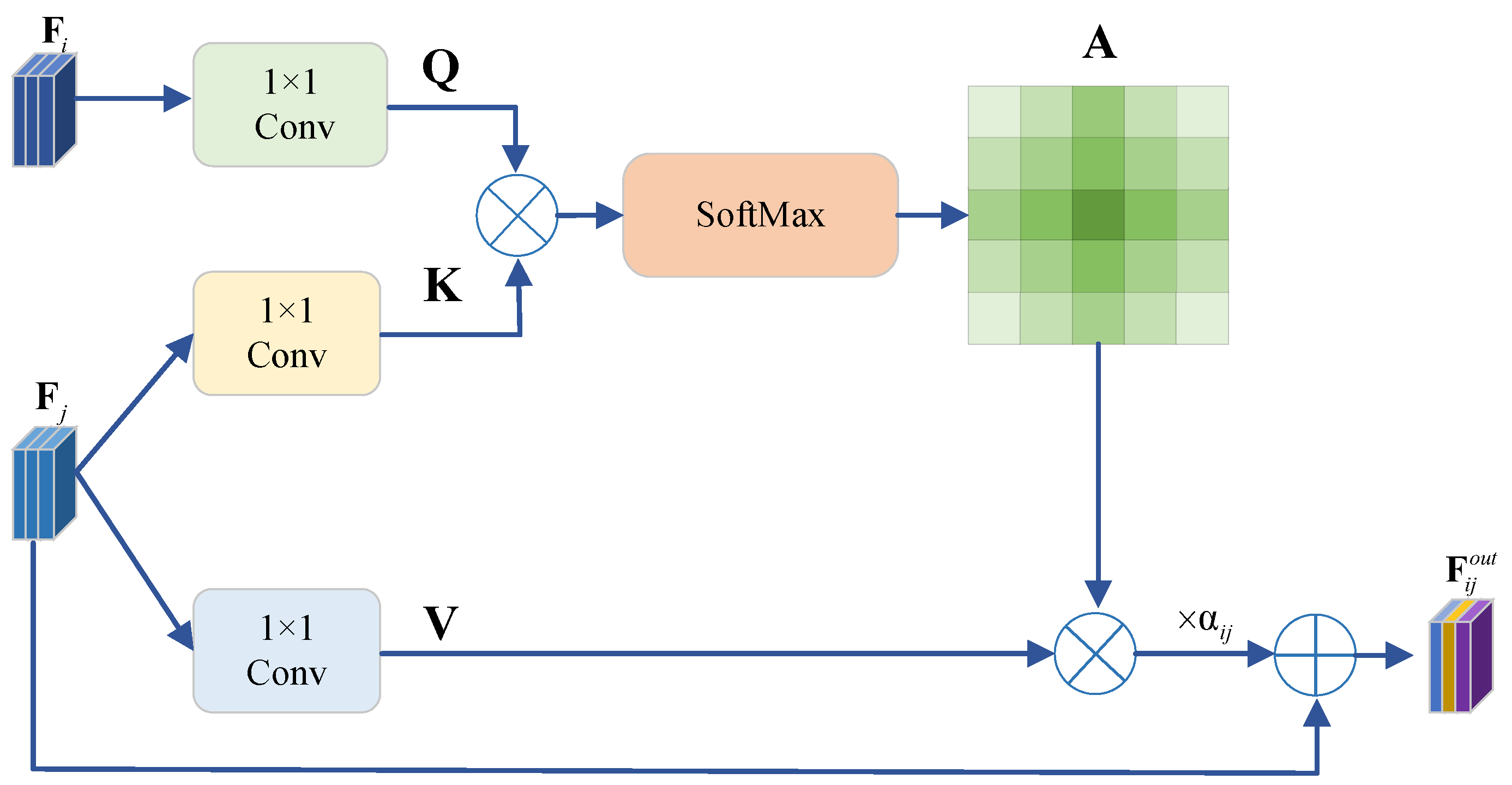
- In response to the semantic gap in the multi-level feature fusion stage, we propose a cross-level adaptive feature aggregation mechanism, which resorts to the cross-level feature similarity to achieve multi-scale adaptive feature fusion. The proposed module utilizes the self-attention-based similarity calculation mechanism but is equipped with a unique cross-level global acceptance field, which enables shallow features extracted from shallow layers of the backbone to capture similarities with deep features extracted from later deep layers. Briefly speaking, the proposed method is capable of assigning weights to shallow features based on similarity to ensure consistency between features at different levels, thereby solving the semantic gap problem inherent in feature pyramids.
- (2)
- To effectively address the angle period ambiguity problem of rotated bounding box detection, we propose a frequency-selective phase-shifting coder. By mapping angles to cosine functions, it achieves a continuous representation of angles. Moreover, considering the inherent differences in periodic ambiguity between rectangular and square shapes, the encoder uses frequency selection to map angles of different shapes, ensuring the correctness of shape-specific encoding.
- (3)
- To demonstrate the effectiveness of the proposed approach, extensive qualitative and quantitative experiments are carried out on two publicly accessible baseline datasets. A set of ablation tests and analytical experiments comprehensively demonstrate the reliability of the proposed method. Moreover, the experimental results of two types of comprehensive evaluation protocols and precision–recall (PR) curves on two public datasets illustrate that the proposed method is superior to state-of-the-art SAR ship detection methods.
2. Methodology
2.1. Overview
2.2. Cross-Level Feature Fusion
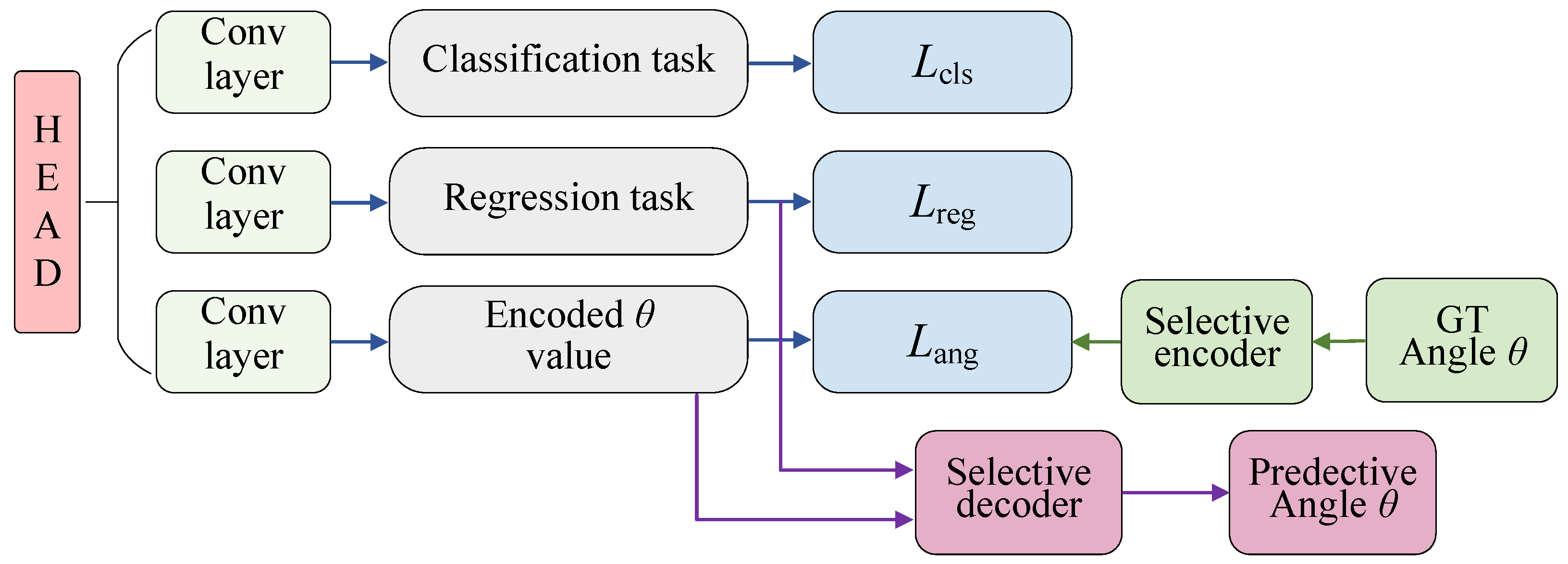
2.3. Multi-Task Detection Heads
2.3.1. Regression Task
2.3.2. Classification Task
2.3.3. Orientation Prediction Task
- : the orientation angle, which lies within the range of [/2, /2);
- : the first phase corresponding to the first frequency, lying within the range of [, );
- : the number of phase-shifting steps;
- : data encoded on the basis of the first phase, = { |n = 1,2,…, }.
- : the orientation angle, which lies within the range of [/4, /4);
- : the second phase corresponding to second frequency, which lies within the range of [,);
- : data encoded on the basis of the second phase, = { |n = 1,2, …,}.
2.4. Loss Function
3. Experimental Results
3.1. Dataset Description
3.2. Evaluation Metrics
3.3. Experimental Settings
3.4. Ablation Experiments
3.5. Contrastive Experiments
3.5.1. Comprehensive Assessment
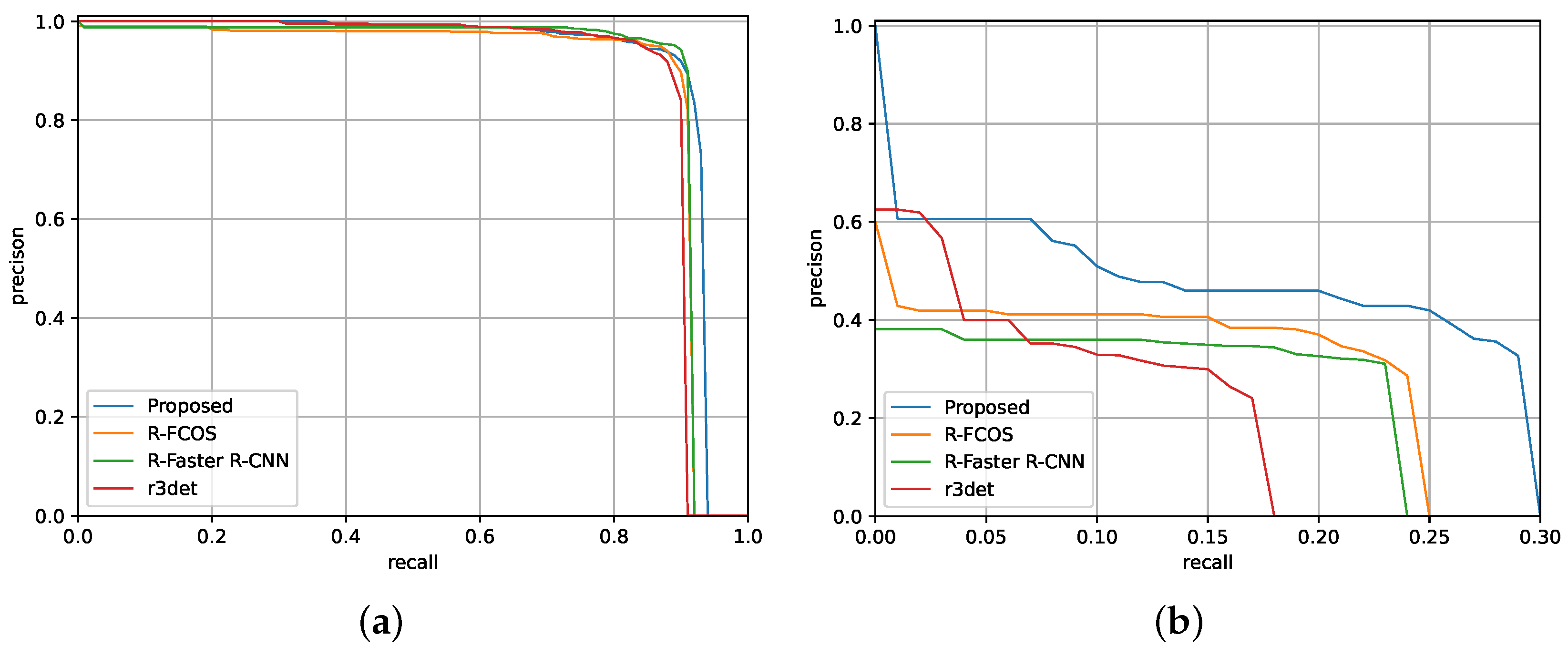
3.5.2. PRC Analysis
3.5.3. Visual Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- di Bisceglie, M.; Galdi, C. CFAR detection of extended objects in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 833–843. [Google Scholar] [CrossRef]
- Conte, E.; De Maio, A.; Ricci, G. Recursive estimation of the covariance matrix of a compound-Gaussian process and its application to adaptive CFAR detection. IEEE Trans. Signal Process. 2002, 50, 1908–1915. [Google Scholar] [CrossRef]
- An, W.; Xie, C.; Yuan, X. An improved iterative censoring scheme for CFAR ship detection with SAR imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4585–4595. [Google Scholar]
- Ai, J.; Mao, Y.; Luo, Q.; Xing, M.; Jiang, K.; Jia, L.; Yang, X. Robust CFAR ship detector based on bilateral-trimmed-statistics of complex ocean scenes in SAR imagery: A closed-form solution. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1872–1890. [Google Scholar] [CrossRef]
- Shi, H.; Fang, Z.; Wang, Y.; Chen, L. An adaptive sample assignment strategy based on feature enhancement for ship detection in SAR images. Remote Sens. 2022, 14, 2238. [Google Scholar] [CrossRef]
- Yao, C.; Xie, P.; Zhang, L.; Fang, Y. ATSD: Anchor-free two-stage ship detection based on feature enhancement in SAR images. Remote Sens. 2022, 14, 6058. [Google Scholar] [CrossRef]
- Wang, J.; Cui, Z.; Jiang, T.; Cao, C.; Cao, Z. Lightweight deep neural networks for ship target detection in SAR imagery. IEEE Trans. Image Process. 2022, 32, 565–579. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, R.; Ai, J.; Zou, H.; Li, J. Global and local context-aware ship detector for high-resolution SAR images. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4159–4167. [Google Scholar] [CrossRef]
- Tang, H.; Gao, S.; Li, S.; Wang, P.; Liu, J.; Wang, S.; Qian, J. A lightweight SAR image ship detection method based on improved convolution and YOLOv7. Remote Sens. 2024, 16, 486. [Google Scholar] [CrossRef]
- Yu, N.; Ren, H.; Deng, T.; Fan, X. A lightweight radar ship detection framework with hybrid attentions. Remote Sens. 2023, 15, 2743. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, S.; Sun, Z.; Liu, C.; Sun, Y.; Ji, K.; Kuang, G. Cross-sensor SAR image target detection based on dynamic feature discrimination and center-aware calibration. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–17. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, X.; Liu, N.; Cao, Z.; Yang, J. Ship detection in large-scale SAR images via spatial shuffle-group enhance attention. IEEE Trans. Geosci. Remote Sens. 2020, 59, 379–391. [Google Scholar] [CrossRef]
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. Centernet: Keypoint triplets for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 6569–6578. [Google Scholar]
- Fan, X.; Hu, Z.; Zhao, Y.; Chen, J.; Wei, T.; Huang, Z. A small ship object detection method for satellite remote sensing data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 11886–11898. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Fu, J.; Sun, X.; Wang, Z.; Fu, K. An anchor-free method based on feature balancing and refinement network for multiscale ship detection in SAR images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1331–1344. [Google Scholar] [CrossRef]
- Guo, H.; Yang, X.; Wang, N.; Gao, X. A CenterNet++ model for ship detection in SAR images. Pattern Recognit. 2021, 112, 107787. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Ren, H.; Hu, J.; Zou, L.; Wang, X. Multi-Level Feature-Refinement Anchor-Free Framework with Consistent Label-Assignment Mechanism for Ship Detection in SAR Imagery. Remote Sens. 2024, 16, 975. [Google Scholar] [CrossRef]
- Sun, Z.; Leng, X.; Zhang, X.; Zhou, Z.; Xiong, B.; Ji, K.; Kuang, G. Arbitrary-Direction SAR Ship Detection Method for Multiscale Imbalance. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–21. [Google Scholar] [CrossRef]
- Xie, X.; You, Z.H.; Chen, S.B.; Huang, L.L.; Tang, J.; Luo, B. Feature enhancement and alignment for oriented object detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 778–787. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Y.; Zhang, G.; Yuan, Y.; Cheng, G.; Wu, Y. Shape-Dependent Dynamic Label Assignment for Oriented Remote Sensing Object Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 132–146. [Google Scholar] [CrossRef]
- Fu, K.; Fu, J.; Wang, Z.; Sun, X. Scattering-keypoint-guided network for oriented ship detection in high-resolution and large-scale SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 11162–11178. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, X.; Wang, Z.; Fu, K. Oriented ship detection based on strong scattering points network in large-scale SAR images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Zhou, K.; Zhang, M.; Zhao, H.; Tang, R.; Lin, S.; Cheng, X.; Wang, H. Arbitrary-oriented ellipse detector for ship detection in remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 7151–7162. [Google Scholar] [CrossRef]
- Ju, M.; Niu, B.; Zhang, J. FPDDet: An Efficient Rotated SAR Ship Detector Based on Simple Polar Encoding and Decoding. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5218915. [Google Scholar] [CrossRef]
- Liu, S.; Chen, P.; Zhang, Y. A multi-scale feature pyramid SAR ship detection network with robust background interference. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9904–9915. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, L.; Li, C.; Kuang, G. Pyramid attention dilated network for aircraft detection in SAR images. IEEE Geosci. Remote Sens. Lett. 2020, 18, 662–666. [Google Scholar] [CrossRef]
- Wan, H.; Chen, J.; Huang, Z.; Xia, R.; Wu, B.; Sun, L.; Yao, B.; Liu, X.; Xing, M. AFSar: An anchor-free SAR target detection algorithm based on multiscale enhancement representation learning. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5219514. [Google Scholar] [CrossRef]
- Tang, L.; Tang, W.; Qu, X.; Han, Y.; Wang, W.; Zhao, B. A scale-aware pyramid network for multi-scale object detection in SAR images. Remote Sens. 2022, 14, 973. [Google Scholar] [CrossRef]
- Wan, H.; Chen, J.; Huang, Z.; Du, W.; Xu, F.; Wang, F.; Wu, B. Orientation Detector for Small Ship Targets in SAR Images Based on Semantic Flow Feature Alignment and Gaussian Label Matching. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5218616. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. FCOS: A Simple and Strong Anchor-Free Object Detector. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1922–1933. [Google Scholar] [CrossRef]
- Neubeck, A.; Van Gool, L. Efficient non-maximum suppression. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, 20–24 August 2006; Volume 3, pp. 850–855. [Google Scholar]
- Yu, J.; Jiang, Y.; Wang, Z.; Cao, Z.; Huang, T. Unitbox: An advanced object detection network. In Proceedings of the 24th ACM International Conference on Multimedia, Amsterdam, The Netherlands, 15–19 October 2016; pp. 516–520. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Li, J.; Qu, C.; Shao, J. Ship detection in SAR images based on an improved faster R-CNN. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 13–14 November 2017; pp. 1–6. [Google Scholar]
- Wei, S.; Zeng, X.; Qu, Q.; Wang, M.; Su, H.; Shi, J. HRSID: A high-resolution SAR images dataset for ship detection and instance segmentation. IEEE Access 2020, 8, 120234–120254. [Google Scholar] [CrossRef]
- Cui, Z.; Li, Q.; Cao, Z.; Liu, N. Dense attention pyramid networks for multi-scale ship detection in SAR images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8983–8997. [Google Scholar] [CrossRef]
- Hu, Q.; Hu, S.; Liu, S. BANet: A balance attention network for anchor-free ship detection in SAR images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5222212. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Yang, X.; Yan, J.; Feng, Z.; He, T. R3det: Refined single-stage detector with feature refinement for rotating object. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 35, pp. 3163–3171. [Google Scholar]
- Zhao, J.; Ding, Z.; Zhou, Y.; Zhu, H.; Du, W.L.; Yao, R.; El Saddik, A. OrientedFormer: An End-to-End Transformer-Based Oriented Object Detector in Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5640816. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, M.; Li, J.; Li, Y.; Yang, H.; Li, W. FPNFormer: Rethink the Method of Processing the Rotation-Invariance and Rotation-Equivariance on Arbitrary-Oriented Object Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5605610. [Google Scholar] [CrossRef]







| Method | CLAFA | FSPSC | Params(M) | FPS | P | R | F1 | mAP | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | ✗ | ✗ | 32.1 | 63.1 | 92.1 | 87.0 | 89.5 | 39.1 | 88.4 | 26.6 | 37.2 | 43.0 | 49.1 |
| Model 1 | ✗ | ✓ | 33.2 | 42.6 | 92.9 | 88.5 | 90.2 | 40.8 | 88.4 | 29.4 | 39.4 | 46.7 | 53.5 |
| Model 2 | ✓ | ✗ | 32.1 | 45.0 | 94.0 | 89.1 | 90.9 | 41.7 | 89.6 | 30.2 | 39.4 | 46.5 | 46.4 |
| Proposed | ✓ | ✓ | 33.2 | 36.7 | 93.1 | 90.3 | 91.1 | 42.3 | 91.3 | 31.4 | 39.5 | 48.7 | 56.6 |
| Method | CLAFA | FSPSC | Params(M) | FPS | P | R | F1 | mAP | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline | ✗ | ✗ | 32.1 | 34.9 | 85.7 | 74.0 | 79.4 | 43.2 | 80.6 | 44.8 | 41.0 | 54.2 | 14.1 |
| Model 1 | ✗ | ✓ | 33.2 | 25.2 | 87.4 | 77.3 | 81.8 | 46.0 | 81.9 | 49.1 | 42.0 | 55.5 | 22.2 |
| Model 2 | ✓ | ✗ | 32.1 | 20.4 | 86.7 | 78.4 | 81.4 | 45.0 | 81.0 | 47.7 | 43.2 | 53.1 | 16.5 |
| Proposed | ✓ | ✓ | 33.2 | 19.0 | 88.0 | 80.1 | 83.3 | 47.6 | 83.8 | 51.0 | 45.6 | 57.1 | 19.8 |
| Params(M) | FPS | P | R | F1 | mAP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R-FCOS [35] | 32.1 | 63.1 | 92.1 | 87.0 | 89.5 | 39.1 | 88.4 | 26.6 | 37.2 | 43.0 | 49.1 |
| R3Det [44] | 41.8 | 52.8 | 88.3 | 84.0 | 86.1 | 37.6 | 87.9 | 23.0 | 36.4 | 40.5 | 42.5 |
| R-Faster-R-CNN [43] | 41.4 | 14.0 | 92.2 | 89.0 | 90.6 | 40.6 | 91.3 | 23.5 | 38.9 | 44.7 | 44.5 |
| OrientedFormer [45] | 49.1 | 27.4 | 92.8 | 86.4 | 88.6 | 38.3 | 91.2 | 19.2 | 36.4 | 42.7 | 42.9 |
| FPNFormer [46] | - | - | - | - | - | - | - | - | 35.1 | - | 51.1 |
| CLAFANet | 33.2 | 36.7 | 93.1 | 90.3 | 91.1 | 42.3 | 91.3 | 31.4 | 39.5 | 48.7 | 56.6 |
| Params(M) | FPS | P | R | F1 | mAP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| R-FCOS [35] | 32.1 | 34.9 | 85.7 | 74.0 | 79.4 | 43.2 | 80.6 | 44.8 | 41.0 | 54.2 | 14.1 |
| R3Det [44] | 41.8 | 28.7 | 84.6 | 71.0 | 77.3 | 39.4 | 79.1 | 35.7 | 38.1 | 45.9 | 9.3 |
| R-Faster-R-CNN [43] | 41.4 | 11.4 | 86.3 | 76.0 | 80.8 | 42.5 | 80.9 | 40.8 | 41.4 | 49.3 | 8.5 |
| OrientedFormer [45] | 49.1 | 14.2 | 87.3 | 78.4 | 81.7 | 46.5 | 83.5 | 48.1 | 45.4 | 53.9 | 11.4 |
| CLAFANet | 33.2 | 19.0 | 88.0 | 80.1 | 83.3 | 47.6 | 83.8 | 51.0 | 45.6 | 57.1 | 19.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, L.; Hu, J.; Ren, H.; Lin, J.; Luo, X.; Zou, L.; Zhou, Y. Cross-Level Adaptive Feature Aggregation Network for Arbitrary-Oriented SAR Ship Detection. Remote Sens. 2025, 17, 1770. https://doi.org/10.3390/rs17101770
Qian L, Hu J, Ren H, Lin J, Luo X, Zou L, Zhou Y. Cross-Level Adaptive Feature Aggregation Network for Arbitrary-Oriented SAR Ship Detection. Remote Sensing. 2025; 17(10):1770. https://doi.org/10.3390/rs17101770
Chicago/Turabian StyleQian, Lu, Junyi Hu, Haohao Ren, Jie Lin, Xu Luo, Lin Zou, and Yun Zhou. 2025. "Cross-Level Adaptive Feature Aggregation Network for Arbitrary-Oriented SAR Ship Detection" Remote Sensing 17, no. 10: 1770. https://doi.org/10.3390/rs17101770
APA StyleQian, L., Hu, J., Ren, H., Lin, J., Luo, X., Zou, L., & Zhou, Y. (2025). Cross-Level Adaptive Feature Aggregation Network for Arbitrary-Oriented SAR Ship Detection. Remote Sensing, 17(10), 1770. https://doi.org/10.3390/rs17101770






